Селективное автоматическое дифференцирование пути: за пределами равномерного распределения при обратном распространении дропаута
Невероятная эффективность стохастического Gradient Descent (SGD), пожалуй, является самым большим открытием в области машинного обучения 2010-х годов. SGD лежит в основе почти всех недавних прорывов в машинном обучении. По сути, SGD удивительно прост: обрабатывайте ваш набор данных по одной точке за раз и для каждой точки корректируйте параметры модели в направлении, заданном этой точкой. В более технических терминах «направление» определяется как градиент, а «корректировка» включает небольшой коэффициент масштабирования, обычно именуемый скоростью обучения.
Хотя техника SGD зародилась в 1950-х годах, она оставалась малоизвестной и слабо используемой до тех пор, пока не получила широкое признание с появлением глубокого обучения. Причины, по которым эта техника работает, были неясны и, отчасти, остаются таковыми. Поскольку целью является минимизация ошибки модели на всем наборе данных, неясно, что выбор точек в полной изоляции должен приводить к чему-либо, кроме числового мусора.
Сегодня в основном понимают, что эффективность SGD — то есть, почему он работает — обусловлена двумя факторами. Во-первых, хотя градиент, получаемый методом SGD, очень шумный — каждый шаг учитывает лишь одну точку данных — его вычисление обходится очень дешево. Оказывается, что при заданном бюджете вычислительных ресурсов выполнение множества обновлений градиента низкого качества значительно превосходит выполнение одного обновления градиента высокого качества. Во-вторых, сами шумные обновления помогают модели выйти из огромных плато числовой безразличности, которые существуют в высоких размерностях. На самом деле, в высоких размерностях суть оптимизации заключается не, как считалось долгое время, в уходе из локальных минимумов, а в уходе из локальных плато — областей, где функция потерь изменяется очень слабо.

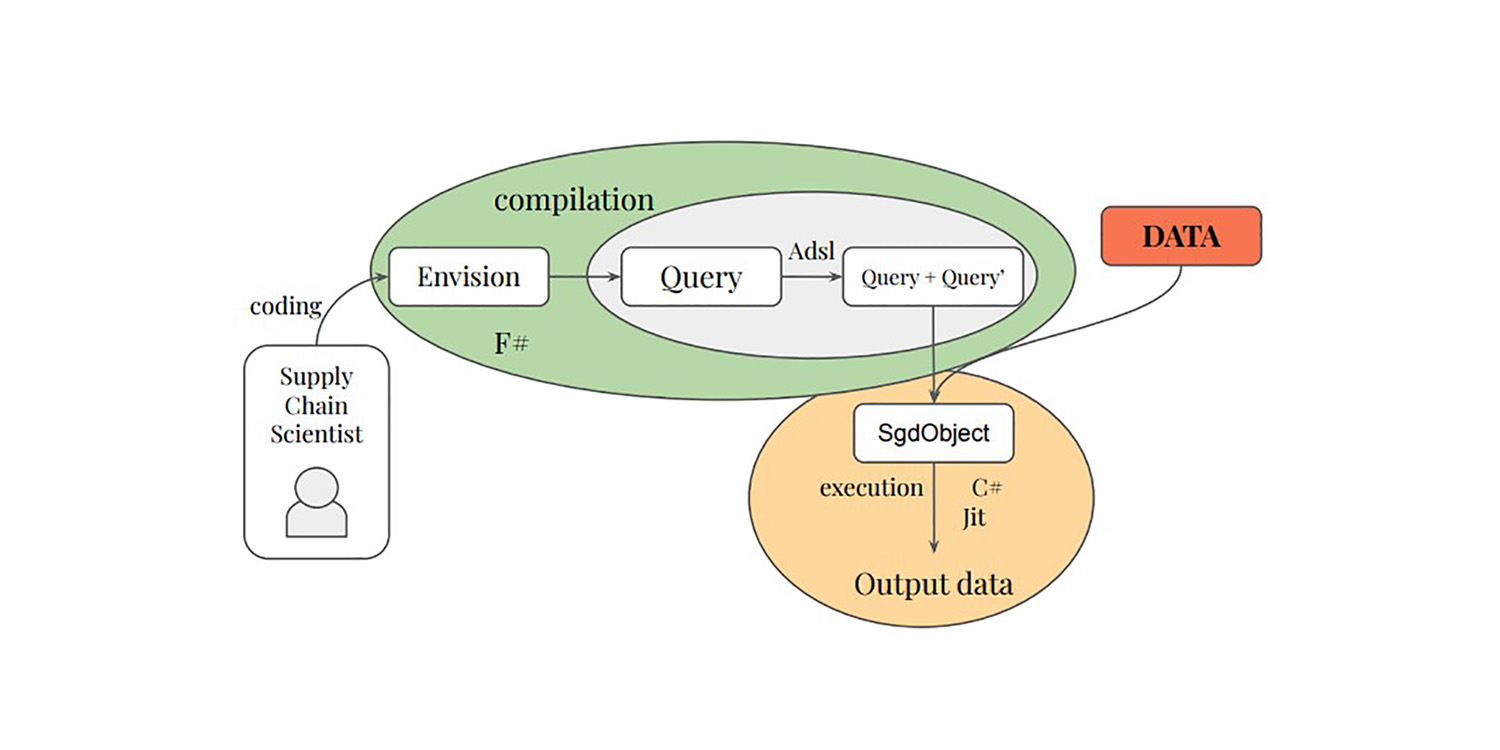
Некоторые из нас, в том числе Пол Пезё и Виктор Николле, решили развить эти идеи дальше. Если SGD работает за счёт обмена качества градиента на вычислительную эффективность, то как насчёт расширения этого принципа ещё дальше? Как насчёт подточечного градиента, который будет ещё дешевле в вычислении, хотя и более шумным? Именно это реализовано в подходе Селективного автоматического дифференцирования пути (SPAD). SPAD переосмысливает один из краеугольных камней современной парадигмы машинного обучения с изюминкой: точка данных может быть «разделена» по градиенту посредством своих оценочных путей.
Ниже представлена статья с вкладом от Пола Пезё (Lokad), Виктора Николле (Lokad), Максима Берара (Litis) и Тьерри Паке (Litis).
Заголовок: Селективное автоматическое дифференцирование пути: за пределами равномерного распределения при обратном распространении дропаута
Авторы: Пол Пезё, Максим Берар, Тьерри Паке, Виктор Николле
Аннотация: В данной статье представлен метод Селективного автоматического дифференцирования пути (SPAD), новый подход к снижению потребления памяти и смягчению переобучения в градиентных моделях для встраиваемого искусственного интеллекта. SPAD расширяет существующее рандомизированное автоматическое дифференцирование, предложенное Октэем и соавторами, которое использует случайные пути через граф обратного распространения с матричным внедрением, за счёт введения альтернативных распределений вероятностей в графе обратного распространения, тем самым улучшая эффективность обучения и управление памятью. В одной конкретной итерации SPAD оценивает и ранжирует несколько путей в графе обратного распространения. В последующих итерациях он преимущественно следует путям с более высоким рейтингом. Эта работа также представляет технику на основе компиляции, позволяющую получить модельно-независимый доступ к случайным путям, что обеспечивает универсальность для различных архитектур моделей, а не только для глубоких сетей. Экспериментальные исследования, проведённые для различных оптимизационных функций, демонстрируют улучшенные показатели минимизации при использовании SPAD. Кроме того, эксперименты с глубоким обучением с использованием SPAD заметно снижают переобучение, предлагая преимущества, аналогичные традиционным методам дропаута, но при этом снижая потребление памяти, что открывает перспективы для применения в других стохастических техниках в этой области.