Selective Path Automatic Differentiation: Beyond Uniform Distribution on Backpropagation Dropout
The unreasonable effectiveness of the Stochastic Gradient Descent (SGD) is probably the biggest machine learning finding of the 2010’s. SGD powers nearly all recent breakthroughs in machine learning. Conceptually, SGD is remarkably simple: process your dataset one data point at a time and, for every point, nudge the model parameters in the direction given by this point. In more technical terms, the “direction” is given as a gradient, and the “nudging” involves a small scaling coefficient usually referred to as the learning rate.
While the SGD technique goes back to the 1950s, it mostly remained an obscure and little-used technique until it came to prominence with the advent of deep learning. The reasons why this technique works were not clear and, to some extent, still aren’t. As the goal is to minimize the model error on the dataset as a whole, it’s not obvious that picking points in strict isolation should yield anything but numerical garbage.
Nowadays, it is generally understood that the effectiveness of SGD - aka, why it works - comes from two factors. First, while the gradient obtained by SGD is very noisy – each step considers a single data point – this gradient is very cheap. It turns out that, for a given budget of computing resources, applying numerous low-quality gradient updates vastly overperforms the application of a single high-quality gradient update. Second, the noisy updates themselves help the model to exit the vast plateaus of numerical indifference that exists in higher dimensions. In fact, in higher dimensions, the crux of optimization is not, as long thought, to escape local minima, but to escape local plateaus - areas where the loss varies very little.

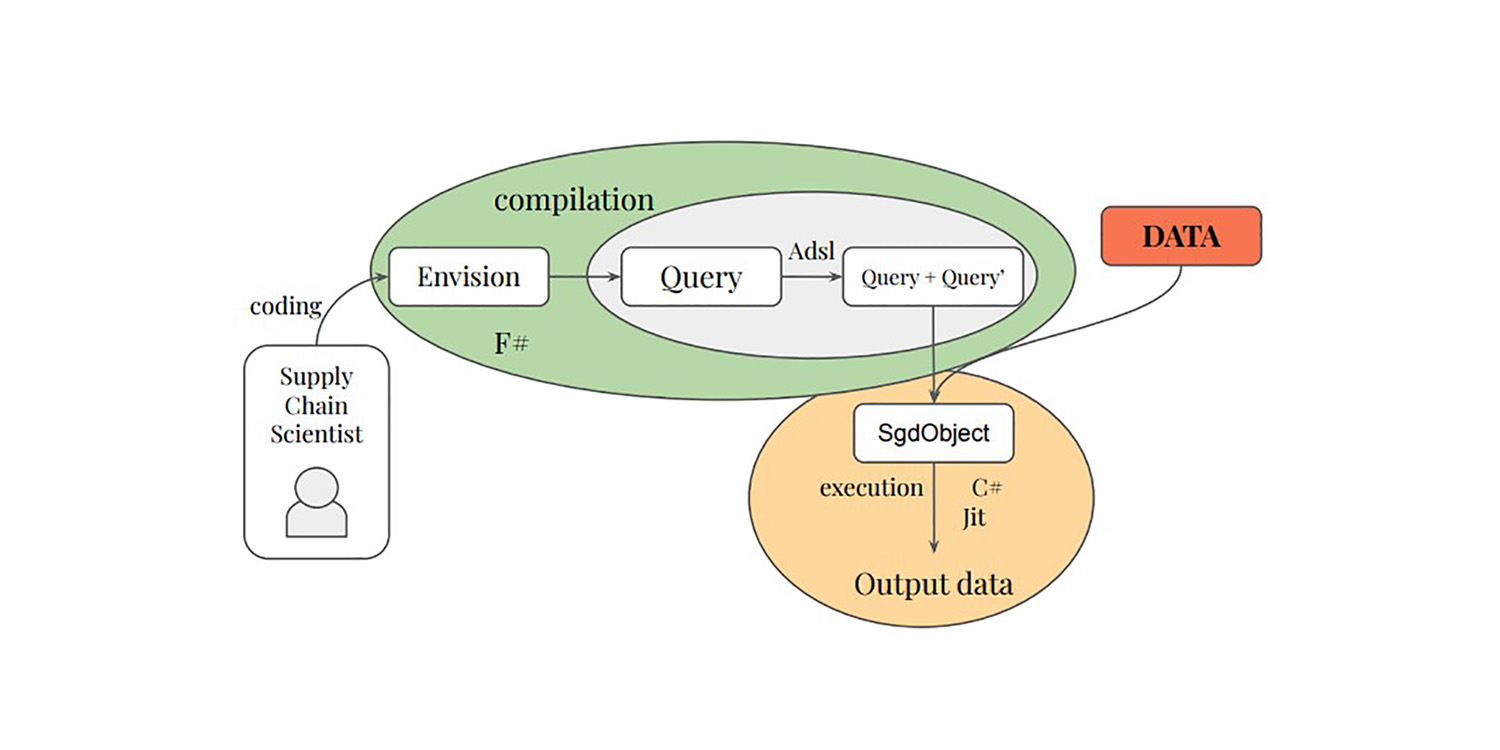
Some of us, including Paul Peseux and Victor Nicollet, decided to advance these ideas further. If SGD works by trading away gradient quality for computing efficiency, what about extending this principle further? What about a sub-point gradient that would be even cheaper to compute, albeit even noisier? This is exactly what has been done with the Selective Path Automatic Differentiation (SPAD). SPAD revisits one of the cornerstones of the modern machine learning paradigm with a twist: a data point can be “split” gradient-wise by its evaluation paths.
The paper below presents a contribution from Paul Peseux (Lokad), Victor Nicollet (Lokad), Maxime Berar (Litis) and Thierry Paquet (Litis).
Title: Selective Path Automatic Differentiation: Beyond Uniform Distribution on Backpropagation Dropout
Authors: Paul Peseux, Maxime Berar, Thierry Paquet, Victor Nicollet
Abstract: This paper introduces Selective Path Automatic Differentiation (SPAD), a novel approach to reducing memory consumption and mitigating overfitting in gradient-based models for embedded artificial intelligence. SPAD extends the existing Randomized Automatic Differentiation, proposed by Oktay et al and which draws random paths through the backpropagation graph with matrix injection, by enabling alternative probability distributions on the backpropagation graph, thereby enhancing learning performance and memory management. In a specific iteration, SPAD evaluates and ranks multiple paths within the backpropagation graph. Over subsequent iterations, it preferentially follows these higher-ranked paths. This work also presents a compilation-based technique allowing model-agnostic access to random paths, ensuring generalizability across various model architectures, not restricted to deep models. Experimental evaluations conducted across various optimization functions demonstrate an enhanced minimization performance when employing SPAD. Additionally, deep learning experiments with SPAD notably mitigate overfitting, offering benefits akin to those of traditional dropout methods, but with a concomitant decrease in memory usage. We conclude by discussing the unique stochasticity implications of our work and the potential for it to augment other stochastic techniques in the field.