Modellazione predittiva strutturata per Supply Chain - Lezione 5.1

00:01 Introduzione
02:44 Panoramica delle esigenze predittive
05:57 Modelli vs. Modellazione
12:26 La storia finora
15:50 Un po’ di teoria e un po’ di pratica
17:41 Programmazione Differenziabile, SGD 1/6
24:56 Programmazione Differenziabile, autodiff 2/6
31:07 Programmazione Differenziabile, funzioni 3/6
35:35 Programmazione Differenziabile, meta-parametri 4/6
37:59 Programmazione Differenziabile, parametri 5/6
40:55 Programmazione Differenziabile, particolarità 6/6
43:41 Walkthrough, previsione della domanda nel retail
45:49 Walkthrough, adattamento dei parametri 1/6
53:14 Walkthrough, condivisione dei parametri 2/6
01:04:16 Walkthrough, mascheramento della perdita 3/6
01:09:34 Walkthrough, integrazione delle covariabili 4/6
01:14:09 Walkthrough, decomposizione sparsa 5/6
01:21:17 Walkthrough, scalatura libera 6/6
01:25:14 Whiteboxing
01:33:22 Ritorno all’ottimizzazione sperimentale
01:39:53 Conclusione
01:44:40 Lezione in arrivo e domande dal pubblico

Descrizione

Programmazione Differenziabile (DP) è un paradigma generativo utilizzato per sviluppare una vasta gamma di modelli statistici, che risultano eccellentemente adatti per le sfide predittive per supply chain challenges. DP supera quasi tutta la letteratura classica delle previsioni basate su modelli parametrici. DP è anche superiore agli algoritmi classici di machine learning - fino alla fine degli anni 2010 - in praticamente ogni dimensione che conta per un uso pratico a scopi della supply chain.

Trascrizione completa

Benvenuti a questa serie di lezioni sulla supply chain. Sono Joannes Vermorel, e oggi presenterò “Structured Predictive Modeling with Differentiable Programming in Supply Chain.” Scegliere il corso d’azione corretto richiede una dettagliata comprensione quantitativa del futuro. Infatti, ogni decisione – acquistare di più, produrre di più – riflette una certa anticipazione del futuro. Invariabilmente, la teoria dominante della supply chain enfatizza il concetto di forecasting per affrontare proprio questa problematica. Tuttavia, la prospettiva del forecasting, almeno nella sua forma classica, presenta carenze su due fronti.

Innanzitutto, enfatizza una prospettiva ristretta di previsione tramite time series, che purtroppo non riesce a cogliere la diversità delle sfide presenti nelle supply chain reali. In secondo luogo, enfatizza un focus limitato sull’forecast accuracy delle serie temporali, che in gran parte sfugge al punto. Guadagnare qualche punto percentuale in più di accuratezza non si traduce automaticamente in un maggior ritorno economico per la supply chain.

L’obiettivo della lezione attuale è scoprire un approccio alternativo al forecasting, che in parte è una tecnologia e in parte una metodologia. La tecnologia sarà la programmazione differenziabile, e la metodologia saranno modelli predittivi strutturati. Al termine di questa lezione, dovresti essere in grado di applicare questo approccio a una situazione della supply chain. Questo approccio non è teorico; è stato il metodo predefinito adottato da Lokad per un paio d’anni ormai. Inoltre, se non hai visto le lezioni precedenti, la lezione attuale non dovrebbe risultare totalmente incomprensibile. Tuttavia, in questa serie di lezioni, stiamo raggiungendo un punto in cui è sicuramente utile seguire le lezioni in sequenza. Nella lezione attuale, riprenderemo numerosi elementi che sono stati introdotti nelle lezioni precedenti.

Il forecasting della future demand è il candidato ovvio quando si tratta di analizzare le esigenze predittive per la nostra supply chain. Infatti, una migliore anticipazione della domanda è un ingrediente critico per decisioni basilari come acquistare di più e produrre di più. Tuttavia, attraverso i principi della supply chain che abbiamo introdotto nel corso del terzo capitolo di questa serie di lezioni, abbiamo visto che esiste un insieme piuttosto diversificato di aspettative in termini di requisiti predittivi per guidare la supply chain.

In particolare, ad esempio, i lead times variano e mostrano pattern stagionali. Praticamente ogni decisione legata all’inventario richiede un’anticipazione della domanda futura ma anche un’anticipazione dei lead times futuri. Pertanto, i lead times devono essere previsti. I resi rappresentano a volte fino alla metà del flusso. Questo è il caso, ad esempio, del fashion e-commerce in Germania. In tali situazioni, anticipare i resi diventa critico, e questi variano notevolmente da un prodotto all’altro. Quindi, in queste situazioni, i resi devono essere previsti.

Dal lato dell’offerta, la produzione stessa può variare e non solo a causa dei ritardi extra o dei lead times variabili. Ad esempio, la produzione può comportare un certo grado di incertezza. Questo accade in settori a bassa tecnologia come l’agricoltura, ma può verificarsi anche in settori high-tech come l’industria farmaceutica. Pertanto, anche i rendimenti produttivi devono essere previsti. Infine, il comportamento dei clienti conta molto. Ad esempio, stimolare la domanda attraverso prodotti che generano acquisizione è molto importante e, al contrario, affrontare stockouts su prodotti che causano un elevato tasso di abbandono quando questi mancano proprio a causa degli stockouts è altrettanto rilevante. Quindi, tali comportamenti richiedono analisi, previsione – in altre parole, devono essere previsti. Il punto fondamentale qui è che il forecasting delle serie temporali è solo un pezzo del puzzle. Abbiamo bisogno di un approccio predittivo che possa abbracciare tutte queste situazioni e altro ancora, poiché è una necessità se vogliamo avere un approccio che abbia qualche possibilità di successo di fronte a tutte le situazioni che una supply chain reale ci presenterà.

L’approccio di riferimento quando si tratta del problema predittivo è presentare un modello. Questo approccio ha guidato la letteratura sul forecasting delle serie temporali per decenni ed è ancora, direi, l’approccio dominante nei circoli del machine learning al giorno d’oggi. Questo approccio incentrato sul modello, così come lo chiamerò, è così pervasivo che potrebbe risultare difficile prendersi un momento per valutare ciò che realmente accade con questa prospettiva incentrata sul modello.

La mia proposta per questa lezione è che la supply chain necessita di una tecnica di modellazione, una prospettiva incentrata sulla modellazione, e che una serie di modelli, per quanto estesa, non sarà mai sufficiente a soddisfare tutti i nostri requisiti così come si presentano nelle supply chain reali. Chiarifichiamo questa distinzione tra l’approccio incentrato sul modello e l’approccio incentrato sulla modellazione.

L’approccio incentrato sul modello enfatizza prima di tutto un modello. Il modello si presenta come un pacchetto, un insieme di numerical recipes che tipicamente assumono la forma di un piece of software che si può effettivamente eseguire. Anche quando non è disponibile un tale software, l’aspettativa è che se hai un modello ma non il software, allora il modello debba essere descritto con precisione matematica, permettendo una completa reimplementazione del modello. Questo pacchetto, il modello trasformato in software, è destinato a essere il risultato finale.

Da una prospettiva idealizzata, questo modello dovrebbe comportarsi esattamente come una funzione matematica: dati in ingresso, risultati in uscita. Se rimane qualche possibilità di configurazione per il modello, tali elementi configurabili vengono trattati come punti non definiti, come problemi che non sono ancora stati completamente risolti. Infatti, ogni opzione configurabile indebolisce il valore del modello. Quando abbiamo configurabilità e troppe opzioni dall’approccio incentrato sul modello, il modello tende a dissolversi in uno spazio di modelli, e improvvisamente, non riusciamo più a ottenere un benchmark affidabile poiché non esiste un modello singolo.

L’approccio della modellazione adotta una visione completamente invertita rispetto all’angolo della configurabilità. Massimizzare l’espressività del modello diventa l’obiettivo finale. Questo non è un difetto; diventa una caratteristica. La situazione può risultare piuttosto confusa quando osserviamo una prospettiva incentrata sulla modellazione, perché se stiamo guardando una presentazione incentrata sulla modellazione, quello che vedremo è una presentazione di modelli. Tuttavia, quei modelli hanno un intento molto diverso.

Se adotti la prospettiva della modellazione, il modello presentato è solo un’illustrazione. Non ha l’intento di essere completo o la soluzione finale al problema. È solo un passo nel percorso per illustrare la tecnica di modellazione stessa. La principale sfida con la tecnica di modellazione è che, improvvisamente, diventa molto difficile valutare l’approccio. Infatti, perdiamo l’opzione del benchmarking ingenuo perché, con questa prospettiva incentrata sulla modellazione, abbiamo le potenzialità dei modelli. Non ci concentriamo specificamente su un modello rispetto a un altro; questo non è nemmeno il giusto approccio mentale. Quello che abbiamo è un’opinione informata.

Tuttavia, vorrei subito sottolineare che non è perché hai un benchmark e dei numeri associati al tuo benchmark che automaticamente si qualifica come scienza. I numeri potrebbero essere del tutto insensati, e al contrario, non è perché si tratta solo di un’opinione informata che sia meno scientifico. In un certo senso, è semplicemente un approccio diverso, e la realtà è che tra le varie comunità i due approcci coesistono.

Ad esempio, se osserviamo il paper “Forecasting at Scale”, pubblicato da un team di Facebook nel 2017, abbiamo qualcosa che è praticamente l’archetipo dell’approccio incentrato sul modello. In questo paper viene presentato il modello Facebook Prophet. E in un altro paper, “Tensor Comprehension”, pubblicato nel 2018 da un altro team di Facebook, abbiamo essenzialmente una tecnica di modellazione. Questo paper può essere visto come l’archetipo dell’approccio della modellazione. Quindi, si può notare che persino i team di ricerca che lavorano nella stessa azienda, quasi contemporaneamente, possono affrontare il problema da un’angolazione all’altra, a seconda della situazione.

Questa lezione fa parte di una serie di lezioni sulla supply chain. Nel primo capitolo, ho presentato le mie opinioni sulla supply chain sia come campo di studio che come pratica. Fin dalla prima lezione, ho sostenuto che la teoria dominante della supply chain non è all’altezza delle sue aspettative. Succede che la teoria dominante della supply chain si basa pesantemente sull’approccio incentrato sul modello, e credo che questo singolo aspetto sia una delle cause principali di attrito tra la teoria dominante della supply chain e le esigenze delle supply chain reali.

Nel secondo capitolo di questa serie di lezioni, ho introdotto una serie di metodologie. Infatti, le metodologie naive vengono tipicamente sconfitte dalla natura episodica e spesso antagonista delle situazioni della supply chain. In particolare, la lezione intitolata “Empirical Experimental Optimization”, che faceva parte del secondo capitolo, è il tipo di prospettiva che adotto oggi in questa lezione.

Nel terzo capitolo, ho introdotto una serie di personae della supply chain. Le personae rappresentano un focus esclusivo sui problemi che cerchiamo di affrontare, ignorando completamente qualsiasi soluzione candidata. Queste personae sono fondamentali per comprendere la diversità delle sfide predittive affrontate dalle supply chain reali. Credo che queste personae siano essenziali per evitare di rimanere intrappolati nella ristretta prospettiva delle serie temporali, che è una caratteristica distintiva di una teoria della supply chain esercitata prestando poca attenzione ai dettagli minuziosi delle supply chain reali.

Nel quarto capitolo, ho introdotto una serie di scienze ausiliarie. Queste scienze sono distinte dalla supply chain, ma una conoscenza di base di queste discipline è essenziale per la pratica moderna della supply chain. Abbiamo già toccato brevemente il tema della programmazione differenziabile in questo quarto capitolo, ma lo reintrodurrò in maniera molto più dettagliata tra qualche minuto.

Infine, nella prima lezione di questo quinto capitolo, abbiamo visto un modello semplice, alcuni direbbero addirittura semplicistico, che ha ottenuto un’accuratezza all’avanguardia nelle previsioni in una competizione mondiale di forecasting competition tenutasi nel 2020. Oggi presento una serie di tecniche che possono essere utilizzate per apprendere i parametri implicati in questo modello che ho presentato nella lezione precedente.

Il resto di questa lezione si suddividerà grossomodo in due blocchi, seguiti da alcune riflessioni finali. Il primo blocco è dedicato alla programmazione differenziabile. Abbiamo già toccato questo argomento nel quarto capitolo; tuttavia, oggi lo esamineremo in maniera molto più approfondita. Alla fine di questa lezione, dovresti essere quasi in grado di creare la tua implementazione di programmazione differenziabile. Dico “quasi” perché i risultati possono variare a seconda dello stack tecnologico che utilizzi. Inoltre, la programmazione differenziabile è un’arte minore a sé stante; ci vuole un po’ di esperienza per farla funzionare senza intoppi nella pratica.

Il secondo blocco di questa lezione è un walkthrough per una situazione di previsione della domanda nel retail. Questo walkthrough è un seguito della lezione precedente, nella quale abbiamo presentato il modello che si è classificato al primo posto nella competizione di forecasting M5 nel 2020. Tuttavia, in quella presentazione non abbiamo dettagliato come sono stati effettivamente calcolati i parametri del modello. Questo walkthrough fornirà esattamente questo, e copriremo anche elementi importanti come gli stockouts e le promotions che sono stati lasciati fuori dalla lezione precedente. Infine, basandomi su tutti questi elementi, discuterò le mie opinioni sull’idoneità della programmazione differenziabile per scopi della supply chain.

Il Stochastic Gradient Descent (SGD) è uno dei due pilastri della programmazione differenziabile. Lo SGD è apparentemente semplice, eppure non è del tutto chiaro il motivo per cui funzioni così bene. È assolutamente chiaro perché funzioni; ciò che non è molto chiaro è perché funzioni così bene.

La storia dello Stochastic Gradient Descent risale agli anni ‘50, quindi ha una storia piuttosto lunga. Tuttavia, questa tecnica ha raggiunto il riconoscimento mainstream solo nell’ultimo decennio con l’avvento del deep learning. Lo Stochastic Gradient Descent è profondamente radicato nella prospettiva dell’ottimizzazione matematica. Abbiamo una funzione di perdita Q che vogliamo minimizzare, e disponiamo di un insieme di parametri reali, indicati con W, che rappresentano tutte le possibili soluzioni. Quello che vogliamo trovare è la combinazione di parametri W che minimizza la funzione di perdita Q.

La funzione di perdita Q dovrebbe rispettare una proprietà fondamentale: può essere decomposta in modo additivo in una serie di termini. L’esistenza di questa decomposizione additiva è ciò che permette allo Stochastic Gradient Descent di funzionare. Se la tua funzione di perdita non può essere decomposta in modo additivo in questo modo, allora lo Stochastic Gradient Descent non si applica come tecnica. In questa prospettiva, X rappresenta l’insieme di tutti i termini che contribuiscono alla funzione di perdita, e Qx rappresenta una perdita parziale che denota la perdita associata a uno dei termini, considerando la funzione di perdita come la somma di termini parziali.

Sebbene lo Stochastic Gradient Descent non sia specifico per situazioni di apprendimento, si adatta perfettamente a tutti i casi d’uso di apprendimento, e quando parlo di apprendimento intendo quello relativo ai casi d’uso del machine learning. Infatti, se disponiamo di un training dataset, questo dataset assumerà la forma di una lista di osservazioni, dove ogni osservazione consiste in una coppia di feature che rappresentano l’input del modello e etichette che rappresentano gli output. In sostanza, ciò che vogliamo dal punto di vista dell’apprendimento è progettare un modello che migliori l’errore empirico e altre metriche osservabili in questo training dataset. Dal punto di vista dell’apprendimento, X sarebbe effettivamente la lista delle osservazioni, e i parametri sarebbero quelli di un modello di machine learning che cerchiamo di ottimizzare per adattarsi al meglio a questo dataset.

Lo Stochastic Gradient Descent è fondamentalmente un processo iterativo che attraversa casualmente le osservazioni, una alla volta. Selezioniamo un’osservazione, un piccolo X, per volta, e per questa osservazione calcoliamo un gradiente locale, rappresentato come nabla di Qx. Si tratta semplicemente di un gradiente locale che si applica solo a un termine della funzione di perdita. Non è il gradiente della funzione di perdita completa, ma un gradiente locale che si applica a un termine della funzione di perdita – si può considerare come un gradiente parziale.

Un passo dello Stochastic Gradient Descent consiste nel prendere questo gradiente locale e spingere leggermente i parametri W basandosi su questa osservazione parziale del gradiente. È esattamente ciò che avviene qui, con W che viene aggiornato come W meno eta per nabla QxW. In sostanza, si dice in forma molto concisa di spostare il parametro W nella direzione del gradiente locale ottenuto con X, dove X è semplicemente una delle osservazioni del tuo dataset, se stiamo affrontando un problema dal punto di vista dell’apprendimento. Successivamente, procediamo in modo casuale, applicando questo gradiente locale e iterando.

Intuitivamente, lo Stochastic Gradient Descent funziona molto bene perché mostra un trade-off tra iterazioni più veloci e gradienti più rumorosi, fino ad arrivare a iterazioni più granulari e quindi ancora più rapide. L’essenza dello Stochastic Gradient Descent è che non ci interessa avere misurazioni del gradiente molto imperfette, purché possiamo ottenerle super velocemente. Se possiamo spostare il trade-off verso iterazioni più rapide, anche a costo di gradienti più rumorosi, facciamolo. È per questo che lo Stochastic Gradient Descent risulta così efficace nel minimizzare la quantità di risorse computazionali necessarie per raggiungere una certa qualità di soluzione per il parametro W.

Infine, abbiamo la variabile eta, conosciuta come learning rate. In pratica, il learning rate non è una costante; questa variabile varia durante l’esecuzione dello Stochastic Gradient Descent. Da Lokad, utilizziamo l’algoritmo Adam per controllare l’evoluzione di questo parametro eta relativo al learning rate. Adam è un metodo pubblicato nel 2014 ed è molto popolare nei circoli del machine learning ogni volta che è coinvolto lo Stochastic Gradient Descent.

Il secondo pilastro della programmazione differenziabile è l’automatic differentiation. Abbiamo già visto questo concetto in una lezione precedente. Rivisitiamo questo concetto osservando un pezzo di codice. Questo codice è scritto in Envision, un linguaggio di programmazione specifico per domini ideato da Lokad allo scopo di ottimizzazione predittiva delle supply chains. Scelgo Envision perché, come vedrete, gli esempi sono molto più concisi e auspicabilmente più chiari rispetto ad altre presentazioni, se dovessi usare Python, Java o C#. Tuttavia, vorrei sottolineare che anche se sto usando Envision, non c’è alcun trucco segreto. Potreste reimplementare completamente tutti questi esempi in altri linguaggi di programmazione. Probabilmente moltiplicherebbe il numero di righe di codice per un fattore di 10, ma, nel quadro generale, è un dettaglio. Qui, per una lezione, Envision ci offre una presentazione molto chiara e concisa.

Vediamo come la programmazione differenziabile possa essere utilizzata per affrontare una regressione lineare. Questo è un problema didattico; non ci serve la programmazione differenziabile per fare una regressione lineare. L’obiettivo è semplicemente familiarizzare con la sintassi della programmazione differenziabile. Dalle righe 1 a 6, dichiariamo la tabella T, che rappresenta la tabella delle osservazioni. Quando dico tabella delle osservazioni, ricordate semplicemente il set dello Stochastic Gradient Descent che era denominato X. È esattamente la stessa cosa. Questa tabella ha due colonne, una feature indicata come X e un’etichetta indicata come Y. Quello che vogliamo è prendere X come input e riuscire a prevedere Y con un modello lineare, o più precisamente, un modello affine. Ovviamente, abbiamo solo quattro punti dati in questa tabella T. Questo è un dataset ridicolmente piccolo; è solo per chiarezza dell’esposizione.

Alla riga 8, introduciamo il blocco autodiff. Il blocco autodiff può essere visto come un ciclo in Envision. È un ciclo che itera su una tabella, in questo caso, la tabella T. Queste iterazioni riflettono i passi dello Stochastic Gradient Descent. Quindi, ciò che accade quando l’esecuzione di Envision entra in questo blocco autodiff è che abbiamo una serie di esecuzioni ripetute in cui selezioniamo righe dalla tabella delle osservazioni per poi applicare i passi dello Stochastic Gradient Descent. Per fare ciò, abbiamo bisogno dei gradienti.

Da dove provengono i gradienti? Qui, abbiamo scritto un programma, una piccola espressione del nostro modello, Ax + B. Introduciamo la funzione di perdita, che è l’errore quadratico medio. Vogliamo ottenere il gradiente. Per una situazione semplice come questa, potremmo scrivere il gradiente manualmente. Tuttavia, l’automatic differentiation è una tecnica che ti permette di compilare un programma in due forme: la prima forma è l’esecuzione in avanti del programma, e la seconda forma è l’esecuzione inversa che calcola i gradienti associati a tutti i parametri presenti nel programma.

Alle righe 9 e 10, abbiamo la dichiarazione di due parametri, A e B, con la parola chiave “auto” che indica a Envision di effettuare un’inizializzazione automatica dei valori di questi due parametri. A e B sono valori scalari. L’automatic differentiation avviene per tutti i programmi contenuti in questo blocco autodiff. Essenzialmente, si tratta di una tecnica a livello di compilatore che compila questo programma due volte: una volta per il forward pass e una seconda volta per un programma che fornirà i valori dei gradienti. La bellezza della tecnica di automatic differentiation è che garantisce che la quantità di CPU necessaria per calcolare il programma regolare sia in linea con quella necessaria per calcolare il gradiente quando si esegue il reverse pass. Questa è una proprietà molto importante. Infine, alla riga 14, stampiamo i parametri che abbiamo appena appreso grazie al blocco autodiff sopra.

La programmazione differenziabile brilla davvero come paradigma di programmazione. È possibile comporre un programma arbitrariamente complesso e ottenere la differenziazione automatica di tale programma. Questo programma può includere, ad esempio, branche e chiamate a funzioni. Questo esempio di codice riprende la funzione di perdita pinball che abbiamo introdotto nella lezione precedente. La funzione di perdita pinball può essere utilizzata per derivare stime dei quantili quando osserviamo deviazioni da una distribuzione di probabilità empirica. Se minimizzi l’errore quadratico medio con la tua stima, ottieni una stima della media della tua distribuzione empirica. Se minimizzi la funzione di perdita pinball, ottieni una stima di un target quantile. Se punti al 90° quantile, significa che è il valore nella tua distribuzione di probabilità per cui il valore futuro osservato ha una probabilità del 90% di essere inferiore alla tua stima (o del 10% di essere superiore). Questo ricorda l’analisi dei service levels che esiste nel supply chain.

Alle righe 1 e 2, introduciamo una tabella delle osservazioni popolata con deviazioni campionate casualmente da una distribuzione di Poisson. I valori della distribuzione di Poisson sono campionati con una media di 3, e otteniamo 10.000 deviazioni. Alle righe 4 e 5, presentiamo la nostra implementazione su misura della funzione di perdita pinball. Questa implementazione è quasi identica al codice che ho introdotto nella lezione precedente. Tuttavia, la parola chiave “autodiff” è ora aggiunta alla dichiarazione della funzione. Questa parola chiave, quando è associata alla dichiarazione della funzione, garantisce che il compilatore di Envision possa differenziare automaticamente questa funzione. Sebbene, in teoria, l’automatic differentiation possa essere applicata a qualsiasi programma, in pratica, ci sono molti programmi per i quali non ha senso differenziarli o molte funzioni per cui non avrebbe senso. Ad esempio, consideri una funzione che prende due valori di testo e li concatena. Dal punto di vista dell’automatic differentiation, non ha senso applicarla a questo tipo di operazione. L’automatic differentiation richiede che ci siano numeri negli input e output delle funzioni che si sta cercando di differenziare.

Alle righe 7 a 9, abbiamo il blocco autodiff, che calcola la stima del quantile target per la distribuzione empirica ottenuta attraverso la tabella delle osservazioni. Sotto sotto, essa è in realtà una distribuzione di Poisson. La stima del quantile è dichiarata come un parametro chiamato “quantile” alla riga 8, e alla riga 9 facciamo una chiamata alla nostra implementazione della funzione di perdita pinball. Il target quantile è impostato a 0,5, quindi stiamo cercando effettivamente una stima mediana della distribuzione. Infine, alla riga 11, stampiamo i risultati del valore che abbiamo appreso tramite l’esecuzione del blocco autodiff. Questo pezzo di codice illustra come un programma che andremo a differenziare automaticamente può includere sia una chiamata di funzione che una biforcazione, e tutto ciò può avvenire in modo completamente automatico.

Ho detto che i blocchi autodiff possono essere interpretati come un ciclo che esegue una serie di passi di stochastic gradient descent (SGD) sulla tabella delle osservazioni, selezionando una riga alla volta da questa tabella. Tuttavia, sono rimasto piuttosto vago riguardo alla condizione di arresto per questa situazione. Quando si ferma lo stochastic gradient descent in Envision? Di default, lo stochastic gradient descent si ferma dopo 10 epoche. Un’epoca, nel gergo del machine learning, rappresenta una traversata completa della tabella delle osservazioni. Alla riga 7, un attributo chiamato “epochs” può essere associato ai blocchi autodiff. Questo attributo è opzionale; di default, il valore è 10, ma se specifichi questo attributo, puoi scegliere un conteggio diverso. Qui, stiamo specificando 100 epoche. Tieni presente che il tempo totale per il calcolo è quasi strettamente lineare rispetto al numero di epoche. Quindi, se hai il doppio delle epoche, il tempo di calcolo durerà il doppio.

Inoltre, alla riga 7, introduciamo anche un secondo attributo chiamato “learning_rate”. Questo attributo è anch’esso opzionale, e di default assume il valore 0,01, associato al blocco autodiff. Questo learning rate è un fattore utilizzato per inizializzare l’algoritmo Adam che controlla l’evoluzione del learning rate. Questo è il parametro eta che abbiamo visto nel passo dello stochastic gradient descent. Esso controlla l’algoritmo Adam. In sostanza, si tratta di un parametro che non dovresti modificare frequentemente, ma a volte regolare questo parametro può far risparmiare una porzione significativa della potenza di elaborazione. Non è inaspettato che, perfezionando questo learning rate, si possano risparmiare circa il 20% del tempo totale di calcolo per il tuo stochastic gradient descent.

L’inizializzazione dei parametri appresi nel blocco autodiff richiede anch’essa un esame più approfondito. Finora, abbiamo usato la parola chiave “auto,” e in Envision, ciò significa semplicemente che Envision inizializzerà il parametro estraendo casualmente un valore da una distribuzione gaussiana con media 1 e deviazione standard 0,1. Questa inizializzazione si discosta dalla pratica abituale nel deep learning, dove i parametri vengono inizializzati casualmente con gaussiane centrate intorno a zero. Il motivo per cui Lokad ha adottato questo approccio diverso diventerà più chiaro più avanti in questa lezione, quando procederemo con una situazione reale di forecasting della domanda nel retail.

In Envision, è possibile sovrascrivere e controllare l’inizializzazione dei parametri. Il parametro “quantile”, per esempio, è dichiarato a linea 9 ma non necessita di essere inizializzato. Infatti, a linea 7, subito sopra il blocco autodiff, abbiamo una variabile “quantile” a cui viene assegnato il valore 4.2, e quindi la variabile è già inizializzata con un dato valore. Non è più necessaria un’inizializzazione automatica. È anche possibile imporre un intervallo di valori consentiti per i parametri, e ciò viene fatto con la parola chiave “in” a linea 9. In sostanza, stiamo definendo che “quantile” debba essere compreso tra 1 e 10, inclusi. Con questi limiti in atto, se viene ottenuto un aggiornamento dall’algoritmo Adam che spinge il valore del parametro al di fuori dell’intervallo accettabile, limitiamo il cambiamento di Adam in modo che rimanga entro questo intervallo. Inoltre, impostiamo a zero i valori di momentum che sono tipicamente associati all’algoritmo Adam sotto il cofano. Imporre limiti ai parametri si discosta dalla pratica classica del deep learning; tuttavia, i benefici di questa funzionalità diventeranno evidenti una volta che inizieremo a discutere di un esempio reale di previsione della domanda nel retail.

La programmazione differenziabile si basa fortemente sulla discesa del gradiente stocastico. L’elemento stocastico è letteralmente ciò che fa funzionare la discesa in modo molto rapido. È una lama a doppio taglio; il rumore ottenuto attraverso le perdite parziali non è solo un difetto, ma anche una caratteristica. Avere un po’ di rumore permette alla discesa di evitare di rimanere bloccata in zone con gradienti molto piatti. Quindi, avere questo gradiente rumoroso non solo accelera notevolmente l’iterazione, ma aiuta anche a spingere l’iterazione a uscire da aree in cui il gradiente è molto piatto e rallenta la discesa. Tuttavia, è bene tenere presente che, quando si utilizza la discesa del gradiente stocastico, la somma dei gradienti non equivale al gradiente della somma. Di conseguenza, la discesa del gradiente stocastico comporta piccoli bias statistici, specialmente per quanto riguarda le distribuzioni a coda. Tuttavia, quando sorgono tali preoccupazioni, è relativamente semplice aggiustare con del nastro adesivo le ricette numeriche, anche se la teoria rimane un po’ confusa.

La programmazione differenziabile (DP) non deve essere confusa con un risolutore arbitrario di ottimizzazione matematica. Il gradiente deve fluire attraverso il programma affinché la programmazione differenziabile funzioni. La programmazione differenziabile può lavorare con programmi arbitrariamente complessi, ma tali programmi devono essere progettati tenendo presente la programmazione differenziabile. Inoltre, la programmazione differenziabile è una cultura; è un insieme di suggerimenti e trucchi che si integrano bene con la discesa del gradiente stocastico. In definitiva, la programmazione differenziabile è nella fascia più accessibile dello spettro del machine learning. È una tecnica molto avvicinabile. Tuttavia, ci vuole un po’ di maestria per padroneggiare questo paradigma e farlo funzionare senza intoppi in produzione.

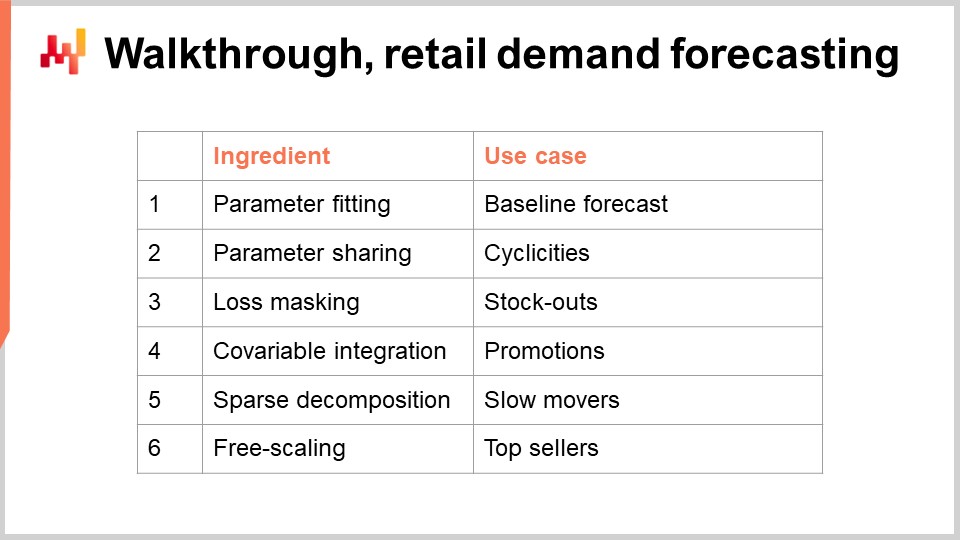
Siamo ora pronti per intraprendere il secondo blocco di questa lezione: il walkthrough. Avremo un walkthrough per il nostro compito di previsione della domanda nel retail. Questo esercizio di modellazione è allineato con la sfida di previsione che abbiamo presentato nella lezione precedente. In breve, vogliamo prevedere la domanda giornaliera a livello di SKU in una rete di vendita al dettaglio. Uno SKU, o stock-keeping unit, è tecnicamente il prodotto cartesiano tra prodotti e punti vendita, filtrato secondo le voci dell’assortimento. Ad esempio, se abbiamo 100 negozi e 10.000 prodotti, e se ogni singolo prodotto è presente in ogni negozio, otteniamo 1 milione di SKU.

Esistono strumenti per trasformare una stima deterministica in una stima probabilistica. Ne abbiamo visto uno nella lezione precedente attraverso la tecnica ESSM. Affronteremo nuovamente questa specifica problematica—trasformare le stime in stime probabilistiche—in maniera più dettagliata nella prossima lezione. Tuttavia, oggi ci occupiamo solo di stimare medie, e tutti gli altri tipi di stime (quantili, probabilistiche) verranno successivamente come estensioni naturali dell’esempio centrale che presenterò oggi. In questo walkthrough, impareremo i parametri di un semplice modello di previsione della domanda. La semplicità di questo modello è ingannevole, poiché questa classe di modello riesce a raggiungere previsioni all’avanguardia, come illustrato nella competizione di forecasting M5 del 2020.

Per il nostro modello di domanda parametrico, introduciamo un singolo parametro per ogni SKU. Questa è una forma di modello assolutamente semplice; la domanda viene modellata come una costante per ogni SKU. Tuttavia, non è la stessa costante per ogni SKU. Una volta ottenuta questa media giornaliera costante, sarà lo stesso valore per tutti i giorni dell’intero ciclo di vita dello SKU.

Vediamo come viene fatto con la programmazione differenziabile. Dalle linee 1 a 4, introduciamo il blocco di dati fittizi. In pratica, questo modello e tutte le sue varianti dipenderebbero dagli input ottenuti dai sistemi aziendali: l’ERP, WMS, TMS, ecc. Tenere una lezione in cui si integra un modello matematico in una rappresentazione realistica dei dati, come quelli ottenuti dall’ERP, introduce un’infinità di complicazioni accidentali irrilevanti per l’argomento della lezione. Quindi, quello che faccio qui è introdurre un blocco di dati fittizi che non pretende affatto di essere realistico, né il tipo di dati che si possono osservare in una situazione retail reale. L’unico scopo di questi dati fittizi è introdurre le tabelle e le relazioni tra di esse, e assicurarsi che l’esempio di codice fornito sia completo, compilabile ed eseguibile. Tutti gli esempi di codice visti finora sono completamente autonomi; non ci sono parti nascoste prima o dopo. Lo scopo unico del blocco di dati fittizi è garantire che abbiamo un pezzo di codice standalone.

In ogni esempio di questo walkthrough, iniziamo con questo blocco di dati fittizi. A linea 1, introduciamo la tabella delle date con “dates” come chiave primaria. Qui, abbiamo un intervallo di date che corrisponde sostanzialmente a due anni e un mese. Poi, a linea 2, introduciamo la tabella degli SKUs, che è l’elenco degli SKU. In questo esempio minimalista, abbiamo solo tre SKU. In una situazione retail reale per una rete di vendita al dettaglio consistente, avremmo milioni, se non decine di milioni, di SKU. Ma qui, per il bene dell’esempio, utilizzo un numero molto ridotto. A linea 3, abbiamo la tabella “T”, che è un prodotto cartesiano tra gli SKU e le date. Essenzialmente, ciò che si ottiene da questa tabella “T” è una matrice in cui ogni SKU è associato a ogni giorno. Ha due dimensioni.

A linea 6, introduciamo il nostro blocco autodiff effettivo. La tabella di osservazione è la tabella degli SKUs, e la discesa del gradiente stocastico qui selezionerà un SKU alla volta. A linea 7, introduciamo il “level”, che sarà il nostro unico parametro. Si tratta di un parametro vettoriale e, finora, nei nostri blocchi autodiff, abbiamo introdotto solo parametri scalari. I parametri precedenti erano solamente un numero; qui, “SKU.level” è in realtà un vettore. È un vettore che contiene un valore per ogni SKU, e questo è letteralmente il nostro modello di domanda costante a livello di SKU. Specifichiamo un intervallo, e vedremo tra poco perché è importante. Deve essere almeno 0.01, e poniamo 1,000 come limite superiore della media giornaliera della domanda per questo parametro. Questo parametro viene inizializzato automaticamente con un valore vicino a uno, che è un punto di partenza ragionevole. In questo modello, abbiamo solo un grado di libertà per SKU. Infine, a linee 8 e 9, implementiamo effettivamente il modello in sé. A linea 8, calcoliamo “dot.delta”, che è la domanda prevista dal modello meno quella osservata, ossia “T.sold”. Il modello è solo un termine singolo, una costante, e poi abbiamo l’osservazione, che è “T.sold”.

Per capire cosa sta succedendo qui, si osservano alcuni comportamenti di broadcasting. La tabella “T” è una tabella incrociata tra SKU e data. Il blocco autodiff è un’iterazione che scorre le righe della tabella di osservazione. A linea 9, essendo all’interno del blocco autodiff, abbiamo scelto una riga per la tabella degli SKU. Il valore “SKUs.level” non è un vettore qui; è solo uno scalare, un singolo valore, perché abbiamo selezionato solo una riga della tabella di osservazione. Successivamente, “T.sold” non è più una matrice perché abbiamo già selezionato un SKU. Ciò che rimane è che “T.sold” è in realtà un vettore, un vettore la cui dimensione è pari a quella della tabella delle date. Quando eseguiamo la sottrazione “SKUs.level - T.sold”, otteniamo un vettore allineato con la tabella delle date, e lo assegnamo a “D.delta”, che è un vettore con una riga per ogni giorno, per due anni e un mese. Infine, a linea 9, calcoliamo la funzione di perdita, che è semplicemente l’errore quadratico medio. Questo modello è estremamente semplice. Vediamo cosa si può fare per i pattern del calendario.

La condivisione dei parametri è probabilmente una delle tecniche di programmazione differenziabile più semplici e utili. Un parametro si dice condiviso se contribuisce a più righe di osservazione. Condividendo i parametri tra le osservazioni, possiamo stabilizzare la discesa del gradiente e mitigare i problemi di overfitting. Consideriamo il pattern del giorno della settimana. Potremmo introdurre sette parametri che rappresentano i vari pesi per ogni singolo SKU. Finora, un SKU ha solo un parametro, che corrisponde alla domanda costante. Se vogliamo arricchire questa percezione della domanda, potremmo affermare che ogni singolo giorno della settimana ha il suo peso, e dato che abbiamo sette giorni della settimana, possiamo avere sette pesi da applicare in maniera moltiplicativa.

Tuttavia, è improbabile che ogni singolo SKU possieda un pattern unico per il giorno della settimana. La realtà è che è molto più ragionevole supporre l’esistenza di una categoria o di una qualche gerarchia, come una famiglia di prodotti, categoria, sotto-categoria o addirittura un reparto del negozio, che catturi correttamente questo pattern del giorno della settimana. L’idea è che non vogliamo introdurre sette parametri per SKU; ciò che desideriamo è introdurre sette parametri per categoria, ovvero il livello di raggruppamento in cui si assume un comportamento omogeneo per i pattern del giorno della settimana.

Se decidiamo di introdurre questi sette parametri con un effetto moltiplicativo sul level, questo è esattamente l’approccio adottato nella lezione precedente per questo modello, che ha ottenuto il primo posto a livello di SKU nella competizione M5. Abbiamo un level e un effetto moltiplicativo con il pattern del giorno della settimana.

Nel codice, dalle linee 1 a 5, abbiamo il blocco di dati fittizi proprio come in precedenza, e introduciamo una tabella extra chiamata “category”. Questa tabella è una tabella di raggruppamento degli SKU, e concettualmente, per ogni singola riga della tabella degli SKU, esiste una e una sola riga corrispondente nella tabella category. Nel linguaggio Envision, si dice che la categoria è upstream della tabella SKUs. A linea 7, viene introdotta la tabella del giorno della settimana. Questa tabella è fondamentale, e la definiamo con una forma specifica che riflette il pattern ciclico che vogliamo catturare. A linea 7, creiamo la tabella del giorno della settimana aggregando le date in base al loro valore modulo sette. Stiamo creando una tabella che avrà esattamente sette righe, e queste sette righe rappresenteranno ciascuno dei sette giorni della settimana. Per ogni riga nella tabella delle date, esiste una e una sola corrispondenza nella tabella del giorno della settimana. Pertanto, secondo il linguaggio Envision, la tabella del giorno della settimana è upstream della tabella “date”.

Ora abbiamo la tabella “CD”, che è un prodotto cartesiano tra categoria e giorno della settimana. In termini di numero di righe, questa tabella avrà tante righe quante sono le categorie moltiplicate per sette, poiché la tabella del giorno della settimana ha sette righe. A linea 12, introduciamo un nuovo parametro chiamato “CD.DOW” (DOW sta per day of the week), che è un altro parametro vettoriale appartenente alla tabella CD. In termini di gradi di libertà, avremo esattamente sette valori per parametro per ogni categoria, che è ciò che cerchiamo. Vogliamo un modello in grado di catturare questo pattern del giorno della settimana, ma con un solo pattern per categoria, non uno per SKU.

Dichiariamo questo parametro e usiamo la parola chiave “in” per specificare che il valore di “CD.DOW” deve essere compreso tra 0.1 e 100. A linea 13, definiamo la domanda come espressa dal modello. La domanda è “SKUs.level * CD.DOW”, che rappresenta la domanda. Prendiamo la domanda e sottraiamo l’osservato “T.sold”, ottenendo così un delta. Quindi, calcoliamo l’errore quadratico medio.

A linea 13, si assiste a una notevole magia di broadcasting. “CD.DOW” è una tabella incrociata tra categoria e giorno della settimana. Poiché siamo all’interno del blocco autodiff, la tabella CD è una tabella incrociata tra categoria e giorno della settimana. Essendo nel blocco autodiff, questo itera sulla tabella degli SKUs. In sostanza, quando selezioniamo un SKU, abbiamo effettivamente selezionato una categoria, dato che la tabella category è upstream. Ciò significa che CD.DOW non è più una matrice, ma un vettore di dimensione sette. Tuttavia, essendo upstream della tabella “date”, quelle sette righe possono essere trasmesse (broadcast) alla tabella delle date. Esiste un solo modo per effettuare questo broadcasting, poiché ogni riga della tabella del giorno della settimana ha affinità con specifiche righe della tabella delle date. Si ha un doppio broadcasting, e alla fine si ottiene una domanda costituita da una serie di valori ciclici a livello di giorno della settimana per lo SKU. Questo è il nostro modello a questo punto, mentre il resto della funzione di perdita rimane invariato.

Si osserva un modo molto elegante per affrontare le ciclicità combinando i comportamenti di broadcasting, derivanti dalla natura relazionale di Envision, con le sue capacità di programmazione differenziabile. Possiamo esprimere le ciclicità del calendario in sole tre righe di codice. Questo approccio funziona bene anche quando si lavora con dati molto sparsi. Funzionerebbe perfettamente anche se si considerassero prodotti che vendono in media solo un’unità al mese. In tali casi, l’approccio saggio sarebbe quello di avere una categoria che includa decine, se non centinaia, di prodotti. Questa tecnica può anche essere utilizzata per riflettere altri pattern ciclici, come il mese dell’anno o il giorno del mese.

Il modello introdotto nella lezione precedente, che ha raggiunto risultati all’avanguardia nella competizione M5, era una combinazione moltiplicativa di tre ciclicità: giorno della settimana, mese dell’anno e giorno del mese. Tutti questi schemi sono stati concatenati come una moltiplicazione. L’implementazione delle altre due varianti è lasciata al pubblico attento, ma si tratta solo di poche righe di codice per ogni schema ciclico, rendendolo molto conciso.

Nella lezione precedente abbiamo introdotto un modello di previsione delle vendite. Tuttavia, non sono le vendite ad interessarci, ma la domanda. Non dobbiamo confondere vendite nulle con domanda nulla. Se in un determinato giorno nel negozio non rimaneva scorta disponibile per l’acquisto da parte del cliente, a Lokad si utilizza la tecnica del mascheramento delle perdite per gestire gli esaurimenti delle scorte. Questa è la tecnica più semplice utilizzata per fronteggiare gli esaurimenti delle scorte, ma non è l’unica. Per quanto ne so, abbiamo almeno altre due tecniche che vengono impiegate in produzione, ognuna con i propri pro e contro. Queste altre tecniche non saranno trattate oggi, ma verranno affrontate in lezioni successive.

Tornando all’esempio di codice, le linee da 1 a 3 rimangono invariate. Esaminiamo ciò che segue. Alla linea 6, stiamo arricchendo i dati fittizi con la flag booleana in-stock. Per ogni singolo SKU e per ogni giorno, abbiamo un valore booleano che indica se alla fine della giornata nel negozio si è verificato un esaurimento delle scorte. Alla linea 15, stiamo modificando la funzione di perdita per escludere, azzerando tali giorni, quelli in cui è stato osservato un esaurimento delle scorte alla fine della giornata. Azzerando questi giorni, garantiamo che nessun gradiente venga retropropagato in situazioni che presentano un bias dovuto al verificarsi dell’esaurimento delle scorte.

L’aspetto più sconcertante della tecnica di mascheramento delle perdite è che essa non modifica affatto il modello. Infatti, se osserviamo il modello espresso alla linea 14, è esattamente lo stesso; non è stato toccato. È solo la funzione di perdita stessa ad essere modificata. Questa tecnica può apparire semplice, ma si discosta profondamente da una prospettiva incentrata sul modello. In sostanza, si tratta di una tecnica focalizzata sulla modellizzazione. Stiamo migliorando la situazione riconoscendo il bias causato dagli esaurimenti delle scorte e riflettendolo nei nostri sforzi di modellizzazione. Tuttavia, lo facciamo modificando la metrica di accuratezza, non il modello stesso. In altre parole, stiamo cambiando la perdita che ottimizziamo, rendendo questo modello non comparabile con altri modelli in termini di puro errore numerico.

Per una situazione come quella di Walmart, come discusso nella lezione precedente, la tecnica del mascheramento delle perdite è adeguata per la maggior parte dei prodotti. Come regola generale, questa tecnica funziona bene se la domanda non è così scarsa da avere la disponibilità di una sola unità la maggior parte del tempo. Inoltre, bisognerebbe evitare i prodotti in cui gli esaurimenti delle scorte sono molto frequenti, poiché potrebbe essere la strategia esplicita del rivenditore terminare la giornata con uno stockout. Questo accade tipicamente per alcuni prodotti ultra-freschi, per i quali il rivenditore punta a una situazione di esaurimento delle scorte entro la fine della giornata. Tecniche alternative possono rimediare a queste limitazioni, ma oggi non abbiamo tempo per trattarle.

Le promozioni sono un aspetto importante del retail. Più in generale, esistono numerosi modi per il rivenditore di influenzare e modellare la domanda, come la determinazione dei prezzi o lo spostamento dei prodotti su una gondola. Le variabili che forniscono informazioni extra a fini predittivi sono generalmente indicate come covariate nei circoli della supply chain. Esiste molta illusione riguardo a covariate complesse come i dati meteorologici o quelli dei social media. Tuttavia, prima di addentrarci in argomenti avanzati, dobbiamo affrontare l’elefante nella stanza, ossia le informazioni sui prezzi, che ovviamente hanno un impatto significativo sulla domanda che si osserverà. Così, alla linea 7 in questo esempio di codice, introduciamo per ogni singolo giorno, alla linea 14, “category.ed”, dove “ed” sta per elasticity of demand. Questo è un parametro vettoriale condiviso con un grado di libertà per categoria, inteso come rappresentazione dell’elasticità della domanda. Alla linea 16, introduciamo una forma esponenziale di price elasticity come l’esponenziale di (-category.ed * t.price). In maniera intuitiva, con questa formula, quando il prezzo aumenta, la domanda converge rapidamente a zero a causa della funzione esponenziale. Al contrario, quando il prezzo converge a zero, la domanda aumenta in modo esplosivo.

Questa forma esponenziale di risposta ai prezzi è semplicistica, e la condivisione dei parametri garantisce un alto grado di stabilità numerica anche con questa funzione esponenziale nel modello. In contesti reali, specialmente per situazioni come quella di Walmart, avremmo diverse informazioni sui prezzi, come sconti, il delta rispetto al prezzo normale, covariate che rappresentano spinte di marketing eseguite dal fornitore, o variabili categoriche che introducono elementi come le gondole. Con la programmazione differenziabile, è semplice creare risposte al prezzo arbitrariamente complesse che si adattano perfettamente alla situazione. Integrare covariate di quasi ogni tipo è molto semplice con la programmazione differenziabile.

I prodotti a lento movimento sono una realtà nel retail e in molti altri settori. Il modello fin qui introdotto ha un parametro, un grado di libertà per SKU, e ancora di più se si considerano i parametri condivisi. Tuttavia, ciò potrebbe risultare già eccessivo, soprattutto per gli SKU che ruotano solo una volta all’anno o poche volte all’anno. In tali situazioni, non possiamo neppure permetterci un grado di libertà per SKU, perciò la soluzione è basarsi esclusivamente sui parametri condivisi e rimuovere tutti i parametri che presentano gradi di libertà a livello di SKU.

Alle linee 2 e 4, introduciamo due tabelle chiamate “products” e “stores”, e la tabella “SKUs” viene costruita come una sottotabella filtrata dal prodotto cartesiano tra products e stores, che rappresenta la vera definizione di assortimento. Alle linee 15 e 16, abbiamo introdotto due parametri vettoriali condivisi: un livello in affinità con la tabella products e un altro livello in affinità con la tabella stores. Questi parametri sono anche definiti all’interno di un intervallo specifico, da 0.01 a 100, che rappresenta il valore massimo.

Ora, alla linea 18, il livello per SKU è composto dalla moltiplicazione del livello del prodotto e del livello del negozio. Il resto dello script rimane invariato. Allora, come funziona? Alla linea 19, SKU.level è uno scalare. Abbiamo il blocco autodesk che itera sulla tabella SKUs, che è la tabella delle osservazioni. Quindi, SKUs.level alla linea 18 è solo un valore scalare. Successivamente, abbiamo products.level. Dal momento che la tabella products è a monte della tabella SKUs, per ogni singolo SKU c’è una ed una sola riga nella tabella products. Di conseguenza, products.level è semplicemente un numero scalare. Lo stesso vale per la tabella stores, che anch’essa è a monte della tabella SKUs. Alla linea 18, c’è un solo store associato a questo specifico SKU. Pertanto, ciò che otteniamo è la moltiplicazione di due valori scalari, che ci dà il SKU.level. Il resto del modello rimane invariato.

Queste tecniche offrono una prospettiva completamente nuova sull’affermazione che a volte non ci sono dati sufficienti o che i dati siano troppo scarsi. Infatti, dalla prospettiva della programmazione differenziabile, tali affermazioni non hanno nemmeno un reale senso. Non esiste il concetto di dati troppo pochi o di dati eccessivamente scarsi, almeno non in termini assoluti. Esistono soltanto modelli che possono essere modificati in direzione della scarsità, e possibilmente verso una scarsità estrema. La struttura imposta è come delle rotaie guida che rendono il processo di apprendimento non solo possibile, ma anche numericamente stabile.

Rispetto ad altre tecniche di machine learning che cercano di far scoprire al modello tutti i pattern ex nihilo, questo approccio strutturato stabilisce la struttura stessa che dobbiamo apprendere. Di conseguenza, il meccanismo statistico in gioco qui ha una libertà limitata su ciò che deve essere appreso. In termini di efficienza dei dati, quindi, può essere incredibilmente efficiente. Naturalmente, tutto ciò dipende dal fatto che abbiamo scelto la struttura giusta.

Come si può vedere, sperimentare è molto semplice. Stiamo già facendo qualcosa di molto complicato, e in meno di 50 righe potremmo gestire una situazione piuttosto complessa, simile a quella di Walmart. Questo è davvero un risultato notevole. C’è un po’ di processo empirico, ma la realtà è che non si tratta di molto. Parliamo di poche decine di righe. Tenete presente che un ERP come quello che gestisce una grande azienda o una vasta rete retail ha tipicamente mille tabelle e 100 campi per tabella. Quindi, chiaramente, la complessità dei sistemi aziendali è assolutamente gigantesca rispetto alla complessità di questo modello predittivo strutturato. Se dobbiamo dedicare un po’ di tempo alle iterazioni, è praticamente trascurabile.

Inoltre, come dimostrato nella competizione di forecasting M5, la realtà è che i supply chain practitioners conoscono già i pattern. Quando il team M5 ha utilizzato tre pattern calendaristici – il giorno della settimana, il mese dell’anno e il giorno del mese – tutti questi pattern erano evidenti per qualsiasi esperto supply chain practitioner. La realtà nella supply chain è che non stiamo cercando di scoprire qualche pattern nascosto. Il fatto che, per esempio, abbassando drasticamente il prezzo la domanda aumenti in modo massiccio, non sorprenderà nessuno. L’unica questione che rimane è qual è esattamente l’entità dell’effetto e qual è la forma precisa della risposta. Questi sono dettagli relativamente tecnici e, se vi concedete l’opportunità di fare qualche esperimento, potrete affrontare questi problemi con relativa facilità.

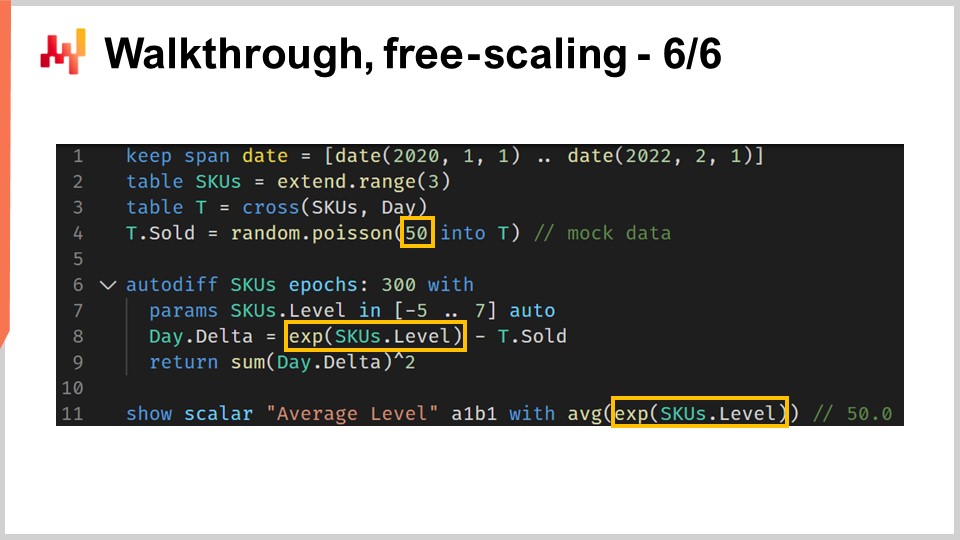
Come ultimo passaggio di questa guida, vorrei evidenziare una piccola stranezza della programmazione differenziabile. La programmazione differenziabile non va confusa con un generico risolutore di ottimizzazione matematica. Dobbiamo tenere presente che è in corso una discesa del gradiente. Più specificamente, l’algoritmo usato per ottimizzare e aggiornare i parametri ha una velocità massima di discesa pari al tasso di apprendimento fornito dall’algoritmo ADAM. In Envision, il tasso di apprendimento predefinito è 0.01.

Se osserviamo il codice, alla linea 4 abbiamo introdotto un’inizializzazione in cui le quantità vendute sono campionate da una distribuzione di Poisson con una media di 50. Se vogliamo apprendere un livello, tecnicamente, dovremmo avere un livello dell’ordine di 50. Tuttavia, quando eseguiamo un’inizializzazione automatica del parametro, partiamo da un valore intorno a uno, e possiamo aumentare solo in incrementi di 0.01. Ci vorrebbero qualcosa come 5.000 epoche per raggiungere effettivamente questo valore di 50. Poiché abbiamo un parametro non condiviso, SKU.level, questo parametro viene toccato una sola volta per epoca. Pertanto, sarebbero necessarie 5.000 epoche, rallentando inutilmente il calcolo.

Potremmo aumentare il tasso di apprendimento per accelerare la discesa, il che sarebbe una soluzione. Tuttavia, non consiglierei di gonfiare il tasso di apprendimento, in quanto solitamente non è il modo giusto per affrontare il problema. In una situazione reale, avremmo parametri condivisi oltre a questo parametro non condiviso. Questi parametri condivisi verrebbero aggiornati dalla discesa del gradiente stocastico molte volte durante ogni epoca. Se aumentate eccessivamente il tasso di apprendimento, rischiate di creare instabilità numeriche per i parametri condivisi. Potreste accelerare il cambiamento del livello SKU, ma creare problemi di stabilità numerica per gli altri parametri.

Una tecnica migliore sarebbe utilizzare un trucco di riscalatura e incapsulare il parametro in una funzione esponenziale, che è esattamente ciò che viene fatto alla linea 8. Con questo wrapper, possiamo ora raggiungere valori di parametro per il livello che possono essere sia molto bassi che molto alti con un numero di epoche molto minore. Questa stranezza è fondamentalmente l’unica anomalia che avrei bisogno di introdurre per avere un esempio realistico in questa guida sulla previsione della domanda nel retail. Tutto considerato, si tratta di una piccola stranezza. Tuttavia, è un promemoria che la programmazione differenziabile richiede attenzione al flusso dei gradienti. La programmazione differenziabile offre un’esperienza di progettazione fluida nel complesso, ma non è magia.

Alcune considerazioni finali: i modelli strutturati ottengono effettivamente una precisione all’avanguardia nelle previsioni. Questo punto è stato ampiamente evidenziato nella lezione precedente. Tuttavia, basandomi sugli elementi presentati oggi, sostengo che l’accuratezza non sia neppure il fattore decisivo a favore della programmazione differenziabile con un modello parametrico strutturato. Quello che otteniamo è comprensione; non ci limitiamo a ottenere un pezzo di software in grado di fare previsioni, ma acquisiamo anche intuizioni dirette sui pattern che stiamo cercando di catturare. Ad esempio, il modello introdotto oggi ci fornirebbe direttamente una previsione della domanda che include pesi espliciti per i giorni della settimana e un’esplicita elasticità della domanda. Se volessimo estendere questa previsione, ad esempio, per introdurre un aumento associato al Black Friday, un evento quasi-stagionale che non si verifica ogni anno nello stesso periodo, potremmo farlo. Basterebbe aggiungere un fattore, e si otterrebbe una stima dell’incremento del Black Friday isolata da tutti gli altri pattern, come quello del giorno della settimana. Questo è di primaria importanza.

Quello che otteniamo con l’approccio strutturato è comprensione, ed è molto più del semplice modello grezzo. Ad esempio, se dovessimo ottenere un’elasticità negativa, una situazione in cui il modello suggerisce che aumentando il prezzo la domanda aumenta, in un contesto simile a quello di Walmart, si tratta di un risultato molto dubbio. Molto probabilmente, ciò riflette il fatto che l’implementazione del modello è difettosa, oppure che ci sono problemi profondi in atto. Indipendentemente da ciò che indica la metrica di accuratezza, se vi trovate in una situazione tipo Walmart in cui un risultato suggerisce che rendendo un prodotto più costoso le persone ne acquistino di più, dovreste mettere seriamente in discussione l’intera vostra pipeline di dati, perché probabilmente c’è qualcosa di molto sbagliato. Questo è ciò che significa avere comprensione.

Anche, il modello è aperto al cambiamento. La programmazione differenziabile è incredibilmente espressiva. Il modello che abbiamo è solo un’iterazione in un percorso. Se il mercato viene trasformato o se la stessa azienda viene trasformata, possiamo essere certi che il modello che abbiamo sarà in grado di catturare questa evoluzione in modo naturale. Non esiste un’evoluzione automatica; ci vorrà l’impegno di un Supply Chain Scientist per catturare questa evoluzione. Tuttavia, ci si può aspettare che questo impegno sia relativamente minimo. In sostanza, se hai un modello molto piccolo e ordinato, allora quando dovrai rivederlo in seguito per aggiustarne la struttura, sarà un compito relativamente contenuto rispetto a una situazione in cui il tuo modello sarebbe una vera bestia ingegneristica.

Quando, se ingegnerizzati con cura, i modelli prodotti con la programmazione differenziabile risultano essere molto stabili. La stabilità si riduce alla scelta della struttura. Essa non è scontata per nessun programma che ottimizzi attraverso la programmazione differenziabile; è qualcosa che ottieni quando disponi di una struttura molto chiara in cui i parametri hanno un significato specifico. Per esempio, se hai un modello in cui, ogni volta che lo riaddestri, ottieni pesi completamente differenti per i giorni della settimana, allora la realtà del tuo business non sta cambiando così rapidamente. Se esegui il modello due volte, dovresti ottenere valori per i giorni della settimana abbastanza stabili. Se non dovesse essere così, allora c’è qualcosa di molto sbagliato nel modo in cui hai modellato la tua domanda. Quindi, se fai una scelta saggia per la struttura del tuo modello, puoi ottenere risultati numerici incredibilmente stabili. In questo modo, evitiamo insidie che tendono a colpire i complessi modelli di machine learning quando cerchiamo di impiegarli in un contesto di supply chain. Infatti, dalla prospettiva della supply chain, le instabilità numeriche sono letali perché si innescano effetti a scatto ovunque. Se possiedi una stima della domanda che fluttua, significa che, casualmente, attiverai un ordine d’acquisto o un ordine di produzione senza motivo. Una volta attivato il tuo ordine di produzione, non puoi decidere la settimana successiva che è stato un errore e che non avresti dovuto farlo. Rimarrai vincolato alla decisione appena presa. Se hai un estimatore della domanda futura che continua a fluttuare, finirai per ottenere riapprovvigionamento e ordini di produzione gonfiati. Questo problema può essere risolto garantendo la stabilità, che è una questione di design.

Uno dei maggiori ostacoli per mettere il machine learning in produzione è la fiducia. Quando operi con milioni di euro o dollari, comprendere cosa succede nella tua ricetta numerica è fondamentale. Gli errori nella supply chain possono risultare estremamente costosi, e ci sono numerosi esempi di disastri nella supply chain causati dalla scorretta applicazione di algoritmi poco compresi. Sebbene la programmazione differenziabile sia molto potente, i modelli che possono essere ingegnerizzati sono incredibilmente semplici. Questi modelli potrebbero essere eseguiti in un spreadsheet di Excel, poiché sono tipicamente modelli moltiplicativi lineari con ramificazioni e funzioni. L’unico aspetto che non potrebbe essere eseguito in un foglio Excel è la differenziazione automatica e, ovviamente, se hai milioni di SKU, non tentare di farlo in un foglio di calcolo. Tuttavia, in termini di semplicità, è perfettamente compatibile con ciò che inseriresti in un foglio di calcolo. Questa semplicità è fondamentale per stabilire fiducia e portare il machine learning in produzione, invece di lasciarlo come un prototipo sofisticato a cui le persone non riescono mai a fidarsi completamente.

Infine, quando mettiamo insieme tutte queste proprietà, otteniamo una tecnologia molto precisa. Questo aspetto è stato discusso nel primissimo capitolo di questa serie di lezioni. Vogliamo trasformare tutti gli sforzi investiti nella supply chain in investimenti capitalisti, anziché trattare gli esperti e i professionisti della supply chain come consumabili che devono fare sempre le stesse cose. Con questo approccio, possiamo considerare tutti questi sforzi come investimenti che genereranno e continueranno a generare ritorni sull’investimento nel tempo. La programmazione differenziabile si integra molto bene con questa prospettiva capitalistica per la supply chain.

Nel secondo capitolo, abbiamo introdotto una lezione importante intitolata “Experimental Optimization”, che ha fornito una possibile risposta alla domanda semplice ma fondamentale: cosa significa migliorare o fare meglio in una supply chain? La prospettiva della programmazione differenziabile offre un’intuizione molto specifica su molte delle difficoltà affrontate dai professionisti della supply chain. I software vendors aziendali solitamente incolpano i dati scadenti per i loro fallimenti nella supply chain. Tuttavia, credo che questo sia semplicemente il modo sbagliato di analizzare il problema. I dati sono quel che sono. Il tuo ERP non è mai stato ingegnerizzato per la data science, ma ha funzionato senza intoppi per anni, se non decenni, e le persone in azienda riescono comunque a gestire la supply chain. Anche se il tuo ERP, che cattura i dati sulla supply chain, non è perfetto, va bene così. Se ti aspetti che siano disponibili dati perfetti, questo è solo un desiderio irrealizzabile. Stiamo parlando di supply chain; il mondo è molto complesso, quindi i sistemi sono imperfetti. Realisticamente, non disponi di un solo sistema aziendale; ne hai circa mezza dozzina, e non sono completamente coerenti tra loro. Questo è un dato di fatto. Tuttavia, quando i vendor aziendali incolpano i dati scadenti, la realtà è che viene utilizzato un modello di previsione molto specifico dal fornitore, e questo modello è stato ingegnerizzato con un insieme particolare di assunzioni sull’azienda. Il problema è che se la tua azienda viola anche solo una di queste assunzioni, la tecnologia crolla completamente. In questa situazione, hai un modello di previsione basato su assunzioni irragionevoli; fornisci i dati, che non sono perfetti, e di conseguenza la tecnologia fallisce. È del tutto irragionevole dire che la colpa sia dell’azienda. La tecnologia in colpa è quella spinta dal vendor che formula assunzioni completamente irrealistiche su quali dati possano persino esistere in un contesto di supply chain.

Non ho presentato alcun benchmark per nessuna metrica di accuratezza oggi. Tuttavia, la mia proposta è che quelle metriche sono per lo più irrilevanti. Un modello predittivo è uno strumento per guidare le decisioni. Ciò che conta è se quelle decisioni — cosa acquistare, cosa produrre, se aumentare o diminuire il prezzo — sono buone o cattive. È vero che decisioni errate possono essere ricondotte al modello predittivo. Tuttavia, nella maggior parte dei casi, non si tratta di un problema di accuratezza. Per esempio, avevamo un modello di previsione delle vendite e abbiamo corretto l’aspetto dello stock out che non era gestito in modo corretto. Ma correggendo quell’aspetto, abbiamo di fatto corretto la metrica di accuratezza stessa. Quindi, sistemare il modello predittivo non significa migliorare l’accuratezza; molto spesso significa rivedere letteralmente il problema e la prospettiva in cui operi, modificando così la metrica di accuratezza o qualcosa di ancor più profondo. Il problema con la prospettiva classica è che essa presume che la metrica di accuratezza sia un obiettivo da perseguire. Non è del tutto così.

Le supply chain operano in un mondo reale, e ci sono molti eventi inaspettati e persino anomali. Per esempio, può verificarsi un’ostruzione del Canale di Suez a causa di una nave; questo è un evento completamente anomalo. In una situazione del genere, verrebbero immediatamente invalidati tutti i modelli di previsione dei tempi di consegna esistenti che considerano quella parte del mondo. Ovviamente, questo è qualcosa che non era mai accaduto prima, quindi non possiamo davvero fare backtest in una simile situazione. Tuttavia, anche se ci troviamo in una situazione eccezionale con una nave che blocca il Canale di Suez, possiamo comunque sistemare il modello, almeno se adottiamo questo tipo di approccio white-box che propongo oggi. Questa correzione comporterà un certo grado di approssimazione, il che va bene. È meglio essere approssimativamente corretti piuttosto che esattamente sbagliati. Per esempio, se consideriamo il blocco del Canale di Suez, puoi semplicemente dire: “aggiungiamo un mese al tempo di consegna per tutte le forniture che dovevano transitare per questa rotta.” Questa è una stima molto approssimativa, ma è meglio presumere che non ci saranno ritardi, pur avendo già l’informazione. Inoltre, il cambiamento spesso proviene dall’interno. Per esempio, consideriamo una rete di vendita al dettaglio che dispone di un vecchio centro di distribuzione e di uno nuovo che serve una dozzina di negozi. Supponiamo che ci sia in corso una migrazione, in cui sostanzialmente le forniture per i negozi vengono trasferite dal vecchio centro al nuovo. Questa situazione si verifica quasi una sola volta nella storia di quel determinato retailer e non può essere facilmente back-testata. Eppure, con un approccio come la programmazione differenziabile, è del tutto semplice implementare un modello che si adatti a questa migrazione graduale.

In conclusione, la programmazione differenziabile è una tecnologia che ci fornisce un approccio per strutturare le nostre intuizioni sul futuro. Essa ci permette di modellare, in maniera letterale, il modo in cui osserviamo il futuro. La programmazione differenziabile riguarda il lato della percezione di questo quadro. Basandoci su questa percezione, possiamo prendere decisioni migliori per le supply chain, e quelle decisioni guidano le azioni che si collocano nell’altro ambito. Uno dei fraintendimenti più grandi della teoria tradizionale della supply chain è che si possano trattare la percezione e l’azione come componenti strettamente isolate. Questo si manifesta, ad esempio, con un team incaricato della pianificazione (cioè la percezione) e un team indipendente incaricato del riapprovvigionamento (cioè l’azione).

Tuttavia, il ciclo di feedback percezione-azione è estremamente importante; è di importanza primaria. Questo è letteralmente il meccanismo che ti guida verso una percezione corretta. Senza questo ciclo di feedback, non è nemmeno chiaro se stai osservando la cosa giusta o se ciò che osservi è davvero ciò che pensi. Hai bisogno di questo meccanismo di feedback ed è grazie a esso che puoi guidare i tuoi modelli verso una valutazione quantitativa corretta del futuro, rilevante per le azioni da intraprendere nella tua supply chain. Gli approcci tradizionali della supply chain tendono a ignorare quasi completamente questo aspetto perché, sostanzialmente, credo siano bloccati in una forma molto rigida di previsione. Questa modalità, incentrata sul modello, può consistere in un modello datato, come il modello di previsione Holt-Winters, o in uno più recente come Facebook Prophet. La situazione è la stessa: se sei vincolato a un solo modello di previsione, tutto il feedback che puoi raccogliere dal lato azione diventa inutile, poiché non puoi fare nulla se non ignorarlo completamente.

Se sei vincolato a un determinato modello di previsione, non puoi riformattare o ristrutturare il tuo modello man mano che ricevi informazioni dal lato azione. D’altra parte, la programmazione differenziabile, con il suo approccio di modellizzazione strutturata, ti offre un paradigma completamente diverso. Il modello predittivo è del tutto usa e getta—tutto. Se il feedback che ricevi dalle azioni richiede cambiamenti radicali nella tua prospettiva predittiva, allora implementa semplicemente quei cambiamenti radicali. Non esiste alcun attaccamento specifico a una determinata iterazione del modello. Mantenere il modello molto semplice è essenziale per assicurarsi che, una volta in produzione, tu possa continuare a modificarlo. Perché, ancora una volta, se ciò che hai ingegnerizzato è come una bestia, un mostro ingegneristico, allora una volta in produzione diventa incredibilmente difficile da cambiare. Uno degli aspetti chiave è che, se desideri poter continuare a modificare, devi avere un modello molto parsimonioso in termini di righe di codice e complessità interna. Ed è qui che la programmazione differenziabile brilla. Non si tratta di raggiungere una maggiore accuratezza; si tratta di ottenere una rilevanza superiore. Senza rilevanza, tutte le metriche di accuratezza diventano del tutto irrilevanti. La programmazione differenziabile e la modellizzazione strutturata ti offrono il percorso per raggiungere la rilevanza e mantenerla nel tempo.

Questo concluderà la lezione di oggi. La prossima volta, il due marzo, alla stessa ora, alle 15:00 ora di Parigi, presenterò la modellizzazione probabilistica per la supply chain. Esamineremo più da vicino le implicazioni tecniche di considerare tutti i futuri possibili anziché sceglierne uno solo e dichiararlo quello giusto. Infatti, considerare tutti i futuri possibili è molto importante se vuoi che la tua supply chain sia effettivamente resiliente contro il rischio. Se ne scegli uno solo, è una ricetta per finire con qualcosa di incredibilmente fragile se la tua previsione non dovesse essere perfettamente corretta. E, indovina un po’, la previsione non è mai completamente corretta. Ecco perché è fondamentale abbracciare l’idea che bisogna considerare tutti i futuri possibili, e vedremo come farlo con moderne ricette numeriche.

Domanda: Il rumore stocastico viene aggiunto per evitare minimi locali, ma come viene sfruttato o scalato per evitare grandi deviazioni in modo che il gradient descent non venga spinto troppo lontano dal suo obiettivo?

Questa è una domanda molto interessante, e la risposta si articola in due parti.

In primo luogo, è per questo che l’algoritmo Adam è molto conservativo in termini di ampiezza dei movimenti. Il gradiente è fondamentalmente illimitato; può avere valori dell’ordine delle migliaia o milioni. Tuttavia, con Adam, il passo massimo è effettivamente limitato superiormente dal tasso di apprendimento. Quindi, in sostanza, Adam incorpora una ricetta numerica che impone letteralmente un passo massimo, e si spera che ciò eviti enormi instabilità numeriche.

Ora, se a caso, nonostante il fatto che abbiamo questo tasso di apprendimento, potremmo dire che, per pura fluttuazione, ci muoveremo iterativamente, un passo alla volta, ma molte volte in una direzione sbagliata, e questa è una possibilità. Per questo dico che lo stochastic gradient descent non è ancora del tutto compreso. Funziona incredibilmente bene in pratica, ma perché funzioni così bene, perché converga così rapidamente e perché non si verifichino più problemi di quelli potenziali, non è del tutto chiaro, soprattutto se consideri che lo stochastic gradient descent avviene in spazi ad alta dimensione. Quindi, in genere, hai letteralmente decine, se non centinaia, di parametri che vengono modificati ad ogni passo. L’intuizione che puoi avere in due o tre dimensioni è molto fuorviante; le cose si comportano in modo molto diverso quando guardi a dimensioni superiori.

Quindi, il succo della questione è: è molto rilevante. Da un lato c’è quella magia di Adam che è molto conservativa nella scala dei passi del gradiente, e dall’altro c’è quella parte, poco compresa, ma che in pratica funziona molto bene. A proposito, credo che il fatto che lo stochastic gradient descent non sia del tutto intuitivo sia anche la ragione per cui, per quasi 70 anni, questa tecnica è stata conosciuta ma non riconosciuta come efficace. Per quasi 70 anni, la gente sapeva che esisteva, ma era molto scettica. Ci è voluto il successo massiccio del deep learning perché la comunità riconoscesse e ammettesse che in realtà funziona molto bene, anche se non capiamo davvero il perché.

Question: Come si capisce quando un determinato pattern è debole e quindi dovrebbe essere rimosso dal modello?

Ancora una domanda molto valida. Non esiste un criterio rigoroso; è letteralmente una scelta discrezionale da parte dello supply chain scientist. Il motivo è che, se il pattern che introduci apporta benefici minimi, ma in termini di modellazione si tratta solo di due righe di codice e l’impatto in termini di tempo computazionale è insignificante, e se mai volessi rimuovere il pattern in seguito risulta semi-triviale, potresti pensare: “Beh, posso semplicemente lasciarlo. Non sembra arrecare danni, non offre molti benefici. Posso immaginare situazioni in cui questo pattern, attualmente debole, potrebbe effettivamente diventare forte.” In termini di manutenibilità, va bene così.

Tuttavia, puoi anche considerare l’altro lato della medaglia, in cui hai un pattern che non cattura molto e aggiunge un notevole carico computazionale al modello. Quindi non è gratuito; ogni volta che aggiungi un parametro o una logica, aumenti la quantità di risorse di calcolo necessarie per il tuo modello, rendendolo più lento e meno gestibile. Se pensi che questo pattern, attualmente debole, potrebbe effettivamente diventare forte, ma in modo negativo, generando instabilità e creando scompiglio nella modellazione predittiva, questa è tipicamente la situazione in cui penseresti: “No, probabilmente dovrei rimuoverlo.”

Vedi, si tratta davvero di una questione di scelta discrezionale. La differentiable programming è una cultura; non sei da solo. Hai colleghi e pari che magari hanno provato cose diverse da Lokad. Questo è il tipo di cultura che cerchiamo di coltivare. So che può risultare un po’ deludente rispetto alla prospettiva dell’IA onnipotente, l’idea che potremmo avere un’intelligenza artificiale tutto-potente che risolve tutti quei problemi per noi. Ma la realtà è che le supply chain sono così complesse, e le nostre tecniche di intelligenza artificiale così grezze, che non abbiamo nessun sostituto realistico per l’intelligenza umana. Quando dico “scelta discrezionale”, intendo dire che serve una sana dose di intelligenza applicata, molto umana, al caso, perché tutti i trucchi algoritmici non si avvicinano nemmeno a fornire una risposta soddisfacente.

Tuttavia, ciò non significa che non si possa progettare qualche tipo di strumento. Sarebbe un altro argomento; vedrò se tratterò effettivamente il tipo di strumenti che forniamo da Lokad per facilitare il design. Un pattern tangenziale sarebbe, se dobbiamo prendere una decisione discrezionale, cercare di fornire tutta l’instrumentation in modo che questa scelta possa essere fatta molto rapidamente, minimizzando il dolore che accompagna questo tipo di indecisione in cui lo supply chain scientist deve decidere qualcosa sul destino dello stato attuale del modello.

Question: Qual è la soglia di complessità di una supply chain dopo la quale il machine learning e la programmazione differenziabile portano risultati notevolmente migliori?

Da Lokad, normalmente riusciamo a ottenere risultati sostanziali per aziende che hanno un fatturato di 10 milioni di dollari all’anno e oltre. Direi che inizia davvero a brillare se possiedi un’azienda con un fatturato annuo di 50 milioni di dollari e oltre.

La ragione è che, fondamentalmente, devi stabilire una pipeline di dati molto affidabile. Devi essere in grado di estrarre tutti i dati rilevanti dall’ERP su base giornaliera. Non intendo dire che i dati saranno buoni o cattivi, semplicemente i dati a tua disposizione possono presentare numerosi difetti. Tuttavia, questo significa che occorre fare molta opera di integrazione solo per poter estrarre quotidianamente le transazioni più basilari. Se l’azienda è troppo piccola, solitamente non hanno nemmeno un dipartimento IT, e non riescono a garantire un’estrazione quotidiana affidabile, compromettendo davvero i risultati.

Ora, in termini di verticali o complessità, il punto è che, nella maggior parte delle aziende e nelle maggiori supply chain, a mio parere, non hanno nemmeno iniziato a ottimizzare. Come ho detto, la teoria mainstream della supply chain sottolinea che dovresti cercare previsioni più accurate. Avere una percentuale ridotta di errore nella previsione è un obiettivo, e molte aziende, per esempio, lo affrontano avvalendosi di un team di pianificazione o di un team di forecasting. A mio parere, tutto ciò non aggiunge valore al business perché fondamentalmente fornisce risposte molto sofisticate a un insieme errato di domande.

Potrebbe sembrare sorprendente, ma la differentiable programming brilla davvero non perché sia fondamentalmente super potente – e lo è – ma perché di solito è la prima volta che viene implementato qualcosa di veramente rilevante per il business all’interno dell’azienda. Se vuoi un esempio, la maggior parte di ciò che viene implementato nella supply chain sono tipicamente modelli come il modello di safety stock, che hanno assolutamente zero rilevanza per una supply chain reale. Ad esempio, nel modello di safety stock, si assume che sia possibile avere un lead time negativo, nel senso che ordini ora e la consegna avvenga ieri. Non ha alcun senso, e di conseguenza i risultati operativi degli safety stock sono solitamente insoddisfacenti.

La differentiable programming si distingue per il conseguimento della rilevanza, non per una sorta di grandiosa supremazia numerica o per essere migliore rispetto ad altre tecniche alternative di machine learning. L’obiettivo è davvero quello di conseguire rilevanza in un mondo che è molto complesso, caotico, ostile, in continuo cambiamento, e dove devi affrontare un panorama applicativo semi-da incubo che rappresenta i dati da elaborare.

Sembra che non ci siano altre domande. In questo caso, immagino che ci vedremo il mese prossimo per la lezione sulla modellazione probabilistica for the supply chain.