Modélisation prédictive structurée pour Supply Chain - Lecture 5.1

00:01 Introduction
02:44 Enquête sur les besoins prédictifs
05:57 Modèles vs. Modélisation
12:26 L’histoire jusqu’ici
15:50 Un peu de théorie et un peu de pratique
17:41 Programmation Différentiable, SGD 1/6
24:56 Programmation Différentiable, autodiff 2/6
31:07 Programmation Différentiable, fonctions 3/6
35:35 Programmation Différentiable, méta-paramètres 4/6
37:59 Programmation Différentiable, paramètres 5/6
40:55 Programmation Différentiable, particularités 6/6
43:41 Explication pas à pas, prévision de la demande au détail
45:49 Explication pas à pas, calibration des paramètres 1/6
53:14 Explication pas à pas, partage des paramètres 2/6
01:04:16 Explication pas à pas, masquage de la perte 3/6
01:09:34 Explication pas à pas, intégration des covariables 4/6
01:14:09 Explication pas à pas, décomposition parcimonieuse 5/6
01:21:17 Explication pas à pas, free-scaling 6/6
01:25:14 Whiteboxing
01:33:22 Retour à l’optimisation expérimentale
01:39:53 Conclusion
01:44:40 Lecture à venir et questions du public

Description

Programmation Différentiable (DP) est un paradigme génératif utilisé pour concevoir une large classe de modèles statistiques, qui se révèlent être particulièrement adaptés aux défis prédictifs de la supply chain. DP surpasse presque toute la littérature de prévision « classique » basée sur des modèles paramétriques. DP est également supérieur aux algorithmes de machine learning « classiques » – jusqu’à la fin des années 2010 – dans pratiquement toutes les dimensions qui importent pour une utilisation pratique dans la supply chain, y compris la facilité d’adoption par les praticiens.

Transcription complète

Bienvenue dans cette série de conférences sur la supply chain. Je suis Joannes Vermorel, et aujourd’hui je vais présenter “Modélisation Prédictive Structurée avec Programmation Différentiable en Supply Chain.” Choisir la bonne ligne d’action nécessite une connaissance quantitative détaillée du futur. En effet, chaque décision – acheter plus, produire plus – reflète une certaine anticipation de l’avenir. Invariablement, la théorie dominante de la supply chain met l’accent sur la notion de prévision pour aborder ce problème. Cependant, la perspective de prévision, du moins sous sa forme classique, présente deux lacunes.

Premièrement, elle met l’accent sur une perspective de prévision limitée aux séries temporelles, qui malheureusement ne parvient pas à aborder la diversité des défis tels qu’ils se présentent dans les supply chains réelles. Deuxièmement, elle se concentre de manière étroite sur la précision des prévisions, ce qui passe en large sur l’essentiel. Gagner quelques points de pourcentage supplémentaires en précision ne se traduit pas automatiquement par une génération de dollars supplémentaires pour votre supply chain.

L’objectif de la présente conférence est de découvrir une approche alternative à la prévision, qui est en partie une technologie et en partie une méthodologie. La technologie sera la programmation différentiable, et la méthodologie consistera en des modèles prédictifs structurés. À la fin de cette conférence, vous devriez être capables d’appliquer cette approche à une situation de supply chain. Cette approche n’est pas théorique ; elle est devenue l’approche de référence chez Lokad depuis quelques années maintenant. De plus, si vous n’avez pas regardé les conférences précédentes, la présente conférence ne devrait pas être totalement incompréhensible. Toutefois, dans cette série de conférences, nous atteignons un point où il serait nettement utile de regarder les conférences dans l’ordre. Dans la présente conférence, nous revisiterons plusieurs éléments qui ont été introduits dans les conférences précédentes.

La prévision de la demande future est la candidate évidente lorsqu’il s’agit de dresser un état des besoins prédictifs pour notre supply chain. En effet, une meilleure anticipation de la demande constitue un ingrédient essentiel pour des décisions très basiques telles qu’acheter plus et produire plus. Cependant, à travers les principes de supply chain que nous avons introduits au cours du troisième chapitre de cette série de conférences, nous avons constaté qu’il existe un ensemble assez diversifié d’attentes en matière de requis prédictifs pour piloter votre supply chain.

En particulier, par exemple, les délais d’approvisionnement varient et présentent des schémas saisonniers. Pratiquement chaque décision liée aux stocks nécessite une anticipation de la demande future mais aussi des délais futurs. Ainsi, les délais d’approvisionnement doivent être prévus. Les retours représentent parfois jusqu’à la moitié du flux. C’est le cas, par exemple, pour le e-commerce de mode en Allemagne. Dans ces situations, anticiper les retours devient crucial, et ces retours varient considérablement d’un produit à l’autre. Ainsi, dans ces situations, les retours doivent être prévus.

Du côté de l’offre, la production elle-même peut varier et pas uniquement à cause des retards supplémentaires ou des délais d’approvisionnement variables. Par exemple, la production peut s’accompagner d’un certain degré d’incertitude. Cela se produit dans des secteurs à basse technologie tels que l’agriculture, mais cela peut également arriver dans des secteurs à haute technologie comme l’industrie pharmaceutique. Ainsi, les rendements de production doivent également être prévus. Enfin, le comportement des clients compte énormément. Par exemple, stimuler la demande grâce à des produits qui génèrent de l’acquisition est très important, et inversement, faire face à des ruptures de stock sur des produits qui provoquent un important taux de désabonnement lorsque ces produits se retrouvent indisponibles justement en raison de ruptures de stock, revêt également une grande importance. Ainsi, ces comportements nécessitent une analyse, une prédiction – autrement dit, ils doivent être prévus. Le point clé à retenir ici est que la prévision des séries temporelles n’est qu’une partie de l’équation. Nous avons besoin d’une approche prédictive capable d’englober toutes ces situations et plus encore, car c’est une nécessité si nous voulons disposer d’une approche susceptible de réussir face à toutes les situations que peut présenter une supply chain réelle.

L’approche de référence lorsqu’il s’agit du problème prédictif consiste à présenter un modèle. Cette approche a dominé la littérature sur la prévision des séries temporelles pendant des décennies, et c’est encore, je dirais, l’approche courante dans les cercles du machine learning de nos jours. Cette approche centrée sur le modèle, voilà comment je vais la désigner, est si omniprésente qu’il peut même être difficile de prendre du recul un instant pour évaluer ce qui se passe réellement avec cette perspective centrée sur le modèle.

Ma proposition pour cette conférence est que la supply chain nécessite une technique de modélisation, une approche centrée sur la modélisation, et qu’une série de modèles, si exhaustive soit-elle, ne sera jamais suffisante pour répondre à tous nos besoins tels qu’ils se présentent dans les supply chains réelles. Clarifions cette distinction entre l’approche centrée sur le modèle et l’approche centrée sur la modélisation.

L’approche centrée sur le modèle met d’abord et avant tout l’accent sur un modèle. Le modèle se présente comme un ensemble, un ensemble de recettes numériques qui sont généralement fournies sous la forme d’un logiciel que vous pouvez effectivement exécuter. Même en l’absence de tel logiciel, l’attente est que si vous disposez d’un modèle mais pas du logiciel, le modèle doit être décrit avec une précision mathématique, permettant une réimplémentation complète du modèle. Ce package, le modèle transformé en logiciel, est censé être le but ultime.

D’un point de vue idéal, ce modèle est censé se comporter exactement comme une fonction mathématique : entrées en, résultats en sortie. S’il reste une quelconque configurabilité pour le modèle, ces éléments configurables sont alors traités comme des éléments incomplets, comme des problèmes qui ne sont pas encore résolus de manière complète. En effet, chaque option de configuration affaiblit la force du modèle. Lorsque nous avons de la configurabilité et trop d’options dans l’approche centrée sur le modèle, le modèle a tendance à se dissoudre dans un espace de modèles, et soudainement, nous ne pouvons plus vraiment effectuer de benchmark car il n’existe pas de modèle unique.

L’approche de modélisation prend une approche complètement inversée en ce qui concerne la configurabilité. Maximiser l’expressivité du modèle devient alors le but ultime. Ce n’est pas un défaut ; cela devient une caractéristique. La situation peut être assez déroutante lorsque l’on observe une perspective centrée sur la modélisation, car si nous assistons à une présentation de cette perspective, ce que nous voyons est une présentation de modèles. Cependant, ces modèles ont une intention tout à fait différente.

Si vous adoptez la perspective de la modélisation, le modèle présenté n’est qu’une illustration. Il n’a pas pour vocation d’être complet ou d’être la solution définitive au problème. Il représente simplement une étape dans le parcours visant à illustrer la technique de modélisation elle-même. Le principal défi de la technique de modélisation est que, soudainement, il devient très difficile d’évaluer l’approche. En effet, nous perdons l’option naïve du benchmark, car avec cette approche centrée sur la modélisation, nous disposons de potentialités de modèles. Nous ne nous concentrons pas spécifiquement sur un modèle par rapport à un autre ; ce n’est même pas le bon état d’esprit. Ce que nous avons, c’est une opinion éclairée.

Cependant, je tiens à souligner immédiatement que ce n’est pas parce que vous disposez d’un benchmark et de chiffres associés qui qualifient automatiquement cela de science. Les chiffres peuvent être tout simplement dénués de sens, et inversement, ce n’est pas parce qu’il s’agit simplement d’une opinion éclairée que c’est moins scientifique. D’une certaine manière, il s’agit simplement d’une approche différente, et la réalité est que, parmi les diverses communautés, ces deux approches coexistent.

Par exemple, si l’on se réfère à l’article “Forecasting at Scale”, publié par une équipe de Facebook en 2017, nous avons quelque chose qui est à peu près l’archétype de l’approche centrée sur le modèle. Dans cet article, il est présenté le modèle Facebook Prophet. Et dans un autre article, “Tensor Comprehension”, publié en 2018 par une autre équipe de Facebook, nous avons essentiellement une technique de modélisation. Cet article peut être considéré comme l’archétype de l’approche de modélisation. Ainsi, vous pouvez voir que même les équipes de recherche travaillant dans la même entreprise, pratiquement en même temps, peuvent aborder le problème d’un angle à l’autre, selon la situation.

Cette conférence fait partie d’une série de conférences sur la supply chain. Dans le premier chapitre, j’ai présenté mes points de vue sur la supply chain en tant que discipline à la fois théorique et pratique. Dès la toute première conférence, j’ai soutenu que la théorie dominante de la supply chain ne répondait pas à ses attentes. Il se trouve que la théorie dominante de la supply chain s’appuie fortement sur l’approche centrée sur le modèle, et je crois que cet aspect unique est l’une des principales causes de friction entre la théorie dominante de la supply chain et les besoins des supply chains réelles.

Dans le deuxième chapitre de cette série de conférences, j’ai présenté une série de méthodologies. En effet, les méthodologies naïves sont généralement vaincues par la nature épisodique et souvent antagoniste des situations de supply chain. En particulier, la conférence intitulée “Empirical Experimental Optimization”, qui faisait partie du deuxième chapitre, est exactement le type de perspective que j’adopte aujourd’hui dans cette conférence.

Dans le troisième chapitre, j’ai présenté une série de personae de la supply chain. Les personae représentent une focalisation exclusive sur les problèmes que nous tentons de résoudre, en écartant totalement toute solution candidate. Ces personae sont essentiels pour comprendre la diversité des défis prédictifs auxquels sont confrontées les supply chains réelles. Je pense que ces personae sont indispensables pour éviter de se retrouver enfermé dans la perspective étroite des séries temporelles, qui est la marque d’une théorie de la supply chain mise en œuvre en accordant peu d’attention aux détails concrets des supply chains réelles.

Dans le quatrième chapitre, j’ai présenté une série de sciences auxiliaires. Ces disciplines sont distinctes de la supply chain, mais une maîtrise de base de ces disciplines est essentielle pour la pratique moderne de la supply chain. Nous avons déjà abordé brièvement le sujet de la programmation différentiable dans ce quatrième chapitre, mais je vais réintroduire ce paradigme de programmation avec beaucoup plus de détails dans quelques minutes.

Enfin, dans la première conférence de ce cinquième chapitre, nous avons vu un modèle simple, certains diraient même simpliste, qui a atteint une précision de prévision de pointe lors d’une compétition de prévision mondiale qui a eu lieu en 2020. Aujourd’hui, je présente une série de techniques pouvant être utilisées pour apprendre les paramètres impliqués dans ce modèle que j’ai présenté lors de la conférence précédente.

Le reste de cette conférence se divisera globalement en deux parties, suivi de quelques réflexions finales. La première partie est consacrée à la programmation différentiable. Nous avons déjà abordé ce sujet dans le quatrième chapitre ; cependant, nous y jetterons un regard beaucoup plus approfondi aujourd’hui. À la fin de cette conférence, vous devriez être presque capables de créer votre propre implémentation de programmation différentiable. Je dis “presque” parce que vos résultats peuvent varier en fonction de la pile technologique que vous utilisez. De plus, la programmation différentiable est un art mineur à part entière ; il faut un peu d’expérience pour la faire fonctionner sans accroc en pratique.

Le second bloc de cette conférence est un tutoriel pour une situation de prévision de la demande au détail. Ce tutoriel fait suite à la conférence précédente, où nous avons présenté le modèle qui a obtenu la première place lors du concours M5 de prévision en 2020. Cependant, lors de cette présentation précédente, nous n’avons pas détaillé comment les paramètres du modèle étaient effectivement calculés. Ce tutoriel va apporter exactement cela, et nous aborderons également des éléments importants tels que les ruptures de stocks et les promotions qui n’avaient pas été traités dans la conférence précédente. Enfin, en nous appuyant sur tous ces éléments, je discuterai de mes points de vue sur l’adéquation de la programmation différentiable à des fins de supply chain.

La descente de gradient stochastique (SGD) est l’un des deux piliers de la programmation différentiable. La SGD est d’une simplicité trompeuse, et pourtant il n’est pas entièrement clair pourquoi elle fonctionne si bien. Il est tout à fait évident pourquoi elle fonctionne ; ce qui n’est pas très clair, c’est pourquoi elle fonctionne si bien.

L’histoire de la descente de gradient stochastique remonte aux années 1950, elle a donc une histoire assez longue. Cependant, cette technique n’est entrée dans le courant dominant qu’au cours de la dernière décennie avec l’avènement du deep learning. La descente de gradient stochastique est profondément ancrée dans la perspective de l’optimisation mathématique. Nous disposons d’une fonction de perte Q que nous souhaitons minimiser, et nous avons un ensemble de paramètres réels, notés W, qui représentent toutes les solutions possibles. Ce que nous voulons trouver, c’est la combinaison de paramètres W qui minimise la fonction de perte Q.

La fonction de perte Q est censée respecter une propriété fondamentale : elle peut être décomposée de manière additive en une série de termes. L’existence de cette décomposition additive permet à la descente de gradient stochastique de fonctionner. Si votre fonction de perte ne peut pas être décomposée de manière additive, alors la descente de gradient stochastique ne s’applique pas en tant que technique. Dans cette perspective, X représente l’ensemble de tous les termes qui contribuent à la fonction de perte, et Qx représente une perte partielle, c’est-à-dire la perte associée à l’un de ces termes dans cette vision de la fonction de perte comme somme de termes partiels.

Bien que la descente de gradient stochastique ne soit pas spécifique aux situations d’apprentissage, elle s’adapte très bien à tous les cas d’usage de l’apprentissage, et par apprentissage, j’entends l’apprentissage dans le cadre du machine learning. En effet, si nous disposons d’un jeu de données d’entraînement, celui-ci prendra la forme d’une liste d’observations, chaque observation étant une paire de caractéristiques représentant l’entrée du modèle et des étiquettes représentant les sorties. Essentiellement, ce que nous recherchons, du point de vue de l’apprentissage, c’est de concevoir un modèle qui performe au mieux sur l’erreur empirique et d’autres aspects observés dans ce jeu de données d’entraînement. Dans cette optique, X serait en réalité la liste des observations, et les paramètres seraient ceux d’un modèle de machine learning que nous essayons d’optimiser pour mieux correspondre à ce jeu de données.

La descente de gradient stochastique est fondamentalement un processus itératif qui parcourt aléatoirement les observations, une observation à la fois. Nous choisissons une observation, un petit X, à la fois, et pour cette observation, nous calculons un gradient local, représenté par nabla de Qx. Il s’agit simplement d’un gradient local qui ne s’applique qu’à un terme de la fonction de perte. Ce n’est pas le gradient de la fonction de perte complète, mais un gradient local qui ne s’applique qu’à un terme de la fonction de perte – vous pouvez le considérer comme un gradient partiel.

Une étape de la descente de gradient stochastique consiste à prendre ce gradient local et à ajuster légèrement les paramètres W en se basant sur cette observation partielle du gradient. C’est exactement ce qui se passe ici, avec W mis à jour selon W moins eta multiplié par nabla QxW. Cela signifie simplement, de manière très concise, pousser le paramètre W dans la direction du gradient très local obtenu avec X, où X n’est qu’une des observations de votre jeu de données, si nous abordons un problème d’apprentissage. Ensuite, nous procédons de manière aléatoire, en appliquant ce gradient local et en itérant.

Intuitivement, la descente de gradient stochastique fonctionne très bien car elle présente un compromis entre une itération plus rapide et des gradients plus bruyants, conduisant à une itération plus granulaire et donc plus rapide. L’essence de la descente de gradient stochastique est que nous ne nous soucions pas d’avoir des mesures très imparfaites de nos gradients tant que nous pouvons les obtenir extrêmement rapidement. Si nous pouvons pousser ce compromis vers une itération plus rapide, même au prix de gradients plus bruyants, faisons-le. C’est pourquoi la descente de gradient stochastique est si efficace pour minimiser la quantité de ressources informatiques nécessaires afin d’atteindre une certaine qualité de solution pour le paramètre W.

Enfin, nous avons la variable eta, qui est appelée le taux d’apprentissage. En pratique, le taux d’apprentissage n’est pas constant ; cette variable varie pendant l’exécution de la descente de gradient stochastique. Chez Lokad, nous utilisons l’algorithme Adam pour contrôler l’évolution de ce paramètre eta du taux d’apprentissage. Adam est une méthode publiée en 2014, et elle est très populaire dans les cercles du machine learning chaque fois que la descente de gradient stochastique est utilisée.

Le deuxième pilier de la programmation différentiable est la différentiation automatique. Nous avons déjà abordé ce concept dans une conférence précédente. Revenons sur ce concept en examinant un extrait de code. Ce code est écrit en Envision, un langage de programmation spécifique élaboré par Lokad dans le but de l’optimisation prédictive des supply chains. Je choisis Envision car, comme vous le verrez, les exemples sont beaucoup plus concis et, espérons-le, bien plus clairs que dans des présentations alternatives si j’utilisais Python, Java ou C#. Toutefois, je tiens à souligner que même si j’utilise Envision, il n’y a pas de formule secrète. Vous pourriez entièrement réimplémenter tous ces exemples dans d’autres langages de programmation. Cela multiplierait sans doute le nombre de lignes de code par un facteur de 10, mais dans le grand schéma des choses, ce n’est qu’un détail. Ici, pour une conférence, Envision nous offre une présentation très claire et concise.

Voyons comment la programmation différentiable peut être utilisée pour aborder une régression linéaire. Il s’agit d’un problème pédagogique ; nous n’avons pas besoin de la programmation différentiable pour effectuer une régression linéaire. Le but est simplement de se familiariser avec la syntaxe de la programmation différentiable. De la ligne 1 à la ligne 6, nous déclarons la table T, qui représente la table d’observation. Quand je dis table d’observation, rappelez-vous simplement de l’ensemble X de la descente de gradient stochastique. C’est exactement la même chose. Cette table comporte deux colonnes, une caractéristique notée X et une étiquette notée Y. Ce que nous voulons, c’est prendre X en entrée et être capables de prédire Y avec un modèle linéaire, ou plus précisément, un modèle affine. Évidemment, nous avons seulement quatre points de données dans cette table T. Il s’agit d’un jeu de données ridiculement petit ; c’est juste pour la clarté de l’exposé.

À la ligne 8, nous introduisons le bloc autodiff. Le bloc autodiff peut être vu comme une boucle en Envision. C’est une boucle qui itère sur une table, dans ce cas, la table T. Ces itérations reflètent les étapes de la descente de gradient stochastique. Ainsi, ce qui se passe lorsque l’exécution d’Envision entre dans ce bloc autodiff, c’est que nous avons une série d’exécutions répétées où nous sélectionnons des lignes de la table d’observations, puis appliquons les étapes de la descente de gradient stochastique. Pour ce faire, nous avons besoin des gradients.

D’où viennent les gradients ? Ici, nous avons écrit un programme, une petite expression de notre modèle, Ax + B. Nous introduisons la fonction de perte, qui est l’erreur quadratique moyenne. Nous voulons obtenir le gradient. Pour une situation aussi simple que celle-ci, nous pourrions écrire le gradient manuellement. Cependant, la différentiation automatique est une technique qui permet de compiler un programme sous deux formes : la première étant l’exécution avant du programme, et la seconde étant l’exécution inverse qui calcule les gradients associés à tous les paramètres présents dans le programme.

Aux lignes 9 et 10, nous avons la déclaration de deux paramètres, A et B, avec le mot-clé “auto” qui indique à Envision de procéder à une initialisation automatique pour les valeurs de ces deux paramètres. A et B sont des valeurs scalaires. La différentiation automatique s’effectue pour tous les programmes contenus dans ce bloc autodiff. Essentiellement, c’est une technique au niveau du compilateur qui compile ce programme deux fois : une fois pour la passe avant et une seconde fois pour un programme qui fournira les valeurs des gradients. La beauté de la différentiation automatique est qu’elle garantit que la quantité de CPU nécessaire pour calculer le programme régulier est alignée avec celle nécessaire pour calculer le gradient lors de la passe inverse. C’est une propriété très importante. Enfin, à la ligne 14, nous affichons les paramètres que nous venons d’apprendre grâce au bloc autodiff ci-dessus.

La programmation différentiable brille vraiment en tant que paradigme de programmation. Il est possible de composer un programme d’une complexité arbitraire et d’en obtenir la différentiation automatique. Ce programme peut inclure des branchements et des appels de fonctions, par exemple. Cet exemple de code reprend la fonction de perte pinball que nous avons introduite dans la conférence précédente. La fonction de perte pinball peut être utilisée pour dériver des estimations de quantiles lorsqu’on observe des écarts par rapport à une distribution de probabilité empirique. Si vous minimisez l’erreur quadratique moyenne avec votre estimation, vous obtenez une estimation de la moyenne de votre distribution empirique. Si vous minimisez la fonction de perte pinball, vous obtenez une estimation d’une cible de quantile. Si vous visez un 90ème quantile, cela signifie que c’est la valeur dans votre distribution de probabilité pour laquelle la valeur future à observer a 90 % de chances d’être inférieure à votre estimation si vous avez une cible de 90 %, ou 10 % de chances d’être supérieure. Cela rappelle l’analyse des taux de service qui existe en supply chain.

Aux lignes 1 et 2, nous introduisons une table d’observations remplie d’écarts échantillonnés de manière aléatoire à partir d’une distribution de Poisson. Les valeurs de la distribution de Poisson sont échantillonnées avec une moyenne de 3, et nous obtenons 10 000 écarts. Aux lignes 4 et 5, nous déployons notre implémentation sur mesure de la fonction de perte pinball. Cette implémentation est presque identique au code que j’ai présenté dans la conférence précédente. Cependant, le mot-clé “autodiff” est désormais ajouté à la déclaration de la fonction. Ce mot-clé, lorsqu’il est attaché à la déclaration de la fonction, garantit que le compilateur Envision peut différencier automatiquement cette fonction. Bien qu’en théorie, la différentiation automatique puisse être appliquée à n’importe quel programme, en pratique, il existe de nombreux programmes pour lesquels la différentiation n’a pas de sens ou de nombreuses fonctions pour lesquelles cela n’aurait pas de sens. Par exemple, considérez une fonction qui prend deux valeurs textuelles et les concatène. D’un point de vue de la différentiation automatique, il n’a pas de sens d’appliquer la différentiation automatique à ce type d’opération. La différentiation automatique requiert que des nombres soient présents dans les entrées et les sorties des fonctions que vous essayez de différencier.

Aux lignes 7 à 9, nous avons le bloc autodiff, qui calcule l’estimation du quantile cible pour la distribution empirique recueillie via la table d’observations. En réalité, il s’agit d’une distribution de Poisson. L’estimation du quantile est déclarée comme un paramètre nommé “quantile” à la ligne 8, et à la ligne 9, nous effectuons un appel de fonction à notre propre implémentation de la fonction de perte pinball. La cible de quantile est fixée à 0,5, ce qui signifie que nous recherchons en réalité une estimation médiane de la distribution. Enfin, à la ligne 11, nous affichons les résultats pour la valeur que nous avons apprise grâce à l’exécution du bloc autodiff. Cet extrait de code illustre comment un programme que nous allons différencier automatiquement peut inclure à la fois un appel de fonction et une branche, et tout cela peut se faire de manière entièrement automatique.

J’ai dit que les blocs autodiff pouvaient être interprétés comme une boucle qui effectue une série d’étapes de descente de gradient stochastique (SGD) sur la table d’observations, en sélectionnant une ligne de cette table à la fois. Cependant, je suis resté assez évasif sur la condition d’arrêt dans cette situation. Quand la descente de gradient stochastique s’arrête-t-elle dans Envision ? Par défaut, la descente de gradient stochastique s’arrête après 10 époques. Une époque, dans la terminologie du machine learning, représente un passage complet à travers la table d’observations. À la ligne 7, un attribut nommé “epochs” peut être attaché aux blocs autodiff. Cet attribut est optionnel ; par défaut, la valeur est 10, mais si vous spécifiez cet attribut, vous pouvez choisir un nombre différent. Ici, nous spécifions 100 époques. Gardez à l’esprit que le temps total de calcul est presque strictement proportionnel au nombre d’époques. Ainsi, si vous avez deux fois plus d’époques, le temps de calcul sera deux fois plus long.

De plus, à la ligne 7, nous introduisons également un second attribut nommé “learning_rate”. Cet attribut est également optionnel, et par défaut, il a la valeur 0,01, attaché au bloc autodiff. Ce taux d’apprentissage est un facteur utilisé pour initialiser l’algorithme Adam qui contrôle l’évolution du taux d’apprentissage. C’est le paramètre eta que nous avons vu dans l’étape de la descente de gradient stochastique. Il contrôle l’algorithme Adam. Essentiellement, c’est un paramètre que vous n’avez pas besoin de modifier fréquemment, mais parfois l’ajuster peut économiser une portion significative de la puissance de traitement. Il n’est pas surprenant que, en ajustant finement ce taux d’apprentissage, vous puissiez économiser environ 20 % du temps total de calcul pour votre descente de gradient stochastique.

L’initialisation des paramètres appris dans le bloc autodiff nécessite également un examen plus approfondi. Jusqu’à présent, nous avons utilisé le mot-clé “auto”, et en Envision, cela signifie simplement qu’Envision initialisera le paramètre en tirant aléatoirement une valeur à partir d’une distribution gaussienne de moyenne 1 et d’écart type 0,1. Cette initialisation diverge de la pratique habituelle dans le deep learning, où les paramètres sont initialisés aléatoirement avec des gaussiennes centrées autour de zéro. La raison pour laquelle Lokad a adopté cette approche différente deviendra plus claire plus tard dans cette conférence lorsque nous aborderons une situation réelle de prévision de la demande au détail.

Dans Envision, il est possible de remplacer et de contrôler l’initialisation des paramètres. Le paramètre “quantile”, par exemple, est déclaré à la ligne 9 mais n’a pas besoin d’être initialisé. En effet, à la ligne 7, juste au-dessus du bloc d’autodiff, nous avons une variable “quantile” à laquelle est assignée la valeur 4.2, et ainsi la variable est déjà initialisée avec une valeur donnée. Il n’est plus nécessaire d’effectuer une initialisation automatique. Il est également possible d’imposer une plage de valeurs autorisées pour les paramètres, et cela se fait avec le mot-clé “in” à la ligne 9. Essentiellement, nous définissons que “quantile” doit être compris entre 1 et 10, inclusivement. Avec ces limites en place, si une mise à jour obtenue via l’algorithme Adam pousse la valeur du paramètre en dehors de la plage acceptable, nous limitons la modification issue d’Adam de manière à ce qu’elle reste dans cette plage. De plus, nous remettons à zéro les valeurs de momentum qui sont typiquement associées à l’algorithme Adam en coulisse. Imposer des limites sur les paramètres diverge de la pratique classique du deep learning; cependant, les avantages de cette fonctionnalité deviendront évidents une fois que nous commencerons à aborder un véritable exemple de prévision de la demande au détail.

La programmation différentiable repose largement sur la descente de gradient stochastique. L’aspect stochastique est littéralement ce qui permet à la descente de fonctionner très rapidement. C’est une arme à double tranchant : le bruit obtenu par le biais des pertes partielles n’est pas seulement un défaut, mais également une caractéristique. En introduisant un peu de bruit, la descente peut éviter de se retrouver bloquée dans des zones où les gradients sont très plats. Ainsi, disposer de ce gradient bruité rend non seulement l’itération beaucoup plus rapide, mais aide aussi à pousser l’itération à sortir des zones où le gradient est très plat et ralentit la descente. Cependant, il faut garder à l’esprit que lorsque la descente de gradient stochastique est utilisée, la somme des gradients n’est pas égale au gradient de la somme. En conséquence, la descente de gradient stochastique présente de légers biais statistiques, notamment lorsque les distributions en queue sont concernées. Toutefois, lorsque ces problèmes surviennent, il est relativement simple de bidouiller les recettes numériques, même si la théorie reste quelque peu obscure.

La programmation différentiable (DP) ne doit pas être confondue avec un solveur quelconque d’optimisation mathématique. Le gradient doit circuler à travers le programme pour que la programmation différentiable fonctionne. La programmation différentiable peut s’appliquer à des programmes d’une complexité arbitraire, mais ces programmes doivent être conçus dans l’esprit de la programmation différentiable. De plus, la programmation différentiable est une culture ; c’est un ensemble d’astuces et de conseils qui s’accordent bien avec la descente de gradient stochastique. Tout bien considéré, la programmation différentiable se situe dans la partie accessible du spectre du machine learning. C’est une technique très abordable. Néanmoins, il faut un certain savoir-faire pour maîtriser ce paradigme et l’exploiter efficacement en production.

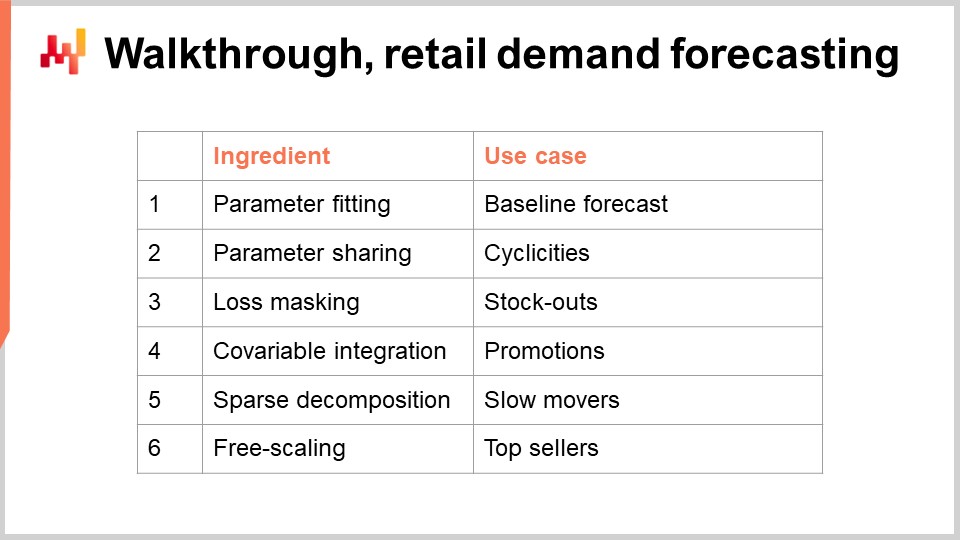
Nous sommes maintenant prêts à entamer le deuxième bloc de cette conférence : le walkthrough. Nous allons réaliser un walkthrough pour notre tâche de prévision de la demande au détail. Cet exercice de modélisation s’inscrit dans le cadre du défi de prévision présenté lors de la conférence précédente. En bref, nous souhaitons prévoir la demande quotidienne au niveau des SKU dans un réseau de vente au détail. Un SKU, ou stock-keeping unit, est techniquement le produit cartésien entre les produits et les magasins, filtré selon les entrées de l’assortiment. Par exemple, si nous disposons de 100 magasins et de 10 000 produits, et si chaque produit est présent dans chaque magasin, nous obtenons 1 million de SKU.

Il existe des outils permettant de transformer une estimation déterministe en une estimation probabiliste. Nous avons découvert l’un de ces outils lors de la conférence précédente grâce à la technique ESSM. Nous reviendrons plus en détail sur cette problématique — transformer des estimations en estimations probabilistes — lors de la prochaine conférence. Cependant, aujourd’hui, nous nous focalisons uniquement sur l’estimation des moyennes, et tous les autres types d’estimations (quantiles, probabilistes) viendront plus tard comme des extensions naturelles de l’exemple principal que je vais présenter aujourd’hui. Dans ce walkthrough, nous allons apprendre les paramètres d’un modèle simple de prévision de la demande. La simplicité de ce modèle est trompeuse, car cette classe de modèle parvient à réaliser des prévisions de pointe, comme l’illustre le concours de prévision M5 en 2020.

Pour notre modèle de demande paramétrique, introduisons un paramètre unique pour chaque SKU. Il s’agit d’une forme de modèle absolument simpliste ; la demande est modélisée comme une constante pour chaque SKU. Cependant, cette constante n’est pas la même pour tous les SKU. Une fois établie, cette moyenne journalière constante sera identique pour tous les jours de l’ensemble du cycle de vie du SKU.

Voyons comment cela se fait grâce à la programmation différentiable. De la ligne 1 à la ligne 4, nous introduisons le bloc de données factices. En pratique, ce modèle et toutes ses variantes dépendraient des entrées issues des systèmes d’entreprise : l’ERP, WMS, TMS, etc. Présenter une conférence dans laquelle j’intégrerais un modèle mathématique dans une représentation réaliste des données, telle qu’elle est obtenue de l’ERP, introduirait une multitude de complications accidentelles qui ne sont pas pertinentes par rapport au sujet actuel de la conférence. Ainsi, ce que je fais ici, c’est introduire un bloc de données factices qui ne prétend même pas être réaliste, ni ressembler aux données que l’on peut observer dans une situation de vente au détail réelle. Le seul objectif de ces données factices est d’introduire les tables et les relations entre ces tables, et de s’assurer que l’exemple de code donné soit complet, compilable et exécutable. Tous les exemples de code que vous avez vus jusqu’à présent sont complètement autonomes ; il n’y a aucune partie cachée avant ou après. Le seul but du bloc de données factices est de garantir que nous disposions d’un code autonome.

Dans chaque exemple de ce walkthrough, nous commençons par ce bloc de données factices. À la ligne 1, nous introduisons la table des dates avec “dates” comme clé primaire. Ici, nous avons une plage de dates qui couvre essentiellement deux ans et un mois. Puis, à la ligne 2, nous introduisons la table des SKUs, qui est la liste des SKUs. Dans cet exemple minimaliste, nous n’avons que trois SKUs. Dans une situation de vente au détail réelle pour un réseau de vente de grande envergure, nous aurions des millions, voire dizaines de millions, de SKUs. Mais ici, pour l’exemple, j’utilise un très petit nombre. À la ligne 3, nous avons la table “T”, qui est un produit cartésien entre les SKUs et la date. Essentiellement, ce que vous obtenez avec cette table “T” est une matrice où chaque SKU et chaque jour est présent. Elle possède deux dimensions.

À la ligne 6, nous introduisons notre bloc d’autodiff réel. La table d’observation est la table des SKUs, et la descente de gradient stochastique ici sélectionnera un SKU à la fois. À la ligne 7, nous présentons le “level”, qui sera notre unique paramètre. Il s’agit d’un paramètre vecteur, et jusqu’ici, dans nos blocs d’autodiff, nous n’avions introduit que des paramètres scalaires. Les paramètres précédents n’étaient qu’un nombre ; ici, “SKU.level” est en réalité un vecteur. C’est un vecteur qui comporte une valeur par SKU, et c’est littéralement notre demande constante modélisée au niveau du SKU. Nous spécifions une plage, et nous verrons bientôt pourquoi cela est important. Il doit être au moins de 0,01, et nous fixons 1 000 comme borne supérieure de la demande moyenne journalière pour ce paramètre. Ce paramètre est initialisé automatiquement avec une valeur proche de un, ce qui constitue un point de départ raisonnable. Dans ce modèle, nous disposons d’un degré de liberté par SKU. Enfin, aux lignes 8 et 9, nous mettons en œuvre le modèle en lui-même. À la ligne 8, nous calculons “dot.delta”, qui correspond à la demande prédite par le modèle moins l’observé, c’est-à-dire “T.sold”. Le modèle se résume à un seul terme, une constante, puis nous avons l’observation, qui est “T.sold”.

Pour comprendre ce qui se passe ici, nous assistons à certains comportements de broadcasting. La table “T” est une table croisée entre SKU et date. Le bloc d’autodiff est une itération qui parcourt les lignes de la table d’observations. À la ligne 9, nous sommes dans le bloc d’autodiff, donc nous avons sélectionné une ligne de la table des SKUs. La valeur “SKUs.level” n’est pas un vecteur ici ; c’est simplement un scalaire, une seule valeur puisque nous avons sélectionné une unique ligne de la table d’observations. Ensuite, “T.sold” n’est plus une matrice car nous avons déjà sélectionné un SKU. Il en résulte que “T.sold” est en réalité un vecteur, un vecteur dont la dimension correspond à celle des dates. Lorsque nous effectuons la soustraction “SKUs.level - T.sold”, nous obtenons un vecteur aligné avec la table des dates, que nous assignons à “D.delta”, qui est un vecteur comportant une ligne par jour, durant deux ans et un mois. Enfin, à la ligne 9, nous calculons la fonction de perte, qui n’est rien d’autre que l’erreur quadratique moyenne. Ce modèle est extrêmement simpliste. Voyons ce qui peut être fait concernant les effets calendaires.

Le partage de paramètres est sans doute l’une des techniques de programmation différentiable les plus simples et les plus utiles. On dit qu’un paramètre est partagé s’il contribue à plusieurs lignes d’observation. En partageant les paramètres entre les observations, nous pouvons stabiliser la descente de gradient et atténuer les problèmes de surapprentissage. Considérons le schéma du jour de la semaine. Nous pourrions introduire sept paramètres représentant les différents poids pour chaque SKU. Jusqu’à présent, un SKU ne possède qu’un seul paramètre, qui correspond à la demande constante. Si nous voulons enrichir cette perception de la demande, nous pourrions dire que chaque jour de la semaine possède son propre poids, et comme il y a sept jours dans la semaine, nous pouvons disposer de sept poids que nous appliquerions de manière multiplicative.

Cependant, il est peu probable que chaque SKU ait son propre schéma unique pour le jour de la semaine. En réalité, il est bien plus raisonnable de supposer qu’il existe une catégorie ou une forme de hiérarchie, comme une famille de produits, une catégorie de produits, une sous-catégorie, voire un département dans le magasin, qui capture correctement ce schéma du jour de la semaine. L’idée est de ne pas introduire sept paramètres par SKU, mais plutôt d’introduire sept paramètres par catégorie, c’est-à-dire un niveau de regroupement où l’on suppose un comportement homogène en termes de schémas du jour de la semaine.

Si nous décidons d’introduire ces sept paramètres avec un effet multiplicatif sur le level, c’est exactement l’approche qui a été adoptée lors de la conférence précédente pour ce modèle, lequel s’est classé numéro un au niveau des SKU dans la compétition M5. Nous disposons d’un level et d’un effet multiplicatif associé au schéma du jour de la semaine.

Dans le code, aux lignes 1 à 5, nous avons le bloc de données factices comme précédemment, et nous introduisons une table supplémentaire nommée “category.” Cette table sert à regrouper les SKUs, et conceptuellement, pour chaque ligne de la table des SKUs, il y a une et une seule ligne correspondante dans la table des catégories. Dans le langage Envision, nous disons que la catégorie est en amont de la table des SKUs. La ligne 7 introduit la table des jours de la semaine. Cette table est essentielle, et nous la créons avec une forme spécifique qui reflète le schéma cyclique que nous souhaitons capturer. À la ligne 7, nous créons la table des jours de la semaine en regroupant les dates selon leur valeur modulo sept. Nous créons ainsi une table qui comportera exactement sept lignes, ces sept lignes représentant chacun des sept jours de la semaine. Pour chaque ligne de la table des dates, il y a une correspondance unique dans la table des jours de la semaine. Ainsi, selon le langage Envision, la table des jours de la semaine est en amont de la table “date.”

Nous disposons maintenant de la table “CD”, qui est un produit cartésien entre la catégorie et le jour de la semaine. En termes de nombre de lignes, cette table comportera autant de lignes qu’il y a de catégories multiplié par sept, puisque la table du jour de la semaine compte sept lignes. À la ligne 12, nous introduisons un nouveau paramètre nommé “CD.DOW” (DOW signifiant day of the week), qui est un autre paramètre vecteur appartenant à la table CD. En termes de degrés de liberté, nous aurons exactement sept valeurs de paramètres multipliées par le nombre de catégories, ce que nous recherchons. Nous souhaitons obtenir un modèle capable de saisir ce schéma du jour de la semaine mais avec un unique schéma par catégorie, et non un schéma par SKU.

Nous déclarons ce paramètre, et nous utilisons le mot-clé “in” pour spécifier que la valeur de “CD.DOW” doit être comprise entre 0.1 et 100. À la ligne 13, nous exprimons la demande telle qu’indiquée par le modèle. La demande est “SKUs.level * CD.DOW”, représentant la demande. Nous avons la demande moins l’observé “T.sold”, ce qui nous donne un delta. Ensuite, nous calculons l’erreur quadratique moyenne.

À la ligne 13, une part considérable de magie de broadcasting opère. “CD.DOW” est une table croisée entre la catégorie et le jour de la semaine. Puisque nous sommes dans le bloc d’autodiff, la table CD est une table croisée entre la catégorie et le jour de la semaine. Comme le bloc parcourt la table des SKUs, en sélectionnant un SKU, nous avons en effet sélectionné une catégorie, puisque la table des catégories est en amont. Cela signifie que CD.DOW n’est plus une matrice, mais plutôt un vecteur de dimension sept. Cependant, elle est en amont de la table “date”, de sorte que ces sept lignes peuvent être diffusées dans la table des dates. Il n’existe qu’une seule manière de réaliser cette diffusion, car chaque ligne de la table des jours de la semaine est associée à des lignes spécifiques de la table des dates. Nous assistons ainsi à une double diffusion, et au final, nous obtenons une demande constituée d’une série de valeurs cycliques au niveau du jour de la semaine pour le SKU. Voilà notre modèle à ce stade, et le reste de la fonction de perte demeure inchangé.

Nous découvrons ici une manière très élégante d’aborder les cyclicités en combinant les comportements de broadcasting issus de la nature relationnelle d’Envision avec ses capacités de programmation différentiable. Nous pouvons exprimer les cyclicités calendaires en seulement trois lignes de code. Cette approche fonctionne parfaitement même lorsque nous traitons des données très rares. Elle fonctionnerait tout aussi bien si nous examinions des produits qui se vendaient en moyenne à une unité par mois. Dans de tels cas, la solution judicieuse serait de regrouper, au sein d’une même catégorie, des dizaines, voire des centaines de produits. Cette technique peut également être utilisée pour refléter d’autres schémas cycliques, tels que le mois de l’année ou le jour du mois.

Le modèle présenté dans la conférence précédente, qui a obtenu des résultats à la pointe de l’état de l’art lors de la compétition M5, était une combinaison multiplicative de trois cyclicités : le jour de la semaine, le mois de l’année et le jour du mois. Tous ces motifs ont été enchaînés par multiplication. La mise en œuvre des deux autres variantes est laissée à l’audience attentive, mais cela ne nécessite qu’une paire de lignes de code par motif cyclique, ce qui le rend très concis.

Dans la conférence précédente, nous avons présenté un modèle de prévision des ventes. Cependant, ce ne sont pas les ventes qui nous intéressent, mais la demande. Il ne faut pas confondre zéro vente avec zéro demande. S’il n’y avait plus de stock pour que le client puisse acheter dans le magasin un jour donné, la technique de masquage de la perte est utilisée chez Lokad pour faire face aux ruptures de stock. Il s’agit de la technique la plus simple employée pour gérer les ruptures de stock, mais ce n’est pas la seule. Autant que je sache, nous disposons d’au moins deux autres techniques utilisées en production, chacune avec ses propres avantages et inconvénients. Ces autres techniques ne seront pas abordées aujourd’hui, mais elles le seront dans des conférences ultérieures.

Revenant à l’exemple de code, les lignes 1 à 3 restent inchangées. Examinons ce qui suit. À la ligne 6, nous enrichissons les données fictives avec le drapeau booléen indiquant la disponibilité en stock. Pour chaque SKU et pour chaque jour, nous avons une valeur booléenne qui indique s’il y a eu une rupture de stock à la fin de la journée dans le magasin. À la ligne 15, nous modifions la fonction de perte afin d’exclure, en mettant à zéro, les jours pour lesquels une rupture de stock a été constatée à la fin de la journée. En mettant ces jours à zéro, nous nous assurons qu’aucun gradient ne soit rétropropagé dans des situations présentant un biais dû à l’occurrence de la rupture de stock.

L’aspect le plus déconcertant de la technique de masquage de la perte est qu’elle ne modifie même pas le modèle. En effet, si l’on observe le modèle exprimé à la ligne 14, il est exactement le même ; il n’a pas été touché. Seule la fonction de perte a été modifiée. Cette technique peut être simple, mais elle diverge profondément d’une perspective centrée sur le modèle. En réalité, c’est une approche axée sur la modélisation. Nous améliorons la situation en reconnaissant le biais causé par les ruptures de stock, ce qui se reflète dans nos efforts de modélisation. Cependant, nous procédons ainsi en modifiant la métrique d’exactitude, et non le modèle lui-même. Autrement dit, nous changeons la fonction de perte que nous optimisons, rendant ce modèle non comparable avec d’autres modèles en termes d’erreur numérique pure.

Pour une situation comme Walmart, comme évoqué dans la conférence précédente, la technique de masquage de la perte est adéquate pour la plupart des produits. En règle générale, cette technique fonctionne bien si la demande n’est pas si rare que vous n’ayez généralement qu’une seule unité en stock. De plus, il convient d’éviter les produits pour lesquels les ruptures de stock sont très fréquentes, car il s’agit de la stratégie explicite du détaillant de terminer la journée en rupture de stock. Cela se produit typiquement pour certains produits ultra-frais où le détaillant vise à provoquer une rupture de stock en fin de journée. Des techniques alternatives remédient à ces limitations, mais nous n’avons pas le temps de les aborder aujourd’hui.

Les promotions sont un aspect important du retail. Plus généralement, il existe de nombreuses manières pour le détaillant d’influencer et de façonner la demande, telles que la tarification ou le déplacement de marchandises vers une gondole. Les variables qui fournissent des informations supplémentaires à des fins prédictives sont généralement appelées covariables dans les cercles de supply chain. On nourrit beaucoup d’espoirs quant à des covariables complexes, telles que les données météorologiques ou celles issues des réseaux sociaux. Cependant, avant de nous plonger dans des sujets avancés, nous devons aborder l’éléphant dans la pièce, à savoir l’information sur les prix, qui a évidemment un impact significatif sur la demande observée. Ainsi, à la ligne 7 de cet exemple de code, nous introduisons pour chaque jour, à la ligne 14, “category.ed”, où “ed” signifie élasticité de la demande. Il s’agit d’un paramètre vecteur partagé avec un degré de liberté par catégorie, destiné à représenter l’élasticité de la demande. À la ligne 16, nous introduisons une forme exponentielle de élasticité des prix en prenant l’exponentielle de (-category.ed * t.price). Intuitivement, avec cette forme, lorsque le prix augmente, la demande converge rapidement vers zéro en raison de la fonction exponentielle. Inversement, lorsque le prix converge vers zéro, la demande augmente de manière explosive.

Cette forme exponentielle de réponse aux prix est simpliste, et le partage des paramètres garantit un haut degré de stabilité numérique, même avec cette fonction exponentielle dans le modèle. Dans des contextes réels, notamment pour des situations comme Walmart, nous disposerions de plusieurs informations sur les prix, telles que des remises, l’écart par rapport au prix normal, des covariables représentant les actions marketing menées par le fournisseur, ou des variables catégorielles qui introduisent des éléments comme les gondoles. Avec la programmation différentiable, il est très simple d’élaborer des réponses aux prix arbitrairement complexes qui s’adaptent étroitement à la situation. L’intégration de covariables de presque tout type est très aisée grâce à la programmation différentiable.

Les produits à rotation lente sont une réalité dans le retail et de bien d’autres secteurs. Le modèle présenté jusqu’à présent comporte un paramètre, un degré de liberté par SKU, voire plus si l’on tient compte des paramètres partagés. Cependant, cela peut déjà être excessif, en particulier pour des SKU qui ne se renouvellent qu’une fois par an ou seulement quelques fois par an. Dans de telles situations, nous ne pouvons même pas nous permettre un degré de liberté par SKU, de sorte que la solution consiste à se reposer uniquement sur des paramètres partagés et à supprimer tous les paramètres ayant des degrés de liberté au niveau du SKU.

Aux lignes 2 et 4, nous introduisons deux tables nommées “products” et “stores”, et la table “SKUs” est construite comme une sous-table filtrée du produit cartésien entre products et stores, ce qui est la définition même de l’assortiment. Aux lignes 15 et 16, nous avons introduit deux paramètres vecteur partagés : un niveau avec une affinité avec la table products et un autre niveau ayant une affinité avec la table stores. Ces paramètres sont également définis dans une plage spécifique, de 0.01 à 100, qui est la valeur maximale.

Maintenant, à la ligne 18, le niveau par SKU est constitué de la multiplication du niveau de produit et du niveau de magasin. Le reste du script reste inchangé. Alors, comment cela fonctionne-t-il ? À la ligne 19, SKU.level est un scalaire. Nous avons le bloc autodesk qui itère sur la table SKUs, qui est la table d’observation. Ainsi, SKUs.level à la ligne 18 n’est qu’une valeur scalaire. Ensuite, nous avons products.level. Puisque la table products est en amont de la table SKUs, pour chaque SKU, il n’existe qu’une seule table products. Donc, products.level est simplement un nombre scalaire. Il en va de même pour la table stores, qui est également en amont de la table SKUs. À la ligne 18, il n’y a qu’un seul magasin associé à ce SKU spécifique. Par conséquent, ce que nous obtenons, c’est la multiplication de deux valeurs scalaires, ce qui nous donne SKU.level. Le reste du modèle reste inchangé.

Ces techniques apportent un éclairage tout à fait nouveau sur l’affirmation selon laquelle il n’y a parfois pas assez de données ou que celles-ci sont trop rares. En effet, d’un point de vue différentiable, ces affirmations n’ont même pas vraiment de sens. Il n’existe pas de notion de données insuffisantes ou de données trop rares, du moins pas en termes absolus. Il existe simplement des modèles qui peuvent être adaptés à la rareté, voire à une rareté extrême. La structure imposée agit comme des rails directeurs qui rendent le processus d’apprentissage non seulement possible, mais aussi numériquement stable.

Comparé à d’autres techniques de machine learning qui tentent de laisser le modèle découvrir tous les motifs ex nihilo, cette approche structurée établit la structure même que nous devons apprendre. Ainsi, le mécanisme statistique en jeu a une liberté limitée quant à ce qu’il doit apprendre. Par conséquent, en termes d’efficacité sur le plan des données, il peut être incroyablement performant. Naturellement, tout cela repose sur le fait que nous avons choisi la bonne structure.

Comme vous pouvez le constater, effectuer des expériences est très simple. Nous réalisons déjà quelque chose de très compliqué, et en moins de 50 lignes, nous pouvons traiter une situation de type Walmart assez complexe. C’est tout un exploit. Il y a une part d’empirisme dans le processus, mais en réalité, ce n’est pas tant que cela. Nous parlons de quelques dizaines de lignes. N’oubliez pas qu’un ERP, tel que celui qui gère une entreprise ou un grand réseau de distribution, comporte généralement un millier de tables et 100 champs par table. La complexité des systèmes d’entreprise est donc absolument gigantesque comparée à celle de ce modèle prédictif structuré. Si nous devons consacrer un peu de temps aux itérations, ce n’est presque rien.

De plus, comme démontré lors de la compétition M5 de prévision, la réalité est que les praticiens de la supply chain connaissent déjà les motifs. Lorsque l’équipe M5 a utilisé trois motifs calendaires — le jour de la semaine, le mois de l’année et le jour du mois — tous ces motifs étaient évidents pour tout praticien expérimenté de la supply chain. La réalité en supply chain est que nous ne cherchons pas à découvrir un motif caché. Le fait que, par exemple, une forte baisse de prix entraîne une augmentation massive de la demande ne surprendra personne. La seule question qui se pose est de déterminer exactement l’ampleur de l’effet et la forme précise de la réponse. Ce sont des détails relativement techniques et, si vous vous offrez la possibilité de mener quelques expériences, vous pourrez résoudre ces problèmes relativement facilement.

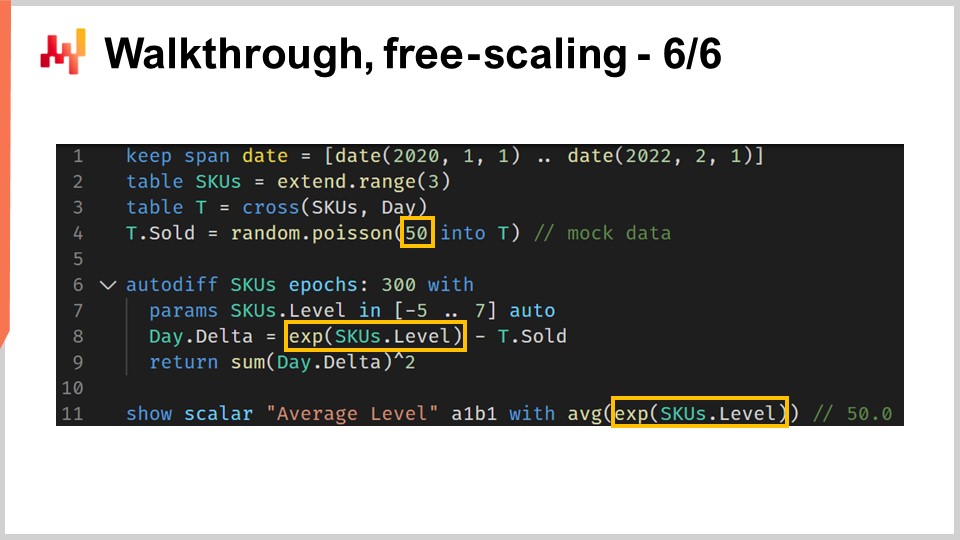
Comme dernière étape de cette démonstration, je souhaiterais souligner une particularité mineure de la programmation différentiable. Celle-ci ne doit pas être confondue avec un solveur générique d’optimisation mathématique. Il faut garder à l’esprit qu’un gradient descendant est en action. Plus précisément, l’algorithme utilisé pour optimiser et mettre à jour les paramètres dispose d’une vitesse de descente maximale égale au taux d’apprentissage fourni par l’algorithme ADAM. Dans Envision, le taux d’apprentissage par défaut est de 0.01.

Si nous regardons le code, à la ligne 4, nous avons introduit une initialisation où les quantités vendues sont échantillonnées à partir d’une distribution de Poisson d’une moyenne de 50. Si nous souhaitons apprendre un niveau, techniquement, il nous faudrait un niveau de l’ordre de 50. Cependant, lors de l’initialisation automatique du paramètre, nous commençons avec une valeur d’environ un, et nous ne pouvons avancer que par incréments de 0.01. Il faudrait environ 5 000 époques pour atteindre réellement cette valeur de 50. Puisque nous avons un paramètre non partagé, SKU.level, ce paramètre n’est modifié qu’une seule fois par époque. Ainsi, nous aurions besoin de 5 000 époques, ce qui ralentirait inutilement le calcul.

Nous pourrions augmenter le taux d’apprentissage pour accélérer la descente, ce qui serait une solution. Cependant, je ne recommanderais pas d’augmenter exagérément le taux d’apprentissage, car ce n’est généralement pas la bonne approche du problème. Dans une situation réelle, nous disposerions de paramètres partagés en plus de ce paramètre non partagé. Ces paramètres partagés seront ajustés par la descente de gradient stochastique de nombreuses fois au cours de chaque époque. Si vous augmentez considérablement le taux d’apprentissage, vous risquez de créer des instabilités numériques pour vos paramètres partagés. Vous pourriez augmenter la vitesse de variation du niveau de SKU, mais cela créerait des problèmes de stabilité numérique pour les autres paramètres.

Une meilleure technique serait d’utiliser une astuce de rescaling et d’envelopper le paramètre dans une fonction exponentielle, ce qui est exactement ce qui est fait à la ligne 8. Grâce à ce wrapper, nous pouvons désormais atteindre des valeurs de paramètre pour le niveau qui peuvent être très faibles ou très élevées avec un nombre d’époques bien inférieur. Cette particularité est fondamentalement la seule que je devrais introduire pour proposer un exemple réaliste de cette démonstration de prévision de la demande en retail. Tout bien considéré, c’est une particularité mineure. Néanmoins, cela rappelle que la programmation différentiable requiert de prêter attention au flux des gradients. La programmation différentiable offre une expérience de conception fluide dans l’ensemble, mais ce n’est pas de la magie.

Quelques réflexions pour finir : les modèles structurés permettent d’atteindre une précision de prévision à la pointe de l’état de l’art. Ce point a été largement développé lors de la conférence précédente. Cependant, d’après les éléments présentés aujourd’hui, je soutiendrais que la précision n’est même pas le facteur décisif en faveur de la programmation différentiable associée à un modèle paramétrique structuré. Ce que nous obtenons, c’est de la compréhension ; nous n’obtenons pas seulement un logiciel capable de faire des prédictions, mais nous accédons également à des informations directes sur les motifs que nous cherchons à capturer. Par exemple, le modèle présenté aujourd’hui nous fournirait directement une prévision de la demande accompagnée de poids explicites pour chaque jour de la semaine et d’une élasticité explicite de la demande. Si nous devions étendre cette prévision, par exemple, pour introduire un uplift associé au Black Friday, un événement quasi-saisonnier qui ne se produit pas à la même période chaque année, nous pourrions le faire. Il suffirait d’ajouter un facteur, et nous obtiendrions alors une estimation de l’uplift du Black Friday, isolée de tous les autres motifs, tels que le motif du jour de la semaine. Cela revêt un intérêt primordial.

Ce que nous obtenons grâce à l’approche structurée, c’est de la compréhension, et c’est bien plus que le simple modèle brut. Par exemple, si nous aboutissons à une élasticité négative, c’est-à-dire une situation où le modèle vous indique qu’en augmentant le prix, vous augmentez la demande, dans un contexte de type Walmart, cela constitue un résultat très douteux. Très probablement, cela reflète que l’implémentation de votre modèle est défectueuse, ou qu’il existe des problèmes profonds. Quelle que soit la métrique de précision, si vous vous retrouvez dans une situation de type Walmart avec un résultat indiquant qu’en rendant un produit plus cher, les gens en achètent davantage, vous devriez sérieusement remettre en question l’ensemble de votre pipeline de données, car il y a vraisemblablement quelque chose qui ne va pas. C’est cela, la compréhension.

De plus, le modèle est ouvert au changement. La programmation différentiable est incroyablement expressive. Le modèle que nous avons n’est qu’une itération dans un parcours. Si le marché se transforme ou si l’entreprise elle-même est transformée, nous pouvons être assurés que le modèle que nous possédons sera capable de capter cette évolution naturellement. Il n’existe pas d’évolution automatique ; il faudra l’effort d’un Supply Chain Scientist pour capter cette évolution. Cependant, cet effort peut être supposé relativement minimal. Cela se résume au fait que si vous avez un modèle très petit et bien organisé, alors, lorsque vous devrez y revenir ultérieurement pour ajuster sa structure, la tâche sera relativement minime comparée à une situation où votre modèle serait une véritable bête d’ingénierie.

Lorsque, conçu avec soin, les modèles produits par programmation différentiable sont très stables. Cette stabilité dépend du choix de la structure. La stabilité n’est pas acquise pour n’importe quel programme que vous optimisez grâce à la programmation différentiable ; c’est le genre de résultat que l’on obtient lorsque l’on dispose d’une structure très claire où les paramètres ont une sémantique spécifique. Par exemple, si vous avez un modèle dans lequel, chaque fois que vous le réentraînez, vous obtenez des poids complètement différents pour le jour de la semaine, alors la réalité de votre entreprise ne change pas si rapidement. Si vous exécutez votre modèle deux fois, vous devriez obtenir des valeurs pour le jour de la semaine relativement stables. Dans le cas contraire, quelque chose cloche profondément dans la façon dont vous avez modélisé votre demande. Ainsi, en faisant un choix judicieux quant à la structure de votre modèle, vous pouvez obtenir des résultats numériques d’une stabilité incroyable. Ce faisant, nous évitons les écueils qui ont tendance à affecter les modèles complexes de deep learning lorsque nous essayons de les utiliser dans un contexte supply chain. En effet, du point de vue supply chain, les instabilités numériques sont fatales, car nous observons des effets de cliquet partout. Si vous disposez d’une estimation de la demande qui fluctue, cela signifie que, de manière aléatoire, vous allez déclencher une commande d’achat ou une commande de production pour rien. Une fois que vous avez déclenché votre commande de production, vous ne pouvez pas décider la semaine suivante que c’était une erreur et que vous n’auriez pas dû le faire. Vous êtes condamné à vivre avec la décision que vous venez de prendre. Si vous disposez d’un estimateur de la demande future qui continue de fluctuer, vous finirez par obtenir des replenishment gonflés et des commandes de production exagérées. Ce problème peut être résolu en assurant la stabilité, ce qui relève de la conception.

Un des plus grands obstacles à la mise en production du deep learning est la confiance. Lorsque vous opérez avec des millions d’euros ou de dollars, comprendre ce qui se passe dans votre recette numérique est crucial. Les erreurs en supply chain peuvent être extrêmement coûteuses, et il existe de nombreux exemples de disasters en supply chain dus à une mauvaise application d’algorithmes mal compris. Bien que la programmation différentiable soit très puissante, les modèles que l’on peut concevoir sont incroyablement simples. Ces modèles pourraient en réalité être exécutés dans une spreadsheet, car il s’agit typiquement de modèles multiplicatifs simples avec des branches et des fonctions. Le seul aspect qui ne pourrait être exécuté dans une feuille Excel est la différentiation automatique, et évidemment, si vous avez des millions de SKUs, n’essayez pas de faire cela sur une feuille de calcul. Cependant, du point de vue de la simplicité, c’est tout à fait compatible avec ce que vous pourriez mettre dans une feuille de calcul. Cette simplicité joue un rôle majeur dans l’établissement de la confiance et dans la mise en production du deep learning, au lieu de les cantonner à de jolis prototypes auxquels on n’arrive jamais à accorder une confiance totale.

Enfin, lorsque nous réunissons toutes ces propriétés, nous obtenons une technologie d’une grande précision. Cet angle a été abordé dans le tout premier chapitre de cette série de conférences. Nous souhaitons transformer tous les efforts investis dans la supply chain en investissements capitalistes, plutôt que de traiter les experts et praticiens de la supply chain comme des consommables contraints de répéter inlassablement les mêmes tâches. Avec cette approche, nous pouvons considérer tous ces efforts comme des investissements qui généreront et continueront de générer un retour sur investissement au fil du temps. La programmation différentiable s’accorde parfaitement avec cette perspective capitaliste pour la supply chain.

Dans le deuxième chapitre, nous avons introduit une conférence importante intitulée “Experimental Optimization”, qui apportait une réponse possible à la question simple mais fondamentale : Qu’est-ce que cela signifie réellement d’améliorer ou de faire mieux dans une supply chain ? La perspective de la programmation différentiable offre un éclairage très précis sur les nombreux défis auxquels sont confrontés les praticiens de la supply chain. Les software vendors d’entreprise reprochent fréquemment les échecs en supply chain aux mauvaises données. Cependant, je pense qu’il s’agit tout simplement d’une mauvaise façon d’aborder le problème. Les données sont ce qu’elles sont. Votre ERP n’a jamais été conçu pour la data science, mais il fonctionne sans accroc depuis des années, voire des décennies, et les personnes de l’entreprise parviennent néanmoins à gérer la supply chain. Même si votre ERP, qui capture les données de votre supply chain, n’est pas parfait, ce n’est pas préoccupant. Si vous vous attendez à ce que des données parfaites soient disponibles, c’est purement du souhait. Nous parlons de supply chains ; le monde est très complexe, donc les systèmes sont imparfaits. En réalité, vous ne disposez pas d’un unique système d’entreprise ; vous en avez environ une demi-douzaine, et ils ne sont pas entièrement cohérents les uns avec les autres. C’est un fait de la vie. Cependant, lorsque les vendors d’entreprise blâment les mauvaises données, la réalité est qu’un modèle de prévision très spécifique est utilisé par le vendeur, et ce modèle a été conçu selon un ensemble d’hypothèses précises concernant l’entreprise. Le problème est que si votre entreprise venait à violer l’une de ces hypothèses, la technologie s’effondrerait complètement. Dans ce cas, vous avez un modèle de prévision qui repose sur des hypothèses déraisonnables, vous y alimentez des données imparfaites, et ainsi la technologie s’effondre. Il est complètement déraisonnable de dire que l’entreprise est en faute. La technologie en cause est celle promue par le vendor, qui formule des hypothèses totalement irréalistes quant à ce que les données peuvent être dans un contexte supply chain.

Je n’ai présenté aucun benchmark pour une quelconque métrique d’exactitude aujourd’hui. Cependant, ma proposition est que ces métriques d’exactitude sont en grande partie sans conséquence. Un modèle prédictif est un outil pour orienter les décisions. Ce qui importe, c’est de savoir si ces décisions – quoi acheter, quoi produire, s’il faut augmenter ou baisser votre prix – sont bonnes ou mauvaises. Il est vrai que de mauvaises décisions peuvent être imputées au modèle prédictif. Cependant, la plupart du temps, il ne s’agit pas d’un problème d’exactitude. Par exemple, nous avions un modèle de prévision des ventes, et nous avons corrigé l’aspect de la rupture de stock qui n’était pas géré de manière appropriée. Pourtant, en corrigeant cet aspect, nous avons en réalité ajusté la métrique d’exactitude elle-même. Ainsi, améliorer le modèle prédictif ne signifie pas nécessairement améliorer l’exactitude ; très souvent, cela implique littéralement de revisiter le problème et la perspective dans lesquels vous opérez, et donc de modifier la métrique d’exactitude ou quelque chose d’encore plus profond. Le problème avec la perspective classique, c’est qu’elle suppose que la métrique d’exactitude est un objectif digne en soi. Ce n’est pas entièrement le cas.

Les supply chains opèrent dans le monde réel, et de nombreux événements inattendus, voire extraordinaires, peuvent survenir. Par exemple, un navire peut provoquer une obstruction du canal de Suez ; il s’agit d’un événement véritablement exceptionnel. Dans une telle situation, tous les modèles de prévision des délais existants, qui se concentraient sur cette partie du monde, seraient immédiatement invalidés. Évidemment, c’était un phénomène qui ne s’était pas réellement produit auparavant, de sorte qu’il est impossible de procéder à des tests rétrospectifs dans une telle situation. Cependant, même face à cette situation exceptionnelle avec un navire bloquant le canal de Suez, nous pouvons toujours corriger le modèle, du moins si nous adoptons ce type d’approche en boîte blanche que je propose aujourd’hui. Cette correction impliquera un certain degré de conjecture, ce qui est acceptable. Il vaut mieux être approximativement correct plutôt qu’exactement faux. Par exemple, si nous envisageons le blocage du canal de Suez, vous pouvez simplement dire « ajoutons un mois au délai pour tous les approvisionnements qui étaient censés transiter par cette route ». C’est très approximatif, mais il vaut mieux supposer qu’il n’y aura aucun retard, même si vous disposez déjà de l’information. De plus, le changement provient souvent de l’intérieur. Par exemple, considérons un réseau de distribution qui dispose d’un ancien centre de distribution et d’un nouveau centre de distribution approvisionnant quelques dizaines de magasins. Disons qu’une migration est en cours, où les approvisionnements des magasins sont progressivement transférés de l’ancien centre de distribution vers le nouveau. Cette situation se produit presque une seule fois dans l’histoire de ce détaillant spécifique, et il est impossible de la tester rétroactivement. Pourtant, avec une approche telle que la programmation différentiable, il est tout à fait simple de mettre en œuvre un modèle adapté à cette migration graduelle.

En conclusion, la programmation différentiable est une technologie qui nous offre une approche pour structurer nos perspectives sur l’avenir. Elle nous permet de façonner, littéralement, notre manière d’envisager le futur. La programmation différentiable se situe dans le domaine de la perception. Sur la base de cette perception, nous pouvons prendre de meilleures décisions pour les supply chains, et ces décisions déterminent les actions qui se situent de l’autre côté du schéma. L’un des plus grands malentendus de la théorie dominante de la supply chain est qu’on peut traiter la perception et l’action comme des composants strictement isolés. Cela se traduit, par exemple, par le fait d’avoir une équipe chargée de la planification (la perception) et une équipe indépendante chargée du replenishment (l’action).

Cependant, la boucle de rétroaction perception-action est d’une importance capitale. C’est littéralement le mécanisme même qui vous guide vers une perception correcte. Sans ce mécanisme de feedback, il n’est même pas certain que vous regardiez la bonne chose, ou que ce que vous observez soit réellement ce que vous pensez être. Vous avez besoin de ce mécanisme de rétroaction, et c’est grâce à lui que vous pouvez orienter vos modèles vers une évaluation quantitative correcte de l’avenir, pertinente pour la conduite des actions de votre supply chain. Les approches classiques de la supply chain négligent presque entièrement ce point, car, en substance, je crois qu’elles sont enfermées dans une forme très rigide de prévision. Cette approche centrée sur un modèle de prévision peut être un modèle ancien, comme le modèle de prévision Holt-Winters, ou un modèle récent, comme Facebook Prophet. La situation est la même : si vous êtes enfermé dans un modèle de prévision unique, tous les retours provenant du côté action deviennent caduques, car vous ne pouvez rien faire de ces retours à part les ignorer complètement.

Si vous êtes enfermé dans un modèle de prévision donné, vous ne pouvez pas reformater ou restructurer votre modèle au fur et à mesure que vous recevez des informations du côté action. En revanche, la programmation différentiable, avec son approche de modélisation structurée, vous offre un paradigme complètement différent. Le modèle prédictif est entièrement jetable – dans son ensemble. Si les retours que vous obtenez de vos actions exigent des changements radicaux dans votre perspective prédictive, implémentez tout simplement ces changements radicaux. Il n’existe aucun attachement particulier à une itération donnée du modèle. Garder le modèle très simple permet de s’assurer qu’une fois en production, vous conservez la possibilité de continuer à le modifier. Car, encore une fois, si ce que vous avez conçu est tel une bête, un monstre d’ingénierie, alors une fois en production, il devient incroyablement difficile à modifier. L’un des aspects clés est que, si vous voulez pouvoir continuer à évoluer, vous devez disposer d’un modèle très parcimonieux en termes de lignes de code et de complexité interne. C’est là que la programmation différentiable brille. Il ne s’agit pas d’atteindre une exactitude supérieure ; il s’agit d’obtenir une pertinence accrue. Sans pertinence, toutes les métriques d’exactitude sont complètement caduques. La programmation différentiable et la modélisation structurée vous offrent le chemin pour atteindre la pertinence et ensuite la maintenir au fil du temps.

Cela conclura la conférence d’aujourd’hui. La prochaine fois, le deux mars, à la même heure, 15 h, heure de Paris, je présenterai la modélisation probabiliste pour la supply chain. Nous examinerons de plus près les implications techniques d’envisager tous les futurs possibles plutôt que de simplement en choisir un et de le déclarer comme le bon. En effet, considérer tous les futurs possibles est très important si vous souhaitez que votre supply chain soit véritablement résiliente face aux risques. Si vous ne choisissez qu’un seul futur, c’est une recette pour aboutir à quelque chose d’incroyablement fragile si votre prévision ne se révèle pas parfaitement exacte. Et devinez quoi, la prévision n’est jamais complètement correcte. C’est pourquoi il est si important d’adopter l’idée qu’il faut envisager tous les futurs possibles, et nous verrons comment faire cela avec des recettes numériques modernes.

Question: Un bruit stochastique est ajouté pour éviter les minima locaux, mais comment est-il exploité ou mis à l’échelle pour éviter de grandes déviations afin que la descente de gradient ne soit pas projetée loin de son objectif ?

C’est une question très intéressante, et il y a deux volets dans cette réponse.

Tout d’abord, c’est pourquoi l’algorithme Adam est très conservateur en termes de magnitude des mouvements. Le gradient est fondamentalement non borné ; il peut atteindre des valeurs équivalentes à des milliers, voire des millions. Cependant, avec Adam, le pas maximal est en réalité limité par le taux d’apprentissage. Ainsi, en pratique, Adam s’accompagne d’une recette numérique qui impose littéralement un pas maximal et, espérons-le, évite ainsi une instabilité numérique massive.

Maintenant, si par hasard, malgré le fait que nous ayons ce taux d’apprentissage, nous pouvions dire que, rien que par pure fluctuation, nous allons avancer de manière itérative, une étape à la fois, mais souvent dans une direction incorrecte, c’est une possibilité. C’est pourquoi je dis que la descente de gradient stochastique n’est toujours pas complètement comprise. Elle fonctionne incroyablement bien en pratique, mais pourquoi elle fonctionne si bien, et pourquoi elle converge si rapidement, et pourquoi nous n’observons pas davantage les problèmes qui peuvent survenir, n’est pas entièrement élucidé, surtout si l’on considère que la descente de gradient stochastique s’effectue en haute dimension. Ainsi, typiquement, vous avez littéralement des dizaines, voire des centaines, de paramètres qui sont modifiés à chaque étape. L’intuition que vous pouvez avoir en deux ou trois dimensions est très trompeuse ; les choses se comportent de manière très différente lorsque l’on considère des dimensions supérieures.

Donc, en résumé pour cette question : c’est très pertinent. Il y a une partie où c’est la magie d’Adam consistant à être très conservateur quant à l’échelle de vos pas de gradient, et une autre partie, qui est mal comprise mais qui, en pratique, fonctionne très bien. D’ailleurs, je pense que le fait que la descente de gradient stochastique ne soit pas complètement intuitive est aussi la raison pour laquelle, pendant près de 70 ans, cette technique a été connue sans être reconnue comme efficace. Pendant près de 70 ans, les gens savaient qu’elle existait, mais ils en étaient très sceptiques. Il a fallu le succès massif du deep learning pour que la communauté reconnaisse et admette qu’elle fonctionne réellement très bien, même si nous ne comprenons pas vraiment pourquoi.

Question: Comment comprend-on lorsqu’un certain pattern est faible et doit donc être retiré du modèle ?

Encore une très bonne question. Il n’existe aucun critère strict ; c’est littéralement un jugement laissé au Supply Chain Scientist. La raison en est que, si le pattern que vous introduisez vous apporte des bénéfices minimaux, mais qu’en termes de modélisation il ne représente que deux lignes de code et que l’impact en termes de temps de calcul est insignifiant, et si jamais vous souhaitez retirer le pattern par la suite, c’est relativement trivial, vous pourriez dire : “Eh bien, je peux simplement le garder. Il ne semble pas nuire, il n’apporte pas grand-chose de positif. Je peux imaginer des situations où ce pattern, faible aujourd’hui, pourrait en réalité devenir fort.” En ce qui concerne la maintenabilité, cela va.

Cependant, vous pouvez également observer l’autre facette du problème, où vous avez un pattern qui n’apporte pas grand-chose, tout en ajoutant une charge de calcul considérable au modèle. Ce n’est donc pas gratuit ; à chaque fois que vous ajoutez un paramètre ou de la logique, vous augmentez les ressources informatiques nécessaires pour votre modèle, le rendant ainsi plus lent et moins maniable. Si vous pensez que ce pattern, faible à présent, pourrait en fait devenir fort, mais de manière négative, en générant de l’instabilité et en créant le chaos dans votre modélisation prédictive, c’est typiquement le genre de situation dans laquelle vous vous direz : “Non, je devrais probablement le retirer.”

Vous voyez, il s’agit vraiment d’une question de jugement. La programmation différentiable est une culture ; vous n’êtes pas seuls. Vous avez des collègues et des pairs qui ont peut-être essayé différentes approches chez Lokad. C’est le type de culture que nous essayons de cultiver. Je sais que cela peut être un peu décevant par rapport à la perspective d’une IA toute-puissante, l’idée que nous pourrions bénéficier d’une intelligence artificielle omnipotente résolvant tous ces problèmes pour nous. Mais la réalité est que les supply chains sont si complexes, et que nos techniques d’intelligence artificielle sont si rudimentaires, que nous n’avons aucun substitut réaliste à l’intelligence humaine. Quand je parle de jugement, je veux simplement dire que vous avez besoin d’une bonne dose d’intelligence appliquée, très humaine, car tous les artifices algorithmiques sont loin de fournir une réponse satisfaisante.

Néanmoins, cela ne signifie pas que vous ne pouvez pas concevoir une sorte d’outillage. Ce serait un autre sujet ; je verrai si je couvrirais effectivement le type d’outillage que nous fournissons chez Lokad pour faciliter la conception. Un pattern tangentiel serait, si nous devons prendre une décision par jugement, d’essayer de fournir toute l’instrumentation nécessaire afin que ce jugement puisse être effectué très rapidement, minimisant ainsi la douleur liée à ce genre d’indécision où le Supply Chain Scientist doit décider du sort de l’état actuel du modèle.

Question: Quel est le seuil de complexité d’une supply chain à partir duquel le machine learning et la programmation différentiable apportent des résultats nettement meilleurs ?

Chez Lokad, nous parvenons généralement à obtenir des résultats substantiels pour des entreprises ayant un chiffre d’affaires de 10 millions de dollars par an et plus. Je dirais que cela commence vraiment à briller si vous avez une entreprise avec un chiffre d’affaires annuel de 50 millions de dollars et plus.

La raison en est que, fondamentalement, vous devez établir un pipeline de données très fiable. Vous devez être capable d’extraire toutes les données pertinentes de l’ERP sur une base quotidienne. Je ne veux pas dire qu’il s’agit de bonnes ou de mauvaises données, simplement que les données dont vous disposez peuvent présenter de nombreux défauts. Néanmoins, cela signifie qu’il faut mettre en place pas mal d’infrastructures rien que pour extraire quotidiennement les transactions de base. Si l’entreprise est trop petite, alors généralement, elle ne dispose même pas d’un département informatique, et elle ne parvient pas à réaliser une extraction quotidienne fiable, ce qui compromet véritablement les résultats.

Maintenant, en termes de secteurs ou de complexité, il faut constater que, à mon avis, dans la plupart des entreprises et la plupart des supply chains, l’optimisation n’a même pas encore véritablement commencé. Comme je l’ai dit, la théorie conventionnelle de la supply chain insiste sur le fait qu’il faut rechercher des prévisions plus précises. Réduire le pourcentage d’erreur de prévision est un objectif, et de nombreuses entreprises, par exemple, s’y attellent en constituant une équipe de planification ou une équipe de prévision. À mon avis, tout cela n’apporte aucune valeur ajoutée à l’entreprise, car cela fournit fondamentalement des réponses très sophistiquées à un mauvais ensemble de questions.

Cela peut surprendre, mais la programmation différentiable brille réellement non pas parce qu’elle est fondamentalement super puissante – ce qu’elle est –, mais parce que c’est généralement la première fois qu’une solution véritablement pertinente pour l’entreprise est mise en place. Si vous voulez prendre un exemple, la plupart des implémentations dans la supply chain reposent typiquement sur des modèles tels que le modèle de safety stock, qui n’ont absolument aucune pertinence pour une supply chain réelle. Par exemple, dans le modèle de safety stock, vous supposez qu’il est possible d’avoir un délai négatif, c’est-à-dire que vous commandez maintenant et que vous êtes livré hier. Cela n’a aucun sens, et par conséquent, les résultats opérationnels des safety stocks sont généralement insatisfaisants.

La programmation différentiable se distingue par sa capacité à atteindre la pertinence, et non par une suprématie numérique éclatante ou en étant meilleure que d’autres techniques alternatives de machine learning. L’enjeu est véritablement d’atteindre la pertinence dans un monde très complexe, chaotique, antagoniste, en perpétuel changement, et où vous devez faire face à un paysage applicatif semi-cauchemardesque qui représente les données à traiter.

Il semble qu’il n’y ait plus de questions. Dans ce cas, je suppose que nous nous retrouverons le mois prochain pour la conférence sur la modélisation probabiliste pour la supply chain.