Разреженность: когда мера точности дает сбой
Три года назад мы публиковали [Переобучение: когда мера точности дает сбой](/blog/2009/4/22/overfitting-when-accuracy-measure-goes-wrong/), однако переобучение далеко не единственная ситуация, когда простые показатели точности могут быть очень вводящими в заблуждение. Сегодня мы фокусируемся на ситуации, склонной к ошибкам: прерывистый спрос, который обычно наблюдается при анализе продаж на уровне магазина (или Ecommerce).
Мы считаем, что одна только эта проблема помешала большинству ритейлеров перейти к продвинутым системам прогнозирования на уровне магазина. Как и в большинстве задач прогнозирования, они бывают тонкими, неинтуитивными и некоторые компании берут большие деньги за некачественные ответы.
Наиболее популярными метриками ошибок в прогнозировании продаж являются средняя абсолютная ошибка (MAE) и средняя абсолютная процентная ошибка (MAPE). В качестве общего руководства мы предлагаем придерживаться MAE, так как MAPE работает очень плохо, когда временные ряды не являются гладкими, то есть постоянно, насколько это касается ритейлеров. Однако есть ситуации, когда MAE тоже дает сбой. Низкие объемы продаж попадают в эту категорию.
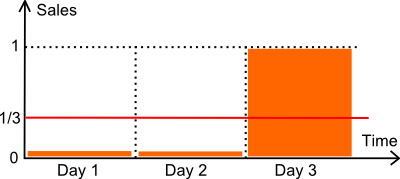
Давайте рассмотрим приведенную выше иллюстрацию. У нас есть товар, продающийся в течение 3 дней. Количество проданных единиц в первые два дня равно нулю. В третий день была продана одна единица. Предположим, что спрос на самом деле составляет ровно 1 единицу каждые 3 дня. Технически это распределение Пуассона с λ=1/3.
В следующем примере мы сравниваем две модели прогнозирования:
- плоская модель M, предсказывающая 1/3 каждый день (среднее значение).
- плоская модель Z, предсказывающая ноль каждый день.
Что касается оптимизации запасов, модель ноль (Z) является крайне вредной. Если предположить, что анализ резервного запаса будет использован для вычисления точки пополнения запасов, то прогноз, равный нулю, с большой вероятностью даст точку пополнения равную нулю, что приведет к частым отсутствиям.
Давайте сравним наши две модели с точки зрения MAPE (*) и MAE.
- M имеет MAPE равный 44%.
- Z имеет MAPE равный 33%.
- M имеет MAE равный 0.44.
- Z имеет MAE равный 0.33.
(*) Классическое определение MAPE предполагает деление на ноль, когда фактическое значение равно нулю. Здесь мы предполагаем, что вместо нуля используется значение 1. Альтернативно, можно было бы делить на прогноз (вместо фактического значения) или использовать sMAPE. Эти изменения не влияют на окончательные выводы.
В заключение, согласно как MAPE, так и MAE, модель ноль оказывается предпочтительнее.
Однако можно утверждать, что эта ситуация слишком упрощена и не отражает сложность реального магазина. Это не совсем так. Мы провели бенчмарки для десятков розничных магазинов, и обычно выигрышной моделью (с точки зрения MAE или MAPE) оказывается модель ноль — модель, которая всегда возвращает ноль. Более того, эта модель обычно выигрывает с удобным запасом по сравнению со всеми другими моделями.
На практике, на уровне магазина, использование MAE или MAPE для оценки качества моделей прогнозирования – это призыв к беде: метрика благоприятствует моделям, которые возвращают нули; чем больше нулей, тем лучше. Этот вывод справедлив для практически каждого магазина, который мы анализировали (за исключением немногих товаров с большим объемом продаж, у которых этой проблемы нет).
Читатели, знакомые с метриками точности, могут предложить использовать вместо этого среднеквадратичную ошибку (MSE), которая не будет благоприятствовать модели ноль. Это верно, однако MSE, применяемая к нестабильным данным — а продажи на уровне магазина нестабильны — не является численно устойчивой. На практике любой выброс в истории продаж значительно исказит конечные результаты. Именно поэтому статистики так долго работали над устойчивой статистикой. Бесплатного обеда здесь нет.
Как же оценивать прогнозы на уровне магазина?
Нам потребовалось очень долгое время, чтобы найти удовлетворительное решение проблемы количественной оценки точности прогнозов на уровне магазина. Еще в 2011 году и раньше мы фактически прибегали к хитростям. Вместо того чтобы анализировать данные по дням, когда данные о продажах были слишком разреженными, мы обычно переходили на агрегаты по неделям (или даже по месяцам для крайне разреженных данных). Переходя к более длительным периодам агрегации, мы искусственно увеличивали объем продаж на период, тем самым снова делая MAE пригодной для использования.
Прорыв произошел всего несколько месяцев назад благодаря квантили. По сути, озарением стало следующее: забудьте о прогнозах, важны лишь точки пополнения запасов. Пытаясь оптимизировать наши классические прогнозы по метрикам X, Y или Z, мы пытались решить неправильную задачу.
Подождите! Так как точки повторного заказа вычисляются на основе прогнозов, как можно утверждать, что прогнозы не имеют значения?
Мы не утверждаем, что прогнозы и их точность не важны. Однако мы заявляем, что важна только точность самих точек повторного заказа. Прогноз или любая другая переменная, используемая для вычисления точек повторного заказа, не может оцениваться отдельно. Оценивать следует только точность точек повторного заказа.
Оказывается, что существует метрика для оценки точек повторного заказа: это функция квантильных потерь (пинбол), функция, известная статистикам десятилетиями. Функция квантильных потерь значительно превосходит другие не благодаря своим математическим свойствам, а просто потому, что она соответствует компромиссу между избытком запасов и дефицитом товара.


