Shortage vs. Stock, forecasting accuracy matters
Demand forecasting is a cornerstone of inventory optimization. Yet, the exact relationship between:
- the service level (probability of not having a shortage),
- the safety stock (amount of inventory above the expected demand),
- and the forecasting accuracy
is sometime a bit fuzzy. Hence, let’s try to clarify the situation.
Shortages costs money: customers are dissatisfied and less likely to return, money invested in customer acquisition gets wasted, indirect sales may be lost too, …
Yet inventory costs money too: more stocks mean more working capital, more product obsolescence, more warehousing costs; excess inventory means higher advertising costs and lower selling points, …
Hence, serving customers is a financial tradeoff between the amount of inventory and the amount of shortages.
We are implicitly considering a retail situation here, but a near identical reasoning applies to manufacturers as well.
At this point, it’s still unclear how the forecasting accuracy gets into the picture. In particular, for some companies, it might look like as if no forecasts were produced in the first place. Ex: just min-max reorder policies, and no forecasting.
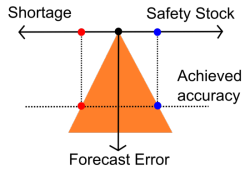
In fact, even if no one in your company explicitly produce forecasts, your inventory still get an implicit forecasting accuracy (illustration here above, the orange triangle representing the constraint). Indeed, it is possible - albeit a bit complicated - to compute the implicit accuracy by companies in your safety stock levels with your shortage frequencies.
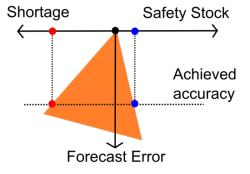
A****djusting the tradeoff either in favor of the service level, or in favor of inventory reduction does not improve the implicit accuracy, as one cost is exchanged for another (illustration on the right, the constraint is rotated, not reduced). Forecasts might be hidden by your processes, it won’t prevent your company to suffer financial losses if those forecasts happen to be incorrect.
Unless there is a deep lack of analysis in your inventory policies, the improvement brought by adjusting the shortage vs. stock tradeoff is expected to be marginal (which could yet represent substantial savings nonetheless, especially if the margin is thin).
In order to improve both sides of the equation, you need better forecasts.
The impact of an improved accuracy is illustrated in the graphic on the left. Compared to the previous situations, we see that reducing the accuracy let you reduce both the frequency of shortages and the amount of safety stock.
The theory roughly says that reducing the forecast error from 1% (relative) can be used to either reduce the shortage frequency from 1% (relative) or reduce the amount of safety stock from 1% (relative).
In practice, there might be obstacles to fully leverage the improvement brought by the extra accuracy, such as the service levels offered by your own suppliers. Yet, with a conservative position, we can still estimate that 1% extra accuracy bring either 0.5% of shortage reduction, or 0.5% of safety stock reduction.
Then again the tradeoff shortage vs. stock can readjusted keeping the new improved accuracy.
Reader Comments (6)
Hi Benhard, Most safety stock formula relies on the variance of the forecasts, yet, as this value is harder to compute, a typical heuristic consists of replacing the variances of the forecasts by the variance of the historical data, but this is an approximation. Hence, if you want to integrate the forecast error into your safety stock calculation, just replace ‘sigma’ coefficient of the historical variance, by the expected variance of the forecasts themselves. Hope it helps.
Joannes Vermorel (7 years ago)
Hi Joannes, I really find this article interesting. I am in the middle of determining inventory policy based on demand forecasting instead of demand history. Most websites shows how to determine inventory policy based on variance of historical data. I wonder how to put forecast error into equation of safety stock. I am sorry if my question out of the topic above. Any kind of help would be appreciated. Thanks Jo. ben
Benhard Adolf (7 years ago)
Actually, it’s not the triangle that really matters but its two edges (right and left). Intuitively, the primary angle is a constant that cannot be changed, so if you move one edge, the other one moves too. The shape somehow looks like a triangle, other only two edges and one angle really matter.
Joannes Vermorel (8 years ago)
Dear Joannes, I find your explanation very clear, but I do not understand the orange triangle. It represents the constraint. But I do not get it in the drawing. Do you have an extra word of explanation. Thank you
Piet Buyck (8 years ago)
Hi Achyut, in the classical safety stock model, we typically assume a normal distribution (Gaussian distribution) of the demand. The normal distribution is defined by two parameters: its mean and its variance. The amount of safety stock (aka the extra stock above the mean demand level), for a given service level, is linearly proportional to the variance. Hence, if you reduce the variance (aka the forecast error) of 1%, you also reduce the safety stock of 1% in this ideal model. Then, the other part about reducing the shortage frequency while maintaining the same amount of safety stock is more complicated, and would require a blog post of its own. I will try to get back to that one when I get the time.
Joannes Vermorel (8 years ago)
Hi Joannes, It is a very useful article. I just need some more clarity on one of the things which you have mentioned in this article. You have said that “The theory roughly says that reducing the forecast error from 1% (relative) can be used to either reduce the shortage frequency from 1% (relative) or reduce the amount of safety stock from 1% (relative).” Can you please elaborate on the concept on which it is based on? I understand that a better forecast would reduce the inventory levels, but i am finding it difficult to quantify it. Thanks in advance
Achyut Koushik A (8 years ago)


