Pénurie vs. Stock, la précision des prévisions compte

Joannes Vermorel

La prévision de la demande est une pierre angulaire de l’optimisation de stocks. Pourtant, la relation exacte entre:

• le taux de service (probabilité de ne pas avoir de rupture),
• le stocks de sécurité (quantité de stocks au-dessus de la demande prévue),
• et la précision des prévisions

est parfois un peu floue. Par conséquent, essayons de clarifier la situation.

Les ruptures coûtent de l’argent : les clients sont insatisfaits et moins susceptibles de revenir, l’argent investi dans l’acquisition de clients est gaspillé, des ventes indirectes peuvent également être perdues, …

Or, les coûts de stocks coûtent de l’argent aussi : plus de stocks signifient plus de fonds de roulement, plus d’obsolescence de produits, plus de coûts d’entreposage ; un excès de stocks signifie des coûts publicitaires plus élevés et des points de vente plus bas, …

Par conséquent, servir les clients est un compromis financier entre la quantité de stocks et le nombre de ruptures.

Nous considérons ici implicitement une situation de commerce de détail, mais un raisonnement presque identique s’applique également aux fabricants.

À ce stade, il n’est toujours pas clair comment la précision des prévisions entre en jeu. En particulier, pour certaines entreprises, il pourrait sembler qu’aucune prévision n’ait été produite dès le départ. Exemple : simplement des politiques de min-max réapprovisionnement, et aucune prévision.

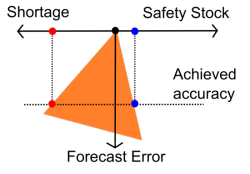
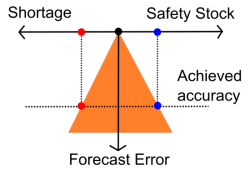
En fait, même si personne dans votre entreprise ne produit explicitement de prévisions, vos stocks bénéficient tout de même d’une précision de prévision implicite (illustration ci-dessus, le triangle orange représentant la contrainte). En effet, il est possible - quoique un peu compliqué - de calculer la précision implicite par les entreprises dans vos niveaux de stocks de sécurité avec vos fréquences de rupture.

Ajuster le compromis soit en faveur du taux de service, soit en faveur de la réduction des stocks, n’améliore pas la précision implicite, car un coût est échangé contre un autre (illustration à droite, la contrainte est pivotée, non réduite). Les prévisions peuvent être masquées par vos processus, cela n’empêchera pas votre entreprise de subir des pertes financières si ces prévisions se révèlent incorrectes.

À moins qu’il n’y ait un manque flagrant d’analyse dans vos politiques de stocks, l’amélioration apportée par l’ajustement du compromis rupture vs. stock devrait être marginale (ce qui pourrait néanmoins représenter des économies substantielles, surtout si la marge est mince).

Afin d’améliorer les deux côtés de l’équation, vous avez besoin de meilleures prévisions.

L’impact d’une précision améliorée est illustré dans le graphique à gauche. Comparé aux situations précédentes, nous constatons que réduire la précision vous permet de réduire à la fois la fréquence des ruptures et la quantité de stocks de sécurité.

La théorie dit approximativement que la réduction de l’erreur de prévision de 1 % (relative) peut être utilisée soit pour réduire la fréquence des ruptures de 1 % (relative), soit pour réduire la quantité de stocks de sécurité de 1 % (relative).

En pratique, il peut y avoir des obstacles à exploiter pleinement l’amélioration apportée par la précision supplémentaire, comme les taux de service offerts par vos propres fournisseurs. Pourtant, avec une position conservatrice, nous pouvons encore estimer qu’une précision supplémentaire de 1 % apporte soit une réduction de 0,5 % des ruptures, soit une réduction de 0,5 % des stocks de sécurité.

Ensuite, le compromis rupture vs. stock peut être réajusté en conservant la nouvelle précision améliorée.

Commentaires des lecteurs (6)

Salut Benhard, La plupart des formules de stocks de sécurité reposent sur la variance des prévisions, mais comme cette valeur est plus difficile à calculer, une heuristique typique consiste à remplacer les variances des prévisions par la variance des données historiques, ce qui reste une approximation. Ainsi, si vous souhaitez intégrer l’erreur de prévision dans le calcul de vos stocks de sécurité, remplacez simplement le coefficient ‘sigma’ de la variance historique par la variance attendue des prévisions elles-mêmes. J’espère que cela aidera. Joannes Vermorel (il y a 7 ans)

Salut Joannes, Je trouve vraiment cet article intéressant. Je suis en train de déterminer une politique de stocks basée sur la prévision de la demande plutôt que sur l’historique de la demande. La plupart des sites montrent comment déterminer une politique de stocks basée sur la variance des données historiques. Je me demande comment intégrer l’erreur de prévision dans l’équation des stocks de sécurité. Je suis désolé si ma question s’écarte du sujet ci-dessus. Toute aide serait appréciée. Merci Jo. ben Benhard Adolf (il y a 7 ans)

En réalité, ce n’est pas le triangle qui importe vraiment, mais ses deux côtés (droit et gauche). Intuitivement, l’angle principal est une constante qui ne peut pas être modifiée, donc si vous déplacez un côté, l’autre se déplace également. La forme ressemble en quelque sorte à un triangle, alors que seuls deux côtés et un angle importent réellement. Joannes Vermorel (il y a 8 ans)

Cher Joannes, Je trouve votre explication très claire, mais je ne comprends pas le triangle orange. Il représente la contrainte. Mais je ne le saisis pas dans le dessin. Auriez-vous un mot supplémentaire d’explication ? Merci Piet Buyck (il y a 8 ans)

Salut Achyut, dans le modèle classique des stocks de sécurité, nous supposons généralement une distribution normale (distribution gaussienne) de la demande. La distribution normale est définie par deux paramètres : sa moyenne et sa variance. La quantité de stocks de sécurité (c’est-à-dire le stock supplémentaire au-dessus du niveau de demande moyen), pour un taux de service donné, est proportionnelle de manière linéaire à la variance. Ainsi, si vous réduisez la variance (c’est-à-dire l’erreur de prévision) de 1 %, vous réduisez également les stocks de sécurité de 1 % dans ce modèle idéal. Ensuite, l’autre aspect concernant la réduction de la fréquence des ruptures tout en maintenant la même quantité de stocks de sécurité est plus compliqué, et nécessiterait un article de blog à part entière. J’essaierai d’y revenir dès que j’aurai le temps. Joannes Vermorel (il y a 8 ans)

Salut Joannes, C’est un article très utile. J’aurais juste besoin de plus de précisions sur l’un des points que vous avez mentionnés dans cet article. Vous avez dit que “La théorie dit approximativement que la réduction de l’erreur de prévision de 1 % (relative) peut être utilisée soit pour réduire la fréquence des ruptures de 1 % (relative), soit pour réduire la quantité de stocks de sécurité de 1 % (relative).” Pourriez-vous s’il vous plaît élaborer sur le concept sur lequel c’est basé ? Je comprends qu’une meilleure prévision réduirait les niveaux de stocks, mais j’ai du mal à le quantifier. Merci d’avance Achyut Koushik A (il y a 8 ans)