Selektive Pfad-Automatische Differenzierung: Jenseits gleichmäßiger Verteilung beim Backpropagation-Dropout
Die unglaubliche Effektivität des stochastischen Gradientenabstiegs (SGD) ist vermutlich die bedeutendste maschinelles Lernen Entdeckung der 2010er Jahre. SGD treibt nahezu alle jüngsten Durchbrüche im maschinellen Lernen an. Konzeptuell ist SGD bemerkenswert einfach: Verarbeite deinen Datensatz einen Datenpunkt nach dem anderen und passe bei jedem Punkt die Modellparameter in die durch diesen Punkt vorgegebene Richtung an. Technischer ausgedrückt wird die „Richtung“ als Gradient angegeben, und das „Anpassen“ erfolgt durch einen kleinen Skalierungsfaktor, der üblicherweise als Lernrate bezeichnet wird.
Obwohl die SGD-Technik aus den 1950er Jahren stammt, blieb sie weitgehend eine obskure und kaum genutzte Methode, bis sie mit dem Aufkommen des Deep Learning an Bedeutung gewann. Die Gründe, weshalb diese Technik funktioniert, waren nicht klar und sind es bis zu einem gewissen Grad immer noch nicht. Da das Ziel darin besteht, den Modellfehler für den gesamten Datensatz zu minimieren, ist es nicht offensichtlich, dass die isolierte Auswahl einzelner Punkte mehr als nur numerischen Unsinn liefern sollte.
Heutzutage ist allgemein anerkannt, dass die Effektivität von SGD – also warum es funktioniert – auf zwei Faktoren beruht. Erstens, obwohl der durch SGD erhaltene Gradient sehr verrauscht ist – jeder Schritt berücksichtigt nur einen einzelnen Datenpunkt – ist dieser Gradient äußerst kostengünstig. Es hat sich gezeigt, dass bei einem gegebenen Budget an Rechenressourcen zahlreiche Aktualisierungen mit minderwertigen Gradienten die Anwendung einer einzigen Aktualisierung mit hochwertigem Gradienten bei Weitem übertreffen. Zweitens helfen die verrauschten Aktualisierungen dem Modell, den weiten Plateaus der numerischen Gleichgültigkeit, die in höheren Dimensionen existieren, zu entkommen. Tatsächlich besteht in höheren Dimensionen der Kern der Optimierung längst nicht mehr – wie lange angenommen – darin, lokalen Minima zu entkommen, sondern lokalen Plateaus, also Bereichen, in denen sich der Verlust kaum ändert.

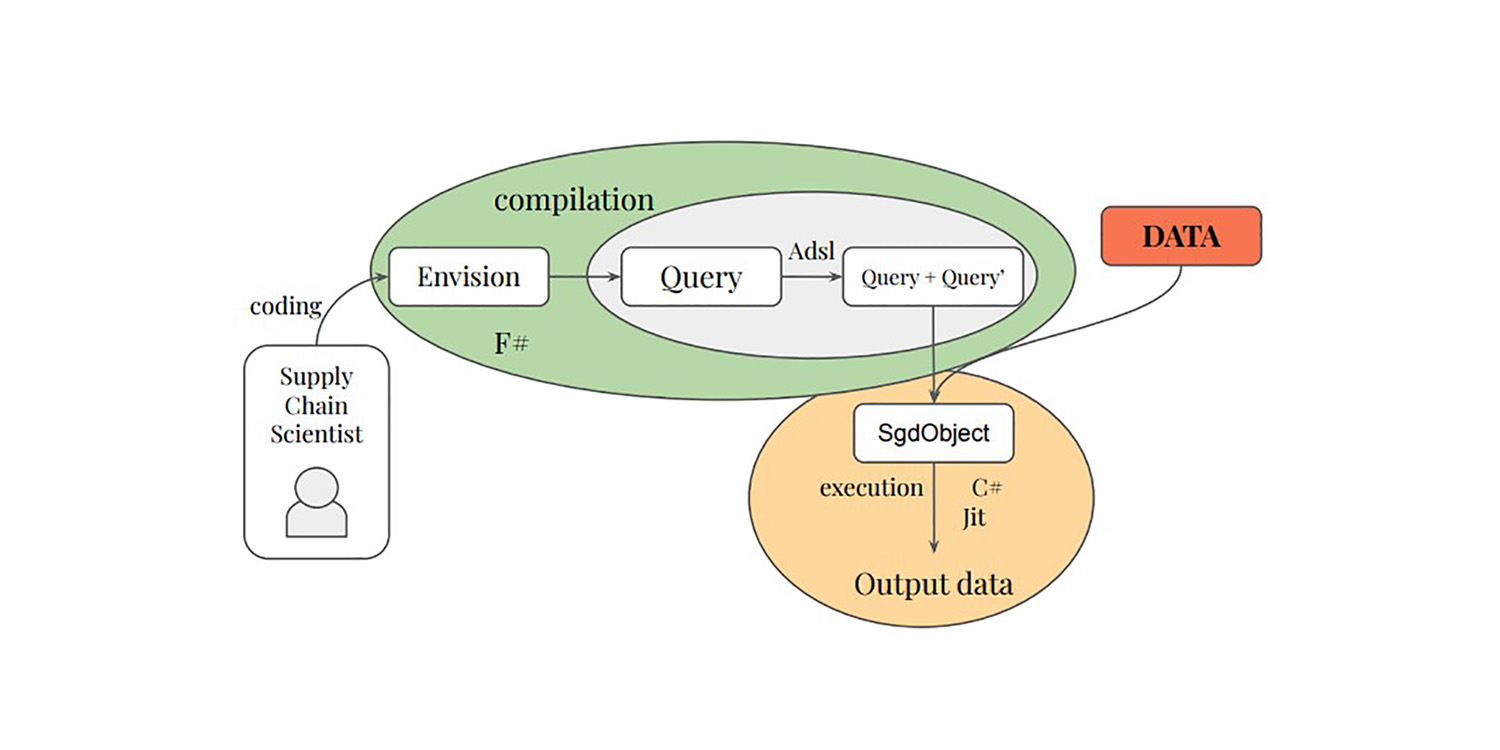
Einige von uns, darunter Paul Peseux und Victor Nicollet, haben beschlossen, diese Ideen weiter voranzutreiben. Wenn SGD funktioniert, indem es Gradientenqualität gegen Rechen-Effizienz eintauscht, wie wäre es, dieses Prinzip noch weiter auszubauen? Wie wäre es mit einem Sub-Datenpunkt-Gradienten, der sogar noch günstiger in der Berechnung ist, wenn auch noch verrauschter? Genau das wurde mit der Selektiven Pfad-Automatischen Differenzierung (SPAD) erreicht. SPAD greift einen der Grundpfeiler des modernen maschinellen Lernparadigmas auf, allerdings mit einem Twist: Ein Datenpunkt kann gradientenmäßig durch seine Evaluationspfade „aufgeteilt“ werden.
Das nachfolgende Papier stellt einen Beitrag von Paul Peseux (Lokad), Victor Nicollet (Lokad), Maxime Berar (Litis) und Thierry Paquet (Litis) vor.
Title: Selektive Pfad-Automatische Differenzierung: Jenseits gleichmäßiger Verteilung beim Backpropagation-Dropout
Autoren: Paul Peseux, Maxime Berar, Thierry Paquet, Victor Nicollet
Abstract: Dieses Papier stellt die Selektive Pfad-Automatische Differenzierung (SPAD) vor, einen neuartigen Ansatz zur Reduzierung des Speicherverbrauchs und zur Abschwächung von Overfitting in gradientenbasierten Modellen für eingebettete künstliche Intelligenz. SPAD erweitert die bestehende Randomized Automatic Differentiation, die von Oktay et al. vorgeschlagen wurde und zufällige Pfade durch den Backpropagation-Graphen mittels Matrixinjektion zieht, indem alternative Wahrscheinlichkeitsverteilungen im Backpropagation-Graphen ermöglicht werden, wodurch Lernleistung und Speichermanagement verbessert werden. In einer spezifischen Iteration bewertet und ordnet SPAD mehrere Pfade innerhalb des Backpropagation-Graphen. In nachfolgenden Iterationen folgt es bevorzugt diesen höher bewerteten Pfaden. Diese Arbeit stellt zudem eine compilierungsbasierte Technik vor, die modellagnostischen Zugang zu zufälligen Pfaden ermöglicht und damit die Generalisierbarkeit über verschiedene Modellarchitekturen hinweg sicherstellt, nicht nur auf tiefe Modelle beschränkt. Experimentelle Auswertungen, die an verschiedenen Optimierungsfunktionen durchgeführt wurden, zeigen eine verbesserte Minimierungsleistung bei Einsatz von SPAD. Darüber hinaus mildern Deep-Learning-Experimente mit SPAD das Overfitting erheblich, was Vorteile bietet, die den herkömmlichen Dropout-Methoden ähneln, jedoch mit einem gleichzeitigen Rückgang des Speicherverbrauchs. Wir schließen mit einer Diskussion der einzigartigen stochastischen Implikationen unserer Arbeit und des Potenzials, damit andere stochastische Techniken in diesem Bereich zu verstärken.