Ottimizzazione matematica per supply chain - Lezione 4.3

00:18 Introduzione
02:18 Contesto
12:08 Perché ottimizzare? 1/2 Previsione con Holt-Winters
17:32 Perché ottimizzare? 2/2 - Problema di instradamento dei veicoli
20:49 La storia finora
22:21 Scienze ausiliarie (ripasso)
23:45 Problemi e soluzioni (ripasso)
27:12 Ottimizzazione matematica
28:09 Convessità
34:42 Stocasticità
42:10 Multi-obiettivo
46:01 Progettazione del solver
50:46 Lezioni di Deep Learning
01:10:35 Ottimizzazione matematica
01:10:58 “True” programming
01:12:40 Ricerca locale
01:19:10 Discesa del gradiente stocastico
01:26:09 Differenziazione automatica
01:31:54 Programmazione differenziale (circa 2018)
01:35:36 Conclusione
01:37:44 Lezione in arrivo e domande dal pubblico

Descrizione

Ottimizzazione matematica è il processo di minimizzazione di una funzione matematica. Quasi tutte le moderne tecniche di apprendimento statistico – ossia la previsione se adottiamo una supply chain perspective – si fondano sull’ottimizzazione matematica. Inoltre, una volta stabilite le previsioni, anche l’identificazione delle decisioni più redditizie si basa, nel suo nucleo, sull’ottimizzazione matematica. I problemi della supply chain coinvolgono frequentemente molte variabili. Sono solitamente di natura stocastica. L’ottimizzazione matematica è una pietra miliare di una moderna pratica di supply chain.

Trascrizione completa

Benvenuti a questa serie di lezioni sulla supply chain. Sono Joannes Vermorel, e oggi presenterò “Mathematical Optimization for Supply Chain.” L’ottimizzazione matematica è il metodo ben definito, formalizzato e computazionalmente praticabile per identificare la migliore soluzione per un dato problema. Tutti i problemi di previsione possono essere considerati come problemi di ottimizzazione matematica. Tutte le situazioni di decision-making sia nella supply chain che al di fuori possono essere considerate problemi di ottimizzazione matematica. In realtà, la prospettiva dell’ottimizzazione matematica è così radicata nella nostra visione moderna del mondo che è diventato molto difficile definire il verbo “to optimize” al di fuori del ristretto ambito offerto dal paradigma dell’ottimizzazione matematica.

Ora, la letteratura scientifica sull’ottimizzazione matematica è immensa, così come l’ecosistema software che fornisce gli strumenti per l’ottimizzazione matematica. Sfortunatamente, la maggior parte di esso è di scarso utilizzo e rilevanza per quanto riguarda la supply chain. L’obiettivo di questa lezione sarà duplice: in primo luogo, vogliamo capire come approcciare l’ottimizzazione matematica per ottenere qualcosa di veramente prezioso e di uso pratico da una prospettiva supply chain. Il secondo aspetto consisterà nell’identificare, in questo vasto panorama, alcuni degli elementi più preziosi che esistono.

La definizione formale dell’ottimizzazione matematica è semplice: si considera una funzione che solitamente viene chiamata la loss function, e questa funzione assume valori reali, producendo semplicemente numeri. Ciò che si desidera è identificare l’input (X0) che rappresenta il valore migliore in grado di minimizzare la loss function. Questo è tipicamente il paradigma dell’ottimizzazione matematica, ed è ingenuamente semplice. Vedremo che ci sono molte cose da dire su questa prospettiva generale.

Questo campo, credo, quando si pensa all’ottimizzazione matematica applicata, si è sviluppato principalmente sotto il nome di ricerca operativa, che definiamo più specificamente come la classica ricerca operativa che si è estesa dagli anni ‘40 fino alla fine degli anni ‘70 del XX secolo. L’idea è che la classica ricerca operativa, a differenza dell’ottimizzazione matematica, si occupava realmente dei problemi aziendali. L’ottimizzazione matematica si interessa della forma generale del problema di ottimizzazione, ben meno se il problema abbia o meno una rilevanza aziendale. Al contrario, la classica ricerca operativa consisteva essenzialmente nell’ottimizzazione, ma non su qualsiasi tipo di problema – bensì su problemi identificati come rilevanti per le aziende.

Curiosamente, siamo passati dalla ricerca operativa all’ottimizzazione matematica in maniera molto simile a come siamo passati dalla previsione, che emerse all’inizio del XX secolo come campo interessato alla previsione generale dei livelli di attività economica futuri, tipicamente associata alle previsioni di time series. Questo ambito è stato essenzialmente superato dal machine learning, che si occupa in maniera più ampia di effettuare predizioni su una gamma molto più vasta di problemi. Potremmo dire che abbiamo avuto, in senso lato, lo stesso tipo di transizione dalla ricerca operativa all’ottimizzazione matematica quanto quella avvenuta dalla previsione al machine learning. Ora, quando ho detto che l’era classica della ricerca operativa durò fino alla fine degli anni ‘70, avevo in mente una data molto specifica. Nel febbraio 1979, Russell Ackoff pubblicò un articolo sorprendente intitolato “The Future of Operational Research is Past.” Per comprendere questo articolo, che credo sia veramente una pietra miliare nella storia della scienza dell’ottimizzazione, bisogna capire che Russell Ackoff è essenzialmente uno dei padri fondatori della ricerca operativa.

Quando pubblicò questo articolo, non era più un giovane; aveva 60 anni. Ackoff nacque nel 1919 e aveva trascorso praticamente tutta la sua carriera lavorando sulla ricerca operativa. Quando pubblicò il suo articolo, sosteneva fondamentalmente che la ricerca operativa aveva fallito. Non solo non aveva prodotto risultati, ma l’interesse nel settore era in calo, tanto che alla fine degli anni ‘90 l’interesse era minore rispetto a quello di 20 anni prima.

Ciò che è molto interessante da capire è che la causa non risiede affatto nel fatto che i computer dell’epoca fossero molto più deboli rispetto a quelli odierni. Il problema non ha nulla a che fare con la limitazione in termini di potenza di calcolo. Siamo alla fine degli anni ‘70; i computer erano molto modesti rispetto a quelli che abbiamo oggi, ma erano comunque in grado di eseguire milioni di operazioni aritmetiche in un lasso di tempo ragionevole. Il problema non è legato alla limitazione della potenza di calcolo, specialmente in un’epoca in cui essa progredisce a ritmi incredibilmente veloci.

A proposito, questo articolo è una lettura fantastica. Consiglio vivamente al pubblico di leggerlo; potete trovarlo facilmente utilizzando il vostro motore di ricerca preferito. L’articolo è molto accessibile e ben scritto. Sebbene i tipi di problemi che Ackoff evidenzia in questo articolo risuonino ancora con forza, anche dopo quattro decenni, in molti modi esso è molto presciente di molti dei problemi che ancora affliggono le supply chain odierne.

Allora, qual è il problema? Il problema è che questo paradigma, in cui si prende una funzione e la si ottimizza, può dimostrare che il processo di ottimizzazione identifica una soluzione buona o forse ottimale. Tuttavia, come si può dimostrare che la loss function che si sta effettivamente ottimizzando sia di interesse per l’azienda? Il problema è che, quando dico che possiamo ottimizzare un determinato problema o una determinata funzione, cosa succede se ciò che stiamo ottimizzando è in realtà una fantasia? E se questo elemento non avesse nulla a che fare con la realtà dell’azienda che si sta cercando di ottimizzare?

Qui risiede il nocciolo del problema, ed è la ragione per cui quei primi tentativi hanno essenzialmente fallito. Perché si è scoperto che, quando si concepisce una qualche espressione matematica destinata a rappresentare l’interesse dell’azienda, ciò che si ottiene è una fantasia matematica. Questo è letteralmente ciò che Russell Ackoff sottolinea in questo articolo, ed egli, al punto della sua carriera in cui aveva giocato a questo gioco per molto tempo, riconosceva che stava conducendo a un vicolo cieco. Nel suo articolo, condivide l’opinione che il campo aveva fallito, e propone la sua diagnosi, ma non ha molte soluzioni da offrire. È molto interessante perché uno dei padri fondatori, un ricercatore molto rispettato e riconosciuto, afferma che l’intero campo di ricerca è un vicolo cieco. Avrà il resto della sua vita, che era ancora abbastanza lunga, a transitare completamente da una prospettiva quantitativa sull’ottimizzazione aziendale verso una prospettiva qualitativa. Trascorrerà gli ultimi tre decenni della sua vita adottando metodi qualitativi e riuscirà comunque a produrre lavori molto interessanti nella seconda parte della sua vita dopo questo punto di svolta.

Ora, per quanto riguarda questa serie di lezioni, cosa facciamo, dato che i punti sollevati da Russell Ackoff sulla ricerca operativa rimangono ancora molto validi al giorno d’oggi? In realtà, ho già iniziato ad affrontare i maggiori problemi che Ackoff evidenziava e, al tempo, lui e i suoi colleghi non avevano soluzioni da proporre. Potevano diagnosticare il problema, ma non avevano una soluzione. In questa serie di lezioni, le soluzioni che propongo sono di natura metodologica, proprio come il fatto che Ackoff sottolinea l’esistenza di un profondo problema metodologico in questa prospettiva della ricerca operativa.

I metodi che propongo sono essenzialmente duplice: da un lato, il personale della supply chain, e dall’altro, il metodo denominato experimental optimization che risulta davvero complementare all’ottimizzazione matematica. Inoltre, posiziono – a differenza della ricerca operativa, che sostiene di avere un interesse o una rilevanza aziendale – il modo in cui affronto il problema oggi non attraverso l’angolo o le lenti della ricerca operativa, ma attraverso quelle dell’ottimizzazione matematica, che posiziono come una scienza ausiliaria pura per la supply chain. Dico che non c’è nulla di intrinsecamente fondamentale nell’ottimizzazione matematica per la supply chain; è semplicemente di interesse fondamentale. È solo un mezzo, non un fine. È qui che risiede la differenza. Il concetto può essere molto semplice, ma ha una grande importanza quando si tratta di ottenere risultati a livello predittivo con l’insieme.

Ora, perché vogliamo addirittura ottimizzare? La maggior parte degli algoritmi di previsione ha alla sua base un problema di ottimizzazione matematica. Su questo schermo, ciò che potete vedere è il classico algoritmo di previsione per serie temporali Holt-Winters moltiplicativo. Questo algoritmo è principalmente di interesse storico; non consiglierei a nessuna supply chain attuale di sfruttare questo specifico algoritmo. Ma per semplicità, questo è un metodo parametrico molto semplice, ed è così conciso che può essere interamente visualizzato su un unico schermo. Non è nemmeno così prolisso.

Tutte le variabili che vedete sullo schermo sono semplici numeri; non sono coinvolti vettori. Essenzialmente, Y(t) è la vostra stima; questa è la previsione per la vostra serie temporale. Qui sullo schermo, si prevede H periodi in avanti, quindi H rappresenta l’orizzonte. E potete pensare di lavorare su Y(t), che è essenzialmente la vostra serie temporale. Potete pensare a dati di vendita aggregati settimanalmente o mensilmente. Questo modello ha essenzialmente tre componenti: Lt, che rappresenta il livello (avete un livello per periodo), Bt, che rappresenta il trend, e St, che è un componente stagionale. Quando dite che volete apprendere il modello Holt-Winters, disponete di tre parametri: alpha, beta e gamma. Questi tre parametri sono essenzialmente semplici numeri compresi tra zero e uno. Quindi, avete tre parametri, tutti numeri tra zero e uno, e quando dite che volete applicare l’algoritmo Holt-Winters, significa semplicemente che identificherete i valori appropriati per questi tre parametri, e basta. L’idea è che questi parametri, alpha, beta e gamma, saranno i migliori se riescono a minimizzare l’errore da voi specificato per la previsione. Su questo schermo, potete vedere un errore quadratico medio, che è molto classico.

Il punto dell’ottimizzazione matematica è concepire un metodo per identificare i valori corretti dei parametri per alpha, beta e gamma. Cosa possiamo fare? Beh, il metodo più semplice e basilare è qualcosa come la grid search. La grid search prevede di esplorare tutti i valori. Poiché questi sono numeri frazionari, esiste un numero infinito di valori, perciò si sceglie una risoluzione, diciamo degli incrementi di 0,1, e si procede per passi di 0,1. Dato che abbiamo tre variabili comprese tra 0 e 1, con incrementi di 0,1 si arriva a circa 1.000 iterazioni per identificare il valore migliore, considerando questa risoluzione.

Tuttavia, questa risoluzione è piuttosto debole. 0,1 offre circa una risoluzione del 10% rispetto alla scala dei parametri. Quindi, magari vorrete utilizzare 0,01, che è molto migliore; significa una risoluzione dell’1%. Tuttavia, se fate così, il numero di combinazioni esplode veramente. Si passa da 1.000 combinazioni a un milione di combinazioni, ed ecco qual è il problema della grid search: molto rapidamente si raggiunge un muro combinatorio, con un numero enorme di opzioni.

L’ottimizzazione matematica mira a concepire algoritmi che offrano un rendimento maggiore per le risorse computazionali impiegate nel problema. Si può ottenere una soluzione molto migliore rispetto alla semplice ricerca esaustiva? La risposta è sì, assolutamente.

Quindi, cosa possiamo fare in questo caso per ottenere effettivamente una soluzione migliore investendo meno risorse computazionali? Innanzitutto, potremmo usare una sorta di gradiente. L’intera espressione per Holt-Winters è completamente differenziabile, eccetto per un’unica divisione che è un piccolo caso limite relativamente facile da gestire. Quindi, questa intera espressione, compresa la funzione di perdita, è interamente differenziabile. Potremmo usare un gradiente per guidare la nostra ricerca; quella sarebbe un’opzione.

Un altro approccio direbbe che in supply chain, potresti avere tonnellate di serie temporali. Quindi, forse invece di trattare ogni singola serie temporale in maniera indipendente, ciò che vuoi fare è una grid search per le prime 1.000 serie temporali, ed investirai, e poi identificherai le combinazioni per alpha, beta e gamma che siano buone. Poi, per tutte le altre serie temporali, sceglierai semplicemente da questa lista ristretta di candidati per identificare la soluzione migliore.

Vedi, ci sono moltissime idee semplici su come effettivamente poter fare molto meglio che limitarsi a un approccio di grid search puro, e l’essenza dell’ottimizzazione matematica, oltre a vari tipi di problemi decisionali, può essere vista tipicamente come un problema di ottimizzazione matematica.

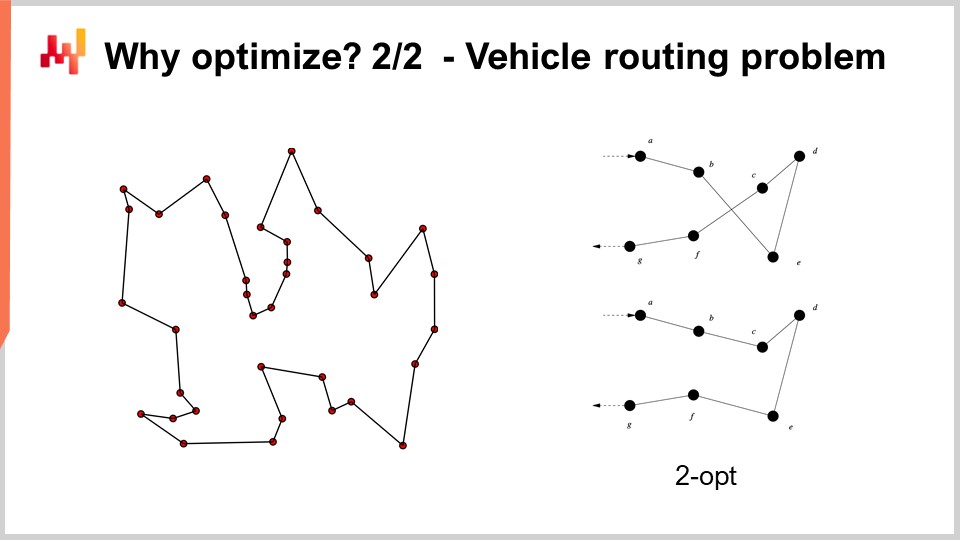
Ad esempio, il problema del vehicle routing che puoi vedere sullo schermo può essere visto come un problema di ottimizzazione matematica. Si tratta di scegliere l’elenco dei punti. Non ho riportato la versione formale del problema perché è relativamente variabile e non offre molti spunti. Ma se vuoi pensarci, puoi semplicemente dire: “Ho dei punti, posso assegnare a ciascun punto una specie di pseudo-rango, che è semplicemente un punteggio, e poi ho un algoritmo che ordina tutti i punti in base ai pseudo-ranghi in ordine ascendente, e questo è il mio percorso.” L’obiettivo dell’algoritmo sarà identificare i valori di quei pseudo-ranghi che ti danno i percorsi migliori.

Ora, con questo problema, vediamo che abbiamo una situazione in cui improvvisamente la grid search non è nemmeno lontanamente un’opzione. Abbiamo dozzine di punti e, se provassimo tutte le combinazioni, sarebbe decisamente troppo. Inoltre, il gradiente non ci sarà d’aiuto, almeno non è ovvio come potrebbe esserlo, perché il problema è di natura molto discreta, e non esiste qualcosa che assomigli a una discesa del gradiente per questo tipo di problema.

Tuttavia, risulta che se vogliamo affrontare questo tipo di problema, esistono euristiche molto potenti che sono state identificate in letteratura. Ad esempio, l’euristica two-opt, pubblicata da Croes nel 1958, ti offre un approccio molto semplice. Parti da un percorso casuale, e in questo percorso, ogni volta che il percorso si incrocia con se stesso, applichi una permutazione per rimuovere l’incrocio. Quindi, parti da un percorso casuale, e al primo incrocio che osservi, esegui la permutazione per eliminarlo, e poi ripeti il processo. Continui con l’euristica finché non rimane più alcun incrocio. Quello che otterrai da questa euristica molto semplice è in realtà una soluzione molto buona. Potrebbe non essere ottimale nel vero senso matematico, quindi non è necessariamente la soluzione perfetta; tuttavia, è una soluzione molto valida, e puoi ottenerla con una quantità relativamente minima di risorse computazionali.

Il problema con l’euristica two-opt è che, pur essendo molto raffinata, è incredibilmente specifica per questo particolare problema. Ciò che interessa veramente nell’ottimizzazione matematica è identificare metodi che funzionino su vaste classi di problemi, anziché disporre di un’euristica che funzioni solo per una versione specifica di un problema. Quindi, vogliamo avere metodi molto generali.

Ora, la storia fino ad ora in questa serie di lezioni: questa lezione fa parte di una serie, e questo presente capitolo è dedicato alle scienze ausiliarie della supply chain. Nel primo capitolo, ho presentato le mie opinioni sulla supply chain sia come campo di studio che come pratica. Il secondo capitolo è stato dedicato alla metodologia, e in particolare abbiamo introdotto una metodologia di massima rilevanza per la presente lezione, che è l’ottimizzazione sperimentale. Questa è la chiave per affrontare il problema molto valido identificato da Russell Ackoff decenni fa. Il terzo capitolo è interamente dedicato al personale della supply chain. In questa lezione, ci concentriamo sull’identificare il problema che stiamo per risolvere, anziché mescolare insieme soluzione e problema. In questo quarto capitolo, stiamo esaminando tutte le scienze ausiliarie della supply chain. C’è una progressione dal livello più basso in termini di hardware, passando a quello degli algoritmi, fino all’ottimizzazione matematica. Stiamo progredendo in termini di livelli di astrazione lungo tutta questa serie.

Solo un breve riepilogo sulle scienze ausiliarie: esse offrono una prospettiva sulla supply chain stessa. La presente lezione non riguarda la supply chain in sé, ma piuttosto una delle scienze ausiliarie della supply chain. Questa prospettiva fa una differenza significativa rispetto alla classica visione della ricerca operativa, che doveva essere un fine, a differenza dell’ottimizzazione matematica, che è un mezzo per un fine ma non un fine in sé, almeno per quanto riguarda la supply chain. L’ottimizzazione matematica non si interessa delle specificità aziendali, e la relazione tra l’ottimizzazione matematica e la supply chain è simile al rapporto tra la chimica e la medicina. Da una prospettiva moderna, non è necessario essere un chimico brillante per essere un ottimo medico; tuttavia, un medico che afferma di non conoscere nulla di chimica potrebbe sembrare sospetto.

L’ottimizzazione matematica presuppone che il problema sia noto. Non si interessa della validità del problema, ma si concentra nel trarre il massimo da ciò che è possibile fare per un dato problema in termini di ottimizzazione. In un certo senso, è come un microscopio – molto potente ma con un campo di messa a fuoco incredibilmente limitato. Il pericolo, come abbiamo accennato nella discussione sul futuro della ricerca operativa, è che se punti il microscopio nel posto sbagliato, potresti distrarti con sfide intellettuali interessanti ma, alla fine, irrilevanti.

Ecco perché l’ottimizzazione matematica deve essere utilizzata in combinazione con l’ottimizzazione sperimentale. L’ottimizzazione sperimentale, che abbiamo trattato nella lezione precedente, è il processo mediante il quale puoi iterare, grazie al feedback del mondo reale, verso versioni migliori del problema stesso. L’ottimizzazione sperimentale è un processo per mutare non la soluzione, ma il problema, in modo che iterativamente tu possa convergere verso un problema ben definito. Questo è il nocciolo della questione, ed è qui che Russell Ackoff e i suoi colleghi dell’epoca non avevano una soluzione. Avevano gli strumenti per ottimizzare un determinato problema, ma non gli strumenti per modificarlo fino a renderlo valido. Se prendi un problema matematico come lo puoi scrivere nella tua torre d’avorio, senza il feedback del mondo reale, quello che ottieni è una fantasia. Il tuo punto di partenza, quando inizi un processo di ottimizzazione sperimentale, è semplicemente una fantasia. Ci vuole il feedback del mondo reale per farlo funzionare. L’idea è oscillare tra ottimizzazione matematica e ottimizzazione sperimentale. In ogni fase del processo di ottimizzazione sperimentale, utilizzerai gli strumenti dell’ottimizzazione matematica. L’obiettivo è minimizzare sia le risorse computazionali che gli sforzi ingegneristici, permettendo al processo di iterare verso la successiva versione del problema.

In questa lezione, affineremo innanzitutto la nostra comprensione della prospettiva dell’ottimizzazione matematica. La definizione formale è ingannevolmente semplice, ma ci sono complessità di cui dobbiamo essere consapevoli per ottenere una rilevanza pratica per scopi della supply chain. Esploreremo poi due ampie classi di solutori che rappresentano lo stato dell’arte nell’ottimizzazione matematica da una prospettiva supply chain.

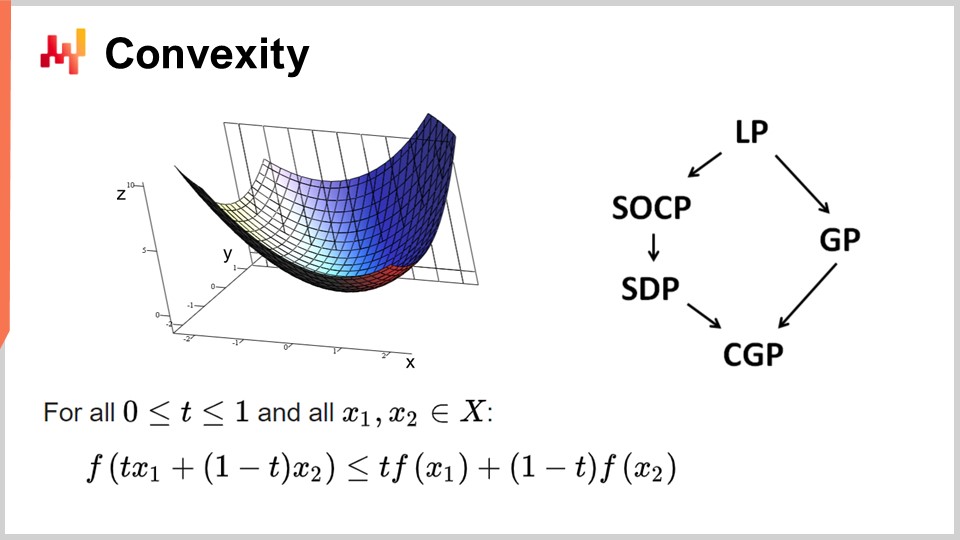
Innanzitutto, discutiamo della convessità e dei primi studi nell’ottimizzazione matematica. La ricerca operativa inizialmente si è concentrata su funzioni di perdita convesse. Una funzione si dice convessa se rispetta certe proprietà. Intuitivamente, una funzione è convessa se, per ogni due punti sul dominio definito dalla funzione, la linea retta che collega quei punti sarà sempre al di sopra dei valori assunti dalla funzione tra quei punti.

La convessità è fondamentale per consentire una vera ottimizzazione matematica, in cui è possibile dimostrare dei risultati. Intuitivamente, quando hai una funzione convessa, significa che per ogni punto della funzione (ogni soluzione candidata), puoi sempre guardarti intorno e trovare una direzione in cui scendere. Non importa da dove inizi, puoi sempre scendere, e scendere è sempre una mossa vantaggiosa. L’unico punto in cui non puoi scendere ulteriormente è essenzialmente il punto ottimale. Sto semplificando qui; ci sono casi limite in cui si possono avere soluzioni non uniche o addirittura nessuna soluzione. Ma, mettendo da parte alcuni casi limite, l’unico punto in cui non puoi ulteriormente ottimizzare con una funzione convessa è quello ottimale. Altrimenti, puoi sempre scendere, e scendere è sempre una buona scelta.

C’è stata un’enorme quantità di ricerca sulle funzioni convesse, e nel corso degli anni sono emersi vari paradigmi di programmazione. LP sta per programmazione lineare, e altri paradigmi includono la programmazione conica di secondo ordine, la programmazione geometrica (che si occupa dei polinomi), la programmazione semidefinita (che coinvolge matrici con autovalori positivi) e la programmazione conica geometrica. Questi framework hanno in comune il fatto che affrontano problemi convessi strutturati. Sono convessi sia nella loro funzione di perdita che nei vincoli che limitano le soluzioni ammissibili.

Questi framework hanno suscitato un interesse molto elevato, con una vasta produzione di letteratura scientifica. Tuttavia, nonostante i loro nomi impressionanti, questi paradigmi offrono pochissima espressività. Anche problemi semplici superano le capacità di questi framework. Ad esempio, l’ottimizzazione dei parametri di Holt-Winters, un modello di previsione di base sviluppato negli anni ‘60, già supera ciò che uno qualsiasi di questi framework può gestire. Allo stesso modo, il problema del vehicle routing e il problema del commesso viaggiatore, entrambi relativamente semplici, superano le capacità di questi framework.

Ecco perché dicevo fin dall’inizio che esiste un’enorme quantità di letteratura, ma serve a molto poco. Sto semplificando qui; ci sono casi limite in cui si possono avere soluzioni non uniche o addirittura nessuna soluzione. Ma, mettendo da parte alcuni casi limite, l’unico punto in cui non puoi ulteriormente ottimizzare con una funzione convessa è quello ottimale. Altrimenti, puoi sempre scendere, e scendere è sempre una buona scelta.

C’è stata un’enorme quantità di ricerca sulle funzioni convesse, e nel corso degli anni sono emersi vari paradigmi di programmazione. LP sta per programmazione lineare, e altri paradigmi includono la programmazione conica di secondo ordine, la programmazione geometrica (che si occupa dei polinomi), la programmazione semidefinita (che coinvolge matrici con autovalori positivi) e la programmazione conica geometrica. Questi framework hanno in comune il fatto che affrontano problemi convessi strutturati. Sono convessi sia nella loro funzione di perdita che nei vincoli che limitano le soluzioni ammissibili.

Questi framework hanno suscitato un interesse molto elevato, con una vasta produzione di letteratura scientifica. Tuttavia, nonostante i loro nomi impressionanti, questi paradigmi offrono pochissima espressività. Anche problemi semplici superano le capacità di questi framework. Ad esempio, l’ottimizzazione dei parametri di Holt-Winters, un modello di previsione di base sviluppato negli anni ‘60, già supera ciò che uno qualsiasi di questi framework può gestire. Allo stesso modo, il problema del vehicle routing e il problema del commesso viaggiatore, entrambi relativamente semplici, superano le capacità di questi framework.

Ecco perché dicevo fin dall’inizio che esiste un’enorme quantità di letteratura, ma serve a molto poco. Una parte del problema era una focalizzazione errata sui solutori basati esclusivamente sull’ottimizzazione matematica. Questi solutori sono molto interessanti dal punto di vista matematico perché permettono di produrre dimostrazioni formali, ma possono essere utilizzati solo per problemi da laboratorio o completamente ipotetici. Una volta che ci si trova nel mondo reale, essi falliscono, e negli ultimi decenni c’è stato ben pochi progressi in questi campi. Per quanto riguarda la supply chain, quasi nulla, a eccezione di alcune nicchie, ha rilevanza per questi solutori.

Un altro aspetto, che è stato completamente scartato e ignorato durante l’era classica della ricerca operativa, è la casualità. La casualità o stocasticità è di importanza critica in due modi radicalmente differenti. Il primo modo in cui dobbiamo affrontare la casualità è all’interno dello stesso solutore. Al giorno d’oggi, tutti i solutori all’avanguardia sfruttano ampiamente processi stocastici internamente. Questo è molto interessante in confronto ad un processo totalmente deterministico. Sto parlando del funzionamento interno del solutore, il pezzo di software che implementa le tecniche di ottimizzazione matematica.

La ragione per cui tutti i solutori all’avanguardia sfruttano ampiamente i processi stocastici ha a che fare con il modo in cui è strutturato l’hardware informatico moderno. L’alternativa alla casualità nell’esplorare le soluzioni sarebbe ricordare ciò che hai fatto in passato, in modo da non rimanere bloccato nella stessa situazione. Se devi ricordare, consumerai memoria. Il problema sta nel fatto che dobbiamo effettuare numerosi accessi alla memoria. Un modo per introdurre la casualità è solitamente un’ottima soluzione per alleviare notevolmente la necessità di accessi casuali alla memoria.

Rendendo il tuo processo stocastico, puoi evitare di sondare il tuo stesso database su ciò che hai testato o non testato tra le possibili soluzioni per il problema che vuoi ottimizzare. Lo fai in modo parzialmente casuale, ma non del tutto. Questo ha un’importanza fondamentale in praticamente tutti i solver moderni. Uno degli aspetti un po’ controintuitivi del possedere un processo stocastico è che, sebbene tu possa avere un solver stocastico, l’output può essere comunque piuttosto deterministico. Per capire questo, considera l’analogia di una serie di setacci. Un setaccio è fondamentalmente un processo fisico stocastico, in cui applichi movimenti casuali e avviene il processo di setacciatura. Anche se il processo è completamente stocastico, il risultato è completamente deterministico. Alla fine, ottieni un risultato completamente prevedibile dal processo di setacciatura, anche se il tuo processo era fondamentalmente casuale. Questa è esattamente la specie di cosa che accade con i solver stocastici ben ingegnerizzati. Questo è uno degli ingredienti chiave dei solver moderni.

Un altro aspetto, che è ortogonale rispetto alla casualità, è la natura stocastica dei problemi stessi. Questo era per lo più assente nell’era classica della ricerca operativa – l’idea che la tua loss function sia rumorosa e che qualsiasi misura tu ottenga di essa presenti un certo grado di rumore. Questo è quasi sempre il caso in supply chain. Perché? La realtà è che in supply chain, ogni volta che prendi una decisione, è perché prevedi qualche tipo di evento futuro. Se decidi di acquistare qualcosa, è perché prevedi che in seguito ci sarà necessità per quell’oggetto. Il futuro non è scritto, quindi puoi avere alcune intuizioni su di esso, ma tali intuizioni non saranno mai perfette. Se decidi di produrre un prodotto ora, è perché ti aspetti che in futuro ci sarà domanda per questo prodotto. La qualità della tua decisione, ossia produrre oggi, dipende da condizioni future incerti e, quindi, ogni decisione che prendi in supply chain avrà una loss function che varierà a seconda di queste condizioni future incontrollabili. La sorta di casualità dovuta al trattare eventi futuri è irriducibile, ed è questo un aspetto di interesse fondamentale perché significa che stiamo fondamentalmente affrontando problemi stocastici.

Tuttavia, se torniamo ai solver matematici classici, vediamo che questo aspetto è completamente assente, il che rappresenta un grosso problema. Significa che abbiamo classi di solver che non sono neppure in grado di comprendere il tipo di problemi che affronteremo, poiché i problemi di interesse, a cui vogliamo applicare l’ottimizzazione matematica, saranno di natura stocastica. Sto parlando del rumore presente nella loss function.

Esiste un’obiezione secondo cui, se hai un problema stocastico, puoi sempre trasformarlo in un problema deterministico tramite il campionamento. Se valutassi la tua loss function rumorosa 10.000 volte, potresti ottenere una loss function approssimativamente deterministica. Tuttavia, questo approccio è incredibilmente inefficiente perché introduce un sovraccarico di 10.000 volte sul tuo processo di ottimizzazione. La prospettiva dell’ottimizzazione matematica riguarda l’ottenimento dei migliori risultati possibili con le risorse computazionali limitate a disposizione. Non si tratta di investire una quantità infinitamente grande di risorse computazionali per risolvere il problema. Dobbiamo far fronte a una quantità finita di risorse computazionali, anche se tale quantità è piuttosto elevata. Pertanto, quando esaminiamo i solver in seguito, dobbiamo tenere presente che è di primaria importanza avere solver che possano affrontare nativamente i problemi stocastici anziché ricorrere per default all’approccio deterministico.

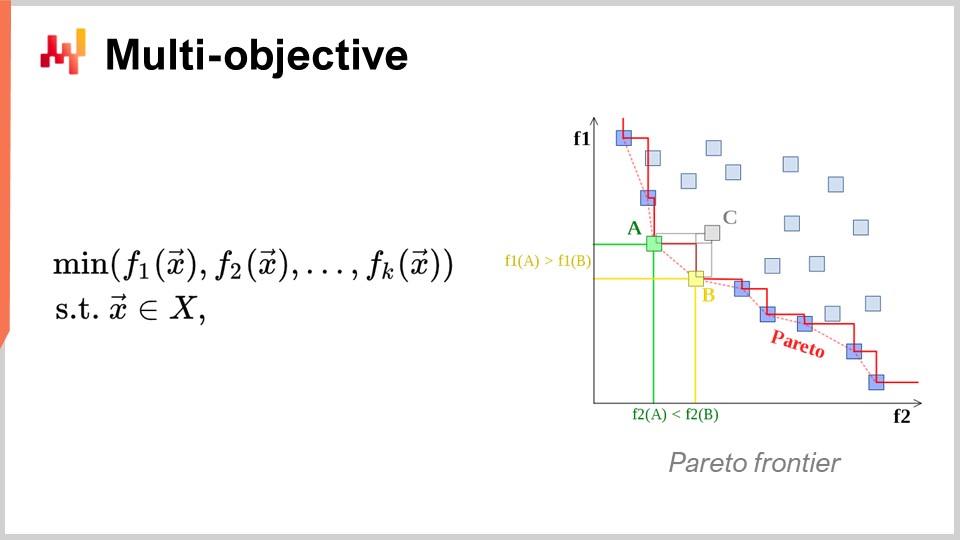
Un altro punto di vista, anch’esso di primaria importanza, è l’ottimizzazione multi-obiettivo. Nella formulazione ingenua del problema di ottimizzazione matematica, ho affermato che la loss function fosse essenzialmente a valore singolo, quindi avevamo un solo valore che volevamo minimizzare. Ma cosa succede se abbiamo un vettore di valori, e quello che vogliamo fare è trovare la soluzione che garantisca il punto più basso secondo l’ordine lessicografico di tutti i vettori, come f1, f2, f3, ecc.?

Perché questo è rilevante anche dal punto di vista della supply chain? La realtà è che, se adotti questa prospettiva multi-obiettivo, puoi esprimere tutti i tuoi vincoli come un’unica loss function dedicata. Puoi, per esempio, avere una funzione che conteggi le violazioni dei vincoli. Perché ci sono vincoli in supply chain? Beh, i vincoli sono presenti ovunque. Ad esempio, se effettui un ordine di acquisto, devi assicurarti di avere abbastanza spazio nel tuo warehouse per immagazzinare le merci al loro arrivo. Quindi, ci sono vincoli sullo spazio di stoccaggio, sulla capacità produttiva e altro ancora. L’idea è che, invece di disporre di un solver in cui devi trattare i vincoli come casi speciali, sia più interessante avere un solver che possa gestire nativamente l’ottimizzazione multi-obiettivo e in cui i vincoli possano essere espressi come uno degli obiettivi. Basta conteggiare il numero di violazioni dei vincoli e minimizzarlo, azzerando tale numero.

Il motivo per cui questo approccio mentale è così rilevante per la supply chain è che i problemi di ottimizzazione che le supply chain devono affrontare non sono enigmi crittografici. Non si tratta di problemi combinatori super stringenti dove o hai una soluzione valida oppure, essendo solo leggermente lontano, non hai nulla. Nella supply chain, ottenere quella che viene comunemente chiamata soluzione ammissibile – una soluzione che soddisfa tutti i vincoli – è solitamente del tutto banale. Identificare una soluzione che rispetti i vincoli non rappresenta un’impresa ardua. Quello che risulta molto difficile è, tra tutte le soluzioni che soddisfano i vincoli, identificare quella che risulta maggiormente profittevole per l’azienda. Qui risiede la difficoltà. Trovare una soluzione che non violi i vincoli è molto semplice. Questo non è il caso in altri campi, ad esempio nell’ottimizzazione matematica per il design industriale, dove si desidera posizionare i componenti all’interno di un cellulare. È un problema incredibilmente vincolato, e non puoi aggirare tale vincolo rinunciando a uno di essi e accettando una piccola imperfezione sul tuo cellulare. È un problema estremamente stringente e combinatorio, in cui è davvero necessario trattare i vincoli come cittadini di prima classe. Ritengo che questo non sia necessario per la stragrande maggioranza dei problemi della supply chain. Pertanto, risulta nuovamente di altissima importanza disporre di tecniche in grado di affrontare nativamente l’ottimizzazione multi-obiettivo.

Ora, discutiamo un po’ di più sul design del solver. Da una prospettiva molto generale su come vogliamo ingegnerizzare un software in grado di produrre soluzioni per una classe molto ampia di problemi, ci sono due aspetti di design particolarmente notevoli che vorrei evidenziare. Il primo aspetto da considerare è se opereremo con una prospettiva white box o black box. L’idea di una prospettiva black box è che possiamo processare qualsiasi programma arbitrario, quindi la loss function può essere qualsiasi programma arbitrario. Non ci interessa; lo trattiamo come una scatola nera completa. L’unica cosa che desideriamo è un programma nel quale possiamo valutare il programma e ottenere il valore di una soluzione provvisoria. Al contrario, un approccio white box enfatizza il fatto che la loss function stessa possiede una struttura che possiamo ispezionare e sfruttare. Possiamo infatti guardare all’interno della loss function. A proposito, quando ho discusso di convessità qualche slide fa, tutti quei modelli e solver matematici puri erano veramente approcci white box. Rappresentano l’estremo caso degli approcci white box, in cui non solo puoi vedere all’interno del problema, ma il problema possiede una struttura molto rigida, come nella programmazione semidefinita, dove la forma è molto ristretta. Tuttavia, senza ricorrere a qualcosa di rigido come un framework matematico, puoi, per esempio, dire che, come parte dell’approccio white box, hai a disposizione qualcosa come il gradiente che ti può aiutare. Il gradiente della loss function è di importanza fondamentale perché, improvvisamente, puoi sapere in quale direzione andare per scendere, anche se non hai un problema convesso in cui il semplice gradient descent garantisca un buon risultato. In linea di massima, se puoi rendere il tuo solver white box, avrai un solver che è di ordini di grandezza più performante rispetto ad un solver black box.

Ora, come secondo aspetto, abbiamo i solver offline contro quelli online. Il solver offline opera tipicamente in batch, quindi un solver offline si limiterà a prendere il problema, eseguirlo, e dovrai aspettare fino al completamento. In quel momento, quando il solver ha terminato, ti fornisce la migliore soluzione o la soluzione migliore identificata. Al contrario, un solver online funziona con un approccio best-effort. Identificherà una soluzione che sia accettabile e poi investirà risorse computazionali per iterare verso soluzioni sempre migliori col passare del tempo e con il maggior investimento di risorse computazionali. Ciò che è veramente di importanza fondamentale è che, affrontando un problema con un solver online, significa che puoi praticamente sospendere il processo in qualsiasi momento e ottenere una soluzione candidata anticipata. Puoi addirittura riprendere il processo. Se torniamo ai solver matematici, questi sono tipicamente solver batch nei quali devi attendere fino al termine del processo.

Sfortunatamente, operare nel mondo della supply chain può essere un percorso molto accidentato, come trattato in una delle lezioni precedenti di questa serie. Ci saranno situazioni in cui di solito puoi permetterti di impiegare, diciamo, tre ore per eseguire questo processo di ottimizzazione matematica. Ma a volte possono verificarsi malfunzionamenti IT, problemi reali o un’emergenza nella supply chain. In tali casi, è fondamentale che ciò che di solito richiede tre ore possa essere interrotto dopo cinque minuti e fornire una risposta, anche se non perfetta, piuttosto che non fornire alcuna risposta. C’è un detto nell’esercito secondo il quale il peggior piano è non avere un piano, quindi è meglio avere un piano molto approssimativo piuttosto che niente. Questo è esattamente ciò che offre un solver online. Questi sono gli elementi chiave del design che terremo a mente nella discussione che segue.

Ora, per concludere questa prima sezione della lezione sull’approccio all’ottimizzazione matematica, diamo un’occhiata alle lezioni di deep learning. Il deep learning ha rappresentato una vera rivoluzione nel campo del machine learning. Tuttavia, al suo interno, il deep learning ha anche un problema di ottimizzazione matematica. Credo che il deep learning abbia generato una rivoluzione all’interno stessa dell’ottimizzazione matematica e abbia completamente cambiato il modo in cui affrontiamo i problemi di ottimizzazione. Il deep learning ha ridefinito ciò che consideriamo lo stato dell’arte dell’ottimizzazione matematica.

Al giorno d’oggi, i modelli di deep learning più grandi gestiscono più di un trilione di parametri, ovvero mille miliardi. Solo per fare un paragone, la maggior parte dei solver matematici fatica anche solo a gestire 1.000 variabili e tipicamente crolla con sole poche decine di migliaia di variabili, non importa quanta potenza hardware vi venga messa addosso. Al contrario, il deep learning riesce, possibilmente usando una grande quantità di risorse computazionali, ma comunque è fattibile. Esistono modelli di deep learning in produzione che vantano oltre un trilione di parametri, e tutti quei parametri sono ottimizzati, il che significa che abbiamo processi di ottimizzazione matematica che possono scalare fino a un trilione di parametri. Questo è assolutamente stupefacente e radicalmente diverso dalle performance viste con le prospettive classiche di ottimizzazione.

La cosa interessante è che anche problemi completamente deterministici, come giocare a Go o a scacchi, che sono non statistici, discreti e combinatori, sono stati risolti con maggior successo mediante metodi completamente stocastici e statistici. Questo è sconcertante, perché giocare a Go o a scacchi può essere considerato come un problema di ottimizzazione discreta, eppure oggi vengono risolti in maniera più efficiente con metodi completamente stocastici e statistici. Ciò contrasta con l’intuizione che la comunità scientifica aveva riguardo a questi problemi due decenni fa.

Rivediamo la comprensione che il deep learning ha sbloccato riguardo l’ottimizzazione matematica. La prima cosa è riconsiderare completamente la maledizione della dimensionalità. Credo che questo concetto sia in gran parte errato, e il deep learning sta dimostrando che non è così che si dovrebbe considerare la difficoltà di un problema di ottimizzazione. Si scopre che, osservando le classi di problemi matematici, è possibile dimostrare matematicamente che certi problemi sono estremamente difficili da risolvere in modo perfetto. Ad esempio, se hai mai sentito parlare di problemi NP-hard, sai che aggiungendo dimensioni al problema questo diventa esponenzialmente più difficile da risolvere. Ogni dimensione extra rende il problema più arduo, e vi è una barriera cumulativa. Si può dimostrare che nessun algoritmo può mai sperare di risolvere il problema perfettamente con una quantità limitata di risorse computazionali. Tuttavia, il deep learning ha dimostrato che questa prospettiva era in gran parte errata.

Prima di tutto, dobbiamo differenziare tra la complessità rappresentazionale del problema e la complessità intrinseca del problema. Permettetemi di chiarire questi due termini con un esempio. Diamo un’occhiata all’esempio di previsione delle serie temporali fornito inizialmente. Supponiamo di avere una storia delle vendite, aggregata giornalmente su tre anni, quindi abbiamo un vettore temporale giornaliero di circa 1.000 giorni. Questa è la rappresentazione del problema.

Ora, cosa succede se passo a una rappresentazione della serie temporale per secondo? Questa è la stessa storia delle vendite, ma invece di rappresentare i dati di vendita con aggregazioni giornaliere, rappresenterò questa serie temporale, la medesima serie, con aggregazioni per secondo. Ciò significa che ci sono 86.400 secondi in ogni singolo giorno, gonfiando così la dimensione della rappresentazione del problema di un fattore pari a 86.000.

Ma se iniziamo a considerare la dimensione intrinseca, non è perché ho una storia delle vendite o perché passo da un’aggregazione giornaliera a una per secondo che sto aumentando la complessità, o la complessità dimensionale interessante del problema, di 1.000 volte. Molto probabilmente, se analizzo le vendite aggregate per secondo, la serie temporale sarà incredibilmente sparsa, con per lo più zeri in quasi tutti i bucket. Non sto aumentando la dimensionalità interessante del problema di un fattore di 100.000. Il deep learning chiarisce che non è perché hai una rappresentazione del problema con molte dimensioni che il problema è fondamentalmente difficile.

Un altro aspetto associato alla dimensionalità è che, sebbene tu possa dimostrare che alcuni problemi sono NP-completi, per esempio, il problema del commesso viaggiatore (una versione semplificata del problema di vehicle routing presentato all’inizio di questa lezione), il commesso viaggiatore è tecnicamente ciò che viene definito un problema NP-hard. Quindi, è un problema in cui, se vuoi trovare la soluzione migliore nel caso generale, il costo aumenterà esponenzialmente man mano che aggiungi punti alla tua mappa. Ma la realtà è che questi problemi sono molto facili da risolvere, come illustrato con l’euristica two-opt; puoi ottenere soluzioni eccellenti con una quantità minima di risorse computazionali. Quindi, stai attento al fatto che le dimostrazioni matematiche, che dimostrano che alcuni problemi sono molto difficili, possono essere ingannevoli. Non ti dicono che, se ti accontenti di una soluzione approssimativa, l’approssimazione può essere eccellente, e a volte non è neanche un’approssimazione; otterrai la soluzione ottimale. È solo che non puoi dimostrare che essa sia ottimale. Questo non dice nulla sul fatto che il problema possa essere approssimato e, molto frequentemente, quei problemi suppostamente afflitti dalla maledizione della dimensionalità sono semplici da risolvere perché le loro dimensioni interessanti non sono così elevate. Il deep learning ha dimostrato con successo che molti problemi ritenuti incredibilmente difficili non lo erano in realtà.

La seconda intuizione chiave è stata quella dei minimi locali. La maggior parte dei ricercatori che lavorano nell’ottimizzazione matematica e nella ricerca operativa ha scelto funzioni convesse perché non esistono minimi locali. Per molto tempo, coloro che non lavoravano con funzioni convesse si sono chiesti come evitare di bloccarsi in un minimo locale. La maggior parte degli sforzi è stata dedicata a lavorare su tematiche quali le metaeuristiche. Il deep learning ha fornito una nuova comprensione: non ci interessano i minimi locali. Questa comprensione proviene da lavori recenti originati dalla comunità del deep learning.

Se hai una dimensione molto elevata, puoi dimostrare che i minimi locali scompaiono man mano che aumenta la dimensione del problema. I minimi locali sono molto frequenti nei problemi a bassa dimensione, ma se incrementi la dimensione dei problemi fino a centinaia o migliaia, statisticamente parlando, i minimi locali diventano incredibilmente improbabili. Al punto che, osservando dimensioni molto grandi come milioni, essi scompaiono completamente.

Invece di pensare che una dimensione più elevata sia il tuo nemico, come era associata alla maledizione della dimensionalità, cosa succederebbe se potessi fare esattamente il contrario e aumentare la dimensione del problema fino a renderla così elevata da rendere banale una discesa pulita senza alcun minimo locale? Si scopre che questo è esattamente ciò che viene fatto nella comunità del deep learning e con modelli che hanno un trilione di parametri. Questo approccio ti offre un modo molto chiaro per procedere per gradiente.

In sostanza, la comunità del deep learning ha dimostrato che era irrilevante avere una prova riguardo alla qualità della discesa o alla convergenza finale. Ciò che conta è la rapidità della discesa. Vuoi iterare e discendere molto rapidamente verso una soluzione molto buona. Se puoi ottenere un processo che discende più velocemente, alla fine otterrai prestazioni migliori in termini di ottimizzazione. Queste intuizioni vanno contro la concezione generale dell’ottimizzazione matematica, o quella che era la comprensione mainstream due decenni fa.

Ci sono altre lezioni da trarre dal deep learning, poiché è un campo molto ricco. Una di queste è la hardware sympathy. Il problema con i solver matematici, come la programmazione conica o la programmazione geometrica, è che si concentrano prima sull’intuizione matematica e non sull’hardware di calcolo. Se progetti un solver che fondamentalmente si oppone al tuo hardware di calcolo, non importa quanto sia sofisticata la tua matematica, è probabile che sarai disperatamente inefficiente a causa di un cattivo impiego delle risorse computazionali.

Una delle intuizioni chiave della comunità del deep learning è che devi collaborare bene con l’hardware di calcolo e progettare un solver che lo sfrutti appieno. Questo è il motivo per cui ho iniziato questa serie di lezioni sulle scienze ausiliarie per supply chain con modern computers for supply chain. È importante comprendere l’hardware che possiedi e come sfruttarlo al meglio. Questa hardware sympathy è il modo in cui si possono ottenere modelli con un trilione di parametri, sebbene ciò richieda un grande cluster di computer o un supercomputer.

Un’altra lezione dal deep learning è l’uso delle funzioni surrogate. Tradizionalmente, i solver matematici miravano ad ottimizzare il problema così com’era, senza discostarsene. Tuttavia, il deep learning ha dimostrato che a volte è meglio utilizzare funzioni surrogate. Ad esempio, molto spesso per le previsioni, i modelli di deep learning usano cross-entropy come metrica di errore invece del mean square. Praticamente nessuno nel mondo reale è interessato al cross-entropy come metrica, poiché risulta piuttosto bizzarro.

Allora, perché le persone usano il cross-entropy? Fornisce gradienti incredibilmente ripidi e, come ha dimostrato il deep learning, tutto ruota attorno alla velocità della discesa. Se hai gradienti molto ripidi, puoi discendere molto rapidamente. Qualcuno potrebbe obiettare dicendo: “Se voglio ottimizzare il mean square, perché dovrei usare il cross-entropy? Non è neanche lo stesso obiettivo.” La realtà è che, se ottimizzi il cross-entropy, otterrai gradienti molto accentuati e, alla fine, se valuti la tua soluzione rispetto al mean square, otterrai una soluzione migliore secondo il criterio del mean square, molto frequentemente, se non sempre. Sto semplificando solo per questa spiegazione. L’idea delle funzioni surrogate è che il vero problema non è un valore assoluto; è solo qualcosa che utilizzi per il controllo al fine di valutare la validità finale della tua soluzione. Non è necessariamente qualcosa che userai mentre il solver è in esecuzione. Questo va completamente contro le idee alla base dei solver matematici che sono stati popolari negli ultimi decenni.

Infine, c’è l’importanza di lavorare in paradigmi. Con l’ottimizzazione matematica, esiste implicitamente una divisione del lavoro nell’organizzazione del tuo team di ingegneria. La divisione del lavoro implicita legata ai solver matematici prevede ingegneri matematici da una parte, responsabili della progettazione del solver, e ingegneri di problema dall’altra parte, la cui responsabilità è esprimere il problema in una forma adatta all’elaborazione da parte dei solver matematici. Questa divisione del lavoro era prevalente e l’idea era renderla il più semplice possibile per l’ingegnere di problema, in modo che dovesse solo esprimere il problema nella maniera più minimalista e pura, lasciando al solver il compito di fare il resto.

Il deep learning ha dimostrato che questa prospettiva era profondamente inefficiente. Questa divisione arbitraria del lavoro non era affatto il miglior modo per affrontare il problema. Se lo fai, ti ritroverai in situazioni impossibilmente difficili, superando di gran lunga lo stato dell’arte per qualsiasi ingegnere matematico impegnato sul problema di ottimizzazione. Un modo molto migliore è far sì che gli ingegneri di problema si impegnino di più per riformulare i problemi in modi che li rendano molto più adatti all’ottimizzazione da parte dell’ottimizzatore matematico.

Il deep learning riguarda un insieme di ricette che ti permettono di inquadrare il problema sopra il tuo solver, in modo da ottenere il massimo dal tuo ottimizzatore. La maggior parte degli sviluppi nella comunità del deep learning si è concentrata sulla creazione di queste ricette, estremamente efficaci nell’apprendimento e compatibili con il paradigma dei solver utilizzati (ad es. TensorFlow, PyTorch, MXNet). La conclusione è che devi davvero collaborare con l’ingegnere di problema, o, in termini di supply chain, il supply chain scientist.

Adesso passiamo alla seconda e ultima sezione di questa lezione sugli elementi più preziosi della letteratura. Daremo un’occhiata a due ampie classi di solver: la ricerca locale e la programmazione differenziabile.

Innanzitutto, lasciami soffermare nuovamente sul termine “programming”. Questa parola riveste un’importanza critica perché, da una prospettiva di supply chain, vogliamo davvero essere in grado di esprimere il problema che affrontiamo, o il problema che pensiamo di affrontare. Non vogliamo una specie di versione a bassa risoluzione del problema che si adatti a una ipotesi matematica semi-assurda, come dover esprimere il problema in un cono o qualcosa del genere. Ciò che ci interessa veramente è avere accesso a un vero paradigma di programming.

Ricorda, quei solver matematici come la programmazione lineare, la programmazione conica di secondo ordine e la programmazione geometrica includevano tutti una parola chiave “programming”. Tuttavia, negli ultimi decenni, le nostre aspettative verso un paradigma di programming si sono evolute drasticamente. Oggi vogliamo qualcosa che ti permetta di gestire programmi quasi arbitrari, programmi in cui ci sono cicli, rami, e possibilmente allocazioni di memoria, ecc. Vuoi veramente qualcosa il più vicino possibile a un programma arbitrario, non una sorta di versione giocattolo super limitata dotata di alcune proprietà matematiche particolari. Nel supply chain, è meglio essere approssimativamente corretti piuttosto che esattamente sbagliati.

Per affrontare l’ottimizzazione generica, iniziamo con la ricerca locale. La ricerca locale è una tecnica di ottimizzazione matematica apparentemente semplice. Il pseudocodice prevede di partire da una soluzione casuale, che rappresenti come un insieme di bit. Quindi, inizializzi la tua soluzione in modo casuale e inizi a invertire i bit in maniera casuale per esplorare l’intorno della soluzione. Se, attraverso questa esplorazione casuale, trovi una soluzione che risulta migliore, questa diventa la tua nuova soluzione di riferimento.

Questo approccio sorprendentemente potente può funzionare con letteralmente qualsiasi programma, trattandolo come una scatola nera, e può anche ripartire da qualsiasi soluzione nota. Esistono molti modi per migliorare questo approccio. Uno di questi è il calcolo differenziale, da non confondere con il calcolo differenziabile. Il calcolo differenziale è l’idea che, se esegui il tuo programma su una determinata soluzione e poi inverto un bit, puoi rieseguire lo stesso programma con un’esecuzione differenziale, senza dover rieseguire l’intero programma. Ovviamente, i risultati possono variare e dipende molto dalla struttura del problema. Un modo per accelerare il processo non è sfruttare qualche tipo di informazione extra sul programma black box che stiamo utilizzando, ma semplicemente riuscire ad accelerare il programma stesso, continuandolo a trattare per lo più come una scatola nera, perché non riesegui l’intero programma ogni volta.

Esistono altri approcci per migliorare la ricerca locale. Puoi perfezionare il tipo di mosse che esegui. La strategia più basilare è chiamata k-flips, in cui inverti un numero k di bit, con k essendo un numero molto piccolo, qualcosa come una coppia fino a una dozzina. Invece di limitarti a invertire i bit, puoi lasciare che l’ingegnere di problema stabilisca il tipo di mutazioni da applicare alla soluzione. Ad esempio, potresti esprimere il desiderio di applicare una sorta di permutazione al tuo problema. L’idea è che queste mosse intelligenti spesso preservano il soddisfacimento di alcuni vincoli del tuo problema, il che può aiutare il processo di ricerca locale a convergere più rapidamente.

Un altro modo per migliorare la ricerca locale è evitare di esplorare lo spazio del tutto in maniera casuale. Invece di invertire i bit a caso, puoi cercare di apprendere le direzioni giuste, identificando le aree più promettenti per le inversioni. Alcuni articoli recenti hanno dimostrato che è possibile integrare un piccolo modulo di deep learning sopra la ricerca locale, fungendo da generatore. Tuttavia, questo approccio può essere complicato dal punto di vista ingegneristico, poiché devi assicurarti che il sovraccarico introdotto dal processo di machine learning produca un ritorno positivo in termini di risorse computazionali.

Esistono altre euristiche ben note e, se desideri una visione sintetica molto accurata di ciò che serve per implementare un moderno motore di ricerca locale, puoi leggere il paper “LocalSolver: A Black-Box Local-Search Solver for 0-1 Programs.” L’azienda che opera LocalSolver ha anche un prodotto con lo stesso nome. In questo articolo forniscono una visione ingegneristica di ciò che avviene dietro le quinte nel loro solver di livello produttivo. Utilizzano multi-start e simulated annealing per ottenere risultati migliori.

Una nota che aggiungerei riguardo la ricerca locale è che non gestisce molto bene, o in modo nativo, i problemi stocastici. Con i problemi stocastici non è così semplice come dire “ho una soluzione migliore” e decidere immediatamente che essa diventa la migliore. È molto più complicato, e devi impegnarti ulteriormente prima di saltare alla soluzione valutata come la nuova migliore.

Ora passiamo alla seconda classe di solver di cui parleremo oggi, ovvero la programmazione differenziabile. Ma prima, per comprendere la programmazione differenziabile, dobbiamo capire lo stochastic gradient descent. Lo stochastic gradient descent è una tecnica iterativa di ottimizzazione basata sul gradiente. È emerso come una serie di tecniche pionieristiche nei primi anni ‘50, il che lo rende quasi 70 anni vecchio. È rimasto abbastanza di nicchia per quasi sei decenni, e abbiamo dovuto aspettare l’avanzamento del deep learning per realizzare il vero potenziale e la potenza dello stochastic gradient descent.

Lo stochastic gradient descent assume che la funzione di perdita possa essere scomposta in modo additivo in una serie di componenti. Nella formula, Q(W) rappresenta la funzione di perdita, che viene suddivisa in una serie di funzioni parziali, Qi. Questo è rilevante perché la maggior parte dei problemi di apprendimento può essere vista come l’apprendimento di una previsione basata su una serie di esempi. L’idea è che puoi scomporre la tua funzione di perdita come l’errore medio commesso sull’intero dataset, con un errore locale per ogni dato. Molti problemi di supply chain possono essere scomposti in maniera additiva in questo modo. Ad esempio, puoi scomporre la tua rete di supply chain in una serie di prestazioni per ogni singolo SKU, con una funzione di perdita associata a ciascun SKU. La vera funzione di perdita che vuoi ottimizzare è il totale.

Quando hai in atto questa decomposizione, che è molto naturale per problemi di apprendimento, puoi iterare con il processo di discesa del gradiente stocastico (SGD). Il vettore di parametri W può essere una serie molto grande, dato che i modelli di deep learning più avanzati hanno un trilione di parametri. L’idea è che ad ogni passo del processo aggiorni i tuoi parametri applicando una piccola quantità di gradiente. Eta è il tasso di apprendimento, un numero piccolo tipicamente compreso tra 0 e 1, spesso intorno a 0,01. Nabla di Q è il gradiente per una funzione di perdita parziale Qi. Sorprendentemente, questo processo funziona bene.

Si dice che lo SGD sia stocastico perché scegli casualmente il tuo prossimo elemento i, saltando attraverso il tuo dataset e applicando un piccolo gradiente ai tuoi parametri ad ogni singolo passo. Questa è l’essenza della discesa del gradiente stocastico.

È rimasto relativamente di nicchia e in gran parte ignorato dalla comunità per quasi sei decenni, perché è piuttosto sorprendente che la discesa del gradiente stocastico funzioni. Funziona perché fornisce un eccellente trade-off tra il rumore nella funzione di perdita e il costo computazionale per accedervi. Invece di avere una funzione di perdita che necessita di essere valutata sull’intero dataset, con la discesa del gradiente stocastico possiamo prendere un dato alla volta e applicare comunque un piccolo gradiente. Questa misura sarà molto frammentaria e rumorosa, eppure questo rumore va bene perché è molto veloce. Puoi eseguire ordini di grandezza in più di piccole ottimizzazioni rumorose rispetto all’elaborazione dell’intero dataset.

Sorprendentemente, il rumore introdotto aiuta la discesa del gradiente. Uno dei problemi negli spazi ad alta dimensionalità è che i minimi locali diventano relativamente inesistenti. Tuttavia, potresti comunque incorrere in vaste aree di plateau dove il gradiente è molto piccolo e la discesa del gradiente non ha una direzione chiara da seguire. Il rumore ti fornisce gradienti più ripidi e rumorosi che facilitano la discesa.

Ciò che è anche interessante con la discesa del gradiente è che, pur essendo un processo stocastico, può affrontare problemi stocastici gratuitamente. Se Qi è una funzione stocastica con rumore e restituisce un risultato casuale che varia ogni volta che la valuti, non serve neppure modificare una singola riga dell’algoritmo. La discesa del gradiente stocastico è di primaria importanza perché ti fornisce qualcosa che è completamente in linea con il paradigma rilevante per scopi di supply chain.

La seconda domanda è: da dove proviene il gradiente? Abbiamo un programma e prendiamo il gradiente della funzione di perdita parziale, ma da dove deriva questo gradiente? Come si ottiene il gradiente per un programma arbitrario? Si scopre che esiste una tecnica molto elegante e minimalista, scoperta molto tempo fa, chiamata differentiamento automatico.

Il differentiamento automatico emerse negli anni ‘60 ed è stato perfezionato nel tempo. Esistono due tipologie: la modalità forward, scoperta nel 1964, e la modalità reverse, scoperta nel 1980. Il differentiamento automatico può essere considerato come un trucco di compilazione. L’idea è che hai un programma da compilare e, grazie al differentiamento automatico, possiedi il tuo programma che rappresenta la funzione di perdita. Puoi ricompilare questo programma per ottenere un secondo programma, e l’output del secondo programma non è la funzione di perdita, ma i gradienti di tutti i parametri coinvolti nel calcolo della funzione di perdita.

Inoltre, il differentiamento automatico ti fornisce un secondo programma con una complessità computazionale sostanzialmente identica a quella del programma iniziale. Ciò significa che non solo hai un metodo per creare un secondo programma che calcola i gradienti, ma anche il secondo programma ha le stesse caratteristiche prestazionali del primo. È un’inflazione a fattore costante in termini di costo computazionale. La realtà, tuttavia, è che il secondo programma ottenuto non possiede esattamente le stesse caratteristiche di memoria del programma iniziale. Sebbene i dettagli vadano oltre l’ambito di questa lezione, ne discuteremo durante le domande. In sostanza, il secondo programma, chiamato reverse, richiederà più memoria e, in alcune situazioni patologiche, potrebbe richiederne molto di più rispetto al programma iniziale. Ricorda che una maggiore richiesta di memoria comporta problemi nelle prestazioni computazionali, poiché non si può assumere un accesso uniforme alla memoria.

Per illustrare un po’ come funziona il differentiamento automatico, come ho accennato, esistono due modalità: forward e reverse. Dal punto di vista dell’apprendimento o dell’ottimizzazione per supply chain, l’unica modalità di interesse per noi è quella reverse. Quello che puoi vedere sullo schermo è una funzione di perdita F, completamente inventata. Puoi osservare la traccia forward, una sequenza di operazioni aritmetiche o elementari eseguite per calcolare la funzione per due valori di input dati, X1 e X2. Questo ti mostra tutti i passaggi elementari eseguiti per calcolare il valore finale.

L’idea è che per ogni operazione elementare, e la maggior parte di esse sono semplici operazioni aritmetiche come la moltiplicazione o l’addizione, la modalità reverse costituirà un programma che esegue gli stessi passaggi ma in ordine inverso. Invece di avere i valori calcolati nel forward, otterrai gli adjoints. Per ogni operazione aritmetica, avrai il suo corrispettivo reverse. La transizione dall’operazione forward al corrispettivo è molto diretta.

Anche se sembra complicato, hai un’esecuzione forward e una reverse, dove quest’ultima non è altro che una trasformazione elementare applicata a ciascuna operazione. Al termine del reverse, ottieni i gradienti. Il differentiamento automatico può sembrare complicato, ma non lo è. Il primo prototipo che abbiamo implementato era di meno di 100 righe di codice, quindi è molto semplice ed essenzialmente un trucco di transpilation economico.

Ora, questo è interessante perché abbiamo la discesa del gradiente stocastico, un meccanismo di ottimizzazione estremamente potente. È incredibilmente scalabile, online, whiteboard, e funziona nativamente con problemi stocastici. L’unico problema rimasto era come ottenere il gradiente e, grazie al differentiamento automatico, lo otteniamo con un sovraccarico fisso o un fattore costante, praticamente per qualsiasi programma arbitrario. Quello che otteniamo alla fine è la programmazione differenziabile.

Curiosamente, la programmazione differenziabile è una combinazione di discesa del gradiente stocastico e differentiamento automatico. Sebbene queste due tecniche, la discesa del gradiente stocastico e il differentiamento automatico, abbiano decenni alle spalle, la programmazione differenziabile è salita alla ribalta solo all’inizio del 2018, quando Yann LeCun, il responsabile AI di Facebook, iniziò a parlarne. LeCun non ha inventato questo concetto, ma è stato determinante nel renderlo popolare.

Ad esempio, la comunità del deep learning inizialmente utilizzava il backpropagation anziché il differentiamento automatico. Per chi ha dimestichezza con le reti neurali, il backpropagation è un processo complesso che risulta di ordini di grandezza più complicato da implementare rispetto al differentiamento automatico. Il differentiamento automatico è superiore sotto tutti gli aspetti. Con questa intuizione, la comunità del deep learning ha affinato la sua visione di cosa costituisce l’apprendimento nel deep learning. Il deep learning ha combinato l’ottimizzazione matematica con varie tecniche di apprendimento e la programmazione differenziabile è emersa come un concetto pulito che isolava le parti non legate all’apprendimento del deep learning.

Le tecniche moderne di deep learning, come il modello transformer, presuppongono un ambiente di programmazione differenziabile sottostante. Ciò permette ai ricercatori di concentrarsi sugli aspetti dell’apprendimento che si sviluppano sopra. La programmazione differenziabile, pur essendo alla base del deep learning, è anche estremamente rilevante per l’ottimizzazione di supply chain e per supportare i processi di apprendimento in supply chain, come la previsione statistica.

Proprio come nel deep learning, il problema si articola in due parti: la programmazione differenziabile come strato di base e le tecniche di ottimizzazione o apprendimento che vi si sovrappongono. La comunità del deep learning mira a identificare architetture che funzionino bene con la programmazione differenziabile, come i transformer. Allo stesso modo, bisogna individuare le architetture che performano bene per scopi di ottimizzazione. Questo è stato il caso per imparare a giocare a Go o a scacchi in contesti altamente combinatori. In lezioni successive discuteremo tecniche che funzionano bene per l’ottimizzazione specifica di supply chain.

Ma ora, è il momento di concludere. Una buona parte della letteratura sulla supply chain e persino la maggior parte delle implementazioni software sono alquanto confuse quando si tratta di ottimizzazione matematica. Questo aspetto di solito non viene nemmeno identificato correttamente come tale e, di conseguenza, i professionisti, i ricercatori e persino gli ingegneri del software che lavorano per aziende di enterprise software mescolano in maniera piuttosto casuale le loro ricette numeriche in ambito di ottimizzazione matematica. Hanno un grosso problema, poiché un componente non viene riconosciuto come avente natura di ottimizzazione matematica, e poiché le persone non sono nemmeno consapevoli di ciò che è disponibile in letteratura, spesso ricorrono a ricerche a griglia rozze o ad euristiche affrettate che producono prestazioni erratiche e incoerenti. In conclusione di questa lezione, d’ora in poi, ogni volta che ti imbatti in un metodo numerico di supply chain o in un software di supply chain che sostiene di offrire qualsiasi tipo di funzionalità analitica, devi chiederti cosa sta succedendo in termini di ottimizzazione matematica e cosa viene fatto. Se ti rendi conto che i fornitori non offrono una visione chiarissima di questa prospettiva, è probabile che tu sia sul lato sinistro dell’illustrazione, e questo non è il posto in cui vuoi essere.

Ora, diamo un’occhiata alle domande.

Domanda: La transizione verso metodi computazionali è una competenza pre-requisito nelle operazioni, e i ruoli operativi diventeranno obsoleti, o viceversa?

Prima di tutto, permettetemi di chiarire alcune cose. Credo sia un errore incolpare il CIO per questo genere di preoccupazioni. Le persone si aspettano troppo dai loro CIO. In qualità di Chief Information Officer, devi già occuparti dello strato base della tua infrastruttura software, come le risorse computazionali, i sistemi transazionali a basso livello, l’integrità della rete e la cybersecurity. Non ci si dovrebbe aspettare che il CIO comprenda cosa serve per fare qualcosa di veramente significativo per la supply chain.

Il problema è che in molte aziende le persone sono così disperatamente ignoranti in tutto ciò che riguarda l’informatica che il CIO diventa il punto di riferimento per tutto. La realtà è che il CIO dovrebbe occuparsi dello strato di base dell’infrastruttura, e poi spetta a ciascun specialista affrontare le proprie esigenze specifiche con le risorse computazionali e gli strumenti software a disposizione.

Per quanto riguarda il fatto che i ruoli operativi diventino obsoleti, se il tuo ruolo consiste nello scorrere manualmente per tutto il giorno i fogli di calcolo Excel spreadsheets, allora sì, è molto probabile che il tuo ruolo diventi obsoleto. Questo problema è noto fin dal 1979, quando Russell Ackoff pubblicò il suo articolo. Il problema è che sapevano che questo metodo per prendere decisioni non era il futuro, ma rimase lo status quo per molto tempo. Il nocciolo della questione è che le aziende devono comprendere il processo sperimentale. Credo che si verificherà una transizione in cui le aziende ricupereranno queste competenze. Molte grandi aziende nordamericane, dopo la Seconda Guerra Mondiale, avevano una certa conoscenza della ricerca operativa tra i loro dirigenti. Era un argomento di grande attualità e i consigli di amministrazione delle grandi aziende conoscevano la ricerca operativa. Come sottolinea Russell Ackoff, a causa della mancanza di risultati, queste idee vennero spinte giù nella gerarchia aziendale fino a essere addirittura esternalizzate completamente, in quanto per lo più irrilevanti e incapaci di produrre risultati tangibili. Credo che la ricerca operativa tornerà solo se le persone impareranno le lezioni del perché l’era classica della ricerca operativa non ha prodotto risultati. Il CIO avrà solo un contributo modesto in questo processo; si tratta soprattutto di ripensare il valore aggiunto delle persone all’interno dell’azienda.

Vuoi avere un contributo capitalista, e questo ritorna a una delle mie precedenti lezioni sulla consegna orientata al prodotto, intesa come software per supply chain. Il punto cruciale è: che tipo di valore aggiunto capitalista offri alla tua azienda? Se la risposta è nessuno, allora potresti non far parte di ciò che la tua azienda dovrebbe e diventerà in futuro.

Domanda: Che dire dell’utilizzo del risolutore di Excel per minimizzare il valore MRMSC e trovare il valore ottimale per alfa, beta e gamma?

Credo che questa domanda sia rilevante per il caso Holt-Winters, dove in realtà è possibile trovare una soluzione con una ricerca a griglia. Tuttavia, cosa sta succedendo in questo risolutore di Excel? Si tratta di una discesa del gradiente o di qualcos’altro? Se ti riferisci al risolutore lineare di Excel, non è un problema lineare, quindi Excel non può fare nulla per te in quel caso. Se disponi di altri risolutori in Excel o di componenti aggiuntivi, sì, possono operare, ma questa è una prospettiva molto datata. Non abbraccia una visione più stocastica; il tipo di previsione che ottieni è una previsione non probabilistica, che rappresenta un approccio superato.

Non sto dicendo che Excel non possa essere utilizzato, ma la domanda è: quali capacità di programmazione vengono sbloccate in Excel? Puoi fare la discesa del gradiente stocastico in Excel? Probabilmente, se aggiungi qualche componente aggiuntivo dedicato. Excel ti permette di integrare qualsiasi programma arbitrario. Potresti, in linea di principio, fare programmazione differenziabile in Excel? Sì. È una buona idea farlo in Excel? No. Per capire perché, devi tornare al concetto di consegna del software orientato al prodotto, che espone cosa non va in Excel. La questione si riduce al modello di programmazione e alla possibilità di mantenere il proprio lavoro nel tempo con un impegno di squadra.

Domanda: I problemi di ottimizzazione sono tipicamente sbilanciati verso il vehicle routing o la previsione. Perché non considerare anche l’ottimizzazione dell’intera supply chain? Non ridurrebbe i costi rispetto a esaminare aree isolate?

Sono completamente d’accordo. La maledizione dell’ottimizzazione della supply chain è che quando esegui un’ottimizzazione locale su un sottoproblema, molto probabilmente sposterai il problema, anziché risolverlo per l’intera supply chain. Sono completamente d’accordo, e non appena inizi ad affrontare un problema più complesso, ti trovi di fronte a un problema ibrido – per esempio, un problema di vehicle routing combinato con una strategia di riapprovvigionamento. Il problema è che hai bisogno di un solver molto generico per affrontarlo perché non vuoi essere limitato. Se hai un solver molto generico, devi avere meccanismi altrettanto generici invece di affidarti a euristiche intelligenti come il two-opt, che funziona bene solo per il vehicle routing e non per qualcosa che sia un ibrido di riapprovvigionamento e vehicle routing allo stesso tempo.

Per passare a questa prospettiva olistica, non devi avere paura della maledizione della dimensionalità. Vent’anni fa, si diceva che questi problemi fossero già estremamente difficili e NP-completi, come il problema del commesso viaggiatore, e tu vuoi risolvere un problema ancora più difficile intrecciandolo con un altro problema. La risposta è sì; devi essere in grado di farlo, ed è per questo che è essenziale avere un solver che ti permetta di gestire programmi arbitrari perché la tua risoluzione potrebbe essere la consolidazione di molti problemi intrecciati e intercalati.

Infatti, l’idea di risolvere questi problemi in isolamento è molto più debole rispetto a risolvere tutto. È meglio essere approssimativamente corretti che esattamente sbagliati. È molto meglio avere un solver debole che affronta l’intera supply chain come un sistema, come un blocco, piuttosto che avere ottimizzazioni locali avanzate che creano problemi in altre aree mentre ottimizzi in maniera microscopica localmente. La vera ottimizzazione del sistema non è necessariamente la migliore per ogni parte, per cui è naturale che se ottimizzi per l’interesse dell’intera azienda e della sua supply chain, non sarà localmente ottimale perché prendi in considerazione anche gli altri aspetti dell’azienda e della sua supply chain.

Domanda: Dopo aver eseguito un’ottimizzazione, quando dovremmo riesaminare lo scenario considerando che nuove restrizioni possono comparire in qualsiasi momento? La risposta è che dovresti rivedere l’ottimizzazione frequentemente. Questo è il ruolo dello supply chain scientist che ho presentato nella seconda lezione di questa serie. Lo supply chain scientist rivedrà l’ottimizzazione tutte le volte che sarà necessario. Se emerge una nuova restrizione, come una nave gigantesca che blocca il Canale di Suez, inaspettata, devi affrontare questa disruption nella tua supply chain. Non hai altra scelta se non quella di affrontare questi problemi; altrimenti, il sistema che hai messo in atto genererà risultati insensati perché opererà in condizioni false. Anche se non hai un’emergenza da affrontare, vuoi comunque investire tempo per riflettere sull’angolo che probabilmente genererà il maggior ritorno per l’azienda. Questo è fondamentalmente ricerca e sviluppo. Hai il sistema in atto, funziona, e stai semplicemente cercando di identificare le aree in cui puoi migliorarlo. Diventa un processo di ricerca applicata che è altamente capitalista ed erratico. Come supply chain scientist, ci sono giorni in cui trascorri l’intera giornata testando metodi numerici, nessuno dei quali fornisce risultati migliori di quelli che hai già. In alcuni giorni, apporti una piccola modifica e, con molta fortuna, salvi milioni per l’azienda. È un processo erratico, ma in media il risultato può essere enorme.

Domanda: Quali sarebbero i casi d’uso per problemi di ottimizzazione oltre alla programmazione lineare, alla programmazione intera, alla programmazione mista, e nel caso di Weber e del costo delle merci?

Invertirei la domanda: dove vedi che la programmazione lineare abbia qualche rilevanza per un problema della supply chain? Praticamente non esiste alcun problema della supply chain che sia lineare. La mia obiezione è che questi framework sono molto semplicistici e non riescono nemmeno ad affrontare problemi da gioco. Come ho detto, questi framework matematici, come la programmazione lineare, non riescono nemmeno ad affrontare un problema da gioco come l’ottimizzazione per un inverno rigido per un antico modello di previsione parametrica a bassa dimensionalità. Non riescono neanche ad affrontare il problema del commesso viaggiatore o praticamente qualsiasi altra cosa.

La programmazione intera o la programmazione mista-intera è solo un termine generico per indicare che alcune delle variabili saranno intere, ma questo non cambia il fatto che questi framework sono semplicemente dei modelli matematici da gioco, lontani dall’espressività necessaria per affrontare i problemi della supply chain.

Quando chiedi dei casi d’uso dei problemi di ottimizzazione, ti invito a dare un’occhiata a tutte le mie lezioni sulle personas della supply chain. Abbiamo già una serie di personas della supply chain, e sto elencando letteralmente tonnellate di problemi che possono essere affrontati tramite l’ottimizzazione matematica. Nelle lezioni sulle personas della supply chain, abbiamo Parigi, Miami, Amsterdam e una world series, con altri in arrivo. Ci sono molti problemi che necessitano di essere affrontati e che meritano un approccio di ottimizzazione matematica adeguato. Tuttavia, vedrai che per ognuno di questi problemi non sarai in grado di inquadrarli all’interno delle restrizioni super strette e, per lo più, bizzarre che emergono da questi framework matematici. Ancora una volta, questi framework riguardano principalmente la convessità, e questa non è la prospettiva giusta per la supply chain. La maggior parte dei problemi che affrontiamo sono non convessi. Ma va bene; non è perché sono non convessi che sono impossibilmente difficili. Vedi, è solo che non sarai in grado di avere una prova matematica alla fine della giornata. Ma il tuo capo o la tua azienda si preoccupano del profitto, non se hai una prova matematica a supporto della decisione. Si concentrano sul fatto che tu possa prendere la decisione giusta in termini di produzione, riapprovvigionamento, prezzi, assortimenti e via dicendo, non sul fatto che tu abbia una prova matematica alle spalle di quelle decisioni.

Domanda: Per quanto tempo dovrebbero essere conservati i dati dell’algoritmo di apprendimento per favorire l’apprendimento?

Beh, direi che, considerando che l’archiviazione dei dati oggigiorno è incredibilmente economica, perché non conservarli per sempre? L’archiviazione dei dati è così economica; ad esempio, basta andare in un supermercato e puoi vedere che il prezzo di un hard disk da un terabyte è intorno a 60 o qualcosa del genere. Quindi, è incredibilmente economico.

Ora, ovviamente, c’è una preoccupazione separata: se nei tuoi dati sono inclusi dati personali, allora i dati che conservi diventano una responsabilità. Ma da un punto di vista della supply chain, se assumiamo che tu abbia prima eliminato tutti i dati personali – perché di solito non è necessario averli – non devi conservare numeri di carte di credito o i nomi dei tuoi clienti. Ti bastano gli identificatori dei clienti e simili. Se elimini tutti i dati personali dai tuoi dati, direi: per quanto tempo? Beh, conservali per sempre.

Uno dei punti nella supply chain è che i dati sono limitati. Non è come nei problemi di deep learning, per esempio il riconoscimento delle immagini, dove puoi elaborare tutte le immagini presenti sul web e avere accesso a database quasi infiniti. Nella supply chain, i tuoi dati sono sempre limitati. Infatti, se vuoi prevedere la domanda futura, ci sono pochissimi settori in cui guardare a oltre un decennio nel passato è veramente rilevante, statisticamente parlando, per prevedere la domanda del trimestre successivo. Tuttavia, direi che è sempre più facile troncare i dati se necessario, piuttosto che rendersi conto che hai eliminato dati e ora mancano. Quindi il mio suggerimento è di conservare tutto, eliminare i dati personali e, alla fine del tuo data pipeline, valutare se sia meglio filtrare i dati molto vecchi. Potrebbe essere utile, oppure no; dipende dal settore in cui operi. Ad esempio, nell’aerospaziale, quando hai parti e aeromobili con una durata operativa di quattro decenni, avere dati nel sistema relativi agli ultimi quattro decenni è rilevante.

Domanda: La programmazione multi-obiettivo è una funzione di due o più obiettivi, come la somma o la minimizzazione di più funzioni in un unico obiettivo?

Esistono diverse varianti per affrontare gli obiettivi multipli. Non si tratta di avere una funzione che sia una somma perché, se la somma è presente, allora è solo una questione di decomposizione e struttura della funzione di perdita. No, si tratta veramente di avere un vettore. Infatti, esistono sostanzialmente molteplici varianti della programmazione multi-obiettivo. La variante più interessante è quella in cui si opta per un ordinamento lessicografico. Per quanto riguarda la supply chain, la minimizzazione, ad esempio decidendo di prendere la media o il massimo delle diverse funzioni, potrebbe essere interessante, ma non ne sono troppo sicuro. Credo che l’approccio multi-obiettivo, in cui puoi effettivamente iniettare vincoli e trattare i vincoli come parte integrante della tua ottimizzazione tradizionale, sia estremamente interessante per le finalità della supply chain. Le altre varianti potrebbero essere interessanti anch’esse, ma non sono del tutto sicuro. Non sto dicendo che non lo siano; sto solo dicendo che non ne sono certo.

Domanda: Come decidi quando utilizzare una soluzione approssimativa invece della soluzione ottimizzata?

Voglio dire, non sono sicuro di aver capito bene la domanda. L’idea è che, se c’è una lezione da apprendere dal deep learning, è che non esiste una soluzione ottimale unica. Tutto è un’approssimazione in una certa misura. Anche quando parli di numeri, nei computer i numeri non hanno precisione infinita; hanno una precisione finita. E questa precisione finita può, in certe circostanze, ritorcersi contro di te. Quindi la risposta è: è sempre approssimativo. Direi che la lezione più grande è che è un’illusione pensare che esista una soluzione perfetta. Non esiste una soluzione perfetta e ottimale. Tutte le soluzioni che hai sono approssimazioni, alcune delle quali sono, direi, leggermente meno o più approssimative. Quindi, non sono troppo sicuro del senso della tua domanda, ma, dalla prospettiva dell’ottimizzazione matematica, significa che hai una funzione di perdita per valutare la qualità e, alla fine, se hai due soluzioni concorrenti, puoi usare la funzione di perdita per stabilire quale sia la migliore. È così che funziona.

Domanda: Perché la serie temporale, in termini di dati storici, è stata divisa per 86.400 in primo luogo?

Non lo è stata. Era un esempio. Volevo semplicemente delineare e spingere la situazione a uno stato assurdo in cui, quando si utilizza una serie temporale, un classico algoritmo di previsione per serie temporali, adotti quella che viene definita una serie temporale equispaziata. Esistono molti modi per rappresentare le serie temporali, e il modo più tipico è quello equispaziato, dove si procede aggregando in “bucket” di uguale lunghezza. Questo è tipicamente ciò che si ottiene con aggregazioni giornaliere o settimanali. Hai bucket della stessa lunghezza, e la tua serie ha una bella struttura vettoriale.

Ma ciò che sto sottolineando è che, in larga misura, è arbitrario. Puoi decidere di rappresentare i dati a livello giornaliero, ma potresti anche rappresentarli al secondo. Ha mai senso rappresentare i dati al secondo? La risposta è sì; dipende dal tipo di problema. Ad esempio, se sei un fornitore di elettricità e devi gestire una rete, allora devi gestire la potenza a ogni secondo in modo da mantenere esattamente l’equilibrio tra l’offerta di elettricità e il consumo. E questo equilibrio viene tarato al secondo. Quindi, potrebbero esserci situazioni in cui rappresentare i dati al secondo ha senso. Per le vendite nel tuo negozio locale, invece, potrebbe non esserlo. Quello che volevo evidenziare con quel 86.400, a proposito, è semplicemente 24 ore per 60 minuti per 60 secondi, e volevo chiarire il fatto che hai sempre una rappresentazione dei tuoi dati, e non dovresti confonderla con la dimensione intrinseca dei tuoi dati, che potrebbe essere completamente diversa. La rappresentazione è, in larga misura, totalmente fittizia e arbitraria. Ti fornisce un indicatore numerico, ad esempio avere dati per tre anni, in modo da avere un vettore di dimensione mille. Ma questo mille è in gran parte un’invenzione, perché si basa sulla decisione di aggregare i dati su base giornaliera. Se scegliessi un altro intervallo, otterresti una dimensione diversa. Questo è il punto che volevo sottolineare, ed è ciò che il deep learning ha veramente centrato: non farti ingannare da scelte arbitrarie nella rappresentazione dei dati. Vuoi essere, in un certo senso, agnostico rispetto alla rappresentazione.

Domanda: Introducendo la previsione probabilistica, passiamo a una funzione di costo e a vincoli che sono probabilistici per natura. Quale implicazione ha questo sul processo di trovare una soluzione?

Beh, ha una restrizione molto basilare e fondamentale. Se hai un solver che non riesce ad elaborare certi problemi, e ricorda che puoi sempre passare da un problema stocastico a uno deterministico semplicemente mediando il risultato su un numero molto elevato di campioni, allora potresti trovarti in difficoltà in termini di costi computazionali. Ciò significa che dovrai spendere circa 10.000 volte in più in potenza di elaborazione per ottenere una soluzione soddisfacente rispetto a un’alternativa. L’implicazione è che devi davvero assicurarti che i tuoi strumenti di ottimizzazione matematica, l’infrastruttura che possiedi, siano nativamente in grado di gestire problemi stocastici. È esattamente ciò che ottieni con il differentiable programming, non tanto con la local search, anche se quest’ultima può essere migliorata o rivista affinché operi in modo più fluido in tali situazioni.

Fondamentalmente, quando si opta per le previsioni probabilistiche, non si mette in discussione solo il modo in cui si guarda al futuro; si mettono in discussione in maniera profonda anche gli strumenti e le strumentazioni con cui bisogna lavorare per queste previsioni. Esattamente questo è il genere di strumenti che Lokad ha sviluppato nell’ultimo decennio. Il motivo è che abbiamo bisogno di strumenti in grado di operare bene con quei tipi di problemi stocastici che emergono invariabilmente nella supply chain, perché praticamente tutti i problemi nelle supply chain contengono un elemento di incertezza e, quindi, in una certa misura, trattano un problema stocastico.

Eccellente. Quindi, la prossima lezione si terrà nello stesso giorno della settimana, un mercoledì. Ci saranno delle vacanze tra adesso e quel momento. La prossima lezione sarà il 22 settembre, e spero di vedervi tutti. Questa volta discuteremo di machine learning per supply chain. A presto.

Riferimenti

• Il futuro della ricerca operativa è passato, Russell L. Ackoff, febbraio 1979
• LocalSolver 1.x: Un risolutore black-box di local-search per la programmazione 0-1, Thierry Benoist, Bertrand Estellon, Frédéric Gardi, Romain Megel, Karim Nouioua, settembre 2011
• Differenziazione automatica nell’apprendimento automatico: una rassegna, Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind, ultima revisione febbraio 2018