00:18 Introduction
02:18 Contexte
12:08 Pourquoi optimiser ? 1/2 Prévision avec Holt-Winters
17:32 Pourquoi optimiser ? 2/2 - Problème de tournées de véhicules
20:49 L’histoire jusqu’à présent
22:21 Sciences auxiliaires (récap)
23:45 Problèmes et solutions (récap)
27:12 Optimisation mathématique
28:09 Convexité
34:42 Stochasticité
42:10 Multi-objectif
46:01 Conception de solveur
50:46 Leçons de deep learning
01:10:35 Optimisation mathématique
01:10:58 “Vraie” programmation
01:12:40 Recherche locale
01:19:10 Descente de gradient stochastique
01:26:09 Différentiation automatique
01:31:54 Programmation différentielle (vers 2018)
01:35:36 Conclusion
01:37:44 Prochaine conférence et questions du public
Description
L’optimisation mathématique est le processus de minimisation d’une fonction mathématique. Presque toutes les techniques modernes d’apprentissage statistique – c’est-à-dire la prévision si nous adoptons une perspective supply chain – reposent fondamentalement sur l’optimisation mathématique. De plus, une fois les prévisions établies, l’identification des décisions les plus rentables repose, en son cœur, sur l’optimisation mathématique. Les problèmes de supply chain impliquent fréquemment de nombreuses variables. Ils sont aussi généralement de nature stochastique. L’optimisation mathématique est une pierre angulaire d’une pratique moderne de supply chain.
Transcription complète

Bienvenue dans cette série de conférences sur supply chain. Je suis Joannes Vermorel, et aujourd’hui je vais présenter « Optimisation mathématique pour supply chain ». L’optimisation mathématique est la méthode bien définie, formalisée et computationnellement tractable permettant d’identifier la meilleure solution pour un problème donné. Tous les problèmes de prévision peuvent être considérés comme des problèmes d’optimisation mathématique. Toutes les situations de prise de décision en supply chain et en dehors de supply chain peuvent également être considérées comme des problèmes d’optimisation mathématique. En réalité, la perspective de l’optimisation mathématique est si ancrée dans notre vision moderne du monde qu’il est devenu très difficile de définir le verbe « optimiser » en dehors de la toute petite boîte qui nous est donnée par le paradigme de l’optimisation mathématique.
Maintenant, la littérature scientifique sur l’optimisation mathématique est vaste, tout comme l’écosystème logiciel qui fournit des outils pour l’optimisation mathématique. Malheureusement, la plupart d’entre eux sont de très peu d’utilité et de pertinence en ce qui concerne supply chain. L’objectif de cette conférence sera double : d’une part, nous voulons comprendre comment aborder l’optimisation mathématique pour obtenir quelque chose de précieux et d’utilisable pratiquement d’un point de vue supply chain. L’autre point sera d’identifier, dans ce vaste paysage, certains des éléments les plus précieux qui s’y trouvent.

La définition formelle de l’optimisation mathématique est simple : on pense à une fonction qui est généralement appelée la fonction de perte, et cette fonction est à valeurs réelles, c’est-à-dire qu’elle produit de simples nombres. Ce que vous souhaitez, c’est identifier l’entrée (X0) qui représente la meilleure valeur minimisant la fonction de perte. C’est typiquement le paradigme de l’optimisation mathématique, qui est d’une simplicité trompeuse. Nous verrons qu’il y a beaucoup de choses à dire sur cette perspective générale.
Je pense que ce domaine, lorsqu’on envisage l’optimisation mathématique appliquée, s’est principalement développé sous le nom de recherche opérationnelle, que nous définissons plus précisément comme la recherche opérationnelle classique qui s’est étendue des années 1940 à la fin des années 1970 au 20ème siècle. L’idée est que la recherche opérationnelle classique, par rapport à l’optimisation mathématique, se préoccupait véritablement des problèmes business. L’optimisation mathématique se focalise sur la forme générale du problème d’optimisation, bien moins sur le fait que le problème ait une quelconque importance pour les entreprises. Au contraire, la recherche opérationnelle classique faisait essentiellement de l’optimisation, mais pas sur n’importe quels problèmes – sur des problèmes identifiés comme étant d’importance pour les entreprises.
Fait intéressant, nous sommes passés de la recherche opérationnelle à l’optimisation mathématique de manière similaire à la transition de la prévision, qui a émergé au début du 20ème siècle en tant que domaine consacré à la prévision générale des niveaux d’activité économique future, généralement associée aux prévisions de séries temporelles. Ce domaine a été essentiellement supplanté par le machine learning, qui se souciait de manière plus large de faire des prédictions sur un éventail beaucoup plus vaste de problèmes. On pourrait dire que nous avons connu une transition similaire de la recherche opérationnelle à l’optimisation mathématique, tout comme celle de la prévision vers le machine learning. Maintenant, quand j’ai dit que l’ère classique de la recherche opérationnelle s’est étendue jusqu’à la fin des années 70, j’avais une date très précise en tête. En février 1979, Russell Ackoff a publié un article remarquable intitulé “The Future of Operational Research is Past.” Pour comprendre cet article, que je considère réellement comme une référence dans l’histoire de la science de l’optimisation, il faut comprendre que Russell Ackoff est essentiellement l’un des pères fondateurs de la recherche opérationnelle.
Lorsqu’il a publié cet article, il n’était plus un jeune homme; il avait 60 ans. Ackoff est né en 1919 et avait passé la majeure partie de sa carrière à travailler sur la recherche opérationnelle. Quand il a publié son article, il déclarait essentiellement que la recherche opérationnelle avait échoué. Non seulement elle n’apportait pas de résultats, mais l’intérêt pour le secteur était en déclin, de sorte qu’à la fin des années 90, l’intérêt était moindre qu’il ne l’était il y a 20 ans dans ce domaine.
Ce qu’il est très intéressant de comprendre, c’est que la cause n’est absolument pas le fait que les ordinateurs de l’époque étaient bien moins puissants que ceux que nous avons aujourd’hui. Le problème n’a rien à voir avec la limitation en termes de puissance de calcul. Il s’agit de la fin des années 70; les ordinateurs étaient très modestes par rapport à ceux d’aujourd’hui, mais ils étaient quand même capables d’effectuer des millions d’opérations arithmétiques en un temps raisonnable. Le problème n’est pas lié à la limitation de la puissance de calcul, surtout à une époque où celle-ci progresse incroyablement vite.
Au fait, cet article est une lecture fantastique. Je recommande vivement au public de le consulter ; vous pouvez facilement le trouver via votre moteur de recherche préféré. Cet article est très accessible et bien rédigé. Bien que le genre de problèmes qu’Ackoff souligne dans cet article résonne encore très fortement quatre décennies plus tard, d’une certaine manière, l’article se montre très prémonitoire quant à nombre des problèmes qui affligent encore les supply chains d’aujourd’hui.
Alors, quel est le problème ? Le problème est que ce paradigme, où vous prenez une fonction et l’optimisez, peut vous prouver que votre processus d’optimisation identifie une solution bonne, voire optimale. Cependant, comment prouver que la fonction de perte que vous optimisez réellement présente un intérêt pour l’entreprise ? Le problème est que lorsque je dis que nous pouvons optimiser un problème ou une fonction donnée, que se passe-t-il si ce que vous optimisez est en réalité une fantaisie ? Et si cela n’avait rien à voir avec la réalité de l’entreprise que vous tentez d’optimiser ?
Voici le cœur du problème, et voici la raison pour laquelle toutes ces premières tentatives ont essentiellement échoué. C’est parce qu’il s’est avéré que lorsque vous imaginez une sorte d’expression mathématique censée représenter l’intérêt de l’entreprise, ce que vous obtenez est une fantaisie mathématique. C’est littéralement ce que Russell Ackoff souligne dans cet article, et il en est arrivé à un stade de sa carrière où il jouait à ce jeu depuis très longtemps et reconnaît que cela ne mène à rien. Dans son article, il partage l’avis que le domaine a échoué, et il propose son diagnostic, sans pour autant offrir beaucoup de solution. C’est très intéressant car l’un des pères fondateurs, un chercheur très respecté et reconnu, affirme que l’ensemble de ce domaine de recherche est une impasse. Il passera le reste de sa vie, qui est encore assez longue, à passer d’une perspective quantitative sur l’optimisation business à une perspective qualitative. Il passera les trois dernières décennies de sa vie à adopter des méthodes qualitatives tout en produisant un travail très intéressant dans la seconde partie de sa vie après ce tournant.
Maintenant, en ce qui concerne cette série de conférences, que faisons-nous puisque les points soulevés par Russell Ackoff concernant la recherche opérationnelle restent très valides de nos jours ? En réalité, j’ai déjà commencé à aborder les plus grands problèmes qu’Ackoff pointait du doigt, et à l’époque, lui et ses pairs n’avaient pas de solutions à proposer. Ils pouvaient diagnostiquer le problème, mais ils n’avaient pas de solution. Dans cette série de conférences, les solutions que je propose sont de nature méthodologique, tout comme le fait qu’Ackoff souligne qu’il existe un profond problème méthodologique avec cette perspective de recherche opérationnelle.
Les méthodes que je propose sont essentiellement doubles : d’une part, le personnel de supply chain, et d’autre part, la méthode intitulée optimisation expérimentale qui se révèle réellement complémentaire à l’optimisation mathématique. De plus, contrairement à la recherche opérationnelle qui prétend être d’intérêt ou de pertinence business, la manière dont j’aborde le problème aujourd’hui ne l’est pas sous l’angle ou à travers le prisme de la recherche opérationnelle. J’aborde le problème à travers le prisme de l’optimisation mathématique, que je positionne comme une science auxiliaire pure pour supply chain. Je dis qu’il n’y a rien d’intrinsèquement fondamental dans l’optimisation mathématique pour supply chain ; c’est simplement d’un intérêt fondationnel. Ce n’est qu’un moyen, et non une fin. C’est là que réside la différence. Le point peut être très simple, mais il revêt une grande importance quand il s’agit d’obtenir effectivement des résultats de niveau prédictif avec l’ensemble.

Maintenant, pourquoi voulons-nous optimiser dès le départ ? La plupart des algorithmes de prévision ont au cœur d’eux un problème d’optimisation mathématique. Sur cet écran, ce que vous pouvez voir est l’algorithme de prévision des séries temporelles multiplicatif classique de Holt-Winters. Cet algorithme est principalement d’intérêt historique ; je ne recommanderais à aucune supply chain contemporaine de tirer parti de cet algorithme spécifique. Mais par souci de simplicité, il s’agit d’une méthode paramétrique très simple, et elle est tellement concise que vous pouvez en faire tenir l’intégralité sur un seul écran. Elle n’est même pas si verbeuse.
Toutes les variables que vous voyez à l’écran ne sont que de simples nombres ; il n’y a pas de vecteurs impliqués. Essentiellement, Y(t) est votre estimation ; c’est votre prévision de séries temporelles. Ici, à l’écran, il s’agira de prévoir H périodes à l’avance, donc H représente l’horizon. Et vous pouvez considérer que vous travaillez effectivement sur Y(t), qui est essentiellement votre série temporelle. Vous pouvez penser à des données de ventes agrégées par semaine ou par mois. Ce modèle comporte essentiellement trois composantes : il y a Lt, qui représente le niveau (vous avez un niveau par période), Bt, qui représente la tendance, et St, qui constitue une composante saisonnière. Lorsque vous dites que vous souhaitez apprendre le modèle de Holt-Winters, vous avez trois paramètres : alpha, beta et gamma. Ces trois paramètres ne sont essentiellement que de simples nombres compris entre zéro et un. Ainsi, vous avez trois paramètres, tous des nombres entre zéro et un, et lorsque vous dites que vous souhaitez appliquer l’algorithme de Holt-Winters, cela signifie simplement que vous identifierez les valeurs appropriées pour ces trois paramètres, et c’est tout. L’idée est que ces paramètres, alpha, beta et gamma, seront les meilleurs s’ils minimisent le type d’erreur que vous avez spécifié pour votre prévision. Sur cet écran, vous pouvez voir une erreur quadratique moyenne, qui est très classique.
L’objectif de l’optimisation mathématique est d’inventer une méthode permettant d’identifier les bonnes valeurs de paramètres pour alpha, beta et gamma. Que pouvons-nous faire ? Eh bien, la méthode la plus simple et la plus élémentaire est quelque chose comme la recherche par grille. La recherche par grille consisterait à explorer toutes les valeurs. Étant donné qu’il s’agit de nombres fractionnaires, il y a une infinité de valeurs, donc nous allons en fait choisir une résolution, disons des pas de 0,1, et nous avancerons par incréments de 0,1. Comme nous avons trois variables comprises entre 0 et 1, nous progressons par incréments de 0,1 ; cela représente environ 1 000 itérations pour parcourir et identifier la meilleure valeur, compte tenu de cette résolution.
Cependant, cette résolution est assez faible. Un pas de 0,1 vous donne environ une résolution de 10 % sur l’échelle que vous avez pour vos paramètres. Vous souhaiterez donc peut-être opter pour 0,01, ce qui est bien meilleur ; cela correspond à une résolution de 1 %. Cependant, si vous faites cela, le nombre de combinaisons explose réellement. Vous passez d’environ 1 000 combinaisons à un million de combinaisons, et vous voyez bien que c’est là le problème de la recherche par grille : très rapidement, vous atteignez une impasse combinatoire, et vous vous retrouvez avec un nombre énorme d’options.
L’optimisation mathématique consiste à concevoir des algorithmes qui vous offrent un meilleur rapport qualité-prix pour une quantité donnée de ressources informatiques que vous souhaitez consacrer au problème. Pouvez-vous obtenir une solution bien meilleure que la simple recherche exhaustive ? La réponse est oui, absolument.
Alors, que pouvons-nous faire dans ce cas pour obtenir réellement une meilleure solution en investissant moins de ressources computationnelles ? Tout d’abord, nous pourrions utiliser une sorte de gradient. L’expression complète pour Holt-Winters est entièrement différentiable, sauf pour une division unique qui constitue un cas limite relativement facile à traiter. Ainsi, toute cette expression, y compris la fonction de perte, est entièrement différentiable. Nous pourrions utiliser un gradient pour guider notre recherche ; ce serait une approche.
L’autre approche consisterait à dire qu’en pratique, dans la supply chain, vous avez peut-être des tonnes de séries temporelles. Donc, peut-être qu’au lieu de traiter chaque série temporelle indépendamment, ce que vous voulez faire, c’est une recherche sur grille pour les 1 000 premières séries temporelles, puis investir et identifier des combinaisons pour alpha, beta et gamma qui sont bonnes. Ensuite, pour toutes les autres séries temporelles, vous choisirez simplement parmi cette liste restreinte de candidats afin d’identifier la meilleure solution.
Vous voyez, il existe de nombreuses idées simples sur la façon de faire bien mieux que de se contenter d’une approche de pure recherche sur grille, et l’essence de l’optimisation mathématique, ainsi que toutes sortes de problèmes de prise de décision, peut également être considérée typiquement comme des problèmes d’optimisation mathématique.
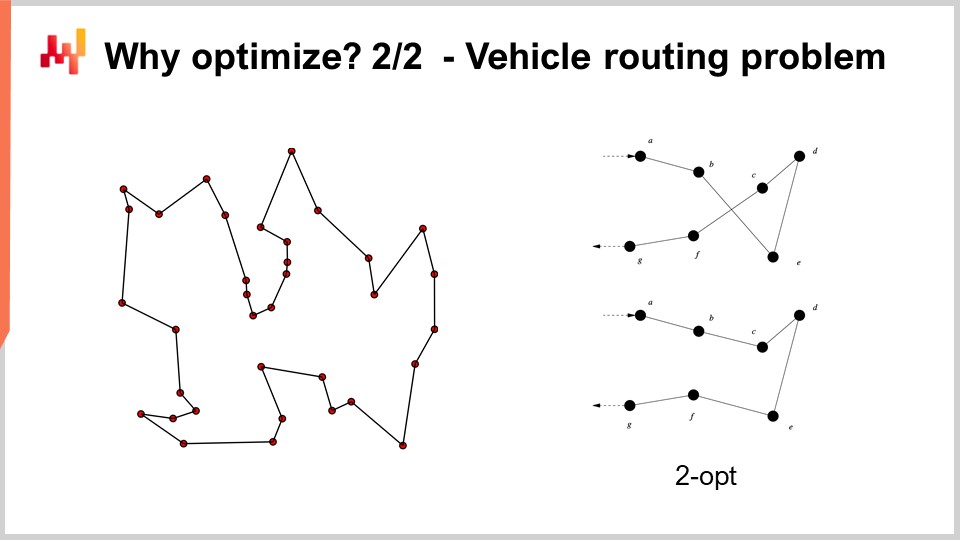
Par exemple, le problème de l’acheminement des véhicules que vous pouvez voir à l’écran peut être considéré comme un problème d’optimisation mathématique. Il s’agit de choisir la liste des points. Je n’ai pas écrit la version formelle du problème car celle-ci est relativement variable et n’apporte pas beaucoup d’éclaircissements. Mais si vous voulez y réfléchir, vous pouvez simplement penser : “J’ai des points, je peux attribuer une sorte de pseudo-ordre, c’est-à-dire un score à chaque point, puis j’ai un algorithme qui trie tous les points par pseudo-ordre en ordre croissant, et voilà ma route.” L’objectif de l’algorithme sera d’identifier les valeurs de ces pseudo-ordres qui vous donnent les meilleures routes.
Maintenant, avec ce problème, nous voyons que la recherche sur grille n’est même pas une option envisageable. Nous avons des dizaines de points, et si nous essayions toutes les combinaisons, ce serait bien trop conséquent. De plus, le gradient ne va pas nous aider, du moins il n’est pas évident en quoi il pourrait nous aider, car le problème est de nature très discrète, et il n’existe pas de descente de gradient évidente pour ce genre de problème.
Cependant, il s’avère que si nous voulons aborder ce type de problème, il existe des heuristiques très puissantes qui ont été identifiées dans la littérature. Par exemple, l’heuristique two-opt, publiée par Croes en 1958, vous propose une approche très simple. Vous commencez par une route aléatoire, et dans cette route, chaque fois qu’elle se croise, vous appliquez une permutation pour éliminer le croisement. Ainsi, vous débutez avec une route aléatoire, et dès le premier croisement observé, vous effectuez la permutation pour le supprimer, puis vous répétez l’opération. Vous répétez le processus avec l’heuristique jusqu’à ce qu’il n’y ait plus aucun croisement. Ce que vous obtenez de cette heuristique très simple est en réalité une très bonne solution. Elle peut ne pas être optimale au sens mathématique pur, donc ce n’est pas forcément la solution parfaite ; cependant, c’est une très bonne solution, et vous pouvez l’obtenir avec une quantité de ressources computationnelles relativement minimale.
Le problème avec l’heuristique two-opt, c’est qu’il s’agit d’une très bonne heuristique, mais elle est incroyablement spécifique à ce problème précis. Ce qui intéresse vraiment dans l’optimisation mathématique, c’est d’identifier des méthodes qui fonctionnent sur de grandes classes de problèmes, plutôt que d’avoir une heuristique qui ne fonctionnerait que pour une version spécifique d’un problème. Nous voulons donc disposer de méthodes très générales.
Maintenant, voici le récit jusqu’ici dans cette série de conférences : cette conférence fait partie d’une série, et ce chapitre est dédié aux sciences auxiliaires de la supply chain. Dans le premier chapitre, j’ai présenté mes vues sur la supply chain, à la fois en tant que domaine d’étude et en tant que pratique. Le deuxième chapitre était dédié à la méthodologie, et en particulier, nous avons introduit une méthodologie d’une importance capitale pour la présente conférence, qui est l’optimisation expérimentale. C’est la clé pour aborder le problème très pertinent identifié par Russell Ackoff il y a des décennies. Le troisième chapitre est entièrement dédié au personnel de la supply chain. Dans cette conférence, nous nous concentrons sur l’identification du problème que nous sommes sur le point de résoudre, plutôt que de confondre solution et problème. Dans ce quatrième chapitre, nous étudions toutes les sciences auxiliaires de la supply chain. Il y a une progression du niveau le plus bas en termes de matériel, montant au niveau des algorithmes, puis à l’optimisation mathématique. Nous progressons en termes de niveaux d’abstraction tout au long de cette série.

Un bref rappel sur les sciences auxiliaires : elles offrent une perspective sur la supply chain elle-même. La présente conférence ne porte pas sur la supply chain en tant que telle, mais plutôt sur l’une des sciences auxiliaires de la supply chain. Cette perspective fait une différence significative entre la perspective classique de la recherche opérationnelle, qui était censée être une fin, et l’optimisation mathématique, qui est un moyen pour atteindre un objectif mais pas une fin en soi, du moins en ce qui concerne la supply chain. L’optimisation mathématique ne se préoccupe pas des spécificités commerciales, et la relation entre l’optimisation mathématique et la supply chain est similaire à celle entre la chimie et la médecine. D’un point de vue moderne, il n’est pas nécessaire d’être un brillant chimiste pour être un brillant médecin ; cependant, un médecin qui prétend ne rien savoir en chimie semblerait suspect.

L’optimisation mathématique part du principe que le problème est connu. Elle ne se préoccupe pas de la validité du problème, mais se concentre sur l’optimisation maximale de ce que vous pouvez faire pour un problème donné. En quelque sorte, c’est comme un microscope – très puissant, mais avec un focus incroyablement étroit. Le danger, comme nous le voyons dans la discussion sur l’avenir de la recherche opérationnelle, est que si vous pointez votre microscope dans la mauvaise direction, vous risquez d’être distrait par des défis intellectuels intéressants mais finalement sans importance.
C’est pourquoi l’optimisation mathématique doit être utilisée conjointement avec l’optimisation expérimentale. L’optimisation expérimentale, que nous avons abordée dans la conférence précédente, est le processus par lequel vous pouvez itérer avec des retours du monde réel pour améliorer les versions du problème lui-même. L’optimisation expérimentale est un processus qui consiste à modifier non la solution, mais le problème, afin de converger itérativement vers un bon problème. C’est là l’essence même du sujet, et là où Russell Ackoff et ses pairs de l’époque n’avaient pas de solution. Ils disposaient des outils pour optimiser un problème donné, mais pas des outils pour modifier le problème jusqu’à ce qu’il soit bon. Si vous prenez un problème mathématique tel que vous pouvez l’écrire dans votre tour d’ivoire, sans retour du monde réel, ce que vous obtenez, c’est une fantaisie. Votre point de départ, lorsque vous initiez un processus d’optimisation expérimentale, n’est qu’une fantaisie. Il faut le retour du monde réel pour que cela fonctionne. L’idée est d’alterner entre l’optimisation mathématique et l’optimisation expérimentale. À chaque étape de votre processus d’optimisation expérimentale, vous utiliserez des outils d’optimisation mathématique. Le but est de minimiser à la fois les ressources computationnelles et les efforts d’ingénierie, permettant ainsi au processus d’itérer vers la prochaine version du problème.

Dans cette conférence, nous allons d’abord affiner notre compréhension de la perspective de l’optimisation mathématique. La définition formelle est trompeusement simple, mais il existe des complexités dont nous devons être conscients pour atteindre une pertinence pratique pour la supply chain. Nous explorerons ensuite deux grandes catégories de solveurs qui représentent l’état de l’art en optimisation mathématique du point de vue de la supply chain.
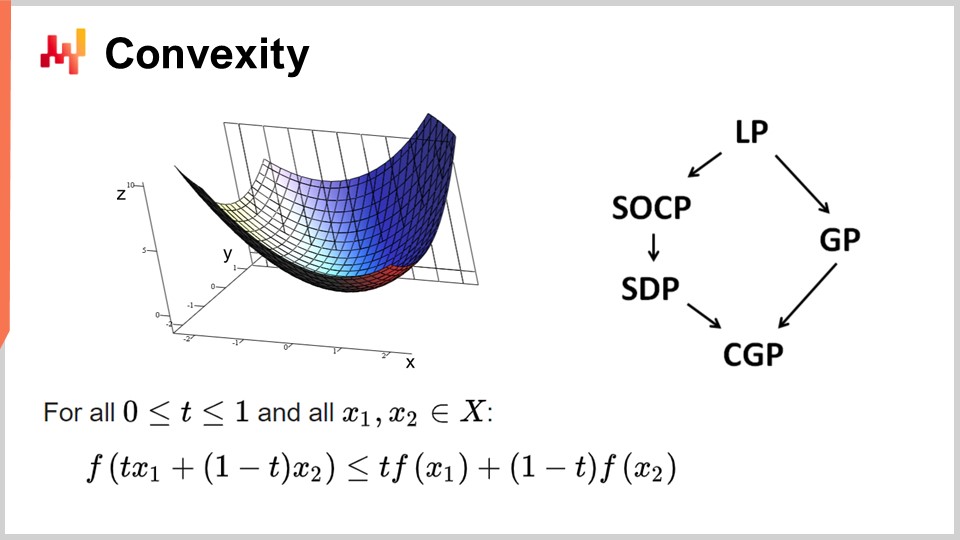
Tout d’abord, parlons de convexité et des premiers travaux en optimisation mathématique. La recherche opérationnelle s’est d’abord focalisée sur les fonctions de perte convexes. On dit qu’une fonction est convexe si elle respecte certaines propriétés. Intuitivement, une fonction est convexe si, pour deux points quelconques sur la variété définie par la fonction, la ligne droite qui relie ces points se trouve toujours au-dessus des valeurs prises par la fonction entre ces points.
La convexité est essentielle pour permettre une véritable optimisation mathématique, où vous pouvez démontrer des résultats. Intuitivement, lorsqu’une fonction est convexe, cela signifie que pour n’importe quel point de la fonction (n’importe quelle solution candidate), vous pouvez toujours regarder autour de vous et trouver une direction dans laquelle vous pouvez descendre. Peu importe d’où vous partez, vous pouvez toujours descendre, et descendre est toujours une bonne démarche. Le seul point où vous ne pouvez pas descendre davantage est essentiellement le point optimal. Je simplifie ici ; il existe des cas limites où les solutions ne sont pas uniques ou bien où il n’y a aucune solution. Mais, mis à part quelques cas limites, le seul point où vous ne pouvez pas optimiser davantage avec une fonction convexe est le point optimal. Sinon, vous pouvez toujours descendre, et descendre est une bonne démarche.
Il y a eu une quantité énorme de recherches sur les fonctions convexes, et divers paradigmes de programmation ont émergé au fil des années. LP signifie programmation linéaire, et d’autres paradigmes incluent la programmation conique du second ordre, la programmation géométrique (traitant des polynômes), la programmation semi-définie (impliquant des matrices aux valeurs propres positives) et la programmation géométrique conique. Ces cadres ont tous en commun qu’ils traitent de problèmes convexes structurés. Ils sont convexes aussi bien dans leur fonction de perte que dans les contraintes qui restreignent les solutions admissibles.
Ces cadres ont suscité un grand intérêt, avec une littérature scientifique intense produite. Cependant, malgré leurs noms impressionnants, ces paradigmes ont très peu d’expressivité. Même des problèmes simples dépassent les capacités de ces cadres. Par exemple, l’optimisation des paramètres de Holt-Winters, un modèle de prévision de base des années 1960, dépasse déjà ce que chacun de ces cadres peut faire. De même, le problème de l’acheminement des véhicules et le problème du voyageur de commerce, qui sont tous deux des problèmes simples, dépassent les capacités de ces cadres.
Voilà pourquoi je disais dès le début qu’il y avait un énorme corpus littéraire, mais très peu d’utilité. Le seul point où vous ne pouvez pas descendre davantage est essentiellement le point optimal. Je simplifie ici ; il existe des cas limites où les solutions ne sont pas uniques ou bien où il n’y a aucune solution. Mais, en mettant de côté quelques cas limites, le seul point où vous ne pouvez pas optimiser davantage avec une fonction convexe est le point optimal. Sinon, vous pouvez toujours descendre, et descendre est une bonne démarche.
Il y a eu une quantité énorme de recherches sur les fonctions convexes, et divers paradigmes de programmation ont émergé au fil des années. LP signifie programmation linéaire, et d’autres paradigmes incluent la programmation conique du second ordre, la programmation géométrique (traitant des polynômes), la programmation semi-définie (impliquant des matrices aux valeurs propres positives) et la programmation géométrique conique. Ces cadres ont tous en commun qu’ils traitent de problèmes convexes structurés. Ils sont convexes aussi bien dans leur fonction de perte que dans les contraintes qui restreignent les solutions admissibles.
Ces cadres ont suscité un grand intérêt, avec une littérature scientifique intense produite. Cependant, malgré leurs noms impressionnants, ces paradigmes ont très peu d’expressivité. Même des problèmes simples dépassent les capacités de ces cadres. Par exemple, l’optimisation des paramètres de Holt-Winters, un modèle de prévision de base des années 1960, dépasse déjà ce que chacun de ces cadres peut faire. De même, le problème de l’acheminement des véhicules et le problème du voyageur de commerce, qui sont tous deux des problèmes simples, dépassent les capacités de ces cadres.
C’est pourquoi je disais dès le début qu’il y avait un énorme corpus littéraire, mais très peu d’utilité. Une partie du problème résidait dans une focalisation erronée sur les solveurs de pure optimisation mathématique. Ces solveurs sont très intéressants d’un point de vue mathématique car ils permettent de produire des preuves mathématiques, mais ils ne peuvent être utilisés qu’avec des problèmes littéralement jouets ou complètement fictifs. Une fois que l’on se retrouve dans le monde réel, ils échouent, et il y a eu très peu de progrès dans ces domaines au cours des dernières décennies. En ce qui concerne la supply chain, presque rien, à quelques niches près, n’a de pertinence pour ces solveurs.

Un autre aspect, qui a été entièrement écarté et ignoré pendant l’ère classique de la recherche opérationnelle, est l’aléa. L’aléa ou la stochasticité est d’une importance cruciale de deux manières radicalement différentes. La première approche de l’aléa concerne le solveur lui-même. De nos jours, tous les solveurs de pointe tirent largement parti des processus stochastiques en interne. Cela est très intéressant comparé à un processus entièrement déterministe. Je parle ici du fonctionnement interne du solveur, le logiciel qui implémente les techniques d’optimisation mathématique.
La raison pour laquelle tous les solveurs de pointe tirent largement parti des processus stochastiques est liée à la manière dont le matériel informatique moderne fonctionne. L’alternative à l’aléa lors de l’exploration des solutions serait de se souvenir de ce que vous avez fait par le passé, afin de ne pas rester bloqué dans la même boucle. Si vous devez vous souvenir, vous consommerez de la mémoire. Le problème réside dans le fait que nous devons effectuer de nombreux accès mémoire. Introduire de l’aléa est généralement un moyen de réduire considérablement le besoin d’accès mémoire aléatoires.
En rendant votre processus stochastique, vous pouvez éviter de sonder votre propre base de données sur ce que vous avez testé ou non parmi les solutions possibles pour le problème que vous souhaitez optimiser. Vous le faites un peu de manière aléatoire, mais pas complètement. Cela revêt une importance capitale dans pratiquement tous les solveurs modernes. L’un des aspects quelque peu contre-intuitifs d’avoir un processus stochastique est que, bien que vous puissiez avoir un solveur stochastique, la sortie peut demeurer assez déterministe. Pour comprendre cela, considérez l’analogie d’une série de tamis. Un tamis est fondamentalement un processus stochastique physique, où vous appliquez des mouvements aléatoires et où le processus de tamisage se déroule. Bien que le processus soit complètement stochastique, le résultat est entièrement déterministe. Au final, vous obtenez un résultat totalement prévisible issu du processus de tamisage, même si votre procédé était fondamentalement aléatoire. C’est exactement ce genre de phénomène qui se produit avec des solveurs stochastiques bien conçus. C’est l’un des ingrédients clés des solveurs modernes.
Un autre aspect, qui est orthogonal en ce qui concerne l’aléatoire, est la nature stochastique des problèmes eux-mêmes. Cela était essentiellement absent de l’ère classique de la recherche opérationnelle – l’idée que votre fonction de perte est bruitée et que toute mesure que vous en ferez comportera un certain degré de bruit. Cela est presque toujours le cas dans la supply chain. Pourquoi ? La réalité est que dans la supply chain, chaque fois que vous prenez une décision, c’est parce que vous anticipez certains événements futurs. Si vous décidez d’acheter quelque chose, c’est parce que vous anticipez qu’il y aura un besoin ultérieur. L’avenir n’est pas écrit, donc vous pouvez avoir quelques aperçus du futur, mais cet aperçu n’est jamais parfait. Si vous décidez de produire un produit maintenant, c’est parce que vous vous attendez à ce que, plus tard, il y ait une demande pour ce produit. La qualité de votre décision de produire aujourd’hui dépend de conditions futures incertaines, et ainsi toute décision que vous prenez dans la supply chain aura une fonction de perte qui varie en fonction de ces conditions futures incontrôlables. Ce type d’aléatoire dû aux événements futurs est irréductible, et cela est d’un intérêt majeur car cela signifie que nous traitons fondamentalement des problèmes stochastiques.
Cependant, si nous revenons aux solveurs mathématiques classiques, nous constatons que cet aspect est complètement absent, ce qui pose un gros problème. Cela signifie que nous disposons de classes de solveurs qui ne peuvent même pas appréhender le type de problèmes auxquels nous serons confrontés, car les problèmes qui nous intéresseront, ceux où nous souhaitons appliquer l’optimisation mathématique, seront de nature stochastique. Je parle ici du bruit dans la fonction de perte.
Il y a une objection selon laquelle, si vous avez un problème stochastique, vous pouvez toujours le transformer en un problème déterministe par échantillonnage. Si vous évaluez votre fonction de perte bruitée 10 000 fois, vous pouvez obtenir une fonction de perte approximativement déterministe. Cependant, cette approche est incroyablement inefficace car elle introduit une surcharge multipliée par 10 000 dans votre processus d’optimisation. La perspective de l’optimisation mathématique consiste à obtenir les meilleurs résultats avec vos ressources informatiques limitées. Il ne s’agit pas d’investir une quantité infiniment grande de ressources pour résoudre le problème. Nous devons composer avec une quantité finie de ressources informatiques, même si cette quantité est assez importante. Ainsi, quand nous examinerons les solveurs par la suite, nous devons garder à l’esprit qu’il est primordial d’avoir des solveurs capables de comprendre nativement les problèmes stochastiques plutôt que de par défaut adopter l’approche déterministe.
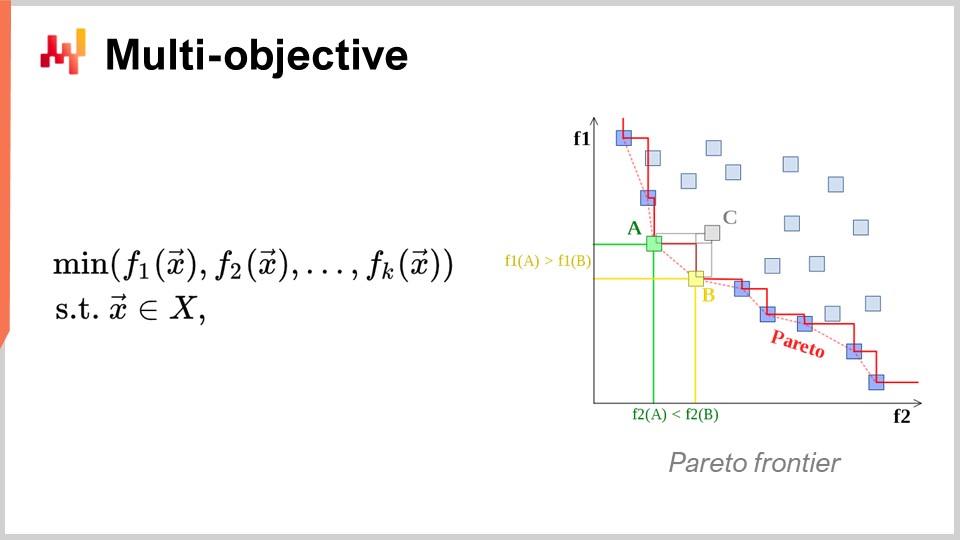
Un autre angle, qui est également d’un intérêt majeur, est l’optimisation multi-objectifs. Dans l’expression naïve du problème d’optimisation mathématique, j’ai dit que la fonction de perte était essentiellement à valeur unique, donc nous avions une seule valeur à minimiser. Mais que se passe-t-il si nous avons un vecteur de valeurs, et que ce que nous voulons, c’est trouver la solution qui fournit le point le plus bas selon l’ordre lexicographique de tous les vecteurs, comme f1, f2, f3, etc.?
Pourquoi cela est-il même d’intérêt du point de vue de la supply chain ? La réalité est que si vous adoptez cette perspective multi-objectifs, vous pouvez exprimer toutes vos contraintes sous la forme d’une unique fonction de perte dédiée. Vous pouvez, par exemple, définir une fonction qui compte le nombre de violations de contraintes. Pourquoi y a-t-il des contraintes dans la supply chain ? Eh bien, elles se trouvent partout. Par exemple, si vous passez une commande d’achat, vous devez vous assurer que vous disposez de suffisamment d’espace dans votre warehouse pour stocker les marchandises lorsqu’elles arrivent. Ainsi, vous avez des contraintes d’espace de stockage, de capacité de production, et bien d’autres. L’idée est que, plutôt que d’avoir un solveur où vous devez traiter les contraintes au cas par cas, il est plus intéressant d’avoir un solveur capable de gérer l’optimisation multi-objectifs et dans lequel vous pouvez exprimer les contraintes comme l’un des objectifs. Vous comptez simplement le nombre de violations de contraintes et vous souhaitez le minimiser, ramenant ce nombre à zéro.
La raison pour laquelle cet état d’esprit est très pertinent pour la supply chain est que les problèmes d’optimisation auxquels les supply chains sont confrontées ne sont pas des énigmes cryptographiques. Ce ne sont pas ces problèmes combinatoires extrêmement serrés où soit vous avez une solution et elle est excellente, soit vous êtes à une infinitésimale différence de la solution et vous n’avez rien. Dans la supply chain, obtenir ce que l’on appelle typiquement une solution faisable – une solution qui satisfait toutes les contraintes – est généralement complètement trivial. Identifier une solution qui satisfait les contraintes n’est pas une tâche ardue. Ce qui est très difficile, c’est, parmi toutes les solutions qui satisfont les contraintes, identifier celle qui est la plus rentable pour l’entreprise. C’est là que cela devient vraiment complexe. Trouver une solution qui ne viole pas les contraintes est très simple. Ce n’est pas le cas dans d’autres domaines, par exemple dans l’optimisation mathématique pour le design industriel, où vous souhaitez placer des composants à l’intérieur d’un téléphone portable. C’est un problème aux contraintes incroyablement serrées, et vous ne pouvez pas tricher en abandonnant une contrainte et en acceptant une légère imperfection sur votre téléphone. C’est un problème extrêmement serré et combinatoire, et où il faut réellement traiter les contraintes comme une priorité. Ce n’est pas nécessaire, je le crois, pour la grande majorité des problèmes de supply chain. Ainsi, il est de nouveau primordial d’avoir des techniques capables de gérer nativement l’optimisation multi-objectifs.
Maintenant, discutons un peu plus de la conception du solveur. D’un point de vue très global sur la manière dont nous souhaitons concevoir un logiciel qui produira des solutions pour une très large classe de problèmes, il y a deux aspects de conception remarquables que je voudrais mettre en avant. Le premier aspect à considérer est de savoir si nous adopterons une perspective boîte noire ou boîte blanche. L’idée d’une approche boîte noire est que nous pouvons traiter n’importe quel programme arbitraire, de sorte que la fonction de perte peut être n’importe quel programme arbitraire. Nous nous en moquons ; nous le traitons comme une boîte complètement noire. La seule exigence est d’avoir un programme qui nous permette d’évaluer et d’obtenir la valeur d’une solution provisoire. Au contraire, une approche boîte blanche insiste sur le fait que la fonction de perte possède une structure que nous pouvons examiner et exploiter. Nous pouvons regarder à l’intérieur de la fonction de perte. D’ailleurs, lorsque je parlais de convexité quelques diapositives plus tôt, tous ces modèles et solveurs mathématiques purs étaient véritablement des approches boîte blanches. Ils représentent l’extrême des approches boîte blanches, où non seulement vous pouvez voir à l’intérieur du problème, mais le problème possède une structure très rigide, comme dans la programmation semi-définie, où la forme est très étroite. Cependant, sans adopter un cadre aussi rigide qu’un modèle mathématique, vous pouvez, par exemple, dire qu’en adoptant une approche boîte blanche, vous bénéficiez d’éléments tels que le gradient pour vous aider. Le gradient de la fonction de perte est d’un intérêt majeur car, soudainement, vous savez dans quelle direction aller pour descendre, même si vous ne disposez pas d’un problème convexe où la descente de gradient garantit un bon résultat. En règle générale, si vous pouvez opérer en boîte blanche, votre solveur sera d’ordres de grandeur plus performant qu’un solveur boîte noire.
Maintenant, en second lieu, nous avons les solveurs offline versus online. Le solveur offline fonctionne typiquement par lots, de sorte qu’il va simplement prendre le problème, l’exécuter, et vous devrez attendre qu’il se termine. Une fois le solveur terminé, il vous fournit la meilleure solution ou du moins la meilleure solution identifiée. En revanche, un solveur online fonctionne beaucoup plus sur une approche de meilleur effort. Il va identifier une solution passable, puis investir des ressources informatiques pour itérer vers des solutions de plus en plus performantes au fil du temps, à mesure que vous investissez davantage de ressources. L’intérêt majeur réside dans le fait qu’avec un solveur online, vous pouvez interrompre le processus à tout moment et obtenir une solution candidate préliminaire. Vous pouvez même reprendre le processus. Si nous revenons aux solveurs mathématiques, ils sont généralement basés sur un fonctionnement par lots où vous devez attendre la fin du processus.
Malheureusement, évoluer dans le domaine de la supply chain peut s’avérer être un parcours semé d’embûches, comme cela a été abordé dans l’une des conférences précédentes de cette série. Il y aura des situations où, habituellement, vous pouvez vous permettre de consacrer, disons, trois heures à exécuter ce processus d’optimisation mathématique. Mais parfois, vous pouvez être confronté à des dysfonctionnements informatiques, à des problèmes du monde réel ou à une urgence dans votre supply chain. Dans de tels cas, ce sera salvateur que ce qui prenait normalement trois heures puisse être interrompu après cinq minutes et fournir une réponse, même imparfaite, plutôt que de n’obtenir aucune réponse du tout. Comme le dit un adage militaire, le pire plan est l’absence de plan, donc il vaut mieux avoir un plan très approximatif plutôt que rien du tout. C’est exactement ce qu’un solveur online vous offre. Ce sont les éléments clés de conception que nous garderons à l’esprit dans la discussion suivante.
Pour conclure cette première section de la conférence sur l’approche de l’optimisation mathématique, examinons les leçons du deep learning. Le deep learning a constitué une révolution totale dans le domaine du machine learning. Cependant, au fond, le deep learning repose également sur un problème d’optimisation mathématique. Je crois que le deep learning a provoqué une révolution au sein même de l’optimisation mathématique et a complètement transformé notre manière d’envisager les problèmes d’optimisation.
De nos jours, les plus grands modèles de deep learning traitent plus d’un trillion de paramètres, soit mille milliards. Pour replacer cela dans un contexte, la plupart des solveurs mathématiques peinent même à gérer 1 000 variables et s’effondrent généralement avec seulement quelques dizaines de milliers de variables, peu importe la puissance de calcul mise à leur disposition. En revanche, le deep learning réussit, certes en mobilisant une grande quantité de ressources informatiques, mais demeure faisable. Il existe des modèles de deep learning en production qui comportent plus d’un trillion de paramètres, et tous ces paramètres sont optimisés, ce qui signifie que nous disposons de processus d’optimisation mathématique capables de se déployer jusqu’à un trillion de paramètres. C’est absolument stupéfiant et radicalement différent des performances observées avec les approches d’optimisation classiques.
L’aspect intéressant est que même des problèmes complètement déterministes, comme jouer au Go ou aux échecs – qui sont non statistiques, discrets et combinatoires – ont été résolus avec le plus grand succès par des méthodes entièrement stochastiques et statistiques. Cela est déconcertant car jouer au Go ou aux échecs peut être considéré comme des problèmes d’optimisation discrets, pourtant ils sont résolus de manière extrêmement efficace aujourd’hui par des méthodes complètement stochastiques et statistiques. Cela va à l’encontre de l’intuition que la communauté scientifique avait à leur sujet il y a deux décennies.
Revisitons la compréhension que le deep learning a apportée en matière d’optimisation mathématique. La première chose est de repenser complètement la malédiction de la dimensionnalité. Je crois que ce concept est en grande partie erroné, et le deep learning démontre que ce n’est pas ainsi que l’on doit appréhender la difficulté d’un problème d’optimisation. Il s’avère que, lorsque l’on examine certaines classes de problèmes mathématiques, on peut démontrer, d’un point de vue mathématique, que certains problèmes sont extrêmement difficiles à résoudre parfaitement. Par exemple, vous avez sans doute entendu parler des problèmes NP-difficiles ; vous savez qu’en ajoutant des dimensions, le problème devient exponentiellement plus difficile à résoudre. Chaque dimension supplémentaire complexifie le problème, et il existe une barrière cumulative. On peut prouver qu’aucun algorithme ne peut espérer résoudre parfaitement le problème avec une quantité limitée de ressources informatiques. Cependant, le deep learning a montré que cette perspective était en grande partie erronée.
D’abord, nous devons différencier la complexité représentative du problème de sa complexité intrinsèque. Permettez-moi de clarifier ces deux termes avec un exemple. Prenons l’exemple de prévision des séries temporelles donné initialement. Supposons que nous ayons un historique de ventes, agrégé quotidiennement sur trois ans, de sorte que nous disposions d’un vecteur temporel quotidien d’environ 1 000 jours. C’est la représentation du problème.
Maintenant, que se passe-t-il si je passe à une représentation des séries temporelles par seconde ? Il s’agit du même historique de ventes, mais au lieu de représenter mes données de ventes sous forme d’agrégats quotidiens, je vais représenter ces mêmes séries temporelles sous forme d’agrégats par seconde. Cela signifie qu’il y a 86 400 secondes dans chaque jour, gonflant ainsi la taille et la dimension de la représentation du problème d’un facteur de 86 000.
Mais si nous commençons à réfléchir à la dimension intrinsèque, ce n’est pas parce que j’ai un historique de ventes, ni parce que je passe d’une agrégation journalière à une agrégation par seconde, que j’augmente la complexité ou la complexité dimensionnelle du problème par 1 000. Très probablement, si je passe à des ventes agrégées par seconde, la série temporelle sera incroyablement creuse, étant quasiment constituée de zéros dans presque tous les compartiments. Je n’augmente pas l’intéressante dimensionnalité du problème par un facteur de 100 000. Le deep learning clarifie que ce n’est pas parce que vous avez une représentation du problème avec de nombreuses dimensions que le problème devient fondamentalement difficile.
Un autre angle associé à la dimensionnalité est que, bien que l’on puisse prouver que certains problèmes sont NP-complets, par exemple le problème du voyageur de commerce (une version simplifiée du problème de tournées de véhicules présenté au début de ce cours), le voyageur de commerce est techniquement ce que l’on appelle un problème NP-difficile. Ainsi, c’est un problème pour lequel, si vous voulez trouver la meilleure solution dans le cas général, le coût augmente de façon exponentielle à mesure que vous ajoutez des points sur votre carte. Mais la réalité est que ces problèmes sont très faciles à résoudre, comme l’illustre l’heuristique two-opt ; vous pouvez obtenir d’excellentes solutions avec une quantité minimale de ressources informatiques. Ainsi, attention, les démonstrations mathématiques qui montrent que certains problèmes sont très difficiles peuvent être trompeuses. Elles ne vous indiquent pas que, si une solution approximative vous suffit, l’approximation peut être excellente, et parfois ce n’est même pas une approximation ; vous allez obtenir la solution optimale. C’est juste que vous ne pouvez pas prouver son optimalité. Cela ne dit rien quant à savoir si vous pouvez approcher le problème, et très fréquemment, ces problèmes supposément frappés par la malédiction de la dimensionnalité sont simples à résoudre parce que leurs dimensions intéressantes ne sont pas si élevées. Deep learning a démontré avec succès que de nombreux problèmes considérés comme incroyablement difficiles ne l’étaient pas vraiment dès le départ.
La deuxième idée clé était celle des minima locaux. La majorité des chercheurs travaillant sur l’optimisation mathématique et la recherche opérationnelle s’est orientée vers les fonctions convexes parce qu’il n’y avait pas de minima locaux. Pendant longtemps, les personnes ne travaillant pas sur des fonctions convexes se sont préoccupées de comment éviter de rester bloquées dans un minimum local. La plupart des efforts ont été consacrés à explorer des approches telles que les méta-heuristiques. Deep learning a apporté une compréhension renouvelée : nous nous passons des minima locaux. Cette compréhension provient de travaux récents issus de la communauté du deep learning.
Si vous avez une dimension très élevée, vous pouvez démontrer que les minima locaux disparaissent à mesure que la dimension du problème augmente. Les minima locaux sont très fréquents dans les problèmes de faible dimension, mais si vous augmentez la dimension des problèmes à des centaines ou des milliers, statistiquement parlant, les minima locaux deviennent incroyablement improbables. Au point que, pour des dimensions très élevées comme des millions, ils disparaissent complètement.
Au lieu de penser qu’une dimension plus élevée est votre ennemie, comme cela était associé à la malédiction de la dimensionnalité, que se passerait-il si vous pouviez faire exactement le contraire et augmenter la dimension du problème jusqu’à ce qu’elle devienne si grande qu’une descente nette sans minima locaux devienne triviale ? Il s’avère que c’est exactement ce qui se fait dans la communauté du deep learning et avec des modèles comportant un billion de paramètres. Cette approche vous offre une manière très limpide de progresser par gradient.
Essentiellement, la communauté du deep learning a montré qu’il n’était pas pertinent de fournir une preuve concernant la qualité de la descente ou la convergence ultime. Ce qui compte, c’est la vitesse de descente. Vous souhaitez itérer et descendre très rapidement vers une très bonne solution. Si vous pouvez disposer d’un processus qui descend plus rapidement, vous irez, en définitive, plus loin en termes d’optimisation. Ces idées vont à l’encontre de la compréhension générale de l’optimisation mathématique, ou de ce qui était la compréhension dominante il y a deux décennies.
Il y a d’autres leçons à tirer du deep learning, car c’est un domaine très riche. L’une d’elles est la sympathie matérielle. Le problème avec les solveurs mathématiques, tels que la programmation conique ou la programmation géométrique, est qu’ils se concentrent d’abord sur l’intuition mathématique et non sur le matériel informatique. Si vous conçevez un solveur qui antagonise fondamentalement votre matériel informatique, peu importe l’ingéniosité de vos mathématiques, il y a de fortes chances que vous soyez désespérément inefficace en raison d’une mauvaise utilisation du matériel de calcul.
L’une des idées clés de la communauté du deep learning est que vous devez bien vous entendre avec le matériel informatique et concevoir un solveur qui l’intègre. C’est pourquoi j’ai commencé cette série de conférences sur les sciences auxiliaires pour supply chain avec des ordinateurs modernes pour supply chain. Il est important de comprendre le matériel dont vous disposez et comment en tirer le meilleur parti. Cette sympathie matérielle est la manière dont vous pouvez obtenir des modèles avec un billion de paramètres, bien qu’elle nécessite un grand cluster d’ordinateurs ou un superordinateur.
Une autre leçon du deep learning est l’utilisation de fonctions de substitution. Traditionnellement, les solveurs mathématiques visaient à optimiser le problème tel quel, sans en dévier. Toutefois, le deep learning a montré que parfois il est préférable d’utiliser des fonctions de substitution. Par exemple, très fréquemment pour les prédictions, les modèles de deep learning utilisent cross-entropy comme métrique d’erreur au lieu du carré moyen. Pratiquement personne dans le monde réel ne s’intéresse à la cross-entropy comme métrique, car cela est assez absurde.
Alors, pourquoi les gens utilisent-ils la cross-entropy ? Elle fournit des gradients incroyablement abrupts, et comme le deep learning l’a démontré, tout est question de la vitesse de la descente. Si vous disposez de gradients très abrupts, vous pouvez descendre très rapidement. Certains pourraient objecter en disant : “Si je veux optimiser le carré moyen, pourquoi devrais-je utiliser la cross-entropy ? Ce n’est même pas le même objectif.” La réalité est que si vous optimisez la cross-entropy, vous obtiendrez des gradients très abrupts, et, en fin de compte, si vous évaluez votre solution par rapport au carré moyen, vous obtiendrez, très fréquemment, sinon toujours, une meilleure solution selon le critère du carré moyen. Je simplifie ici pour l’explication. L’idée des fonctions de substitution est que le vrai problème n’est pas absolu ; c’est simplement quelque chose que vous utiliserez pour contrôler et évaluer la validité finale de votre solution. Ce n’est pas nécessairement ce que vous utiliserez pendant l’exécution du solveur. Cela va complètement à l’encontre des idées sous-jacentes aux solveurs mathématiques qui étaient populaires durant les dernières décennies.
Enfin, il y a l’importance de travailler selon des paradigmes. Avec l’optimisation mathématique, il existe implicitement une division du travail dans l’organisation de votre équipe d’ingénierie. La division du travail implicite associée aux solveurs mathématiques est que vous aurez d’un côté des ingénieurs mathématiciens, responsables de concevoir le solveur, et de l’autre des ingénieurs problèmes, dont la responsabilité est d’exprimer le problème sous une forme adaptée au traitement par les solveurs mathématiques. Cette division du travail était répandue, et l’idée était de la rendre aussi simple que possible pour l’ingénieur problèmes, afin qu’il n’ait qu’à exprimer le problème de la manière la plus minimaliste et la plus pure, en laissant le solveur faire le travail.
Deep learning a montré que cette perspective était profondément inefficace. Cette division arbitraire du travail n’était pas la meilleure manière d’aborder le problème. En procédant ainsi, vous vous retrouvez avec des situations d’une difficulté insurmontable, dépassant de loin l’état de l’art pour les ingénieurs mathématiques travaillant sur le problème d’optimisation. Une approche bien meilleure consiste à ce que les ingénieurs problèmes fassent un effort supplémentaire pour reformuler les problèmes de manière à les rendre beaucoup plus adaptés à l’optimisation par le solveur mathématique.
Deep learning consiste en un ensemble de recettes qui vous permettent de formuler le problème en complément de votre solveur, afin de tirer le meilleur parti de votre optimiseur. La plupart des développements dans la communauté du deep learning se sont concentrés sur la conception de ces recettes, très efficaces pour l’apprentissage tout en s’intégrant parfaitement dans le paradigme des solveurs dont ils disposent (par exemple, TensorFlow, PyTorch, MXNet). La conclusion est que vous souhaitez vraiment collaborer avec l’ingénieur problème, ou en terminologie supply chain, le Supply Chain Scientist.

Passons maintenant à la deuxième et dernière partie de cette conférence sur les éléments les plus précieux de la littérature. Nous allons examiner deux grandes classes de solveurs : la recherche locale et la programmation différentiable.

Premièrement, permettez-moi de revenir sur le terme “programming.” Ce mot revêt une importance cruciale car, d’un point de vue supply chain, nous voulons vraiment être en mesure d’exprimer le problème auquel nous sommes confrontés, ou le problème que nous pensons affronter. Nous ne voulons pas une sorte de version en très basse résolution du problème qui se contente de satisfaire une hypothèse mathématique semi-absurde, comme l’obligation d’exprimer votre problème sous forme de cône ou quelque chose du genre. Ce qui nous intéresse vraiment, c’est d’avoir accès à un véritable paradigme de programming.
Souvenez-vous, ces solveurs mathématiques tels que la programmation linéaire, la programmation conique du second ordre et la programmation géométrique comportaient tous un mot-clé programming. Cependant, au cours des dernières décennies, nos attentes vis-à-vis d’un paradigme de programming ont évolué de façon spectaculaire. De nos jours, nous voulons quelque chose qui vous permette de traiter des programmes presque arbitraires, des programmes dans lesquels vous avez des boucles, des branchements, et éventuellement des allocations de mémoire, etc. Vous voulez vraiment quelque chose d’aussi proche que possible d’un programme arbitraire, et non une version jouet super limitée qui possède quelques propriétés mathématiques intéressantes. En supply chain, il vaut mieux être approximativement correct plutôt qu’exactement faux.

Pour aborder l’optimisation générique, commençons par la recherche locale. La recherche locale est une technique d’optimisation mathématique apparemment simple. Le pseudocode consiste à démarrer avec une solution aléatoire, que vous représentez sous forme d’un ensemble de bits. Vous initialisez ensuite votre solution de manière aléatoire et commencez à inverser les bits de façon aléatoire afin d’explorer le voisinage de la solution. Si, grâce à cette exploration aléatoire, vous trouvez une solution qui s’avère être meilleure, celle-ci devient votre nouvelle solution de référence.
Cette approche, étonnamment puissante, peut fonctionner avec littéralement n’importe quel programme, en le considérant comme une boîte noire, et peut également redémarrer à partir de n’importe quelle solution connue. Il existe de nombreuses façons d’améliorer cette approche. L’une d’elles est le calcul différentiel, à ne pas confondre avec le calcul différentiable. Le calcul différentiel repose sur l’idée que, si vous exécutez votre programme sur une solution donnée puis que vous inversez un bit, vous pouvez réexécuter le même programme grâce à une exécution différentielle, sans avoir à réexécuter l’ensemble du programme. Évidemment, vos résultats peuvent varier, et cela dépend fortement de la structure du problème. Une manière d’accélérer le processus consiste non pas à exploiter une sorte d’information supplémentaire sur le programme boîte noire que nous utilisons, mais simplement à accélérer le programme lui-même, en le considérant toujours majoritairement comme une boîte noire, car vous ne réexécutez pas l’ensemble du programme à chaque fois.
Il existe d’autres approches pour améliorer la recherche locale. Vous pouvez optimiser le type de mouvements que vous effectuez. La stratégie la plus basique s’appelle les k-flips, où vous inversez un certain nombre k de bits, k étant un très petit nombre, de l’ordre de quelques-uns à une dizaine. Plutôt que de simplement inverser des bits, vous pouvez laisser l’ingénieur problème déterminer le type de mutations à appliquer à la solution. Par exemple, vous pourriez indiquer que vous souhaitez appliquer une sorte de permutation dans votre problème. L’idée est que ces mouvements intelligents préservent souvent la satisfaction de certaines contraintes de votre problème, ce qui peut aider le processus de recherche locale à converger plus rapidement.
Une autre manière d’améliorer la recherche locale consiste à ne pas explorer l’espace de manière entièrement aléatoire. Plutôt que d’inverser les bits aléatoirement, vous pouvez essayer d’apprendre les bonnes directions, en identifiant les zones les plus prometteuses pour les inversions. Certains articles récents ont montré que vous pouvez intégrer un petit module de deep learning au-dessus de la recherche locale, agissant comme un générateur. Toutefois, cette approche peut s’avérer délicate du point de vue de l’ingénierie, car vous devez vous assurer que la surcharge introduite par le processus d’apprentissage automatique apporte un rendement positif en termes de ressources informatiques.
Il existe d’autres heuristiques bien connues, et si vous souhaitez obtenir une vue synthétique très complète de ce qu’il faut pour implémenter un moteur de recherche locale moderne, vous pouvez lire l’article “LocalSolver: A Black-Box Local-Search Solver for 0-1 Programs.” L’entreprise qui exploite LocalSolver possède également un produit du même nom. Dans cet article, ils donnent une perspective d’ingénierie sur le fonctionnement interne de leur solveur de niveau production. Ils utilisent le multi-start et le recuit simulé pour de meilleurs résultats.
Un avertissement que j’ajouterais concernant la recherche locale est qu’elle ne traite pas très bien, ou de façon native, les problèmes stochastiques. Avec les problèmes stochastiques, il n’est pas aussi simple de dire “J’ai une meilleure solution” et de décider immédiatement qu’elle devient la meilleure solution. C’est plus compliqué que cela, et vous devez fournir un effort supplémentaire avant de vous engager sur la solution évaluée comme la nouvelle meilleure.

Maintenant, passons à la deuxième catégorie de solveurs dont nous allons discuter aujourd’hui, à savoir la programmation différentiable. Mais d’abord, pour comprendre la programmation différentiable, nous devons appréhender la descente de gradient stochastique. La descente de gradient stochastique est une technique d’optimisation itérative basée sur le gradient. Elle est apparue sous la forme d’une série de techniques initiées au début des années 1950, ce qui lui donne aujourd’hui presque 70 ans. Elle est restée plutôt marginale pendant près de six décennies, et nous avons dû attendre l’avènement du deep learning pour réaliser le véritable potentiel et la puissance de la descente de gradient stochastique.
La descente de gradient stochastique suppose que la fonction de perte peut être décomposée de manière additive en une série de composantes. Dans l’équation, Q(W) représente la fonction de perte, qui est décomposée en une série de fonctions partielles, Qi. Ceci est pertinent car la plupart des problèmes d’apprentissage peuvent être envisagés comme nécessitant l’apprentissage d’une prédiction basée sur une série d’exemples. L’idée est que vous pouvez décomposer votre fonction de perte en l’erreur moyenne commise sur l’ensemble du jeu de données, avec une erreur locale pour chaque point de données. De nombreux problèmes supply chain peuvent également être décomposés de manière additive de cette façon. Par exemple, vous pouvez décomposer votre réseau supply chain en une série de performances pour chaque SKU, avec une fonction de perte associée à chaque SKU. La véritable fonction de perte que vous souhaitez optimiser est le total.
Lorsque vous avez cette décomposition en place, qui est très naturelle pour les problèmes d’apprentissage, vous pouvez itérer avec le processus de descente de gradient stochastique (SGD). Le vecteur de paramètres W peut être une très grande série, puisque les plus grands modèles de deep learning possèdent un trillion de paramètres. L’idée est qu’à chaque étape du processus, vous mettez à jour vos paramètres en appliquant une petite quantité de gradient. Eta est le taux d’apprentissage, un petit nombre typiquement compris entre 0 et 1, souvent autour de 0,01. Nabla de Q est le gradient pour une fonction de perte partielle Qi. Étonnamment, ce processus fonctionne bien.
On dit que le SGD est stochastique parce que vous choisissez aléatoirement votre prochain élément i, en parcourant votre ensemble de données et en appliquant une infime quantité de gradient à vos paramètres à chaque étape. C’est l’essence de la descente de gradient stochastique.
Il est resté relativement de niche et largement ignoré par la communauté en général pendant près de six décennies, car il est assez surprenant que la descente de gradient stochastique fonctionne du tout. Elle fonctionne parce qu’elle offre un excellent trade-off entre le bruit dans la fonction de perte et le coût computationnel d’accès à la fonction de perte elle-même. Au lieu d’avoir une fonction de perte qui doit être évaluée sur l’ensemble du jeu de données, avec la descente de gradient stochastique, nous pouvons prendre un point de données à la fois et appliquer quand même un peu de gradient. Cette mesure sera très fragmentaire et bruitée, et pourtant ce bruit est acceptable car le processus est très rapide. Vous pouvez réaliser d’ordres de grandeur plus d’optimisations minuscules et bruitées comparé au traitement de l’ensemble du jeu de données.
Étonnamment, le bruit introduit aide la descente de gradient. L’un des problèmes dans les espaces de haute dimension est que les minima locaux deviennent relativement inexistants. Cependant, vous pouvez encore rencontrer de vastes zones de plateau où le gradient est très faible, et la descente de gradient n’a pas de direction claire pour descendre. Le bruit vous fournit des gradients plus raides et plus bruités qui facilitent la descente.
Ce qui est également intéressant avec la descente de gradient, c’est qu’il s’agit d’un processus stochastique, mais qu’il peut gérer gratuitement des problèmes stochastiques. Si Qi est une fonction stochastique avec du bruit et donne un résultat aléatoire qui varie à chaque évaluation, vous n’avez même pas besoin de modifier une seule ligne de l’algorithme. La descente de gradient stochastique est d’un intérêt primordial car elle vous fournit quelque chose qui est complètement en phase avec le paradigme pertinent pour la supply chain.

La deuxième question est : d’où vient le gradient ? Nous avons un programme, et nous prenons simplement le gradient de la fonction de perte partielle, mais d’où provient ce gradient ? Comment obtient-on un gradient pour un programme arbitraire ? Il s’avère qu’il existe une technique très élégante et minimaliste, découverte il y a longtemps, appelée différentiation automatique.
La différentiation automatique est apparue dans les années 1960 et a été perfectionnée au fil du temps. Il en existe deux types : le mode avant, découvert en 1964, et le mode reverse, découvert en 1980. La différentiation automatique peut être considérée comme une astuce de compilation. L’idée est que vous avez un programme à compiler, et avec la différentiation automatique, vous avez votre programme qui représente la fonction de perte. Vous pouvez recompiler ce programme pour obtenir un second programme, dont la sortie n’est pas la fonction de perte mais les gradients de tous les paramètres impliqués dans le calcul de la fonction de perte.
De plus, la différentiation automatique vous fournit un second programme dont la complexité de calcul est essentiellement identique à celle de votre programme initial. Cela signifie que non seulement vous avez un moyen de créer un second programme qui calcule les gradients, mais également que ce second programme présente les mêmes caractéristiques de calcul en termes de performance que le premier. Il s’agit d’une inflation à facteur constant en termes de coût de calcul. La réalité, cependant, est que le second programme obtenu n’a pas exactement les mêmes caractéristiques mémoire que le programme initial. Bien que les détails relèvent d’un niveau de précision dépassant le cadre de cette conférence, nous pourrons en discuter lors des questions. Essentiellement, le second programme, appelé le mode reverse, va nécessiter plus de mémoire, et dans certaines situations pathologiques, il peut nécessiter beaucoup plus de mémoire que le programme initial. Rappelez-vous que plus de mémoire crée des problèmes de performance de calcul, car vous ne pouvez pas supposer un accès uniforme à la mémoire.
Pour illustrer un peu ce à quoi ressemble la différentiation automatique, comme je l’ai mentionné, il existe deux modes : le mode avant et le mode reverse. D’un point de vue d’apprentissage ou d’optimisation de la supply chain, le seul mode qui nous intéresse est le mode reverse. Ce que vous voyez à l’écran est une fonction de perte F, entièrement fictive. Vous pouvez observer la trace en avant, une séquence d’opérations arithmétiques ou élémentaires qui se déroulent pour calculer votre fonction pour deux valeurs d’entrée données, X1 et X2. Cela vous donne toutes les étapes élémentaires effectuées pour calculer la valeur finale.
L’idée est que pour chaque étape élémentaire, et la plupart d’entre elles ne sont que des opérations arithmétiques de base comme la multiplication ou l’addition, le mode reverse est un programme qui exécute les mêmes étapes mais dans l’ordre inverse. Au lieu d’avoir les valeurs en avant, vous aurez les adjoints. Pour chaque opération arithmétique, vous disposerez de sa contrepartie reverse. La transition de l’opération en avant vers sa contrepartie est très simple.
Même si cela semble compliqué, vous disposez d’une exécution en avant et d’une exécution reverse, où l’exécution reverse n’est rien d’autre qu’une transformation élémentaire appliquée à chaque opération. À la fin du reverse, vous obtenez les gradients. La différentiation automatique peut sembler compliquée, mais ce ne l’est pas. Le premier prototype que nous avons implémenté faisait moins de 100 lignes de code, il est donc très simple et constitue essentiellement une astuce de transpilation peu coûteuse.
C’est intéressant car nous avons la descente de gradient stochastique, qui est un mécanisme d’optimisation incroyablement puissant. Il est incroyablement scalable, en ligne, sur tableau blanc, et fonctionne nativement avec des problèmes stochastiques. Le seul problème qui restait était de savoir comment obtenir le gradient, et avec la différentiation automatique, nous avons le gradient moyennant une surcharge fixe ou un facteur constant, pour pratiquement n’importe quel programme arbitraire. Ce que nous obtenons au final, c’est la programmation différentiable.
De manière intéressante, la programmation différentiable est une combinaison de descente de gradient stochastique et de différentiation automatique. Bien que ces deux techniques, la descente de gradient stochastique et la différentiation automatique, datent de plusieurs décennies, la programmation différentiable n’a gagné en popularité qu’au début de 2018, lorsque Yann LeCun, le responsable de l’IA chez Facebook, a commencé à communiquer sur ce concept. LeCun n’a pas inventé ce concept, mais il a joué un rôle déterminant dans sa popularisation.
Par exemple, la communauté du deep learning utilisait initialement la rétropropagation plutôt que la différentiation automatique. Pour ceux qui connaissent les réseaux de neurones, la rétropropagation est un processus complexe qui est d’ordres de grandeur plus compliqué à implémenter que la différentiation automatique. La différentiation automatique est supérieure à tous égards. Forts de cette compréhension, la communauté du deep learning a affiné sa vision de ce qui constitue l’apprentissage dans le deep learning. Le deep learning a combiné l’optimisation mathématique avec diverses techniques d’apprentissage, et la programmation différentiable est apparue comme un concept épuré qui isolait les parties non-apprentissage du deep learning.
Les techniques modernes de deep learning, telles que le modèle transformer, supposent un environnement de programmation différentiable fonctionnant en arrière-plan. Cela permet aux chercheurs de se concentrer sur les aspects d’apprentissage qui se construisent par-dessus. La programmation différentiable, bien qu’elle soit fondamentale pour le deep learning, est également extrêmement pertinente pour l’optimisation de la supply chain et pour soutenir les processus d’apprentissage supply chain, tels que la prévision statistique.
Tout comme dans le deep learning, il y a deux volets dans le problème : la programmation différentiable en tant que couche de base et les techniques d’optimisation ou d’apprentissage par-dessus. La communauté du deep learning vise à identifier les architectures qui fonctionnent bien avec la programmation différentiable, telles que les transformers. De même, il faut identifier les architectures performantes pour l’optimisation. C’est ce qui a été fait pour apprendre à jouer au Go ou aux échecs dans des environnements fortement combinatoires. Nous aborderons des techniques adaptées à l’optimisation spécifique de la supply chain lors de conférences ultérieures.

Mais maintenant, il est temps de conclure. Une bonne partie de la littérature sur la supply chain et même la majorité de ses implémentations logicielles sont assez confuses en ce qui concerne l’optimisation mathématique. Cet aspect n’est généralement même pas correctement identifié comme tel, et par conséquent, les praticiens, chercheurs et même les ingénieurs logiciels travaillant pour des entreprises de enterprise software se mêlent souvent à leurs recettes numériques de manière plutôt hasardeuse en ce qui concerne l’optimisation mathématique. Ils ont un gros problème, car un composant n’a pas été identifié comme étant de nature optimisation mathématique, et parce que les gens ne sont même pas conscients de ce qui est disponible dans la littérature, ils recourent souvent à des recherches en grille rudimentaires ou à des heuristiques précipitées qui donnent des performances erratiques et inconsistantes. En conclusion de cette conférence, dorénavant, chaque fois que vous rencontrez une méthode numérique de supply chain ou un logiciel de supply chain qui prétend offrir une quelconque fonctionnalité analytique, vous devez vous interroger sur ce qui se passe en termes d’optimisation mathématique et sur ce qui est mis en œuvre. Si vous constatez que les fournisseurs n’offrent pas une vision limpide à ce sujet, il y a de fortes chances que vous vous trouviez du côté gauche de l’illustration, et ce n’est pas l’endroit où vous souhaitez être.
Maintenant, regardons les questions.

Question: La transition vers des méthodes computationnelles est-elle une compétence préalable dans les opérations, et les rôles opérationnels deviendront-ils obsolètes, ou inversement ?
Tout d’abord, laissez-moi préciser quelques points. Je pense qu’il est erroné d’imputer ce genre de préoccupations au CIO. Les gens attendent beaucoup trop de leurs CIO. En tant que Chief Information Officer, vous devez déjà gérer la couche de base de votre infrastructure logicielle, comme les ressources computationnelles, les systèmes transactionnels de bas niveau, l’intégrité du réseau et la cybersécurité. On ne devrait pas attendre du CIO qu’il comprenne ce qu’il faut pour réellement apporter une valeur ajoutée à votre supply chain.
Le problème est que, dans de nombreuses entreprises, les gens sont tellement ignorants en matière d’informatique que le CIO devient la personne de référence pour tout. La réalité est que le CIO devrait s’occuper de la couche de base de l’infrastructure, et qu’il revient ensuite à chaque spécialiste de répondre à ses besoins spécifiques avec les ressources computationnelles et les outils logiciels disponibles.
En ce qui concerne l’obsolescence des rôles opérationnels, si votre rôle consiste à passer la journée à parcourir manuellement des spreadsheets Excel, alors oui, il est fort probable que votre rôle devienne obsolète. Ce problème est connu depuis 1979, lorsque Russell Ackoff a publié son article. Le problème est que l’on savait que cette méthode de prise de décision n’était pas l’avenir, mais elle est restée le statu quo pendant très longtemps. Le cœur du problème est que les entreprises doivent comprendre le processus expérimental. Je suis convaincu qu’il y aura une transition où les entreprises recommenceront à acquérir ces compétences. De nombreuses grandes entreprises nord-américaines après la Seconde Guerre mondiale possédaient une certaine connaissance de la recherche opérationnelle parmi leurs dirigeants. C’était un sujet brûlant, et les conseils d’administration des grandes entreprises avaient une expertise en recherche opérationnelle. Comme le souligne Russell Ackoff, en raison du manque de résultats, ces idées ont été reléguées à l’échelon inférieur de l’entreprise, jusqu’à être complètement externalisées, car elles étaient pour la plupart irrélevantes et n’apportaient pas de résultats tangibles. Je crois que la recherche opérationnelle ne reviendra que si les gens tirent les leçons de l’échec de l’ère classique de la recherche opérationnelle à produire des résultats. Le CIO n’aura qu’une contribution modeste dans cette entreprise ; il s’agit principalement de repenser la valeur ajoutée des personnes au sein de l’entreprise.
Vous souhaitez apporter une contribution capitalistique, et cela revient à l’une de mes conférences précédentes sur la livraison orientée produit dans le sens des produits logiciels pour la supply chain. L’essentiel est : quelle sorte de valeur ajoutée capitalistique apportez-vous à votre entreprise ? Si la réponse est aucune, alors vous pourriez ne pas faire partie de ce que votre entreprise devrait être et deviendra à l’avenir.
Question: Qu’en est-il de l’utilisation du solveur Excel pour minimiser la valeur MRMSC et trouver la valeur optimale pour alpha, beta et gamma ?
Je crois que cette question est pertinente pour le cas de Holt-Winters, où vous pouvez en fait trouver une solution grâce à une recherche en grille. Cependant, que se passe-t-il dans ce solveur Excel ? S’agit-il d’une descente de gradient ou de quelque chose d’autre ? Si vous faites référence au solveur linéaire d’Excel, il ne s’agit pas d’un problème linéaire, donc Excel ne peut rien faire pour vous dans ce cas. Si vous disposez d’autres solveurs dans Excel ou d’add-ins, oui, ils peuvent fonctionner, mais c’est une perspective très dépassée. Elle n’adhère pas à une vision plus stochastique ; le type de prévision que vous obtenez est une prévision non probabiliste, ce qui constitue une approche obsolète.
Je ne dis pas qu’Excel ne peut pas être utilisé, mais la question est : quelles capacités de programmation se libèrent dans Excel ? Pouvez-vous effectuer une descente de gradient stochastique dans Excel ? Probablement, si vous ajoutez un add-in dédié. Excel vous permet de brancher n’importe quel programme arbitraire par-dessus. Pourriez-vous potentiellement faire de la programmation différentiable dans Excel ? Oui. Est-ce une bonne idée de le faire dans Excel ? Non. Pour comprendre pourquoi, vous devez revenir au concept de livraison logiciel orientée produit, qui explique ce qui ne va pas avec Excel. Cela se résume au modèle de programmation et à la capacité de maintenir réellement votre travail sur le long terme en collaborant en équipe.
Question: Les problèmes d’optimisation sont généralement orientés vers le routage de véhicules ou la prévision. Pourquoi ne pas envisager d’optimiser l’ensemble de la supply chain également ? Ne réduirait-on pas les coûts par rapport à une approche sectorisée ?
Je suis tout à fait d’accord. La malédiction de l’optimization de la supply chain est que lorsque vous effectuez une optimisation locale sur un sous-problème, vous allez très probablement déplacer le problème au lieu de le résoudre pour l’ensemble de la supply chain. Je suis tout à fait d’accord, et dès que vous commencez à examiner un problème plus complexe, vous êtes face à un problème hybride – par exemple, un problème de routage de véhicules combiné avec une stratégie de replenishment. Le problème est que vous avez besoin d’un solveur très générique pour aborder cela, car vous ne voulez pas être limité. Si vous disposez d’un solveur très générique, il vous faut des mécanismes tout aussi génériques au lieu de vous fier à des heuristiques intelligentes comme le two-opt, qui ne fonctionnent bien que pour le routage de véhicules et non pour quelque chose qui est un hybride de reapprovisionnement et de routage de véhicules en même temps.
Pour adopter cette perspective holistique, il faut ne pas avoir peur de la malédiction de la dimensionnalité. Il y a vingt ans, on aurait dit que ces problèmes étaient déjà extrêmement difficiles et NP-complets, comme le problème du voyageur de commerce, et vous voulez résoudre un problème encore plus difficile en l’entremêlant avec un autre problème. La réponse est oui ; vous devez être capable de le faire, et c’est pourquoi il est essentiel de disposer d’un solveur qui vous permette de traiter des programmes arbitraires, car votre résolution peut être la consolidation de nombreux problèmes entrelacés et imbriqués.
En effet, l’idée de résoudre ces problèmes isolément est bien moins efficace que de tout résoudre. Il vaut mieux être approximativement correct que parfaitement faux. Il est bien préférable de disposer d’un solveur très faible qui aborde l’ensemble de la supply chain en tant que système, en bloc, plutôt que d’avoir des optimisations locales avancées qui ne font que créer des problèmes ailleurs lorsqu’on micro-optimise localement. La véritable optimisation du système n’est pas nécessairement la meilleure optimisation pour chaque partie, il est donc naturel que, si vous optimisez dans l’intérêt de l’ensemble de l’entreprise et de sa supply chain, cela ne soit pas optimal localement, car vous tenez compte des autres aspects de l’entreprise et de sa supply chain.
Question : Après avoir réalisé un exercice d’optimisation, quand devons-nous revisiter le scenario étant donné que de nouvelles contraintes peuvent apparaître à tout moment ? La réponse est que vous devez revoir l’optimisation fréquemment. C’est le rôle du Supply Chain Scientist que j’ai présenté dans la deuxième conférence de cette série. Le Supply Chain Scientist revisitera l’optimisation aussi souvent que nécessaire. Si une nouvelle contrainte apparaît, comme un navire gigantesque bloquant le canal de Suez – ce fut inattendu –, vous devez faire face à cette disruption dans votre supply chain. Vous n’avez d’autre option que de traiter ces problèmes ; sinon, le système que vous avez mis en place produira des résultats insensés parce qu’il fonctionnera dans de fausses conditions. Même si vous n’avez pas d’urgence à gérer, vous souhaitez tout de même investir votre temps pour réfléchir à l’angle susceptible de générer le plus grand retour pour l’entreprise. Il s’agit fondamentalement de recherche et développement. Vous avez le système en place, il fonctionne, et vous essayez simplement d’identifier des domaines dans lesquels vous pouvez l’améliorer. Cela devient un processus de recherche appliquée, hautement capitaliste et erratique. En tant que Supply Chain Scientist, il y a des jours où vous passez toute la journée à tester des méthodes numériques, aucune ne fournissant de meilleurs résultats que ceux que vous possédez déjà. Certains jours, vous effectuez un tout petit ajustement, et vous avez beaucoup de chance, économisant ainsi des millions pour l’entreprise. C’est un processus erratique, mais en moyenne, le résultat peut être colossal.
Question : Quels seraient les cas d’usage pour des problèmes d’optimisation autres que la programmation linéaire, la programmation en nombres entiers, la programmation mixte, et dans le cas de Weber et du coût des marchandises ?
Je renverserais la question : où voyez-vous que la programmation linéaire a une quelconque pertinence pour un problème de supply chain ? Il n’existe pratiquement aucun problème de supply chain qui soit linéaire. Mon objection est que ces cadres sont très simplistes et ne peuvent même pas aborder des problèmes ludiques. Comme je l’ai dit, ces cadres mathématiques, comme la programmation linéaire, ne peuvent même pas aborder un problème ludique comme l’optimisation d’un hiver rigoureux pour un ancien modèle de prévision paramétrique à basse dimension. Ils ne peuvent même pas traiter le problème du voyageur de commerce ou pratiquement quoi que ce soit d’autre.
La programmation en nombres entiers ou la programmation mixte-integer n’est qu’un terme générique pour indiquer que certaines variables vont être des entiers, mais cela ne change rien au fait que ces cadres de programmation sont de simples cadres mathématiques ludiques, loin de posséder l’expressivité nécessaire pour traiter des problèmes de supply chain.
Lorsque vous demandez quels sont les cas d’utilisation des problèmes d’optimisation, je vous invite à consulter toutes mes conférences sur les personae de la supply chain. Nous disposons déjà d’une série de personae de la supply chain, et j’énumère littéralement une tonne de problèmes qui peuvent être abordés par l’optimisation mathématique. Dans les conférences sur les personae de la supply chain, nous avons Paris, Miami, Amsterdam et une série mondiale, avec d’autres à venir. Nous avons de nombreux problèmes qui mériteraient d’être abordés avec une véritable approche d’optimisation mathématique. Cependant, vous verrez que pour chacun de ces problèmes, vous ne pourrez pas les cadrer dans les contraintes très serrées et souvent bizarres qui émergent de ces cadres mathématiques. Encore une fois, ces cadres mathématiques reposent principalement sur la convexité, et ce n’est pas la bonne perspective pour la supply chain. La plupart des aspects que nous traitons sont non convexes. Mais ce n’est pas grave ; ce n’est pas parce qu’ils sont non convexes qu’ils sont impossiblement difficiles. Vous voyez, c’est simplement que vous ne pourrez pas obtenir de preuve mathématique à la fin de la journée. Mais votre patron ou votre entreprise se préoccupent du profit, pas de savoir si vous disposez d’une preuve mathématique pour étayer la décision. Ils se préoccupent du fait que vous puissiez prendre la bonne décision en termes de production, de reapprovisionnement, de prix, d’assortiments, etc., et non du fait que vous ayez une preuve mathématique attachée à ces décisions.
Question : Combien de temps les données de l’algorithme d’apprentissage doivent-elles être conservées pour faciliter l’apprentissage ?
Eh bien, je dirais que, étant donné que le stockage des données est aujourd’hui incroyablement bon marché, pourquoi ne pas le conserver indéfiniment ? Le stockage des données est si peu coûteux ; par exemple, allez simplement dans un supermarché, et vous verrez que le prix d’un disque dur d’un téraoctet tourne autour de 60 ou quelque chose dans ce genre. C’est donc incroyablement bon marché.
Maintenant, évidemment, il y a une préoccupation distincte : si vos données contiennent des informations personnelles, alors les données que vous conservez deviennent une responsabilité. Mais d’un point de vue supply chain, si nous supposons que vous avez d’abord épuré toutes les données personnelles – car, en général, vous n’avez pas besoin d’avoir des données personnelles – vous n’avez pas besoin de conserver des numéros de carte de crédit ou le nom de vos clients. Il vous suffit d’avoir des identifiants clients, etc. Si vous éliminez simplement toutes les données personnelles de vos données, je dirais : combien de temps ? Eh bien, conservez-les indéfiniment.
Un des points concernant la supply chain est que vous disposez de données limitées. Ce n’est pas comme les problèmes de deep learning tels que la reconnaissance d’images, où vous pouvez traiter toutes les images du web et avoir accès à des bases de données presque infinies à analyser. Dans la supply chain, vos données sont toujours limitées. En effet, si vous voulez prévoir la demande future, il y a très peu d’industries pour lesquelles remonter à plus d’une décennie dans le passé est véritablement pertinent, d’un point de vue statistique, pour prévoir la demande du trimestre suivant. Néanmoins, je dirais qu’il est toujours plus facile de tronquer les données si besoin, plutôt que de se rendre compte que vous en avez écarté et qu’il manque quelque chose. Ma suggestion est donc de tout conserver, d’épurer les données personnelles, et qu’à la toute fin de votre data pipeline, vous verrez s’il est préférable de filtrer les données très anciennes. Cela pourrait être le cas, ou non ; cela dépend de l’industrie dans laquelle vous opérez. Par exemple, dans l’aéronautique, lorsque vous avez des pièces et des avions avec une durée de vie opérationnelle de quatre décennies, avoir dans votre système les données des quatre dernières décennies est pertinent.
Question : La programmation multi-objectifs consiste-t-elle à avoir deux ou plusieurs objectifs, par exemple en additionnant ou en minimisant plusieurs fonctions en un seul objectif ?
Il existe plusieurs variantes pour aborder les problèmes multi-objectifs. Il ne s’agit pas d’avoir une fonction qui soit une somme, car si vous avez la somme, ce n’est qu’une question de décomposition et de structure de la fonction de perte. Non, il s’agit réellement d’avoir un vecteur. En effet, il existe essentiellement plusieurs approches de la programmation multi-objectifs. L’approche la plus intéressante est celle qui privilégie un ordre lexicographique. En ce qui concerne la supply chain, la minimisation – lorsque vous souhaitez dire que vous prenez la moyenne ou le maximum de plusieurs fonctions – peut présenter un intérêt, mais je n’en suis pas trop sûr. Je pense que l’approche multi-objectifs, où vous pouvez effectivement injecter des contraintes et les traiter comme faisant partie intégrante de votre optimisation habituelle, présente un intérêt considérable pour la supply chain. Les autres variantes pourraient aussi être intéressantes, mais j’en doute un peu. Je ne dis pas qu’elles ne le sont pas ; je dis simplement que j’en doute.
Question : Comment décideriez-vous quand utiliser une solution approximative plutôt qu’une solution optimisée ?
Je veux dire, je ne suis pas sûr de bien comprendre la question. L’idée est que, s’il y a une leçon à tirer du deep learning, c’est qu’il n’existe pas de solution optimale unique. Tout est une approximation, dans une certaine mesure. Même lorsque vous affirmez disposer de chiffres, dans les ordinateurs, les nombres ne sont pas exprimés avec une précision infinie ; ils ont une précision finie. Et cette précision finie peut, dans certaines circonstances, se retourner contre vous. La réponse est donc : c’est toujours approximatif. Je dirais que la plus grande leçon est qu’il est illusoire de penser qu’il existe une solution parfaite. Il n’existe pas de solution parfaite et optimale. Toutes les solutions que vous obtenez sont des approximations, et certaines d’entre elles sont, je dirais, légèrement plus ou moins approximatives. Je ne suis donc pas certain du sens de votre question, mais du point de vue de l’optimisation mathématique, cela signifie que vous disposez d’une fonction de perte pour en évaluer la qualité, et qu’au final, si vous avez deux solutions concurrentes, vous utilisez cette fonction de perte pour déterminer laquelle est la meilleure. Voilà comment cela fonctionne.
Question : Pourquoi les séries temporelles, en termes de données historiques, ont-elles été divisées par 86 400 en premier lieu ?
Ce n’était pas le cas. C’était un exemple. Je voulais simplement illustrer et pousser la situation jusqu’à l’absurde, où l’on voit que, lorsque vous optez pour des séries temporelles, avec un algorithme classique de prévision des séries temporelles, vous adoptez ce que l’on appelle des séries temporelles à intervalles réguliers. Il existe de nombreuses manières de représenter des séries temporelles, et la façon la plus typique de les représenter est la version à intervalles réguliers, où vous procédez à une agrégation en tranches de durée égale. C’est typiquement ce que vous obtenez avec une agrégation quotidienne ou hebdomadaire. Vous avez des tranches de même longueur, et votre série adopte une structure de type vecteur.
Mais ce que je souligne, c’est que cela est en grande partie arbitraire. Vous pouvez décider de représenter les données sous forme quotidienne, mais vous pourriez aussi choisir de les représenter à la seconde. Est-ce que cela aurait du sens de représenter les données à la seconde ? La réponse est oui ; cela dépend du type de problèmes. Par exemple, si vous êtes fournisseur d’électricité et que vous souhaitez gérer un réseau, alors vous devez gérer la puissance à chaque seconde afin d’obtenir exactement l’équilibre entre l’offre d’électricité dans votre réseau et la consommation d’énergie. Et cet équilibre est en réalité réglé à la seconde. Il peut donc exister des situations où représenter les données à la seconde a du sens. Pour la vente dans votre magasin local, cela pourrait ne pas être pertinent. Ce que je voulais souligner avec ces 86 400, d’ailleurs, c’est simplement 24 heures multipliées par 60 minutes multipliées par 60 secondes, et je voulais clarifier le fait que vous avez toujours une représentation de vos données, et que vous ne devez pas confondre cette représentation, qui repose sur une certaine dimensionnalité, avec la dimension intrinsèque de vos données, qui peut être complètement différente. La représentation est, dans une large mesure, totalement inventée et arbitraire. Elle vous donne un indicator numérique, par exemple en ayant trois années de données, ce qui vous fournit un vecteur de dimension mille. Mais ce mille est en grande partie fictif car il repose sur la décision d’agréger les données de manière quotidienne. Si vous optiez pour une autre périodicité, vous obtiendriez une dimension différente. C’est le point que je voulais faire valoir, et c’est ce que le deep learning a vraiment bien compris : disposer d’alternatives qui vous empêchent d’être trompé par des choix arbitraires de représentation des données. Vous devez rester, en quelque sorte, agnostique quant à la représentation.
Question : En introduisant la prévision probabiliste, nous passons à une fonction de coût et à des contraintes de nature probabiliste. Quelle implication cela a-t-il sur le processus de recherche d’une solution ?
Eh bien, cela présente une contrainte fondamentale très basique. Si vous avez un solveur qui ne peut pas traiter de tels problèmes – et rappelez-vous que vous pouvez toujours revenir d’un problème stochastique à un problème déterministe en moyennant simplement vos résultats sur un très grand nombre d’échantillons – alors vous êtes en difficulté en termes de coûts de calcul. Cela signifie que vous devrez dépenser environ 10 000 fois plus de puissance de traitement pour obtenir une solution satisfaisante comparativement à une solution alternative. L’implication est qu’il faut vraiment s’assurer que vos outils d’optimisation mathématique, l’infrastructure dont vous disposez, soient nativement capables de traiter des problèmes stochastiques. C’est exactement ce que vous obtenez avec la differentiable programming, pas autant avec la recherche locale, bien que l’on puisse améliorer ou réviser la recherche locale pour qu’elle fonctionne plus harmonieusement dans ce genre de situations.
Fondamentalement, lorsque vous optez pour une prévision probabiliste, cela ne remet pas uniquement en question votre manière de concevoir l’avenir ; cela remet également en cause en profondeur le type d’outils et d’instrumentation avec lesquels vous devez travailler pour exploiter ces prévisions. C’est exactement le genre d’outils que Lokad développe depuis la dernière décennie. La raison en est que nous devons disposer d’outils capables de bien fonctionner avec le type de problèmes stochastiques qui surgissent invariablement dans la supply chain, car pratiquement tous les problèmes dans les supply chains comportent un ingrédient d’incertitude, et traitent donc, dans une certaine mesure, d’un problème stochastique.
Excellent. Ainsi, le prochain cours aura lieu le même jour de la semaine, un mercredi. Il y aura quelques vacances entre-temps. Le prochain cours sera le 22 septembre, et j’espère vous y voir tous. Cette fois, nous aborderons le machine learning pour supply chain. À bientôt.
Références
- L’avenir de la recherche opérationnelle appartient au passé, Russell L. Ackoff, février 1979
- LocalSolver 1.x : un solveur de recherche locale en boîte noire pour la programmation 0-1, Thierry Benoist, Bertrand Estellon, Frédéric Gardi, Romain Megel, Karim Nouioua, septembre 2011
- La différentiation automatique dans le machine learning : une revue, Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind, dernière révision en février 2018


