Previsione dei lead time - Lezione 5.3

00:00 Introduzione
02:55 Il caso dei lead time
09:25 Lead time reali (1/3)
12:13 Lead time reali (2/3)
13:44 Lead time reali (3/3)
16:12 La storia finora
19:31 ETA: 1 ora da adesso
22:16 CPRS (riepilogo) (1/2)
23:44 CPRS (riepilogo) (2/2)
24:52 Validazione incrociata (1/2)
27:00 Validazione incrociata (2/2)
27:40 Smussamento dei lead time (1/2)
31:29 Smussamento dei lead time (2/2)
40:51 Composizione del lead time (1/2)
44:19 Composizione del lead time (2/2)
47:52 Lead time quasi-stagionale
54:45 Modello log-logistico per il lead time (1/4)
57:03 Modello log-logistico per il lead time (2/4)
01:00:08 Modello log-logistico per il lead time (3/4)
01:03:22 Modello log-logistico per il lead time (4/4)
01:05:12 Modello incompleto per il lead time (1/4)
01:08:04 Modello incompleto per il lead time (2/4)
01:09:30 Modello incompleto per il lead time (3/4)
01:11:38 Modello incompleto per il lead time (4/4)
01:14:33 Domanda nel lead time (1/3)
01:17:35 Domanda nel lead time (2/3)
01:24:49 Domanda nel lead time (3/3)
01:28:27 Modularità delle tecniche predittive
01:31:22 Conclusione
01:32:52 Lezione successiva e domande dal pubblico

Descrizione

Lead times sono una componente fondamentale della maggior parte delle situazioni di supply chain. I lead time possono e devono essere previsti proprio come la domanda. I modelli di previsione probabilistica dedicati ai lead time possono essere utilizzati. Viene presentata una serie di tecniche per elaborare previsioni probabilistiche dei lead time a fini di supply chain. La composizione di queste previsioni, per il lead time e per la domanda, è un pilastro della modellazione predittiva nella supply chain.

Trascrizione completa

Benvenuti in questa serie di lezioni di supply chain. Sono Joannes Vermorel e oggi presenterò “Previsione dei lead time”. I lead time, e più in generale tutti i ritardi applicabili, sono un aspetto fondamentale della supply chain quando si cerca di bilanciare offerta e domanda. Bisogna considerare i ritardi coinvolti. Ad esempio, consideriamo la domanda per un giocattolo. Una corretta anticipazione del picco stagionale della domanda prima di Natale non ha importanza se le merci vengono ricevute a gennaio. I lead time determinano i dettagli della pianificazione tanto quanto la domanda.

I lead time variano; variano molto. Questo è un dato di fatto, e tra un attimo presenterò alcune evidenze. Tuttavia, a prima vista, questa affermazione risulta sconcertante. Non è chiaro perché il lead time debba variare così tanto in primo luogo. Abbiamo processi produttivi che possono operare con tolleranze inferiori a un micrometro. Inoltre, come parte del processo produttivo, possiamo controllare un effetto, ad esempio l’applicazione di una fonte luminosa, fino a un microsecondo. Se possiamo controllare la trasformazione della materia con una precisione del micrometro e del microsecondo, con sufficiente dedizione, dovremmo essere in grado di controllare il flusso della domanda con un grado di precisione comparabile. O forse no.

Questo modo di pensare potrebbe spiegare perché i lead time sembrano essere così sottovalutati nella letteratura sulla supply chain. I libri sulla supply chain e, di conseguenza, il supply chain software riconoscono a malapena l’esistenza dei lead time, limitandosi a introdurli come parametro di ingresso per il loro modello di inventario. Per questa lezione, ci saranno tre obiettivi:

Vogliamo comprendere l’importanza e la natura dei lead time. Vogliamo capire come i lead time possano essere previsti, con un particolare interesse per i modelli probabilistici che ci permettono di abbracciare l’incertezza. Vogliamo combinare le previsioni dei lead time con quelle della domanda in modi che risultino utili per la supply chain.

Secondo la letteratura mainstream della supply chain, i lead time valgono a malapena poche note a piè di pagina. Questa affermazione potrebbe sembrare un’esagerazione stravagante, ma temo che non lo sia. Secondo Google Scholar, un motore di ricerca specializzato nella letteratura scientifica, la query “demand forecasting” per l’anno 2021 restituisce 10.500 articoli. Un’ispezione superficiale dei risultati indica che, in effetti, la stragrande maggioranza di tali voci discute la previsione della domanda in ogni tipo di situazione e mercato. La stessa query, sempre per l’anno 2021, su Google Scholar per “lead time forecasting” restituisce 71 risultati. I risultati per la query sulla previsione dei lead time sono così limitati che bastano pochi minuti per esaminare l’intero volume di ricerche di un anno.

Risulta che ci siano solo circa una dozzina di voci che discutono realmente la previsione dei lead time. Infatti, la maggior parte dei risultati si trova in espressioni come “long lead time forecast” o “short lead time forecast”, che in realtà si riferiscono alla previsione della domanda, e non a quella del lead time. È possibile ripetere questo esercizio con “demand prediction” e “lead time prediction” e altre espressioni simili in altri anni. Lascio questo esercizio al pubblico.

Pertanto, come stima approssimativa, abbiamo circa mille volte più articoli sulla previsione della domanda rispetto a quelli sulla previsione del lead time. I libri sulla supply chain e il supply chain software seguono la medesima tendenza, relegando il lead time a cittadino di seconda classe e a una questione tecnica di poco conto. Tuttavia, il personale della supply chain presentato in questa serie di lezioni racconta una storia diversa. Questi personaggi possono rappresentare aziende fittizie, ma riflettono archetipi della supply chain. Ci raccontano il tipo di situazione che dovrebbe essere considerata tipica. Vediamo cosa ci dicono in merito ai lead time.

Paris è un marchio di moda fittizio che gestisce la propria rete di vendita al dettaglio. Paris effettua ordini a fornitori esteri, con lead time lunghi e talvolta superiori a sei mesi. Questi lead time sono conosciuti in modo imperfetto eppure la nuova collezione deve arrivare in negozio al momento giusto, così come definito dall’operazione di marketing associata alla nuova collezione. I lead time dei fornitori richiedono un’adeguata anticipazione; in altre parole, necessitano di una previsione.

Amsterdam è un’azienda FMCG fittizia specializzata nella produzione di formaggi, creme e burro. Il processo di stagionatura del formaggio è noto e controllato, ma varia, con deviazioni di alcuni giorni. Tuttavia, pochi giorni corrispondono proprio alla durata delle promozioni intense innescate dalle retail chains che risultano essere il canale di vendita principale di Amsterdam. Questi lead time di produzione richiedono una previsione.

Miami è un MRO aviation fittizio. MRO sta per maintenance, repair, and overhaul. Ogni aeromobile necessita di migliaia di pezzi ogni anno per poter continuare a volare. Anche un singolo pezzo mancante può far rimanere a terra l’aereo. La durata della riparazione per un pezzo riparabile, noto anche come TAT (turnaround time), definisce quando il pezzo rotabile torna operativo. Tuttavia, il TAT varia da giorni a mesi, a seconda dell’entità delle riparazioni, che non sono note al momento della rimozione del pezzo dall’aeromobile. Questi TAT richiedono una previsione.

San Jose è un’azienda e-commerce fittizia che distribuisce una varietà di articoli per la casa e accessori. Come parte del suo servizio, San Jose fornisce un impegno per una data di consegna per ogni transazione. Tuttavia, la consegna stessa dipende da società terze che sono tutt’altro che perfettamente affidabili. Pertanto, San Jose necessita di una stima informata sulla data di consegna che può essere promessa per ogni transazione. Questa stima informata equivale implicitamente a una previsione del lead time.

Infine, Stuttgart è un’azienda fittizia dell’automotive aftermarket. Gestisce filiali che offrono riparazioni auto. Il prezzo d’acquisto più basso per i pezzi di ricambio può essere ottenuto dai grossisti che offrono lead time lunghi e piuttosto irregolari. Esistono fornitori più affidabili, seppur più costosi e più vicini. Scegliere il fornitore giusto per ogni pezzo richiede un’adeguata analisi comparativa dei relativi lead time associati ai vari fornitori.

Come possiamo vedere, ogni singolo operatore della supply chain presentato finora richiede l’anticipazione di almeno un lead time, e spesso di diversi. Sebbene si possa sostenere che prevedere la domanda richieda più attenzione e impegno rispetto alla previsione dei lead time, in definitiva, entrambi sono necessari in quasi tutte le situazioni della supply chain.

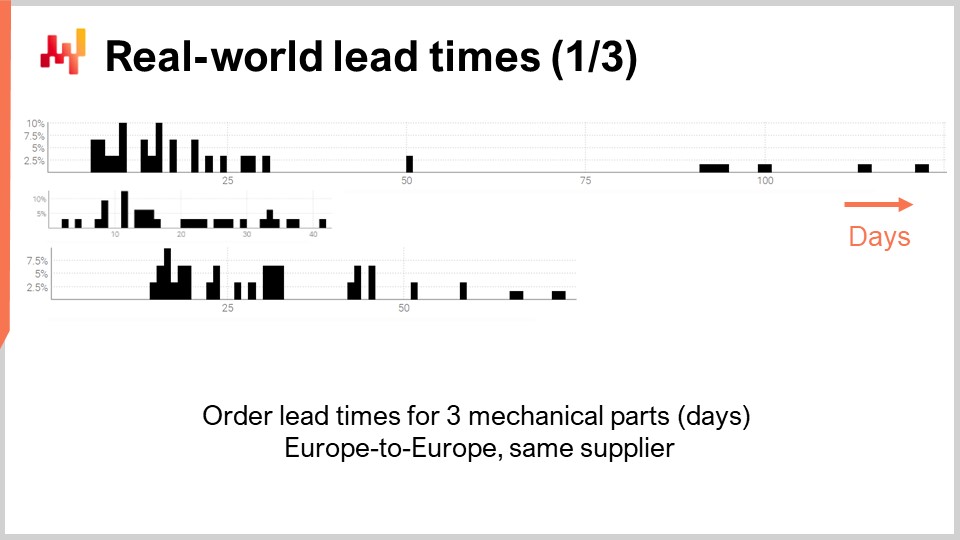
Esaminiamo alcuni lead time reali. Sullo schermo compaiono tre istogrammi che sono stati tracciati compilando i lead time osservati associati a tre componenti meccanici. Questi componenti sono ordinati dallo stesso fornitore situato in Europa occidentale. Gli ordini provengono da un’azienda anch’essa situata in Europa occidentale. L’asse x indica la durata dei lead time osservati espressa in giorni, mentre l’asse y indica il numero di osservazioni espresso in percentuale. Nei seguenti istogrammi, saranno adottate le stesse convenzioni, con l’asse x associato a durate espresse in giorni e l’asse y che riflette la frequenza. Da queste tre distribuzioni, possiamo già trarre alcune osservazioni.

In primo luogo, i dati sono scarsi. Abbiamo solo qualche dozzina di punti dati, e queste osservazioni sono state raccolte nel corso di diversi anni. Questa situazione è tipica; se l’azienda effettua ordini solo una volta al mese, ci vuole quasi un decennio per raccogliere oltre 100 osservazioni sui lead time. Pertanto, qualunque operazione statistica intraprendiamo, essa dovrebbe essere orientata verso numeri piccoli piuttosto che grandi. Infatti, avremo raramente il lusso di lavorare con grandi quantità di dati.

In secondo luogo, i lead time sono irregolari. Abbiamo osservazioni che spaziano da pochi giorni a un trimestre. Pur essendo sempre possibile calcolare un lead time medio, fare affidamento su un valore medio per uno qualsiasi di tali componenti sarebbe poco saggio. È inoltre chiaro che nessuna di queste distribuzioni è minimamente normale.

In terzo luogo, abbiamo tre parti che sono in qualche modo comparabili per dimensioni e prezzo, eppure i lead time variano notevolmente. Sebbene possa essere allettante raggruppare queste osservazioni per rendere i dati meno scarsi, è ovviamente poco saggio farlo, poiché verrebbero mescolate distribuzioni altamente dissimili. Queste distribuzioni non hanno la stessa media, mediana, né lo stesso valore minimo o massimo.

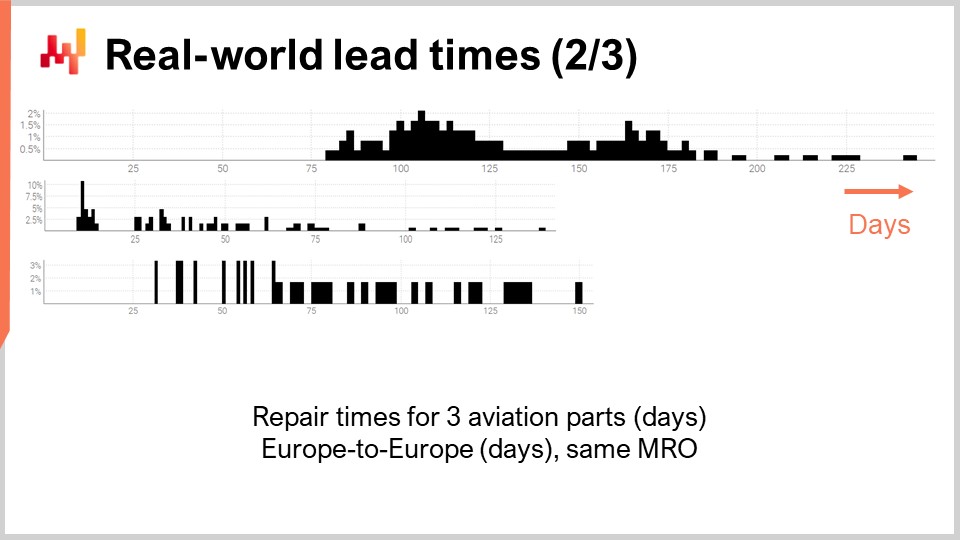
Esaminiamo un secondo gruppo di lead time. Queste durate riflettono il tempo necessario per riparare tre distinti componenti aeronautici. La prima distribuzione sembra presentare due modalità oltre a una coda. Quando una distribuzione presenta due modalità, solitamente questo suggerisce l’esistenza di una variabile nascosta che spiega tali modalità. Ad esempio, potrebbero esserci due tipi distinti di operazioni di riparazione, ciascuno associato a un proprio lead time. La seconda distribuzione sembra presentare una modalità oltre a una coda. Questa modalità corrisponde a una durata relativamente breve, circa due settimane. Potrebbe riflettere un processo in cui il componente viene ispezionato prima, e talvolta il componente viene ritenuto utilizzabile senza ulteriori interventi, garantendo così un lead time molto più breve. La terza distribuzione appare completamente dispersa, senza una modalità o coda evidente. Potrebbero esserci diversi processi di riparazione in gioco che vengono raggruppati insieme. La scarsità dei dati, con solo tre dozzine di osservazioni, rende difficile dire di più. Rivedremo questa terza distribuzione più avanti in questa lezione.

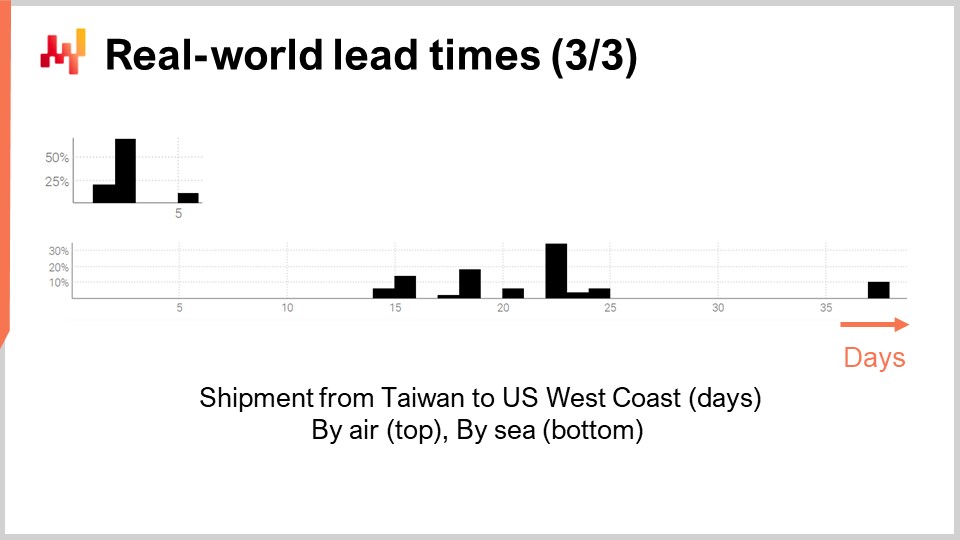
Infine, esaminiamo due lead time che riflettono i ritardi di spedizione da Taiwan alla costa occidentale degli Stati Uniti, sia via aereo che via nave. Non sorprende che gli aerei cargo siano più veloci delle navi cargo. La seconda distribuzione sembra suggerire che a volte una spedizione via mare possa perdere la nave originaria e essere poi caricata sulla nave successiva, raddoppiando quasi il ritardo. Lo stesso fenomeno potrebbe verificarsi anche con la spedizione aerea, anche se i dati sono così limitati da renderlo solo una congettura. Va notato che avere accesso a sole un paio di osservazioni non è inusuale per quanto riguarda i lead time. Queste situazioni sono frequenti. È importante tenere presente che in questa lezione cerchiamo strumenti che ci permettano di lavorare con i dati relativi ai lead time a nostra disposizione, anche se si tratta di poche osservazioni, e non con i dati sui lead time che vorremmo avere, come migliaia di osservazioni. Le brevi interruzioni in entrambe le distribuzioni suggeriscono inoltre la presenza di un andamento ciclico settimanale, anche se l’attuale visualizzazione con istogrammi non è adeguata per convalidare questa ipotesi.

Da questa breve panoramica dei lead time reali, possiamo già comprendere alcuni dei fenomeni sottostanti in gioco. Infatti, i lead time sono altamente strutturati; i ritardi non si verificano senza una causa, e tali cause possono essere identificate, scomposte e quantificate. Tuttavia, i dettagli della scomposizione del lead time non sono frequentemente registrati nei sistemi IT, almeno non ancora. Anche quando è disponibile una scomposizione dettagliata del lead time osservato, come può avvenire in alcune industrie, come quella aeronautica, ciò non implica che i lead time possano essere anticipati perfettamente. I sotto-segmenti o le fasi all’interno del lead time probabilmente mostrano una loro incertezza irreducibile.

Questa serie di lezioni di supply chain presenta le mie opinioni e intuizioni sia sullo studio che sulla pratica della supply chain. Cerco di mantenere queste lezioni in una certa indipendenza, ma hanno più senso se guardate in sequenza. Il resto di questa lezione dipende da elementi che sono stati precedentemente introdotti in questa serie, anche se tra poco fornirò un ripasso.

Il primo capitolo è una introduzione generale al campo e allo studio di supply chain. Chiarisce la prospettiva che caratterizza questa serie di lezioni. Come avrete già intuito, questa prospettiva si discosta sostanzialmente da quella che sarebbe considerata la visione mainstream su supply chain.

Il secondo capitolo introduce una serie di metodologie. Infatti, supply chain supera le metodologie naive. Le supply chain sono costituite da persone che hanno propri interessi; non esiste una parte neutrale in supply chain. Questo capitolo affronta tali complicazioni, incluso il mio conflitto di interesse in quanto CEO di Lokad, un’azienda di software aziendale specializzata in supply chain optimization.

Il terzo capitolo esamina una serie di supply chain “personas.” Queste personas sono aziende fittizie che abbiamo brevemente esaminato oggi, e sono intese a rappresentare archetipi di situazioni di supply chain. Lo scopo di queste personas è concentrarsi esclusivamente sui problemi, posticipando la presentazione delle soluzioni.

Il quarto capitolo rivede le scienze ausiliarie di supply chain. Queste scienze non riguardano supply chain in sé, ma dovrebbero essere considerate essenziali per una pratica moderna di supply chain. Questo capitolo include una progressione attraverso i livelli di astrazione, partendo dall’hardware informatico fino alle questioni legate alla cybersecurity.

Il quinto e presente capitolo è dedicato al predictive modeling. Il predictive modeling è una prospettiva più generale rispetto alla previsione; non riguarda solo la previsione della domanda. Si tratta della progettazione di modelli che possono essere utilizzati per stimare e quantificare i futuri fattori della supply chain di interesse. Oggi, ci immergiamo nei lead time, ma più in generale in supply chain, qualsiasi cosa non sia conosciuta con un grado ragionevole di certezza merita una previsione.

Il sesto capitolo spiega come le decisioni ottimizzate possano essere calcolate sfruttando i modelli predittivi, e più specificamente i modelli probabilistici che sono stati introdotti nel quinto capitolo. Il settimo capitolo ritorna a una prospettiva ampiamente non tecnica per discutere l’effettiva esecuzione aziendale di un’iniziativa di quantitative supply chain.

Oggi, ci concentriamo sui lead time. Abbiamo appena visto perché i lead time sono importanti, e abbiamo appena esaminato una breve serie di lead time reali. Pertanto, procederemo con elementi di modellizzazione dei lead time. Poiché adotterò una prospettiva probabilistica, reintrodurrò brevemente il Continuous Rank Probability Score (CRPS), una metrica per valutare la bontà di una previsione probabilistica. Introducirò anche la cross-validation e una variante della cross-validation che sia adatta alla nostra prospettiva probabilistica. Con questi strumenti a disposizione, introdurremo e valuteremo il nostro primo modello probabilistico non naive per i lead time. I dati sui lead time sono scarsi, e il primo punto all’ordine del giorno è lisciare queste distribuzioni. I lead time possono essere scomposti in una serie di fasi intermedie. Pertanto, assumendo che siano disponibili alcuni dati di lead time scomposti, abbiamo bisogno di uno strumento per ricomporre quei lead time mantenendo l’approccio probabilistico.

Successivamente, reintrodurremo la differentiable programming. La differentiable programming è già stata utilizzata in questa serie di lezioni per prevedere la domanda, ma può essere impiegata anche per prevedere i lead time. Lo faremo, a partire da un semplice esempio inteso a catturare l’impatto del Capodanno cinese sui lead time, un tipico schema osservato quando si importano merci dall’Asia.

Procederemo quindi con un modello probabilistico parametrico per i lead time, sfruttando la distribuzione log-logistica. Ancora una volta, la differentiable programming sarà fondamentale per apprendere i parametri del modello. Estenderemo poi questo modello considerando osservazioni incomplete dei lead time. Infatti, anche gli ordini d’acquisto non ancora completati ci forniscono alcune informazioni sul lead time.

Infine, combiniamo una previsione probabilistica dei lead time e una previsione probabilistica della domanda all’interno di una singola situazione di replenishment dell’inventario. Questa sarà l’occasione per dimostrare perché la modularità rappresenta una preoccupazione essenziale nel predictive modeling, ancor più importante persino delle sottigliezze dei modelli stessi.

Nella Lezione 5.2 sulla previsione probabilistica, abbiamo già introdotto alcuni strumenti per valutare la qualità di una previsione probabilistica. Infatti, le solite metriche di accuratezza come l’errore quadratico medio o l’errore assoluto medio si applicano solo alle previsioni puntuali, non a quelle probabilistiche. Tuttavia, non è perché le nostre previsioni diventano probabilistiche che l’accuratezza nel senso generale diventa irrilevante. Ci basta uno strumento statistico che sia compatibile con la prospettiva probabilistica.

Tra questi strumenti, c’è il Continuous Rank Probability Score (CRPS). La formula è mostrata sullo schermo. Il CRPS è una generalizzazione della metrica L1, ossia l’errore assoluto, ma applicata alle distribuzioni di probabilità. La versione abituale del CRPS confronta una distribuzione, chiamata F qui, con un’osservazione, chiamata X qui. Il valore ottenuto dalla funzione CRPS è omogeneo con l’osservazione. Per esempio, se X è un lead time espresso in giorni, allora il valore del CRPS è anch’esso espresso in giorni.

Il CRPS può essere generalizzato per il confronto di due distribuzioni. Questo è ciò che viene mostrato sullo schermo. È solo una lieve variazione della formula precedente. L’essenza di questa metrica rimane invariata. Se F è la vera distribuzione dei lead time e F_hat è una stima della distribuzione dei lead time, allora il CRPS è espresso in giorni. Il CRPS riflette la quantità di differenza tra le due distribuzioni. Il CRPS può anche essere interpretato come la minima quantità di energia necessaria per trasportare tutta la massa dalla prima distribuzione in modo che essa assuma l’esatta forma della seconda distribuzione.

Ora abbiamo uno strumento per confrontare due distribuzioni di probabilità unidimensionali. Questo diventerà interessante a breve quando introdurremo il nostro primo modello probabilistico per i lead time.

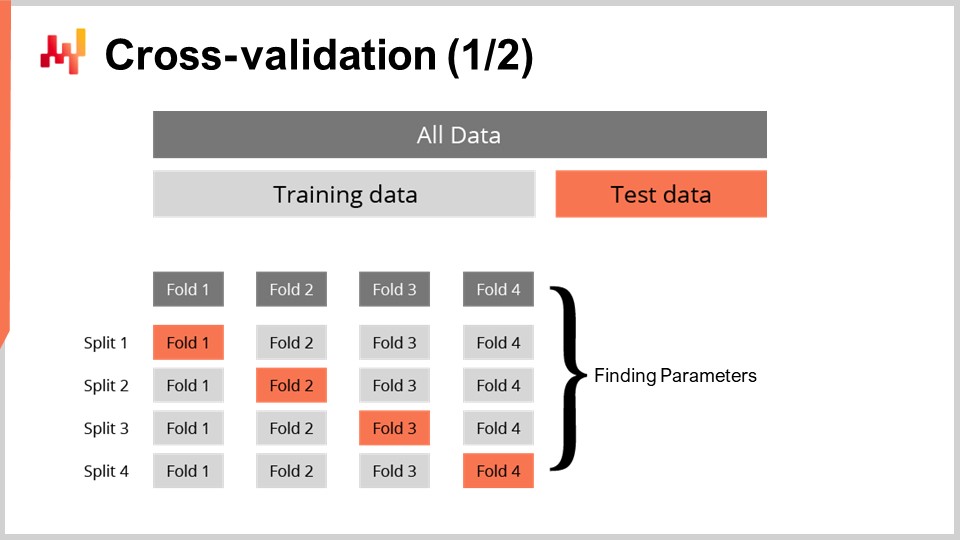
Avere una metrica per misurare la bontà di una previsione probabilistica non è del tutto sufficiente. La metrica misura la bontà sui dati a nostra disposizione; tuttavia, ciò che desideriamo veramente è essere in grado di valutare la bontà della nostra previsione su dati che non abbiamo. Infatti, sono i lead time futuri a interessarci, non quelli già osservati in passato. La nostra capacità di fare in modo che un modello funzioni bene sui dati che non possediamo si definisce generalizzazione. La cross-validation è una tecnica generale di validazione del modello esattamente finalizzata a valutare la capacità di un modello di generalizzare bene.

Nella sua forma più semplice, la cross-validation consiste nel suddividere le osservazioni in un piccolo numero di sottoinsiemi. Per ogni iterazione, un sottoinsieme viene messo da parte e definito come il sottoinsieme di test. Il modello viene quindi generato o addestrato basandosi sugli altri sottoinsiemi di dati, definiti come i sottoinsiemi di training. Dopo l’addestramento, il modello viene validato sul sottoinsieme di test. Questo processo viene ripetuto un certo numero di volte, e la bontà media ottenuta in tutte le iterazioni rappresenta il risultato finale della cross-validation.

La cross-validation è raramente usata nel contesto della previsione di time series a causa della dipendenza temporale tra le osservazioni. Infatti, la cross-validation, come appena presentata, presume che le osservazioni siano indipendenti. Quando sono coinvolte serie temporali, viene usato invece il backtesting. Il backtesting può essere visto come una forma di cross-validation che tiene conto della dipendenza temporale.

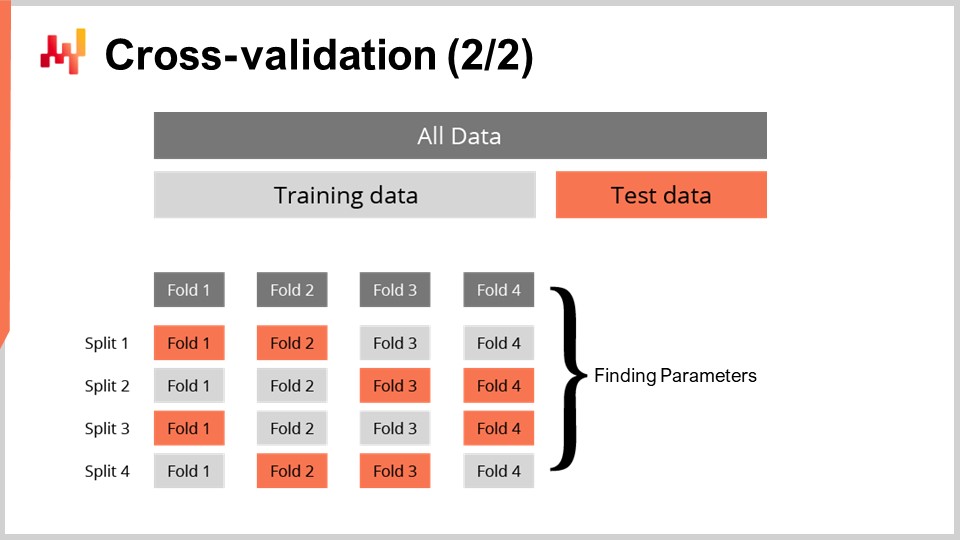
La tecnica della cross-validation presenta numerose varianti che riflettono una vasta gamma di possibili angolazioni da considerare. Non esamineremo queste varianti ai fini di questa lezione. Utilizzerò una variante specifica in cui, ad ogni divisione, il sottoinsieme di training e quello di test hanno all’incirca la stessa dimensione. Questa variante è stata introdotta per affrontare la validazione di un modello probabilistico, come vedremo tra un attimo con del codice.

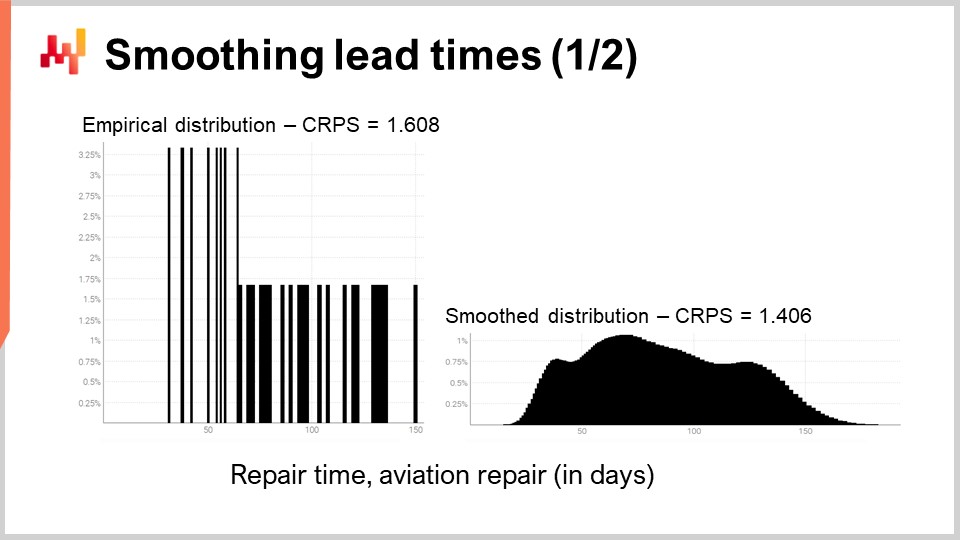
Rivisitiamo uno dei lead time reali che abbiamo visto precedentemente sullo schermo. A sinistra, l’istogramma è associato alla terza distribuzione dei tempi di riparazione in ambito aviazione. Si tratta delle stesse osservazioni viste in precedenza, e l’istogramma è stato semplicemente esteso verticalmente. In questo modo, i due istogrammi a sinistra e a destra condividono la stessa scala. Per l’istogramma a sinistra, abbiamo circa 30 osservazioni. Non è molto, ma è già più di quanto otterremo frequentemente.

L’istogramma a sinistra è definito come una distribuzione empirica. È letteralmente l’istogramma grezzo ottenuto dalle osservazioni. L’istogramma ha un contenitore per ogni durata espressa in un numero intero di giorni. Per ogni contenitore, contiamo il numero di lead time osservati. A causa della scarsità dei dati, la distribuzione empirica assomiglia a un codice a barre.

C’è un problema qui. Se abbiamo due lead time osservati esattamente a 50 giorni, ha senso affermare che la probabilità di osservare 49 giorni o 51 giorni sia esattamente zero? Non lo è. Chiaramente, esiste uno spettro di durate; semplicemente non abbiamo abbastanza dati per osservare la vera distribuzione sottostante, che molto probabilmente è molto più liscia di questa distribuzione simile a un codice a barre.

Pertanto, quando si tratta di lisciare questa distribuzione, esiste un numero indefinito di modi per eseguire questa operazione di smoothing. Alcuni metodi di smoothing potrebbero sembrare validi ma non sono statisticamente solidi. Come buon punto di partenza, vorremmo assicurarci che un modello liscio sia più accurato rispetto a quello empirico. Si scopre che abbiamo già introdotto due strumenti, il CRPS e la cross-validation, che ce lo permettono.

Tra un attimo, i risultati sono visibili. L’errore CRPS associato alla distribuzione a barcode è di 1,6 giorni, mentre l’errore CRPS associato alla distribuzione liscia è di 1,4 giorni. Queste due cifre sono state ottenute tramite cross-validation. L’errore inferiore indica che, in termini di CRPS, la distribuzione a destra è la più accurata delle due. La differenza di 0,2 tra 1,4 e 1,6 non è molta; tuttavia, la proprietà fondamentale qui è che abbiamo una distribuzione liscia che non lascia in modo erratico alcune durate intermedie con probabilità zero. Ciò è ragionevole, poiché la nostra comprensione delle riparazioni ci dice che quelle durate probabilmente si verificherebbero se le riparazioni fossero ripetute. Il CRPS non riflette l’effettiva portata del miglioramento ottenuto lisciando la distribuzione. Tuttavia, almeno, la riduzione del CRPS conferma che questa trasformazione è ragionevole dal punto di vista statistico.

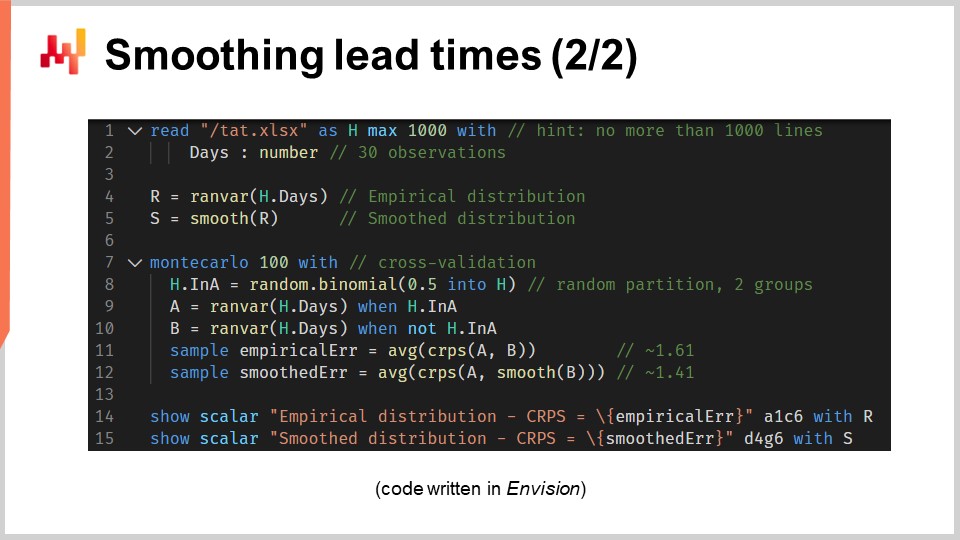
Diamo ora un’occhiata al codice sorgente che ha prodotto quei due modelli e ha mostrato quei due istogrammi. In totale, questo è realizzato in 12 righe di codice, escludendo le righe vuote. Come al solito in questa serie di lezioni, il codice è scritto in Envision, il linguaggio di programmazione specifico di dominio di Lokad dedicato all’ottimizzazione predittiva delle supply chain. Tuttavia, non c’è alcuna magia; questa logica avrebbe potuto essere scritta in Python. Ma per il tipo di problemi che stiamo considerando in questa lezione, Envision è più conciso e più autonomo.

Rivediamo quelle 12 righe di codice. Alle righe 1 e 2, stiamo leggendo un spreadsheet Excel che contiene una singola colonna di dati. Lo spreadsheet contiene 30 osservazioni. Questi dati sono raccolti all’interno di una tabella chiamata “H” che ha una singola colonna denominata “days.” Alla riga 4, stiamo costruendo una distribuzione empirica. La variabile “R” ha il tipo di dato “ranvar,” e a destra dell’assegnazione, la funzione “ranvar” è un aggregatore che prende le osservazioni in input e restituisce l’istogramma rappresentato con un tipo di dato “ranvar.” Di conseguenza, il tipo di dato “ranvar” è dedicato alle distribuzioni intere unidimensionali. Abbiamo introdotto il tipo di dato “ranvar” in una lezione precedente di questo capitolo. Questo tipo di dato garantisce un utilizzo costante di memoria e un tempo di calcolo costante per ogni operazione. Lo svantaggio del “ranvar” come tipo di dato è che è coinvolta una compressione lossy, sebbene la perdita di dati causata dalla compressione sia stata progettata per essere irrilevante per scopi di supply chain.

Alla riga 5, stiamo lisciando la distribuzione con la funzione integrata chiamata “smooth.” Sotto il cofano, questa funzione sostituisce la distribuzione originale con una miscela di distribuzioni di Poisson. Ogni contenitore dell’istogramma viene trasformato in una distribuzione di Poisson con una media pari alla posizione intera del contenitore, e infine la miscela assegna a ciascuna distribuzione di Poisson un peso proporzionale al peso del contenitore stesso. Un altro modo per comprendere cosa faccia la funzione “smooth” è considerare che equivale a sostituire ogni singola osservazione con una distribuzione di Poisson la cui media è pari all’osservazione stessa. Tutte queste distribuzioni di Poisson, una per ogni osservazione, vengono poi mescolate. Mescolare significa fare la media dei valori dei rispettivi contenitori dell’istogramma. Le variabili “ranvar” “R” e “S” non verranno utilizzate nuovamente prima delle righe 14 e 15, dove verranno visualizzate.

Alla riga 7, iniziamo un blocco Monte Carlo. Questo blocco è una sorta di ciclo e verrà eseguito 100 volte, come specificato dai 100 valori che appaiono subito dopo la parola chiave Monte Carlo. Il blocco Monte Carlo è inteso a raccogliere osservazioni indipendenti generate secondo un processo che comporta un grado di casualità. Ti starai chiedendo perché esista un costrutto Monte Carlo specifico in Envision invece di un semplice ciclo, come avviene di solito nei linguaggi di programmazione tradizionali. Si scopre che avere un costrutto dedicato offre benefici sostanziali. In primo luogo, garantisce che le iterazioni siano veramente indipendenti, fino ai semi utilizzati per derivare la pseudocasualità. In secondo luogo, offre un obiettivo esplicito per la distribuzione automatizzata del carico di lavoro su più core della CPU o addirittura su più macchine.

Alla riga 8, creiamo un vettore casuale di valori Booleani all’interno della tabella “H.” Con questa riga, stiamo creando valori casuali indipendenti, chiamati deviate (vero o falso), per ogni riga della tabella “H.” Come di consueto con Envision, i cicli sono astratti tramite la programmazione con array. Con questi valori Booleani, stiamo suddividendo la tabella “H” in due gruppi. Questa suddivisione casuale è utilizzata per il processo di validazione incrociata.

Alle righe 9 e 10, stiamo creando due “ranvars” chiamati “A” e “B”, rispettivamente. Stiamo utilizzando nuovamente l’aggregatore “ranvar”, ma questa volta applichiamo un filtro con la parola chiave “when” subito dopo la chiamata all’aggregatore. “A” viene generato utilizzando solo le righe in cui il valore in “a” è vero; per “B”, il contrario. “B” viene generato utilizzando solo le righe in cui il valore in “a” è falso.

Alle righe 11 e 12, raccogliamo le figure di interesse dal blocco Monte Carlo. In Envision, la parola chiave “sample” può essere posizionata solo all’interno di un blocco Monte Carlo. Viene usata per raccogliere le osservazioni che vengono effettuate iterando più volte attraverso il processo Monte Carlo. Alla riga 11, stiamo calcolando l’errore medio, espresso in termini CRPS, tra due distribuzioni empiriche: un sottocampione dell’insieme originale dei tempi di consegna. La parola chiave “sample” specifica i valori raccolti durante le iterazioni Monte Carlo. L’aggregatore “AVG”, che sta per “average” sul lato destro dell’assegnazione, viene utilizzato per produrre una singola stima al termine del blocco.

Alla riga 12, facciamo qualcosa di quasi identico a quanto avvenuto alla riga 11. Questa volta, tuttavia, applichiamo la funzione “smooth” al “ranvar” “B.” Vogliamo valutare quanto la variante smooth sia vicina alla distribuzione empirica naif. Si scopre che è più vicina, almeno in termini CRPS, rispetto alle sue controparti empiriche originali.

Alle righe 14 e 15, mettiamo in mostra gli istogrammi e i valori CRPS. Queste righe generano le figure che abbiamo visto nella diapositiva precedente. Questo script ci fornisce il riferimento per la qualità della distribuzione empirica del nostro modello. In effetti, mentre questo modello, quello “barcode”, è discutibilmente naif, rimane comunque un modello, e probabilistico a questo proposito. Così, questo script ci offre anche un modello migliore, almeno nel senso del CRPS, attraverso una variante smooth della distribuzione empirica originale.

In questo momento, a seconda della tua familiarità con i linguaggi di programmazione, potrebbe sembrare molto da assimilare. Tuttavia, vorrei sottolineare quanto sia semplice produrre una distribuzione di probabilità ragionevole, anche quando non abbiamo più di poche osservazioni. Sebbene abbiamo 12 righe di codice, solo le righe 4 e 5 rappresentano la vera parte di modellazione dell’esercizio. Se fossimo interessati solo alla variante smooth, allora il “ranvar” “S” potrebbe essere scritto con una singola riga di codice. Quindi, si tratta letteralmente di una riga: prima, applicare un’aggregazione ranvar, e poi applicare un operatore smooth, ed è fatto. Il resto è solo strumentazione e visualizzazione. Con gli strumenti adeguati, la modellazione probabilistica, che si tratti di lead time o altro, può essere resa estremamente semplice. Non c’è matematica grandiosa coinvolta, né algoritmi complessi, né enormi componenti software. È semplice e notevolmente così.

Come si fa a far sì che una spedizione arrivi con sei mesi di ritardo? La risposta è ovvia: un giorno alla volta. Più seriamente, i tempi di consegna possono solitamente essere scomposti in una serie di ritardi. Ad esempio, il tempo di consegna di un fornitore può essere scomposto in un ritardo di attesa mentre l’ordine viene inserito in una coda arretrata, seguito da un ritardo di produzione mentre le merci vengono prodotte, e infine seguito da un ritardo di transito mentre le merci vengono spedite. Quindi, se i tempi di consegna possono essere scomposti, è interessante anche poterli ricomporre.

Se vivessimo in un mondo altamente deterministico in cui il futuro potesse essere previsto con precisione, allora ricomporre i tempi di consegna sarebbe semplicemente una questione di somme. Tornando all’esempio appena menzionato, comporre il tempo di consegna dell’ordine significherebbe sommare il ritardo in coda in giorni, il ritardo di produzione in giorni e il ritardo di transito in giorni. Eppure, non viviamo in un mondo in cui il futuro possa essere previsto con precisione. Le distribuzioni dei tempi di consegna nel mondo reale che abbiamo presentato all’inizio di questa lezione supportano questa affermazione. I tempi di consegna sono erratici e ci sono poche ragioni per credere che questo cambierà fondamentalmente nelle prossime decadi.

Pertanto, i tempi di consegna futuri dovrebbero essere affrontati come variabili casuali. Queste variabili casuali abbracciano e quantificano l’incertezza invece di ignorarla. Più specificamente, ciò significa che ogni componente del tempo di consegna dovrebbe essere modellato individualmente come una variabile casuale. Tornando al nostro esempio, il tempo di consegna dell’ordine è una variabile casuale ed è ottenuto come la somma di tre variabili casuali rispettivamente associate al ritardo in coda, al ritardo di produzione e al ritardo di transito.

La formula per la somma di due variabili casuali indipendenti, monodimensionali e a valori interi è presentata sullo schermo. Questa formula afferma semplicemente che se otteniamo una durata totale di Z giorni, e se abbiamo K giorni per la prima variabile casuale X, allora dobbiamo avere Z meno K giorni per la seconda variabile casuale Y. Questo tipo di somma è noto, in generale, in matematica come convoluzioni.

Sebbene sembri che vi sia un numero infinito di termini in questa convoluzione, in pratica ci interessano solo un numero finito di termini. In primo luogo, tutte le durate negative hanno probabilità zero; infatti, ritardi negativi significherebbero viaggiare indietro nel tempo. In secondo luogo, per ritardi lunghi, le probabilità diventano così basse che, per scopi pratici della supply chain, possono essere approssimate in modo affidabile a zero.

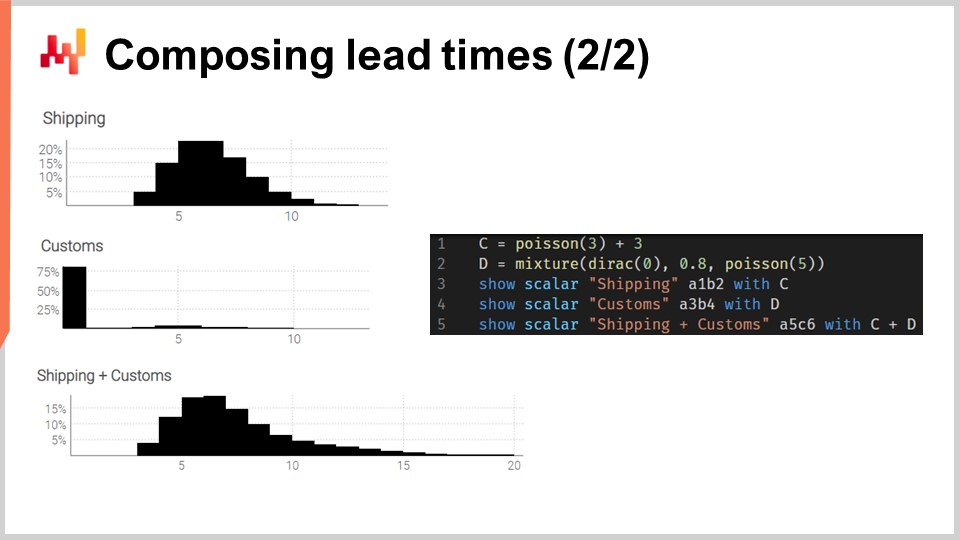
Mettiamo in pratica queste convoluzioni. Consideriamo un tempo di transito che può essere scomposto in due fasi: un ritardo di spedizione seguito da un ritardo per lo sdoganamento. Vogliamo modellare queste due fasi con due variabili casuali indipendenti e poi ricomporre il tempo di transito sommando queste due variabili casuali.

Sullo schermo, gli istogrammi a sinistra sono prodotti dallo script a destra. Alla riga 1, il ritardo di spedizione è modellato come una convoluzione di una distribuzione di Poisson più una costante. La funzione Poisson restituisce un tipo di dato “ranvar”; aggiungere tre ha l’effetto di spostare la distribuzione verso destra. Il “ranvar” risultante viene assegnato alla variabile “C”. Questo “ranvar” viene visualizzato alla riga 3. Si può vedere a sinistra come l’istogramma superiore. Riconosciamo la forma di una distribuzione di Poisson spostata verso destra di alcune unità, tre unità in questo caso. Alla riga due, lo sdoganamento è modellato come una miscela di un Dirac a zero e un Poisson a cinque. Il Dirac a zero si verifica nell’ottanta percento dei casi; è questo il significato della costante 0.8. Riflette situazioni in cui, nella maggior parte dei casi, le merci non sono nemmeno ispezionate dalla dogana e passano senza alcun ritardo notevole. In alternativa, nel venti percento dei casi, le merci vengono ispezionate dalla dogana e il ritardo è modellato come una distribuzione di Poisson con una media di cinque. Il ranvar risultante viene assegnato a una variabile chiamata D. Questo ranvar viene visualizzato alla riga quattro e può essere visto a sinistra come l’istogramma intermedio. Questo aspetto asimmetrico riflette che, nella maggior parte dei casi, la dogana non aggiunge alcun ritardo.

Infine, alla riga cinque, calcoliamo C più D. Questa somma è una convoluzione, poiché sia C che D sono ranvars, non numeri. Questa è la seconda convoluzione in questo script, poiché una convoluzione si è già verificata alla riga uno. Il ranvar risultante viene visualizzato ed è visibile a sinistra come il terzo e ultimo istogramma. Questo terzo istogramma è simile al primo, tranne per il fatto che la coda si estende molto più a destra. Ancora una volta, vediamo che con poche righe di codice possiamo affrontare effetti reali non banali, come i ritardi dello sdoganamento.

Tuttavia, si potrebbero fare due critiche a questo esempio. In primo luogo, non si specifica da dove provengano le costanti; in pratica, vogliamo apprendere queste costanti dai dati storici. In secondo luogo, mentre la distribuzione di Poisson ha il vantaggio della semplicità, potrebbe non essere una forma molto realistica per la modellazione dei tempi di consegna, soprattutto considerando situazioni con code lunghe. Pertanto, affronteremo questi due punti a seguire.

Per apprendere i parametri dai dati, rivedremo un paradigma di programmazione che abbiamo già introdotto in questa serie di lezioni, ovvero la differentiable programming. Se non hai visto le lezioni precedenti in questo capitolo, ti invito a guardarle al termine della lezione attuale. La differentiable programming è introdotta in modo più dettagliato in quelle lezioni.

La differentiable programming è una combinazione di due tecniche: la discesa del gradiente stocastica e l’autodifferenziazione. La discesa del gradiente stocastica è una tecnica di ottimizzazione che spinge i parametri, osservazione per osservazione, nella direzione opposta a quella dei gradienti. L’autodifferenziazione è una tecnica di compilazione, come nel compilatore di un linguaggio di programmazione; calcola i gradienti per tutti i parametri che compaiono all’interno di un programma generico.

Illustriamo la differentiable programming con un problema sui tempi di consegna. Questo servirà sia da ripasso che da introduzione, a seconda della tua familiarità con questo paradigma. Vogliamo modellare l’impatto del Capodanno Cinese sui tempi di consegna associati alle importazioni dalla Cina. Infatti, poiché le fabbriche chiudono per due o tre settimane durante il Capodanno Cinese, i tempi di consegna si allungano. Il Capodanno Cinese è ciclico; accade ogni anno. Tuttavia, non è strettamente stagionale, almeno non nel senso del calendario gregoriano.

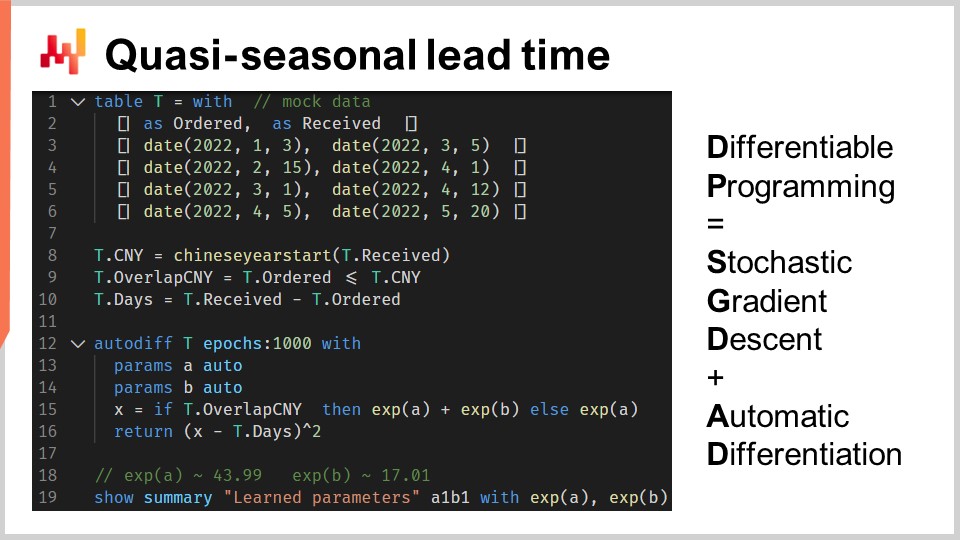
Alle righe da uno a sei, introduciamo alcuni ordini di acquisto fittizi con quattro osservazioni, con una data d’ordine e una data di ricezione. In pratica, questi dati non verrebbero inseriti manualmente, ma verrebbero caricati dai sistemi aziendali. Alle righe otto e nove, calcoliamo se il tempo di consegna si sovrappone al Capodanno Cinese. La variabile “T.overlap_CNY” è un vettore Booleano; indica se l’osservazione è influenzata o meno dal Capodanno Cinese.

Alla riga 12, introduciamo un blocco “autodiff”. La tabella T viene utilizzata come tabella delle osservazioni, e ci sono 1000 epoche. Ciò significa che ogni osservazione, cioè ogni riga della tabella T, verrà visitata mille volte. Un passo della discesa del gradiente stocastica corrisponde a un’esecuzione della logica all’interno del blocco “autodiff”.

Alle righe 13 e 14, vengono dichiarati due parametri scalari. Il blocco “autodiff” apprenderà questi parametri. Il parametro A riflette il tempo di consegna base senza l’effetto del Capodanno Cinese, e il parametro B riflette il ritardo extra associato al Capodanno Cinese. Alla riga 15, calcoliamo X, la previsione del tempo di consegna del nostro modello. Questo è un modello deterministico, non probabilistico; X è una previsione puntuale del tempo di consegna. Il lato destro dell’assegnazione è semplice: se l’osservazione si sovrappone al Capodanno Cinese, allora restituiamo il valore base più il componente del Nuovo Anno; altrimenti, restituiamo solo il valore base. Poiché il blocco “autodiff” prende in esame una singola osservazione alla volta, alla riga 15 la variabile T.overlap_CNY si riferisce a un valore scalare e non a un vettore. Questo valore corrisponde alla singola riga scelta come osservazione all’interno della tabella T.

I parametri A e B sono racchiusi nella funzione esponenziale “exp”, che è un piccolo trucco della differentiable programming. Infatti, l’algoritmo che guida la discesa del gradiente stocastica tende ad essere relativamente conservativo quando si tratta delle variazioni incrementali dei parametri. Quindi, se vogliamo apprendere un parametro positivo che può crescere oltre, diciamo, 10, racchiudere questo parametro in un processo esponenziale accelera la convergenza.

Alla riga 16, restituiamo un errore quadratico medio tra la nostra previsione X e la durata osservata, espressa in giorni (T.days). Anche all’interno di questo blocco “autodiff”, T.days è un valore scalare e non un vettore. Poiché la tabella T viene usata come tabella delle osservazioni, il valore restituito viene trattato come il loss che viene minimizzato tramite la discesa del gradiente stocastica. L’autodifferenziazione propaga i gradienti dal loss ai parametri A e B. Infine, alla riga 19, visualizziamo i due valori che abbiamo appreso, rispettivamente per A e B, che sono il tempo base e il componente del Nuovo Anno del nostro tempo di consegna.

Questo conclude la nostra reintroduzione della differentiable programming come strumento versatile per apprendere pattern statistici. Da qui in poi, rivedremo i blocchi “autodiff” in situazioni più elaborate. Tuttavia, sottolineiamo ancora una volta che, anche se può sembrare un po’ opprimente, non c’è nulla di veramente complicato in ciò che sta accadendo. Si potrebbe dire che il pezzo di codice più complicato in questo script sia l’implementazione sottostante della funzione “ChineseYearStart”, chiamata alla riga otto, che fa parte della libreria standard di Envision. In poche righe di codice, introduciamo un modello con due parametri e apprendiamo quei parametri. Ancora una volta, questa semplicità è notevole.

I tempi di consegna spesso presentano code pesanti; cioè, quando un tempo di consegna devia, devia di molto. Pertanto, per modellare il tempo di consegna, è interessante adottare distribuzioni che possano riprodurre questi comportamenti a coda pesante. La letteratura matematica propone un ampio elenco di tali distribuzioni, e parecune sarebbero adatte al nostro scopo. Tuttavia, limitarsi a esaminare il panorama matematico richiederebbe ore. Notate semplicemente che la distribuzione di Poisson non ha una coda pesante. Così, oggi, sceglierò la distribuzione log-logistica, che risulta essere una distribuzione a coda pesante. La giustificazione principale per questa scelta è che i team di Lokad stanno modellando i tempi di consegna con distribuzioni log-logistiche per diversi clienti. Funziona bene con un minimo di complicazioni. Tenete presente, però, che la distribuzione log-logistica non è affatto una soluzione miracolosa, e in numerose situazioni Lokad modella i tempi di consegna in maniera differente.

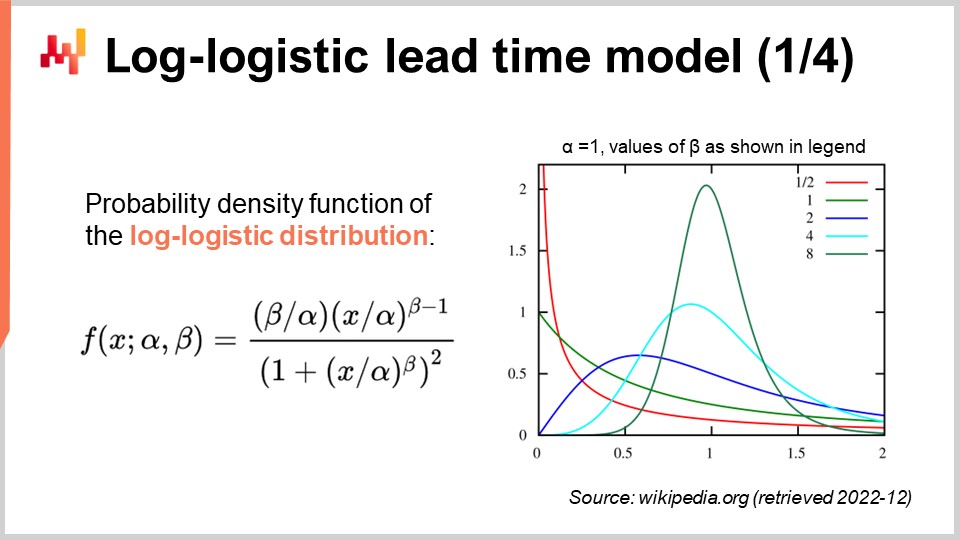
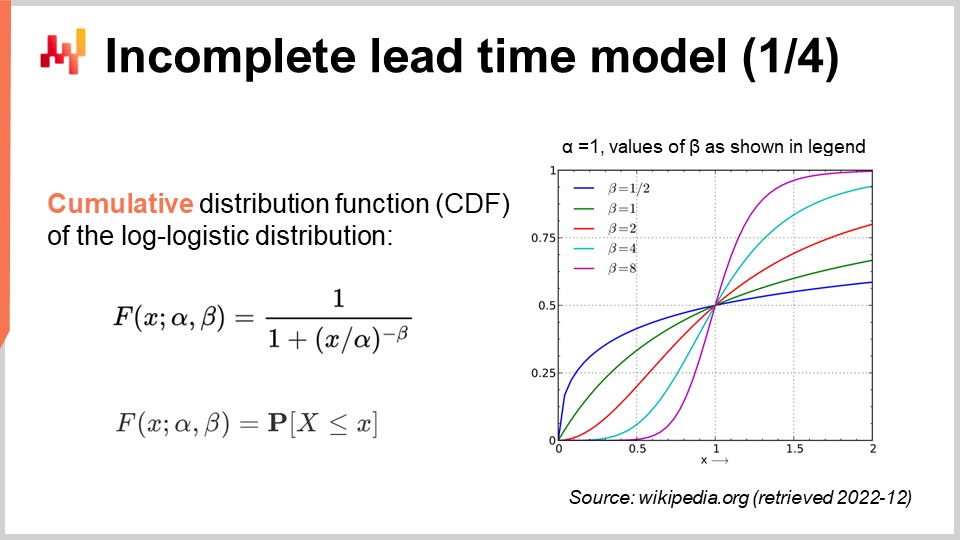
Sullo schermo, vediamo la funzione di densità di probabilità della distribuzione log-logistica. Si tratta di una distribuzione parametrica che dipende da due parametri, alpha e beta. Il parametro alpha corrisponde alla mediana della distribuzione, mentre il parametro beta ne governa la forma. A destra, è possibile ottenere una breve serie di forme variando i valori di beta. Sebbene questa formula della densità possa sembrare intimidatoria, si tratta letteralmente di materiale da libro di testo, proprio come la formula per calcolare il volume di una sfera. Potreste provare a decifrare e memorizzare questa formula, ma non è veramente necessario; basta sapere che esiste una formula analitica. Una volta che sapete che esiste, ritrovarla online richiede meno di un minuto.

Il nostro intento è sfruttare la distribuzione log-logistica per apprendere un modello probabilistico del tempo di consegna. Per fare ciò, minimizzeremo il log-likelihood. Infatti, nella lezione precedente di questo quinto capitolo, abbiamo visto che esistono diverse metriche adatte alla prospettiva probabilistica. Poco fa, abbiamo rivisitato il CRPS (Continuous Ranked Probability Score). Qui, invece, rivisitiamo il log-likelihood, che adotta una prospettiva bayesiana.

In sintesi, dati due parametri, la distribuzione log-logistica ci indica la probabilità di osservare ciascuna osservazione così come si presenta nel dataset empirico. Vogliamo apprendere i parametri che massimizzano questa probabilità. Il logaritmo, e quindi il log-likelihood anziché la semplice likelihood, viene introdotto per evitare underflow numerici. Gli underflow numerici si verificano quando elaboriamo numeri molto piccoli, vicini allo zero; tali numeri non si combinano bene con la rappresentazione in virgola mobile, comunemente presente nell’hardware informatico moderno.

Così, per calcolare il log-likelihood della distribuzione log-logistica, applichiamo il logaritmo alla sua funzione di densità di probabilità. L’espressione analitica è mostrata sullo schermo. Questa espressione può essere implementata, ed è esattamente ciò che viene fatto nelle tre righe di codice sottostanti.

Alla riga uno viene introdotta la funzione “L4”. L4 sta per “log-likelihood of log-logistic” – sì, sono tanti L e tanti logaritmi. Questa funzione prende tre argomenti: i due parametri alpha e beta, oltre all’osservazione x. Essa restituisce il logaritmo della likelihood. La funzione L4 è decorata con la parola chiave “autodiff”; tale parola chiave indica che la funzione è pensata per essere differenziata tramite differenziazione automatica. In altre parole, i gradienti possono fluire a ritroso dal valore restituito da questa funzione fino ai suoi argomenti, cioè i parametri alpha e beta. Tecnicamente, il gradiente fluisce anche attraverso l’osservazione x; tuttavia, poiché manterremo le osservazioni immutabili durante il processo di apprendimento, i gradienti non influenzeranno le osservazioni. Alla riga tre, otteniamo la trascrizione letterale della formula matematica appena sopra lo script.

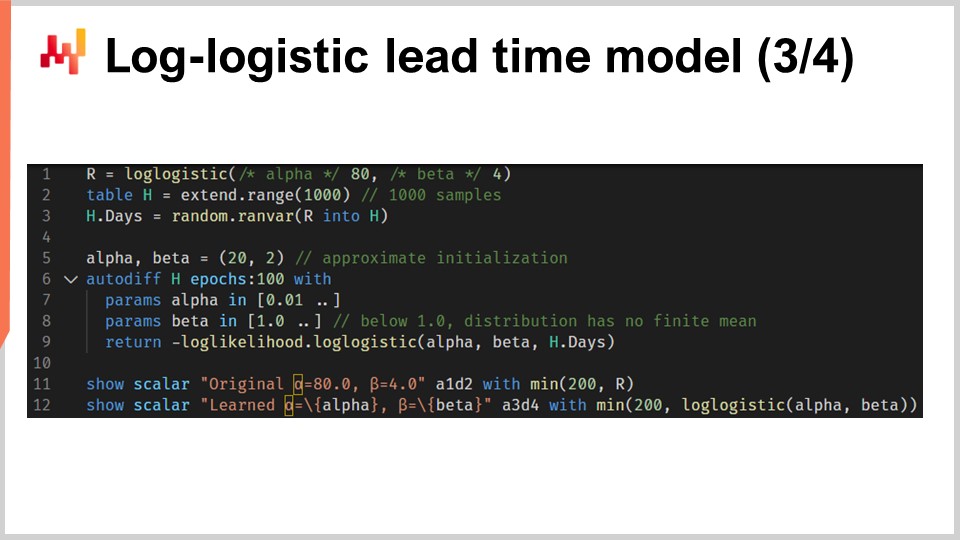
Proviamo ora a mettere insieme il tutto con uno script che apprende i parametri di un modello probabilistico del tempo di consegna basato sulla distribuzione log-logistica. Nella riga uno e nella riga tre, generiamo il nostro mock dataset di addestramento. In contesti reali, useremmo dati storici invece di generare dati fittizi. Alla riga uno, creiamo una “ranvar” che rappresenta la distribuzione originale. Per l’esercizio, vogliamo recuperare quei parametri, alpha e beta. La funzione log-logistica fa parte della libreria standard di Envision e restituisce una “ranvar”. Alla riga due, creiamo la tabella “H”, che contiene 1.000 voci. Alla riga tre, estraiamo 1.000 deviate campionate casualmente dalla distribuzione originale “R”. Questo vettore “H.days” rappresenta il dataset di addestramento.

Alla riga sei, abbiamo un blocco “autodiff”: qui avviene l’apprendimento. Nelle righe sette e otto, dichiariamo due parametri, alpha e beta, e per evitare problemi numerici come la divisione per zero, vengono imposti dei limiti su tali parametri. Alpha deve rimanere maggiore di 0,01 e beta maggiore di 1,0. Alla riga nove, restituiamo il loss, che è l’opposto del log-likelihood. Infatti, per convenzione, i blocchi “autodiff” minimizzano la funzione di loss, e dunque vogliamo massimizzare la likelihood, da qui il segno meno. La funzione “log_likelihood.logistic” fa parte della libreria standard di Envision, ma internamente è semplicemente la funzione “L4” che abbiamo implementato nella slide precedente. Non c’è magia qui; è tutta differenziazione automatica che fa fluire il gradiente dal loss ai parametri alpha e beta.

Alle righe 11 e 12 vengono tracciate sia la distribuzione originale sia quella appresa. Gli istogrammi sono limitati a 200; questo limite rende l’istogramma un po’ più leggibile. Ne parleremo tra poco. Nel caso vi stiate chiedendo come vada in termini di prestazioni la parte “autodiff” di questo script, essa impiega meno di 80 millisecondi per eseguirsi su un singolo core della CPU. La programmazione differenziabile non è solo versatile; sfrutta anche al meglio le risorse computazionali messe a disposizione dall’hardware moderno.

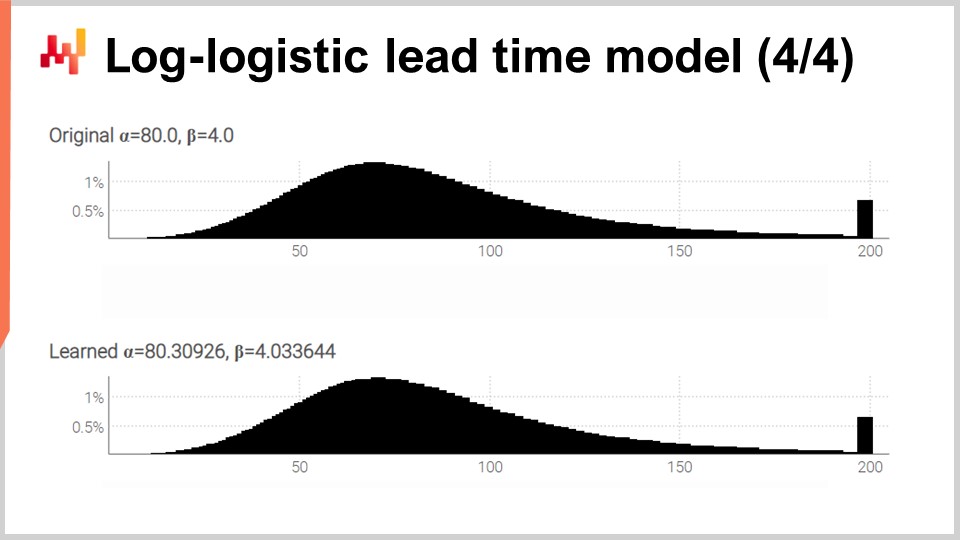
Sullo schermo vediamo i due istogrammi prodotti dallo script che abbiamo appena esaminato. In alto, la distribuzione originale con i suoi due parametri originali, alpha e beta, pari rispettivamente a 80 e 4. In basso, la distribuzione appresa con due parametri ottenuti tramite programmazione differenziabile. Le due punte estreme a destra sono associate alle code che abbiamo troncato, dato che queste code si estendono molto. A proposito, sebbene sia raro, capita che alcuni beni vengano ricevuti più di un anno dopo essere stati ordinati. Non è il caso di ogni settore, certamente non per i latticini, ma per ricambi meccanici o componenti elettronici, infatti, accade occasionalmente.

Anche se il processo di apprendimento non è perfetto, otteniamo risultati entro l’uno percento dei valori originali dei parametri. Questo dimostra, almeno, che la massimizzazione del log-likelihood tramite programmazione differenziabile funziona in pratica. La distribuzione log-logistica può essere o non essere adatta; dipende dalla forma della distribuzione dei tempi di consegna che state affrontando. Tuttavia, possiamo quasi scegliere qualsiasi distribuzione parametrica alternativa. Tutto ciò che serve è un’espressione analitica della funzione di densità di probabilità. Esiste un’ampia varietà di tali distribuzioni. Una volta in possesso di una formula da libro di testo, una semplice implementazione tramite programmazione differenziabile solitamente fa il resto.

I tempi di consegna non vengono osservati solo al termine della transazione. Mentre la transazione è ancora in corso, si dispone già di alcune informazioni; si ottiene un’osservazione incompleta del tempo di consegna. Considerate, ad esempio, che 100 giorni fa avete effettuato un ordine. I beni non sono ancora stati ricevuti; tuttavia, sapete già che il tempo di consegna è di almeno 100 giorni. Questa durata di 100 giorni rappresenta il limite inferiore di un tempo di consegna che non è stato ancora osservato completamente. Tali tempi di consegna incompleti sono spesso di notevole importanza. Come ho accennato all’inizio di questa lezione, i dataset dei tempi di consegna sono spesso scarsamente popolati. Non è insolito disporre di un dataset che includa solo mezza dozzina di osservazioni. In queste situazioni, è importante sfruttare al massimo ogni osservazione, comprese quelle ancora in corso.

Consideriamo il seguente esempio: abbiamo in totale cinque ordini. Tre ordini sono già stati consegnati con valori di tempo di consegna molto vicini a 30 giorni. Tuttavia, gli ultimi due ordini sono in sospeso da 40 e 50 giorni, rispettivamente. In base alle prime tre osservazioni, il tempo medio di consegna dovrebbe aggirarsi intorno ai 30 giorni. Tuttavia, i due ordini ancora incompleti smentiscono questo scenario. I due ordini in sospeso a 40 e 50 giorni suggeriscono un tempo di consegna sostanzialmente più lungo. Quindi, non dovremmo scartare gli ultimi ordini solo perché sono incompleti. Dobbiamo sfruttare queste informazioni e aggiornare la nostra stima verso tempi di consegna maggiori, magari intorno ai 60 giorni.

Rivisitiamo il nostro modello probabilistico del tempo di consegna, ma stavolta tenendo conto delle osservazioni incomplete. In altre parole, vogliamo gestire osservazioni che talvolta rappresentano solo un limite inferiore rispetto al tempo di consegna finale. Per farlo, possiamo utilizzare la funzione di distribuzione cumulativa (CDF) della distribuzione log-logistica. Questa formula è scritta sullo schermo; ancora una volta, si tratta di materiale da libro di testo. La CDF della distribuzione log-logistica beneficia di un’espressione analitica semplice. Di seguito, farò riferimento a questa tecnica come “tecnica della probabilità condizionata” per gestire i dati censurati.

Basandoci su questa espressione analitica della CDF, possiamo rivisitare il log-likelihood della distribuzione log-logistica. Lo script sullo schermo fornisce una versione rivista dell’implementazione precedente della funzione L4. Alla riga uno, abbiamo praticamente la stessa dichiarazione della funzione. Questa funzione prende un quarto argomento in più, un valore Booleano chiamato “is_incomplete” che indica, come suggerisce il nome, se l’osservazione è incompleta o meno. Alle righe due e tre, se l’osservazione è completa, si ricorre alla situazione precedente con la distribuzione log-logistica standard. Quindi, viene chiamata la funzione di log-likelihood che fa parte della libreria standard. Avrei potuto ripetere il codice della precedente implementazione L4, ma questa versione è più concisa. Alle righe quattro e cinque, esprimiamo il log-likelihood di osservare, in definitiva, un tempo di consegna superiore all’attuale osservazione incompleta, “X”. Ciò avviene tramite la CDF e, più precisamente, il logaritmo della CDF.

Possiamo ora ripetere l’impostazione con uno script che apprende i parametri della distribuzione log-logistica, ma questa volta in presenza di tempi di consegna incompleti. Lo script sullo schermo è quasi identico a quello precedente. Dalle righe uno a tre generiamo i dati; queste righe non sono state modificate. Notate che H.N è un vettore generato automaticamente che viene creato implicitamente alla riga due. Questo vettore numerica le righe generate, a partire da uno. La versione precedente di questo script non utilizzava questo vettore auto-generato, ma attualmente il vettore H.N compare alla fine della riga sei.

Le righe cinque e sei sono davvero quelle importanti. Qui, censuriamo i tempi di consegna. È come se effettuassimo un’osservazione del tempo di consegna ogni giorno, troncando le osservazioni troppo recenti per essere informative. Ciò significa, ad esempio, che un tempo di consegna di 20 giorni iniziato sette giorni fa appare come un tempo di consegna incompleto di sette giorni. Alla fine della riga sei, abbiamo generato una lista di tempi di consegna in cui alcune delle osservazioni più recenti (quelle che terminerebbero oltre la data attuale) sono incomplete. Il resto dello script rimane invariato, tranne che alla riga 12, dove il vettore H.is_complete viene passato come quarto argomento della funzione di log-likelihood. Così, alla riga 12, chiamiamo la funzione di programmazione differenziabile che abbiamo appena introdotto un attimo fa.

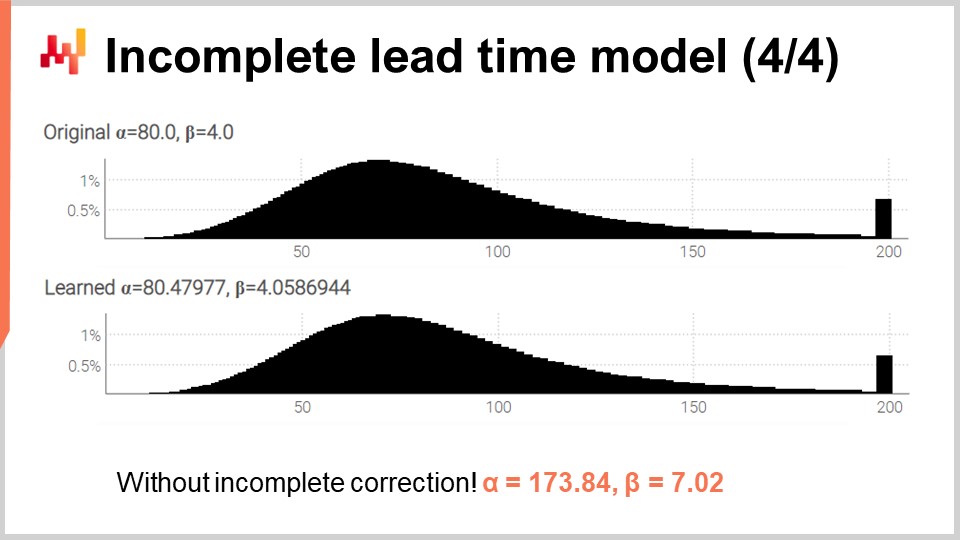
Infine, sullo schermo, vengono prodotti i due istogrammi da questo script rivisto. I parametri vengono ancora appresi con alta precisione, mentre ora siamo in presenza di numerosi tempi di consegna incompleti. Per verificare che gestire i tempi incompleti non fosse una complicazione superflua, ho rieseguito lo script, questa volta con una variazione modificata che utilizza il sovraccarico a tre argomenti della funzione di log-likelihood (quella che abbiamo utilizzato inizialmente e che assumeva che tutte le osservazioni fossero complete). Per alpha e beta otteniamo i valori mostrati in fondo allo schermo. Come previsto, tali valori non corrispondono affatto ai valori originali di alpha e beta.

In questa serie di lezioni, non è la prima volta che viene introdotta una tecnica per gestire dati censurati. Nella seconda lezione di questo capitolo, è stata introdotta la tecnica del loss masking per affrontare gli stockouts. Infatti, solitamente vogliamo prevedere la domanda futura, non le vendite future. Gli stockout introducono un bias negativo, poiché non riusciamo a osservare tutte le vendite che si sarebbero verificate se lo stockout non fosse accaduto. La tecnica della probabilità condizionata può essere utilizzata per gestire la domanda censurata, come avviene con gli stockout. La tecnica della probabilità condizionata è un po’ più complessa del loss masking, quindi probabilmente non dovrebbe essere usata se il loss masking è sufficiente.

Nel caso dei tempi di consegna, la scarsità di dati è la motivazione principale. Potremmo avere così pochi dati da rendere fondamentale sfruttare ogni singola osservazione, anche quelle incomplete. Infatti, la tecnica della probabilità condizionata è più potente del loss masking nel senso che sfrutta le osservazioni incomplete anziché scartarle semplicemente. Ad esempio, se c’è una unità di stock e se questa singola unità viene venduta, allora, suggerendo uno stockout, la tecnica della probabilità condizionata sfrutta comunque l’informazione che la domanda era maggiore o uguale a uno.

Qui otteniamo un sorprendente vantaggio della modellizzazione probabilistica: ci offre un modo elegante per gestire la censura, un effetto che si verifica in numerose situazioni della supply chain. Attraverso la probabilità condizionata, possiamo eliminare intere classi di bias sistematici.

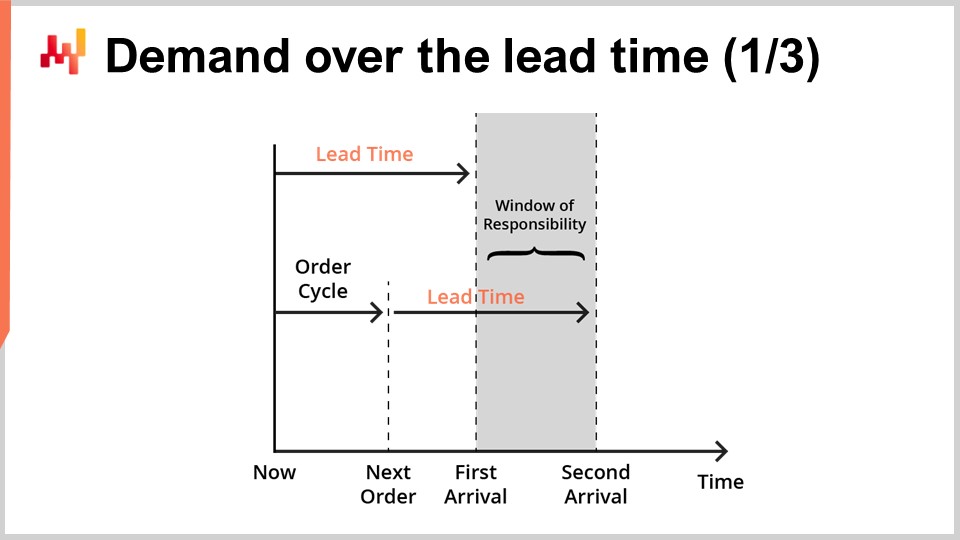
Le previsioni dei lead time sono tipicamente intese per essere combinate con le previsioni della domanda. Infatti, consideriamo ora una semplice situazione di rifornimento dell’inventario, come illustrato sullo schermo.

Serviamo un singolo prodotto e lo stock può essere rifornito effettuando un nuovo ordine a un unico fornitore. Stiamo cercando una previsione che possa supportare la nostra decisione di riordinare o meno dal fornitore. Possiamo riordinare ora e, se lo facciamo, le merci arriveranno al momento indicato come “first arrival.” Successivamente, avremo un’altra opportunità per riordinare. Questa ulteriore opportunità si verifica in un momento indicato come “next order,” e in questo caso le merci arriveranno al momento indicato come “second arrival.” Il periodo indicato come “window of responsibility” è il periodo che conta per quanto riguarda la nostra decisione di riordino.

Infatti, qualunque cosa decidiamo di riordinare non arriverà prima del primo lead time. Pertanto, abbiamo già perso il controllo sul soddisfacimento della domanda per tutto ciò che accade prima del “first arrival.” Successivamente, poiché avremo un’ulteriore opportunità per riordinare, soddisfare la domanda dopo il “second arrival” non è più di nostra responsabilità; è responsabilità del prossimo riordino. Quindi, riordinare con l’intenzione di soddisfare la domanda oltre il “second arrival” dovrebbe essere posticipato fino alla prossima opportunità di riordino.

Per supportare la decisione di riordino, ci sono due fattori che devono essere previsti. In primo luogo, dovremmo prevedere lo stock atteso al momento del “first arrival.” Infatti, se al momento del “first arrival” rimane ancora molto stock, allora non c’è motivo di riordinare ora. In secondo luogo, dovremmo prevedere la domanda attesa per la durata della “window of responsibility.” In un setup reale, dovremmo anche prevedere la domanda oltre la “window of responsibility” per valutare il carrying cost delle merci che stiamo ordinando ora, poiché potrebbero esserci eccedenze che si estendono in periodi successivi. Tuttavia, per motivi di concisione e tempistiche, oggi ci concentreremo sullo stock atteso e sulla domanda attesa per quanto riguarda la “window of responsibility.”

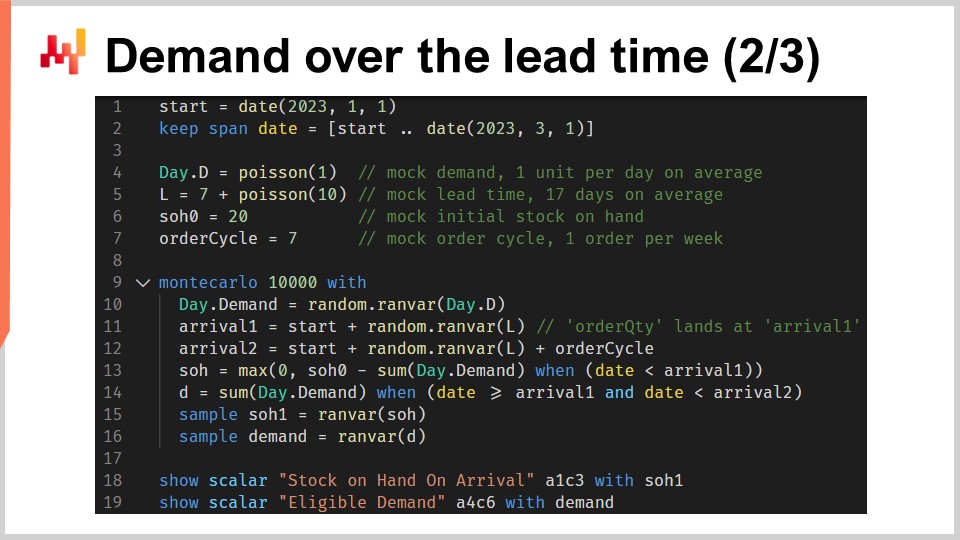
Questo script implementa i fattori della “window of responsibility”, ovvero le previsioni di cui abbiamo appena discusso. Riceve in input una previsione probabilistica dei lead time e una previsione probabilistica della domanda. Restituisce due distribuzioni di probabilità, cioè lo stock disponibile al momento dell’arrivo e la domanda ammissibile definita dalla “window of responsibility.”

Alle righe uno e due, impostiamo le timeline, che iniziano il 1° gennaio e terminano il 1° marzo. In un setup di previsione, questa timeline non sarebbe codificata in modo fisso. Alla riga quattro, viene introdotto un modello probabilistico semplificato della domanda: una distribuzione di Poisson ripetuta giorno per giorno per l’intera durata di questa timeline. La domanda sarà, in media, un’unità al giorno. Sto utilizzando qui un modello semplificato per la domanda per ragioni di chiarezza. In un setup reale, ad esempio, useremmo un ESSM (Ensemble State Space Model). I modelli state space sono probabilistici, e sono stati introdotti nella primissima lezione di questo capitolo.

Alla riga cinque, viene introdotto un altro modello probabilistico semplificato. Questo secondo modello è pensato per i lead time. Si tratta di una distribuzione di Poisson spostata di sette giorni a destra. Lo spostamento viene eseguito tramite una convoluzione. Alla riga sei, definiamo lo stock iniziale disponibile. Alla riga sette, definiamo il ciclo d’ordine. Questo valore è espresso in giorni e caratterizza quando avverrà il prossimo riordino.

Dalla riga 9 alla 16, abbiamo un blocco Monte Carlo che rappresenta la logica centrale dello script. In precedenza, in questa lezione, abbiamo già introdotto un altro blocco Monte Carlo per supportare la nostra logica di cross-validation. Qui, stiamo utilizzando nuovamente questo costrutto, ma per uno scopo diverso. Vogliamo calcolare due variabili casuali che riflettano, rispettivamente, lo stock disponibile al momento dell’arrivo e la domanda ammissibile. Tuttavia, l’algebra delle variabili casuali non è sufficientemente espressiva per eseguire questo calcolo. Pertanto, utilizziamo invece un blocco Monte Carlo.

Nella terza lezione di questo capitolo, ho sottolineato che esiste una dualità tra la previsione probabilistica e le simulazioni. Il blocco Monte Carlo illustra questa dualità. Partiamo da una previsione probabilistica, la trasformiamo in una simulazione e infine convertiamo i risultati della simulazione in un’altra previsione probabilistica.

Diamo un’occhiata ai dettagli. Alla riga 10, generiamo una traiettoria per la domanda. Alla riga 11, generiamo la data di arrivo per il primo ordine, supponendo che stiamo ordinando oggi. Alla riga 12, generiamo la data di arrivo per il secondo ordine, supponendo che stiamo ordinando un ciclo d’ordine da ora. Alla riga 13, calcoliamo ciò che rimane come stock disponibile al momento del primo arrivo. Si tratta dello stock iniziale meno la domanda osservata per la durata del primo lead time. La funzione max zero indica che lo stock non può diventare negativo. In altre parole, assumiamo di non accettare arretrati. Questo presupposto di assenza di arretrati potrebbe essere modificato. Il caso degli arretrati è lasciato come esercizio al pubblico. Come suggerimento, la programmazione differenziabile può essere utilizzata per valutare la percentuale della domanda non soddisfatta che si converte con successo in arretrati, a seconda di quanti giorni mancano alla rinnovata disponibilità dello stock.

Tornando allo script, alla riga 14, calcoliamo la domanda ammissibile, cioè la domanda che si verifica durante la “window of responsibility.” Alle righe 15 e 16, raccogliamo due variabili casuali di interesse tramite la parola chiave “sample.” A differenza del primo script Envision di questa lezione, che trattava la cross-validation, qui intendiamo raccogliere distribuzioni di probabilità da questo blocco Monte Carlo, e non solo medie. In entrambe le righe 15 e 16, la variabile casuale che appare a destra dell’assegnazione è un aggregatore. Alla riga 15, otteniamo una variabile casuale per lo stock disponibile al momento dell’arrivo. Alla riga 16, otteniamo un’altra variabile casuale per la domanda che si verifica all’interno della “window of responsibility.”

Alle righe 18 e 19, quelle due variabili casuali vengono visualizzate. Ora, fermiamoci un attimo e ripensiamo a tutto questo script. Le righe da uno a sette sono dedicate semplicemente all’impostazione dei dati fittizi. Le righe 18 e 19 servono solo a visualizzare i risultati. L’unica logica effettiva si svolge nelle otto righe comprese tra la 9 e la 16. Infatti, tutta la logica effettiva si trova, in un certo senso, alle righe 13 e 14.

Con poche righe di codice, meno di 10 indipendentemente dal conteggio, combiniamo una previsione probabilistica dei lead time con una previsione probabilistica della domanda per comporre una sorta di previsione probabilistica ibrida di reale importanza supply chain. Notiamo che non c’è nulla qui che dipenda realmente dalle specifiche sia della previsione dei lead time sia della previsione della domanda. Sono stati utilizzati modelli semplici, ma si sarebbero potuti usare modelli sofisticati. Non avrebbe fatto alcuna differenza. L’unico requisito è avere due modelli probabilistici in modo da rendere possibile generare quelle traiettorie.

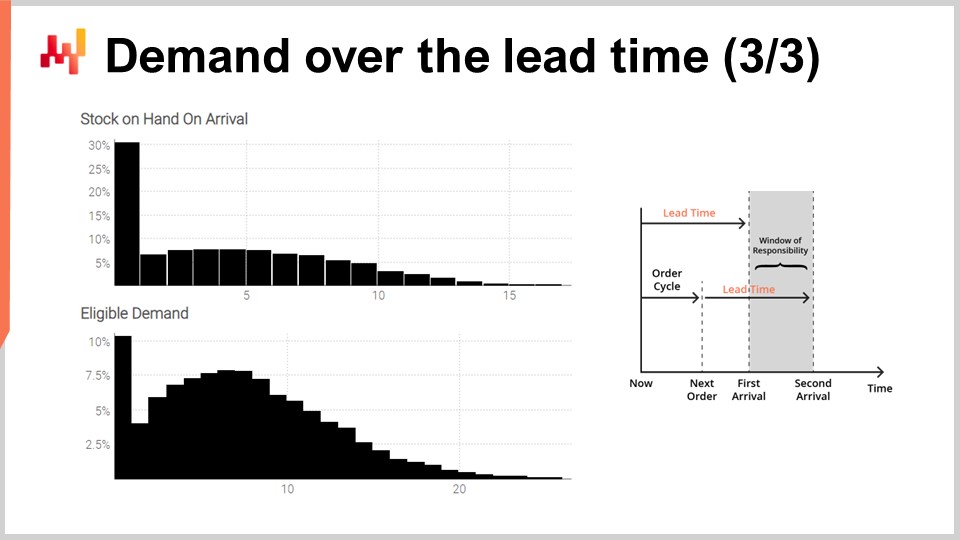
Infine, sullo schermo, gli istogrammi prodotti dallo script. L’istogramma superiore rappresenta lo stock disponibile al momento dell’arrivo. C’è circa il 30% di probabilità di fronteggiare uno stock iniziale pari a zero. In altre parole, c’è il 30% di probabilità che si sia verificato un esaurimento dell’inventario nell’ultimo giorno appena prima della data del “first arrival.” Il valore medio dello stock potrebbe essere di circa cinque unità. Tuttavia, se giudicassimo questa situazione basandoci sulla media, leggeremmo seriamente male la situazione. Una previsione probabilistica è essenziale per riflettere correttamente la situazione dello stock iniziale.

L’istogramma inferiore rappresenta la domanda associata alla “window of responsibility.” Abbiamo circa il 10% di probabilità di fronteggiare una domanda pari a zero. Questo risultato potrebbe anche sembrare sorprendente. Infatti, abbiamo iniziato questo esercizio con una domanda di Poisson stazionaria di un’unità al giorno in media. Abbiamo sette giorni tra gli ordini. Se non fosse stato per la variazione dei lead time, ci sarebbe stata meno dello 0,1% di probabilità di ottenere una domanda pari a zero in sette giorni. Tuttavia, lo script dimostra che questa occorrenza è molto più frequente. La ragione è che una “window of responsibility” ridotta può verificarsi se il primo lead time è più lungo del solito e se il secondo lead time è più corto del solito.

Affrontare una domanda pari a zero durante la “window of responsibility” significa che lo stock disponibile probabilmente diventerà piuttosto elevato in un determinato momento. A seconda della situazione, ciò potrebbe essere critico o meno, ma potrebbe esserlo, ad esempio, se esiste un limite di capacità di stoccaggio o se lo stock è deperibile. Ancora una volta, la domanda media, probabilmente intorno a otto, non fornisce un’indicazione affidabile di come fosse la domanda. Ricordate che abbiamo ottenuto questa distribuzione altamente asimmetrica da una domanda stazionaria iniziale, di un’unità al giorno in media. Questo è l’effetto della variazione dei lead time in azione.

Questo semplice setup dimostra l’importanza dei lead time nelle situazioni di rifornimento dell’inventario. Da un punto di vista supply chain, isolare le previsioni dei lead time da quelle della domanda è, nel migliore dei casi, un’astrazione pratica. La domanda giornaliera non è ciò che ci interessa realmente. Ciò che interessa davvero è la composizione della domanda con il lead time. Se fossero presenti altri fattori stocastici, come arretrati o resi, anche tali fattori farebbero parte del modello.

Il presente capitolo di questa serie di lezioni è intitolato “Predictive Modeling” invece di “Demand Forecasting”, come sarebbe tipicamente il caso nei manuali supply chain tradizionali. La ragione di questo titolo di capitolo dovrebbe essere diventata progressivamente evidente man mano che procediamo con la presente lezione. Infatti, da un punto di vista supply chain, vogliamo prevedere l’evoluzione del sistema supply chain. La domanda è certamente un fattore importante, ma non è l’unico. Altri fattori variabili, come il lead time, devono essere previsti. Ancora più importante, tutti questi fattori devono, alla fine, essere previsti insieme.

Infatti, dobbiamo unire questi componenti predittivi per supportare un processo di decision-making. Quindi, ciò che conta non è cercare un modello finale di previsione della domanda. Questo compito è in gran parte un’impresa futile, in definitiva, perché l’accuratezza extra verrà ottenuta in modi che contraddicono il miglior interesse dell’azienda. Più sofisticazione significa più opacità, più bug, più risorse computazionali. Come regola empirica, quanto più sofisticato è il modello, tanto più diventa difficile comporre operativamente con successo questo modello con un altro. Ciò che conta è assemblare una collezione di tecniche predittive che possano essere composte a piacimento. Questo è il senso della modularità da una prospettiva di predictive modeling. In questa lezione sono state presentate mezza dozzina di tecniche. Queste tecniche sono utili in quanto affrontano aspetti critici del mondo reale, come le osservazioni incomplete. Sono anche semplici; nessuno degli esempi di codice presentati oggi ha superato le 10 righe di logica effettiva. Ancora più importante, queste tecniche sono modulari, come mattoncini Lego. Funzionano bene insieme e possono essere quasi infinitamente ricombinate.

L’obiettivo finale del predictive modeling per supply chain, come dovrebbe essere inteso, è l’identificazione di tali tecniche. Ogni tecnica dovrebbe essere, di per sé, un’opportunità per rivedere qualsiasi modello predittivo preesistente al fine di semplificarlo o migliorarlo.

In conclusione, nonostante i lead time siano in gran parte trascurati dalla comunità accademica, i lead time possono e devono essere previsti. Esaminando una breve serie di distribuzioni reali dei lead time, abbiamo identificato due sfide: in primo luogo, i lead time variano; in secondo luogo, i lead time sono rari. Pertanto, abbiamo introdotto tecniche di modellazione adatte a gestire osservazioni dei lead time che risultano sia scarse che erratiche.

Questi modelli di lead time sono probabilistici e sono, in larga misura, il proseguimento dei modelli che sono stati progressivamente introdotti in questo capitolo. Abbiamo anche visto che la prospettiva della probabilità fornisce una soluzione elegante al problema dell’osservazione incompleta, un aspetto quasi ubiquitario nella supply chain. Questo problema si verifica ogni volta che si verificano esaurimenti dello stock e ogni volta che ci sono ordini pendenti. Infine, abbiamo visto come comporre una previsione probabilistica dei lead time con una previsione probabilistica della domanda per elaborare il modello predittivo di cui abbiamo bisogno per supportare un successivo processo decisionale.

La prossima lezione sarà l'8 marzo. Sarà un mercoledì alla stessa ora del giorno, alle 15:00 ora di Parigi. La lezione di oggi è stata tecnica, ma la prossima sarà in gran parte non tecnica, e discuterò il caso del supply chain scientist. Infatti, i manuali supply chain tradizionali trattano la supply chain come se i modelli di previsione e i modelli di ottimizzazione emergessero dal nulla, ignorando completamente la loro componente “wetware” — cioè, le persone responsabili. Pertanto, daremo uno sguardo più da vicino ai ruoli e alle responsabilità del supply chain scientist, una persona che si prevede guidi l’iniziativa quantitativa supply chain.

Ora procederò con le domande.

Domanda: E se qualcuno volesse mantenere il proprio stock per ulteriori innovazioni o per motivi diversi dal just in time o altri concetti?

Questa è davvero una domanda molto importante. Il concetto è tipicamente affrontato attraverso la modellazione economica della supply chain, che tecnicamente chiamiamo “economic drivers” in questa serie di lezioni. Quello che stai chiedendo è se sia meglio non servire un cliente oggi perché, in un momento successivo, ci sarà l’opportunità di servire la stessa unità a un’altra persona che, per qualsiasi ragione, conta di più. In sostanza, quello che stai dicendo è che c’è un valore maggiore da catturare servendo un altro cliente in seguito, forse un cliente VIP, rispetto a servire un cliente oggi.

Questo potrebbe essere il caso, e succede. Ad esempio, nell’industria dell’aviazione, supponiamo che tu sia un fornitore MRO (Maintenance, Repair, and Overhaul). Hai i soliti clienti VIP—le compagnie aeree che servi abitualmente con contratti a lungo termine, e sono molto importanti. Quando ciò accade, vuoi assicurarti di poter sempre servire quei clienti. Ma cosa succede se un’altra compagnia aerea ti chiama e chiede un’unità? In questo caso, quello che accadrà è che potresti servire questa persona, ma non hai un contratto a lungo termine con loro. Quindi, quello che farai è regolare il prezzo in modo che sia molto alto, assicurandoti di ottenere abbastanza valore per compensare la potenziale esaurimento dello stock che potresti affrontare in un secondo momento. In sostanza, per questa prima domanda, credo che non si tratti davvero di previsione ma più di una corretta modellizzazione dei driver economici. Se vuoi preservare lo stock, ciò che devi fare è generare un modello—un modello di ottimizzazione—in cui la risposta razionale non è servire il cliente che chiede un’unità mentre hai ancora dello stock di riserva.

A proposito, un’altra situazione tipica è quando stai vendendo kit. Un kit è un insieme di molte parti vendute insieme, e ti rimane solo una parte che vale solo una piccola frazione del valore totale del kit. Il problema è che se vendi quest’ultima unità, non potrai più assemblare il kit e venderlo al suo prezzo pieno. Quindi, potresti trovarti in una situazione in cui preferisci tenere l’unità in stock solo per poter vendere il kit in un secondo momento, potenzialmente con qualche incertezza. Ma, ancora una volta, tutto si riduce ai driver economici, e questo sarebbe il modo in cui affronterei la situazione.

Domanda: Negli ultimi anni, la maggior parte dei ritardi nella supply chain sono avvenuti a causa di guerre o pandemie, che sono molto difficili da prevedere perché non abbiamo mai avuto tali situazioni prima. Qual è la tua opinione in merito?

La mia opinione è che i tempi di consegna sono variati da sempre. Sono nel mondo della supply chain dal 2008, e i miei genitori lavoravano nella supply chain anche 30 anni prima di me. Per quanto ne ricordiamo, i tempi di consegna sono sempre stati erratici e variabili. C’è sempre qualcosa che succede, che si tratti di una protesta, una guerra o un cambiamento nelle tariffe. Sì, gli ultimi due anni sono stati estremamente erratici, ma i tempi di consegna erano già molto variabili.

Concordo che nessuno può sostenere di essere in grado di prevedere la prossima guerra o pandemia. Se fosse possibile prevedere matematicamente questi eventi, le persone non si impegnerebbero in guerre o investirebbero nella supply chain; giocherebbero semplicemente in borsa e diventerebbero ricchi anticipando i movimenti del mercato.

La conclusione è che quello che puoi fare è pianificare l’imprevisto. Se non hai fiducia nel futuro, puoi effettivamente gonfiare le variazioni nelle tue previsioni. È l’opposto di cercare di rendere la tua previsione più accurata—mantieni le tue aspettative medie, ma gonfi la coda in modo che le decisioni che prendi basandoti su quelle previsioni probabilistiche siano più resilient alle variazioni. Hai ingegnerizzato le variazioni attese per essere maggiori di quelle che stai attualmente osservando. In definitiva, l’idea che le cose siano facili o difficili da prevedere deriva da una prospettiva di previsione puntuale, in cui vorresti giocare come se fosse possibile avere un’anticipazione precisa del futuro. Questo non è il caso—non esiste un’anticipazione precisa del futuro. L’unica cosa che puoi fare è lavorare con distribuzioni di probabilità con una grande dispersione che manifesta e quantifica la tua ignoranza sul futuro.

Invece di perfezionare decisioni che dipendono criticamente dall’esecuzione minuta del piano esatto, stai tenendo conto e pianificando un interessante grado di variazione, rendendo le tue decisioni più robuste contro tali variazioni. Tuttavia, questo vale solo per quel tipo di variazione che non impatta la tua supply chain in maniera troppo brutale. Ad esempio, puoi gestire tempi di consegna del fornitore più lunghi, ma se il tuo magazzino è stato bombardato, nessuna previsione ti salverà in quella situazione.

Domanda: Possiamo creare questi istogrammi e calcolare il CRPS in Microsoft Excel, per esempio, sfruttando add-in di Excel come itsastat o altri che ospitano molte distribuzioni?

Sì, puoi. Uno di noi a Lokad ha effettivamente prodotto un foglio di calcolo Excel che rappresenta un modello probabilistico per una situazione di rifornimento dell’inventario. Il punto cruciale del problema è che Excel non dispone di un tipo di dato istogramma nativo, quindi tutto ciò che hai in Excel sono numeri—una cella, un numero. Sarebbe elegante e semplice avere un unico valore che rappresenta un istogramma, in cui hai un istogramma completo racchiuso in una singola cella. Tuttavia, per quanto ne so, questo non è possibile in Excel. Tuttavia, se sei disposto a spendere circa 100 righe circa per rappresentare l’istogramma, anche se non sarà compatto e pratico, puoi implementare una distribuzione in Excel e fare un po’ di modellizzazione probabilistica. Pubblicheremo il link all’esempio nella sezione commenti.

Tieni presente che si tratta di un’impresa relativamente laboriosa perché Excel non è idealmente adatto per questo compito. Excel è un linguaggio di programmazione, e con esso puoi fare qualsiasi cosa, quindi non hai nemmeno bisogno di un add-in per realizzarlo. Tuttavia, sarà un po’ verboso, quindi non aspettarti qualcosa di super ordinato.

Domanda: Il lead time può essere scomposto in componenti come il tempo di ordinazione, il tempo di produzione, il tempo di trasporto, ecc. Se si vuole un controllo più granulare sui lead time, come cambierebbe questo approccio?

Prima di tutto, dobbiamo considerare cosa significa avere un maggiore controllo sul lead time. Vuoi ridurre il lead time medio o ridurre la variabilità del lead time? Curiosamente, ho visto molte aziende riuscire a ridurre il lead time medio, ma scambiando qualcosa in più la variazione del lead time. In media, il lead time è più breve, ma di tanto in tanto è molto più lungo.

In questa lezione, ci stiamo cimentando in un esercizio di modellizzazione. Di per sé, non c’è alcuna azione; si tratta solo di osservare, analizzare e prevedere. Tuttavia, se possiamo scomporre il lead time e analizzare la distribuzione sottostante, possiamo utilizzare la modellizzazione probabilistica per valutare quali componenti variano di più e quali hanno l’impatto negativo più significativo sulla nostra supply chain. Possiamo eseguire scenari “what-if” con queste informazioni. Ad esempio, prendi una parte del tuo lead time e chiediti: “E se la coda di questo lead time fosse un po’ più corta, o se la media fosse un po’ più breve?” Puoi quindi riassemblare tutto, rieseguire il tuo modello predittivo per l’intera supply chain e iniziare a valutare l’impatto.

Questo approccio ti permette di ragionare per parti riguardo a determinati fenomeni, compresi quelli erratici. Non sarebbe tanto un cambio di approccio quanto una continuazione di quanto già fatto, che ci porta al Capitolo 6, che tratta l’ottimizzazione delle decisioni reali basata su questi modelli probabilistici.

Domanda: Credo che questo offra l’opportunità di ricalcolare i nostri lead times in SAP per fornire una tempistica più realistica e aiutare a minimizzare i nostri sistemi pull-in e pull-out. È possibile?

Disclaimer: SAP è un concorrente di Lokad nel campo dell’ottimizzazione della supply chain. La mia risposta iniziale è no, SAP non può farlo. La realtà è che SAP dispone di quattro soluzioni distinte che si occupano di ottimizzazione della supply chain, e dipende da quale stack stai parlando. Tuttavia, tutti questi stack hanno in comune una visione incentrata sulle previsioni puntuali. Tutto in SAP è stato ingegnerizzato sul presupposto che le previsioni saranno accurate.

Sì, SAP ha alcuni parametri da regolare, come la distribuzione normale che ho menzionato all’inizio di questa lezione. Tuttavia, le distribuzioni dei lead time che abbiamo osservato non erano distribuite normalmente. Per quanto ne so, le configurazioni mainstream di SAP per l’ottimizzazione della supply chain adottano una distribuzione normale per i lead times. Il problema è che, alla base, il software fa un’ipotesi matematica ampiamente errata. Non puoi recuperare da un’ipotesi ampiamente errata che va dritta al cuore della tua architettura software semplicemente regolando un parametro. Forse, tramite una reverse engineering un po’ folle, potresti trovare un parametro che finisca per generare la decisione corretta. Teoricamente, questo è possibile, ma in pratica presenta così tanti problemi che la domanda è: perché vorresti davvero farlo?

Per adottare una prospettiva probabilistica, devi impegnarti completamente, nel senso che le tue previsioni sono probabilistiche e i tuoi modelli di ottimizzazione sfruttano modelli probabilistici. Il problema qui è che, anche se potessimo regolare la modellizzazione probabilistica per ottenere lead times leggermente migliori, il resto dello stack SAP ricadrebbe nelle previsioni puntuali. Indipendentemente da quello che accade, trasformeremo quelle distribuzioni in punti. L’idea che tu possa approssimare questo con una media è inquietante e semplicemente sbagliata. Quindi, tecnicamente, potresti regolare i lead times, ma incontrerai così tanti problemi dopo che potrebbe non valerne lo sforzo.

Domanda: Ci sono situazioni in cui ordini le stesse parti da fornitori diversi. Questa è un’informazione importante da considerare nella previsione dei lead times. Effettui la previsione dei lead times per articolo o ci sono situazioni in cui sfrutti il raggruppamento degli articoli in famiglie?

Questa è una domanda veramente interessante. Abbiamo due fornitori per lo stesso articolo. La domanda sarà quanto siano simili gli articoli e i fornitori. Per prima cosa, dobbiamo esaminare la situazione. Se un fornitore si trova proprio accanto e l’altro è dall’altra parte del mondo, devi certamente considerarli separatamente. Ma supponiamo l’interessante situazione in cui i due fornitori sono abbastanza simili e si tratta dello stesso articolo. Dovresti aggregare queste osservazioni o meno?

La cosa interessante è che, attraverso la programmazione differenziabile, puoi comporre un modello che assegna un certo peso al fornitore e un certo peso all’articolo, lasciando che la magia dell’apprendimento faccia il suo corso. Il modello si adatterà per stabilire se sia necessario dare più peso al componente dell’articolo del lead time o a quello del fornitore. Potrebbe darsi che due fornitori che offrono sostanzialmente lo stesso tipo di prodotto abbiano un certo bias, per cui in media uno sia un po’ più veloce dell’altro. Ma ci sono articoli che richiedono sicuramente più tempo, e quindi se scegli in modo selettivo gli articoli, non è chiaro che un fornitore sia più veloce dell’altro, perché dipende davvero dagli articoli che stai analizzando. Molto probabilmente avrai pochissimi dati se disaggregationi tutto fino a ogni fornitore e ogni articolo. Pertanto, la cosa interessante, e ciò che consiglierei qui, è di ingegnerizzare utilizzando la programmazione differenziabile. Potremmo addirittura cercare di riprendere questa situazione in una lezione successiva, una situazione in cui assegni dei parametri a livello di parte e altri a livello di fornitore. In questo modo, il numero totale di parametri non sarà il numero di articoli moltiplicato per il numero di fornitori; sarà il numero di articoli più il numero di fornitori, o magari più il numero dei fornitori per categoria, o qualcosa di simile. Non farai esplodere il numero di parametri, ma aggiungerai semplicemente un parametro, un elemento che ha un’affinità verso il fornitore, permettendoti di realizzare una sorta di miscela dinamica guidata dai tuoi dati storici.

Domanda: Credo che la quantità ordinata e il fatto che determinati prodotti vengano ordinati insieme possano influenzare il lead time alla fine. Potresti spiegare la complessità di includere tutte le variabili in questo tipo di problema?

Nell’ultimo esempio, avevamo due tipi di durata: il ciclo d’ordine e il lead time stesso. Il ciclo d’ordine è interessante perché è incerto nella misura in cui non abbiamo ancora preso la decisione. È fondamentalmente qualcosa che puoi decidere praticamente in qualsiasi momento, quindi il ciclo d’ordine è completamente interno e determinato da te. Questo non è l’unico aspetto nella supply chain; i prezzi sono la stessa cosa. Hai la domanda, osservi la domanda, ma puoi effettivamente scegliere il prezzo che desideri. Alcuni prezzi sono ovviamente imprudenti, ma è la stessa logica—è una decisione tua.

Il ciclo d’ordine è una tua scelta. Ora, quello che stai dicendo è che c’è incertezza sul momento esatto per il prossimo lead time d’ordine perché non sai esattamente quando effettuerai l’ordine. Infatti, hai perfettamente ragione. Quello che succede è che, quando hai la capacità di implementare questa modellizzazione probabilistica, improvvisamente, come discusso nel sesto capitolo di questa serie di lezioni, non vuoi dire che il ciclo d’ordine sia di sette giorni. Invece, vuoi adottare una politica di riordino che massimizzi il ritorno sull’investimento per la tua azienda. Quindi, quello che puoi fare è pianificare il futuro in modo che, se riordini ora, prendi una decisione ora e poi applichi la tua politica giorno per giorno. Ad un certo punto nel futuro, effettui un riordino, e quello che hai è una situazione simile a una “serpente che si morde la coda”, perché la migliore decisione odierna dipende dalla decisione del prossimo ordine, quella che non hai ancora preso. Questo tipo di problema è noto come problema di policy, ed è un problema decisionale sequenziale. In sostanza, quello che vuoi veramente è definire una politica, un oggetto matematico che regola il tuo processo decisionale.

Il problema dell’ottimizzazione della policy è piuttosto complicato, e intendo affrontarlo nel sesto capitolo. Ma in sintesi, se torniamo alla tua domanda, abbiamo due componenti distinte. Abbiamo il componente che varia indipendentemente da ciò che fai, cioè il lead time del fornitore, e poi c’è il tempo di ordinazione, che è qualcosa di completamente interno al tuo processo e va trattato come una questione di ottimizzazione.

Concludendo questo discorso, vediamo una convergenza tra ottimizzazione e modellizzazione predittiva. Alla fine, le due finiscono per essere praticamente la stessa cosa, perché ci sono interazioni tra le decisioni che prendi e ciò che accade nel futuro.

Questo è tutto per oggi. Non dimenticare, l'8 marzo, alla stessa ora del giorno, sarà un mercoledì, alle 15:00. Grazie, e ci vediamo alla prossima volta.