Spärlichkeit: Wenn die Genauigkeitsmessung schiefgeht

Joannes Vermorel

Vor drei Jahren haben wir [Overfitting: when accuracy measure goes wrong](/blog/2009/4/22/overfitting-when-accuracy-measure-goes-wrong/) veröffentlicht, jedoch ist overfitting bei weitem nicht die einzige Situation, in der einfache Genauigkeitsmessungen sehr irreführend sein können. Heute konzentrieren wir uns auf eine besonders fehleranfällige Situation: unregelmäßige Nachfrage, die typischerweise auftritt, wenn man sich Verkäufe auf Filialebene (oder E-Commerce) anschaut.

Wir sind überzeugt, dass allein dieses eine Problem die meisten Einzelhändler daran gehindert hat, fortschrittliche Prognosesysteme auf Filialebene einzuführen. Wie bei den meisten Prognoseproblemen ist es subtil, gegenintuiv und einige Unternehmen verlangen hohe Preise, um mangelhafte Antworten auf diese Frage zu liefern.

Die beliebtesten Fehlerkennzahlen in der Verkaufsprognose sind der Mean Absolute Error (MAE) und der Mean Absolute Percentage Error (MAPE). Als allgemeine Richtlinie empfehlen wir, beim MAE zu bleiben, da der MAPE sehr schlecht abschneidet, wenn time-series nicht gleichmäßig verlaufen, das heißt, ständig, zumindest aus Sicht der Einzelhändler. Allerdings gibt es Situationen, in denen auch der MAE schlecht abschneidet. Niedrige Verkaufsvolumina fallen in diese Situationen.

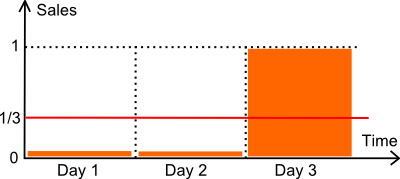
Betrachten wir die obige Darstellung. Wir haben einen Artikel, der über 3 Tage verkauft wird. Die Anzahl der in den ersten beiden Tagen verkauften Einheiten beträgt null. Am dritten Tag wird eine Einheit verkauft. Nehmen wir an, dass die tatsächliche Nachfrage genau 1 Einheit alle 3 Tage beträgt. Technisch gesprochen handelt es sich um eine Poisson-Verteilung mit λ=1/3.

Im Folgenden vergleichen wir zwei Prognosemodelle:

• ein konstantes Modell M mit 1/3 pro Tag (dem Mittelwert).
• ein konstantes Modell Z mit null pro Tag.

Was die Lageroptimierung betrifft, ist das Modell Null (Z) äußerst schädlich. Wenn man annimmt, dass die Sicherheitsbestandsanalyse zur Berechnung eines Nachbestellpunkts herangezogen wird, führt eine Null-Prognose sehr wahrscheinlich ebenfalls zu einem Nachbestellpunkt von Null, was zu häufigen Fehlbeständen führt. Eine Fehlerkennzahl, die das Modell Null gegenüber vernünftigeren Prognosen bevorzugen würde, würde sich also ziemlich schlecht verhalten.

Vergleichen wir unsere beiden Modelle hinsichtlich des MAPE (*) und des MAE.

• M hat einen MAPE von 44%.
• Z hat einen MAPE von 33%.
• M hat einen MAE von 0,44.
• Z hat einen MAE von 0,33.

(*) Die klassische Definition des MAPE beinhaltet eine Division durch Null, wenn der tatsächliche Wert null ist. Wir nehmen hier an, dass der tatsächliche Wert im Fall von Null durch 1 ersetzt wird. Alternativ hätten wir auch durch die Prognose (statt durch den tatsächlichen Wert) teilen oder den sMAPE verwenden können. Diese Änderungen machen keinen Unterschied: Die Schlussfolgerung der Diskussion bleibt dieselbe.

Abschließend lässt sich sagen, dass hier gemäß beiden, MAPE und MAE, das Modell Null dominiert.

Allerdings könnte man argumentieren, dass dies eine vereinfachte Situation sei und die Komplexität eines echten Geschäfts nicht widerspiegele. Das ist nicht ganz richtig. Wir haben Benchmarks in Dutzenden von Einzelhandelsgeschäften durchgeführt, und üblicherweise ist das siegreiche Modell (laut MAE oder MAPE) das Modell Null - das Modell, das stets null zurückgibt. Darüber hinaus gewinnt dieses Modell typischerweise mit einem beachtlichen Vorsprung gegenüber allen anderen Modellen.

In der Praxis ist es auf Filialebene, sich entweder auf den MAE oder den MAPE zu verlassen, um die Qualität von Prognosemodellen zu evaluieren, ein Rezept für Probleme: Das Maß begünstigt Modelle, die Nullen zurückgeben; je mehr Nullen, desto besser. Diese Schlussfolgerung gilt für nahezu jedes Geschäft, das wir bisher analysiert haben (abgesehen von den wenigen Artikeln mit hohem Verkaufsvolumen, die dieses Problem nicht aufweisen).

Leser, die mit Genauigkeitsmetriken vertraut sind, könnten vorschlagen, stattdessen den Mean Square Error (MSE) zu verwenden, der das Modell Null nicht begünstigt. Das mag stimmen, jedoch ist der MSE bei Anwendung auf unregelmäßige Daten – und Verkäufe auf Filialebene sind unregelmäßig – numerisch instabil. In der Praxis wird jeder Ausreißer in der Verkaufshistorie die Endergebnisse stark verzerren. Genau diesem Problem haben sich Statistiker von Anfang an gewidmet, indem sie an robuster Statistik gearbeitet haben. Es gibt hier keinen kostenlosen Mittag.

Wie beurteilt man dann Prognosen auf Filialebene?

Es hat eine sehr, sehr lange Zeit gedauert, bis wir eine zufriedenstellende Lösung für das Problem fanden, die Genauigkeit der Prognosen auf Filialebene zu quantifizieren. Bereits 2011 und davor haben wir im Grunde genommen betrogen. Anstatt tägliche Datenpunkte zu betrachten, wechselten wir, wenn die Verkaufsdaten zu spärlich waren, typischerweise zu wöchentlichen Aggregaten (oder sogar zu monatlichen Aggregaten bei extrem spärlichen Daten). Durch den Wechsel zu längeren Aggregationszeiträumen haben wir die Verkaufsvolumina pro Periode künstlich erhöht und damit den MAE wieder nutzbar gemacht.

Der Durchbruch gelang erst vor ein paar Monaten durch Quantile. Im Wesentlichen lautete die Erleuchtung: Vergessen Sie die Prognosen, nur die Nachbestellpunkte zählen. Indem wir versuchten, unsere klassischen Prognosen an den Kennzahlen X, Y oder Z zu optimieren, versuchten wir, das falsche Problem zu lösen.

Moment! Da Nachbestellpunkte auf Basis der Prognosen berechnet werden, wie können Sie behaupten, dass Prognosen irrelevant sind?

Wir behaupten nicht, dass Prognosen und Prognosegenauigkeit irrelevant sind. Wir stellen jedoch fest, dass nur die Genauigkeit der Nachbestellpunkte selbst zählt. Die Prognose oder welche andere Variable auch zur Berechnung der Nachbestellpunkte herangezogen wird, kann nicht isoliert bewertet werden. Es muss und sollte ausschließlich die Genauigkeit der Nachbestellpunkte bewertet werden.

Es stellt sich heraus, dass eine Kennzahl zur Bewertung von Nachbestellpunkten existiert: Es ist die Pinball Loss Function, eine Funktion, die Statistiker seit Jahrzehnten kennen. Pinball Loss ist nicht aufgrund seiner mathematischen Eigenschaften überlegen, sondern schlicht, weil sie zum Inventartrade-off passt: zu viel Lagerbestand vs. zu viele Fehlbestände.