00:19 Einführung
04:33 Zwei Definitionen für ‘Algorithmus’
08:09 Big-O
13:10 Die bisherige Entwicklung
15:11 Hilfswissenschaften (Rückblick)
17:26 Moderne Algorithmen
19:36 Übertreffen von “Optimalität”
22:23 Datenstrukturen - 1/4 - Liste
25:50 Datenstrukturen - 2/4 - Baum
27:39 Datenstrukturen - 3/4 - Graph
29:55 Datenstrukturen - 4/4 - Hash-Tabelle
31:30 Zauberrezepte - 1/2
37:06 Zauberrezepte - 2/2
39:17 Tensor-Comprehensions - 1/3 - Die ‘Einstein’-Notation
42:53 Tensor-Comprehensions - 2/3 - Durchbruch des Facebook-Teams
46:52 Tensor-Comprehensions - 3/3 - supply chain-Perspektive
52:20 Meta-Techniken - 1/3 - Kompression
56:11 Meta-Techniken - 2/3 - Memoisierung
58:44 Meta-Techniken - 3/3 - Unveränderlichkeit
01:03:46 Fazit
01:06:41 Kommende Vorlesung und Fragen aus dem Publikum
Beschreibung
Die Optimierung von supply chains beruht darauf, zahlreiche numerische Probleme zu lösen. Algorithmen sind hochkodifizierte numerical recipes dazu gedacht, präzise rechnerische Probleme zu lösen. Überlegene Algorithmen bedeuten, dass überlegene Ergebnisse mit weniger Rechenressourcen erzielt werden können. Durch die Konzentration auf die Besonderheiten von supply chain kann die algorithmische Leistung enorm verbessert werden, manchmal um Größenordnungen. „supply chain“-Algorithmen müssen zudem das Design moderner Computer berücksichtigen, das sich in den letzten Jahrzehnten erheblich weiterentwickelt hat.
Gesamtes Transkript

Willkommen zu dieser Reihe von supply chain Vorlesungen. Ich bin Joannes Vermorel, und heute präsentiere ich „Moderne Algorithmen für supply chain.“ Überlegene Rechenkapazitäten sind entscheidend, um eine überlegene supply chain performance zu erreichen. Genauere Vorhersagen, feinere Optimierung und häufigere Optimierung sind alle wünschenswert, um eine überlegene supply chain performance zu erzielen. Es gibt immer eine überlegene numerische Methode, die nur geringfügig jenseits der Rechenressourcen liegt, die Sie sich leisten können.
Algorithmen, einfach ausgedrückt, lassen Computer schneller arbeiten. Algorithmen sind ein Zweig der Mathematik, und dies ist ein sehr aktives Forschungsgebiet. Der Fortschritt in diesem Forschungsgebiet übertrifft häufig den Fortschritt der Rechnerhardware selbst. Das Ziel dieser Vorlesung ist es, zu verstehen, worum es bei modernen Algorithmen geht und, genauer aus supply chain Perspektive, wie man Probleme angeht, sodass man diese modernen Algorithmen für seine supply chain optimal nutzen kann.

Was Algorithmen betrifft, gibt es ein Buch, das ein absolutes Standardwerk ist: Introduction to Algorithms, erstmals 1990 veröffentlicht. Es ist ein Muss. Die Qualität von Präsentation und Schreibstil ist einfach überragend. Dieses Buch verkaufte sich in den ersten 20 Jahren über eine halbe Million Mal und inspirierte eine ganze Generation akademischer Autoren. Tatsächlich wurden die meisten neueren supply chain Bücher, die sich mit supply chain Theorie befassen und in den letzten zehn Jahren veröffentlicht wurden, häufig stark vom Stil und der Präsentation dieses Buches inspiriert.
Persönlich las ich dieses Buch bereits 1997, und es handelte sich tatsächlich um eine französische Übersetzung der allerersten Ausgabe. Es hatte einen tiefgreifenden Einfluss auf meine gesamte Karriere. Nachdem ich dieses Buch gelesen hatte, sah ich Software nie wieder auf dieselbe Weise. Ein Wort der Warnung jedoch: Dieses Buch übernimmt eine Perspektive auf die Rechnerhardware, die Ende der 80er und Anfang der 90er vorherrschte. Wie wir in den vorherigen Vorlesungen dieser Reihe gesehen haben, hat sich die Rechnerhardware in den letzten Jahrzehnten recht dramatisch weiterentwickelt, weshalb einige der im Buch gemachten Annahmen relativ veraltet erscheinen. Zum Beispiel geht das Buch davon aus, dass Speicherzugriffe stets in konstanter Zeit erfolgen, unabhängig davon, wie viel Speicher Sie adressieren möchten. So funktionieren moderne Computer nicht mehr.
Dennoch glaube ich, dass es bestimmte Situationen gibt, in denen Simplizität ein vernünftiger Ansatz ist, wenn man im Gegenzug einen viel höheren Grad an Klarheit und Einfachheit in der Darstellung gewinnt. Dieses Buch leistet in dieser Hinsicht eine erstaunliche Arbeit. Obwohl ich darauf hinweise, dass einige der grundlegenden Annahmen im Buch veraltet sind, bleibt es dennoch ein absolutes Standardwerk, das ich dem gesamten Publikum empfehlen würde.

Lassen Sie uns den Begriff “Algorithmus” für das Publikum klären, das mit diesem Konzept vielleicht nicht so vertraut ist. Es gibt die klassische Definition, bei der es sich um eine endliche Abfolge wohldefinierter Computeranweisungen handelt. Dies ist die Art von Definition, die man in Lehrbüchern oder auf Wikipedia findet. Obwohl die klassische Definition eines Algorithmus ihre Berechtigung hat, glaube ich, dass sie unzureichend ist, da sie nicht die zugrundeliegende Intention von Algorithmen verdeutlicht. Es handelt sich nicht einfach um irgendeine Abfolge von Anweisungen, sondern um eine sehr spezifische Abfolge von Computeranweisungen. Daher schlage ich eine persönliche Definition des Begriffs Algorithmus vor: Ein Algorithmus ist im Wesentlichen eine leistungsorientierte, fein granulierte, problemlösende Softwaremethode.
Lassen Sie uns diese Definition auseinandernehmen, oder? Zunächst der problemlösende Teil: Ein Algorithmus ist vollständig durch das Problem charakterisiert, das er lösen will. Auf diesem Bildschirm sehen Sie den Pseudocode für den Quicksort-Algorithmus, einen populären und bekannten Algorithmus. Quicksort versucht, das Sortierproblem zu lösen, das wie folgt lautet: Sie haben ein Array, das Dateneinträge enthält, und Sie möchten einen Algorithmus, der dasselbe Array zurückgibt, jedoch mit allen Einträgen in aufsteigender Reihenfolge sortiert. Algorithmen konzentrieren sich gänzlich auf ein spezifisches und klar definiertes Problem.
Der zweite Aspekt ist, wie Sie beurteilen, dass Sie einen besseren Algorithmus haben. Ein besserer Algorithmus ermöglicht es, dasselbe Problem mit weniger Rechenressourcen zu lösen, was in der Praxis zu schnelleren Abläufen führt. Schließlich gibt es den fein granulierten Aspekt. Wenn wir vom Begriff “Algorithmen” sprechen, impliziert dies, dass wir sehr elementare Probleme betrachten, die modular aufgebaut und unendlich kombinierbar sind, um wesentlich kompliziertere Probleme zu lösen. Darum geht es bei Algorithmen wirklich.
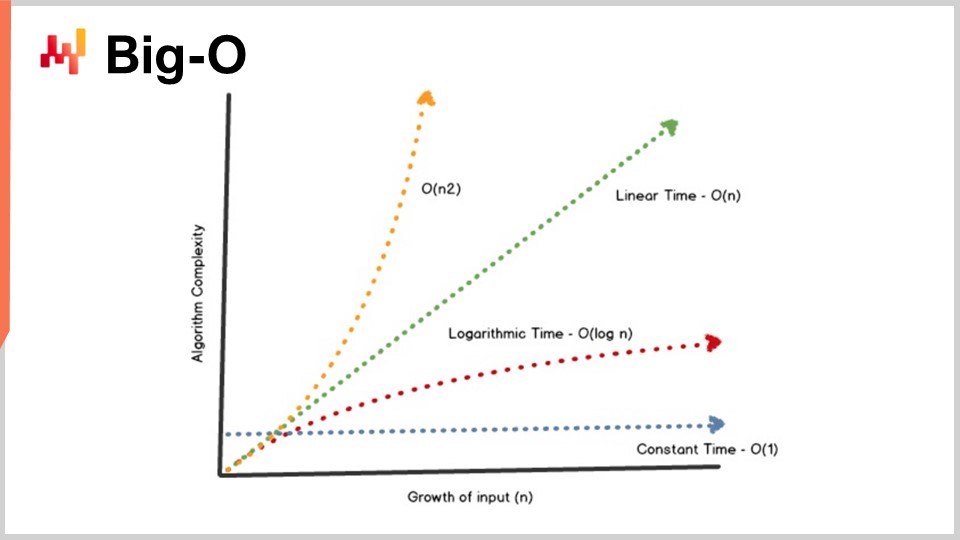
Ein zentrales Ergebnis der Algorithmentheorie ist es, die Leistung von Algorithmen in recht abstrakter Weise zu charakterisieren. Ich werde heute nicht die Zeit haben, in die Details dieser Charakterisierung und des mathematischen Rahmens einzutauchen. Die Idee ist, dass wir zur Charakterisierung eines Algorithmus sein asymptotisches Verhalten betrachten. Wir haben ein Problem, das von einer oder mehreren entscheidenden Engpass-Dimensionen abhängig ist, die das Problem definieren. Beispielsweise ist im zuvor dargestellten Sortierproblem die charakteristische Dimension üblicherweise die Anzahl der zu sortierenden Elemente. Die Frage lautet, was passiert, wenn das Array der zu sortierenden Elemente sehr groß wird? Diese charakteristische Dimension bezeichne ich konventionell mit der Zahl “n”.
Nun habe ich diese Notation, die Big-O-Notation, die Sie vielleicht im Zusammenhang mit Algorithmen schon gesehen haben. Ich werde nur einige Elemente darlegen, um Ihnen ein Gefühl dafür zu geben, was dahintersteckt. Nehmen wir beispielsweise an, wir haben einen Datensatz, und wir möchten einen einfachen statistischen Indikator wie einen Durchschnitt berechnen. Wenn ich sage, ich habe einen Algorithmus mit Big-O von 1, bedeutet dies, dass ich in der Lage bin, eine Lösung für dieses Problem (das Berechnen des Durchschnitts) in konstanter Zeit zu liefern, unabhängig davon, ob der Datensatz klein oder groß ist. Konstante Zeit, also Big-O von 1, ist eine absolute Voraussetzung, wann immer Sie etwas in Echtzeit im Sinne der Maschinen-zu-Maschinen-Kommunikation tun wollen. Ohne etwas Konstantes ist es sehr schwierig, manchmal unmöglich, Echtzeitleistung zu erzielen.
Typischerweise ist ein weiterer wichtiger Leistungsaspekt Big-O von N. Big-O von N bedeutet, dass die Komplexität des Algorithmus strikt linear zur Größe des betreffenden Datensatzes ist. Dies erreichen Sie, wenn Sie eine effiziente Implementierung haben, die das Problem durch einmaliges oder eine feste Anzahl von Durchläufen der Daten löst. Eine Big-O von N-Komplexität ist in der Regel nur mit Batch-Ausführung vereinbar. Wenn Sie etwas Online und in Echtzeit wünschen, können Sie nicht den gesamten Datensatz durchlaufen, es sei denn, Sie wissen, dass dieser eine feste Größe besitzt.
Jenseits der Linearität haben wir Big-O von N-Quadrat. Big-O von N-Quadrat ist ein sehr interessanter Fall, denn es ist der Knackpunkt der Produktionsexplosion. Es bedeutet, dass die Komplexität quadratisch in Bezug auf die Größe des Datensatzes wächst, was heißt, dass wenn Sie zehnmal mehr Daten haben, Ihre Leistung 100-mal schlechter wird. Dies ist typischerweise die Art von Leistung, bei der im Prototyp keine Probleme auffallen, weil mit kleinen Datensätzen gearbeitet wird. Auch in der Testphase treten meist keine Probleme auf, da eben kleine Datensätze verwendet werden. Sobald Sie in Produktion gehen, haben Sie jedoch eine Software, die völlig träge reagiert. Sehr häufig in der Welt der Enterprise Software, besonders in der Welt der supply chain Enterprise Software, werden die meisten gravierenden Leistungsprobleme, die im Feld beobachtet werden, tatsächlich durch quadratische Algorithmen verursacht, die nicht identifiziert wurden. Infolgedessen zeigt sich dieses quadratische Verhalten als extrem langsam. Dieses Problem wurde anfangs nicht erkannt, weil moderne Computer recht schnell sind, und N-Quadrat ist nicht so schlimm, solange N ziemlich klein ist. Sobald Sie jedoch mit einem großen, produktionsreifen Datensatz arbeiten, wird es richtig schmerzhaft.
Diese Vorlesung ist tatsächlich die zweite Vorlesung meines vierten Kapitels in dieser Reihe von supply chain Vorlesungen. Im ersten Kapitel, dem Prolog, habe ich meine Ansichten über supply chain sowohl als Forschungsgebiet als auch als Praxis vorgestellt. Was wir gesehen haben, ist, dass supply chain eine große Sammlung von Wicked-Problemen ist, im Gegensatz zu einfachen Problemen. Wicked-Probleme können nicht mit naiven Methoden angegangen werden, da überall widersprüchliche Verhaltensweisen auftreten, weshalb der Methode selbst enorme Aufmerksamkeit zukommt. Die meisten naiven Ansätze scheitern auf spektakuläre Weise. Genau das habe ich im zweiten Kapitel getan, das sich vollständig den Methoden widmet, die geeignet sind, supply chains zu untersuchen und die Praxis des supply chain Managements zu verbessern. Das dritte Kapitel, das noch nicht abgeschlossen ist, zoomt im Wesentlichen auf das, was ich “supply chain personnel” nenne – eine sehr spezifische Methodik, bei der der Fokus auf den Problemen selbst liegt und nicht auf den Lösungen, die man sich zur Problemlösung einfallen lässt. In Zukunft werde ich zwischen Kapitel drei und dem vorliegenden Kapitel, das sich mit den Hilfswissenschaften von supply chain befasst, wechseln.
Während der letzten Vorlesung haben wir gesehen, dass wir für unsere supply chain durch bessere, modernere Rechnerhardware mehr Rechenkapazitäten gewinnen können. Heute betrachten wir das Problem aus einem anderen Blickwinkel – wir suchen nach mehr Rechenkapazitäten, weil wir bessere Software haben. Darum geht es bei Algorithmen.

Eine kurze Zusammenfassung: Die Hilfswissenschaften sind im Wesentlichen eine Perspektive auf supply chain selbst. Die heutige Vorlesung handelt nicht strikt von supply chain; es geht um Algorithmen. Dennoch glaube ich, dass dies für supply chain von grundlegender Bedeutung ist. supply chain ist keine Insel; der Fortschritt, der in supply chain erzielt werden kann, hängt stark von den Fortschritten in anderen angrenzenden Bereichen ab. Ich bezeichne diese Bereiche als die Hilfswissenschaften von supply chain.
Ich glaube, dass die Situation der Beziehung zwischen den medizinischen Wissenschaften und der Chemie im 19. Jahrhundert ziemlich ähnlich ist. Zu Beginn des 19. Jahrhunderts kümmerten sich die medizinischen Wissenschaften überhaupt nicht um die Chemie. Die Chemie war noch das neue Kind am Block und wurde nicht als gültige Option für einen tatsächlichen Patienten angesehen. Spult man ins 21. Jahrhundert vor, so wäre das Argument, dass man ein ausgezeichneter Arzt sein kann, ohne etwas über Chemie zu wissen, völlig absurd. Es ist allgemein anerkannt, dass ein ausgezeichneter Chemiker nicht automatisch einen ausgezeichneten Arzt macht, aber es herrscht Einigkeit darüber, dass man – wenn man nichts über die Körperchemie weiß – im Hinblick auf die modernen medizinischen Wissenschaften unmöglich kompetent sein kann. Meiner Auffassung nach wird im 21. Jahrhundert das Feld supply chain Algorithmen beinahe genauso betrachtet werden wie die Medizin im 19. Jahrhundert die Chemie.

Algorithmen sind ein riesiges Forschungsfeld, ein Zweig der Mathematik, und wir werden heute nur an der Oberfläche dieses Gebiets kratzen. Insbesondere haben sich in diesem Forschungsbereich über Jahrzehnte hinweg beeindruckende Ergebnisse angehäuft. Es mag ein recht theoretisches Feld sein, aber das bedeutet nicht, dass es nur Theorie ist. Tatsächlich ist es ein eher theoretisches Forschungsgebiet, in dem jedoch unzählige Erkenntnisse ihren Weg in die Praxis gefunden haben.
Tatsächlich verwendet jedes Smartphone oder jeder Computer, den Sie heute nutzen, buchstäblich Zehntausende von Algorithmen, die ursprünglich irgendwo veröffentlicht wurden. Diese Erfolgsbilanz ist im Vergleich zur supply chain theory besonders beeindruckend, denn der Großteil der supply chains basiert bislang nicht auf den Erkenntnissen der supply chain theory. Bei modernen Computern und modernen Algorithmen wird praktisch alles, was softwarebezogen ist, vollständig durch all diese jahrzehntelangen Erkenntnisse der algorithmischen Forschung angetrieben. Das steht im Kern fast jedes einzelnen Computers, den wir heute benutzen.
Für die heutige Vorlesung habe ich eine Auswahl an Themen getroffen, die meiner Meinung nach sehr anschaulich das illustrieren, was Sie wissen sollten, um sich dem Thema moderner Algorithmen zu nähern. Zuerst werden wir besprechen, wie wir angeblich optimale Algorithmen tatsächlich übertreffen können, besonders für supply chain. Anschließend werfen wir einen kurzen Blick auf Datenstrukturen, gefolgt von magischen Rezepten, Tensor-Kompression und schließlich Meta-Techniken.
Zunächst möchte ich klarstellen, dass ich mit „Algorithmen für supply chain“ nicht Algorithmen meine, die dazu bestimmt sind, spezifische Probleme der supply chain zu lösen. Die korrekte Perspektive besteht darin, klassische Algorithmen für klassische Probleme zu betrachten und diese klassischen Probleme aus der Perspektive der supply chain erneut zu beleuchten, um zu sehen, ob wir tatsächlich etwas Besseres erreichen können. Die Antwort lautet: Ja, das können wir.
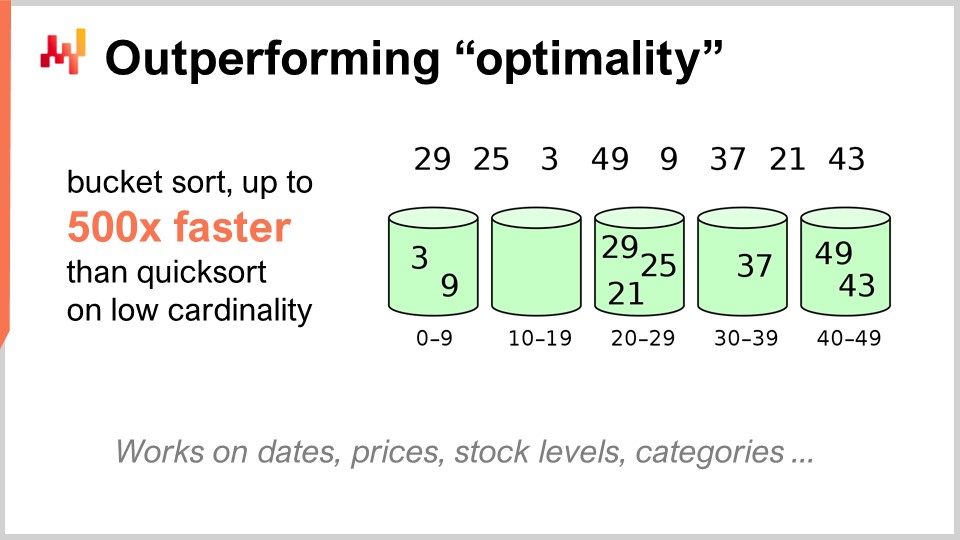
Zum Beispiel ist der Quicksort-Algorithmus laut der allgemeinen Theorie der Algorithmen optimal in dem Sinne, dass man keinen Algorithmus einführen kann, der beliebig besser als Quicksort ist. Insofern ist Quicksort so gut, wie er jemals sein kann. Wenn wir uns jedoch speziell auf supply chain konzentrieren, ist es möglich, atemberaubende Geschwindigkeitssteigerungen zu erzielen. Insbesondere, wenn wir Sortierprobleme betrachten, bei denen die Kardinalität der interessierenden Datensätze niedrig ist, wie etwa Termine, Preise, Lagerbestände oder Kategorien – all das sind Datensätze mit niedriger Kardinalität. Wenn Sie also zusätzliche Annahmen haben, wie etwa eine Situation mit niedriger Kardinalität, dann können Sie den Bucket-Sort verwenden. In der Praxis gibt es zahlreiche Situationen, in denen Sie absolut monumentale Geschwindigkeitssteigerungen erzielen können, beispielsweise 500 Mal schneller als Quicksort. So können Sie um Größenordnungen schneller sein als das vermeintlich Optimale, nur weil Sie sich nicht im allgemeinen Fall, sondern im supply chain-Fall befinden. Das ist etwas sehr Wichtiges, und ich glaube, dass hierin der Kern der beeindruckenden Ergebnisse liegt, die wir durch den Einsatz von Algorithmen für supply chain erzielen können.
Ich bin der Meinung, dass diese Sichtweise aus mindestens zwei Gründen fehlgeleitet ist. Erstens, wie wir gesehen haben, ist nicht unbedingt der Standardalgorithmus von Interesse. Wir haben gesehen, dass es einen vermeintlich optimalen Algorithmus wie Quicksort gibt, aber wenn man dasselbe Problem aus der Perspektive der supply chain betrachtet, kann man tatsächlich massive Geschwindigkeitssteigerungen erzielen. Daher ist es von zentraler Bedeutung, mit Algorithmen vertraut zu sein, wenn auch nur, um die Klassiker neu zu überdenken und enorme Geschwindigkeitsvorteile zu erreichen, gerade weil man sich nicht im allgemeinen Fall, sondern im supply chain-Fall befindet.
Der zweite Grund, warum ich diese Sichtweise als fehlgeleitet erachte, ist, dass es bei Algorithmen sehr um Datenstrukturen geht. Datenstrukturen sind Möglichkeiten, Daten so zu organisieren, dass man effizienter mit ihnen arbeiten kann. Das Interessante daran ist, dass all diese Datenstrukturen eine Art Vokabular bilden, und der Zugang zu diesem Vokabular ist essenziell, um supply chain-Situationen in einer Weise beschreiben zu können, die sich leicht in Software übersetzen lässt. Wenn Sie mit einer Beschreibung in Laientermini beginnen, enden Sie in der Regel mit Dingen, die äußerst schwer in Software umzusetzen sind. Wenn Sie von einem Softwareingenieur erwarten, der nichts von supply chain versteht, dass diese Übersetzung für Sie vornimmt, könnte das ein Rezept für Probleme sein. Es ist tatsächlich viel einfacher, wenn Sie dieses Vokabular kennen, sodass Sie direkt die Begriffe verwenden können, die sich leicht in die Umsetzung Ihrer Ideen in Software übertragen lassen.
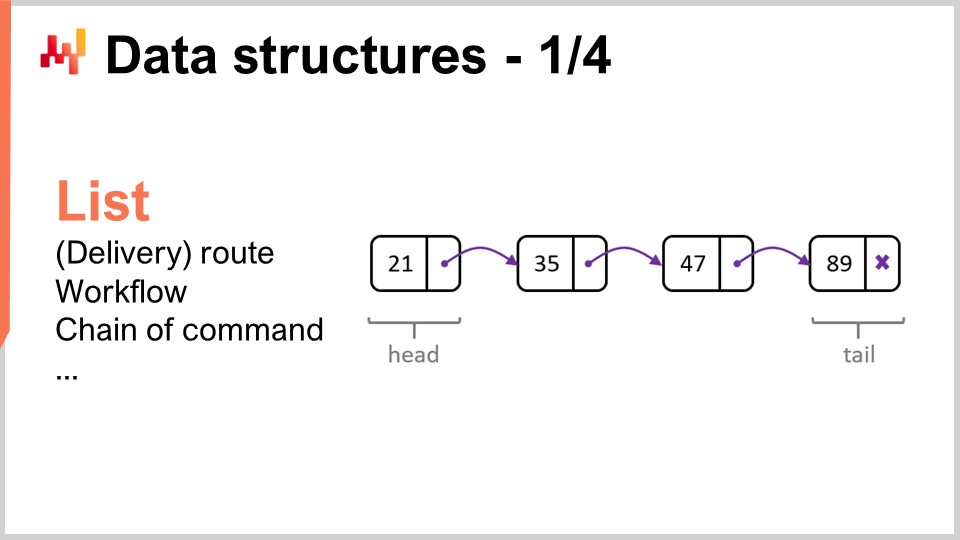
Lassen Sie uns die beliebtesten und einfachsten Datenstrukturen durchgehen. Die erste davon ist die Liste. Eine Liste kann beispielsweise verwendet werden, um eine Lieferroute darzustellen, also die Abfolge der zu tätigen Lieferungen, mit einem Eintrag pro Lieferung. Sie können die Lieferroute fortlaufend nummerieren, während Sie sie abarbeiten. Eine Liste kann auch einen workflow darstellen, also eine Abfolge von Operationen, die benötigt werden, um ein bestimmtes Gerät herzustellen, oder eine Befehlskette, die festlegt, wer welche Entscheidungen treffen soll.
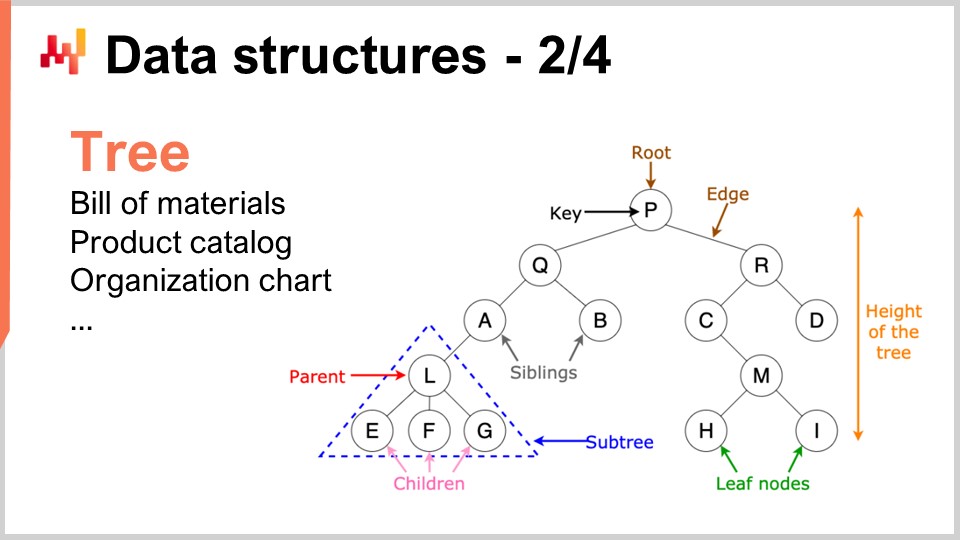
Ähnlich sind Bäume eine weitere allgegenwärtige Datenstruktur. Übrigens sind algorithmische Bäume verkehrt herum angeordnet, mit der Wurzel oben und den Ästen unten. Bäume ermöglichen es, alle Arten von Hierarchien zu beschreiben, und supply chains weisen überall Hierarchien auf. Zum Beispiel ist eine bill of material ein Baum; Sie haben ein Gerät, das Sie herstellen möchten, und dieses Gerät besteht aus Baugruppen. Jede Baugruppe besteht aus Unterbaugruppen, und jede Unterbaugruppe besteht aus Einzelteilen. Wenn Sie die bill of material vollständig aufschlüsseln, erhalten Sie einen Baum. Ebenso hat ein Produktkatalog, in dem Sie Produktfamilien, Produktkategorien, Produkte, Unterkategorien usw. haben, sehr häufig eine baumartige Architektur. Ein Organigramm, mit dem CEO an der Spitze, den Führungskräften auf C-Level darunter und so weiter, wird ebenfalls durch einen Baum dargestellt. Die algorithmische Theorie bietet Ihnen eine Vielzahl von Werkzeugen und Methoden, um Bäume zu verarbeiten und Operationen effizient an Bäumen durchzuführen. Wann immer Sie Daten als Baum darstellen können, verfügen Sie über ein komplettes Arsenal mathematischer Methoden, um effizient mit diesen Bäumen zu arbeiten. Aus diesem Grund ist dies von großem Interesse.
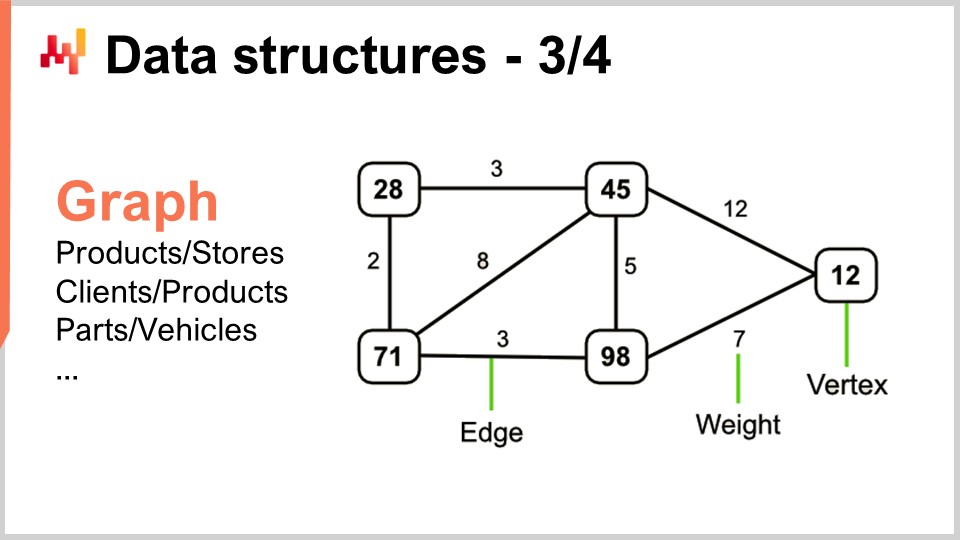
Nun ermöglichen Graphen die Beschreibung aller möglichen Netzwerke. Übrigens ist ein Graph im mathematischen Sinne eine Menge von Knoten und eine Menge von Kanten, wobei die Kanten jeweils zwei Knoten verbinden. Der Begriff „Graph“ mag ein wenig irreführend sein, da er nichts mit Grafiken zu tun hat. Ein Graph ist lediglich ein mathematisches Objekt, keine Zeichnung oder etwas Grafisches. Sobald Sie wissen, wie man nach Graphen sucht, werden Sie feststellen, dass supply chains überall Graphen aufweisen.
Einige Beispiele: Ein Sortiment in einem Einzelhandelsnetzwerk, das im Grunde ein bipartiter Graph ist, verbindet Produkte und Geschäfte. Wenn Sie ein loyalty Programm haben, bei dem Sie aufzeichnen, welcher Kunde welches Produkt über die Zeit gekauft hat, entsteht ein weiterer bipartiter Graph, der Kunden und Produkte verbindet. Im automobilen Aftermarket, wo Sie Reparaturen durchführen müssen, brauchen Sie typischerweise eine Kompatibilitätsmatrix, die Ihnen die Liste der Teile liefert, die mechanisch mit dem betreffenden Fahrzeug kompatibel sind. Diese Kompatibilitätsmatrix ist im Wesentlichen ein Graph. Es gibt eine enorme Menge an Literatur zu allen möglichen Algorithmen, mit denen Sie mit Graphen arbeiten können – daher ist es sehr interessant, wenn Sie ein Problem als von einer Graphstruktur unterstützt charakterisieren können, da alle in der Literatur bekannten Methoden dann sofort zur Verfügung stehen.
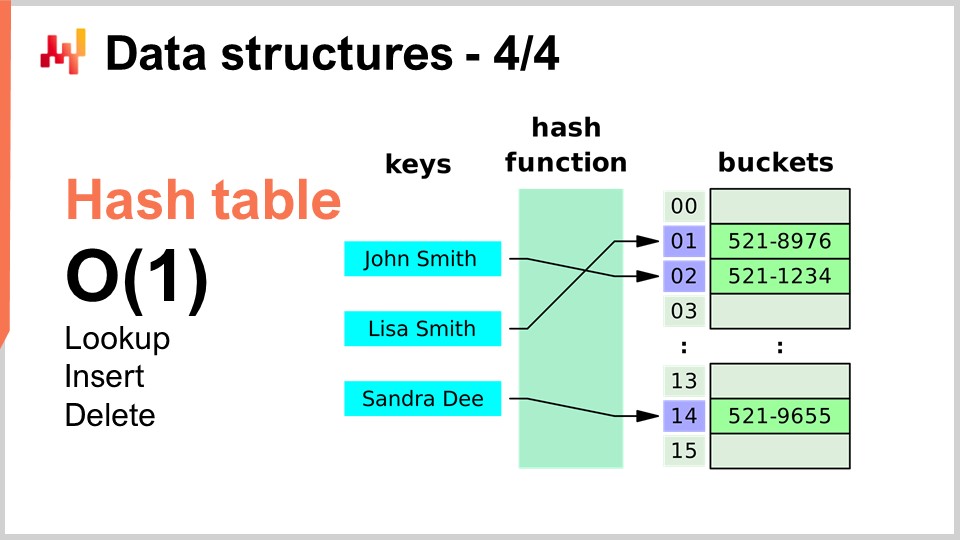
Abschließend möchte ich die letzte Datenstruktur, die ich heute behandle, vorstellen: die Hash-Tabelle. Die Hash-Tabelle ist im Wesentlichen das Schweizer Taschenmesser der Algorithmen. Sie ist nicht neu; keine der zuvor vorgestellten Datenstrukturen ist in irgendeiner Hinsicht neu. Die Hash-Tabelle ist wahrscheinlich die jüngste von allen und stammt aus den 1950er Jahren – also nicht aktuell, aber dennoch ist sie eine unglaublich nützliche Datenstruktur. Es handelt sich um einen Container, der Schlüssel-Wert-Paare enthält. Die Idee ist, dass Sie mit diesem Container eine große Menge an Daten speichern können, und er bietet Ihnen Big-O(1) Leistung beim Suchen, Einfügen und Löschen. Sie haben einen Container, in dem Sie in konstanter Zeit Daten hinzufügen, überprüfen können, ob Daten vorhanden sind (durch Überprüfung des Schlüssels), und gegebenenfalls Daten entfernen können. Das ist sehr interessant und nützlich. Hash-Tabellen sind buchstäblich überall anzutreffen und werden in anderen Algorithmen umfangreich verwendet.
Eines möchte ich noch anmerken, und diesen Punkt werden wir später noch einmal aufgreifen: Die Leistung einer Hash-Tabelle hängt maßgeblich von der Leistung der von Ihnen verwendeten Hash-Funktion ab.

Werfen wir nun einen Blick auf magische Rezepte, und wir wechseln dabei vollständig die Perspektive. Magische Zahlen sind im Grunde ein Anti-Pattern. In der vorherigen Vorlesung, jener über negatives Wissen für supply chain, haben wir besprochen, wie Anti-Patterns typischerweise mit guten Absichten beginnen, aber in unbeabsichtigte Konsequenzen münden, die die angeblichen Vorteile der Lösung zunichte machen. Magische Zahlen sind ein wohlbekanntes Programmier-Anti-Pattern. Dieses Programmier-Anti-Pattern besteht darin, Code so zu schreiben, dass er mit Konstanten übersät ist, die völlig unerwartet erscheinen und Ihre Software sehr schwer wartbar machen. Wenn Sie Unmengen von Konstanten haben, ist oft unklar, warum diese Einschränkungen bestehen und wie sie gewählt wurden.
Normalerweise ist es, wenn man magische Zahlen in einem Programm sieht, besser, all diese Konstanten an einem Ort zu isolieren, wo sie besser verwaltet werden können. Allerdings gibt es Situationen, in denen eine sorgfältige Auswahl von Konstanten etwas völlig Unerwartetes bewirkt, und man nahezu magische, völlig unbeabsichtigte Vorteile durch die Verwendung von Zahlen erzielt, die so wirken, als wären sie vom Himmel gefallen. Genau darum geht es in dem sehr kurzen Algorithmus, den ich hier präsentiere.
Im supply chain möchten wir häufig in der Lage sein, eine Art Simulation zu erreichen. Simulationen oder Monte-Carlo-Prozesse sind einer der grundlegenden Tricks, die Sie in unzähligen supply chain-Situationen einsetzen können. Die Leistung Ihrer Simulation hängt jedoch stark von Ihrer Fähigkeit ab, Zufallszahlen zu generieren. Um Simulationen zu erzeugen, ist in der Regel ein gewisses Maß an erzeugter Zufälligkeit notwendig, und deshalb benötigen Sie einen Algorithmus, um diese Zufälligkeit zu erzeugen. Für Computer handelt es sich typischerweise um Pseudorandomness – es ist keine echte Zufälligkeit, sondern lediglich etwas, das wie Zufallszahlen aussieht und die statistischen Eigenschaften von Zufallszahlen aufweist, aber eigentlich nicht zufällig ist.
Die Frage ist also: Wie effizient können Sie Zufallszahlen generieren? Es stellt sich heraus, dass es einen Algorithmus namens “Shift” gibt, veröffentlicht im Jahr 2003 von George Marsaglia, der ziemlich beeindruckend ist. Dieser Algorithmus erzeugt Zufallszahlen von sehr hoher Qualität, indem er eine vollständige Permutation von 2 hoch 64 minus 1 Bits erzeugt. Er durchläuft alle 64-Bit-Kombinationen, abzüglich einer, wobei die Null als Fixpunkt dient. Dies geschieht im Wesentlichen mit sechs Operationen: drei Binärverschiebungen und drei XOR (exklusiv oder) Operationen, die bitweise Operationen sind. Die Verschiebungen sind ebenfalls bitweise Operationen.
Was wir sehen, ist, dass da drei magische Zahlen in der Mitte stehen: 13, 7 und 17. Übrigens sind alle diese Zahlen Primzahlen; das ist kein Zufall. Es stellt sich heraus, dass, wenn Sie genau diese spezifischen Konstanten wählen, Sie einen ausgezeichneten Zufallszahlengenerator erhalten, der zufällig super schnell ist. Wenn ich super schnell sage, meine ich, dass Sie buchstäblich 10 Megabyte pro Sekunde an Zufallszahlen generieren können. Das ist absolut enorm. Wenn wir zur vorherigen Vorlesung zurückkehren, können wir erkennen, warum dieser Algorithmus auch so effizient ist. Wir haben nicht nur lediglich sechs Anweisungen, die direkt auf von der zugrunde liegenden Hardware, wie dem Prozessor, nativ unterstützte Befehle abgebildet werden, sondern es gibt auch keinen Verzweigungsbefehl. Es gibt keinen Test, was bedeutet, dass dieser Algorithmus nach der Ausführung die maximale Pipeline-Kapazität des Prozessors ausschöpfen wird, weil es keine Verzweigung gibt. Wir können buchstäblich die tiefe Pipeline-Kapazität, die in einem modernen Prozessor vorhanden ist, voll auslasten. Das ist sehr interessant.
Die Frage ist also: Könnten wir andere Zahlen wählen, damit dieser Algorithmus funktioniert? Die Antwort lautet nein. Es gibt nur wenige Dutzend oder vielleicht etwa hundert verschiedene Zahlenkombinationen, die tatsächlich funktionieren würden, während alle anderen Ihnen einen Zufallszahlengenerator von sehr geringer Qualität liefern. Genau hier liegt der magische Aspekt. Sehen Sie, dies ist ein aktueller Trend in der algorithmischen Entwicklung: Etwas völlig Unerwartetes zu finden, bei dem Sie eine halb-magische Konstante entdecken, die Ihnen durch die Kombination sehr unerwarteter binärer Operationen völlig unbeabsichtigte Vorteile verschafft. Die Erzeugung von Zufallszahlen ist von entscheidender Bedeutung für supply chain.

Aber wie gesagt, Hash-Tabellen sind überall anzutreffen, und es ist auch von großem Interesse, eine superleistungsfähige generische Hash-Funktion zu haben. Existiert sie? Ja. Es gibt seit Jahrzehnten ganze Klassen von Hash-Funktionen, aber 2019 wurde ein weiterer Algorithmus veröffentlicht, der rekordverdächtige Leistungen erbringt. Dies ist derjenige, den Sie auf dem Bildschirm sehen können, “WyHash” von Wang Yi. Im Wesentlichen können Sie erkennen, dass die Struktur dem XORShift-Algorithmus sehr ähnlich ist. Es handelt sich um einen Algorithmus, der wie XORShift keine Verzweigung enthält und ebenfalls die XOR-Operation verwendet. Der Algorithmus nutzt sechs Anweisungen: vier XOR-Operationen und zwei Multiply-No-Flags-Operationen.
Multiply-No-Flags ist einfach die Standardmultiplikation zweier 64-Bit-Ganzzahlen, bei der Sie die oberen 64 Bits und die unteren 64 Bits erhalten. Dies ist eine tatsächlich in modernen Prozessoren verfügbare Anweisung, die auf Hardwareebene implementiert ist, sodass sie als nur eine Computeranweisung zählt. Wir haben zwei davon. Wieder haben wir drei magische Zahlen, geschrieben in hexadezimaler Form. Übrigens, diese sind ebenfalls Primzahlen und völlig halb-magisch. Wenn Sie diesen Algorithmus anwenden, erhalten Sie eine absolut hervorragende, nicht-kryptografische Hash-Funktion, die fast mit der Geschwindigkeit von memcpy arbeitet. Sie ist sehr schnell und von größtem Interesse.

Nun wechseln wir zu etwas völlig Anderem. Der Erfolg von deep learning und vielen anderen modernen Methoden des maschinellen Lernens beruht auf einigen wesentlichen algorithmischen Einsichten in Probleme, die massiv durch spezialisierte Rechenhardware beschleunigt werden können. Genau das habe ich in meiner vorherigen Vorlesung angesprochen, als ich über Prozessoren mit superskalaren Befehlen und – wenn ihr mehr wissen wollt – über GPUs und sogar TPUs sprach. Lassen Sie uns diesen Einblick noch einmal aufgreifen, um zu sehen, wie das Ganze eher chaotisch entstanden ist. Ich glaube jedoch, dass sich die relevanten Einsichten in den letzten Jahren kristallisiert haben. Um zu verstehen, wo wir heutzutage stehen, müssen wir zurückgehen zur Einstein-Notation, die vor etwas mehr als einem Jahrhundert von Albert Einstein in einem seiner Aufsätze eingeführt wurde. Die Intuition ist einfach: Man hat einen Ausdruck y, der eine Summe von i = 1 bis i = 3 von c_y mal x_y darstellt. Wir haben Ausdrücke, die so geschrieben sind, und die Intuition der Einstein-Notation besteht darin, in solchen Situationen die Summation vollständig wegzulassen. In Software-Begriffen wäre die Summation eine for-Schleife. Die Idee ist, die Summation ganz wegzulassen und per Konvention über alle sinnvollen Indizes der Variablen i zu summieren.
Diese einfache Intuition führt zu zwei sehr überraschenden, aber positiven Ergebnissen. Das erste ist die Designkorrektheit. Wenn wir die Summe explizit schreiben, riskieren wir, nicht die richtigen Indizes zu verwenden, was in der Software zu Index-Out-of-Bounds-Fehlern führen kann. Indem wir die explizite Summation entfernen und festlegen, dass wir definitionsgemäß alle gültigen Indexpositionen berücksichtigen, erhalten wir einen correct-by-design-Ansatz. Dies allein ist von primärem Interesse und hängt mit der Array-Programmierung zusammen, einem Programmierparadigma, das ich in einer meiner früheren Vorlesungen kurz angesprochen habe.
Die zweite Erkenntnis, die neuer ist und heutzutage von großem Interesse, besteht darin, dass wenn man sein Problem in einer Form formulieren kann, in der die Einstein-Notation anwendbar ist, das Problem in der Praxis von massiver Hardwarebeschleunigung profitieren kann. Dies ist ein bahnbrechendes Element.

Um zu verstehen, warum, gibt es ein sehr interessantes Papier namens “Tensor Comprehensions”, das 2018 vom Facebook-Forschungsteam veröffentlicht wurde. Sie führten den Begriff der Tensor Comprehensions ein. Zunächst möchte ich die beiden Begriffe definieren. Im Bereich der Informatik ist ein Tensor im Wesentlichen eine mehrdimensionale Matrix (in der Physik sind Tensoren jedoch völlig anders). Ein Skalarwert ist ein Tensor nullter Dimension, ein Vektor ist ein Tensor erster Dimension, eine Matrix ist ein Tensor zweiter Dimension, und es gibt auch Tensoren mit noch höheren Dimensionen. Tensoren sind Objekte, an die array-ähnliche Eigenschaften geknüpft sind.
Comprehension ist etwas Ähnliches wie eine Algebra mit den vier Grundoperationen – plus, minus, mal und geteilt – sowie weiteren Operationen. Sie ist umfangreicher als die gewöhnliche arithmetische Algebra; deshalb gibt es eine Tensor Comprehension anstelle einer Tensoralgebra. Sie ist umfassender, aber nicht so ausdrucksstark wie eine vollwertige Programmiersprache. Wenn man eine Comprehension verwendet, ist diese restriktiver als eine komplette Programmiersprache, in der man alles machen kann, was man möchte.
Die Idee ist, dass, wenn man sich die MV-Funktion (def MV) ansieht, es grundsätzlich eine Funktion ist, wobei MV für matrix-vector steht. In diesem Fall handelt es sich um eine Matrix-Vektor-Multiplikation, und diese Funktion führt im Wesentlichen eine Multiplikation zwischen der Matrix A und dem Vektor X durch. In dieser Definition kommt die Einstein-Notation zum Einsatz: Wir schreiben C_i = A_ik * X_k. Welche Werte sollen wir für i und k wählen? Die Antwort lautet: alle gültigen Kombinationen dieser Indizes. Wir nehmen alle gültigen Indexwerte, summieren sie, und in der Praxis erhalten wir so eine Matrix-Vektor-Multiplikation.
Am unteren Bildschirmrand sieht man dieselbe MV-Methode, die mit for-Schleifen umgeschrieben wurde, wobei die Wertebereiche explizit angegeben sind. Die entscheidende Leistung des Facebook-Forschungsteams besteht darin, dass wann immer man ein Programm mit dieser Syntax der Tensor Comprehension schreiben kann, sie einen Compiler entwickelt haben, der es ermöglicht, umfangreich von der Hardwarebeschleunigung durch GPUs zu profitieren. Grundsätzlich erlauben sie es, jedes Programm, das man mit dieser Tensor-Comprehension-Syntax schreiben kann, zu beschleunigen. Wann immer man ein solches Programm schreibt, profitiert man von massiver Hardwarebeschleunigung – und wir sprechen hier von etwas, das zwei Größenordnungen schneller ist als ein herkömmlicher Prozessor. Dies ist ein beeindruckendes Ergebnis für sich.

Nun werfen wir einen Blick darauf, was wir aus der supply chain-Perspektive mit diesem Ansatz erreichen können. Ein zentrales Interessensgebiet der modernen supply chain-Praxis ist probabilistic forecasting. Probabilistic forecasting, das ich in einer früheren Vorlesung behandelt habe, basiert auf der Idee, dass man keine Punktprognose erstellt, sondern vielmehr alle verschiedenen Wahrscheinlichkeiten für eine interessierende Variable vorhersagt. Nehmen wir zum Beispiel eine Durchlaufzeit Prognose. Man möchte seine Durchlaufzeit vorhersagen und eine probabilistische Durchlaufzeit-Prognose erstellen.
Nehmen wir nun an, dass sich Ihre Durchlaufzeit in die Fertigungsdurchlaufzeit und die Transportdurchlaufzeit zerlegen lässt. Tatsächlich haben Sie höchstwahrscheinlich eine probabilistische Prognose für die Fertigungsdurchlaufzeit, die eine diskrete Zufallsvariable darstellt und Ihnen die Wahrscheinlichkeit angibt, dass eine Dauer von einem Tag, zwei Tagen, drei Tagen, vier Tagen usw. auftritt. Man kann es sich als ein großes Histogramm vorstellen, das die Wahrscheinlichkeiten für das Auftreten dieser Dauer in der Fertigungsdurchlaufzeit zeigt. Anschließend gibt es einen ähnlichen Prozess für die Transportdurchlaufzeit, bei dem eine weitere diskrete Zufallsvariable eine probabilistische Prognose liefert.
Nun möchten Sie die gesamte Durchlaufzeit berechnen. Würden die prognostizierten Durchlaufzeiten als Zahlen vorliegen, könnte man einfach addieren. Da es sich jedoch nicht um Zahlen handelt, sondern um Wahrscheinlichkeitsverteilungen, müssen wir diese beiden Verteilungen kombinieren, um eine dritte Wahrscheinlichkeitsverteilung zu erhalten – die Wahrscheinlichkeitsverteilung der gesamten Durchlaufzeit. Es stellt sich heraus, dass, wenn wir annehmen, dass die beiden Durchlaufzeiten – Fertigungsdurchlaufzeit und Transportdurchlaufzeit – unabhängig voneinander sind, die Operation, mit der wir diese Zufallsvariablen summieren, eine eindimensionale Faltung ist. Das mag komplex klingen, ist es aber in Wirklichkeit nicht. Was ich implementiert habe – und was Sie auf dem Bildschirm sehen – ist die Implementierung einer eindimensionalen Faltung zwischen einem Vektor, der das Histogramm der Wahrscheinlichkeiten der Fertigungsdurchlaufzeit (A) darstellt, und dem Histogramm, das die Wahrscheinlichkeiten der Transportdurchlaufzeit (B) repräsentiert. Das Ergebnis ist die gesamte Zeit, die die Summe dieser probabilistischen Durchlaufzeiten darstellt. Verwendet man die Tensor-Comprehension-Notation, kann dies in einem sehr kompakten Einzeiler-Algorithmus ausgedrückt werden.
Wenn wir nun zur Big-O-Notation zurückkehren, die ich zu Beginn dieser Vorlesung eingeführt habe, sehen wir, dass wir im Grunde einen quadratischen Algorithmus haben. Es ist Big-O von N², wobei N die charakteristische Größe der Arrays für A und B darstellt. Wie erwähnt, ist quadratische Performance ein kritischer Punkt bei Prognoseproblemen. Was können wir also tun, um dieses Problem anzugehen? Zunächst müssen wir bedenken, dass es sich um ein supply chain-Problem handelt und wir das Gesetz der kleinen Zahlen zu unserem Vorteil nutzen können. Wie in der vorherigen Vorlesung besprochen, drehen sich supply chains überwiegend um kleine Zahlen. Wenn wir uns die Durchlaufzeiten ansehen, können wir vernünftigerweise davon ausgehen, dass diese Durchlaufzeiten kleiner als, sagen wir, 400 Tage sind. Für dieses Wahrscheinlichkeits-Histogramm ist das bereits eine recht lange Zeit.
Somit verbleibt uns ein Big-O von N², allerdings mit einem N, das kleiner als 400 ist. 400 kann durchaus groß sein, denn 400 mal 400 ergeben 160.000. Das ist eine beträchtliche Zahl, und bedenken Sie, dass das Addieren in dieser Wahrscheinlichkeitsverteilung eine sehr grundlegende Operation ist. Sobald wir mit probabilistic forecasting beginnen, wollen wir unsere Prognosen auf verschiedene Weise kombinieren – und höchstwahrscheinlich werden wir Millionen dieser Faltungen durchführen, da diese Faltungen im Grunde nichts anderes sind als verherrlichte Additionen im Bereich der Zufallsvariablen. Selbst wenn wir N also auf weniger als 400 beschränken, ist es von großem Interesse, Hardwarebeschleunigung einzusetzen – und genau das können wir mit Tensor Comprehension erreichen.
Das Wichtigste, woran man sich erinnern sollte, ist, dass sobald man diesen Algorithmus formulieren kann, man das Wissen über die supply chain-Konzepte nutzen sollte, um die anwendbaren Annahmen zu präzisieren, und anschließend die verfügbaren Toolkits einsetzt, um von Hardwarebeschleunigung zu profitieren.

Nun wollen wir über Meta-Techniken sprechen. Meta-Techniken sind von großem Interesse, weil sie auf bestehende Algorithmen aufgesetzt werden können. Wenn man also einen Algorithmus hat, besteht die Chance, dass man eine dieser Meta-Techniken zur Leistungsverbesserung einsetzen kann. Die erste wesentliche Erkenntnis ist die Kompression, schlichtweg, weil kleinere Daten eine schnellere Verarbeitung bedeuten. Wie wir in der vorherigen Vorlesung gesehen haben, gibt es keinen einheitlichen Speicherzugriff. Wenn Sie auf mehr Daten zugreifen möchten, müssen Sie verschiedene Arten von physischem Speicher ansprechen, und je größer der Speicher wird, desto weniger effizient sind diese Speichertypen. Der L1-Cache im Prozessor ist sehr klein – etwa 64 Kilobyte –, aber sehr schnell. Der RAM, also der Hauptspeicher, ist mehrere hundert Mal langsamer als dieser kleine Cache, aber man kann buchstäblich ein Terabyte RAM haben. Daher ist es von großem Interesse, sicherzustellen, dass Ihre Daten so klein wie möglich sind, da dies fast immer zu schnelleren Algorithmen führt. Es gibt eine Reihe von Tricks, die Sie in dieser Hinsicht anwenden können.
Zunächst können Sie Ihre Daten bereinigen und ordnen. Dies fällt in den Bereich der Unternehmenssoftware. Wenn Sie einen Algorithmus haben, der mit Daten arbeitet, gibt es oft viele ungenutzte Daten, die nicht zur Lösung des eigentlichen Problems beitragen. Es ist essentiell, dafür zu sorgen, dass die relevanten Daten nicht mit solchen vermischt werden, die ignoriert werden.
Die zweite Idee ist das Bitpacking. Es gibt zahlreiche Situationen, in denen Sie einige Flags in andere Elemente – beispielsweise in Zeiger – einbetten können. Man mag einen 64-Bit-Zeiger besitzen, aber es ist sehr selten notwendig, den vollständigen 64-Bit-Adressbereich auszuschöpfen. Sie können einige Bits Ihres Zeigers opfern, um Flags einzufügen, wodurch Sie Ihre Daten nahezu ohne Leistungsverlust minimieren können.
Außerdem können Sie die Genauigkeit anpassen. Benötigen Sie in der supply chain 64 Bit Fließkommagenauigkeit? Es ist sehr selten, dass Sie diese Präzision tatsächlich benötigen. In der Regel genügen 32 Bit, und es gibt sogar viele Situationen, in denen 16 Bit ausreichend sind. Vielleicht denken Sie, dass eine Reduktion der Präzision unbedeutend ist, aber häufig, wenn Sie die Datenmenge um den Faktor zwei reduzieren können, beschleunigt sich Ihr Algorithmus nicht bloß um den Faktor 2, sondern um den Faktor 10. Das Packen der Daten bringt völlig nichtlineare Vorteile in Bezug auf die Ausführungsgeschwindigkeit.
Schließlich gibt es noch die Entropiekodierung, die im Grunde genommen einer Kompression entspricht. Allerdings möchten Sie nicht zwangsläufig Algorithmen einsetzen, die so effizient komprimieren wie beispielsweise der Algorithmus, der für ZIP-Archive verwendet wird. Vielmehr wünschen Sie sich etwas, das in puncto Kompression vielleicht etwas weniger effizient, dafür aber in der Ausführung wesentlich schneller ist.
Die Kompression basiert im Wesentlichen auf der Idee, dass man einen kleinen Mehrverbrauch an CPU-Ressourcen in Kauf nehmen kann, um den Druck auf den Speicher zu verringern – und in fast allen Fällen ist genau dies der entscheidende Trick.
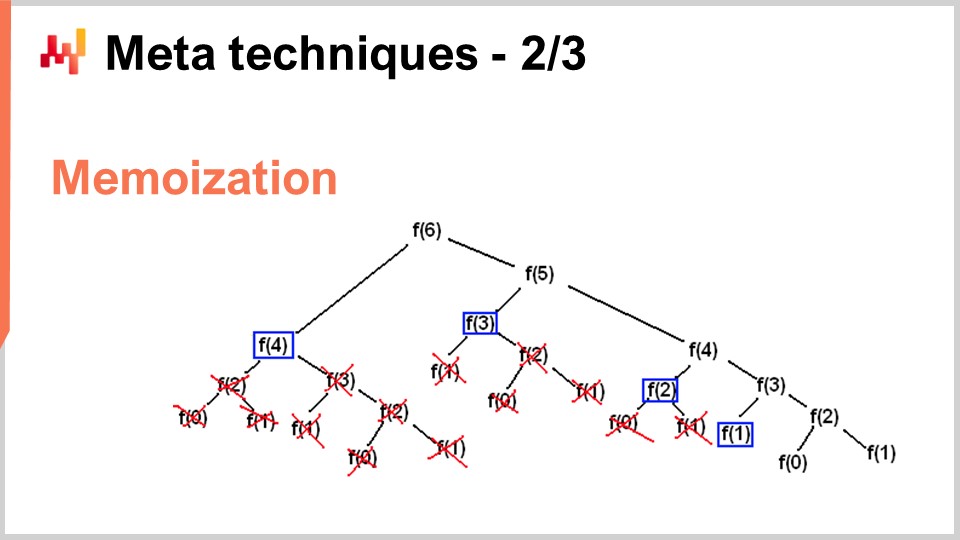
Allerdings gibt es Situationen, in denen Sie genau das Gegenteil erreichen möchten – also Speicher opfern, um den CPU-Verbrauch drastisch zu senken. Genau das wird mit dem Memoization-Trick erreicht. Memoization beruht darauf, dass, wenn eine Funktion während der Ausführung Ihrer Lösung viele Male mit exakt denselben Eingabewerten aufgerufen wird, es nicht nötig ist, die Funktion erneut zu berechnen. Stattdessen können Sie das Ergebnis speichern, beispielsweise in einer Hashtabelle, und beim erneuten Aufruf prüfen, ob das Ergebnis bereits vorhanden ist. Wenn die Funktion, die Sie memoisieren, sehr rechenintensiv ist, können Sie eine massive Beschleunigung erzielen. Besonders interessant wird es, wenn Sie Memoization nicht im Hauptspeicher einsetzen – denn wie in der vorherigen Vorlesung gesehen, ist DRAM sehr teuer –, sondern die Ergebnisse auf Festplatten oder SSDs ablegen, die günstig und reichlich vorhanden sind. Die Idee ist, SSDs gegen eine Reduzierung des CPU-Drucks einzutauschen, was in gewisser Weise genau das Gegenteil der zuvor beschriebenen Kompression darstellt.
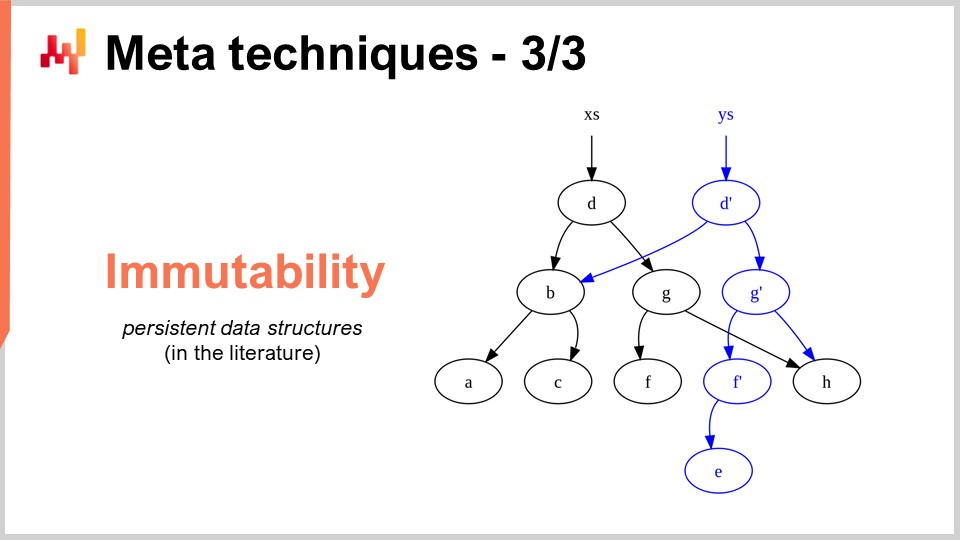
Die letzte Meta-Technik ist die Immutabilität. Unveränderliche (immutable) Datenstrukturen sind im Grunde solche, die nie modifiziert werden. Die Idee ist, dass Änderungen darüber “geschichtet” werden. Beispielsweise gibt eine immutable Hashtabelle, wenn ein Element hinzugefügt wird, eine neue Hashtabelle zurück, die alles der alten Hashtabelle plus das neue Element enthält. Die naive Methode, dies zu erreichen, wäre, die gesamte Datenstruktur zu kopieren und die Kopie zurückzugeben – was jedoch sehr ineffizient ist. Der entscheidende Gedanke bei unveränderlichen Datenstrukturen ist, dass bei einer Modifikation eine neue Datenstruktur zurückgegeben wird, die nur die Änderung implementiert, während alle unberührten Teile der alten Datenstruktur wiederverwendet werden.
Fast alle klassischen Datenstrukturen – wie Listen, Bäume, Graphen und Hashtabellen – haben ihre unveränderlichen Gegenstücke. In vielen Situationen ist es von großem Vorteil, diese zu verwenden. Übrigens gibt es moderne Programmiersprachen, die vollkommen auf Immutabilität setzen, wie zum Beispiel Clojure, falls Ihnen diese Sprache bekannt ist.
Warum ist das von großem Interesse? Erstens, weil es die Parallelisierung von Algorithmen massiv vereinfacht. Wie wir in der vorherigen Vorlesung gesehen haben, ist es bei allgemeinen Desktop-Prozessoren nicht möglich, einen Prozessor zu finden, der mit 100 GHz läuft. Was Sie jedoch finden können, ist eine Maschine mit 50 Kernen, von denen jeder mit 2 GHz arbeitet. Wenn Sie diese vielen Kerne nutzen möchten, müssen Sie Ihre Ausführung parallelisieren, und dann läuft Ihre Parallelisierung Gefahr, sehr fiese Fehler – sogenannte Race Conditions – hervorzurufen. Es wird sehr schwierig zu erkennen, ob der von Ihnen geschriebene Algorithmus korrekt ist, da möglicherweise mehrere Prozessoren gleichzeitig versuchen, in denselben Speicherbereich des Computers zu schreiben.
Wenn Sie jedoch unveränderliche Datenstrukturen haben, passiert das per Design nie – einfach weil, sobald eine Datenstruktur existiert, sie sich niemals ändert, sondern nur eine neue Datenstruktur entsteht. Dadurch können Sie mit dem unveränderlichen Ansatz eine massive Leistungssteigerung erzielen, da Sie parallele Versionen Ihrer Algorithmen leichter implementieren können. Bedenken Sie, dass in der Regel der Engpass bei der Implementierung algorithmischer Beschleunigungen die Zeit ist, die benötigt wird, um die Algorithmen tatsächlich umzusetzen. Wenn Sie etwas haben, das es Ihnen per Design ermöglicht, ein gewisses furchtloses Nebenläufigkeitsprinzip anzuwenden, können Sie algorithmische Beschleunigungen viel schneller realisieren – mit weniger Ressourcen in Bezug auf die Anzahl der beteiligten Programmierer. Ein weiterer wichtiger Vorteil unveränderlicher Datenstrukturen ist, dass sie die Fehlersuche erheblich erleichtern. Wenn Sie eine Datenstruktur destruktiv verändern und dabei auf einen Fehler stoßen, kann es sehr schwierig sein nachzuvollziehen, wie es dazu kam. Mit einem Debugger kann es ein ziemliches Ärgernis sein, das Problem genau zu lokalisieren. Das Interessante an unveränderlichen Datenstrukturen ist, dass Änderungen nicht destruktiv erfolgen, sodass Sie die vorherige Version der Datenstruktur einsehen und leichter nachvollziehen können, wie es zu dem Punkt kam, an dem ein inkorrektes Verhalten auftritt.

Zusammenfassend können sich bessere Algorithmen wie Superkräfte anfühlen. Mit besseren Algorithmen holen Sie mehr aus derselben Computerhardware heraus, und diese Vorteile sind unbegrenzt. Es ist eine einmalige Anstrengung, und danach haben Sie einen unbegrenzten Mehrwert, da Sie Zugang zu überlegenen Rechenkapazitäten erlangt haben – bedenkt man die gleiche Menge an Rechenressourcen, die einem bestimmten supply chain Problem von Interesse zugeordnet sind. Ich glaube, dass diese Perspektive Möglichkeiten für massive Verbesserungen im supply chain management bietet.
Wenn wir uns ein völlig anderes Gebiet ansehen, wie beispielsweise Videospiele, haben diese ihre eigenen algorithmischen Traditionen und Erkenntnisse entwickelt, die dem Spielerlebnis gewidmet sind. Die atemberaubende Grafik, die Sie mit modernen Videospielen erleben, ist das Produkt einer Gemeinschaft, die Jahrzehnte damit verbracht hat, den gesamten Algorithmus-Stack neu zu überdenken, um die Qualität des Spielerlebnisses zu maximieren. In der Gaming-Welt geht es nicht darum, ein 3D-Modell zu haben, das aus physikalischer oder wissenschaftlicher Sicht korrekt ist, sondern darum, die wahrgenommene Qualität des grafischen Erlebnisses für den Spieler zu maximieren – wofür Algorithmen bis ins kleinste Detail optimiert wurden, um beeindruckende Ergebnisse zu erzielen.
Ich glaube, dass eine derartige Arbeit für supply chains gerade erst begonnen hat. Enterprise supply chain Software steckt fest, und nach meiner eigenen Wahrnehmung nutzen wir nicht einmal 1 % dessen, was moderne Computerhardware für uns leisten kann. Die meisten Chancen liegen noch vor uns und können durch Algorithmen erschlossen werden – nicht nur durch supply chain Algorithmen wie beispielsweise Fahrzeug-Routing-Algorithmen, sondern auch indem wir klassische Algorithmen aus einer supply chain Perspektive neu überdenken, um massiven Geschwindigkeitszuwachs zu erzielen.

Nun werde ich einen Blick auf die Fragen werfen.
Frage: Sie haben über die supply chain-spezifischen Details gesprochen, wie zum Beispiel kleine Zahlen. Wenn wir im Voraus wissen, dass wir bei all unseren potenziellen Entscheidungen nur mit kleinen Zahlen zu tun haben, welche Art von Vereinfachung bringt das mit sich? Zum Beispiel: Wenn wir wissen, dass wir höchstens einen oder zwei Container bestellen können, fällt Ihnen ein konkretes Beispiel ein, wie sich dies auf das Granularitätsniveau ganzheitlicher Prognosen auswirken würde, die zur Berechnung der Lagerbelohnungsfunktion verwendet werden?
Zunächst einmal ist alles, was ich heute präsentiert habe, bei Lokad in Produktion. All diese Erkenntnisse sind – auf die eine oder andere Weise – sehr gut auf supply chain anwendbar, weil sie bei Lokad in der Produktion eingesetzt werden. Sie müssen sich bewusst sein, dass das, was Sie von moderner Software erhalten, nicht darauf optimiert wurde, das Potenzial der Computerhardware voll auszuschöpfen. Denken Sie nur daran, dass wir, wie ich in meiner letzten Vorlesung gezeigt habe, heutzutage Computer haben, die tausendmal leistungsfähiger sind als die Computer vor einigen Jahrzehnten. Laufen sie tausendmal schneller? Nein. Können sie Probleme lösen, die fantastischerweise viel komplexer sind als die, die wir vor einigen Jahrzehnten hatten? Nein. Unterschätzen Sie also nicht das enorme Verbesserungspotenzial.
Der Bucketsort, den ich in dieser Vorlesung vorgestellt habe, ist ein einfaches Beispiel. In der supply chain gibt es Sortieroperationen nahezu überall, und soweit ich weiß, ist es sehr selten, dass irgendeine Enterprise-Software spezialisierte Algorithmen einsetzt, die hervorragend zu supply chain-Situationen passen. Nun, wenn wir wissen, dass wir ein oder zwei Container haben, nutzen wir diese Elemente bei Lokad? Ja, das tun wir ständig, und es gibt unzählige Tricks, die auf dieser Ebene implementiert werden können.
Die Tricks finden in der Regel auf einer niedrigeren Ebene statt, und die Vorteile fließen dann in die Gesamtlösung ein. Man muss daran denken, Probleme des Container-Füllens in all ihre Teilprobleme zu zerlegen. Sie können Vorteile erzielen, indem Sie die Ideen und Tricks anwenden, die ich heute auf der unteren Ebene vorgestellt habe.
Beispielsweise, welche Art von numerischer Präzision benötigen wir, wenn wir über Container sprechen? Vielleicht genügen 16-Bit-Zahlen mit einer Genauigkeit von 16 Bit. Dadurch werden die Daten kleiner. Wie viele unterschiedliche Produkte bestellen wir? Vielleicht bestellen wir nur ein paar tausend verschiedene Produkte, sodass wir den Bucketsort einsetzen können. Die Wahrscheinlichkeitsverteilung bezieht sich auf eine kleinere Zahl – theoretisch könnten wir Histogramme haben, die von null Einheiten, über eine Einheit, drei Einheiten bis hin zu unendlich reichen, aber gehen wir wirklich bis ins Unendliche? Nein, das tun wir nicht. Vielleicht können wir intelligente Annahmen darüber treffen, dass es sehr selten vorkommt, dass wir auf ein Histogramm stoßen, in dem wir mehr als 1.000 Einheiten erreichen. Wenn das der Fall ist, können wir approximieren. Wir benötigen nicht unbedingt eine Genauigkeit von zwei Einheiten, wenn es um einen Container geht, der 1.000 Einheiten enthält. Wir können approximieren und ein Histogramm mit größeren Buckets und Ähnlichem verwenden. Es geht, würde ich sagen, nicht so sehr darum, algorithmische Prinzipien wie tensor comprehension einzuführen, die unglaublich sind, weil sie alles auf eine sehr coole Art vereinfachen. Allerdings führen die meisten algorithmischen Beschleunigungen letztlich zu einem schnelleren, aber etwas komplizierteren Algorithmus. Er ist nicht unbedingt einfacher, denn normalerweise ist der einfachste Algorithmus auch etwas ineffizient. Ein passenderer Algorithmus für einen bestimmten Fall mag etwas länger zu schreiben und komplexer sein, aber letztlich wird er schneller laufen. Das ist nicht immer so, wie wir bei den magischen Rezepten gesehen haben, aber was ich zeigen wollte, war, dass wir die grundlegenden Bausteine dessen, was wir tun, neu überdenken müssen, um tatsächlich Enterprise-Software zu entwickeln.
Frage: Wie weitreichend sind diese Erkenntnisse bei ERP Anbietern, APS und Best-of-Breeds wie GTA implementiert?
Das Interessante ist, dass diese Erkenntnisse im Grunde – die meisten davon – völlig unvereinbar mit transaktionaler Software sind. Die meisten Enterprise-Softwarelösungen basieren auf einem Kern, der eine transaktionale Datenbank ist, und alles wird über diese Datenbank abgewickelt. Diese Datenbank ist keine speziell für supply chain entwickelte Datenbank; sie ist eine generische Datenbank, die in der Lage sein soll, mit allen möglichen Situationen umzugehen, an die Sie denken können – von Finanzen über wissenschaftliches Rechnen bis hin zu medizinischen Aufzeichnungen und mehr.
Das Problem ist, dass wenn die Software, die Sie betrachten, im Kern eine transaktionale Datenbank besitzt, die von mir vorgeschlagenen Erkenntnisse per Design nicht umgesetzt werden können. Es ist gewissermaßen Spiel aus. Wenn Sie sich Videospiele ansehen, wie viele davon basieren auf einer transaktionalen Datenbank? Die Antwort ist null. Warum? Weil man keine gute Grafikleistung auf Basis einer transaktionalen Datenbank realisieren kann. Computergrafik lässt sich in einer transaktionalen Datenbank nicht umsetzen.
Eine transaktionale Datenbank ist zwar sehr nützlich, da sie Transaktionalität bietet, aber sie schließt Sie in eine Welt ein, in der nahezu alle algorithmischen Beschleunigungen, an die Sie denken könnten, schlichtweg nicht anwendbar sind. Ich glaube, wenn wir über APS nachdenken, gibt es an diesen Systemen nichts Fortschrittliches. Sie sind seit Jahrzehnten in der Vergangenheit festgefahren, weil sie im Kern komplett um eine transaktionale Datenbank herum entworfen wurden, die sie daran hindert, einige der in den letzten vermutlich vier Jahrzehnten im Bereich der Algorithmen gewonnenen Erkenntnisse zu nutzen.
Das ist der Kern des Problems im Bereich der Enterprise-Software. Die Designentscheidungen, die Sie im ersten Monat der Gestaltung Ihres Produkts treffen, werden Sie Jahrzehnte lang verfolgen – im Grunde genommen bis ans Ende der Zeit. Sobald Sie sich für ein bestimmtes Design Ihres Produkts entschieden haben, können Sie nicht einfach ein Upgrade durchführen; Sie sind damit festgelegt. Genauso wie man ein Auto nicht einfach so zu einem Elektroauto umbauen kann – wenn Sie ein wirklich gutes Elektroauto wollen, müssen Sie das Auto komplett um die Idee herum neu konzipieren, dass der Antriebsstrang elektrisch sein wird. Es geht nicht einfach darum, den Motor auszutauschen und zu sagen: “Hier ist ein Elektroauto.” So funktioniert das nicht. Dies ist eines dieser grundlegenden Designprinzipien, bei denen, sobald Sie sich dazu entschlossen haben, ein Elektroauto zu produzieren, Sie alles rund um den Motor neu überdenken müssen, damit es passt. Leider können ERPs und APS, die stark datenbankzentriert sind, keine dieser Erkenntnisse nutzen, fürchte ich. Es ist immer möglich, eine isolierte Blase zu schaffen, in der Sie von diesen Tricks profitieren, aber es wird immer ein angebundenes Add-on bleiben; es wird nie zum Kernsystem werden.
Bezüglich der beeindruckenden Fähigkeiten von Blue Yonder bitte ich um Nachsicht, da Lokad ein direkter Konkurrent von Blue Yonder ist und es mir schwerfällt, vollkommen unvoreingenommen zu sein. Im Enterprise-Software-Markt muss man absurd kühne Behauptungen aufstellen, um wettbewerbsfähig zu bleiben. Ich bin nicht überzeugt, dass diesen Behauptungen irgendeine Substanz zugrunde liegt. Ich stelle die Annahme infrage, dass irgendjemand in diesem Markt etwas vorzuweisen hat, das als beeindruckend gilt.
Wenn Sie etwas Atemberaubendes und ultrabeindruckendes sehen wollen, schauen Sie sich die neueste Demo der Unreal Engine oder spezialisierte Videospiel-Algorithmen an. Betrachten Sie die Computergrafik auf der nächsten PlayStation 5-Hardware – sie ist absolut beeindruckend. Haben wir im Bereich der Enterprise-Software etwas in derselben Liga technologischer Errungenschaften? Was Lokad betrifft, habe ich eine stark voreingenommene Meinung, aber betrachtet man den Markt allgemein, so sehe ich ein Meer von Menschen, die seit Jahrzehnten versuchen, relationale Datenbanken maximal auszureizen. Manchmal bringen sie andere Arten von Datenbanken ins Spiel, wie etwa Graph-Datenbanken, aber das verfehlt vollkommen den Kern der von mir präsentierten Erkenntnisse. Es liefert nichts Substanzielles, um der Welt der supply chain einen Mehrwert zu bieten.
Die zentrale Botschaft für das Publikum ist, dass es eine Frage des Designs ist. Wir müssen sicherstellen, dass die anfänglichen Entscheidungen, die in das Design Ihrer Enterprise-Software eingeflossen sind, nicht derart beschaffen sind, dass sie per Design verhindern, dass diese Techniken überhaupt eingesetzt werden können.
Die nächste Vorlesung findet in drei Wochen statt, am Mittwoch um 15 Uhr Pariser Zeit. Es wird der 13. Juni sein, und wir werden das dritte Kapitel erneut aufgreifen, das sich mit supply chain personnel, überraschenden Persönlichkeitseigenschaften und fiktiven Unternehmen beschäftigt. Nächstes Mal werden wir über Käse sprechen. Bis dann!


