Probabilistische Vorhersage für Supply Chain - Lecture 5.2

00:01 Einführung
02:18 Die moderne Vorhersage
06:37 Probabilistisch ausflippen
11:58 Die bisherige Geschichte
15:10 Wahrscheinlicher Plan für heute
17:18 Biestarium der Vorhersagen
28:10 Metriken - CRPS - 1/2
33:21 Metriken - CRPS - 2/2
37:20 Metriken - Monge-Kantorovich
42:07 Metriken - likelihood - 1/3
47:23 Metriken - likelihood - 2/3
51:45 Metriken - likelihood - 3/3
55:03 1D Verteilungen - 1/4
01:01:13 1D Verteilungen - 2/4
01:06:43 1D Verteilungen - 3/4
01:15:39 1D Verteilungen - 4/4
01:18:24 Generatoren - 1/3
01:24:00 Generatoren - 2/3
01:29:23 Generatoren - 3/3
01:37:56 Bitte warten Sie, während wir Sie ignorieren
01:40:39 Fazit
01:43:50 Anstehende Vorlesung und Publikumsfragen

Beschreibung

Eine Vorhersage gilt als probabilistisch statt deterministisch, wenn sie eine Menge von Wahrscheinlichkeiten enthält, die allen möglichen zukünftigen Ergebnissen zugeordnet sind, anstatt ein bestimmtes Ergebnis als die Vorhersage festzulegen. Probabilistische Vorhersagen sind besonders wichtig, wenn die Unsicherheit irreduzibel ist – was fast immer der Fall ist, wenn komplexe Systeme betroffen sind. Für supply chains sind probabilistische Vorhersagen unerlässlich, um robuste Entscheidungen angesichts unsicherer zukünftiger Bedingungen zu treffen.

Vollständiges Transkript

Willkommen zu dieser Reihe von supply chain Vorträgen. Ich bin Joannes Vermorel, und heute präsentiere ich “Probabilistic Forecasting for Supply Chain.” Probabilistische Vorhersagen sind einer der wichtigsten – wenn nicht sogar der wichtigste – Paradigmenwechsel in über einem Jahrhundert statistischer Vorhersage Wissenschaft. Dennoch ist es auf technischer Ebene größtenteils dasselbe. Wenn wir uns probabilistische Vorhersagemodelle oder deren nicht-probabilistische Alternativen ansehen, handelt es sich um dieselbe Statistik, dieselben Wahrscheinlichkeiten. Probabilistische Vorhersagen spiegeln einen Wandel in der Art und Weise wider, wie wir selbst über Vorhersagen denken sollten. Der größte Wandel, den probabilistische Vorhersagen für supply chain mit sich bringen, liegt nicht in der Vorhersagewissenschaft. Der größte Wandel liegt in der Art und Weise, wie supply chains betrieben und optimiert werden, wenn prädiktive Modelle zum Einsatz kommen.

Das Ziel der heutigen Vorlesung ist eine sanfte technische Einführung in die probabilistische Vorhersage. Am Ende dieser Vorlesung sollten Sie in der Lage sein zu verstehen, worum es bei probabilistischen Vorhersagen geht, wie man probabilistische Vorhersagen von nicht-probabilistischen Vorhersagen unterscheidet, wie man die Qualität einer probabilistischen Vorhersage bewertet und sogar in der Lage ist, ein eigenes Einsteiger-Modell für probabilistische Vorhersagen zu entwickeln. Heute werde ich nicht darauf eingehen, wie probabilistische Vorhersagen im Kontext von supply chains für entscheidungsbasierte Optimierung genutzt werden können. Der aktuelle Schwerpunkt liegt ausschließlich darauf, die Grundlagen der probabilistischen Vorhersage zu vermitteln. Die Verbesserung von Entscheidungsprozessen in supply chain durch probabilistische Vorhersagen wird in der nächsten Vorlesung behandelt.

Um die Bedeutung probabilistischer Vorhersagen zu verstehen, ist ein wenig historischer Kontext notwendig. Die moderne Form der Vorhersage, die statistische Vorhersage – im Gegensatz zur Wahrsagerei – entstand zu Beginn des 20. Jahrhunderts. Die Vorhersage entwickelte sich in einem breiteren wissenschaftlichen Kontext, in dem die Naturwissenschaften, einige wenige sehr erfolgreiche Disziplinen wie Kinetik, Elektromagnetismus und Chemie, scheinbar willkürlich präzise Ergebnisse erzielen konnten. Diese Ergebnisse wurden im Wesentlichen durch einen jahrhundertealten Aufwand erzielt, der beispielsweise bis zu Galileo Galilei zurückverfolgt werden kann, als er überlegene Technologien entwickelte, die überlegene Messmethoden ermöglichten. Genauere Messungen wiederum würden die weitere wissenschaftliche Entwicklung vorantreiben, indem sie es den Wissenschaftlern ermöglichten, ihre Theorien und Vorhersagen noch präziser zu testen und herauszufordern.

In diesem breiteren Kontext, in dem einige Wissenschaften unglaublich erfolgreich waren, machte sich das entstehende Vorhersagefeld zu Beginn des 20. Jahrhunderts im Wesentlichen daran, das nachzuahmen, was diese Naturwissenschaften im Bereich der Wirtschaft erreicht hatten. Beispielsweise gründete einer der Pioniere, Roger Babson – einer der Väter der modernen Wirtschaftsprognose – zu Beginn des 20. Jahrhunderts ein erfolgreiches Unternehmen für Wirtschaftsprognosen in den Vereinigten Staaten. Das Motto des Unternehmens lautete buchstäblich: “For every action, there is an equal and opposite reaction.” Babsons Vision war es, den Erfolg der newtonschen Physik in den Bereich der Wirtschaft zu übertragen und letztlich ebenso präzise Ergebnisse zu erzielen.

Allerdings bleibt nach über einem Jahrhundert statistischer akademischer Vorhersagen, in denen supply chains operieren, die Idee, willkürlich präzise Ergebnisse zu erzielen – was in prognostischen Begriffen bedeutet, willkürlich genaue Vorhersagen zu erreichen – ebenso schwer fassbar wie vor über einem Jahrhundert. Seit einigen Jahrzehnten gibt es Stimmen in der weiteren supply chain-Welt, die Bedenken geäußert haben, dass diese Vorhersagen niemals präzise genug werden. Es hat sich eine Bewegung entwickelt, wie etwa Lean Manufacturing, die unter anderem starke Befürworter dafür war, die Abhängigkeit von supply chains von diesen unzuverlässigen Vorhersagen weitgehend zu verringern. Darum geht es beim Just-in-Time: Wenn Sie alles, was der Markt benötigt, genau zur richtigen Zeit produzieren und bereitstellen können, dann brauchen Sie plötzlich keine verlässliche, genaue Vorhersage mehr.

In diesem Kontext ist probabilistische Vorhersage eine Rehabilitierung der Vorhersage, allerdings mit viel bescheideneren Ambitionen. Probabilistische Vorhersagen gehen von der Idee aus, dass eine irreduzible Unsicherheit über die Zukunft besteht. Alle Zukünfte sind möglich, sie sind nur nicht alle gleich wahrscheinlich, und das Ziel probabilistischer Vorhersagen ist es, die jeweilige Wahrscheinlichkeit all dieser alternativen Zukünfte vergleichend zu bewerten, anstatt alle möglichen Zukünfte auf eine einzige zu reduzieren.

Die newtonsche Perspektive auf statistische Wirtschaftsprognosen ist im Wesentlichen gescheitert. Die Auffassung in unserer Gemeinschaft, dass willkürlich genaue Vorhersagen jemals erreicht werden können, ist weitgehend verloren gegangen. Und doch, erstaunlicherweise, beruhen fast alle supply chain software und ein großer Teil der gängigen supply chain practices im Kern auf der Annahme, dass solche Vorhersagen letztlich verfügbar sein werden.

Beispielsweise basiert Sales and Operations Planning (S&OP) auf der Idee, dass eine einheitliche, quantifizierte Vision für das Unternehmen erreicht werden kann, wenn alle Beteiligten zusammengebracht werden und gemeinsam an der Erstellung einer Vorhersage arbeiten. Ebenso ist open-to-buy im Wesentlichen eine Methode, die auf der Annahme beruht, dass ein Top-down-Budgetierungsprozess möglich ist, basierend auf der Idee, dass willkürlich präzise Top-down-Vorhersagen konstruiert werden können. Darüber hinaus richten sich – wenn wir uns viele Werkzeuge ansehen, die im Bereich der Vorhersage und Planung in supply chains sehr verbreitet sind – wie business intelligence und spreadsheets diese Werkzeuge umfangreich auf eine Punkt-time-series Vorhersage aus. Im Wesentlichen besteht die Idee darin, dass Ihre historischen Daten in die Zukunft fortgeschrieben werden können, sodass für jede relevante Zeitperiode ein Datenpunkt existiert. Diese Werkzeuge haben per Design einen enormen Reibungsverlust, wenn es darum geht, die Art der Berechnungen nachzuvollziehen, die mit einer probabilistischen Vorhersage einhergehen – bei der es nicht nur eine Zukunft, sondern alle möglichen Zukünfte gibt.

In der Tat geht es bei probabilistischen Vorhersagen nicht darum, eine klassische Vorhersage mit irgendeiner Art von Unsicherheit zu schmücken. Probabilistische Vorhersagen dienen auch nicht dazu, eine Auswahlliste von Szenarien zu erstellen, wobei jedes Szenario für sich eine klassische Vorhersage darstellt. Herkömmliche supply chain Methoden arbeiten typischerweise nicht mit probabilistischen Vorhersagen, da sie im Kern implizit oder explizit auf der Annahme beruhen, dass es eine Art Referenzvorhersage gibt, um die sich dann alles dreht. Im Gegensatz dazu stellt die probabilistische Vorhersage die direkte numerische Bewertung aller möglichen Zukünfte dar.

Natürlich sind wir durch die verfügbaren Rechenressourcen begrenzt, sodass wir in der Praxis, wenn ich von “allen möglichen Zukünften” spreche, nur eine endliche Anzahl von Zukünften betrachten können. Angesichts der modernen Rechenleistung, die uns zur Verfügung steht, kann die Anzahl der Zukünfte, die wir tatsächlich berücksichtigen können, in die Millionen gehen. Hier stoßen business intelligence und spreadsheets an ihre Grenzen. Sie sind nicht auf die Art von Berechnungen ausgelegt, die bei probabilistischen Vorhersagen anfallen. Dies ist ein Problem des Softwaredesigns. Sehen Sie, ein Spreadsheet hat Zugang zu denselben Computern und derselben Rechenleistung, aber wenn die Software nicht mit dem richtigen Design ausgestattet ist, können manche Aufgaben unglaublich schwer zu bewältigen sein, selbst wenn Sie über eine enorme Rechenleistung verfügen.

Aus supply chain-Sicht besteht die größte Herausforderung bei der Einführung probabilistischer Vorhersagen darin, sich von jahrzehntelangen Werkzeugen und Praktiken zu lösen, die auf ein sehr ambitioniertes, aber meines Erachtens fehlgeleitetes Ziel ausgerichtet sind – nämlich die Erzielung willkürlich genauer Vorhersagen. Ich möchte gleich darauf hinweisen, dass es äußerst fehlgeleitet wäre, probabilistische Vorhersagen als Mittel zur Erreichung genauerer Vorhersagen zu betrachten. Das ist nicht der Fall. Probabilistische Vorhersagen sind nicht genauer, und sie können nicht als direkter Ersatz für klassische, herkömmliche Vorhersagen verwendet werden. Ihre Überlegenheit liegt in den Möglichkeiten, wie diese Vorhersagen für supply chain-Zwecke, insbesondere im Rahmen von Entscheidungsfindungsprozessen in supply chains, genutzt werden können. Unser Ziel heute ist es jedoch nur, zu verstehen, worum es bei diesen probabilistischen Vorhersagen geht, während deren Ausnutzung in der nächsten Vorlesung behandelt wird.

Diese Vorlesung ist Teil einer Reihe von supply chain Vorträgen. Ich versuche, diese Vorlesungen weitgehend unabhängig voneinander zu halten. Dennoch kommen wir an einen Punkt, an dem es dem Publikum wirklich helfen wird, wenn diese Vorlesungen in Zusammenhang angesehen werden, da ich häufig auf Inhalte früherer Vorlesungen Bezug nehmen werde.

Diese Vorlesung ist also die dritte des fünften Kapitels, das sich predictive modeling widmet. Im allerersten Kapitel dieser Serie habe ich meine Ansichten zu supply chains sowohl als Studienfach als auch als Praxis präsentiert. Im zweiten Kapitel stellte ich Methodologien vor. Tatsächlich sind die meisten supply chain-Situationen von Natur aus adversarial, und diese Situationen neigen dazu, naive Methodologien zu entwaffnen. Wir müssen über geeignete Methodologien verfügen, wenn wir im Bereich der supply chains irgendeinen Erfolg erzielen wollen.

Das dritte Kapitel widmete sich der supply chain Sparsamkeit, mit einem ausschließlichen Fokus auf das Problem und die eigentliche Natur der Herausforderung, der wir in den verschiedenen Situationen, die supply chains betreffen, gegenüberstehen. Die Idee hinter supply chain Sparsamkeit besteht darin, sämtliche Aspekte der Lösungsseite vollständig zu ignorieren, da wir uns ausschließlich auf das Problem konzentrieren wollen, bevor wir die Lösung auswählen, die wir zu dessen Bewältigung einsetzen möchten.

Im vierten Kapitel habe ich eine breite Palette von Hilfswissenschaften untersucht. Diese Wissenschaften sind nicht supply chain an sich; sie sind andere Forschungsfelder, die angrenzend oder unterstützend wirken. Dennoch bin ich der Meinung, dass ein grundlegendes Verständnis dieser Hilfswissenschaften Voraussetzung für die moderne Praxis von supply chains ist.

Schließlich tauchen wir im fünften Kapitel in die Techniken ein, die es uns ermöglichen, die Zukunft zu quantifizieren und zu bewerten, insbesondere um Aussagen über die Zukunft zu treffen. Tatsächlich spiegelt sich in allem, was wir in supply chains tun, bis zu einem gewissen Grad eine gewisse Erwartung der Zukunft wider. Wenn wir die Zukunft besser voraussehen können, werden wir in der Lage sein, bessere Entscheidungen zu treffen. Darum geht es in diesem fünften Kapitel: um quantifizierbar bessere Einsichten in die Zukunft zu gewinnen. In diesem Kapitel stellen probabilistische Vorhersagen einen zentralen Ansatz dar, um die Zukunft anzugehen.

Der restliche Teil dieser Vorlesung ist in vier Abschnitte ungleicher Länge unterteilt. Zunächst werden wir die gängigsten Arten von Vorhersagen jenseits der klassischen Vorhersage betrachten. Ich werde gleich erläutern, was ich unter einer klassischen Vorhersage verstehe. In supply chain Kreisen wird tatsächlich viel zu wenig erkannt, dass es viele Optionen gibt. Probabilistische Vorhersagen sollten selbst als ein Sammelbegriff verstanden werden, der eine ziemlich vielfältige Palette von Werkzeugen und Techniken umfasst.

Zweitens werden wir Metriken einführen, um die Qualität probabilistischer Vorhersagen zu bewerten. Unabhängig davon, was passiert, wird eine gut gestaltete probabilistische Vorhersage Ihnen stets sagen, “Nun, dafür gab es eine Wahrscheinlichkeit.” Die Frage lautet also: Wie unterscheidet man eine tatsächlich gute probabilistische Vorhersage von einer schlechten? Genau hier kommen diese Metriken ins Spiel. Es gibt spezielle Metriken, die ausschließlich der Situation probabilistischer Vorhersagen gewidmet sind.

Drittens werden wir eine eingehende Untersuchung eindimensionaler Verteilungen vornehmen. Diese sind die einfachste Art von Verteilung, und obwohl sie offensichtliche Einschränkungen aufweisen, sind sie auch der einfachste Einstieg in den Bereich der probabilistischen Vorhersage.

Viertens werden wir kurz auf Generatoren eingehen, die häufig als Monte-Carlo-Methoden bezeichnet werden. Tatsächlich besteht eine Dualität zwischen Generatoren und Dichteschätzern, und diese Monte-Carlo-Methoden werden uns einen Weg eröffnen, höherdimensionale Probleme und Formen der probabilistischen Vorhersage anzugehen.

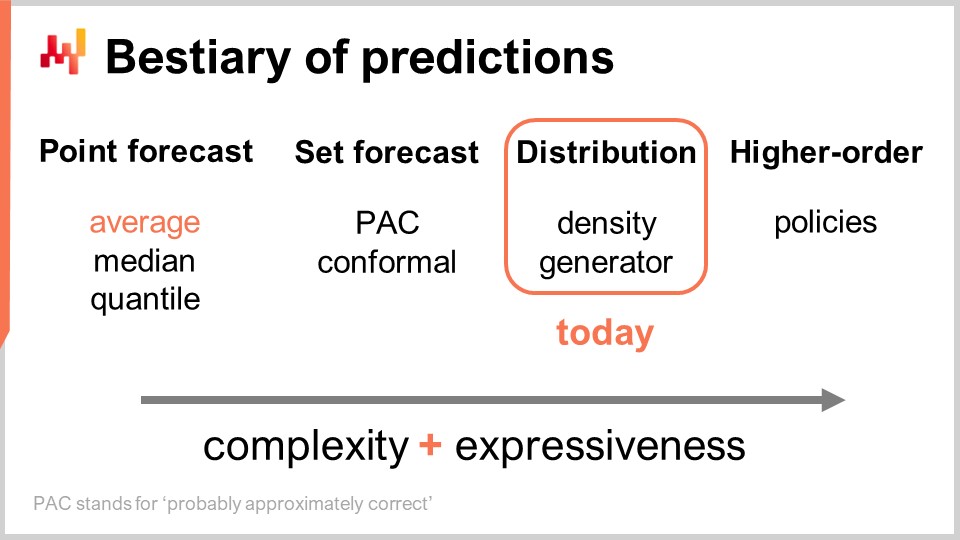
Es gibt mehrere Arten von Vorhersagen, und dieser Aspekt sollte nicht damit verwechselt werden, dass es mehrere Arten von Prognosemodellen gibt. Wenn Modelle nicht demselben Typ oder derselben Prognoseklasse angehören, lösen sie nicht einmal dieselben Probleme. Die gebräuchlichste Art der Vorhersage ist die Punktprognose. Als Beispiel: Wenn ich sage, dass morgen der Gesamtumsatz in Euro in einem Geschäft 10.000 Euro für das Tagesgesamtaggregat betragen wird, mache ich eine Punktprognose darüber, was in diesem Geschäft morgen passieren wird. Wenn ich diese Übung wiederhole und anfange, eine Zeitreihenprognose zu erstellen, indem ich zunächst eine Aussage für morgen und dann eine weitere Aussage für übermorgen treffe, erhalte ich mehrere Datenpunkte. Dennoch bleibt das alles im Wesentlichen eine Punktprognose, da wir im Kern unsere Auseinandersetzung dadurch wählen, dass wir ein bestimmtes Aggregationsniveau festlegen und uns auf diesem Niveau unsere Vorhersagen als eine einzelne Zahl präsentieren, die die Antwort sein soll.

Nun gibt es innerhalb des Typs der Punktprognose mehrere Untertypen von Prognosen, abhängig davon, welche Metrik optimiert wird. Die wahrscheinlich am häufigsten verwendete Metrik ist vermutlich der quadratische Fehler, sodass wir einen mittleren quadratischen Fehler haben, der Ihnen die durchschnittliche Vorhersage liefert. Übrigens neigt dies dazu, die am häufigsten verwendete Prognose zu sein, da sie die einzige ist, die zumindest einigermaßen additiv ist. Keine Prognose ist jemals vollständig additiv; sie kommt immer mit zahlreichen Vorbehalten. Dennoch sind manche Prognosen additiver als andere, und durchschnittliche Prognosen tendieren eindeutig dazu, die additivsten unter ihnen zu sein. Wenn Sie eine durchschnittliche Prognose wünschen, haben Sie im Wesentlichen eine Punktprognose, die gegen den mittleren quadratischen Fehler optimiert wurde. Verwenden Sie eine andere Metrik, wie den absoluten Fehler, und optimieren dagegen, erhalten Sie eine Medianprognose. Nutzen Sie die pinball loss function, die wir in der allerersten Vorlesung dieses fünften Kapitels in dieser Serie von supply chain Vorlesungen eingeführt haben, so erhalten Sie eine quantile forecast. Übrigens, wie wir heute sehen können, klassifiziere ich quantile forecasts als einfach einen weiteren Typ von Punktprognose. Tatsächlich erhalten Sie mit der quantile forecast im Wesentlichen eine einzige Schätzung. Diese Schätzung mag mit einer Verzerrung einhergehen, was beabsichtigt ist. Darum geht es bei Quantilen, aber dennoch qualifiziert sich dies meiner Ansicht nach voll und ganz als Punktprognose, da die Form der Prognose einfach ein einzelner Punkt ist.

Nun gibt es die Set-Prognose, die anstelle eines einzelnen Punktes eine Menge von Punkten zurückgibt. Es gibt Variationen, je nachdem, wie Sie die Menge aufbauen. Wenn wir uns eine PAC-Prognose ansehen – PAC steht für Probably Approximately Correct – handelt es sich im Wesentlichen um einen von Valiant vor etwa zwei Jahrzehnten eingeführten Rahmen, der besagt, dass die Menge, welche Ihre Vorhersage darstellt, mit einer bestimmten Wahrscheinlichkeit ein Ergebnis enthält, das mit dieser bestimmten Wahrscheinlichkeit innerhalb der von Ihnen vorhergesagten Menge beobachtet wird. Die von Ihnen erzeugte Menge umfasst tatsächlich alle Punkte, die in einen Bereich fallen, der durch einen maximalen Abstand zu einem Referenzpunkt charakterisiert ist. In gewisser Weise ist die PAC-Perspektive auf Prognosen bereits eine Set-Prognose, da der Output nicht mehr ein einzelner Punkt ist. Dennoch haben wir immer noch einen Referenzpunkt, ein zentrales Ergebnis, und einen maximalen Abstand zu diesem zentralen Punkt. Wir sagen lediglich, dass es mit einer bestimmten, festgelegten Wahrscheinlichkeit vorkommt, dass das Ergebnis schließlich innerhalb unserer Vorhersagemenge beobachtet wird.

Der PAC-Ansatz kann durch den konformen Ansatz verallgemeinert werden. Conformal prediction besagt: “Hier ist eine Menge, und ich teile Ihnen mit, dass es eine bestimmte Wahrscheinlichkeit gibt, mit der das Ergebnis in dieser Menge liegt.” Wo conformal prediction den PAC-Ansatz verallgemeinert, ist, dass konforme Vorhersagen nicht mehr an einen Referenzpunkt und den Abstand zu diesem Referenzpunkt gebunden sind. Sie können diese Menge beliebig gestalten und bleiben trotzdem Teil des Set-Prognose-Paradigmas.

Die Zukunft kann auf noch granulärere und komplexere Weise dargestellt werden: die Verteilungsprognose. Die Verteilungsprognose liefert Ihnen eine Funktion, die alle möglichen Ergebnisse ihren jeweiligen lokalen Wahrscheinlichkeitsdichten zuordnet. In gewisser Weise beginnen wir mit der Punktprognose, bei der die Vorhersage lediglich ein Punkt ist. Dann wechseln wir zur Set-Prognose, bei der die Vorhersage eine Menge von Punkten ist. Schließlich ist die Verteilungsprognose technisch gesehen eine Funktion oder etwas, das eine Funktion verallgemeinert. Übrigens, wenn ich in dieser Vorlesung den Begriff “Verteilung” verwende, bezieht er sich stets implizit auf eine Wahrscheinlichkeitsverteilung. Verteilungsprognosen stellen etwas noch Reichhaltigeres und Komplexeres dar als eine Menge, und genau darauf werden wir uns heute konzentrieren.

Es gibt zwei gängige Ansätze, um an Verteilungen heranzugehen: den Dichteansatz und den Generatoransatz. Wenn ich von “Dichte” spreche, beziehe ich mich im Grunde auf die lokale Schätzung von Wahrscheinlichkeitsdichten. Der Generatoransatz umfasst einen Monte-Carlo-generativen Prozess, der Ergebnisse erzeugt, sogenannte Deviates, welche die gleiche lokale Wahrscheinlichkeitsdichte reflektieren sollen. Dies sind die beiden Hauptwege, um Verteilungsprognosen anzugehen.

Über die Verteilung hinaus haben wir höherordentliche Konstrukte. Das mag etwas kompliziert zu verstehen sein, aber mein Punkt hier – auch wenn wir heute nicht auf höherordentliche Konstrukte eingehen – ist lediglich, zu verdeutlichen, dass probabilistische Vorhersagen, wenn sie darauf abzielen, Verteilungen zu generieren, nicht das Endziel darstellen; es ist nur ein Schritt, und es gibt noch mehr. Höherordentliche Konstrukte sind wichtig, wenn wir jemals in der Lage sein wollen, befriedigende Antworten auf einfache Situationen zu erhalten.

Um zu verstehen, worum es bei höherordentlichen Konstrukten geht, betrachten wir ein einfaches Einzelhandelsgeschäft, in dem eine Rabattpolitik für Produkte gilt, die kurz vor ihrem Verfallsdatum stehen. Offensichtlich möchte das Geschäft keine veralteten Bestände auf den Regalen haben, weshalb ein automatischer Rabatt in Kraft tritt, sobald Produkte ihrem Verfallsdatum sehr nahekommen. Die Nachfrage, die dieses Geschäft generieren würde, hängt stark von dieser Politik ab. Daher sollte die Prognose, die wir haben möchten – welche als Verteilungsprognose die Wahrscheinlichkeiten für alle möglichen Ergebnisse darstellen kann – von dieser Politik abhängen. Allerdings ist diese Politik ein mathematisches Objekt; es ist eine Funktion. Was wir uns wünschen, ist nicht eine probabilistische Vorhersage, sondern etwas Meta-Höheres – ein höherordentliches Konstrukt, das, gegeben eine Politik, die daraus resultierende Verteilung erzeugen kann.

Aus supply chain Perspektive gewinnen wir, wenn wir von einer Art der Prognose zur nächsten übergehen, deutlich mehr Informationen. Dabei geht es nicht darum, die Prognose genauer zu machen, sondern vielmehr darum, Zugang zu einer völlig anderen Art von Information zu erhalten – als ob man die Welt zunächst in Schwarzweiß sieht und dann plötzlich die Fähigkeit erlangt, Farben zu erkennen, anstatt einfach nur eine höhere Auflösung zu erhalten. Was die Werkzeuge angeht, so sind Tabellenkalkulationen und Business-Intelligence-Tools einigermaßen geeignet, um mit Punktprognosen umzugehen. Je nachdem, welche Art von Set-Prognose Sie in Betracht ziehen, mögen sie ausreichend sein, aber Sie stoßen dabei bereits an die Grenzen ihrer Gestaltungsmöglichkeiten. Sie sind nicht wirklich dafür ausgelegt, mit irgendeiner ausgefallenen Set-Prognose jenseits der offensichtlichen umzugehen, bei der Sie lediglich einen Bereich mit Minimal- und Maximalwerten im Spektrum der erwarteten Werte definieren. Wir werden sehen, dass, wenn wir auch nur annähernd mit Verteilungsprognosen oder höherordentlichen Konstrukten arbeiten wollen, wir völlig andere Werkzeuge benötigen – was in einem Moment klarer werden sollte.

Um mit probabilistischen Prognosen zu beginnen, wollen wir versuchen, zu charakterisieren, was eine gute probabilistische Prognose ausmacht. Tatsächlich wird Ihnen eine probabilistische Prognose, egal welches Ergebnis Sie beobachten, sagen, dass es eine Wahrscheinlichkeit für das Eintreten dieses Ergebnisses gab. Unter diesen Voraussetzungen, wie unterscheidet man also eine gute probabilistische Prognose von einer schlechten? Es liegt sicherlich nicht daran, dass allein die Tatsache, dass sie probabilistisch ist, alle Prognosemodelle plötzlich gut macht.

Genau darum gehen Metriken, die speziell für probabilistische Vorhersagen entwickelt wurden, und der Continuous Ranked Probability Score (CRPS) ist die Generalisierung des absoluten Fehlers für eindimensionale probabilistische Prognosen. Es tut mir wirklich leid für diesen entsetzlich klingenden Namen – der CRPS. Ich habe diese Terminologie nicht selbst erfunden; sie wurde mir übermittelt. Die CRPS-Formel wird auf dem Bildschirm gezeigt. Im Wesentlichen ist die Funktion F die kumulative Verteilungsfunktion; sie stellt die abgegebene probabilistische Prognose dar. Der Punkt x ist die tatsächliche Beobachtung, und der CRPS-Wert ist etwas, das Sie zwischen Ihrer probabilistischen Prognose und der gerade getätigten Beobachtung berechnen.

Wir können sehen, dass im Grunde der Punkt mittels der Heaviside-Stufenfunktion in eine quasi-probabilistische Prognose umgewandelt wird. Die Einführung der Heaviside-Stufenfunktion entspricht gerade dem Vorgang, den soeben beobachteten Punkt in eine Dirac-Wahrscheinlichkeitsverteilung zu überführen – eine Verteilung, die die gesamte Wahrscheinlichkeitsmasse auf ein einzelnes Ergebnis konzentriert. Anschließend folgt ein Integral, und im Wesentlichen führt das CRPS eine Art Formabgleich durch. Wir gleichen die Form der CDF (kumulative Verteilungsfunktion) mit der Form einer anderen CDF ab, nämlich jener, die mit der Dirac-Verteilung übereinstimmt, die zu dem beobachteten Punkt passt.

Aus der Perspektive einer Punktprognose ist das CRPS nicht nur wegen der komplizierten Formel rätselhaft, sondern auch, weil diese Metrik zwei Argumente entgegennimmt, die nicht vom gleichen Typ sind. Eines dieser Argumente ist eine Verteilung, und das andere lediglich ein einzelner Datenpunkt. So besteht eine Asymmetrie, die bei den meisten anderen Metriken für Punktprognosen, wie dem absoluten Fehler und dem mittleren quadratischen Fehler, nicht vorhanden ist. Beim CRPS vergleichen wir im Wesentlichen einen Punkt mit einer Verteilung.

Wenn wir mehr darüber verstehen wollen, was wir mit dem CRPS berechnen, ist eine interessante Beobachtung, dass das CRPS dieselbe Einheit wie die Beobachtung hat. Zum Beispiel, wenn x in Euro angegeben ist und der CRPS-Wert zwischen F und x ebenfalls in derselben Einheit wie Euro vorliegt, ist das der Grund, weshalb ich sage, dass CRPS eine Generalisierung des absoluten Fehlers darstellt. Übrigens, wenn Sie Ihre probabilistische Prognose in eine Dirac-Verteilung zusammenfassen, liefert das CRPS einen Wert, der exakt dem absoluten Fehler entspricht.

Obwohl das CRPS ziemlich einschüchternd und kompliziert erscheinen mag, ist die Implementierung tatsächlich recht unkompliziert. Auf dem Bildschirm ist ein kleines Envision-Skript zu sehen, das veranschaulicht, wie das CRPS aus der Perspektive einer Programmiersprache verwendet werden kann. Envision ist eine domänenspezifische Programmiersprache, die der prädiktiven Optimierung von supply chains gewidmet ist und von Lokad entwickelt wurde. In diesen Vorlesungen verwende ich Envision der Klarheit und Prägnanz halber. Bitte beachten Sie jedoch, dass an Envision nichts Einzigartiges ist; dieselben Ergebnisse könnten in jeder Programmiersprache erzielt werden – sei es Python, Java, JavaScript, C#, F# oder eine andere. Mein Punkt ist, dass es nur mehr Codezeilen erfordern würde, weshalb ich bei Envision bleibe. Alle hier in dieser Vorlesung gezeigten Codeausschnitte – und übrigens auch in den vorherigen – sind eigenständig und vollständig. Sie könnten diesen Code technisch kopieren und einfügen, und er würde laufen. Es sind keine Module involviert, kein versteckter Code und keine Umgebung einzurichten.

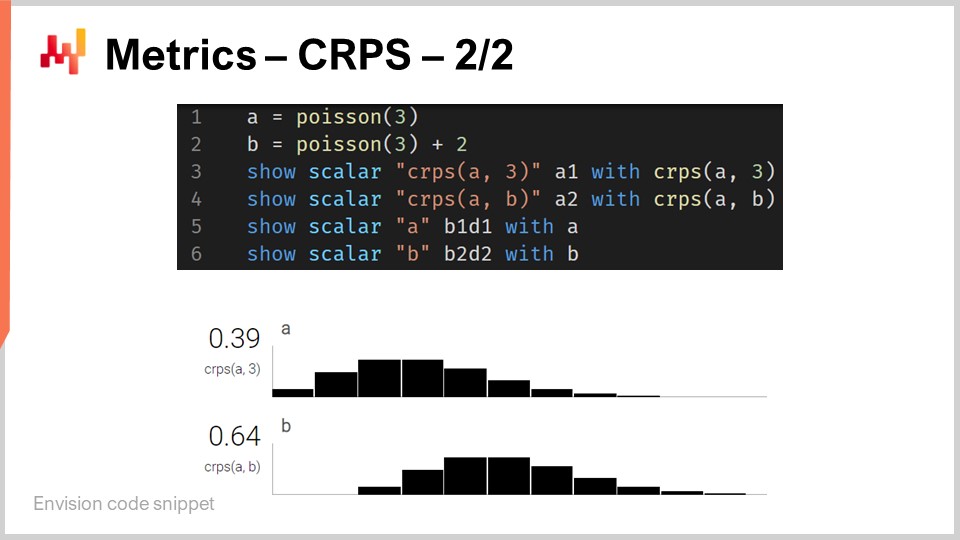
Nun also zurück zum Codeausschnitt. In den Zeilen eins und zwei definieren wir eindimensionale Verteilungen. Ich werde später darauf eingehen, wie diese eindimensionalen Verteilungen in Envision tatsächlich funktionieren, aber wir haben hier zwei Verteilungen: Eine ist eine Poisson-Verteilung, die eine eindimensionale diskrete Verteilung darstellt, und die zweite in Zeile zwei ist dieselbe Poisson-Verteilung, jedoch um zwei Einheiten nach rechts verschoben – daher das “+2”. In Zeile drei berechnen wir die CRPS-Distanz zwischen einer Verteilung und dem Wert 3, welcher eine Zahl ist. So stellen wir fest, dass hier eine Asymmetrie in Bezug auf Datentypen besteht, von der ich gesprochen habe. Anschließend werden die Ergebnisse unten angezeigt, wie Sie am unteren Bildschirmrand sehen können.

In Zeile vier berechnen wir das CRPS zwischen der Verteilung A und der Verteilung B. Obwohl die klassische Definition des CRPS eine Berechnung zwischen einer Verteilung und einem einzelnen Punkt vorsieht, ist es völlig unkompliziert, diese Definition auf ein Paar von Verteilungen zu verallgemeinern. Alles, was Sie tun müssen, ist, dieselbe CRPS-Formel zu nehmen und die Heaviside-Stufenfunktion durch die kumulative Verteilungsfunktion der zweiten Verteilung zu ersetzen. Die “show”-Anweisungen in den Zeilen drei bis sechs führen zu der Anzeige, die Sie unten auf dem Bildschirm sehen – buchstäblich ein Screenshot.

Wir sehen also, dass die Verwendung von CRPS nicht schwieriger oder komplizierter ist als die Nutzung irgendeiner speziellen Funktion, wie beispielsweise der Kosinusfunktion. Natürlich ist es etwas mühsam, wenn Sie den Kosinus selbst implementieren müssten, aber alles in allem ist an CRPS nichts besonders Kompliziertes dran. Kommen wir nun weiter.

Das Monge-Kantorovich-Problem gibt uns Einblick, wie wir den Formabgleich, der im CRPS zum Einsatz kommt, in höheren Dimensionen angehen können. Bedenken Sie, dass das CRPS tatsächlich auf die Dimension eins beschränkt ist. Formabgleich ist konzeptionell etwas, das auf beliebig viele Dimensionen verallgemeinert werden könnte, und das Monge-Kantorovich-Problem ist sehr interessant – doppel so sehr, weil es im Kern tatsächlich ein supply chain Problem ist.

Das Monge-Kantorovich-Problem, das ursprünglich nichts mit probabilistischer Vorhersage zu tun hatte, wurde vom französischen Wissenschaftler Gaspard Monge in einem Memoiren aus dem Jahr 1781 mit dem Titel “Mémoire sur la théorie des déblais et des remblais” eingeführt, was grob übersetzt “Memoiren über die Theorie des Aushubs und der Aufschüttung” bedeuten könnte.

Monge definierte das Kapital C als die Kosten, um das gesamte Erz von den Minen zu den Fabriken zu transportieren. Die Kosten ergeben sich aus der Summe des Transports des gesamten Erzes von jeder Mine zu jeder Fabrik, wobei es natürlich sehr ineffiziente Möglichkeiten gibt, das Erz zu befördern. Wenn wir also sagen, dass wir eine bestimmte Kostenangabe haben, meinen wir, dass diese Kosten den optimalen Transportplan widerspiegeln. Dieses Kapital C repräsentiert die bestmöglichen Kosten, die durch die Berücksichtigung des optimalen Transportplans erzielt werden können.

Dies ist im Wesentlichen ein supply chain Problem, das über Jahrhunderte hinweg ausführlich untersucht wurde. In der vollständigen Problemformulierung gibt es Nebenbedingungen für T. Der Kürze halber habe ich nicht alle Nebenbedingungen auf dem Bildschirm dargestellt. Es gibt beispielsweise eine Nebenbedingung, dass der Transportplan die Produktionskapazität jeder Mine nicht überschreiten darf und dass jede Fabrik vollständig bedient wird, indem ihr eine Zuweisung zukommt, die ihren Anforderungen entspricht. Es gibt zahlreiche Nebenbedingungen, aber sie sind recht umfangreich, weshalb ich sie nicht auf dem Bildschirm dargestellt habe.

Nun, obwohl das Transportproblem für sich genommen interessant ist, haben wir, wenn wir die Liste der Minen und die Liste der Fabriken als zwei Wahrscheinlichkeitsverteilungen interpretieren, einen Weg, eine punktweise Metrik in eine verteilungsweise Metrik umzuwandeln. Dies ist eine Schlüsselerkenntnis über den Formenabgleich in höheren Dimensionen aus der Monge-Kantorovich-Perspektive. Ein anderer Begriff für diese Perspektive ist die Wasserstein-Metrik, obwohl sie sich hauptsächlich auf den nicht-diskreten Fall bezieht, der für uns von geringerer Bedeutung ist.

Die Monge-Kantorovich-Perspektive ermöglicht es uns, eine punktweise Metrik, die den Unterschied zwischen zwei Zahlen oder zwei Vektoren von Zahlen berechnen kann, in eine Metrik umzuwandeln, die auf Wahrscheinlichkeitsverteilungen im gleichen Raum anwendbar ist. Dies ist ein sehr mächtiger Mechanismus. Allerdings ist das Monge-Kantorovich-Problem schwer zu lösen und erfordert erhebliche Rechenleistung. Für den Rest der Vorlesung werde ich mich an Techniken halten, die einfacher zu implementieren und auszuführen sind.

Die bayessche Perspektive besteht darin, eine Reihe von Beobachtungen aus der Sicht eines a priori Glaubens zu betrachten. Die bayessche Perspektive wird üblicherweise im Gegensatz zur frequentistischen Perspektive verstanden, die die Häufigkeit von Ergebnissen auf Basis tatsächlicher Beobachtungen schätzt. Die Idee ist, dass die frequentistische Perspektive keine Vorannahmen mitbringt. Somit liefert uns die bayessche Perspektive ein Werkzeug, bekannt als die Likelihood, um das Maß an Überraschung bei der Betrachtung der Beobachtungen und eines gegebenen Modells zu bewerten. Das Modell, das im Wesentlichen ein probabilistisches Prognosemodell ist, stellt die Formalisierung unserer Vorannahmen dar. Die bayessche Perspektive bietet uns einen Weg, einen Datensatz im Hinblick auf ein probabilistisches Prognosemodell zu bewerten. Um zu verstehen, wie dies geschieht, sollten wir mit der Likelihood für einen einzelnen Datenpunkt beginnen. Die Likelihood, wenn wir eine Beobachtung x haben, ist die Wahrscheinlichkeit, x gemäß dem Modell zu beobachten. Hier wird angenommen, dass das Modell vollständig durch theta, die Parameter des Modells, charakterisiert ist. Die bayessche Perspektive nimmt typischerweise an, dass das Modell eine gewisse parametrische Form besitzt, und theta ist der vollständige Vektor aller Modellparameter.

Wenn wir von theta sprechen, nehmen wir implizit an, dass wir eine vollständige Charakterisierung des probabilistischen Modells haben, die uns eine lokale Wahrscheinlichkeitsdichte für alle Punkte liefert. Somit ist die Likelihood die Wahrscheinlichkeit, diesen einen Datenpunkt zu beobachten. Wenn wir die Likelihood für das Modell theta haben, ist es die gemeinsame Wahrscheinlichkeit, alle Datenpunkte im Datensatz zu beobachten. Wir gehen davon aus, dass diese Punkte unabhängig voneinander sind, sodass die Likelihood ein Produkt von Wahrscheinlichkeiten ist.

Wenn wir tausende Beobachtungen haben, ist die Likelihood, als Produkt von tausenden Werten, die kleiner als eins sind, numerisch wahrscheinlich verschwindend klein. Ein verschwindend kleiner Wert ist typischerweise schwer darzustellen, wie Gleitkommazahlen in Computern repräsentiert werden. Anstatt direkt mit der Likelihood zu arbeiten, die ein verschwindend kleiner Wert ist, tendieren wir dazu, mit der Log-Likelihood zu arbeiten. Die Log-Likelihood ist einfach der Logarithmus der Likelihood, der die unglaubliche Eigenschaft besitzt, Multiplikation in Addition umzuwandeln.

Die Log-Likelihood des Modells theta ist die Summe der Logarithmen aller einzelnen Likelihoods für alle Datenpunkte, wie in der letzten Gleichungszeile auf dem Bildschirm gezeigt wird. Die Likelihood ist eine Metrik, die uns die Güte der Anpassung für eine gegebene probabilistische Vorhersage liefert. Sie gibt uns an, wie wahrscheinlich es ist, dass das Modell den Datensatz erzeugt hat, den wir beobachten. Wenn wir zwei probabilistische Vorhersagen im Wettbewerb haben und alle anderen Anpassungsfragen beiseitelegen, sollten wir das Modell wählen, das die höchste Likelihood oder die höchste Log-Likelihood liefert, denn je höher, desto besser.

Die Likelihood ist sehr interessant, da sie in hohen Dimensionen problemlos arbeitet, im Gegensatz zur Monge-Kantorovich-Methode. Solange wir ein Modell haben, das uns eine lokale Wahrscheinlichkeitsdichte liefert, können wir die Likelihood – oder genauer gesagt, die Log-Likelihood – als Metrik verwenden.

Des Weiteren, sobald wir eine Metrik haben, die die Güte der Anpassung repräsentiert, bedeutet das, dass wir genau gegen diese Metrik optimieren können. Es bedarf lediglich eines Modells mit mindestens einem Freiheitsgrad, was im Grunde mindestens einen Parameter bedeutet. Wenn wir dieses Modell an der Likelihood, unserer Metrik für die Anpassungsgüte, ausrichten, werden wir hoffentlich ein trainiertes Modell erhalten, bei dem wir gelernt haben, zumindest eine anständige probabilistische Vorhersage zu erzeugen. Genau das wird hier auf dem Bildschirm gemacht.

Auf Zeile eins und zwei erzeugen wir einen simulierten Datensatz. Wir erstellen eine Tabelle mit 2.000 Zeilen, und dann generieren wir in Zeile zwei 2.000 Abweichungen, unsere Beobachtungen aus einer Poisson-Verteilung mit einem Mittelwert von zwei. Also haben wir unsere 2.000 Beobachtungen. In Zeile drei starten wir einen autodiff-Block, der Teil des Paradigmas der differentiellen Programmierung ist. Dieser Block wird einen stochastischen Gradientenabstieg ausführen und viele Male über alle Beobachtungen in der Beobachtungstabelle iterieren. Hier ist die Beobachtungstabelle Tabelle T.

Auf Zeile vier deklarieren wir den einen Parameter des Modells, genannt lambda. Wir legen fest, dass dieser Parameter ausschließlich positiv sein soll. Diesen Parameter werden wir mittels des stochastischen Gradientenabstiegs wiederentdecken. In Zeile fünf definieren wir die Verlustfunktion, die einfach das Minus der Log-Likelihood ist. Wir wollen die Likelihood maximieren, aber der autodiff-Block versucht, den Verlust zu minimieren. Daher müssen wir, wenn wir die Log-Likelihood maximieren wollen, dieses Minuszeichen vor die Log-Likelihood setzen, was genau das ist, was wir getan haben.

Der gelernte Lambda-Parameter wird in Zeile sechs angezeigt. Nicht überraschend liegt der gefundene Wert sehr nahe bei zwei, da wir mit einer Poisson-Verteilung mit einem Mittelwert von zwei gestartet sind. Wir haben ein probabilistisches Prognosemodell erstellt, das ebenfalls parametrisch ist und dieselbe Form hat, nämlich eine Poisson-Verteilung. Wir wollten den einen Parameter der Poisson-Verteilung wiederentdecken, und genau das erhalten wir. Wir bekommen ein Modell, das etwa ein Prozent vom ursprünglichen Schätzwert abweicht.

Wir haben gerade unser erstes probabilistisches Prognosemodell erlernt, und es hat im Wesentlichen nur drei Zeilen Code gebraucht. Dies ist offensichtlich ein sehr einfaches Modell; dennoch zeigt es, dass an probabilistischer Prognose nichts von Natur aus Kompliziertes ist. Es ist nicht Ihre übliche Vorhersage mittels mittlerer quadratischer Abweichung, aber abgesehen davon ist es mit den richtigen Werkzeugen wie differentieller Programmierung nicht komplizierter als eine klassische Punktvorhersage.

Die Funktion log_likelihood.poisson, die wir zuvor verwendet haben, ist Teil der Standardbibliothek von Envision. Es steckt jedoch keine Magie dahinter. Schauen wir uns an, wie diese Funktion eigentlich im Hintergrund implementiert ist. Die ersten beiden Zeilen am Anfang geben uns die Implementierung der Log-Likelihood der Poisson-Verteilung. Eine Poisson-Verteilung wird vollständig durch ihren einen Parameter, lambda, charakterisiert, und die Log-Likelihood-Funktion nimmt nur zwei Argumente entgegen: den einen Parameter, der die Poisson-Verteilung vollständig charakterisiert, und die eigentliche Beobachtung. Die tatsächliche Formel, die ich geschrieben habe, ist buchstäblich Lehrbuchmaterial. Es ist das, was man erhält, wenn man die Lehrbuchformel implementiert, die die Poisson-Verteilung charakterisiert. Es gibt hier nichts Besonderes.

Achtet auf die Tatsache, dass diese Funktion mit dem autodiff-Schlüsselwort gekennzeichnet ist. Wie wir in der vorherigen Vorlesung gesehen haben, stellt das autodiff-Schlüsselwort sicher, dass die automatische Differenzierung korrekt durch diese Funktion fließen kann. Die Log-Likelihood der Poisson-Verteilung verwendet außerdem eine weitere spezielle Funktion, log_gamma. Die log_gamma-Funktion ist der Logarithmus der Gammafunktion, die die Verallgemeinerung der Fakultätsfunktion auf komplexe Zahlen darstellt. Hier benötigen wir nur die Verallgemeinerung der Fakultätsfunktion auf reelle positive Zahlen.

Die Implementierung der log_gamma-Funktion ist etwas wortreich, aber wieder Lehrbuchmaterial. Sie verwendet eine Kettenbruchapproximation für die log_gamma-Funktion. Das Schöne daran ist, dass uns die automatische Differenzierung bis in die tiefsten Ebenen unterstützt. Wir beginnen mit dem autodiff-Block, der die Funktion log_likelihood.poisson aufruft, die als autodiff-Funktion implementiert ist. Diese Funktion wiederum ruft die log_gamma-Funktion auf, die ebenfalls mit dem autodiff-Marker implementiert ist. Im Wesentlichen sind wir in der Lage, unsere probabilistischen Prognosemethoden in drei Zeilen Code zu produzieren, weil wir eine gut durchdachte Standardbibliothek haben, die unter Berücksichtigung der automatischen Differenzierung implementiert wurde.

Nun wollen wir uns dem Spezialfall der eindimensionalen diskreten Verteilungen zuwenden. Diese Verteilungen finden sich überall in einer supply chain und repräsentieren unseren Einstiegspunkt in die probabilistische Prognose. Zum Beispiel, wenn wir lead times mit täglicher Granularität prognostizieren wollen, können wir sagen, dass es eine gewisse Wahrscheinlichkeit für eine eintägige Durchlaufzeit gibt, eine andere Wahrscheinlichkeit für eine zweitägige Durchlaufzeit, drei Tage und so weiter. All das bildet ein Histogramm der Wahrscheinlichkeiten für Durchlaufzeiten. Ebenso, wenn wir die Nachfrage für eine gegebene SKU an einem bestimmten Tag betrachten, können wir sagen, dass es eine Wahrscheinlichkeit gibt, null Einheiten Nachfrage, eine Einheit Nachfrage, zwei Einheiten Nachfrage und so weiter zu beobachten.

Wenn wir all diese Wahrscheinlichkeiten zusammenfassen, erhalten wir ein Histogramm, das sie darstellt. Ebenso, wenn wir über den Lagerbestand einer SKU nachdenken, könnten wir daran interessiert sein zu ermitteln, wie viel Bestand für diese bestimmte SKU am Ende der Saison übrig bleibt. Wir können eine probabilistische Vorhersage verwenden, um die Wahrscheinlichkeit zu bestimmen, dass am Ende der Saison null Einheiten auf Lager sind, eine Einheit auf Lager bleibt, zwei Einheiten und so weiter. All diese Situationen passen zu dem Muster, durch ein Histogramm dargestellt zu werden, in dem jedem einzelnen diskreten Ergebnis des interessierenden Phänomens ein Behälter zugeordnet ist.

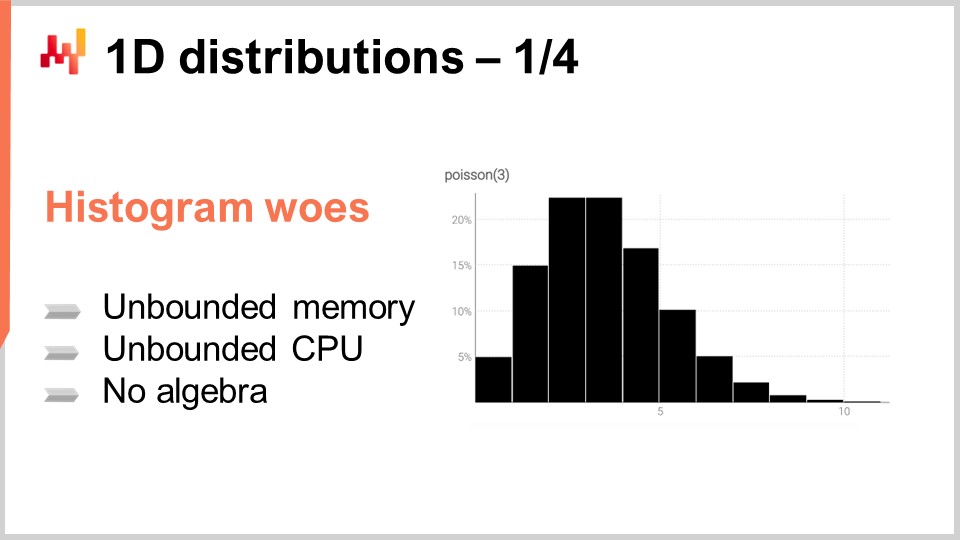
Das Histogramm ist die kanonische Methode, um eine eindimensionale diskrete Verteilung darzustellen. Jeder Behälter ist mit der Wahrscheinlichkeitsmasse des entsprechenden diskreten Ergebnisses verbunden. Abgesehen vom Anwendungsfall der Datenvisualisierung sind Histogramme jedoch etwas unspektakulär. In der Tat ist die Arbeit mit Histogrammen etwas mühsam, wenn wir mehr tun wollen als nur diese Wahrscheinlichkeitsverteilungen zu visualisieren. Wir haben im Wesentlichen zwei Klassen von Problemen mit Histogrammen: Die erste Schwierigkeit hängt mit den Rechenressourcen zusammen, und die zweite Schwierigkeit betrifft den Programmierausdruck von Histogrammen.

Im Hinblick auf Rechenressourcen sollten wir bedenken, dass der Speicherbedarf eines Histogramms grundsätzlich unbegrenzt ist. Man kann ein Histogramm als ein Array betrachten, das beliebig groß werden kann. Wenn man es mit einem einzelnen Histogramm zu tun hat, selbst mit einem außergewöhnlich großen aus supply chain-Sicht, ist der benötigte Speicher für einen modernen Computer unproblematisch. Das Problem entsteht, wenn man nicht nur ein Histogramm, sondern Millionen von Histogrammen für Millionen von SKUs in einem supply chain Kontext hat. Wenn jedes Histogramm ziemlich groß werden kann, kann die Verwaltung dieser Histogramme zu einer Herausforderung werden, insbesondere angesichts des nicht-uniformen Speicherzugriffs moderner Computer.

Umgekehrt ist auch der erforderliche CPU-Bedarf zur Verarbeitung dieser Histogramme unbegrenzt. Obwohl die Operationen an Histogrammen überwiegend linear erfolgen, steigt die Verarbeitungszeit mit zunehmendem Speicherbedarf aufgrund des nicht-uniformen Speicherzugriffs. Folglich besteht großes Interesse daran, strenge Grenzen für den benötigten Speicher und die CPU-Leistung festzulegen.

Die zweite Schwierigkeit bei Histogrammen ist das Fehlen einer zugehörigen Algebra. Zwar kann man die Werte zweier Histogramme bereichsweise addieren oder multiplizieren, allerdings führt dies nicht zu einer sinnvollen Darstellung, wenn man das Histogramm als Repräsentation einer Zufallsvariable interpretiert. Zum Beispiel, wenn man zwei Histogramme nimmt und punktweise multipliziert, erhält man ein Histogramm, das nicht einmal eine Gesamtmasse von eins hat. Dies ist aus der Perspektive einer Algebra von Zufallsvariablen keine gültige Operation. Tatsächlich kann man Histogramme nicht wirklich addieren oder multiplizieren, sodass man in dem, was man mit ihnen tun kann, eingeschränkt ist.

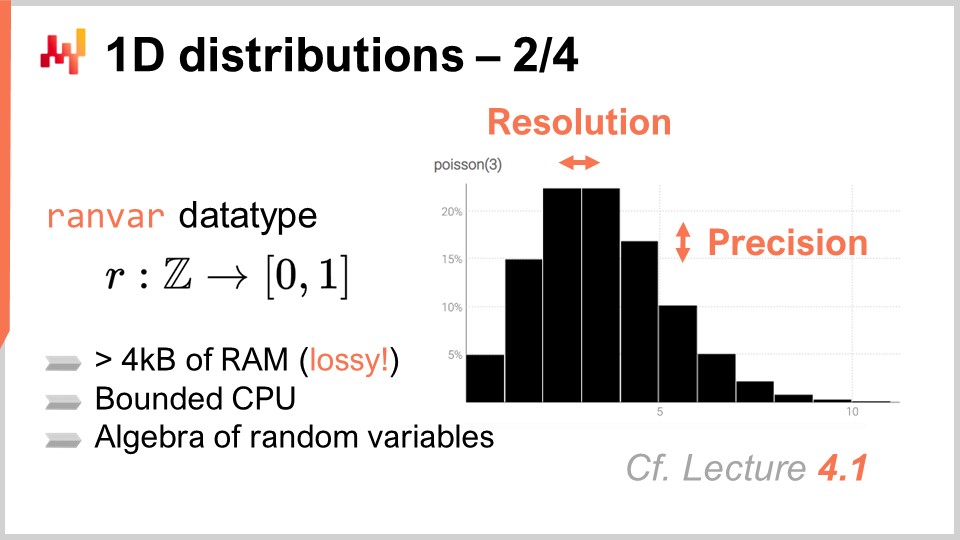
Bei Lokad ist der Ansatz, den wir als am praktikabelsten befunden haben, um mit diesen allgegenwärtigen eindimensionalen diskreten Verteilungen umzugehen, die Einführung eines dedizierten Datentyps. Das Publikum ist wahrscheinlich mit den gängigen Datentypen vertraut, die in den meisten Programmiersprachen existieren, wie Integer, Fließkommazahlen und Strings. Dies sind die typischen primitiven Datentypen, die überall zu finden sind. Dennoch hindert Sie nichts daran, speziellere Datentypen einzuführen, die besonders gut zu unseren Anforderungen aus supply chain-Sicht passen. Genau das hat Lokad mit dem Datentyp ranvar getan.

Der Datentyp ranvar ist speziell für eindimensionale diskrete Verteilungen vorgesehen, und der Name ist eine Abkürzung für random variable. Technisch, aus formaler Sicht, ist der ranvar eine Funktion von Z (der Menge aller ganzen Zahlen, positiv und negativ) zu Wahrscheinlichkeiten, welche Zahlen zwischen null und eins sind. Die Gesamtmasse von Z ist immer gleich eins, da sie Wahrscheinlichkeitsverteilungen repräsentiert.

Aus rein mathematischer Sicht könnte man argumentieren, dass die Menge an Informationen, die in eine solche Funktion einfließen können, beliebig groß werden kann. Das ist zwar wahr; jedoch ist die Realität, dass aus supply chain-Sicht eine sehr klare Grenze besteht, wie viel relevante Information in einem einzelnen ranvar enthalten sein kann. Obwohl es theoretisch möglich ist, eine Wahrscheinlichkeitsverteilung zu konstruieren, die Megabytes zur Darstellung benötigen würde, existiert keine solche Verteilung, die für supply chain-Zwecke relevant ist.

Es ist möglich, eine obere Grenze von 4 Kilobyte für den ranvar-Datentyp zu entwerfen. Indem wir ein Limit für den Speicherplatz festlegen, den dieser ranvar einnehmen kann, erhalten wir auch eine obere Grenze in Bezug auf die CPU-Leistung für alle Operationen, was sehr wichtig ist. Anstatt ein naives Limit zu haben, das die Buckets bei 1.000 begrenzt, führt Lokad ein Komprimierungsschema mit dem ranvar-Datentyp ein. Diese Komprimierung ist im Wesentlichen eine verlustbehaftete Darstellung der ursprünglichen Daten, bei der Auflösung und Genauigkeit verloren gehen. Die Idee besteht jedoch darin, ein Komprimierungsschema zu entwickeln, das eine hinreichend präzise Darstellung der Histogramme liefert, sodass der eingeführte Approximationsgrad aus der supply chain-Perspektive vernachlässigbar ist.

Das Kleingedruckte des Komprimierungsalgorithmus, der mit dem ranvar-Datentyp verbunden ist, liegt außerhalb des Rahmens dieser Vorlesung. Dies ist jedoch ein sehr einfacher Komprimierungsalgorithmus, der um Größenordnungen einfacher ist als die Arten von Komprimierungsalgorithmen, die für Bilder auf Ihrem Computer verwendet werden. Als Nebeneffekt des Speicherbegrenzungslimits, das für diesen ranvar festgelegt wird, erhalten wir ebenfalls eine obere Grenze in Bezug auf die CPU-Leistung für alle Operationen, was sehr wichtig ist. Schließlich ist mit dem ranvar-Datentyp der wichtigste Punkt, dass wir eine Algebra von Variablen erhalten, die uns einen Weg bietet, tatsächlich mit diesen Datentypen zu arbeiten und all die Arten von Operationen durchzuführen, die wir mit primitiven Datentypen durchführen möchten – nämlich alle möglichen Primitive zu kombinieren, um unseren Anforderungen zu genügen.

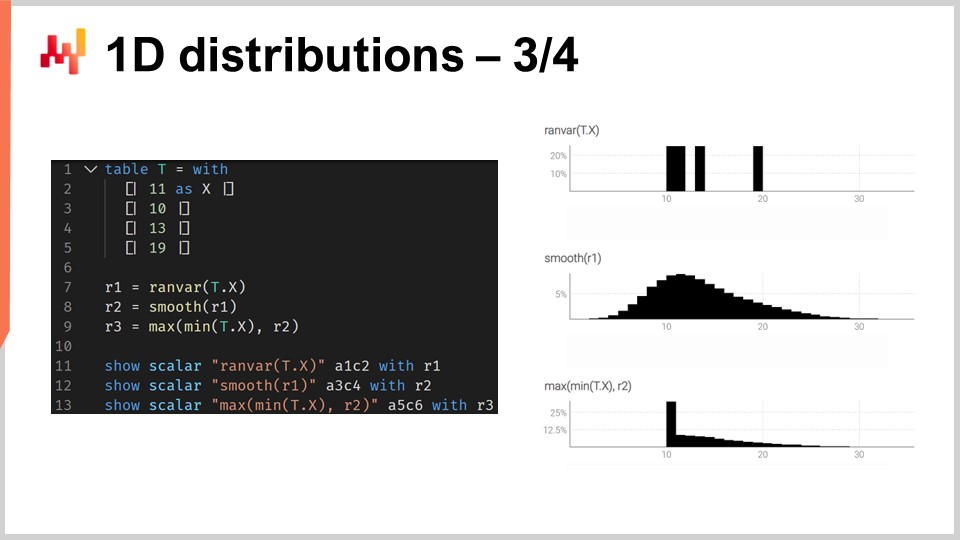
Um zu veranschaulichen, was es bedeutet, mit ranvars zu arbeiten, betrachten wir eine Situation der Durchlaufzeitvorhersage, genauer gesagt, eine probabilistische Vorhersage einer Durchlaufzeit. Auf dem Bildschirm ist ein kurzes Envision-Skript zu sehen, das zeigt, wie man eine solche probabilistische Vorhersage erstellt. In den Zeilen 1–5 führen wir die Tabelle T ein, die die vier Variationen der Durchlaufzeiten enthält, mit Werten von 11 Tagen, 10 Tagen, 13 Tagen und 90 Tagen. Zwar sind vier Beobachtungen sehr wenige, dennoch ist es leider sehr üblich, dass es nur eine äußerst begrenzte Anzahl von Datenpunkten bei Durchlaufzeitbeobachtungen gibt. Tatsächlich, wenn man einen ausländischen Lieferanten betrachtet, der pro Jahr zwei Bestellungen erhält, dauert es zwei Jahre, um diese vier Datenpunkte zu sammeln. Daher ist es wichtig, Techniken zu haben, die auch mit einem unglaublich begrenzten Satz von Beobachtungen arbeiten können.

Auf Zeile 7 erstellen wir einen ranvar, indem wir die vier Beobachtungen direkt aggregieren. Hier ist der Begriff “ranvar”, der in Zeile 7 erscheint, tatsächlich ein Aggregator, der eine Reihe von Zahlen als Eingabe nimmt und einen einzelnen Wert des ranvar-Datentyps zurückgibt. Das Ergebnis wird oben rechts auf dem Bildschirm angezeigt, was ein empirischer ranvar ist.

Dieser empirische ranvar ist jedoch keine realistische Darstellung der tatsächlichen Verteilung. Zum Beispiel, obwohl wir eine Durchlaufzeit von 11 Tagen und eine Durchlaufzeit von 13 Tagen beobachten können, erscheint es unrealistisch, dass eine Durchlaufzeit von 12 Tagen nicht beobachtet werden kann. Wenn wir diesen ranvar als probabilistische Vorhersage interpretieren, würde er besagen, dass die Wahrscheinlichkeit, jemals eine Durchlaufzeit von 12 Tagen zu beobachten, null ist, was inkorrekt erscheint. Dies ist offensichtlich ein Overfitting-Problem.

Um diese Situation zu beheben, glätten wir in Zeile 8 den ursprünglichen ranvar, indem wir die Funktion “smooth” aufrufen. Die Funktion smooth ersetzt im Wesentlichen den ursprünglichen ranvar durch eine Mischung von Verteilungen. Für jeden Bucket der ursprünglichen Verteilung ersetzen wir den Bucket durch eine Poisson-Verteilung mit einem Mittelwert, der auf den Bucket zentriert ist, gewichtet entsprechend der jeweiligen Wahrscheinlichkeit des Buckets. Durch die geglättete Verteilung erhalten wir das Histogramm, das in der Mitte rechts auf dem Bildschirm angezeigt wird. Das sieht schon viel besser aus; wir haben keine bizarren Lücken mehr und auch keine null Wahrscheinlichkeit in der Mitte. Zudem liefert dieses Modell bei der Betrachtung der Wahrscheinlichkeit einer 12-tägigen Durchlaufzeit eine von null verschiedene Wahrscheinlichkeit, was wesentlich plausibler klingt. Es liefert außerdem eine von null verschiedene Wahrscheinlichkeit, auch über 20 Tage hinauszugehen, und angesichts der Tatsache, dass wir vier Datenpunkte hatten und bereits eine Durchlaufzeit von 19 Tagen beobachtet haben, erscheint die Idee, dass eine Durchlaufzeit von bis zu 20 Tagen möglich ist, sehr vernünftig. Somit haben wir mit dieser probabilistischen Vorhersage eine schöne Verteilung, die eine von null verschiedene Wahrscheinlichkeit für diese Ereignisse darstellt, was sehr gut ist.

Auf der linken Seite jedoch haben wir etwas etwas Merkwürdiges. Während es in Ordnung ist, dass sich diese Wahrscheinlichkeitsverteilung nach rechts ausbreitet, gilt dies nicht für die linke Seite. Wenn man bedenkt, dass die beobachteten Durchlaufzeiten das Ergebnis von Transportzeiten waren – da es neun Tage dauert, bis der truck ankommt –, erscheint es unwahrscheinlich, dass wir jemals eine Durchlaufzeit von drei Tagen beobachten. In dieser Hinsicht ist das Modell recht unrealistisch.

Deshalb führen wir in Zeile 9 einen bedingt angepassten ranvar ein, indem wir festlegen, dass er größer sein muss als die kleinste jemals beobachtete Durchlaufzeit. Wir verwenden “min_of(T, x)”, was den kleinsten Wert aus den Zahlen der Tabelle T entnimmt, und nutzen dann “max”, um das Maximum zwischen einer Verteilung und einer Zahl zu bestimmen. Das Ergebnis muss größer als dieser Wert sein. Der angepasste ranvar wird ganz unten rechts angezeigt, und hier sehen wir unsere endgültige Durchlaufzeitvorhersage. Letztere erscheint als eine sehr vernünftige probabilistische Vorhersage der Durchlaufzeit, wenn man bedenkt, dass wir einen unglaublich begrenzten Datensatz mit nur vier Datenpunkten haben. Wir können nicht behaupten, dass es sich um eine hervorragende probabilistische Vorhersage handelt; jedoch würde ich argumentieren, dass dies eine Vorhersage in Produktionsqualität ist und dass derartige Techniken in der Produktion gut funktionieren würden, im Gegensatz zu einer durchschnittlichen Punktvorhersage, die das Risiko variierender Durchlaufzeiten stark unterschätzen würde.

Das Schöne an probabilistischen Vorhersagen ist, dass sie, obwohl sie sehr crude sein können, bereits ein gewisses Maß an Minderungspotenzial für schlecht informierte Entscheidungen bieten, die aus der naiven Anwendung einer Durchschnittsvorhersage basierend auf den beobachteten Daten resultieren würden.

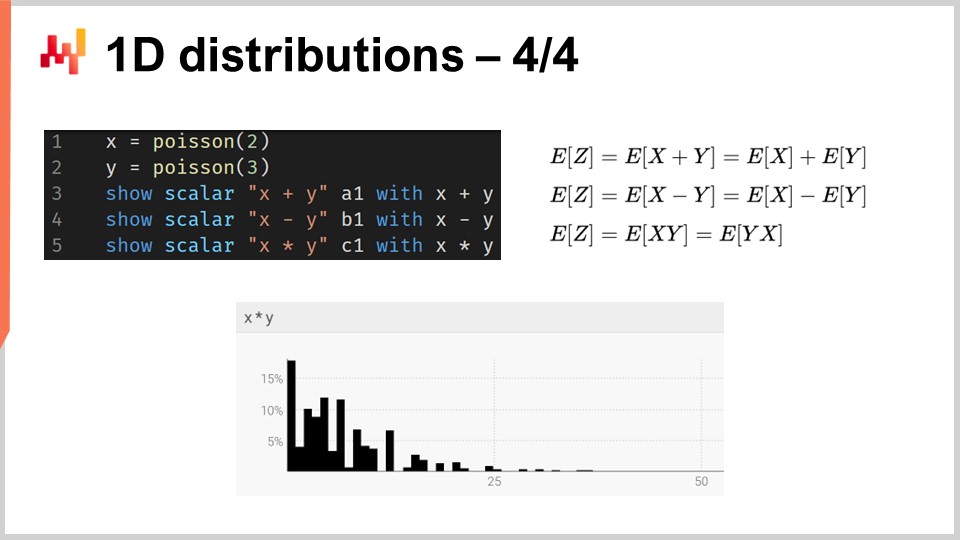
Generell unterstützen ranvars eine ganze Reihe von Operationen: Es ist möglich, ranvars zu addieren, zu subtrahieren und zu multiplizieren, genauso wie es möglich ist, Ganzzahlen zu addieren, zu subtrahieren und zu multiplizieren. Im Hintergrund, da es sich semantisch um diskrete Zufallsvariablen handelt, werden all diese Operationen als Faltungen implementiert. Auf dem Bildschirm wird das unten angezeigte Histogramm durch die Multiplikation von zwei Poisson-Verteilungen, nämlich mit den Mittelwerten zwei und drei, erzeugt. In der supply chain wird die Multiplikation von Zufallsvariablen als direkte Faltung bezeichnet. Im Kontext der supply chain ist die Multiplikation von zwei Zufallsvariablen sinnvoll, um beispielsweise die Ergebnisse darzustellen, die auftreten können, wenn Kunden nach denselben Produkten suchen, jedoch mit unterschiedlichen Multiplikatoren. Nehmen wir an, wir haben einen Buchladen, der zwei Kundenkohorten bedient. Auf der einen Seite haben wir die erste Kohorte, die aus Studenten besteht, die eine Einheit kaufen, wenn sie den Laden betreten. In diesem illustrativen Buchladen haben wir eine zweite Kohorte, die aus Professoren besteht, welche 20 Bücher kaufen, wenn sie den Laden betreten.

Aus modellierungstechnischer Sicht könnten wir eine probabilistische Vorhersage haben, die die Ankunftsraten im Buchladen entweder von Studenten oder von Professoren darstellt. Dies würde uns die Wahrscheinlichkeit anzeigen, an einem Tag null Kunden, einen Kunden, zwei Kunden usw. zu beobachten, und so die Wahrscheinlichkeitsverteilung der Anzahl der Kunden an einem beliebigen Tag offenbaren. Die zweite Variable würde uns die jeweiligen Wahrscheinlichkeiten anzeigen, entweder eine Einheit (Studenten) oder 20 Einheiten (Professoren) zu kaufen. Um eine Darstellung der Nachfrage zu erhalten, würden wir diese beiden Zufallsvariablen einfach multiplizieren, was zu einem scheinbar unregelmäßigen Histogramm führt, das die in den Konsummustern Ihrer Kohorten vorhandenen Multiplikatoren widerspiegelt.

Monte-Carlo-Generatoren oder einfach Generatoren stellen einen alternativen Ansatz zur probabilistischen Vorhersage dar. Anstatt eine Verteilung anzuzeigen, die uns die lokale Wahrscheinlichkeitsdichte liefert, können wir einen Generator präsentieren, der – wie der Name schon sagt – Ergebnisse generiert, von denen erwartet wird, dass sie implizit den gleichen lokalen Wahrscheinlichkeitsverteilungen folgen. Es besteht eine Dualität zwischen Generatoren und Wahrscheinlichkeitsdichten, was bedeutet, dass beide im Wesentlichen zwei Facetten derselben Perspektive darstellen.

Wenn Sie einen Generator haben, ist es immer möglich, die aus diesem Generator erhaltenen Ergebnisse zu mitteln, um Schätzungen der lokalen Wahrscheinlichkeitsdichten zu rekonstruieren. Umgekehrt ist es, falls Sie lokale Wahrscheinlichkeitsdichten haben, stets möglich, Ausreißer gemäß dieser Verteilung zu ziehen. Grundsätzlich sind diese beiden Ansätze lediglich unterschiedliche Wege, um die gleiche probabilistische oder stochastische Natur des Phänomens, das wir modellieren möchten, zu betrachten.

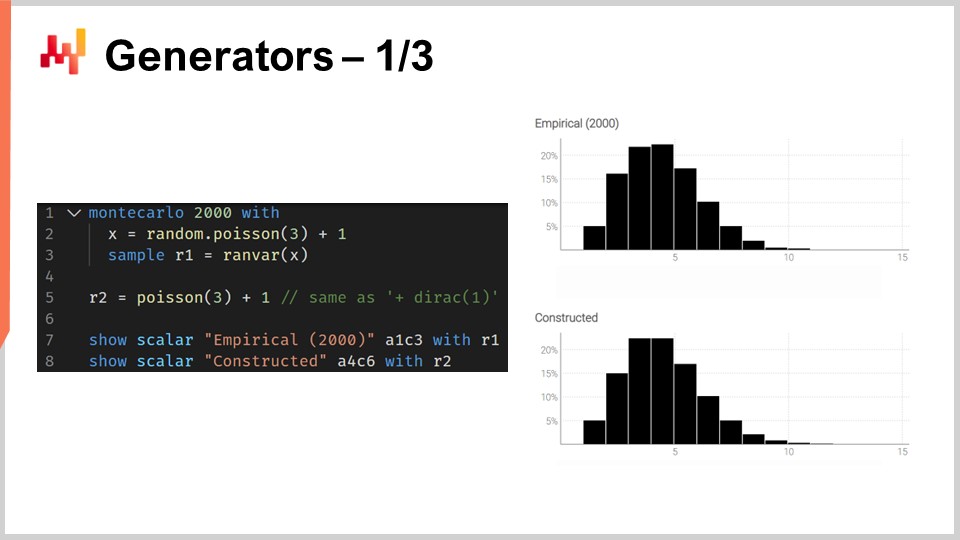
Das auf dem Bildschirm angezeigte Skript veranschaulicht diese Dualität. In Zeile eins führen wir einen Monte-Carlo-Block ein, der vom System iteriert wird, ähnlich wie die Auto-Differentiation-Blöcke durch viele Schritte des stochastischen Gradientenabstiegs iteriert werden. Der Monte-Carlo-Block wird 2.000-mal ausgeführt, und aus diesem Block werden wir 2.000 Abweichungen sammeln.

In Zeile zwei ziehen wir eine Abweichung aus einer Poisson-Verteilung mit einem Mittelwert von drei und addieren anschließend eins zur Abweichung. Im Wesentlichen erhalten wir eine Zufallszahl aus dieser Poisson-Verteilung und addieren dann eins. In Zeile drei sammeln wir diese Abweichung in L1, welche als Akkumulator für den Aggregator ranvar fungiert. Dies ist exakt derselbe Aggregator, den wir zuvor in unserem Beispiel zur Durchlaufzeit eingeführt haben. Hier sammeln wir all diese Beobachtungen in L1, was uns eine eindimensionale Verteilung liefert, die durch einen Monte-Carlo-Prozess gewonnen wurde. In Zeile fünf konstruieren wir dieselbe eindimensionale diskrete Verteilung, diesmal jedoch mit der Algebra der Zufallsvariablen. Wir verwenden also einfach Poisson minus drei und addieren eins. In Zeile fünf läuft kein Monte-Carlo-Prozess ab; es handelt sich dabei rein um diskrete Wahrscheinlichkeiten und Faltungen.

Wenn wir die beiden Verteilungen in den Zeilen sieben und acht visuell vergleichen, sehen wir, dass sie nahezu identisch sind. Ich sage “nahezu”, weil wir zwar 2.000 Iterationen verwenden, was eine Menge ist, aber es ist nicht unendlich. Die Abweichungen zwischen den exakten Wahrscheinlichkeiten, die man mit ranvar erhält, und den approximativen Wahrscheinlichkeiten, die man mit dem Monte-Carlo-Prozess erhält, sind noch bemerkbar, wenn auch nicht groß.

Generatoren werden manchmal Simulatoren genannt, aber irren Sie sich nicht – sie sind dasselbe. Wann immer Sie einen Simulator haben, liegt ein generativer Prozess zugrunde, der implizit einem probabilistischen Vorhersageprozess unterliegt. Immer wenn ein Simulator oder Generator involviert ist, sollte die Frage in den Vordergrund rücken: Wie genau ist diese Simulation? Sie ist von Design her nicht exakt, ebenso wie es sehr gut möglich ist, völlig ungenaue Vorhersagen zu erhalten, ob probabilistisch oder nicht. Es ist sehr leicht, eine völlig ungenaue Simulation zu erhalten.

Bei Generatoren sehen wir, dass Simulationen lediglich eine Möglichkeit sind, die Perspektive der probabilistischen Vorhersage zu betrachten, aber dies ist eher ein technisches Detail. Es ändert nichts an der Tatsache, dass man letztlich etwas haben möchte, das eine genaue Darstellung des Systems liefert, das man mit seiner Vorhersage charakterisieren möchte, ob probabilistisch oder nicht.

Der generative Ansatz ist nicht nur sehr nützlich, wie wir in Kürze an einem konkreten Beispiel sehen werden, sondern auch konzeptionell etwas leichter zu begreifen als der Ansatz mit Wahrscheinlichkeitsdichten. Allerdings ist auch der Monte-Carlo-Ansatz nicht ohne technische Details. Es gibt einige Dinge, die notwendig sind, wenn man diesen Ansatz in einem Produktionskontext für eine tatsächliche realweltliche supply chain funktionsfähig machen möchte.

Erstens müssen Generatoren schnell sein. Monte Carlo ist immer ein trade-off zwischen der Anzahl der gewünschten Iterationen und der Anzahl der Iterationen, die man sich angesichts der verfügbaren Rechenressourcen leisten kann. Ja, moderne Computer verfügen über viel Rechenleistung, aber Monte-Carlo-Prozesse können unglaublich ressourcenintensiv sein. Man möchte von vornherein etwas, das super schnell ist. Wenn wir zu den in der zweiten Vorlesung des vierten Kapitels eingeführten Komponenten zurückkehren, haben wir sehr schnelle Funktionen wie ExhaustShift oder WhiteHash, die wesentlich für den Aufbau der Primitiven sind, mit denen man elementare Zufalls-Generatoren erzeugt, die super schnell sind. Diese sind notwendig, sonst wird es schwierig. Zweitens muss die Ausführung verteilt werden. Die naive Implementierung eines Monte-Carlo-Programms besteht lediglich darin, eine Schleife zu haben, die sequentiell iteriert. Wenn man jedoch nur eine einzige CPU verwendet, um die Monte-Carlo-Anforderungen zu bewältigen, kehrt man im Grunde genommen zu der Rechenleistung zurück, die Computer vor zwei Jahrzehnten kennzeichnete. Dieser Punkt wurde in der allerersten Vorlesung des vierten Kapitels angesprochen. In den letzten zwei Jahrzehnten sind Computer zwar leistungsfähiger geworden, aber hauptsächlich durch Hinzufügen von CPUs und einem höheren Grad an Parallelisierung. Daher muss man für seine Generatoren eine verteilte Perspektive einnehmen.

Zuletzt muss die Ausführung deterministisch sein. Was bedeutet das? Es bedeutet, dass, wenn derselbe Code zweimal ausgeführt wird, er exakt dieselben Ergebnisse liefern sollte. Das mag kontraintuitiv erscheinen, da wir mit randomisierten Methoden arbeiten. Dennoch entstand der Bedarf an Determinismus sehr schnell. Dies wurde auf schmerzhafte Weise in den 90er Jahren festgestellt, als die Finanzwelt begann, Monte-Carlo-Generatoren für ihre Preisberechnungen zu verwenden. Die Finanzwelt hat vor einiger Zeit den Weg der probabilistischen Vorhersage eingeschlagen und machte ausgiebig von Monte-Carlo-Generatoren Gebrauch. Eine der Erkenntnisse war, dass es nahezu unmöglich wird, die Bedingungen, die einen Fehler oder einen Absturz verursacht haben, zu reproduzieren, wenn kein Determinismus vorhanden ist. Aus der Perspektive der supply chain können Fehler in der Berechnung von Bestellungen unglaublich kostspielig sein.

Wenn Sie ein gewisses Maß an Produktionsbereitschaft für die Software erreichen möchten, die Ihre supply chain steuert, müssen Sie diese deterministische Eigenschaft gewährleisten, wann immer Sie mit Monte Carlo arbeiten. Seien Sie sich bewusst, dass viele Open-Source-Lösungen aus der Akademie stammen und sich überhaupt nicht um Produktionsbereitschaft kümmern. Stellen Sie sicher, dass, wenn Sie mit Monte Carlo arbeiten, Ihr Prozess von vornherein super schnell, verteilt und deterministisch gestaltet ist, damit Sie in der Lage sind, die Fehler zu diagnostizieren, die in Ihrem Produktions-Setup im Laufe der Zeit unvermeidlich auftreten werden.

Wir haben eine Situation gesehen, in der ein Generator eingeführt wurde, um das zu replizieren, was sonst mit einem ranvar durchgeführt wurde. Als Faustregel gilt, dass es besser ist, wenn man mit reinen Wahrscheinlichkeitsdichten und Zufallsvariablen auskommen kann, ohne Monte Carlo einzubeziehen. So erhält man präzisere Ergebnisse und muss sich nicht um die numerische Stabilität sorgen, die bei Monte Carlo immer etwas heikel ist. Allerdings ist der Ausdrucksvermögen der Algebra der Zufallsvariablen begrenzt, und hier glänzt Monte Carlo wirklich. Diese Generatoren sind ausdrucksstärker, weil sie es ermöglichen, Situationen zu erfassen, die mit bloßer Algebra der Zufallsvariablen nicht angegangen werden können.

Lassen Sie uns dies anhand einer supply chain-Situation veranschaulichen. Betrachten Sie einen einzelnen SKU mit einem anfänglichen Lagerbestand, einer probabilistischen Prognose für die Nachfrage und einem interessierenden Zeitraum von drei Monaten, mit einer eingehenden Lieferung in der Mitte des Zeitraums. Wir nehmen an, dass die Nachfrage entweder sofort aus dem vorhandenen Lagerbestand bedient wird oder für immer verloren geht. Wir möchten den erwarteten Lagerbestand am Ende des Zeitraums für den SKU kennen, da uns dies dabei hilft, zu entscheiden, wie viel Risiko wir in Bezug auf tote Lagerbestände haben.

Die Situation ist tückisch, weil sie so gestaltet wurde, dass es in der Mitte des Zeitraums eine dritte Möglichkeit für einen Fehlbestand gibt. Der naive Ansatz bestünde darin, den anfänglichen Lagerbestand, die Verteilung der Nachfrage für den gesamten Zeitraum zu übernehmen und die Nachfrage vom Lagerbestand abzuziehen, was zum verbleibenden Lagerbestand führt. Dies berücksichtigt jedoch nicht die Tatsache, dass wir einen erheblichen Teil der Nachfrage verlieren könnten, falls es zu einem Fehlbestand kommt, während die eingehende Lagerauffüllung noch aussteht. Die naive Vorgehensweise würde den Lagerbestand am Ende des Zeitraums unterschätzen und die bediente Nachfrage überschätzen.

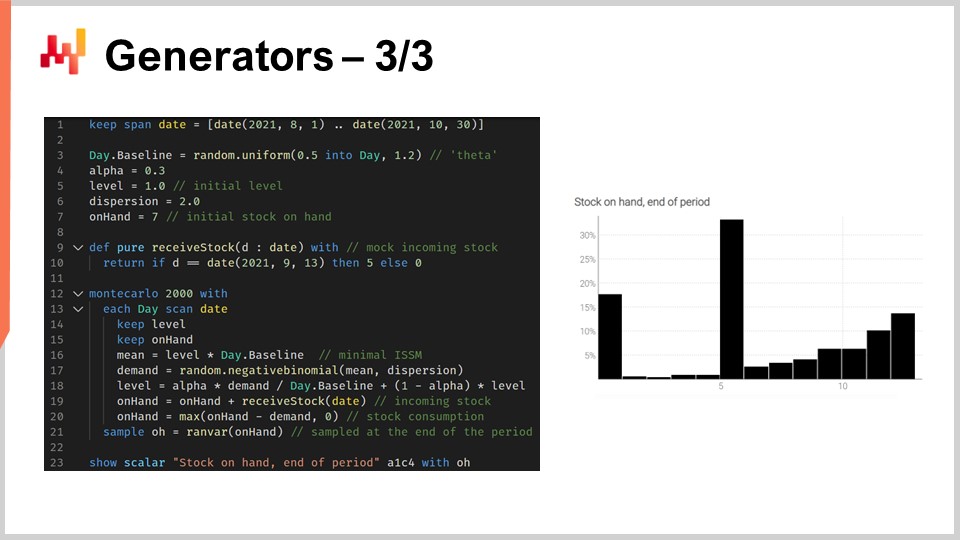
Das angezeigte Skript modelliert das Auftreten von Fehlbeständen, sodass wir einen korrekten Schätzer für den Lagerbestand dieses SKU am Ende des Zeitraums erhalten können. In den Zeilen 1 bis 10 definieren wir die Mock-Daten, die unser Modell charakterisieren. Die Zeilen 3 bis 6 enthalten die Parameter für das ISSM-Modell. Das ICSM-Modell haben wir bereits in der allerersten Vorlesung dieses fünften Kapitels gesehen. Im Wesentlichen generiert dieses Modell eine Nachfrageentwicklung mit einem Datenpunkt pro Tag. Der interessierende Zeitraum wird in der Tages-Tabelle definiert, und die Parameter für diese Entwicklung befinden sich ganz am Anfang.

In den vorherigen Vorlesungen haben wir das AICSM-Modell und die erforderlichen Methoden durch differenzierbares Programmieren eingeführt, um diese Parameter zu erlernen. Heute verwenden wir das Modell in der Annahme, dass wir alles gelernt haben, was wir lernen müssen. In Zeile 7 definieren wir den anfänglichen Lagerbestand, der typischerweise aus dem ERP oder WMS bezogen wird. In den Zeilen 9 und 10 definieren wir die Menge und das Datum für die Lagerauffüllung. Diese Datenpunkte würden typischerweise als geschätzte Ankunftszeit, die vom Lieferanten angegeben und im ERP gespeichert wird, erfasst. Wir gehen davon aus, dass das Lieferdatum exakt bekannt ist; es wäre jedoch unkompliziert, dieses einzelne Datum durch eine probabilistische Prognose der Lieferzeit zu ersetzen.

In den Zeilen 12 bis 21 haben wir das ISSM-Modell, das die Nachfrageentwicklung generiert. Wir befinden uns in einer Monte-Carlo-Schleife, und für jede Monte-Carlo-Iteration iterieren wir über jeden einzelnen Tag des interessierenden Zeitraums. Die Iteration der Tage beginnt in Zeile 13. Die ESSM-Mechaniken sind aktiv, aber in den Zeilen 19 und 20 aktualisieren wir die Variable für den aktuellen Lagerbestand. Diese Variable gehört nicht zum ISSM-Modell; das ist etwas Zusätzliches. In Zeile 19 legen wir fest, dass der aktuelle Lagerbestand dem Lagerbestand vom Vortag plus der eingehenden Lieferung entspricht, die an den meisten Tagen null beträgt und am 13. September fünf Einheiten liefert. Anschließend aktualisieren wir in Zeile 20 den Lagerbestand, indem wir festlegen, dass eine bestimmte Anzahl von Einheiten durch die Nachfrage des Tages verbraucht wird, und wir wenden ein max 0 an, um sicherzustellen, dass der Lagerbestand nicht ins Negative geht.

Abschließend sammeln wir in Zeile 21 den finalen Lagerbestand, und in Zeile 23 wird dieser finale Lagerbestand angezeigt. Dies ist das Histogramm, das Sie rechts auf dem Bildschirm sehen. Hier erkennen wir eine Verteilung mit einer sehr unregelmäßigen Form. Diese Form kann nicht durch die Algebra der Zufallsvariablen erzielt werden. Generatoren sind unglaublich ausdrucksstark; dennoch sollten Sie die Ausdruckskraft dieser Generatoren nicht mit Genauigkeit verwechseln. Obwohl Generatoren sehr ausdrucksstark sind, ist es alles andere als trivial, die Genauigkeit solcher Generatoren zu bewerten. Seien Sie versichert, dass, sobald ein Generator oder Simulator zum Einsatz kommt, auch immer eine Wahrscheinlichkeitsprognose im Spiel ist, und Simulationen können, wie jede Prognose, probabilistisch oder anders, dramatisch ungenau sein.

Es war bereits eine lange Vorlesung, und dennoch gibt es viele Themen, die ich heute noch gar nicht angesprochen habe. Entscheidungsfindung, zum Beispiel: Wenn alle Zukünfte möglich sind, wie treffen wir dann überhaupt Entscheidungen? Diese Frage habe ich nicht beantwortet, aber sie wird in der nächsten Vorlesung behandelt.

Auch höhere Dimensionen sind wichtig zu berücksichtigen. Eine eindimensionale Verteilung ist ein Anfang, aber eine supply chain benötigt mehr. Zum Beispiel, wenn es bei einem bestimmten SKU zu einem Fehlbestand kommt, kann es zu Kannibalisierung kommen, bei der Kunden natürlich auf ein Ersatzprodukt zurückgreifen. Wir möchten dies modellieren, wenn auch in grober Form.

Höherstufige Konstrukte spielen ebenfalls eine Rolle. Wie ich sagte, ist die Prognose der Nachfrage nicht mit der Vorhersage der Bewegungen der Planeten vergleichbar. Wir haben überall selbstprophetische Effekte. Irgendwann wollen wir unsere Preisstrategien und Bestandsauffüllungsrichtlinien berücksichtigen und einbeziehen. Dazu benötigen wir höherstufige Konstrukte, was bedeutet, dass man, gegeben eine Richtlinie, eine probabilistische Prognose des Ergebnisses erhält, jedoch muss die Richtlinie in die höherstufigen Konstrukte eingebracht werden.

Darüber hinaus erfordert das Beherrschen probabilistischer Prognosen zahlreiche numerische Verfahren und fachspezifisches Wissen, um zu wissen, welche Verteilungen am ehesten zu bestimmten Situationen passen. In dieser Vorlesungsreihe werden wir später weitere Beispiele vorstellen.

Schließlich gibt es die Herausforderung des Wandels. Probabilistische Prognosen sind ein radikaler Bruch mit den herkömmlichen Praktiken in der supply chain. Häufig machen die technischen Details, die mit probabilistischen Prognosen verbunden sind, nur einen kleinen Teil der Herausforderung aus. Der schwierige Teil besteht darin, die Organisation selbst neu zu erfinden, sodass sie beginnt, diese probabilistischen Prognosen anstelle von Punktprognosen zu nutzen, die im Grunde genommen Wunschdenken sind. All diese Aspekte werden in späteren Vorlesungen behandelt, aber es wird Zeit brauchen, da viel Stoff abzuhandeln ist.

Zusammenfassend stellen probabilistische Prognosen einen radikalen Bruch mit der Perspektive der Punktprognose dar, bei der man irgendeine Art von Konsens über die eine Zukunft erwartet, die eintreten soll. Die probabilistische Prognose basiert auf der Beobachtung, dass die Unsicherheit der Zukunft irreduzibel ist. Ein Jahrhundert der Prognosewissenschaft hat gezeigt, dass alle Versuche, auch nur annähernd genaue Prognosen zu erstellen, gescheitert sind. Somit sind wir mit vielen unbestimmten Zukünften konfrontiert. Probabilistische Prognosen bieten uns jedoch Techniken und Werkzeuge, um diese Zukünfte zu quantifizieren und zu bewerten. Probabilistische Prognosen sind eine bedeutende Errungenschaft. Es hat fast ein Jahrhundert gedauert, bis man akzeptierte, dass wirtschaftliche Prognosen nicht wie Astronomie sind. Während wir die exakte Position eines Planeten in einem Jahrhundert mit großer Genauigkeit vorhersagen können, haben wir keine Hoffnung, jemals etwas auch nur annähernd Vergleichbares im Bereich der supply chain zu erreichen. Die Idee, eine einzige Prognose zu haben, die alle regiert, kehrt einfach nicht zurück. Dennoch klammern sich viele Unternehmen weiterhin an die Hoffnung, dass irgendwann einmal die eine wahre, genaue Prognose erreicht wird. Nach einem Jahrhundert des Versuchens ist dies im Wesentlichen Wunschdenken.

Mit modernen Computern ist die Perspektive der einen Zukunft nicht die einzige vorherrschende Perspektive. Wir haben Alternativen. Probabilistische Prognosen gibt es bereits seit den 90er Jahren, also vor drei Jahrzehnten. Bei Lokad nutzen wir probabilistische Prognosen seit über einem Jahrzehnt, um supply chains in der Produktion zu steuern. Es mag noch nicht Mainstream sein, aber es ist weit davon entfernt, Science-Fiction zu sein. Es ist seit drei Jahrzehnten in vielen Finanzunternehmen Realität und seit einem Jahrzehnt in der supply chain-Welt.

Obwohl probabilistische Prognosen einschüchternd und hoch technisch erscheinen mögen, sind sie mit den richtigen Werkzeugen nur ein paar Codezeilen. Es gibt nichts grundsätzlich Schwieriges oder Herausforderndes an probabilistischen Prognosen, zumindest nicht im Vergleich zu anderen Arten von Prognosen. Die größte Herausforderung besteht darin, den Komfort aufzugeben, der mit der Illusion verbunden ist, dass die Zukunft perfekt kontrollierbar sei. Die Zukunft ist nicht perfekt kontrollierbar und wird es auch nie sein, und alles in allem ist das wahrscheinlich zum Besten.

Damit endet die heutige Vorlesung. Nächstes Mal, am 6. April, werde ich die Entscheidungsfindung beim Versand des Einzelhandelsinventars präsentieren, und wir werden sehen, wie die heute vorgestellten probabilistischen Prognosen genutzt werden können, um eine grundlegende Entscheidung in der supply chain zu treffen, nämlich die Bestandsauffüllung in einem Einzelhandelsnetz. Die Vorlesung findet am selben Wochentag, Mittwoch, zur selben Tageszeit, 15 Uhr, statt, und zwar am ersten Mittwoch im April.

Frage: Können wir die Auflösung bezüglich Präzision gegenüber dem RAM-Volumen für Envision optimieren?

Ja, absolut, wenn auch nicht in Envision selbst. Dies ist eine Entscheidung, die wir bei der Gestaltung von Envision getroffen haben. Mein Ansatz bei Supply Chain Scientist besteht darin, sie von niedrigstufigen technischen Details zu befreien. Envisions 4 Kilobytes bieten viel Raum, um Ihre supply chain-Situation präzise darzustellen. Die dabei verlorene Genauigkeit in Bezug auf Auflösung und Präzision ist also unerheblich.

Zweifellos gibt es beim Entwurf Ihres Kompressionsalgorithmus zahlreiche Abwägungen zu berücksichtigen. Zum Beispiel müssen Buckets, die sehr nahe bei Null liegen, eine perfekte Auflösung haben. Wenn Sie die Wahrscheinlichkeit berechnen möchten, null Einheiten Nachfrage zu beobachten, möchten Sie nicht, dass Ihre Approximation die Buckets für null, eine oder zwei Einheiten zusammenfasst. Wenn Sie jedoch Buckets für die Wahrscheinlichkeit von 1.000 nachgefragten Einheiten betrachten, ist es wahrscheinlich in Ordnung, wenn 1.000 und 1.001 Einheiten zusammengefasst werden. Es gibt also viele Tricks, um einen Kompressionsalgorithmus zu entwickeln, der wirklich den Anforderungen der supply chain entspricht. Dies ist um Größenordnungen einfacher im Vergleich zu dem, was bei der Bildkompression vor sich geht. Meiner Meinung nach würde ein korrekt gestaltetes Tooling das Problem für die Supply Chain Scientist grundsätzlich abstrahieren. Das ist zu niedrigstufig, und in den meisten Fällen müssen Sie nicht mikro-optimieren. Wenn Sie Walmart wären und nicht nur 1 Million SKUs, sondern mehrere hundert Millionen SKUs hätten, könnte Mikro-Optimierung Sinn machen. Andernfalls, sofern von übermäßig großen supply chains nicht die Rede ist, bin ich überzeugt, dass Sie etwas haben können, das gut genug ist, sodass der Leistungseinbruch durch fehlende vollständige Optimierung größtenteils unerheblich ist.

Frage: Welche praktischen Überlegungen sind aus supply chain-Perspektive bei der Optimierung dieser Parameter zu berücksichtigen?

Bei probabilistischen Prognosen in der supply chain ist eine Präzision von mehr als einem zu 100.000 in der Regel unerheblich, einfach weil man nie genügend Daten hat, um eine Genauigkeit bei der Schätzung der Wahrscheinlichkeiten zu erreichen, die feiner aufgelöst ist als ein Anteil von 1 zu 100.000.

Frage: Welche Branche profitiert am meisten von dem probabilistischen Prognoseansatz?

Die kurze Antwort lautet: Je unregelmäßiger und unvorhersehbarer Ihre Muster sind, desto größer sind die Vorteile. Bei intermittierender Nachfrage gibt es große Vorteile; bei unregelmäßiger Nachfrage ebenso; und wenn die Lieferzeiten stark variieren und Ihre supply chains von unregelmäßigen Schocks betroffen sind, profitieren Sie am meisten. Am anderen Ende des Spektrums, nehmen wir beispielsweise die supply chain der Wasserversorgung, ist der Wasserverbrauch extrem gleichmäßig und weist fast nie große Schocks auf – höchstens Mikroschocks. Dies ist die Art von Problem, das nicht vom probabilistischen Ansatz profitiert. Die Idee ist, dass es einige Situationen gibt, in denen klassische Punktprognosen sehr genaue Vorhersagen liefern. Wenn Sie sich in einer Situation befinden, in der Ihre Prognosen für alle Produkte einen Fehler von weniger als fünf Prozent aufweisen, dann brauchen Sie keine probabilistischen Prognosen; Sie befinden sich in einer Situation, in der eine wirklich genaue Prognose tatsächlich funktioniert. Wenn Sie jedoch wie viele Unternehmen in Situationen sind, in denen Ihre Prognosegenauigkeit sehr niedrig ist, mit Abweichungen von 30% oder mehr, dann profitieren Sie erheblich von probabilistischen Prognosen. Übrigens, wenn ich von einem Prognosefehler von 30% spreche, beziehe ich mich stets auf die sehr disaggregierte Prognose. Viele Unternehmen werden Ihnen sagen, dass ihre Prognosen zu 5% genau sind, aber wenn man alles aggregiert, kann dies ein sehr trügerisches Bild der tatsächlichen Prognosegenauigkeit vermitteln. Ihre Prognosegenauigkeit zählt nur auf der disaggregiertesten Ebene, typischerweise auf SKU-Ebene und auf Tagesbasis, da Ihre Entscheidungen ebenfalls auf SKU- und Tagesebene getroffen werden. Wenn Sie auf SKU-Ebene und Tagesebene Ihre disaggregiertesten Prognosen mit einer Genauigkeit von 5% erreichen, dann brauchen Sie keine probabilistischen Prognosen. Beobachten Sie jedoch zweistellige Ungenauigkeiten in Prozent, so profitieren Sie erheblich von probabilistischen Prognosen.

Frage: Da Lieferzeiten saisonal bedingt sein können, würden Sie die Lieferzeitprognosen in mehrere aufteilen, jeweils eine für jede einzelne Saison, um zu vermeiden, dass man eine multimodale Verteilung sieht?

Das ist eine gute Frage. Die Idee ist, dass man typischerweise ein parametrisches Modell für seine Lieferzeiten erstellt, das ein Saisonalitätsprofil beinhaltet. Der Umgang mit Saisonalität bei Lieferzeiten unterscheidet sich im Grunde nicht wesentlich vom Umgang mit anderen zyklischen Schwankungen, wie wir es in der vorherigen Vorlesung bei der Nachfrage gemacht haben. Der übliche Weg ist, nicht mehrere Modelle zu erstellen, denn wie Sie richtig bemerkt haben, wird man bei mehreren Modellen allerlei bizarre Sprünge beobachten, wenn man von einer Modalität zur nächsten wechselt. Es ist in der Regel besser, einfach ein Modell mit einem Saisonalitätsprofil in der Mitte zu haben. Es wäre wie eine parametrische Zerlegung, bei der man einen Vektor hat, der den wöchentlichen Effekt angibt, der die Lieferzeit in einer bestimmten Woche des Jahres beeinflusst. Vielleicht haben wir in einer späteren Vorlesung Zeit, ein ausführlicheres Beispiel dafür zu geben.

Frage: Ist probabilistic forecasting ein guter Ansatz, wenn man eine intermittierende Nachfrage vorhersagen möchte?

Absolut. Tatsächlich glaube ich, dass wenn Sie intermittierende Nachfrage haben, probabilistic forecasting nicht nur eine gute Methode ist, sondern die klassische Punktprognose völlig unsinnig wäre. Mit der klassischen Prognose hätten Sie typischerweise Schwierigkeiten, mit all den Nullen umzugehen. Was sollen Sie mit diesen Nullen anfangen? Am Ende erhalten Sie einen sehr niedrigen, bruchteiligen Wert, der eigentlich keinen Sinn ergibt. Bei intermittierender Nachfrage ist die Frage, die Sie wirklich beantworten wollen: Ist mein Lagerbestand groß genug, um diese gelegentlichen Nachfragespitzen zu bedienen? Wenn Sie eine Durchschnittsprognose verwenden, werden Sie das niemals herausfinden.

Um zum Beispiel der Buchhandlung zurückzukommen: Wenn Sie sagen, dass in einer gegebenen Woche im Durchschnitt eine Einheit Nachfrage pro Tag beobachtet wird, wie viele Bücher müssen Sie in Ihrer Buchhandlung vorrätig haben, um eine hohe Servicequalität zu gewährleisten? Nehmen wir an, dass die Buchhandlung jeden einzelnen Tag nachgefüllt wird. Wenn die einzigen Kunden Studenten sind und Sie im Durchschnitt täglich eine Nachfrageeinheit haben, führt ein Lagerbestand von drei Büchern zu einer sehr hohen Servicequalität. Sollte jedoch gelegentlich ein Professor hereinkommen, der auf einmal 20 Bücher sucht, wird Ihre Servicequalität – wenn Sie nur drei Bücher im Laden haben – katastrophal sein, weil Sie niemals in der Lage sein werden, einen der Professoren zu bedienen. Dies ist typischerweise der Fall bei intermittierender Nachfrage – es geht nicht nur darum, dass die Nachfrage intermittierend ist, sondern auch darum, dass manche Nachfragespitzen hinsichtlich ihrer Größenordnung erheblich variieren können. Genau hier zeigt probabilistic forecasting seine Stärken, da es die feine Struktur der Nachfrage erfassen kann, anstatt alles in Durchschnittswerten zusammenzufassen, in denen diese feine Struktur verloren geht.

Frage: Wenn wir die Lieferzeit durch eine Verteilung ersetzen, wird dann der Ausschlag, der auf der ersten Folie des Generators als glatte Glockenkurve dargestellt wird?

Bis zu einem gewissen Grad neigen zufällige Prozesse dazu, die Werte zu streuen. Auf der ersten Folie zum Generator müssten wir das Experiment mit verschiedenen Einstellungen durchführen, um zu sehen, was wir erhalten. Die Idee ist, dass wir, wenn wir die Lieferzeit durch eine Verteilung ersetzen, dies tun, weil wir ein Verständnis des Problems haben, das uns zeigt, dass die Lieferzeit variiert. Wenn wir unserem Lieferanten absolut vertrauen und er unglaublich zuverlässig war, dann ist es völlig in Ordnung zu sagen, dass die ETA (estimated time of arrival) das ist, was sie ist, und eine nahezu perfekte Schätzung des tatsächlichen Wertes darstellt. Wenn wir jedoch in der Vergangenheit gesehen haben, dass Lieferanten manchmal unbeständig waren oder ihr Ziel verfehlten, dann ist es besser, die Lieferzeit durch eine Verteilung zu ersetzen.

Die Einführung einer Verteilung zur Ersetzung der Lieferzeit glättet nicht notwendigerweise die Ergebnisse, die man am Ende erhält; es hängt davon ab, worauf man schaut. Zum Beispiel kann bei Betrachtung des extremsten Falls von Überbestand eine variable Lieferzeit sogar das Risiko von abgestorbenem Inventar verschärfen. Warum ist das so? Wenn Sie ein sehr saisonales Produkt und eine variable Lieferzeit haben und das Produkt nach Ende der Saison eintrifft, bleiben Sie mit einem Produkt zurück, das nicht mehr zur Saison passt, was das Risiko von abgestorbenem Inventar am Saisonende vergrößert. Daher ist das heikel. Die Tatsache, dass Sie eine Variable durch ihren probabilistischen Ersatz ersetzen, glättet nicht automatisch das, was Sie beobachten werden; manchmal kann es die Verteilung sogar noch schärfer machen. Die Antwort lautet also: Es kommt darauf an.

Ausgezeichnet, ich denke, das war es für heute. Bis zum nächsten Mal.