Priorisierte Bestandsauffüllung in Excel mit probabilistischen Prognosen
Unsicherheit ist ein unvermeidlicher Aspekt der Prognose. Dennoch entstand im 20. Jahrhundert die statistische Prognose mit der Hoffnung, dass Unsicherheit durch geeignete mathematische Modelle eliminiert werden könnte. Als Ergebnis spielten frühe Supply-Chain-Theorien die Unsicherheit herunter oder lehnten sie ab, da neuere oder bessere Prognoseverfahren erwartet wurden, sie zu eliminieren oder, falls dies nicht gelingt, sie unbedeutend zu machen. Obwohl gut gemeint, waren diese Ansätze fehlerhaft, da die Unsicherheit nach einem Jahrhundert statistischer Modellierung hartnäckig unvermeidlich bleibt. Im Jahr 2012 führte Lokad eine alternative Supply-Chain-Perspektive ein, die Unsicherheit akzeptiert und quantifiziert. Dieser Ansatz nutzt probabilistische Prognosen anstelle der klassischen Punkt-Zeitreihen Prognosen. In diesem Leitfaden und der begleitenden Microsoft Excel-Tabelle wenden wir probabilistische Prognosen auf das Auffüllungsproblem des Bestands an. Dieser Ansatz führt zu einer priorisierten Bestandsauffüllungspolitik, die hier durch Excel demonstriert wird. Unser Ziel ist zweifach: Erstens, diesen Ansatz einem Publikum zu popularisieren, das möglicherweise nicht mit fortschrittlicheren Softwaretools vertraut ist; und zweitens, zu demonstrieren, dass die Akzeptanz von Unsicherheit mehr eine bestimmte Denkweise erfordert als ausgefeilte Werkzeuge.
Download: probabilistic-inventory-replenishment.xlsx
1. Das Problem der Bestandsauffüllung
Das Problem der Bestandsauffüllung konzentriert sich auf die Identifizierung der besten Einkaufsliste - eine, die die Kernfinanzbeschränkungen und -ziele des Unternehmens berücksichtigt. Die Methode zur Erstellung einer solchen Liste sollte ebenso gut funktionieren, unabhängig von Budgetbeschränkungen, da die Methode versucht, die Rendite für jeden ausgegebenen Dollar zu maximieren. Das Problem besteht darin, dass alle SKUs um die gleichen Dollar konkurrieren, daher muss der finanzielle Ertrag der Lagerung einer beliebigen Einheit eines SKU quantifiziert und im Kontext aller zusätzlichen Einheiten jedes SKU eingestuft werden.
1.1 Die Lösung für die priorisierte Bestandsauffüllung
Der Prozess der Bestandsbewertung, wie oben beschrieben, erfordert eine Mikro-Perspektive. Um die Rendite aus der Hinzufügung einer beliebigen Einheit eines SKU zu einer Einkaufsliste zu vergleichen, müssen mehrere Faktoren berücksichtigt werden. Nämlich die Wahrscheinlichkeit seines Verkaufs, wie sie von einer probabilistischen Nachfrageprognose und den wirtschaftlichen Treibern - z.B. Bruttogewinnspanne und Einkaufspreis - bereitgestellt wird. Jede in Betracht gezogene Menge muss wiederum im Hinblick auf interne und externe Beschränkungen (wie begrenzte Lagerhaus Kapazität, Losmultiplikatoren und MOQs/MOVs, etc.) abgewogen werden. Randfälle, wie wenn zwei (oder mehr) Einheiten die gleiche erwartete Rentabilität haben, müssen durch die Bewertung der relativen Bedeutung jedes Produkts in eine Bestandsauffüllungspolitik einbezogen werden. SKUs sollten nicht isoliert betrachtet werden, sondern in Körben. Einige SKUs, obwohl sie in Isolation niedrigere Gewinnspannen haben (wie Milch), sind wichtiger, da sie Verkäufe ermöglichen von Produkten mit hoher Marge. Daher stellt die finanzielle Belohnung für die Aufrechterhaltung von Service Levels eines Produkts mit niedrigerer Marge - eines, das andere Verkäufe ermöglicht - einen weiteren Treiber (“stockout cover”)1 dar. Ein Ansatz zur priorisierten Bestandsauffüllung (PIR), der probabilistische Prognosen als Eingabe nutzt, berücksichtigt alle oben beschriebenen Faktoren.
Kurz gesagt, die PIR-Lösung kann in drei Schritten zusammengefasst werden:
1. Erstellen Sie eine probabilistische Nachfrageprognose.
2. Listen Sie alle möglichen Bestellmengen auf.
3. Bewerten Sie alle möglichen Bestellmengen mit wirtschaftlichen Treibern.
1.2 Priorisierte Lagerauffüllung in Excel
Mit Hilfe von Finanzdaten für einen fiktiven Laden, einschließlich der in dem vorherigen Abschnitt aufgeführten wirtschaftlichen Treiber, modelliert diese Excel-Tabelle die Lagerauffüllungspolitik für drei SKUs (Stifte, Tastaturen und Bücherregale)2. Die finanziellen Auswirkungen jeder zusätzlichen Einheit von SKU (falls bestellt) und die Wahrscheinlichkeit, sie zu verkaufen, sind im Charts-Blatt dargestellt (siehe Abbildung 1). Die Diagramme und Charts werden sich je nach den Eingaben und den Modellannahmen (z.B. Anfangsbestände, Kauf- und Verkaufspreise usw.) im Control Tower-Blatt (Abbildung 2) aktualisieren. Eine detaillierte Liste der möglichen Entscheidungsoptionen wird im Micro purchasing decisions-Blatt (Abbildung 3) auf der Grundlage der Schlüsselinputs erstellt. Diese Inputs sind die probabilistischen Nachfrageprognosen aus dem Distribution generators-Blatt (Abbildung 4) und die Inputs aus dem Control Tower-Blatt. Schließlich wird eine Tabelle mit priorisierten Lagerauffüllungsentscheidungen zusammengestellt und hinsichtlich der erwarteten Rendite auf das investierte Kapital eingestuft (siehe Ranked purchasing decisions-Blatt in Abbildung 5).
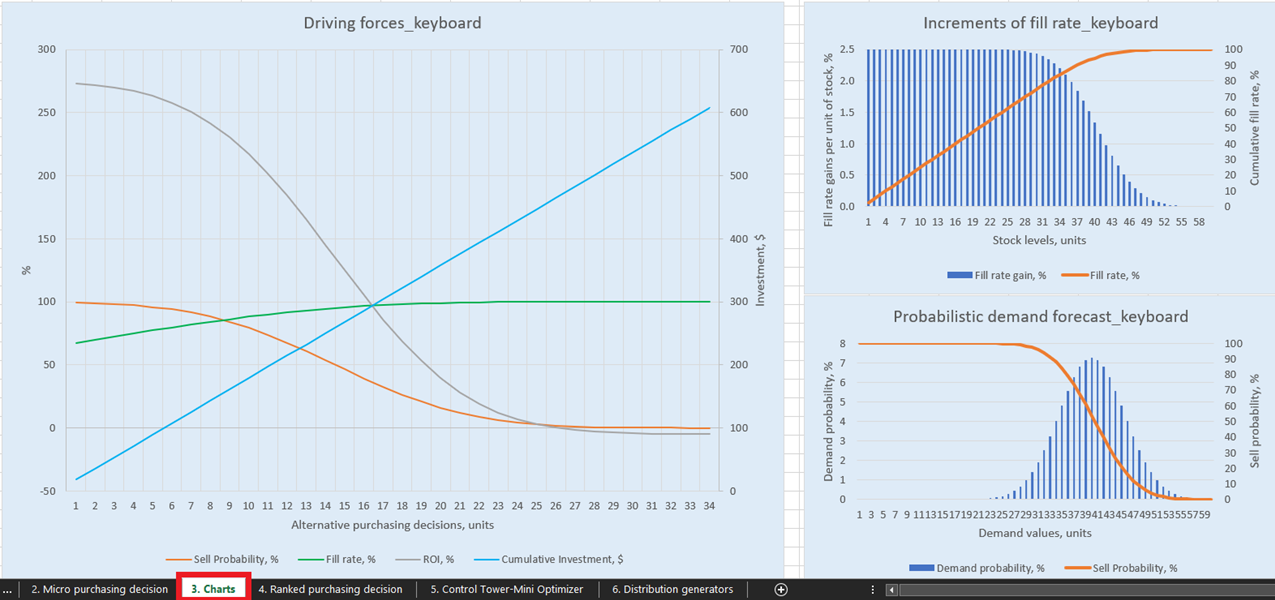
Abbildung 1. Ansicht von "Driving forces keyboard" in Charts, Standort hervorgehoben in rot.
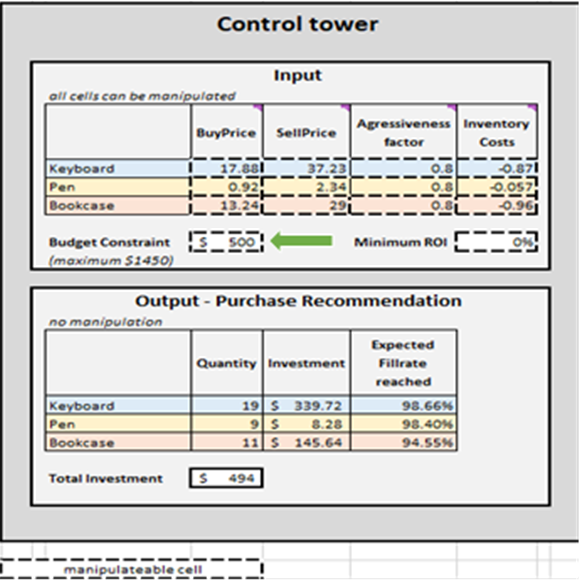
Abbildung 2. Ansicht von "Control Tower" befindet sich in Control Tower – Mini Optimizer (Blatt 5). Man kann die "Budget Constraint" auf einen beliebigen Wert zwischen $0 und $1450 ändern (siehe grüner Pfeil).
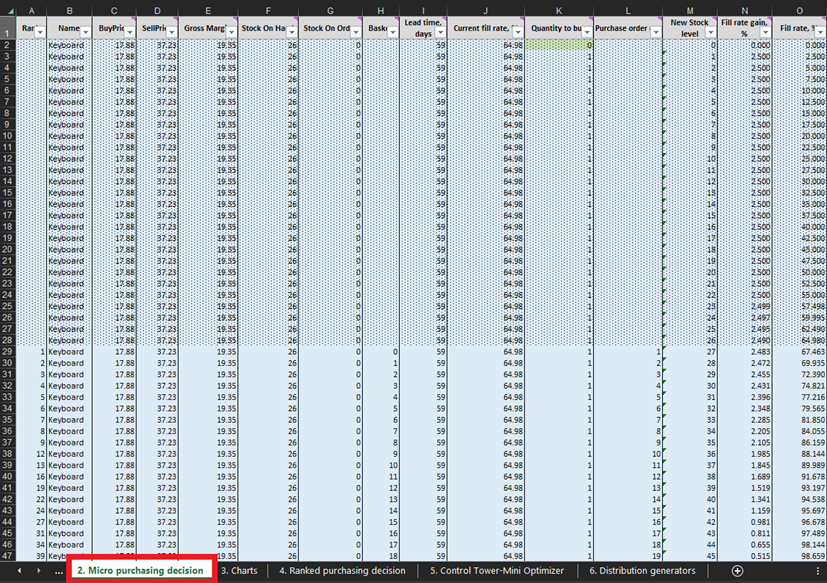
Abbildung 3. Wo man Micro purchasing decisions innerhalb von Excel findet, hervorgehoben in rot. Die Zeilen, die durch bedingte, gepunktete Formatierung abgedeckt sind, sind vergangene Daten (bis einschließlich Zeile 28 im obigen Bild). Diese Informationen repräsentieren frühere Kaufentscheidungen. Wir sind nur an allem unterhalb dieser bedingten Formatierung interessiert. Die gleiche gepunktete Formatierung gilt für die Daten von Stift und Bücherregal.
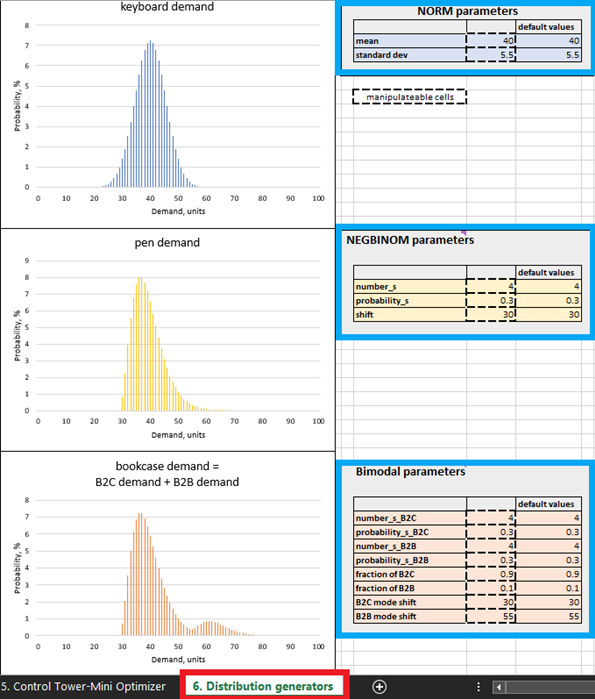
Abbildung 4. Wo man Distribution generators innerhalb von Excel findet, hervorgehoben in rot. Produktsteuerungsfelder sind in blau hervorgehoben. Die Zellen mit gestrichelten Konturen können manipuliert werden.
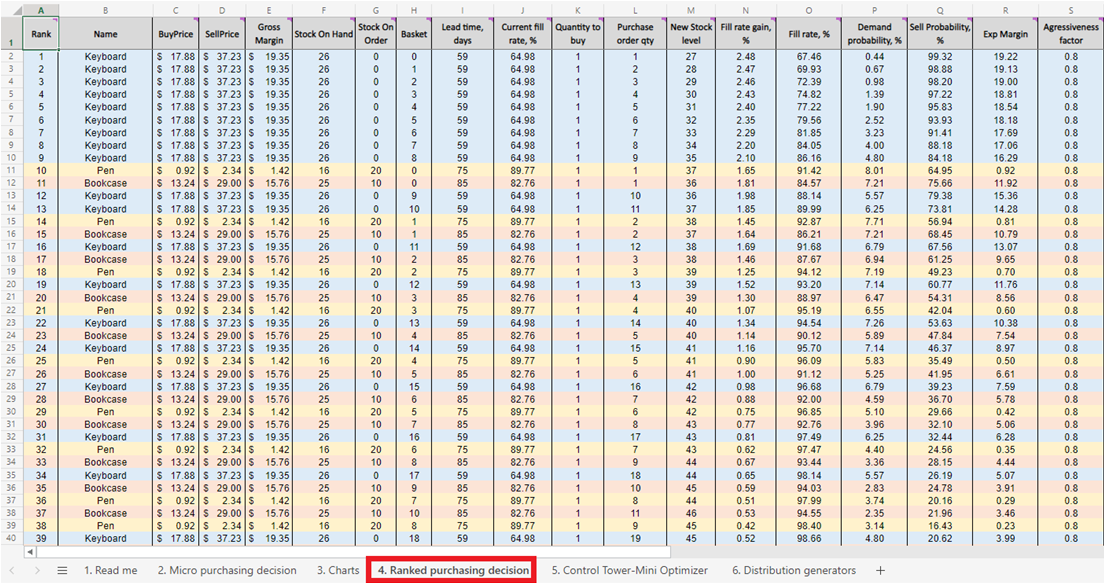
Abbildung 5. Eine priorisierte Liste von Mikrokaufentscheidungen zur Lagerauffüllung, befindet sich in Blatt 4.
2. Probabilistische Nachfrageprognose
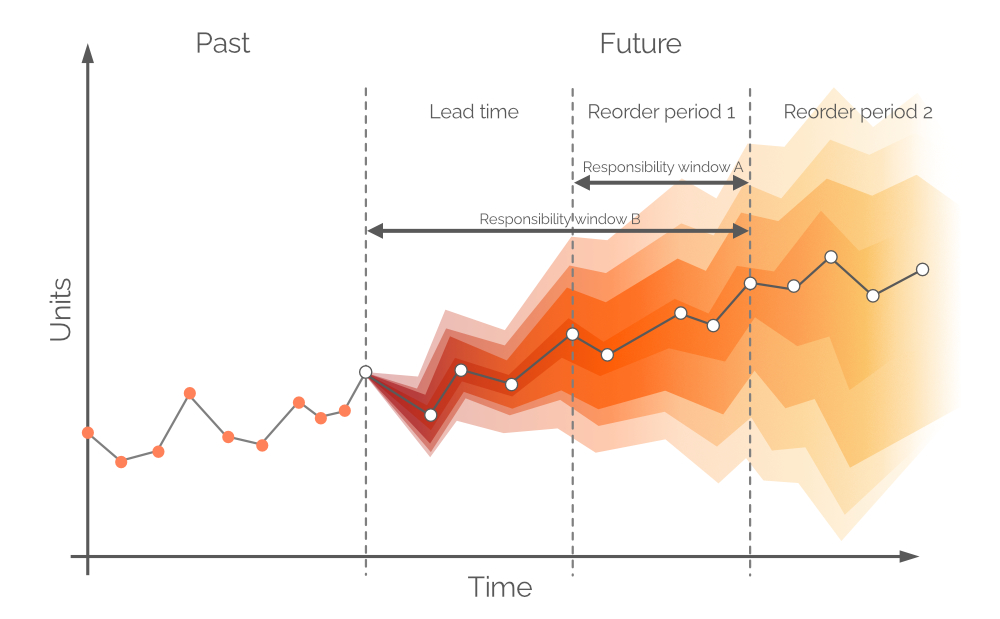
In diesem Kontext ist eine probabilistische Prognose eine Reihe aller wahrscheinlichen zukünftigen Nachfragewerte und ihrer jeweiligen Wahrscheinlichkeiten. Sie berücksichtigt die inhärente Unsicherheit der zukünftigen Nachfrage und kann über jeden Zeitraum erstellt werden. Wie eine traditionelle Zeitreihenprognose gibt es einen einzigen, am wahrscheinlichsten identifizierten Nachfragewert (die weißen Punkte in Abbildung 6) und eine Trendlinie (die graue Linie, die die weißen Punkte verbindet). Eine probabilistische Prognose integriert jedoch Unsicherheit durch die Hinzufügung aller möglichen (wenn auch nicht gleich wahrscheinlichen) Nachfragewerte. Dieser Ansatz ist in Abbildung 6 zu sehen, wo verschiedene Konfidenzintervalle Nachfragewerte mit unterschiedlichen Wahrscheinlichkeiten darstellen.
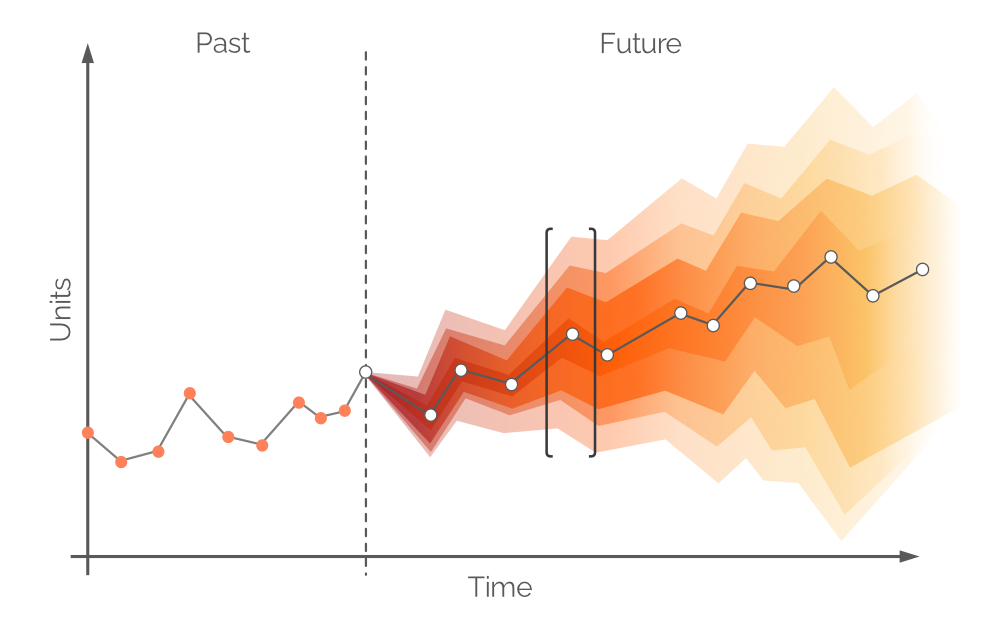
Abbildung 6. Eine probabilistische Prognose (Nachfrage auf der y-Achse; Zeit auf der x-Achse). Die gestrichelte vertikale graue Linie zeigt den aktuellen Moment ("jetzt") an. Die Zeit wird in Tagen gemessen, obwohl dies jedes gewünschte Intervall sein könnte. Der Bereich in schwarzen Klammern wird später besprochen.
Die weißen Punkte in Abbildung 6 repräsentieren die wahrscheinlichsten Nachfragewerte zu festen zukünftigen Intervallen. Es gibt ein begleitendes Farbband, das einer Reihe von alternativen zukünftigen Nachfragewerten entspricht - eine Wahrscheinlichkeitsverteilung in Farbe. Diese Farbe verblasst entlang der vertikalen Achse, je weiter man sich vom weißen Punkt entfernt, was die größere Unsicherheit und geringere Wahrscheinlichkeit darstellt. Insgesamt verblassen die Farbbänder mit der Zeit (entlang der horizontalen Achse), da die Unsicherheit mit der Zeit zunimmt. Unabhängig von der Unsicherheit gibt es jedoch immer mindestens einen Wert, der der wahrscheinlichste ist, und dieser wird zu jeder Zeit durch die weißen Punkte dargestellt. Ein Beispiel für eine Wahrscheinlichkeitsverteilung für einen Zeitpunkt ist in Abbildung 7 dargestellt.
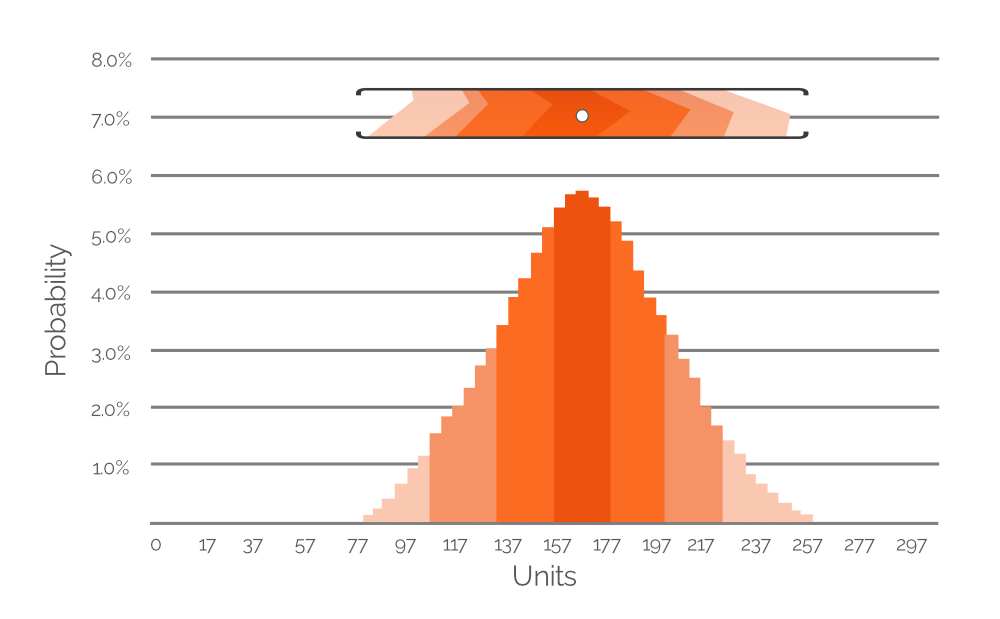
Abbildung 7. Ein Histogramm, das die Wahrscheinlichkeit mehrerer möglicher Nachfragewerte (in 20-Einheiten-Intervallen) darstellt. Die y-Achse ist der Wahrscheinlichkeitswert; die x-Achse ist die Nachfrage in Einheiten. Das Histogramm ist eine Darstellung des hervorgehobenen Wertebereichs in Abbildung 6 (hier zu Referenzzwecken enthalten).
Abbildung 7 drückt die hervorgehobenen Daten aus Abbildung 6 als Wahrscheinlichkeitshistogramm aus, mit expliziten numerischen Werten, die die Wahrscheinlichkeit verschiedener Nachfragewerte bezeichnen. Die Farbkodierung wird zur leichteren Verständlichkeit beibehalten (denken Sie daran, blassere Farben sind weniger wahrscheinlich; dichtere Farben sind wahrscheinlicher). In diesem Beispiel ist der wahrscheinlichste Nachfragewert 167 Einheiten (+/-), weshalb der weiße Punkt im abgeschnittenen Wertebereich aus Abbildung 6 direkt über der höchsten Stange im Histogramm positioniert ist. Wir weisen jedoch auch Nachfragewahrscheinlichkeiten extrem niedrigen und hohen Nachfragewerten zu (rund 80 und 260 Einheiten, beide sehr blasses Orange). Dies zeigt die potenzielle Datenreichtum einer probabilistischen Prognose und ähnliche Histogramme sind in der Excel-Tabelle enthalten - eines für jede unserer SKUs (siehe Abbildung 4). Mit diesen Histogrammen (wie in Abbildung 7 oben) können Nachfragewerte (in Einheiten) mit nichtnull Wahrscheinlichkeiten des Auftretens identifiziert und in die PIR einbezogen werden.
2.1 Die Erstellung einer probabilistischen Prognose
Obwohl es möglich ist, eine echte probabilistische Prognose mit historischen Daten in Excel zu erstellen, ist es wohl das am wenigsten geeignete Werkzeug für diesen Zweck. Insgesamt liegen die Einzelheiten zur Erstellung einer produktionsreifen probabilistischen Prognose außerhalb des Geltungsbereichs dieses Dokuments, daher wurden synthetische probabilistische Prognosen aus Gründen der Einfachheit ausgewählt. Die Parameter dieser synthetischen Prognosen können in Verteilungsgeneratoren manipuliert werden (siehe Abbildung 4). Es wird jedoch empfohlen, dass man zuerst die Standardeinstellungen studiert, bevor man Anpassungen vornimmt.
In gängigen Praktiken der Supply Chain wird die Nachfrage typischerweise als normalverteilt betrachtet, dies ist jedoch selten der Fall. In realen Supply Chains weichen die meisten SKUs von normalen Verteilungsmustern ab. Angesichts dieser Realität haben wir bewusst drei verschiedene Verteilungsmuster ausgewählt: normal (für Tastaturen), negativ binomial (für Stifte) und bimodal (für Bücherregale - eine Mischung aus zwei negativ binomialen Mustern). Die folgenden Ausführungen begründen diese Annahme.
Zum Beispiel gehen wir davon aus, dass Bücherregale sowohl von Einzelpersonen als auch von Unternehmen (z.B. Schulen) gekauft werden, daher verwenden wir eine bimodale Verteilung. In der Standardeinstellung für Bücherregale gibt es häufige Nachfrage von Einzelpersonen, wobei pro Kunde ein oder zwei Einheiten gekauft werden. Dies stellt den ersten Modus der Verteilung dar (siehe Abbildung 4). Unternehmen stellen jedoch weniger häufige Nachfragequellen dar, geben aber größere Bestellungen auf (größer als Einzelpersonen tendieren). Wenn dies geschieht, wird ihre Nachfrage zur Nachfrage hinzugefügt, die durch die Käufe der Einzelpersonen generiert wird, und der zweite Modus der Verteilung erscheint. Dieser zweite Modus ist nach rechts verschoben (was hohe Nachfragewerte darstellt) und ist deutlich kleiner als der erste Modus, was die Tatsache widerspiegelt, dass er weniger häufig vorkommt (Abbildung 4). Unser Modell geht auch davon aus, dass Stifte von Einzelpersonen mit selten hoher Nachfrage gekauft werden (Studenten, die vor Schulprüfungsterminen kaufen, zum Beispiel). Schließlich, um die Tatsache zu reflektieren, dass eine normale Verteilung gelegentlich auftritt, folgen die Tastaturverkäufe einem normalen Verteilungsmuster.
Innerhalb der Verteilungsgeneratoren (Abbildung 4) kann man die Nachfrageverteilungen bearbeiten, indem man die Parameter in den manipulierbaren Zellen ändert. Zum Beispiel wird eine Erhöhung des Mittelwerts für Tastaturen (siehe “NORM-Parameter” in Abbildung 4) von 40 auf 50 dazu führen, dass die Verteilung um 10 Einheiten nach rechts verschoben wird. Als Ergebnis dieser Erhöhung der durchschnittlichen Nachfrage wird der erwartete ROI für alle Tastatureinheiten steigen. Ebenso kann man Änderungen an den Parametern der negativ binomialen (Stifte) und bimodalen (Bücherregale) Verteilungen vornehmen.
Da Excel die Ausdruckskraft für diese Art von Berechnung fehlt, beschränkt diese Demonstration die Änderungen auf 100 Einheiten pro Produkt. Zum Beispiel wird das Setzen des Mittelwerts für die Tastatur auf 99 dazu führen, dass fast 50% der Nachfrageeinheiten in dem Mikro-Einkaufsentscheidungen Blatt nicht berechnet werden können.
2.2 Auswahl eines Horizonts für eine probabilistische Nachfrageprognose
Typischerweise werden Prognosen in tägliche/wochenweise/monatliche Intervalle unterteilt, obwohl diese diskreten Perioden aus Sicht der Nachschubbeschaffung von begrenztem Nutzen und Wert sind. Die Nachfrage über die nächste Lieferzeit kann nicht durch heute getroffene Kaufentscheidungen gedeckt werden, es sei denn, rückständige Aufträge sind erlaubt, da alle gekauften Einheiten nach einer der Lieferzeit entsprechenden Periode eintreffen werden. Daher sollte die Nachfrage mit dem vorhandenen Lagerbestand und den bestellten Einheiten gedeckt werden (siehe Abbildung 8), vorausgesetzt, die bestellten Einheiten treffen vor der Nachfrage ein. Daher befasst sich die probabilistische Prognose mit der Nachfrage zwischen den Nachbestellpunkten oder, anders ausgedrückt, der Nachfrage während des Nachbestellungszeitraums 1 (siehe Abbildung 9). Fernere zukünftige Nachfrage wird mit zukünftigen Bestellungen gedeckt (siehe Nachbestellungszeitraum 2, in Abbildung 9).

Abbildung 8. Lagerbestand (Spalte F) und bestellter Bestand (Spalte G), hervorgehoben in rot, befinden sich in Mikro-Einkaufsentscheidungen. Lieferzeit, Spalte I, ist in blau hervorgehoben.
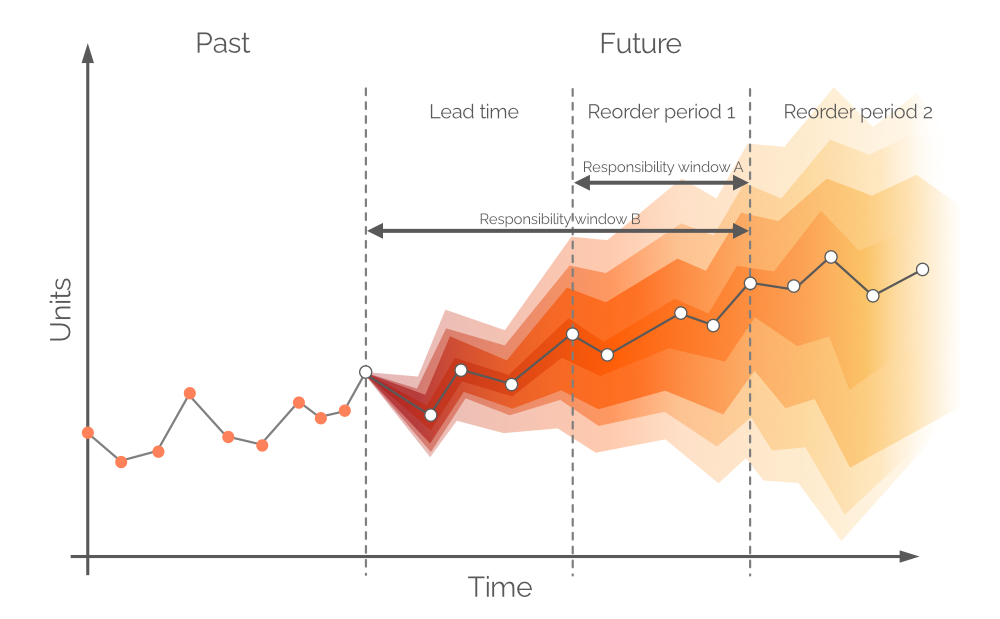
Abbildung 9. Eine visuelle Darstellung alternativer Verantwortungsfenster. Die Nachfrage ist auf der y-Achse, die Zeit auf der x-Achse, wobei die gestrichelte vertikale graue Linie links den aktuellen Moment ("jetzt", wie in Abbildung 6) anzeigt. Die probabilistische Prognose in diesem Dokument bezieht sich auf die Nachfrage über den Horizont gleich Verantwortungsfenster B.
Theoretisch sollte die probabilistische Nachfrageprognose über den Zeitraum gleich Nachbestellungsperiode 1 erstellt werden - dieser Zeitraum wird als Verantwortungsfenster A bezeichnet (siehe Abbildung 9). Um dies zu tun, müssten wir zukünftige Prognosen für den Lagerbestand und den bestellten Bestand am Ende der Lieferzeit erstellen. Allerdings ist die Nachfrage über die Lieferzeit - für die wir bereits Entscheidungen während der vorherigen Bestellperiode getroffen haben - ebenfalls probabilistisch, und dies würde zu Lagerbeständen führen, die selbst Wahrscheinlichkeitsverteilungen sind3. Durch die Zulassung von rückständigen Aufträgen (eine gängige Praxis in einigen Branchen) kann eine probabilistische Prognose kann über einen gemeinsamen Zeitraum (Lieferzeit plus Nachbestellungsperiode 1, wie in Abbildung 9, aka Verantwortungsfenster B) erstellt werden.
Es kann davon ausgegangen werden, dass die aktuellen Mengen an Lagerbestand und bestelltem Bestand die Nachfrage während der Lieferzeit decken werden. Wenn es zu einem Fehlbestand kommt, wird jede nachfolgende Nachfrage mit rückständigen Aufträgen gedeckt. Diese rückständigen Aufträge werden durch die Mikro-Einkaufsentscheidungen bedient, die ab heute getroffen werden. Dies ermöglicht es uns, Lagerbestand und bestellten Bestand als diskrete Werte (anstatt als zufällige) zu behandeln4.
3. Identifizierung möglicher Nachfüllentscheidungsoptionen
In einem realen Bestandsauffüllungsszenario müsste man alle möglichen Entscheidungsoptionen skizzieren, da es keinen direkten Weg gibt, von einer probabilistischen Prognose zur besten Einzelentscheidung (Kaufmenge, in diesem Fall) für jedes Produkt zu gelangen. Anstatt einer einzigen perfekten Wahl präsentiert ein probabilistischer Ansatz eine Reihe von möglichen Entscheidungen, die man in Bezug auf Machbarkeit berücksichtigen muss.
Machbarkeit hat hier die alltägliche Bedeutung, dass eine Entscheidung sofort umsetzbar ist; sie kann “so wie sie ist” ohne weitere Berechnungen oder Überprüfungen ausgeführt werden. Zum Beispiel ist eine Entscheidung “machbar”, wenn sie rentabel ist und alle unsere Einschränkungen erfüllt (z.B. MOQs, EOQs, Losgrößen, volle Containerlieferungen und jede andere Einschränkung, die in unserer Lieferkette bestehen könnte)5.
Bei jeder Zeile des Mikro-Einkaufsentscheidungen Blattes (Abbildungen 3 und 10) müssen wir in Betracht ziehen, eine weitere Einheit des Bestands zu unserer Bestellung für ein bestimmtes Produkt hinzuzufügen6. Unser “Jetzt” (oder Tag 1 dieses Experiments) beginnt bei Zeile 29, die den aktuellen Lagerbestand anzeigt. Dieser wird berechnet als Summe von Lagerbestand und bestelltem Bestand. Wenn wir uns entscheiden, eine Einheit zur Bestellung hinzuzufügen, dann wird die Gesamtkaufmenge in Spalte L als Summe aller bisher für den Kauf in Betracht gezogenen Einheiten berechnet (siehe Anmerkungen in Abbildung 10).
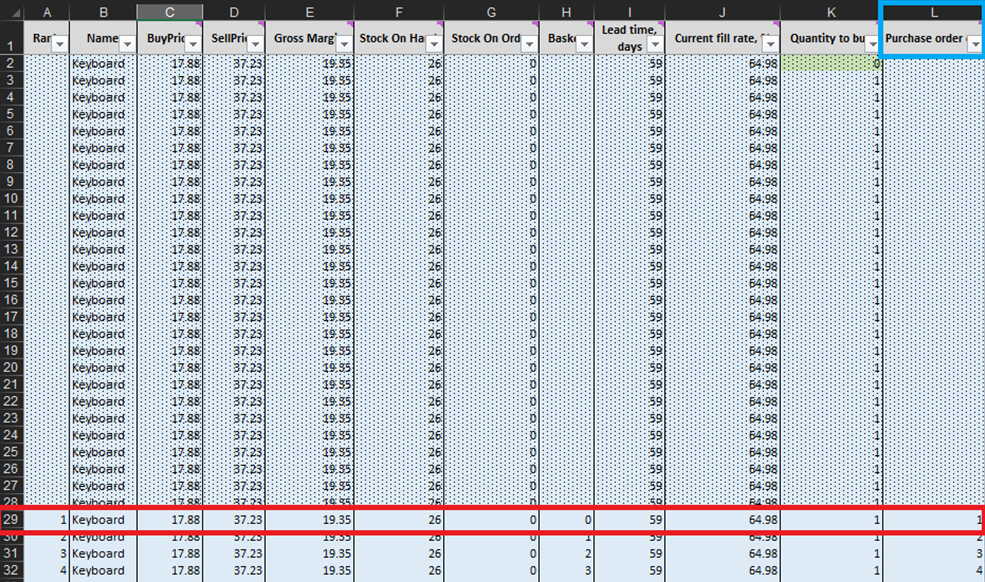
Abbildung 10. Blick in das Mikro-Einkaufsentscheidungsblatt. Zeile 29, hervorgehoben in rot, ist der Beginn unseres Experiments (für Tastaturen). Die Bestellspalte ist in blau hervorgehoben. Das gleiche Prinzip gilt für Zeilen 140 (für Bestellungen von Stiften) und 240 (für Bestellungen von Bücherregalen).
Sobald diese machbaren Bestandsentscheidungen identifiziert wurden, berechnen und bewerten wir die wirtschaftliche Belohnung jeder möglichen Bestellung. Beachten Sie, dass wir die Kaufbelohnung für Einheiten, die derzeit entweder auf Lager oder in Bestellung sind (Spalten F und G in Abbildung 10), nicht bewerten. Da wir diese Einheiten bereits gekauft haben, wurde die theoretische wirtschaftliche Belohnung zu einem früheren Zeitpunkt bestimmt (und bewertet). Zum Beispiel, wenn wir uns die Tastaturdaten in Abbildung 10 ansehen, sind derzeit 26 Einheiten auf Lager. Daher beginnen wir mit den Berechnungen in Zeile 29 und überlegen, ob wir unsere erste zusätzliche Einheit bestellen sollten (was den Lagerbestand von 26 auf 27 Einheiten erhöhen würde).
3.1 Bewertung machbarer Einkaufsentscheidungen
Um die beste Kaufmenge für jedes Produkt zu wählen, ist es notwendig, den erwarteten monetären Ertrag auf Einheitenebene für jede machbare Menge für jedes Produkt zu berechnen (unter Berücksichtigung der unsicheren Zukunft, die durch die probabilistische Prognose dargestellt wird). Dies ist ein erwarteter Wertkonzept, das auf die granularste Ebene der Bestandsentscheidung angepasst ist.
In der Realität sollte jede Art von wirtschaftlichem Treiber berücksichtigt werden, wenn man versucht, den erwarteten Ertrag für jede machbare Entscheidung zu berechnen7. Für die Zwecke dieser Demonstration sind hier die Faktoren, die wir berücksichtigen werden:
- Verkaufspreis: Wie viel wir den Kunden für das Produkt berechnen.
- Lager-/Lagerkosten: Wie viel es uns kostet, das Produkt zu halten.
- Einkaufspreis: Wie viel es uns kostet, das Produkt von unserem Lieferanten/Großhändler zu kaufen.
- Fehlbestandsdeckung: Wird unten im Detail behandelt, da es sich um einen weniger bekannten, aber dennoch wichtigen Treiber handelt8.
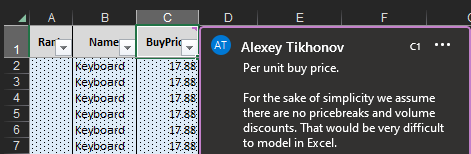
Abbildung 11. Erläuternde Anmerkung zum Einkaufspreis, sichtbar durch Überfahren des Spaltenkopfes mit der Maus. Für jede Spalte in jedem Blatt des Excel-Dokuments gibt es eine Definition.
Fehlbestandsdeckung stellt einen finanziellen Anreiz dar, eine Einheit eines Produkts auf Lager zu halten, jedoch nicht mit dem expliziten Ziel, es zu verkaufen. Dieser wirtschaftliche Treiber wird verwendet, um die relative Bedeutung eines Produkts im Vergleich zu anderen zu modellieren. Er fördert die Vermeidung von Fehlbeständen bei Produkten, die aufgrund ihrer direkten Margenbeiträge als weniger wichtig angesehen werden könnten, da diese Produkte auf indirekte Weise erheblich zu den Gewinnmargen beitragen können. Daher ist es eher ein Belohnungstreiber9. Obwohl dieser Treiber unscharf ist, ist es entscheidend, alle kritischen Produkte zu identifizieren (auch solche, die keine direkten Margentreiber sind).
3.2 Berechnung der Punktzahl jeder machbaren Entscheidung
Die gesamtwirtschaftliche Konsequenz (oder Kaufbelohnung) einer Bestandsauffüllungsentscheidung ist die Summe aller wirtschaftlichen Treiber, einschließlich erwarteter Marge, erwarteter Lagerkosten und Fehlbestandsdeckung (unten im Detail definiert). Lagerkosten sind in diese Berechnungen als negativer Treiber einbezogen, der als Gegenkraft wirkt, um unsere Bestandsauffüllungsentscheidungen auszugleichen.
Unten ist eine Analyse der wirtschaftlichen Auswirkungen der Formeln in jeder Spalte, unter Verwendung der Zeile 29 des Blattes Mikro-Kaufentscheidungen als Beispiel (siehe Abbildung 12)

Abbildung 12. Eine Aufschlüsselung der Treiber pro Schlüsselspalte, unter Verwendung der Zeile 29 von Mikro-Kaufentscheidungen (Excel-Blatt 2). Bestimmte Spalten wurden für die Bequemlichkeit der Abbildung ausgeblendet.
Um die erwartete Belohnung für jede Entscheidung zu berechnen, benötigen wir die folgenden Treiber:
Bruttomarge (Spalte E) = Verkaufspreis – Einkaufspreis.
Verkaufswahrscheinlichkeit (Spalte Q) = überprüfen Sie die Formel im Blatt10.
Nicht-Verkaufswahrscheinlichkeit (keine Spalte) = 100% - Verkaufswahrscheinlichkeit
Erwartete Marge (Spalte R) = Bruttomarge * Verkaufswahrscheinlichkeit/100.
Aggressivitätsfaktor (Spalte S) = Bereich von 0 bis 1. 0.8 wurde für dieses Tool ausgewählt.
Fehlbestandsdeckung (Spalte T) = Verkaufspreis * Aggressivitätsfaktor * Verkaufswahrscheinlichkeit
Lagerkosten (Spalte U)
Erwartete Lagerkosten (Spalte V) = Lagerkosten * Nicht-Verkaufswahrscheinlichkeit11.
Mit den oben genannten Daten wird die Kaufbelohnung für jede mikroebene Bestandsentscheidung (jede Einheit jedes Produkts) wie folgt berechnet:
Kaufbelohnung (Spalte W) = Erwartete Marge + Fehlbestandsdeckung + Erwartete Lagerkosten.
Sobald wir die Schätzung der Kaufbelohnung haben, können wir die endgültige Punktzahl berechnen, die wir später verwenden werden, um alle in Betracht gezogenen Entscheidungen zu bewerten.
Punktzahl (Spalte Y) = Kaufbelohnung / Investition (Spalte X)12.
Da die Fehlbestandsdeckung ein unscharfer Treiber ist, der sowohl direkte als auch indirekte Renditen berücksichtigt, ist die Kaufbelohnung keine strenge Abbildung der erwarteten Rendite einer Bestandsentscheidung isoliert. Wenn man diese Art von Rendite berechnen möchte, würde man die Fehlbestandsdeckung aus dieser Formel ausschließen13.
4. Ranking der machbaren Bestandsauffüllungsentscheidungen
Sobald wir die Punktzahl für jede machbare Bestandskaufentscheidung (für jedes Produkt) haben, wird eine Liste erstellt und in absteigender Reihenfolge (höchste bis niedrigste) in Rangierte Kaufentscheidungen sortiert (siehe Abbildung 13). Jede machbare Bestandsentscheidung wird in Bezug auf positive ROI % sortiert. Ein ordinaler Rang (1., 2., 3., usw.) wird auch jeder Entscheidung zugewiesen (siehe Spalte A in derselben Abbildung).
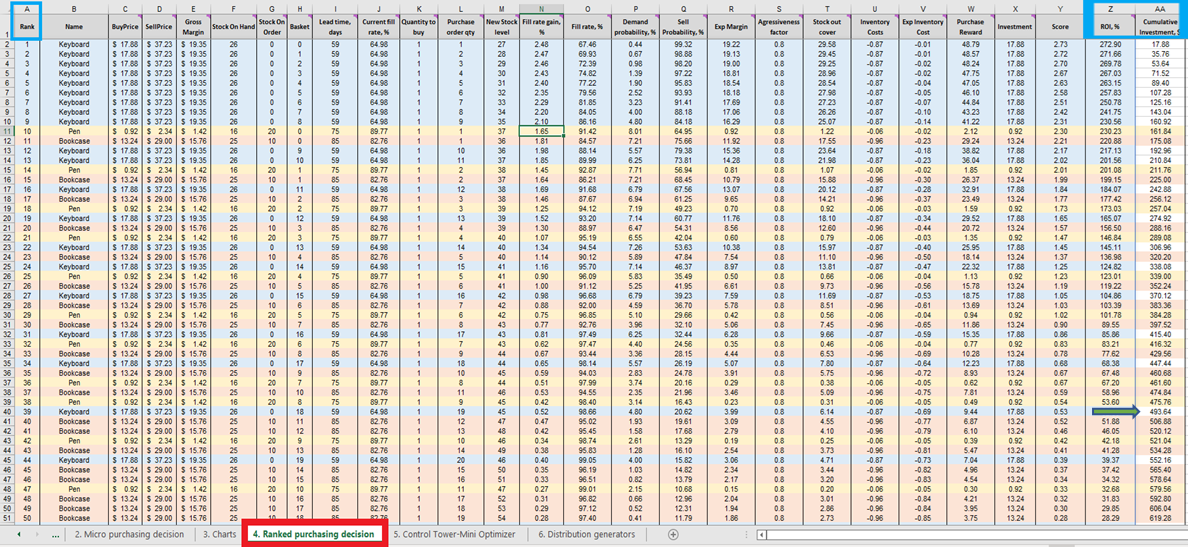
Abbildung 13. Rangierte Kaufentscheidungen hervorgehoben in rot. Spalten A, Z und AA sind in blau hervorgehoben. Zelle 40 (der Cut-off-Punkt für ein Budget von $500 – der Standardwert der Tabelle) wird durch den grünen Pfeil angezeigt.
Rangierte Kaufentscheidungen enthält farbcodierte Zeilen für jedes Produkt (Tastaturen, Stifte und Bücherregale), die hier verwendet werden, um zu demonstrieren, wie die Wahl, eine einzige zusätzliche Einheit eines beliebigen Produkts hinzuzufügen, mit jeder anderen zusätzlichen Einheit jedes anderen Produkts interagiert. Jede dieser Bestandsentscheidungen beeinflusst kollektiv den ROI. Schließlich wird ein kumulierter Investitionswert berechnet (Spalte AA, Abbildung 13). Dieser kann verwendet werden, um anzuzeigen, wo man Kaufentscheidungen angesichts der eigenen Budgetbeschränkungen beenden sollte - obwohl dies nur ein möglicher Beendigungsindikator ist14.
5. Festlegung der Beendigungskriterien
Bei der Auswahl eines Beendigungspunktes (sowohl in Rangierten Kaufentscheidungen als auch in der Realität) variieren die Kriterien je nach einer Vielzahl von Variablen. Zum Beispiel könnte man ein bescheidenes Budget haben und daher ist die Maximierung des ROI problematisch, insbesondere bei sehr engen Margen. Alternativ ist es möglich, dass man ein Gesamtziel für das Servicelevel hat und dann dieses Priorität mit dem Bestreben, die Gewinnmargen zu maximieren, ausbalancieren muss.
Um noch detaillierter zu werden, könnten die Beendigungskriterien ein Streben nach maximiertem ROI mit variierenden Servicelevel-Zielen für jedes Produkt oder jede Kategorie umfassen. Die Beendigungskriterien sind daher eine strategische Wahl, die nach einer ehrlichen Reflexion über die übergeordneten Geschäftsziele eines Unternehmens getroffen werden sollte. Priorisierte Bestandsauffüllung (PIR) ist in dieser Hinsicht bemerkenswert flexibel; die Beendigungskriterien für jeden Kaufzyklus können unter Verwendung des gleichen allgemeinen Rankingverfahrens angepasst werden
Für explizite Visualisierungen unserer möglichen Bestandsauffüllungsentscheidungen gibt es drei Diagramme und Grafiken für jedes Produkt im Charts Dashboard (Blatt 3, siehe Abbildung 14). Von besonderem Interesse ist “Driving forces_product name” (Keyboard-Beispiel wird in Abbildung 14 verwendet), das die Entwicklung des ROI zeigt, gegeben verschiedene Kaufmengen auf der Einheitenebene.
Wie im Diagramm ersichtlich, gibt es einen Punkt, an dem erhöhte Kaufmengen zu einem negativen ROI führen werden. Dies liegt daran, dass es auf einer bestimmten Ebene keinen Sinn macht, mehr Einheiten zu kaufen, da unsere erwarteten Margen durch erhöhte erwartete Bestandskosten kritisch reduziert werden.
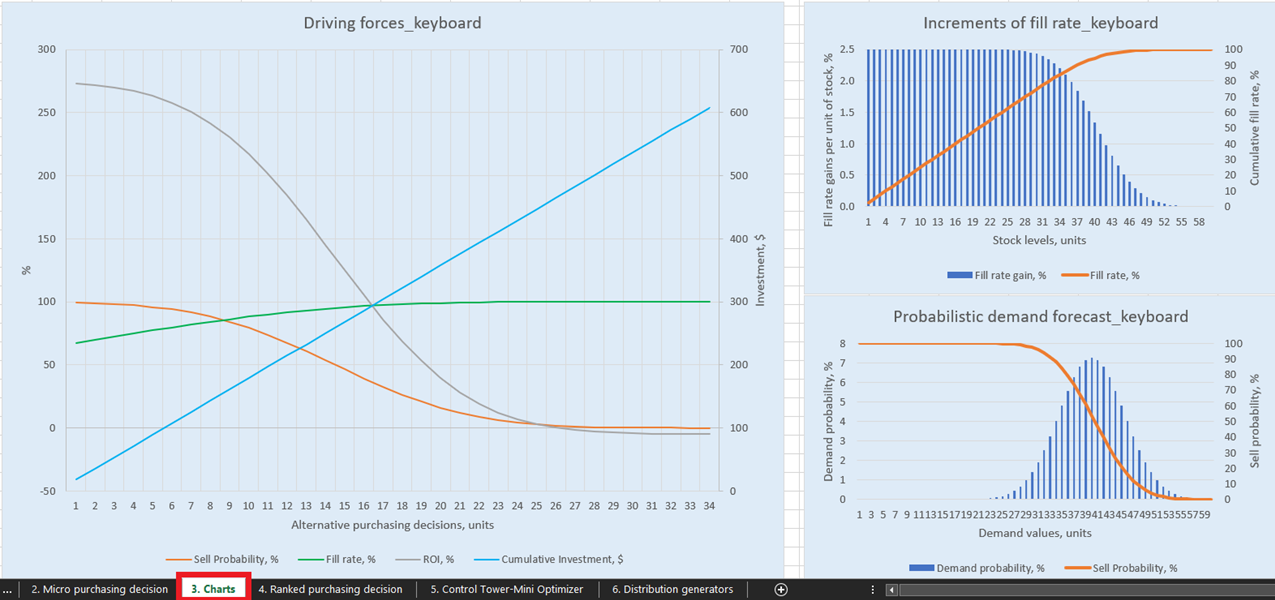
Abbildung 14. Ansicht von “Driving forces_keyboard” in Charts, hervorgehoben in rot.
Sobald die Beendigungskriterien festgelegt sind, werden die priorisierten Bestandsauffüllungsentscheidungen pro SKU aggregiert, was wiederum die Menge, Investition und erwartete Füllrate erreicht in Output-Kaufempfehlung für jede SKU aktualisiert (siehe Abbildung 15). Man kann die Budgetbeschränkungen ($0 bis $1450) ändern, was wiederum die empfohlene Einkaufsliste aktualisiert. Für die Bequemlichkeit verfügt der Kontrollturm über zwei zusätzliche Blöcke: Base Case – hard copy und Änderungen am Basisszenario. Ersteres ist statisch und zeigt die Standardeinstellungen für die Demonstration, wie sie von Lokad entworfen wurden; letzteres zeigt den Unterschied zwischen allen vorgenommenen Änderungen und der Standardeinstellung von Lokad.
Die Kaufempfehlungsliste im Control tower repräsentiert das Ziel dieser Demonstration (siehe Abbildung 15).
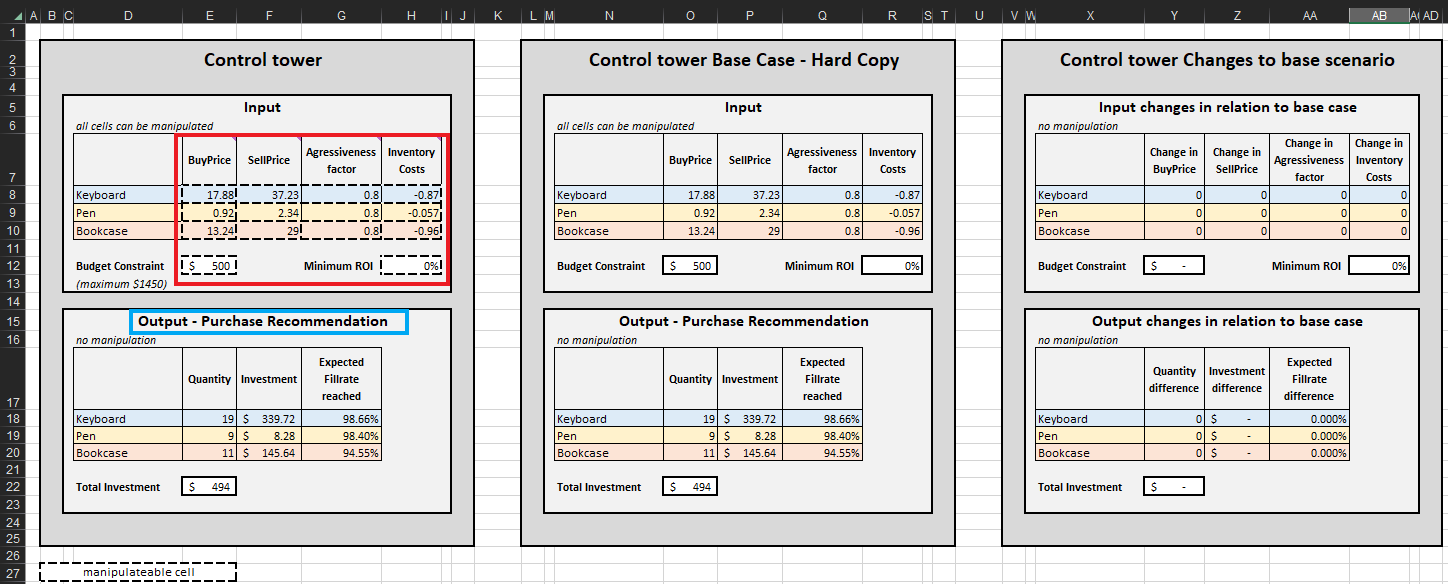
Abbildung 15. Ansicht des Control Tower-Mini Optimizer (Blatt 5). Die manipulierbaren Zellen sind in Rot hervorgehoben. "Kaufempfehlung" ist in Blau hervorgehoben und repräsentiert das Ziel eines priorisierten Bestandsauffüllungsansatzes.
6. Schlussfolgerung
Traditionelle Zeitreihenprognosen sind einfach nicht in der Lage, das Maß an Granularität zu erfassen, das notwendig ist, um Bestandsauffüllungsentscheidungen zu treffen, die zukünftige Unsicherheit und das volle Ausmaß der eigenen Beschränkungen und Treiber widerspiegeln. Dies liegt daran, dass ihnen eine explizite Unsicherheitsdimension fehlt, die durch Wahrscheinlichkeitswerte für erwartete zukünftige Ergebnisse dargestellt wird. Da eine traditionelle Zeitreihe effektiv blind für diese Art von Daten ist, kommt eine klassische Bewältigungsmethode wie Sicherheitsbestand dem Raten gleich; nicht genug und man verliert profitable Verkäufe mit positivem erwartetem ROI; zu viel und man reduziert den eigenen ROI, indem man Einheiten auf Lager hält, die (wie in der Tabelle gezeigt) einen negativen erwarteten ROI haben.
Priorisierte Bestandsauffüllung, unter Verwendung von probabilistischen Prognosen, ist unsere Lösung für dieses Problem. Ein solcher Ansatz betrachtet Bestandsauffüllungsentscheidungen in Kombination, anstatt isoliert. Dadurch kann die erwartete finanzielle Belohnung unserer Bestandsauffüllungsentscheidungen vollständig quantifiziert und offenbart werden. Die Grundlage eines solchen Ansatzes ist die Akzeptanz von Unsicherheit und die Nutzung von probabilistischen Prognoseeingaben. Im Gegenzug kann man auch einen tieferen Einblick in die Servicelevels (pro SKU) gewinnen, die bedeutende finanzielle Belohnungen bringen, anstatt willkürliche Ziele zu setzen.
Der in diesem Dokument demonstrierte PIR-Ansatz wurde mit synthetischen Daten und engen Parametern konstruiert. Diese Entscheidungen wurden getroffen, um ein gängiges Tool (Excel) für einen ungewöhnlichen Zweck (PIR) anzupassen. Unter anderem wurden SKUs und Einheiten begrenzt (auf 3 bzw. 100), um die Verarbeitungszeit zu reduzieren, da eine gesamte Katalogmenge an Daten (geschweige denn die Daten mehrerer Geschäfte) zu aufwändig zu verarbeiten wäre. Darüber hinaus wurden keine Lieferkettenbeschränkungen hinzugefügt. Entscheidend ist, dass Excel nicht darauf ausgelegt ist, Zufallsvariablen zu verarbeiten - ein wichtiger Schritt bei der Erstellung von probabilistischen Prognosen und PIR-Richtlinien. Diese Einschränkungen gelten nicht für eine produktionsreife PIR-Lösung.
Supply-Chain-Praktiker, deren Unternehmen Excel entwachsen sind, können gerne eine E-Mail an contact@lokad.com senden, um eine Demonstration einer produktionsreifen PIR-Lösung zu vereinbaren.
7. Übersicht über die Tabelle
7.1 Lesen Sie mich
Dieses Blatt dient als Startseite für den Benutzer. Es gibt einen Link zu einem Online-Tutorial (das, das Sie gerade lesen).
7.2 Mikro-Einkaufsentscheidungen
Dies ist das zweite Blatt und ist der feingranularen finanziellen Analyse aller machbaren Nachfüllentscheidungsoptionen gewidmet. Bitte beachten Sie, dass hier keine manuelle Datenmanipulation durchgeführt wird. Dieses Blatt zeigt nur die Ergebnisse von Berechnungen an, die auf den Eingaben aus den Blättern Control Tower und Distribution Generators basieren.
Hauptmerkmale:
- Zeilen mit bedingter Formatierung sind “vergangene Entscheidungen” und können nicht geändert werden. Wir empfehlen die Verwendung einer Desktop-App, da die browserbasierte Version von Excel manchmal in Bezug auf die Formatierung unzuverlässig ist.
- Wenn Sie den Mauszeiger über jede Spaltenüberschrift bewegen, wird eine hilfreiche Definition/Anmerkung angezeigt.
7.3 Diagramme
Dies ist das dritte Blatt und ist der Visualisierung der Haupttreiber bei den eigenen Bestandsauffüllungsentscheidungen gewidmet. Bitte beachten Sie, dass hier keine manuelle Datenmanipulation durchgeführt wird. Dieses Blatt soll dem Praktiker helfen, die inneren Abläufe des PIR-Prozesses zu visualisieren (und somit besser zu verstehen).
Hauptmerkmale:
- Drei Diagramme pro SKU (Tastatur, Stift und Bücherregal).
- Das Diagramm “Driving Forces” visualisiert die Haupttreiber für jede Entscheidung auf Einheitenebene (für jede SKU). Deshalb enthält die x-Achse nur Einheiten einer SKU, die noch bestellt werden müssen.
- Zwei weitere Diagramme (“Increments of Fill Rate” und “Probabilistic Demand Forecast”) enthalten alle Bestandseinheiten - vorhandener Bestand und die Einheiten, die bestellt werden können.
7.4 Rangierte Einkaufsentscheidungen
Dies ist das vierte Blatt und dient dazu, alle machbaren Nachfüllentscheidungen aufzulisten, sortiert nach ROI/Punktzahl in absteigender Reihenfolge. Diese Liste wird automatisch aus den Daten des Blattes 2 (Micro purchasing decisions) sortiert. Machbare Entscheidungen werden in Bezug aufeinander angezeigt (siehe “Hauptmerkmale” unten). Bitte beachten Sie, dass hier keine manuelle Datenmanipulation durchgeführt wird. Je nach den Änderungen, die an den Eingaben in den Blättern 5 und 6 vorgenommen wurden, wird sich diese Liste ändern.
Hauptmerkmale:
- Machbare Bestandsauffüllungsentscheidungen werden in absteigender Reihenfolge (von höchster zu niedrigster) nach ROI/Punktzahl sortiert.
- Die kumulative Investition wird für die sortierten Entscheidungen berechnet (siehe Spalte AA in Blatt 4).
- Wenn Sie den Mauszeiger über jede Spaltenüberschrift bewegen, wird eine hilfreiche Definition/Anmerkung angezeigt.
7.5 Control Tower-Mini-Optimierer
Dies ist das fünfte Blatt und fasst die Modellannahmen (Eingaben) und die empfohlenen Entscheidungen (Ausgaben) zusammen. Daten in manipulierbaren Zellen können geändert werden, um die Modellannahmen und damit die Ausgabe des Modells zu ändern.
Hauptmerkmale:
- Drei Blöcke zur Unterstützung der Demonstration: “Control Tower” für die manuelle Manipulation von Eingaben; “Base Case - Hard Copy” zur Anzeige der Standardeinstellungen; und “Changes to base scenario” zur Anzeige der Unterschiede zwischen den aktualisierten und den Standardeinstellungen (siehe Blatt 5).
- Ein vierter Block (“Model Assumptions”), der sich unter “Control Tower” befindet, dient der Manipulation der anfänglichen Bestandsannahmen (siehe Blatt 5).
- Nur Daten in manipulierbaren Zellen können geändert werden.
7.6 Verteilungsgeneratoren
Dies ist das sechste Blatt und ist der Erzeugung von probabilistischen Nachfrageprognosen gewidmet. Parameter in manipulierbaren Zellen können geändert werden, was zur Aktualisierung der Verteilungen und zur Anzeige neuer Wahrscheinlichkeitswerte für die Nachfrage führt.
Hauptmerkmale:
- Ein Verteilungsdiagramm pro SKU.
- Jede SKU hat ein anderes Verteilungsmuster (Begründung in Abschnitt 2.1 erklärt).
- Es gibt eine Tabelle links von der Reihe von Verteilungsdiagrammen, die der Manipulation der Parameter der Verteilungen gewidmet ist.
- Nur Parameter in manipulierbaren Zellen können geändert werden.
- Wenn Sie den Mauszeiger über relevante Spaltenüberschriften (in der Tabelle) bewegen, wird eine hilfreiche Definition/Anmerkung angezeigt.
Anmerkungen
-
Betrachten Sie Milch und Schokolade. Ersteres ist ein Produkt mit geringer Marge, gilt jedoch als Grundnahrungsmittel, während letzteres ein diskretionäres Produkt mit höheren Gewinnmargen ist. Die Menschen neigen dazu, Grundnahrungsmittel und diskretionäre Produkte zusammen zu kaufen, aber die Strafe für das Fehlen von Milch ist anders als für Schokolade. Ein Kunde könnte ein diskretionäres Produkt (Kekse) gegen ein anderes (Schokolade) austauschen, wenn ein Ausverkauf vorliegt, aber wenn er ein Grundnahrungsmittel (Milch) nicht kaufen kann, könnte er den Laden ganz verlassen. Deshalb wäre die Ausverkaufsabdeckung für Milch größer als für Schokolade, unabhängig von der Bruttogewinnmarge. Aus unserer Sicht ist die Ausverkaufsabdeckung eine Belohnung und keine Strafe, da sie dazu bestimmt ist, den Verkauf zu fördern. ↩︎
-
Drei Produkte reichen aus, um das Konzept zu veranschaulichen, aber auch das Dokument kurz und verständlich zu halten. ↩︎
-
Die Lagerbestände werden probabilistisch, wenn wir die probabilistische Nachfrage von diskreten Lagerbestandswerten abziehen (diskreter Wert minus Wahrscheinlichkeitsverteilung ergibt eine weitere Wahrscheinlichkeitsverteilung). All dies würde es zu kompliziert machen, Dinge durch Excel zu erklären, da es nicht geeignet ist, Berechnungen mit Zufallsvariablen durchzuführen (denken Sie an ‘Nachfrage-Wahrscheinlichkeitsverteilungen’). ↩︎
-
Diese Zugeständnisse sind notwendig, um das allgemeine Prinzip eines probabilistischen Ansatzes zu demonstrieren. In Wirklichkeit werden Rückstände nicht immer verwendet und Lieferzeiten sind probabilistisch und können sich ändern. ↩︎
-
Um der Einfachheit willen haben wir keine Supply-Chain-Beschränkungen angewendet. ↩︎
-
Wie bereits erwähnt, müssen wir keine Daten in Micro Purchasing Decisions bearbeiten. Alle Datenmanipulationen werden über die Blätter 5 und 6 durchgeführt. ↩︎
-
In diesem Excel-Blatt werden wirtschaftliche Treiber in Dollar ausgedrückt, obwohl die Währung irrelevant ist. ↩︎
-
Die Liste der oben genannten wirtschaftlichen Treiber ist nicht vollständig und realistische Szenarien zur Bestandsauffüllung (und Supply Chain) werden mit Sicherheit mehr aufweisen. Dies gilt insbesondere bei der Produktion von Waren und Verderblichkeitsbeschränkungen. ↩︎
-
Dieser Treiber ist in einem B2C-Kontext weniger klar als in einem B2B-Kontext. Bei letzterem gibt es oft explizite Strafen, die mit Stockout-Ereignissen verbunden sind, wie vertragliche Strafen; bei ersterem ist es schwierig, die negative Auswirkung eines Stockout-Ereignisses finanziell zu quantifizieren. Im Allgemeinen wird es hoch sein für Produkte, die einem Geschäft einen unverhältnismäßig negativen Einfluss auf die Attraktivität zufügen (unabhängig vom direkten Margenbeitrag des SKU). Milch, wie zuvor erwähnt, ist kein Margentreiber für Supermärkte, aber ihre strategische Platzierung (normalerweise am Ende des Supermarktes) veranlasst die Kunden, Gang für Gang durch andere Produkte zu gehen (fast alle mit höheren Margen). Wenn ein Supermarkt ein Stockout-Ereignis mit diesem Grundnahrungsmittel erlebt (eines, das die Menschen tendenziell sehr regelmäßig und in Körben kaufen), könnte dies die Kunden dazu veranlassen, den Supermarkt zu verlassen, anderswo einzukaufen und möglicherweise nicht zurückzukehren (wenn diese Stockout-Ereignisse regelmäßig sind). ↩︎
-
Die Verkaufswahrscheinlichkeit leitet sich aus den Wahrscheinlichkeitsverteilungen ab, die in den Verteilungsgeneratoren (Blatt 6) erzeugt werden. ↩︎
-
Die laufenden Kosten für den Nichtverkauf und damit die Lagerung einer unverkauften Einheit eines SKU. ↩︎
-
Die Investition ist in diesem Szenario gleich dem Kaufpreis, aber nur, weil unsere Kaufentscheidungen nicht durch MOQs oder Losmultiplikatoren eingeschränkt sind. ↩︎
-
Der einfachste Weg, dies zu tun, besteht darin, den Aggressivitätsfaktor (Spalte S in Abbildung 12) auf null zu setzen, was ein Unternehmen tun könnte, wenn es entscheidet, dass ein Stockout-Ereignis keine negativen Auswirkungen hat. Ein freier Rat: das tut es definitiv. ↩︎
-
Zum Beispiel beträgt unser Standardbudget $500, daher würden wir unsere Kaufentscheidungen bei Zelle 40 beenden (siehe Abbildung 13), da Zelle 41 einen Wert von $506,88 hat und über unserem Budget liegt. Wir würden dann Zahlen pro Produkt zusammenfassen, was unsere Einkaufsliste darstellen würde (siehe Ausgabe - Kaufempfehlung im Control Tower, wie in Abbildung 2). Wie bereits erwähnt, kann man das voreingestellte Budget von $500 (siehe Abbildung 2 für Anweisungen) auf einen beliebigen Wert zwischen $0 und $1450 ändern. Dies wird zeigen, wie sich die Einkaufsliste mit verschiedenen Budgetbeschränkungen ändert. Unabhängig von finanziellen Einschränkungen wird Ranked Purchase Decisions die bestmögliche Kombination von Bestandsentscheidungen aus einer ROI-Perspektive für alle Zeilen zwischen Rang 1 und dem Beendigungspunkt identifizieren. ↩︎