Previsione Probabilistica per Supply Chain - Lezione 5.2

00:01 Introduzione
02:18 La previsione moderna
06:37 Previsione probabilistica in tilt
11:58 La storia fino ad ora
15:10 Piano probabile per oggi
17:18 Bestiario delle previsioni
28:10 Metriche - CRPS - 1/2
33:21 Metriche - CRPS - 2/2
37:20 Metriche - Monge-Kantorovich
42:07 Metriche - verosimiglianza - 1/3
47:23 Metriche - verosimiglianza - 2/3
51:45 Metriche - verosimiglianza - 3/3
55:03 Distribuzioni 1D - 1/4
01:01:13 Distribuzioni 1D - 2/4
01:06:43 Distribuzioni 1D - 3/4
01:15:39 Distribuzioni 1D - 4/4
01:18:24 Generatori - 1/3
01:24:00 Generatori - 2/3
01:29:23 Generatori - 3/3
01:37:56 Attendere prego mentre ti ignoriamo
01:40:39 Conclusione
01:43:50 Prossima lezione e domande del pubblico

Descrizione

Si dice che una previsione sia probabilistica, anziché deterministica, se contiene un insieme di probabilità associate a tutti i possibili esiti futuri, invece di indicare un particolare esito come “la” previsione. Le previsioni probabilistiche sono importanti ogniqualvolta l’incertezza sia irriducibile, il che avviene quasi sempre quando si tratta di sistemi complessi. Per le supply chain, le previsioni probabilistiche sono essenziali per produrre decisioni robuste contro condizioni future incerte.

Trascrizione completa

Benvenuti in questa serie di lezioni sulla supply chain. Sono Joannes Vermorel, e oggi presenterò “Probabilistic Forecasting for Supply Chain.” La previsione probabilistica è uno dei cambiamenti di paradigma più importanti, se non il più importante, in oltre un secolo di statistical forecasting nella scienza. Tuttavia, a livello tecnico, è per lo più più o meno lo stesso. Se osserviamo i modelli di previsione probabilistica o le loro alternative non probabilistiche, si tratta delle stesse statistiche, delle stesse probabilità. La previsione probabilistica riflette un cambiamento nel modo in cui dovremmo concepire la previsione stessa. Il più grande cambiamento portato dalla previsione probabilistica per la supply chain non si trova nella scienza della previsione. Il più grande cambiamento si trova nel modo in cui le supply chain vengono gestite e ottimizzate in presenza di modelli predittivi.

L’obiettivo della lezione di oggi è fornire un’introduzione tecnica delicata alla previsione probabilistica. Al termine di questa lezione, dovreste essere in grado di comprendere di cosa tratta la previsione probabilistica, come differenziare le previsioni probabilistiche da quelle non probabilistiche, come valutare la qualità di una previsione probabilistica, e persino di riuscire a progettare il vostro modello di previsione probabilistica entry-level. Oggi non tratterò l’utilizzo delle previsioni probabilistiche per scopi di decision-making nel contesto delle supply chain. L’attenzione attuale si concentra esclusivamente sul porre le basi della previsione probabilistica. Il miglioramento dei processi decisionali nella supply chain mediante previsioni probabilistiche sarà affrontato nella prossima lezione.

Per comprendere il significato delle previsioni probabilistiche, è necessario un piccolo contesto storico. La forma moderna di previsione, la previsione statistica, a differenza della divinazione, emerse all’inizio del XX secolo. La previsione emerse in un contesto scientifico più ampio in cui le scienze esatte, alcune discipline di grande successo come la cinematica, l’elettromagnetismo e la chimica, erano in grado di ottenere risultati apparentemente arbitrariamente precisi. Questi risultati furono ottenuti attraverso ciò che sostanzialmente si tradusse in uno sforzo che si è protratto per secoli, che può essere fatto risalire, ad esempio, a Galileo Galilei, nello sviluppo di tecnologie superiori che avrebbero permesso forme di misurazioni migliori. Misurazioni più precise, a loro volta, avrebbero alimentato ulteriori sviluppi scientifici, consentendo agli scienziati di testare e mettere in discussione le loro teorie e previsioni in modi ancora più precisi.

In questo contesto più ampio, in cui alcune scienze avevano avuto un successo incredibile, il nascente campo delle previsioni all’inizio del XX secolo si prefiggeva essenzialmente di replicare ciò che quelle scienze esatte avevano realizzato nel campo dell’economia. Ad esempio, se osserviamo pionieri come Roger Babson, uno dei padri della previsione economica moderna, egli fondò una società di previsioni economiche di successo negli Stati Uniti all’inizio del XX secolo. Il motto della compagnia era, in senso letterale, “Per ogni azione esiste una reazione uguale e contraria.” La visione di Babson era quella di trasporre il successo della fisica newtoniana nel campo dell’economia e, in ultima analisi, ottenere risultati altrettanto precisi.

Tuttavia, dopo più di un secolo di previsioni accademiche statistiche, nel quale operano le supply chain, l’idea di ottenere risultati arbitrariamente precisi, che in termini di previsione si traduce nell’ottenere previsioni arbitrariamente accurate forecasts, resta elusiva come lo era oltre un secolo fa. Per un paio di decenni, sono state sollevate voci nel più ampio mondo delle supply chain che hanno espresso preoccupazioni sul fatto che queste previsioni non diventeranno mai sufficientemente accurate. C’è stato un movimento, come il lean manufacturing, che tra gli altri è stato un forte sostenitore della significativa riduzione della dipendenza delle supply chain da queste previsioni inaffidabili. Questo è ciò di cui tratta il just-in-time: se puoi produrre e servire in just-in-time tutto ciò di cui il mercato ha bisogno, allora improvvisamente non hai più bisogno di una previsione affidabile e accurata.

In questo contesto, la previsione probabilistica rappresenta una riabilitazione della previsione, ma con ambizioni molto più modeste. La previsione probabilistica parte dall’idea che esista un’incertezza irriducibile sul futuro. Tutti i futuri sono possibili, ma non sono tutti ugualmente probabili, e l’obiettivo della previsione probabilistica è valutare comparativamente la rispettiva probabilità di tutti quegli scenari alternativi, e non ridurre tutti i futuri possibili a un solo futuro.

La prospettiva newtoniana sulle previsioni economiche statistiche ha essenzialmente fallito. L’opinione, all’interno della nostra comunità, che sia possibile ottenere previsioni arbitrariamente accurate è in gran parte scomparsa. Eppure, stranamente, quasi tutto il supply chain software e una grande quantità di supply chain practices mainstream sono in realtà fondate, alla base, sull’assunzione che tali previsioni saranno in definitiva disponibili.

Ad esempio, il Sales and Operations Planning (S&OP) si basa sull’idea che sia possibile ottenere una visione unificata e quantificata per l’azienda se tutti gli stakeholder vengono riuniti e collaborano nella costruzione di una previsione comune. Analogamente, l’open-to-buy è essenzialmente un metodo basato sull’idea che sia possibile avere un processo di budgeting top-down, fondato sull’idea che sia possibile costruire previsioni top-down arbitrariamente precise. Inoltre, anche se osserviamo molti strumenti molto comuni in ambito di previsione e pianificazione nelle supply chain, come il business intelligence e i spreadsheets, tali strumenti sono ampiamente orientati verso una previsione a punto time-series. Essenzialmente, l’idea è che si possano estendere i dati storici nel futuro, avendo un punto per ogni periodo di interesse. Questi strumenti, per loro natura, presentano un’enorme quantità di attrito quando si tratta di comprendere il tipo di calcoli che sono coinvolti in una previsione probabilistica, in cui non esiste un solo futuro, ma tutti i futuri possibili.

Infatti, la previsione probabilistica non riguarda l’abbellimento di una previsione classica con una qualche forma di incertezza. La previsione probabilistica non riguarda nemmeno l’istituzione di una lista ristretta di scenari, in cui ogni scenario rappresenta, a sé stante, una previsione classica. I metodi mainstream della supply chain tipicamente non lavorano con previsioni probabilistiche perché, alla base, sono implicitamente o esplicitamente basati sull’idea che esista una sorta di previsione di riferimento, attorno a cui tutto ruoterà. Al contrario, la previsione probabilistica rappresenta una valutazione numerica frontale di tutti i futuri possibili.

Naturalmente, siamo limitati dalla quantità di risorse informatiche a nostra disposizione, quindi quando dico “tutti i futuri possibili”, nella pratica considereremo solo un numero finito di futuri. Tuttavia, considerando il potere di elaborazione moderno di cui disponiamo, il numero di futuri che possiamo effettivamente considerare si aggira intorno ai milioni. È qui che il business intelligence e i fogli di calcolo incontrano difficoltà. Non sono pensati per i tipi di calcoli richiesti dalle previsioni probabilistiche. Questo è un problema di progettazione software. Come vedete, un foglio di calcolo ha accesso agli stessi computer e allo stesso potere di elaborazione, ma se il software non è progettato correttamente, alcuni compiti possono risultare incredibilmente difficili da realizzare, anche se si dispone di una grande quantità di potenza computazionale.

Pertanto, dal punto di vista della supply chain, la sfida più grande nell’adottare la previsione probabilistica è lasciar andare decenni di strumenti e pratiche radicate in un obiettivo molto ambizioso, ma che ritengo fuorviante, ossia che sia possibile ottenere previsioni arbitrariamente accurate. Vorrei sottolineare immediatamente che sarebbe incredibilmente fuorviante pensare alla previsione probabilistica come a un modo per ottenere previsioni più accurate. Non è così. Le previsioni probabilistiche non sono più accurate e non possono essere utilizzate come sostituto diretto delle previsioni classiche e mainstream. La superiorità delle previsioni probabilistiche risiede nei modi in cui esse possono essere sfruttate per scopi della supply chain, in particolare per scopi di decision-making nel contesto delle supply chain. Tuttavia, il nostro obiettivo oggi è solo comprendere di cosa trattano queste previsioni probabilistiche, e lo sfruttamento di tali previsioni verrà affrontato nella prossima lezione.

Questa lezione fa parte di una serie di lezioni sulla supply chain. Cerco di mantenere queste lezioni abbastanza indipendenti l’una dall’altra. Tuttavia, stiamo arrivando a un punto in cui sarà davvero utile per il pubblico guardare queste lezioni in sequenza, poiché farò frequenti riferimenti a quanto presentato nelle lezioni precedenti.

Quindi, questa lezione è la terza del quinto capitolo, dedicato al predictive modeling. Nel primissimo capitolo di questa serie, ho presentato le mie opinioni sulle supply chain sia come campo di studio che come pratica. Nel secondo capitolo, ho presentato le metodologie. In effetti, la maggior parte delle situazioni nelle supply chain è di natura avversariale, e tali situazioni tendono a sconfiggere le metodologie naive. Abbiamo bisogno di metodologie adeguate se vogliamo ottenere un minimo di successo nel campo delle supply chain.

Il terzo capitolo era dedicato alla parsimonia nella supply chain, con un focus esclusivo sul problema e sulla natura stessa della sfida che affrontiamo in varie situazioni che le supply chain coprono. L’idea alla base della parsimonia nella supply chain è ignorare completamente tutti gli aspetti relativi alla soluzione, poiché vogliamo poter esaminare esclusivamente il problema prima di scegliere la soluzione da adottare.

Nel quarto capitolo, ho esaminato un’ampia gamma di scienze ausiliarie. Queste scienze non sono la supply chain in sé; sono altri campi di ricerca che sono adiacenti o di supporto. Tuttavia, credo che una padronanza di base di queste scienze ausiliarie sia un requisito per la pratica moderna delle supply chain.

Infine, nel quinto capitolo, ci addentriamo nelle tecniche che ci permettono di quantificare e valutare il futuro, in particolare per produrre affermazioni su di esso. In effetti, tutto ciò che facciamo nelle supply chain riflette, in una certa misura, una certa anticipazione del futuro. Se saremo in grado di anticipare meglio il futuro, allora potremo prendere decisioni migliori. Di questo tratta il quinto capitolo: ottenere intuizioni quantificabili migliori sul futuro. In questo capitolo, le previsioni probabilistiche rappresentano un modo fondamentale nel nostro approccio per affrontare il futuro.

Il resto di questa lezione è diviso in quattro sezioni di lunghezza ineguale. Per prima cosa, esamineremo i tipi di previsioni più comuni, oltre a quella classica. Tra poco chiarirò cosa intendo per previsione classica. In effetti, pochissime persone nel mondo della supply chain si rendono conto che ci sono molte opzioni a disposizione. La previsione probabilistica stessa dovrebbe essere intesa come un ombrello che copre un insieme abbastanza vario di strumenti e tecniche.

In secondo luogo, introdurremo delle metriche per valutare la qualità delle previsioni probabilistiche. Qualunque cosa accada, una previsione probabilistica ben progettata ti dirà sempre: “Beh, c’era una probabilità che questo accadesse.” Quindi la domanda diventa: come si distingue una buona previsione probabilistica da una cattiva? È qui che entrano in gioco queste metriche. Esistono metriche specializzate interamente dedicate alla situazione delle previsioni probabilistiche.

In terzo luogo, esamineremo in dettaglio le distribuzioni unidimensionali. Esse sono il tipo più semplice di distribuzione e, sebbene presentino limiti evidenti, rappresentano anche il punto di ingresso più facile nel mondo della previsione probabilistica.

In quarto luogo, toccheremo brevemente il tema dei generatori, che sono frequentemente indicati come metodi Monte Carlo. Infatti, esiste una dualità tra generatori e stimatori di densità di probabilità, e questi metodi Monte Carlo ci offriranno un percorso per affrontare problemi e forme di previsione probabilistica a dimensioni superiori.

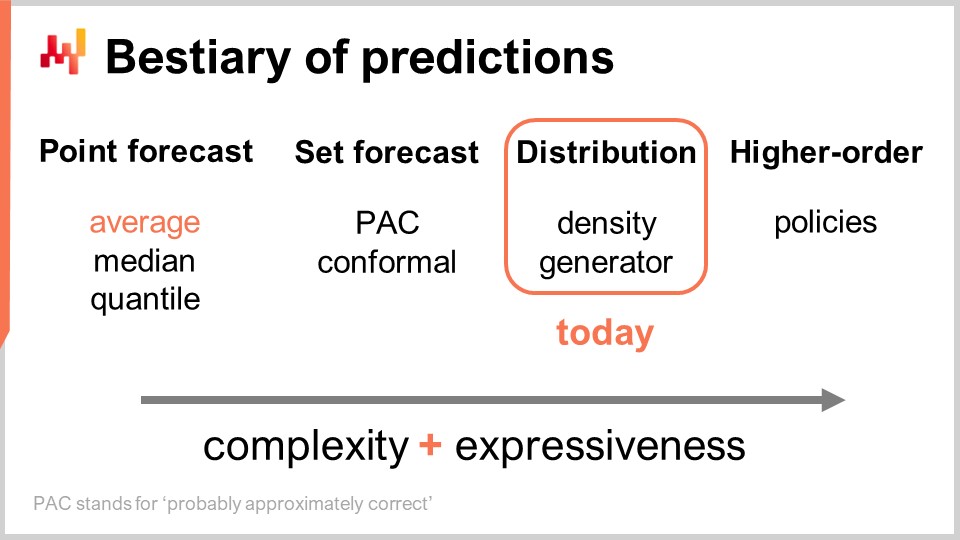
Esistono vari tipi di previsioni, e questo aspetto non va confuso con il fatto che esistano vari tipi di modelli di forecasting. Quando i modelli non appartengono allo stesso tipo o classe di previsione, non stanno nemmeno risolvendo gli stessi problemi. Il tipo di previsione più comune è la previsione puntuale. Ad esempio, se dico che domani le vendite totali in euro in un negozio saranno 10.000 euro per l’aggregato totale della giornata, sto facendo una previsione puntuale su ciò che accadrà in questo negozio domani. Se ripeto questo esercizio e inizio a costruire una previsione di serie temporale formulando un’enunciazione per il giorno di domani, poi un’altra per il giorno dopo, avrò più punti dati. Tuttavia, tutto ciò rimane comunque una previsione puntuale perché, sostanzialmente, stiamo scegliendo la nostra battaglia selezionando un certo livello di aggregazione e, a quel livello, le nostre previsioni ci forniscono un unico numero, che dovrebbe essere la risposta.

Ora, all’interno del tipo di previsione puntuale, esistono molteplici sottotipi di previsioni a seconda della metrica ottimizzata. La metrica più comunemente usata è probabilmente l’errore quadratico, quindi abbiamo l’errore quadratico medio, che fornisce la previsione media. Tra l’altro, questa tende ad essere la previsione più utilizzata perché è l’unica che è almeno in parte additiva. Nessuna previsione è mai completamente additiva; comporta sempre numerosi caveat. Tuttavia, alcune previsioni sono più additive di altre e, chiaramente, le previsioni medie tendono ad essere le più additive in assoluto. Se desideri avere una previsione media, ciò che ottieni è sostanzialmente una previsione puntuale ottimizzata rispetto all’errore quadratico medio. Se usi un’altra metrica, come l’errore assoluto, e la ottimizzi, otterrai una previsione mediana. Se utilizzi la pinball loss function che abbiamo introdotto nella primissima lezione di questo quinto capitolo di questa serie di lezioni di supply chain, otterrai una quantile forecast. Tra l’altro, come possiamo vedere oggi, sto classificando le previsioni quantile come un ulteriore tipo di previsione puntuale. Infatti, con la previsione quantile, ottieni sostanzialmente una singola stima. Questa stima potrebbe avere un bias, che è intenzionale. Questo è ciò che riguarda i quantili, ma, comunque, a mio avviso, si qualifica pienamente come una previsione puntuale perché la forma della previsione è semplicemente un unico punto.

Ora, esiste la previsione tramite insieme, che restituisce un insieme di punti anziché un singolo punto. Esiste una variazione a seconda di come costruisci l’insieme. Se osserviamo una previsione PAC, PAC sta per Probably Approximately Correct. Questo è sostanzialmente un framework introdotto da Valiant circa due decenni fa, e afferma che l’insieme, che rappresenta la tua previsione, ha una certa probabilità affinché un esito venga osservato all’interno dell’insieme che stai prevedendo con quella determinata probabilità. L’insieme che produci è in realtà tutti i punti che ricadono all’interno di una regione caratterizzata da una distanza massima rispetto a un punto di riferimento. In un certo senso, la prospettiva PAC sulla previsione è già una previsione tramite insieme perché l’output non è più un punto. Tuttavia, ciò che abbiamo è ancora un punto di riferimento, un esito centrale, e una distanza massima da questo punto centrale. Stiamo semplicemente affermando che esiste una certa probabilità specificata che l’esito verrà infine osservato all’interno del nostro insieme di previsione.

L’approccio PAC può essere generalizzato attraverso l’approccio conforme. La previsione conforme afferma: “Ecco un insieme, e ti dico che c’è questa data probabilità che l’esito rientri in questo insieme.” Ciò che generalizza l’approccio conforme rispetto a quello PAC è che le previsioni conformi non sono più legate all’avere un punto di riferimento e alla distanza da esso. Puoi modellare questo insieme come preferisci, e rimarrai comunque all’interno del paradigma della previsione tramite insieme.

Il futuro può essere rappresentato in maniera ancora più granulare e complessa: la previsione di distribuzione. La previsione di distribuzione ti fornisce una funzione che mappa tutti i possibili esiti alle rispettive densità di probabilità locali. In un certo senso, partiamo dalla previsione puntuale, dove la previsione è solo un punto. Poi passiamo alla previsione tramite insieme, dove la previsione è un insieme di punti. Infine, la previsione di distribuzione è tecnicamente una funzione o qualcosa che ne generalizza una. Tra l’altro, quando uso il termine “distribuzione” in questa lezione, esso si riferirà implicitamente a una distribuzione di probabilità. Le previsioni di distribuzione rappresentano qualcosa di ancora più ricco e complesso di un insieme, e questo sarà il nostro focus per oggi.

Esistono due modi comuni per affrontare le distribuzioni: l’approccio basato sulla densità e l’approccio generatore. Quando dico “densità”, mi riferisco sostanzialmente alla stima locale delle densità di probabilità. L’approccio generatore prevede un processo generativo Monte Carlo che genera esiti, chiamati deviati, che dovrebbero riflettere la medesima densità di probabilità locale. Questi sono i due modi principali per affrontare le previsioni di distribuzione.

Oltre la distribuzione, abbiamo costrutti di ordine superiore. Questo potrebbe essere un po’ complicato da comprendere, ma il mio intento qui, anche se oggi non affronteremo i costrutti di ordine superiore, è semplicemente quello di delineare che il forecasting probabilistico, quando si concentra sulla generazione di distribuzioni, non è il traguardo finale; è solo un passaggio, e c’è di più. I costrutti di ordine superiore sono importanti se vogliamo essere in grado di ottenere risposte soddisfacenti in situazioni semplici.

Per capire di cosa trattano i costrutti di ordine superiore, consideriamo un semplice punto vendita che applica una politica di sconto per i prodotti prossimi alla scadenza. Ovviamente, il negozio non vuole avere inventario invenduto a magazzino, quindi si attiva uno sconto automatico quando i prodotti sono molto vicini alla data di scadenza. La domanda che questo negozio genererebbe dipende fortemente da questa politica. Pertanto, la previsione che vorremmo avere, che può essere una distribuzione rappresentante le probabilità per tutti i possibili esiti, dovrebbe dipendere da questa politica. Tuttavia, questa politica è un oggetto matematico; è una funzione. Quello che desidereremmo non è una previsione probabilistica ma qualcosa di più meta – un costrutto di ordine superiore che, data una politica, possa generare la distribuzione risultante.

Da una prospettiva della supply chain, quando passiamo da un tipo di previsione all’altro, acquisiamo molte più informazioni. Questo non va confuso con il rendere la previsione più accurata; si tratta di accedere a un tipo di informazione completamente diverso, come passare dal vedere il mondo in bianco e nero al poter vedere i colori anziché semplicemente ottenere una risoluzione maggiore. In termini di strumenti, i fogli di calcolo e gli strumenti di business intelligence sono in certa misura adeguati per trattare previsioni puntuali. A seconda del tipo di previsione tramite insieme che si considera, potrebbero essere sufficienti, ma si stanno già superando le loro capacità progettuali. Non sono infatti progettati per gestire alcun tipo di previsione “fancy” tramite insieme oltre a quella ovvia, in cui si definisce semplicemente un intervallo con valori minimo e massimo nell’insieme dei valori attesi. Vedremo che, sostanzialmente, se vogliamo avere anche la minima possibilità di lavorare con previsioni di distribuzione o con costrutti di ordine superiore, abbiamo bisogno di strumenti completamente diversi, anche se questo diventerà più chiaro a breve.

Per iniziare con le previsioni probabilistiche, proviamo a caratterizzare cosa renda una previsione probabilistica valida. Infatti, qualunque cosa accada, una previsione probabilistica ti dirà che, indipendentemente dall’esito che osservi, c’era una probabilità che quell’evento si verificasse. Quindi, in queste condizioni, come distingui una buona previsione probabilistica da una cattiva? Sicuramente non è perché sia probabilistica che improvvisamente tutti i modelli di forecasting siano buoni.

Questo è esattamente ciò di cui trattano le metriche dedicate al forecasting probabilistico, e il Continuous Ranked Probability Score (CRPS) è la generalizzazione dell’errore assoluto per previsioni probabilistiche unidimensionali. Mi dispiace moltissimo per questo nome orrendo – il CRPS. Non sono stato io a inventare questa terminologia; mi è stata affidata. La formula del CRPS è mostrata sullo schermo. Sostanzialmente, la funzione F è la funzione di distribuzione cumulativa; è la previsione probabilistica che viene effettuata. Il punto x rappresenta l’osservazione effettiva, e il valore del CRPS è qualcosa che si calcola tra la tua previsione probabilistica e l’unica osservazione che hai appena effettuato.

Possiamo vedere che, sostanzialmente, il punto viene trasformato in una previsione quasi-probabilistica di per sé tramite la funzione a gradino di Heaviside. L’introduzione della funzione a gradino di Heaviside equivale semplicemente a trasformare il punto che abbiamo appena osservato in una distribuzione di probabilità di Dirac, ovvero una distribuzione che concentra tutta la massa di probabilità su un singolo esito. Successivamente, abbiamo un integrale e, sostanzialmente, il CRPS esegue una sorta di confronto delle forme. Stiamo confrontando la forma della CDF (funzione di distribuzione cumulativa) con la forma di un’altra CDF, quella associata al Dirac che corrisponde al punto osservato.

Da una prospettiva di previsione puntuale, il CRPS è intrigante non solo per la formula complicata, ma anche perché questa metrica prende due argomenti che non sono dello stesso tipo. Uno di questi è una distribuzione, e l’altro è semplicemente un singolo dato. Quindi, qui abbiamo un’asimmetria che non esiste nella maggior parte delle altre metriche di previsione puntuale, come l’errore assoluto e l’errore quadratico medio. Nel CRPS, stiamo essenzialmente confrontando un punto con una distribuzione.

Se vogliamo comprendere meglio cosa calcoliamo con il CRPS, un’interessante osservazione è che il CRPS ha la stessa unità dell’osservazione. Ad esempio, se x è espresso in euro, e il valore del CRPS tra F e x è anch’esso omogeneo in termini di unità ad euro, è per questo che dico che il CRPS è una generalizzazione dell’errore assoluto. Tra l’altro, se “collassi” la tua previsione probabilistica in un Dirac, il CRPS ti darà un valore che corrisponde esattamente all’errore assoluto.

Anche se il CRPS può sembrare piuttosto intimidatorio e complicato, l’implementazione è in realtà abbastanza semplice. Sullo schermo è presente un piccolo script Envision che illustra come il CRPS possa essere utilizzato dal punto di vista di un linguaggio di programmazione. Envision è un linguaggio di programmazione specifico per il dominio, dedicato all’ottimizzazione predittiva delle supply chain, sviluppato da Lokad. In queste lezioni, sto utilizzando Envision per ragioni di chiarezza e concisione. Tuttavia, nota che non c’è nulla di unico in Envision; gli stessi risultati potrebbero essere ottenuti con qualsiasi linguaggio di programmazione, che si tratti di Python, Java, JavaScript, C#, F# o altro. Il mio punto è che questo richiederebbe semplicemente più righe di codice, perciò rimango su Envision. Tutti gli snippet di codice presentati in questa lezione e, tra l’altro, anche in quelle precedenti, sono autonomi e completi. Potresti tecnicamente copiare e incollare questo codice, e funzionerebbe. Non sono coinvolti moduli, non c’è codice nascosto e non occorre impostare un ambiente.

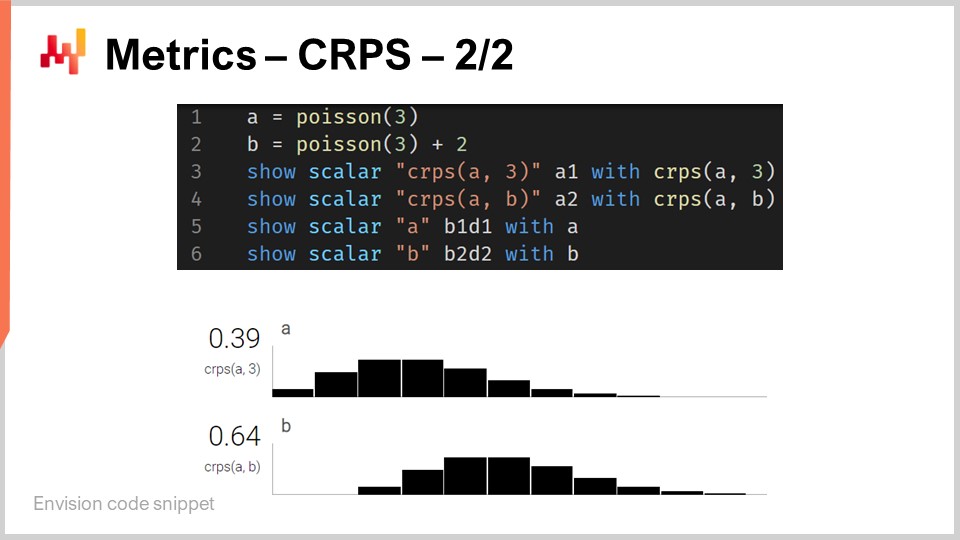
Quindi, torniamo allo snippet di codice. Alle righe uno e due, definiamo distribuzioni unidimensionali. Tornerò in seguito su come funzionano effettivamente queste distribuzioni unidimensionali in Envision, ma qui abbiamo due distribuzioni: una è una distribuzione di Poisson, che è una distribuzione discreta unidimensionale, e la seconda, alla riga due, è la stessa distribuzione di Poisson ma traslata di due unità a destra. È questo che significa il “+2”. Alla riga tre, calcoliamo la distanza CRPS tra una distribuzione e il valore 3, che è un numero. Qui stiamo riscontrando questa asimmetria in termini di tipi di dati di cui parlavo. Successivamente, i risultati vengono visualizzati in basso, come puoi vedere sullo schermo.

Alla riga quattro, calcoliamo il CRPS tra la distribuzione A e la distribuzione B. Sebbene la definizione classica di CRPS sia tra una distribuzione e un singolo punto, è del tutto semplice generalizzare questa definizione a una coppia di distribuzioni. Tutto ciò che devi fare è prendere la medesima formula del CRPS e sostituire la funzione a gradino di Heaviside con la funzione di distribuzione cumulativa della seconda distribuzione. Le istruzioni “show” dalle righe tre a sei danno il risultato visualizzato in basso sullo schermo, che è letteralmente uno screenshot.

Quindi, vediamo che utilizzare il CRPS non è più difficile o complicato che usare qualsiasi funzione speciale, come la funzione coseno. Ovviamente, può essere un po’ fastidioso se devi reimplementare tu stesso il coseno, ma tutto sommato non c’è nulla di particolarmente complicato nel CRPS. Ora, andiamo avanti.

Il problema di Monge-Kantorovich ci offre una visione su come approcciare il processo di abbinamento delle forme presente nel CRPS, ma in dimensioni superiori. Ricorda, il CRPS è in realtà confinato alla dimensione uno. L’abbinamento delle forme è concettualmente qualcosa che potrebbe essere generalizzato a qualsiasi numero di dimensioni, e il problema di Monge-Kantorovich è molto interessante, ancor di più perché, in sostanza, è effettivamente un problema di supply chain.

Il problema di Monge-Kantorovich, originariamente non correlato al forecasting probabilistico, fu introdotto dallo scienziato francese Gaspard Monge in un memoir del 1781 intitolato “Mémoire sur la théorie des déblais et des remblais,” che potrebbe essere tradotto approssimativamente come “Memoir sulla teoria dello spostamento della terra.” Un modo per comprendere il problema di Monge-Kantorovich è immaginare una situazione in cui abbiamo una lista di miniere, indicate come M sullo schermo, e una lista di fabbriche, indicate come F. Le miniere estraggono minerale, e le fabbriche lo consumano. Quello che vogliamo è costruire un piano di trasporto, T, che mappi tutto il minerale prodotto dalle miniere al consumo richiesto dalle fabbriche.

Monge definì il capitale C come il costo per spostare tutto il minerale dalle miniere alle fabbriche. Il costo è la somma per trasportare tutto il minerale da ogni miniera a ogni fabbrica, ma esistono ovviamente modi molto inefficienti per trasportare il minerale. Quindi, quando diciamo di avere un costo specifico, intendiamo che tale costo riflette il piano di trasporto ottimale. Questo capitale C rappresenta il miglior costo raggiungibile considerando il piano di trasporto ottimale.

Questo è essenzialmente un problema di supply chain che è stato studiato ampiamente nel corso dei secoli. Nella formulazione completa del problema, ci sono vincoli su T. Per questioni di concisione, non ho messo tutti i vincoli sullo schermo. C’è un vincolo, ad esempio, secondo il quale il piano di trasporto non deve superare la capacità produttiva di ogni miniera, e ogni fabbrica dovrebbe essere completamente soddisfatta, disponendo di un’allocazione che corrisponde alle sue esigenze. Ci sono molti vincoli, ma sono piuttosto verbosi, quindi non li ho inclusi sullo schermo.

Ora, mentre il problema del trasporto è interessante di per sé, se iniziamo a interpretare la lista delle miniere e la lista delle fabbriche come due distribuzioni di probabilità, abbiamo un modo per trasformare una metrica puntuale in una metrica distribuzionale. Questo è un’idea chiave sul matching di forme in dimensioni superiori attraverso la prospettiva di Monge-Kantorovich. Un altro termine per questa prospettiva è la metrica Wasserstein, sebbene riguardi per lo più il caso non discreto, il che è di minore interesse per noi.

La prospettiva Monge-Kantorovich ci permette di trasformare una metrica puntuale, che può calcolare la differenza tra due numeri o due vettori di numeri, in una metrica che si applica a distribuzioni di probabilità che operano sullo stesso spazio. Questo è un meccanismo molto potente. Tuttavia, il problema di Monge-Kantorovich è difficile da risolvere e richiede una notevole potenza di calcolo. Per il resto della lezione, mi atterrò a tecniche che sono più semplici da implementare ed eseguire.

La prospettiva bayesiana consiste nell’osservare una serie di osservazioni dal punto di vista di una convinzione a priori. La prospettiva bayesiana è di solito intesa in opposizione alla prospettiva frequentista, che stima la frequenza degli esiti basandosi sulle osservazioni effettive. L’idea è che la prospettiva frequentista non venga fornita di convinzioni a priori. Pertanto, la prospettiva bayesiana ci offre uno strumento noto come verosimiglianza per valutare il grado di sorpresa quando si considerano le osservazioni e un dato modello. Il modello, che è sostanzialmente un modello di previsione probabilistica, è la formalizzazione delle nostre convinzioni a priori. La prospettiva bayesiana ci fornisce un modo per valutare un dataset in relazione a un modello di previsione probabilistica. Per capire come ciò avvenga, dovremmo partire dalla verosimiglianza per un singolo punto di dati. La verosimiglianza, quando abbiamo un’osservazione x, è la probabilità di osservare x secondo il modello. Qui, si assume che il modello sia completamente caratterizzato da theta, i parametri del modello. La prospettiva bayesiana tipicamente presuppone che il modello abbia una qualche forma parametrica, e theta è il vettore completo di tutti i parametri del modello.

Quando diciamo theta, assumiamo implicitamente di avere una caratterizzazione completa del modello probabilistico, che ci fornisce una densità di probabilità locale per tutti i punti. Così, la verosimiglianza è la probabilità di osservare questo singolo punto di dati. Quando abbiamo la verosimiglianza per il modello theta, essa rappresenta la probabilità congiunta di osservare tutti i punti del dataset. Presumiamo che questi punti siano indipendenti, quindi la verosimiglianza è un prodotto di probabilità.

Se abbiamo migliaia di osservazioni, la verosimiglianza, essendo un prodotto di migliaia di valori inferiori a uno, tende ad essere numericamente trascurabilmente piccola. Un valore trascurabilmente piccolo è tipicamente difficile da rappresentare nel modo in cui i numeri in virgola mobile sono rappresentati nei computer. Invece di lavorare direttamente con la verosimiglianza, che è un numero trascurabilmente piccolo, tendiamo a lavorare con la log-verosimiglianza. La log-verosimiglianza è semplicemente il logaritmo della verosimiglianza, che ha l’incredibile proprietà di trasformare la moltiplicazione in addizione.

La log-verosimiglianza del modello theta è la somma dei logaritmi di tutte le verosimiglianze individuali per tutti i punti di dati, come mostrato nell’ultima riga dell’equazione sullo schermo. La verosimiglianza è una metrica che ci fornisce una bontà dell’adattamento per una data previsione probabilistica. Ci dice quanto è probabile che il modello abbia generato il dataset che osserviamo. Se abbiamo due previsioni probabilistiche in competizione, e se mettiamo da parte per un momento tutte le altre questioni di fitting, dovremmo scegliere il modello che ci fornisce la verosimiglianza più alta o la log-verosimiglianza più alta, perché più alto è meglio.

La verosimiglianza è molto interessante perché può operare in alte dimensioni senza complicazioni, a differenza del metodo Monge-Kantorovich. Finché abbiamo un modello che ci fornisce una densità di probabilità locale, possiamo utilizzare la verosimiglianza, o più realisticamente, la log-verosimiglianza come metrica.

Inoltre, non appena disponiamo di una metrica che può rappresentare la bontà dell’adattamento, significa che possiamo ottimizzare in base a questa metrica stessa. Basta un modello con almeno un grado di libertà, il che significa fondamentalmente almeno un parametro. Se ottimizziamo questo modello in base alla verosimiglianza, la nostra metrica per la bontà dell’adattamento, speriamo di ottenere un modello addestrato in cui abbiamo imparato a produrre almeno una previsione probabilistica decente. È esattamente ciò che viene fatto qui sullo schermo.

Alle linee uno e due, generiamo un dataset fittizio. Creiamo una tabella con 2.000 righe, e poi alla linea due, generiamo 2.000 deviazioni, le nostre osservazioni da una distribuzione di Poisson con una media di due. Quindi, abbiamo le nostre 2.000 osservazioni. Alla linea tre, avviamo un blocco di autodiff, che fa parte del paradigma della programmazione differenziabile. Questo blocco eseguirà una discesa del gradiente stocastica e itererà molte volte su tutte le osservazioni nella tabella delle osservazioni. Qui, la tabella delle osservazioni è la tabella T.

Alla linea quattro, dichiariamo l’unico parametro del modello, chiamato lambda. Specificiamo che questo parametro deve essere esclusivamente positivo. Questo parametro è quello che cercheremo di ridiscoverare attraverso la discesa del gradiente stocastica. Alla linea cinque, definiamo la funzione di perdita, che è semplicemente il meno della log-verosimiglianza. Vogliamo massimizzare la verosimiglianza, ma il blocco di autodiff cerca di minimizzare la perdita. Pertanto, se vogliamo massimizzare la log-verosimiglianza, dobbiamo aggiungere questo segno meno davanti alla log-verosimiglianza, esattamente come abbiamo fatto.

Il parametro lambda appreso viene mostrato alla linea sei. Non sorprende che il valore trovato sia molto vicino a due, perché abbiamo iniziato con una distribuzione di Poisson con una media di due. Abbiamo creato un modello di previsione probabilistica che è anche parametrico e della stessa forma, una distribuzione di Poisson. Volevamo riscoprire l’unico parametro della distribuzione di Poisson, ed è esattamente ciò che otteniamo. Otteniamo un modello che rientra in circa l’uno per cento della stima originale.

Abbiamo appena appreso il nostro primo modello di previsione probabilistica, e tutto ciò ha richiesto essenzialmente solo tre righe di codice. Ovviamente, questo è un modello molto semplice; tuttavia, dimostra che non c’è nulla di intrinsecamente complicato nella previsione probabilistica. Non si tratta della vostra solita previsione a quadrati medi, ma a parte questo, con gli strumenti appropriati come la programmazione differenziabile, non è più complicata di una classica previsione puntuale.

La funzione log_likelihood.poisson che abbiamo usato in precedenza fa parte della libreria standard di Envision. Tuttavia, non c’è alcun trucco coinvolto. Diamo un’occhiata a come questa funzione è effettivamente implementata internamente. Le prime due righe in alto ci danno l’implementazione della log-verosimiglianza della distribuzione di Poisson. Una distribuzione di Poisson è completamente caratterizzata dal suo unico parametro, lambda, e la funzione di log-verosimiglianza prende solo due argomenti: l’unico parametro che caratterizza completamente la distribuzione di Poisson e l’osservazione effettiva. La formula effettiva che ho scritto è letteralmente materiale da libro di testo. È ciò che si ottiene quando si implementa la formula da libro di testo che caratterizza la distribuzione di Poisson. Non c’è nulla di fantastico qui.

Fai attenzione al fatto che questa funzione è contrassegnata con la parola chiave autodiff. Come abbiamo visto nella lezione precedente, la parola chiave autodiff assicura che la differenziazione automatica possa fluire correttamente attraverso questa funzione. La log-verosimiglianza della distribuzione di Poisson utilizza anche un’altra funzione speciale, log_gamma. La funzione log_gamma è il logaritmo della funzione gamma, che è la generalizzazione della funzione fattoriale ai numeri complessi. Qui, abbiamo bisogno solo della generalizzazione della funzione fattoriale ai numeri reali positivi.

L’implementazione della funzione log_gamma è leggermente verbosa, ma è di nuovo materiale da libro di testo. Essa utilizza un’approssimazione in frazione continua per la funzione log_gamma. La bellezza qui è che abbiamo la differenziazione automatica che funziona per noi fino in fondo. Iniziamo con il blocco autodiff, chiamando la funzione log_likelihood.poisson, che è implementata come funzione autodiff. Questa funzione, a sua volta, chiama la funzione log_gamma, anch’essa implementata con il marcatore autodiff. In sostanza, siamo in grado di produrre i nostri metodi di previsione probabilistici in tre righe di codice perché disponiamo di una libreria standard ben ingegnerizzata che è stata implementata, prestando attenzione alla differenziazione automatica.

Ora, passiamo al caso speciale delle distribuzioni discrete unidimensionali. Queste distribuzioni sono ovunque in una supply chain e rappresentano il nostro punto di ingresso nella previsione probabilistica. Ad esempio, se vogliamo prevedere i tempi di consegna con granularità giornaliera, possiamo dire che c’è una certa probabilità di avere un tempo di consegna di un giorno, un’altra probabilità di avere un tempo di consegna di due giorni, tre giorni, e così via. Tutto ciò si traduce in un istogramma di probabilità per i tempi di consegna. Analogamente, se stiamo osservando la domanda per un determinato SKU in un determinato giorno, possiamo dire che c’è una probabilità di osservare zero unità di domanda, una unità di domanda, due unità di domanda, e così via.

Se raggruppiamo tutte queste probabilità, otteniamo un istogramma che le rappresenta. Analogamente, se stiamo pensando al livello di stock di un SKU, potremmo essere interessati a valutare quanta merce rimarrà per questo determinato SKU alla fine della stagione. Possiamo utilizzare una previsione probabilistica per determinare la probabilità di avere zero unità in stock alla fine della stagione, una unità in stock, due unità, e così via. Tutte queste situazioni si adattano al modello di essere rappresentate attraverso un istogramma con cestelli associati ad ogni singolo esito discreto del fenomeno di interesse.

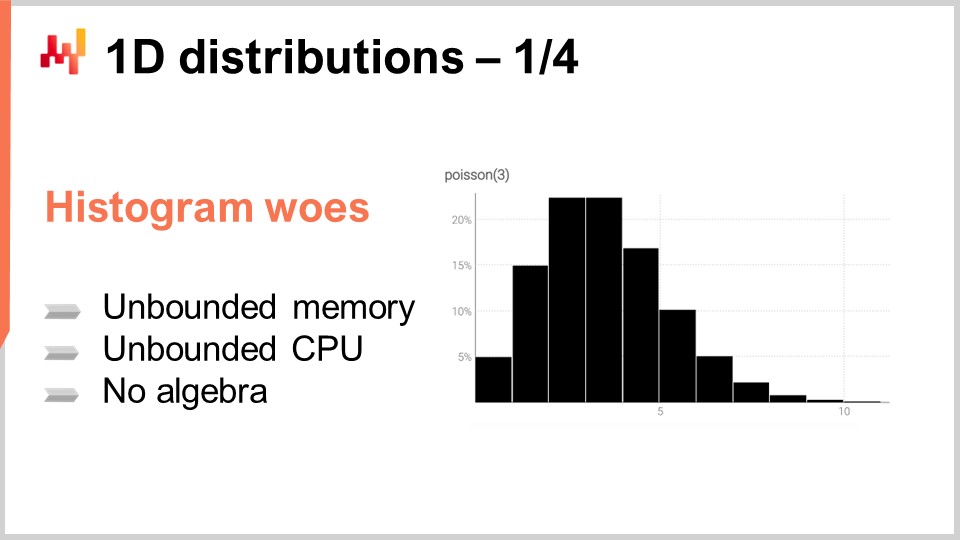
L’istogramma è il modo canonico per rappresentare una distribuzione discreta unidimensionale. Ogni cestello è associato alla massa di probabilità per l’esito discreto. Tuttavia, mettendo da parte il caso d’uso della visualizzazione dei dati, gli istogrammi risultano un po’ deludenti. Infatti, operare sugli istogrammi è una certa sfida se vogliamo fare qualcosa di diverso dalla visualizzazione di quelle distribuzioni di probabilità. Abbiamo essenzialmente due classi di problemi con gli istogrammi: il primo problema è legato alle risorse computazionali e la seconda classe di problemi è legata all’espressività programmativa degli istogrammi.

In termini di risorse computazionali, dovremmo considerare che la quantità di memoria necessaria per un istogramma è fondamentalmente illimitata. Si può pensare a un istogramma come a un array che cresce quanto necessario. Quando si tratta di un singolo istogramma, anche uno eccezionalmente grande da una prospettiva di supply chain, la quantità di memoria richiesta non è un problema per un computer moderno. Il problema sorge quando non si ha un solo istogramma, ma milioni di istogrammi per milioni di SKU in un contesto di supply chain. Se ogni istogramma può crescere abbastanza in grande, la gestione di questi istogrammi può diventare una sfida, soprattutto considerando che i computer moderni tendono ad offrire un accesso alla memoria non uniforme.

Al contrario, la quantità di CPU necessaria per elaborare questi istogrammi è anch’essa illimitata. Sebbene le operazioni sugli istogrammi siano per lo più lineari, il tempo di elaborazione aumenta man mano che la quantità di memoria cresce a causa dell’accesso non uniforme alla memoria. Di conseguenza, c’è un notevole interesse nel mettere limiti rigorosi sulla quantità di memoria e CPU richieste.

Il secondo problema con gli istogrammi è la mancanza di un’algebra associata. Sebbene si possa eseguire un’addizione o una moltiplicazione cestello per cestello quando si considerano due istogrammi, farlo non risulta in qualcosa che abbia senso quando si interpreta l’istogramma come una rappresentazione di una variabile casuale. Ad esempio, se prendi due istogrammi ed esegui una moltiplicazione puntuale, finisci con un istogramma che non ha nemmeno una massa pari a uno. Questa non è un’operazione valida dal punto di vista di un’algebra delle variabili casuali. In realtà, non puoi davvero sommare o moltiplicare istogrammi, quindi sei limitato in ciò che puoi fare con essi.

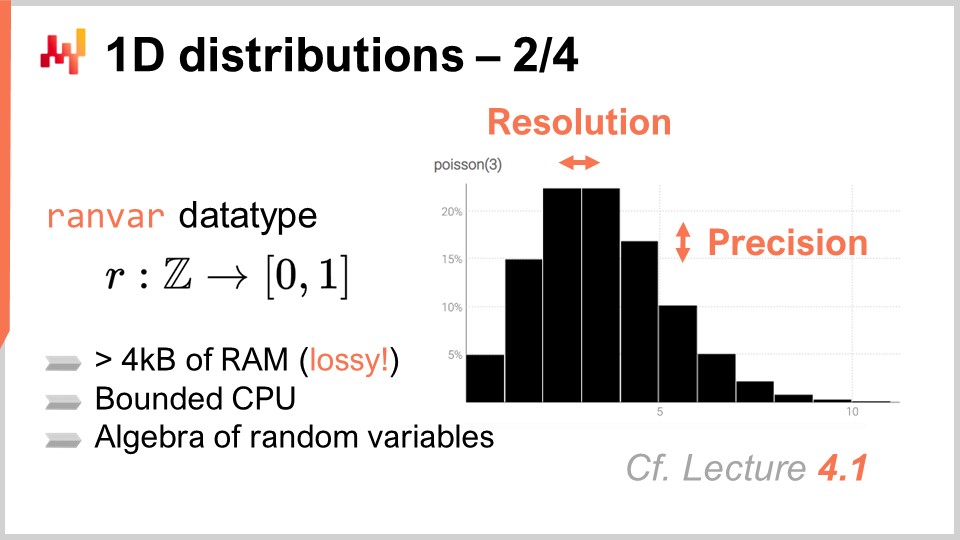
Da Lokad, l’approccio che abbiamo trovato più pratico per affrontare queste distribuzioni discrete unidimensionali onnipresenti è introdurre un tipo di dato dedicato. Il pubblico è probabilmente familiare con i tipi di dato comuni che esistono nella maggior parte dei linguaggi di programmazione, come interi, numeri in virgola mobile e stringhe. Questi sono i tipici tipi di dato primitivi trovati ovunque. Tuttavia, nulla ti impedisce di introdurre tipi di dato più specializzati che siano particolarmente adatti per i nostri requisiti da una prospettiva di supply chain. È esattamente ciò che ha fatto Lokad con il tipo di dato ranvar.

Il tipo di dato ranvar è dedicato alle distribuzioni discrete unidimensionali, e il nome è un’abbreviazione per variabile casuale. Tecnicamente, da una prospettiva formale, il ranvar è una funzione da Z (l’insieme di tutti gli interi, positivi e negativi) alle probabilità, che sono numeri compresi tra zero e uno. La massa totale di Z è sempre pari a uno, poiché rappresenta distribuzioni di probabilità.

Da una prospettiva puramente matematica, alcuni potrebbero sostenere che la quantità di informazione che può essere immessa in tale funzione può diventare arbitrariamente grande. Questo è vero; tuttavia, la realtà è che, da una prospettiva di supply chain, esiste un limite molto chiaro a quanta informazione rilevante possa essere contenuta in un singolo ranvar. Sebbene sia teoricamente possibile ideare una distribuzione di probabilità che richiederebbe megabyte per essere rappresentata, non esiste alcuna distribuzione simile che sia rilevante per scopi di supply chain.

È possibile progettare un limite superiore di 4 kilobyte per il tipo di dato ranvar. Limitando la memoria che questo ranvar può utilizzare, si ottiene anche un limite superiore in termini di CPU per tutte le operazioni, cosa molto importante. Invece di avere un limite naïf che pone un tetto di 1.000 ai bucket, Lokad introduce uno schema di compressione con il tipo di dato ranvar. Questa compressione è essenzialmente una rappresentazione con perdita dei dati originali, con conseguente perdita di risoluzione e precisione. Tuttavia, l’idea è progettare uno schema di compressione che fornisca una rappresentazione sufficientemente precisa degli istogrammi, in modo che il grado di approssimazione introdotto sia trascurabile dal punto di vista della supply chain.

I dettagli tecnici dell’algoritmo di compressione associato al tipo di dato ranvar sono al di fuori dell’ambito di questa lezione. Tuttavia, questo è un algoritmo di compressione molto semplice, di ordini di magnitudine più semplice rispetto ai tipi di algoritmi di compressione usati per le immagini sul tuo computer. Come beneficio secondario del limitare la memoria che questo ranvar può utilizzare, si ottiene anche un limite superiore in termini di CPU per tutte le operazioni, il che è molto importante. Infine, con il tipo di dato ranvar, il punto più importante è che otteniamo un’algebra di variabili che ci offre un modo per operare effettivamente su questi tipi di dato e fare tutte quelle cose che vorremmo fare con i tipi di dato primitivi, ovvero disporre di ogni sorta di primitive da combinare in modi che soddisfino i nostri requisiti.

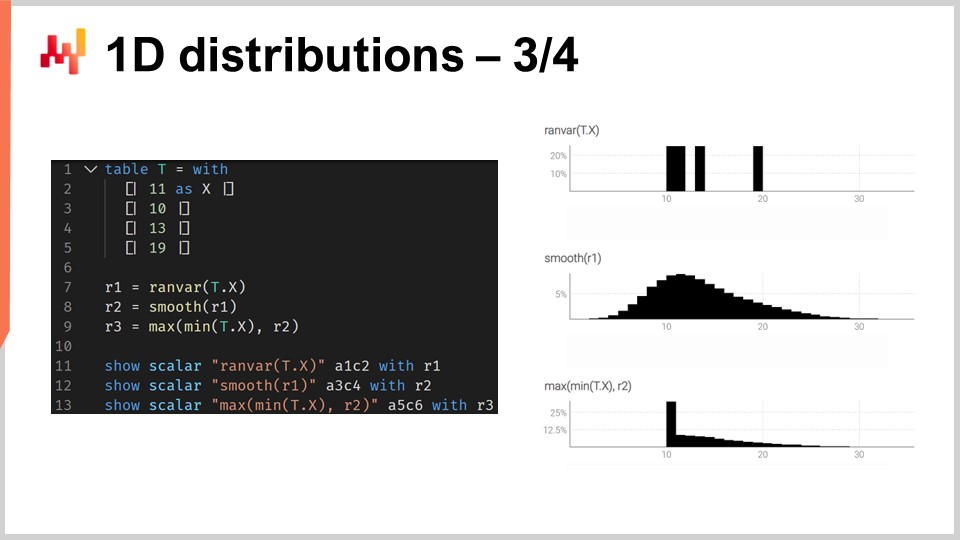
Per illustrare cosa significa lavorare con i ranvar, consideriamo una situazione di previsione dei lead time, più specificamente una previsione probabilistica di un lead time. Sullo schermo appare un breve script Envision che mostra come costruire tale previsione probabilistica. Alle linee 1-5, introduciamo la tabella T che contiene i quattro lead time di variazione, con valori di 11 giorni, 10 giorni, 13 giorni e 90 giorni. Anche se quattro osservazioni sono pochi, purtroppo è molto comune disporre di un set di dati estremamente limitato per quanto riguarda le osservazioni sul lead time. Infatti, se consideriamo un fornitore estero che riceve due ordini di acquisto all’anno, ci vogliono due anni per raccogliere quei quattro dati. Quindi, è importante disporre di tecniche che possano operare anche con un set di osservazioni incredibilmente limitato.

Alla linea 7, creiamo un ranvar aggregando direttamente le quattro osservazioni. Qui, il termine “ranvar” che compare alla linea 7 è in realtà un aggregatore che prende in input una serie di numeri e restituisce un singolo valore del tipo di dato ranvar. Il risultato viene visualizzato in alto a destra dello schermo, ed è un ranvar empirico.

Tuttavia, questo ranvar empirico non rappresenta in modo realistico la distribuzione effettiva. Per esempio, mentre possiamo osservare un lead time di 11 giorni e uno di 13 giorni, risulta irrealistico non poter osservare un lead time di 12 giorni. Se interpretiamo questo ranvar come una previsione probabilistica, implicherebbe che la probabilità di osservare un lead time di 12 giorni sia zero, il che sembra scorretto. Questo è ovviamente un problema di overfitting.

Per risolvere questa situazione, alla linea 8 levighiamo il ranvar originale chiamando la funzione “smooth”. La funzione smooth sostituisce essenzialmente il ranvar originale con una miscela di distribuzioni. Per ogni bucket della distribuzione originale, sostituiamo il bucket con una distribuzione di Poisson con una media centrata sul bucket, ponderata in base alla rispettiva probabilità del bucket. Tramite la distribuzione smooth, otteniamo l’istogramma che viene visualizzato al centro a destra dello schermo. Già appare molto meglio; non abbiamo più buchi strani e non compare una probabilità zero al centro. Inoltre, osservando la probabilità di vedere un lead time di 12 giorni, questo modello ci offre una probabilità non zero, il che risulta molto più ragionevole. Fornisce anche una probabilità non zero di superare i 20 giorni e, considerando che avevamo quattro dati e abbiamo già osservato un lead time di 19 giorni, l’idea che un lead time di 20 giorni sia possibile risulta molto sensata. Quindi, con questa previsione probabilistica, abbiamo una buona distribuzione che rappresenta una probabilità non zero per quegli eventi, e questo è molto positivo.

Tuttavia, sul lato sinistro abbiamo qualcosa di un po’ strano. Se da un lato è accettabile che questa distribuzione di probabilità si estenda verso destra, lo stesso non si può dire per il lato sinistro. Se consideriamo che i lead time osservati sono il risultato dei tempi di trasporto, dato che ci vogliono nove giorni perché il truck arrivi, risulta improbabile che si possa mai osservare un lead time di tre giorni. In questo senso, il modello appare piuttosto irrealistico.

Quindi, alla linea 9, introduciamo un ranvar condizionatamente aggiustato, affermando che deve essere maggiore del lead time più basso mai osservato. Utilizziamo “min_of(T, x)” che prende il valore più piccolo tra i numeri della tabella T, e poi usiamo “max” per determinare il massimo tra una distribuzione e un numero. Il risultato deve essere maggiore di questo valore. Il ranvar aggiustato viene visualizzato in basso a destra, e qui vediamo la nostra previsione finale del lead time. Quest’ultima risulta una previsione probabilistica molto ragionevole del lead time, considerando che abbiamo un dataset incredibilmente limitato costituito da sole quattro osservazioni. Non possiamo dire che sia una previsione probabilistica eccellente; tuttavia, sostengo che si tratti di una previsione a livello di produzione, e che questo genere di tecniche funzioni bene in produzione, a differenza di una previsione puntuale media che sottovaluterebbe enormemente il rischio di lead time variabili.

La bellezza delle previsioni probabilistiche è che, pur potendo essere molto crude, offrono già un certo potenziale di mitigazione contro decisioni mal informate che deriverebbero dall’applicazione naïf di una previsione media basata sui dati osservati.

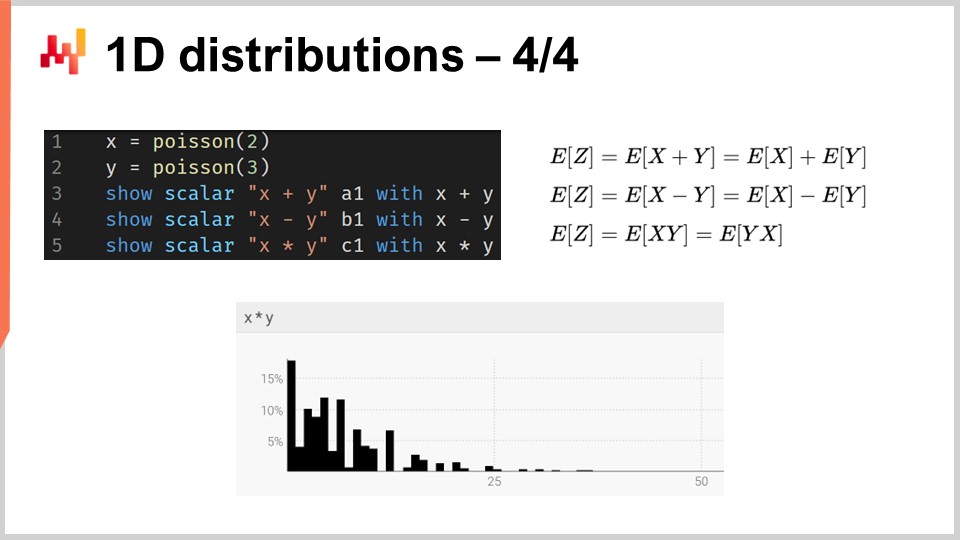
Più in generale, i ranvar supportano un’ampia gamma di operazioni: è possibile sommare, sottrarre e moltiplicare ranvar, proprio come è possibile sommare, sottrarre e moltiplicare interi. Sotto il cofano, dato che stiamo trattando variabili casuali discrete in termini di semantica, tutte queste operazioni sono implementate come convoluzioni. Sullo schermo, l’istogramma visualizzato in basso è ottenuto tramite la moltiplicazione di due distribuzioni di Poisson, rispettivamente con media due e tre. In supply chain, la moltiplicazione di variabili casuali è definita convoluzione diretta. Nel contesto della supply chain, la moltiplicazione di due variabili casuali ha senso per rappresentare, ad esempio, i risultati che si possono ottenere quando i clienti cercano gli stessi prodotti ma con moltiplicatori variabili. Supponiamo di avere una libreria che serve due gruppi di clienti. Da un lato, abbiamo il primo gruppo composto da studenti, che acquistano una unità al loro ingresso in negozio. In questa libreria illustrativa, abbiamo un secondo gruppo composto da professori, che acquistano 20 libri entrando nel negozio.

Da un punto di vista della modellazione, potremmo avere una previsione probabilistica che rappresenta i tassi di arrivo nella libreria sia degli studenti che dei professori. Ciò ci darebbe la probabilità di osservare zero clienti in un giorno, uno, due, ecc., rivelando la distribuzione di probabilità di osservare un certo numero di clienti in un determinato giorno. La seconda variabile fornirebbe le rispettive probabilità di acquistare una (per gli studenti) rispetto a 20 (per i professori). Per avere una rappresentazione della domanda, basterebbe moltiplicare insieme queste due variabili casuali, ottenendo un istogramma apparentemente erratico che riflette i moltiplicatori presenti nei modelli di consumo dei vari gruppi.

I generatori Monte Carlo, o semplicemente generatori, rappresentano un approccio alternativo alla previsione probabilistica. Invece di mostrare una distribuzione che ci fornisce la densità di probabilità locale, possiamo mostrare un generatore che, come suggerisce il nome, genera risultati destinati a seguire implicitamente le medesime distribuzioni di probabilità locali. Esiste una dualità tra generatori e densità di probabilità, il che significa che i due sono essenzialmente due facce della stessa medaglia.

Se si dispone di un generatore, è sempre possibile fare la media dei risultati ottenuti da questo generatore per ricostruire stime delle densità di probabilità locali. Viceversa, se si hanno le densità di probabilità locali, è sempre possibile estrarre deviati secondo questa distribuzione. Fondamentalmente, questi due approcci sono semplicemente modi diversi di osservare la stessa natura probabilistica o stocastica del fenomeno che stiamo cercando di modellare.

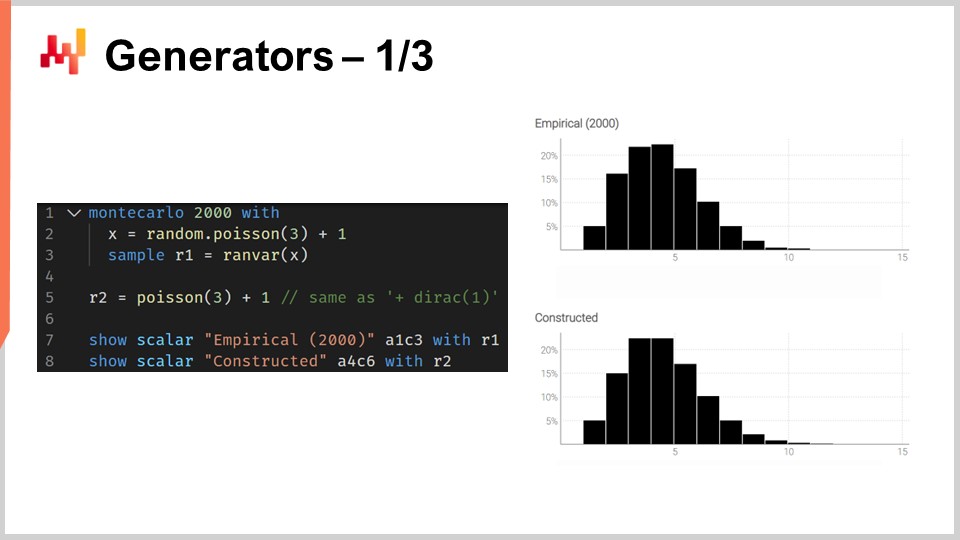
Lo script sullo schermo illustra questa dualità. Alla linea uno introduciamo un blocco Monte Carlo, che verrà iterato dal sistema, proprio come i blocchi di auto-differenziazione vengono iterati attraverso numerosi passaggi di discesa stocastica del gradiente. Il blocco Monte Carlo verrà eseguito 2.000 volte e, da questo blocco, raccoglieremo 2.000 deviati.

Alla linea due, estraiamo un deviato da una distribuzione di Poisson con media tre e poi aggiungiamo uno a tale deviato. In sostanza, otteniamo un numero casuale da questa distribuzione di Poisson e poi aggiungiamo uno. Alla linea tre, raccogliamo questo deviato in L1, che funge da accumulatore per l’aggregatore ranvar. Questo è esattamente lo stesso aggregatore che abbiamo introdotto precedentemente per il nostro esempio sul lead time. Qui raccogliamo tutte quelle osservazioni in L1, ottenendo una distribuzione unidimensionale realizzata tramite un processo Monte Carlo. Alla linea cinque, costruiamo la medesima distribuzione discreta unidimensionale, ma questa volta utilizzando l’algebra delle variabili casuali. Così, usiamo semplicemente Poisson meno tre e aggiungiamo uno. Alla linea cinque non è in corso alcun processo Monte Carlo; si tratta unicamente di probabilità discrete e convoluzioni.

Quando confrontiamo visivamente le due distribuzioni alle linee sette e otto, vediamo che sono quasi identiche. Dico “quasi” perché, pur impiegando 2.000 iterazioni, e anche se sono molte, non sono infinite. Le deviazioni tra le probabilità esatte ottenute con ranvar e quelle approssimative ottenute tramite il processo Monte Carlo sono ancora evidenti, seppur non elevate.

I generatori sono talvolta chiamati simulatori, ma non fraintendete: sono la stessa cosa. Ogni volta che avete un simulatore, c’è un processo generativo che implicitamente sta alla base di una previsione probabilistica. Quando è coinvolto un simulatore o un generatore, la domanda che dovrebbe sorgere è: qual è l’accuratezza di questa simulazione? Non è accurata per progettazione, così come è del tutto possibile ottenere previsioni completamente inesatte, siano esse probabilistiche o meno. È molto facile ottenere una simulazione totalmente inaccurata.

Con i generatori vediamo che le simulazioni sono solo un modo per osservare la prospettiva della previsione probabilistica, ma si tratta più di un dettaglio tecnico. Questo non cambia il fatto che, alla fine, si desidera avere qualcosa che rappresenti in modo accurato il sistema che si sta cercando di caratterizzare con la propria previsione, probabilistica o meno.

L’approccio generativo non è solo molto utile, come vedremo con un esempio specifico tra un attimo, ma è anche concettualmente più facile da comprendere, almeno in parte, rispetto all’approccio basato sulle densità di probabilità. Tuttavia, l’approccio Monte Carlo non è privo di complessità tecniche. Ci sono alcune cose necessarie se si vuole rendere questo approccio praticabile in un contesto di produzione per una supply chain reale.

Prima di tutto, i generatori devono essere veloci. Monte Carlo rappresenta sempre un trade-off tra il numero di iterazioni che si vorrebbero ottenere e quello che si può permettere, considerando le risorse computazionali disponibili. Sì, i computer moderni dispongono di molta potenza di elaborazione, ma i processi Monte Carlo possono richiedere risorse incredibilmente elevate. Si desidera qualcosa che, di default, sia super veloce. Se torniamo agli ingredienti introdotti nella seconda lezione del quarto capitolo, abbiamo funzioni molto veloci come ExhaustShift o WhiteHash, essenziali per la costruzione delle primitive che permettono di generare generatori casuali elementari super veloci. Senza queste, si farà fatica. In secondo luogo, è necessario distribuire l’esecuzione. L’implementazione naïf di un programma Monte Carlo consiste semplicemente in un ciclo che itera in modo sequenziale. Tuttavia, se si utilizza una sola CPU per affrontare i requisiti Monte Carlo, in sostanza si ritorna alla potenza computazionale dei computer di due decenni fa. Questo punto è stato affrontato già nella primissima lezione del quarto capitolo. Negli ultimi vent’anni i computer sono diventati più potenti, ma principalmente grazie all’aggiunta di CPU e a gradi di parallelizzazione. Quindi, è necessario avere una prospettiva distribuita per i propri generatori.

Infine, l’esecuzione deve essere deterministica. Cosa significa? Significa che se lo stesso codice viene eseguito due volte, esso deve produrre esattamente gli stessi risultati. Questo può sembrare controintuitivo, dato che stiamo trattando metodi randomizzati. Tuttavia, la necessità di determinismo è emersa molto rapidamente. È stata scoperta in modo doloroso negli anni ‘90, quando la finanza iniziò a utilizzare generatori Monte Carlo per il pricing. La finanza intraprese la strada della previsione probabilistica già tempo fa e fece ampio uso dei generatori Monte Carlo. Una delle cose che hanno imparato è che se non c’è determinismo, diventa quasi impossibile replicare le condizioni che hanno generato un bug o un crash. Dal punto di vista della supply chain, errori nei calcoli degli ordini di acquisto possono risultare incredibilmente costosi.

Se desideri raggiungere un certo grado di prontezza alla produzione per il software che governa la tua supply chain, devi assicurarti che questa proprietà deterministica sia presente ogni volta che utilizzi Monte Carlo. Attenzione, molte soluzioni open-source provengono dal mondo accademico e non tengono conto della prontezza alla produzione. Assicurati che, quando lavori con Monte Carlo, il tuo processo sia intrinsecamente super veloce, distribuito per design e deterministico, in modo da poter diagnosticare i bug che inevitabilmente sorgeranno nel tempo nel tuo ambiente produttivo.

Abbiamo osservato una situazione in cui è stato introdotto un generatore per replicare ciò che altrimenti veniva svolto con una variabile casuale. In linea di massima, ogni volta che puoi fare a meno delle sole densità di probabilità con variabili casuali senza coinvolgere Monte Carlo, è meglio. Si ottengono risultati più precisi e non devi preoccuparti della stabilità numerica, che è sempre un po’ complicata con Monte Carlo. Tuttavia, l’espressività dell’algebra delle variabili casuali è limitata, ed è qui che Monte Carlo risplende veramente. Questi generatori sono più espressivi perché ti permettono di comprendere situazioni che non possono essere affrontate solo con un’algebra delle variabili casuali.

Illustriamo questo con una situazione di supply chain. Considera un singolo SKU con un livello di scorte iniziale, una previsione probabilistica per la domanda e un periodo di interesse che si estende su tre mesi, con una spedizione in arrivo a metà periodo. Presumiamo che la domanda venga soddisfatta immediatamente dalle scorte disponibili o che venga persa per sempre. Vogliamo conoscere il livello atteso delle scorte al termine del periodo per lo SKU, poiché saperlo ci aiuterà a decidere quanto rischio abbiamo in termini di inventario invenduto.

La situazione è insidiosa perché è stata progettata in modo tale che esista una terza possibilità per un stockout di verificarsi proprio a metà periodo. L’approccio ingenuo sarebbe prendere il livello di scorte iniziale, la distribuzione della domanda per l’intero periodo, e sottrarre la domanda dalle scorte, ottenendo così il livello residuo di scorte. Tuttavia, questo non tiene conto del fatto che potremmo perdere una buona parte della domanda se si verifica un stockout mentre il riapprovvigionamento in arrivo è ancora in sospeso. Farlo in maniera ingenua sottostimerebbe la quantità di scorte che avremo alla fine del periodo e sovrastimerebbe la quantità di domanda che verrà soddisfatta.

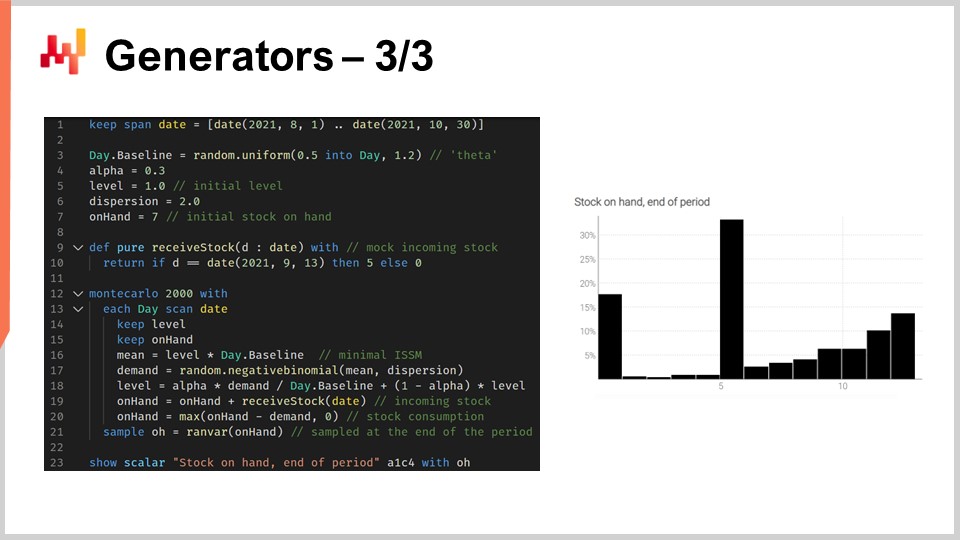
Lo script in esposizione modella l’ocorrenza degli stockout in modo da poter avere un estimatore corretto per il livello delle scorte di questo SKU alla fine del periodo. Dalle linee 1 a 10 definiamo i dati fittizi che caratterizzano il nostro modello. Le linee dalla 3 alla 6 contengono i parametri per il modello ISSM. Abbiamo già visto il modello ICSM nella primissima lezione di questo quinto capitolo. In sostanza, questo modello genera una traiettoria della domanda con un punto dati per ogni giorno. Il periodo di interesse è definito nella tabella dei giorni, e abbiamo i parametri per questa traiettoria fin dall’inizio.

Nelle lezioni precedenti abbiamo introdotto il modello AICSM e i metodi necessari, attraverso la programmazione differenziabile, per apprendere questi parametri. Oggi utilizziamo il modello, presupponendo di aver appreso tutto ciò che occorre. Alla linea 7 definiamo le scorte iniziali disponibili, che tipicamente si ottengono dall’ERP o dal WMS. Alle linee 9 e 10 definiamo la quantità e la data per il riapprovvigionamento. Questi dati verrebbero solitamente ottenuti come tempo stimato di arrivo fornito dal fornitore e registrato nell’ERP. Presumiamo che la data di consegna sia perfettamente nota; tuttavia, sarebbe semplice sostituire questa data singola con una previsione probabilistica del lead time.

Dalle linee 12 a 21 abbiamo il modello ISSM che genera la traiettoria della domanda. Siamo all’interno di un ciclo Monte Carlo e, per ogni iterazione Monte Carlo, attraversiamo ogni singolo giorno del periodo di interesse. L’iterazione dei giorni inizia alla linea 13. Abbiamo in atto la meccanica ESSM, ma alle linee 19 e 20 aggiorniamo la variabile on-hand. La variabile on-hand non fa parte del modello ISSM; rappresenta un’integrazione extra. Alla linea 19 affermiamo che le scorte disponibili sono quelle di ieri più la spedizione in arrivo, che sarà zero per la maggior parte dei giorni e cinque unità per il 13 settembre. Poi, alla linea 20, aggiorniamo le scorte dicendo che un certo numero di unità viene consumato dalla domanda del giorno, usando il max 0 per indicare che il livello di scorte non può scendere in negativo.

Infine, raccogliamo le scorte finali disponibili alla linea 21 e, alla linea 23, queste vengono messe in visualizzazione. Questo è l’istogramma che vedi sulla destra dello schermo. Qui osserviamo una distribuzione con una forma molto irregolare. Tale forma non può essere ottenuta attraverso l’algebra delle variabili casuali. I generatori sono incredibilmente espressivi; tuttavia, non dovresti confondere l’espressività di questi generatori con l’accuratezza. Pur essendo estremamente espressivi, non è banale valutare l’accuratezza di tali generatori. Non fraintendermi, ogni volta che utilizzi un generatore o un simulatore, hai in gioco una previsione probabilistica e le simulazioni possono essere estremamente inaccurate, proprio come qualsiasi altra previsione, probabilistica o meno.

È già stata una lezione lunga, eppure ci sono molti argomenti che oggi non ho neanche toccato. Il processo decisionale, per esempio, se tutti i futuri sono possibili, come decidiamo qualcosa? Non ho risposto a questa domanda, ma verrà affrontata nella prossima lezione.

Anche le dimensioni superiori sono importanti da considerare. Una distribuzione unidimensionale è un punto di partenza, ma una supply chain ha bisogno di molto di più. Per esempio, se si verifica un stock-out per un determinato SKU, potremmo sperimentare la cannibalizzazione, dove i clienti ricorrono naturalmente a un sostituto. Vorremmo modellare questo, anche se in maniera sommaria.

Anche i costrutti di ordine superiore giocano un ruolo. Come ho detto, prevedere la domanda non è come prevedere i movimenti dei pianeti. Abbiamo effetti auto-profetici ovunque. A un certo punto, vogliamo considerare e integrare le nostre politiche di prezzo e di riapprovvigionamento. Per farlo, abbiamo bisogno di costrutti di ordine superiore, il che significa che, data una politica, ottieni una previsione probabilistica dell’esito, ma devi iniettare la politica all’interno dei costrutti di ordine superiore.

Inoltre, padroneggiare le previsioni probabilistiche comporta numerose ricette numeriche e una notevole esperienza nel dominio per sapere quali distribuzioni si adattano meglio a determinate situazioni. In questa serie di lezioni introdurremo ulteriori esempi in seguito.

Infine, c’è la sfida del cambiamento. Le previsioni probabilistiche rappresentano una rottura radicale rispetto alle pratiche tradizionali della supply chain. Spesso, le complessità tecniche legate alle previsioni probabilistiche sono solo una piccola parte della sfida. La parte difficile è reinventare l’organizzazione stessa, affinché essa possa iniziare a utilizzare queste previsioni probabilistiche invece di affidarsi alle previsioni puntuali, che sono essenzialmente frutto di desideri irrealistici. Tutti questi aspetti saranno trattati in lezioni successive, ma richiederanno tempo visto il vasto terreno da coprire.

In conclusione, le previsioni probabilistiche rappresentano una rottura radicale rispetto alla prospettiva delle previsioni puntuali, in cui si attende un consenso su un unico futuro che si suppone debba realizzarsi. La previsione probabilistica si basa sull’osservazione che l’incertezza del futuro è irreducibile. Un secolo di scienze previsionali ha dimostrato che tutti i tentativi di ottenere previsioni anche solo vagamente accurate sono falliti. Quindi, siamo bloccati con molti futuri indefiniti. Tuttavia, le previsioni probabilistiche ci offrono tecniche e strumenti per quantificare e valutare questi futuri. Le previsioni probabilistiche sono un risultato significativo. Ci è voluto quasi un secolo per accettare l’idea che l’analisi economica non fosse come l’astronomia. Mentre possiamo prevedere con grande accuratezza la posizione esatta di un pianeta tra un secolo, non abbiamo alcuna speranza di ottenere qualcosa di remotamente equivalente nel campo della supply chain. L’idea di avere una previsione unica che domini tutto non tornerà mai. Eppure, molte aziende si aggrappano ancora alla speranza che, ad un certo punto, verrà raggiunta la vera previsione accurata. Dopo un secolo di tentativi, questo è essenzialmente un pensiero illusorio.

Con i computer moderni, questa prospettiva di un unico futuro non è l’unica opzione. Esistono alternative. Le previsioni probabilistiche sono in uso dagli anni ‘90, ovvero da tre decenni. In Lokad, utilizziamo le previsioni probabilistiche per gestire le supply chain in produzione da oltre un decennio. Potrebbe non essere ancora la norma, ma è ben lontana dall’essere fantascienza. È una realtà per molte aziende nel settore finanziario da tre decenni e nel mondo della supply chain da un decennio.

Anche se le previsioni probabilistiche possono sembrare intimidatorie e altamente tecniche, con gli strumenti giusti si riducono a poche linee di codice. Non c’è nulla di particolarmente difficile o impegnativo nelle previsioni probabilistiche, almeno non rispetto ad altri tipi di previsioni. La sfida più grande consiste nel rinunciare al comfort dell’illusione che il futuro sia perfettamente sotto controllo. Il futuro non è perfettamente controllato e non lo sarà mai, e, in generale, probabilmente è per il meglio.

Concludiamo qui la lezione di oggi. La prossima volta, il 6 aprile, presenterò il processo decisionale nel dispaccio degli inventari al dettaglio, e vedremo come le previsioni probabilistiche presentate oggi possano essere impiegate per guidare una decisione fondamentale nella supply chain, vale a dire il riapprovvigionamento dell’inventario in una rete di vendita al dettaglio. La lezione si terrà lo stesso giorno della settimana, mercoledì, alla stessa ora, alle 15:00, e sarà il primo mercoledì di aprile.

Domanda: Possiamo ottimizzare la risoluzione in termini di precisione rispetto al volume di RAM per Envision?

Sì, assolutamente, anche se non in Envision stesso. Questa è una scelta che abbiamo fatto nel design di Envision. Il mio approccio, quando si tratta di supply chain scientists, è liberare questi professionisti dalle questioni tecniche di basso livello. I 4 kilobyte di Envision offrono molto spazio, permettendo una rappresentazione accurata della tua situazione di supply chain. Quindi, l’approssimazione che perdi in termini di risoluzione e precisione è irrilevante.

Certamente, quando si tratta del design del tuo algoritmo di compressione, ci sono molti compromessi da considerare. Per esempio, i bucket vicini allo zero devono avere una risoluzione perfetta. Se vuoi ottenere la probabilità di osservare zero unità di domanda, non vuoi che la tua approssimazione raggruppi insieme i bucket per zero domanda, una unità e due unità. Tuttavia, se osservi i bucket per la probabilità di osservare 1.000 unità di domanda, raggruppare 1.000 e 1.001 unità è probabilmente accettabile. Quindi, esistono molti accorgimenti per sviluppare un algoritmo di compressione che si adatti veramente alle esigenze della supply chain. Questo è di gran lunga più semplice rispetto a ciò che avviene nella compressione delle immagini. Il mio punto di vista è che uno strumento progettato correttamente possa fondamentalmente astraere il problema per i supply chain scientists. Questo livello di dettaglio è troppo basso e, nella maggior parte dei casi, non è necessario micro-ottimizzare. Se sei Walmart e non hai solo 1 milione di SKU, ma diversi centinaia di milioni di SKU, allora la micro-ottimizzazione potrebbe avere senso. Tuttavia, a meno che tu non stia parlando di supply chain estremamente grandi, credo sia possibile ottenere qualcosa di sufficientemente buono, in modo che l’impatto prestazionale di una non ottimizzazione completa sia per lo più irrilevante.

Domanda: Quali sono le considerazioni pratiche da tenere in conto da una prospettiva di supply chain durante l’ottimizzazione di tali parametri?

Quando si tratta di previsioni probabilistiche nella supply chain, avere una precisione superiore a una parte su 100.000 è tipicamente irrilevante, semplicemente perché non hai mai abbastanza dati per stimare le probabilità con una granularità superiore a una parte su 100.000.

Domanda: Quale settore beneficia maggiormente dall’approccio delle previsioni probabilistiche?

La risposta breve è: più i tuoi modelli sono erratici e irregolari, maggiori sono i benefici. Se hai una domanda intermittente, i benefici sono enormi; se hai una domanda erratica, i benefici sono notevoli; se i lead time variano ampiamente e le supply chain subiscono shock erratici, i benefici sono massimi. All’estremo opposto, ad esempio, se consideriamo la supply chain della distribuzione dell’acqua, il consumo d’acqua è estremamente regolare e raramente subisce grandi shock – solo micro-shock al massimo. Questo è un tipo di problema che non trae vantaggio dall’approccio probabilistico. L’idea è che in alcune situazioni le previsioni puntuali classiche forniscono risultati molto accurati. Se ti trovi in una situazione in cui le previsioni per tutti i tuoi prodotti hanno un margine di errore inferiore al cinque percento guardando al futuro, allora non hai bisogno di previsioni probabilistiche; in tali casi, una previsione veramente accurata funziona. Tuttavia, se ti trovi in situazioni in cui la precisione delle previsioni è molto bassa, con un margine d’errore del 30% o più, allora beneficerai enormemente dalle previsioni probabilistiche. Tra l’altro, quando dico errore del 30% mi riferisco sempre alla previsione estremamente disaggregata. Molte aziende dichiarano che le loro previsioni hanno un margine d’errore del 5%, ma se si aggrega tutto questo può generare una percezione fuorviante dell’accuratezza reale. L’accuratezza delle previsioni conta soprattutto a livello disaggregato, tipicamente a livello di SKU e giornaliero, poiché le decisioni vengono prese proprio a questi livelli. Se a livello di SKU e a livello giornaliero riesci a ottenere previsioni con un margine d’errore del 5%, allora non hai bisogno di previsioni probabilistiche. Tuttavia, se noti imprecisioni a due cifre in termini percentuali, allora beneficerai enormemente dalle previsioni probabilistiche.

Domanda: Dato che i tempi di consegna possono essere stagionali, decomporresti le previsioni dei lead time in più previsioni, una per ogni stagione distinta, per evitare di osservare una distribuzione multimodale?

Questa è una buona domanda. L’idea qui è che tipicamente costruisci un modello parametrico per i tuoi tempi di consegna che includa un profilo di stagionalità. Affrontare la stagionalità dei tempi di consegna non è fondamentalmente molto diverso dal gestire qualsiasi altra ciclicità, come abbiamo fatto nella lezione precedente per la domanda. Il metodo tipico non è costruire modelli multipli, perché, come hai giustamente sottolineato, se ne hai diversi, osserverai ogni sorta di salti bizzarri quando passi da una modalità all’altra. Di solito è meglio avere un solo modello con un profilo di stagionalità al centro. Sarebbe come una decomposizione parametrica in cui hai un vettore che ti indica l’effetto settimanale che incide sul tempo di consegna in una certa settimana dell’anno. Forse avremo tempo in una lezione successiva per fornire un esempio più esteso di ciò.

Question: La previsione probabilistica è un buon approccio quando si vuole prevedere una domanda intermittente?

Assolutamente. In effetti, credo che quando si ha una domanda intermittente, la previsione probabilistica non sia solo un buon metodo, ma la classica previsione puntuale risulti completamente priva di senso. Con la previsione classica, normalmente fatichi a gestire tutti quegli zeri. Cosa ne fai di quegli zeri? Finisci con un valore molto basso e frazionario, che in realtà non ha molto senso. Con la domanda intermittente, la vera domanda a cui vuoi rispondere è: il mio stock è abbastanza grande da soddisfare quei picchi di domanda che tendono a verificarsi di tanto in tanto? Se usi una previsione media, non lo saprai mai.

Solo per tornare all’esempio della libreria, se dici che in una data settimana osservi in media una unità di domanda al giorno, quanti libri devi tenere nella tua libreria per garantire un’elevata qualità del servizio? Supponiamo che la libreria venga rifornita ogni singolo giorno. Se le uniche persone di cui ti occupi sono studenti, allora, con una media di una unità di domanda ogni giorno, avere tre libri in stock garantirà un’elevata qualità del servizio. Tuttavia, se di tanto in tanto arriva un professore in cerca di 20 libri in una volta, la qualità del servizio, se hai solo tre libri in negozio, sarà pessima perché non sarai mai in grado di servire nessun professore. Questo è tipicamente il caso della domanda intermittente – non è solo il fatto che la domanda sia intermittente, ma anche che alcuni picchi di domanda possano variare significativamente in termini di entità. È qui che la previsione probabilistica risplende veramente, poiché riesce a catturare la struttura fine della domanda invece di raggrupparla tutte insieme in medie, dove questa struttura fine viene persa.

Question: Se sostituiamo il tempo di consegna con una distribuzione, il picco rappresentato da una curva a campana liscia nella prima slide per il generatore?

In una certa misura, se randomizzi di più, tendi a distribuire le cose. Nella prima slide relativa al generatore, dovremmo eseguire l’esperimento con diverse impostazioni per vedere cosa otteniamo. L’idea è che, quando vogliamo sostituire il tempo di consegna con una distribuzione, lo facciamo perché abbiamo un’intuizione sul problema che ci dice che il tempo di consegna sta variando. Se riponiamo completa fiducia nel nostro fornitore e questi si sono dimostrati incredibilmente affidabili, allora è perfettamente accettabile dire che l’ETA (estimated time of arrival) è ciò che è ed è una stima quasi perfetta della realtà. Tuttavia, se in passato abbiamo notato che i fornitori erano talvolta erratici o mancavano l’obiettivo, allora è meglio sostituire il tempo di consegna con una distribuzione.

Introdurre una distribuzione per sostituire il tempo di consegna non liscia necessariamente i risultati che ottieni alla fine; dipende da cosa stai osservando. Ad esempio, se consideri il caso più estremo di sovraccarico di stock, un tempo di consegna variabile può addirittura esacerbare il rischio di avere inventario invenduto. Perché? Se hai un prodotto molto stagionale e un tempo di consegna variabile, e il prodotto arriva dopo la fine della stagione, ti ritrovi con un prodotto fuori stagione, il che amplifica il rischio di avere inventario invenduto al termine della stagione. Quindi, è complicato. Il fatto di convertire una variabile nella sua sostituzione probabilistica non liscia automaticamente ciò che osserverai; a volte, può rendere la distribuzione ancora più accentuata. Quindi, la risposta è: dipende.

Eccellente, penso che per oggi sia tutto. A presto.