00:01 はじめに
02:18 現代の予測
06:37 パニック状態の確率的予測
11:58 これまでの経緯
15:10 本日の見込みプラン
17:18 予測の動物図鑑
28:10 指標 - CRPS - 1/2
33:21 指標 - CRPS - 2/2
37:20 指標 - モンジュ・カントロビッチ
42:07 指標 - 尤度 - 1/3
47:23 指標 - 尤度 - 2/3
51:45 指標 - 尤度 - 3/3
55:03 1次元分布 - 1/4
01:01:13 1次元分布 - 2/4
01:06:43 1次元分布 - 3/4
01:15:39 1次元分布 - 4/4
01:18:24 ジェネレーター - 1/3
01:24:00 ジェネレーター - 2/3
01:29:23 ジェネレーター - 3/3
01:37:56 無視している間、しばらくお待ちください
01:40:39 結論
01:43:50 今後の講義と聴衆からの質問
説明
予測が確率的であるとは、特定の結果を一つだけ指し示すのではなく、すべての可能な未来の結果に関連付けられた確率の集合を含む場合をいいます。確率的予測は、不確実性が解消できない場合、つまり複雑なシステムが関与する際には常に重要です。サプライチェーンにおいて、確率的予測は不確実な未来の状況に対して堅牢な意思決定を行うために不可欠です。
全文書き起こし

このサプライチェーン講義シリーズへようこそ。私はジョアンネス・ヴェルモレルです。本日は「サプライチェーンのための確率的予測」をご紹介します。確率的予測は、過去一世紀以上にわたる統計的予測科学における、最も重要なパラダイムシフトの一つ(あるいは最も重要なもの)です。しかし、技術的な面では、ほとんど従来と同じ統計や確率が用いられているだけです。確率的予測は、予測そのものの捉え方を変えるものです。サプライチェーンにおいて、確率的予測がもたらす最大の変化は、予測科学自体ではなく、予測モデルを前提としたサプライチェーンの運用と最適化の方法にあるのです。
本日の講義の目的は、確率的予測への丁寧な技術的入門を提供することです。この講義の終わりには、確率的予測とは何か、非確率的予測との違い、確率的予測の質を評価する方法、さらには入門レベルの確率的予測モデルを自ら設計する方法が理解できるようになるはずです。本日は、サプライチェーンの文脈における意思決定目的での確率的予測の活用については触れません。今回は、あくまで確率的予測の基礎を固めることに専念します。サプライチェーンにおける意思決定プロセスの改善は、次回の講義で扱います。

確率的予測の意義を理解するためには、少し歴史的な文脈が必要です。現代的な形の予測、すなわち統計的予測は、占いと対照される形で20世紀初頭に登場しました。予測は、物理学や化学など、極めて成功したハードサイエンスが、ほぼ任意に正確な結果を得るという科学的背景の中で発展しました。これらの成果は、何世紀にもわたる努力の結果であり、例えばガリレオ・ガリレイがより優れた測定技術を開発したことにその起源を辿ることができます。より正確な測定は、科学者が自らの理論や予測をさらに精密に検証・挑戦するための原動力となりました。
このように、いくつかの科学が大きな成功を収めた背景の中で、20世紀初頭に新たに登場した予測分野は、経済学の領域でそれらハードサイエンスが達成した成果を模倣しようと試みました。たとえば、近代経済予測の父の一人であるロジャー・バブソンは、20世紀初頭にアメリカで成功した経済予測会社を設立しました。同社のモットーは文字通り「すべての作用には等しく反対の反作用がある」というものでした。バブソンのビジョンは、ニュートン物理学の成功を経済学に転用し、同様の正確さを実現することにありました。
しかし、サプライチェーンが運用される今日までの1世紀以上にわたる統計的な学術予測の後も、理論上は任意に予測の精度が向上しうるという考えは、かつての夢のままです。数十年にわたり、サプライチェーン界では、これらの予測が十分に正確にならないだろうという懸念が上がってきました。リーン生産方式のように、サプライチェーンが信頼性の低い予測に大きく依存しないようにする動きもありました。これがジャストインタイムの考え方の根底にあるのです。市場の需要に合わせて必要なものを必要な時に製造・供給できるのであれば、もはや信頼性の高い正確な予測は不要になるのです。
この文脈において、確率的予測は予測の再生(リハビリテーション)でありながら、その野心ははるかに控えめです。確率的予測は、未来には解消不可能な不確実性が存在するとする考えに基づいています。あらゆる未来が可能であるものの、その発生確率は均一ではなく、確率的予測の目的は、すべての代替的未来の発生確率を比較評価することにあり、あらゆる可能性を一つに収束させることではありません。

統計的経済予測に対するニュートン的視点は、ほぼ失敗に終わりました。我々のコミュニティ内で、任意に正確な予測が実現するという考えはほとんど消え去っています。しかし、奇妙なことに、ほぼすべてのサプライチェーンソフトウェアや多くの主流のサプライチェーンの実践は、その根底に、最終的にはそのような予測が利用可能になるという前提を持っています。
例えば、セールス・アンド・オペレーションズ・プランニング(S&OP)は、すべての関係者が一堂に会して共同で予測を構築することにより、統一された定量的な企業ビジョンが達成できるという考えに基づいています。同様に、オープントゥバイも、本質的には、任意に正確なトップダウン予測を構築できるという考えに根ざした予算編成プロセスの一手法です。さらに、サプライチェーン分野で広く使用されるツール、例えばビジネス・インテリジェンスやスプレッドシート、そして時系列予測すべてが、歴史的なデータを未来に延長し、各期間ごとに一点を割り当てるという考えに基づいて設計されています。
実際、確率的予測は従来の予測に不確実性を付与するだけのものではありません。また、各シナリオごとに古典的予測の短いリストを作成することでもありません。主流のサプライチェーン手法は、本質的にある基準予測を中心に据えて物事が回るという考えに暗黙的または明示的に依拠しているため、通常は確率的予測を扱いません。対照的に、確率的予測はすべての可能な未来に対する数値的な前面評価なのです。
当然ながら、利用可能な計算資源には限りがあるため、「すべての可能な未来」と言っても、実際には有限数の未来しか考慮できません。しかし、現代の処理能力を考慮すると、実際に考慮できる未来の数は何百万にも上ります。これが、ビジネス・インテリジェンスやスプレッドシートが苦手とする点です。これらのツールは、1つの未来ではなくあらゆる未来を扱う計算に対して、大きな障壁を抱えています。これはソフトウェア設計の問題でもあります。つまり、スプレッドシートは同じコンピューターと処理能力にアクセスできるにもかかわらず、適切な設計が施されていなければ、膨大な処理能力を有していても特定のタスクを実行するのは非常に困難になるのです。
したがって、サプライチェーンの観点から、確率的予測を採用する上での最大の課題は、任意に正確な予測が可能であるという、極めて野心的ではあるものの誤った目標に基づく何十年にもわたるツールや慣習を手放すことにあります。ここで強調しておきたいのは、確率的予測をより正確な予測を実現する手段と考えるのは全くの誤りだということです。確率的予測は従来の主流予測の代替として、より正確であるとも言えません。確率的予測の優位性は、特にサプライチェーンの文脈における意思決定で、いかにこれらの予測が活用されうるかという点にあります。しかし、本日の目的は、単に確率的予測が何であるかを理解することであり、その活用方法については次回の講義で扱います。

この講義は、サプライチェーンに関する一連の講義の一部です。これらの講義はできるだけ独立性を保つようにしていますが、以前の講義で提示した内容を頻繁に参照するため、連続して視聴していただくと聴衆にとって非常に有益になる段階に達しています。
さて、本講義は第5章に相当し、予測モデリングに捧げられた講義の第3回目です。このシリーズの第1章では、サプライチェーンを学問としても実践としてもどう捉えるかという私の見解を示しました。第2章では、各種手法を紹介しました。実際、サプライチェーンの状況のほとんどは対立的な性質を持ち、単純な手法では打破できません。サプライチェーンの領域で一定の成功を収めるためには、適切な手法が必要です。
第3章は、サプライチェーンの簡素性に焦点を当て、各状況で直面する問題とその本質的な挑戦のみを徹底して検討するものでした。サプライチェーンの簡素性の考え方は、解決策側の要素をすべて排除し、まず問題そのものだけを詳細に見ることにあります。
第4章では、補助的な科学分野について幅広く概観しました。これらの科学はサプライチェーンそのものではなく、隣接または支援する研究分野ですが、現代のサプライチェーン実践にはこれら補助科学の入門知識が必要であると考えています。
最後に、第5章では、未来を定量化し評価する技術、特に未来に関する記述を作成するための技法に踏み込みます。実際、サプライチェーンで行うすべてのことは、ある程度未来への予測を反映しています。未来をより良く予測できれば、より良い意思決定が可能になるのです。これが第5章の主旨、すなわち未来について定量的に優れた洞察を得ることに関するものです。本章において、確率的予測は未来に取り組むための核心的な手法を提供します。
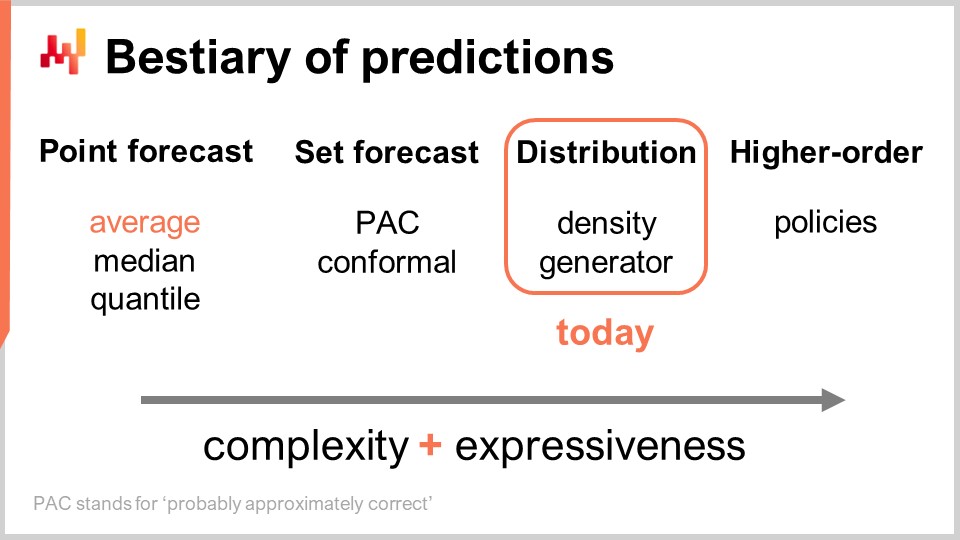
この講義の残りは、長さが異なる4つのセクションに分かれています。まず、従来の予測を超えた、最も一般的な予測の種類を検討します。ここでいう従来の予測の意味は後ほど明確にします。実際、サプライチェーンの分野では、利用可能な選択肢が多いことに気付いている人はほとんどいません。確率的予測自体は、非常に多様なツールと技法を包含する統括概念と理解されるべきです。
次に、確率的予測の質を評価するための指標を導入します。どのような結果になろうとも、よく設計された確率的予測は常に「この事象が起こる確率があった」と示します。では、実際に良い確率的予測と悪い確率的予測をどのように見極めるのでしょうか。そこでこれらの指標が役立ちます。確率的予測専用の専門的な指標が存在するのです。
第三に、1次元分布について詳しく検討します。これらは最も単純な分布であり、明らかな制約はあるものの、確率的予測の世界に入るための最も容易な入り口でもあります。
第四に、モンテカルロ法と呼ばれることが多いジェネレーターについて簡単に触れます。実際、ジェネレーターと確率密度推定器の間には二面性があり、これらのモンテカルロ法によって高次元の問題やその他の形態の確率的予測に取り組む道が拓かれます。

予測には複数の種類があり、この点は予測モデルに複数のタイプがあるという事実と混同してはなりません。同じタイプやクラスに属さないモデルは、そもそも同じ問題を解いているとは言えません。最も一般的な予測の形式はポイント予測です。例えば、「明日、この店舗のユーロでの合計売上が10,000ユーロになる」と言う場合、私はこの店舗の明日の状況についてポイント予測を行っていることになります。同じ作業を繰り返し、まず明日の日付について予測を行い、その次に明後日の日付について発言すれば、複数のデータポイントが得られます。しかし、本質的には、特定の集約レベルを選んでその集約レベルで単一の数字を得るという点において、依然としてポイント予測に過ぎません。
ポイント予測の中にも、最適化する指標に応じて複数のサブタイプがあります。おそらく最も一般的に使用される指標は二乗誤差であり、平均二乗誤差が用いられることで平均的な予測が得られます。ちなみに、これは少なくともある程度加法的である唯一の予測であるため、最も広く使用されています。どの予測も完全に加法的というわけではなく、常に多くの注意点が伴います。しかし、中には他よりも加法性の高い予測があり、平均予測はその中でも特に加法的です。平均予測を得たい場合、本質的には平均二乗誤差に最適化されたポイント予測を作成することになります。逆に、絶対誤差のような別の指標で最適化すれば、得られるのは中央値予測となります。また、このサプライチェーン講義シリーズ第5章の最初の講義で紹介したピンボール 損失関数を使用すれば、分位点予測が得られます。ちなみに、今日ご覧の通り、私は分位点予測を単なるポイント予測の一形式として分類しています。実際、分位点予測でも本質的には単一の推定値が得られ、この推定値には意図されたバイアスが含まれていることがあります。これが分位数の意味するところですが、私の見解では、予測が単一の点で表現されるという点から、十分にポイント予測と見なすことができます。
次に、セット予測というものがあります。これは単一の点ではなく、一連の点の集合を返します。セットの構築方法によっていろいろなバリエーションがあります。例えば、PAC予測を見てみましょう。PACはProbably Approximately Correct(おそらく概ね正しい)の略です。これは約20年前にValiantによって提唱されたフレームワークで、予測としてのセットにおいて、ある確率でその中に結果が観測されると述べています。実際に生成されるセットは、基準点からの最大距離で特徴づけられる領域内に収まるすべての点で構成されます。ある意味で、PACの予測観点は既にセット予測であり、出力が単一の点ではなく集合として表現されるからです。しかし、依然として中心となる参照点が存在し、その参照点からの最大距離が定義されています。すなわち、最終的に結果が予測セット内に収まるという、ある特定の確率が存在することを示しているのです。
PACアプローチは、コンフォーマルアプローチによって一般化することができます。コンフォーマル予測は「これはセットであり、その中に結果が収まる確率がこの値である」と伝えます。コンフォーマル予測がPACアプローチを一般化する点は、もはや参照点やその参照点への距離に依存していないことであり、あなたが望むように自由にセットを形作ることができ、それでもなおセット予測のパラダイムに属するという点です。
未来はさらに細分化され、より複雑な方法で表現することが可能です―それが分布予測です。分布予測は、すべての可能な結果をそれぞれの局所確率密度に写像する関数を提供します。ある意味で、まずは単一の点で表されるポイント予測から始まり、次に一連の点からなるセット予測へと進み、最終的に分布予測は厳密には関数、もしくは関数を一般化した何かであると言えます。ちなみに、本講義で「分布」という用語を使う際は、常に確率の分布を意味するものと解釈してください。分布予測は、セットよりもさらに豊かで複雑な情報を表しており、今日の焦点はそこにあります。
分布にアプローチする一般的な方法は2つあります。すなわち、密度アプローチとジェネレーターアプローチです。「密度」と言う場合、基本的には局所的な確率密度の推定を意味します。一方、ジェネレーターアプローチは、モンテカルロ生成プロセスを用いて結果―偏差と呼ばれる―を生成し、これらが同じ局所確率密度を反映することを意図しています。これらが、分布予測に取り組むための主要な2つの方法です。
分布を超えて、より高次の構造体が存在します。これは理解するのがやや複雑かもしれませんが、本日高次の構造体について詳述しないにしても、確率予測が分布の生成に焦点を当てる際、それが最終目的ではなく、単なる一段階に過ぎず、その先にさらに多くの可能性があることを示すためです。単純な状況に対して満足のいく答えを得るためには、高次の構造体が重要となります。
高次の構造体が何を意味するのかを理解するために、有効期限が近い商品に対して割引ポリシーが設定されている単純な小売店を考えてみましょう。明らかに、店舗は陳腐在庫を抱えたくないため、商品が有効期限に非常に近づくと自動的に割引が適用されます。この店が生み出す需要は、このポリシーに大きく依存します。したがって、あらゆる可能な結果の確率を表す分布としての予測は、このポリシーに依存すべきです。しかしながら、このポリシーは数学的なオブジェクト、すなわち関数です。私たちが求めるのは単なる確率予測ではなく、むしろ、与えられたポリシーに基づいて結果の分布を生成できるメタな高次構造体なのです。
サプライチェーンの観点から見ると、一種類の予測から次のタイプの予測に移行することで、はるかに多くの情報が得られます。これは予測の精度が向上するということではなく、全く異なる種類の情報、例えば白黒でしか見えなかった世界に色が加わるかのような変化を意味します。ツールの面では、スプレッドシートやビジネスインテリジェンスツールはポイント予測を扱うにはある程度十分ですが、考慮しているセット予測のタイプによっては、これらは設計能力の限界に挑むことになります。これらのツールは、予測値の最小値と最大値を定義するという明白なケース以外の、洗練されたセット予測を扱うようには設計されていません。本質的には、もし分布予測や高次の構造体に取り組むチャンスを得たいのであれば、全く異なる種類のツールが必要となることがすぐに明らかになるでしょう。
確率予測を始めるにあたり、良い確率予測とは何かを特徴付けてみましょう。実際、どのような結果が観測されても、確率予測はその事象が発生する確率があったことを示します。では、そのような状況下で、良い確率予測と悪い確率予測をどのように区別するのでしょうか?確率的だからといって、すべての予測モデルが優れているわけではありません。
これこそが、確率予測専用の指標が扱うテーマであり、Continuous Ranked Probability Score(CRPS)は一次元確率予測における絶対誤差の一般化です。この恐ろしい名称――CRPS――については本当に申し訳なく思いますが、私自身がこの用語を考案したのではなく、与えられたものです。CRPSの公式が画面に示されています。基本的に、関数Fは累積分布関数であり、予測そのものを表します。点xは実際の観測値であり、CRPSの値は、確率予測とその直前に観測された一つのデータ点との間で計算されるものです。
本質的には、観測された点はHeavisideステップ関数を介して準確率予測に変換されます。Heavisideステップ関数の導入は、観測した点を、全ての確率質量を単一の結果に集中させるDirac確率分布に変換することと同等です。その後、積分が行われ、本質的にはCRPSは何らかの形状マッチングを行っています。つまり、累積分布関数(CDF)の形状と、観測した点に対応するDiracのCDFの形状とを比較しているのです。
ポイント予測の観点から見ると、CRPSが紛らわしいのは、複雑な公式だけでなく、この指標が同じ型ではない2つの引数を取るためです。一方は分布であり、もう一方は単一のデータポイントです。したがって、絶対誤差や平均二乗誤差といった他の多くのポイント予測指標には存在しない非対称性がここにあります。CRPSでは、本質的に一点と分布を比較しているのです。
CRPSで何が計算されるかを理解するための興味深い点は、CRPSが観測値と同じ単位を持つということです。例えば、xがユーロで表現されているなら、関数Fとxの間で計算されるCRPSの値もユーロと同じ単位であるため、CRPSが絶対誤差の一般化であると言えるのです。ちなみに、確率予測をDiracに収束させた場合、CRPSはちょうど絶対誤差と同じ値を与えます。

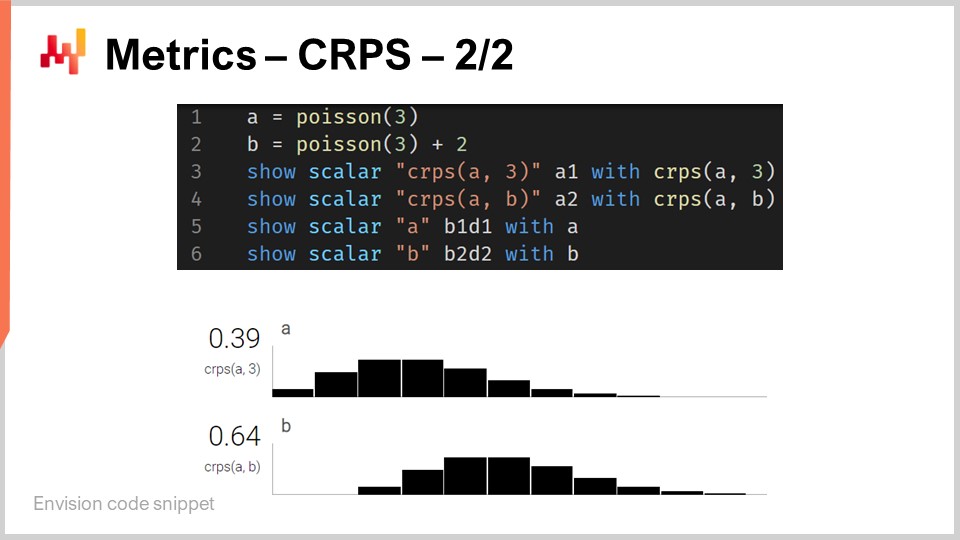
CRPSは非常に複雑で威圧的に見えるかもしれませんが、その実装は実際にはかなり直感的です。画面には、プログラミング言語の観点からCRPSがどのように使用できるかを示す小さなEnvisionスクリプトが表示されています。Envisionは、Lokadによって開発されたサプライチェーンの予測最適化に特化したドメイン固有プログラミング言語です。本講義では、明快さと簡潔さのためにEnvisionを使用しています。しかし、Envisionに特有のものは何もなく、Python、Java、JavaScript、C#、F#、またはその他の言語でも同じ結果が得られます。つまり、単にコード行数が増えるだけなので、ここではEnvisionに従っているのです。ちなみに、本講義および前回の講義で示された全てのコードスニペットは、独立して完全なもので、実際にコピー&ペーストして実行可能です。モジュールや隠れたコード、またセットアップすべき環境は一切ありません。
さて、コードスニペットに戻りましょう。1行目と2行目で一次元の分布を定義しています。Envisionにおけるこれら一次元分布の動作については後で触れますが、ここでは2つの分布が存在します。1つは離散一次元分布であるポアソン分布で、2行目のもう1つは同じポアソン分布を右に2ユニットシフトしたものです。これが「+2」の意味です。3行目では、分布と数値3との間のCRPS距離を計算しています。ここで、先ほど述べたデータ型の非対称性が現れています。そして、結果は画面下部に表示されるのが確認できます。
4行目では、分布Aと分布Bの間でCRPSを計算しています。古典的なCRPSの定義は、分布と単一の点の間での計算ですが、この定義を分布のペアに一般化することは全く問題ありません。同じCRPSの公式を用い、Heavisideステップ関数を2番目の分布の累積分布関数に置き換えるだけでよいのです。3行目から6行目までの"show"文が、画面下部に表示される、実際のスクリーンショットとなる結果を生成します。
このように、CRPSの使用は、コサイン関数のような特殊な関数を用いるのと同じくらい難しくも複雑ともいえません。もちろん、コサインを自分で再実装しなければならないのであれば手間はかかりますが、全体としてCRPS自体が特に複雑なものではないのは明らかです。では、次に進みましょう。

Monge-Kantorovich問題は、CRPSにおける形状マッチングのプロセスを高次元でどのようにアプローチするかについての洞察を与えてくれます。なお、CRPSは実際には一次元に限定されていることを忘れてはなりません。形状マッチングは概念的には任意の次元に一般化可能であり、さらにMonge-Kantorovich問題は、その根底にサプライチェーン問題があるという点でも非常に興味深いです。
もともと確率予測とは無関係であったMonge-Kantorovich問題は、フランスの科学者ガスパール・モンジュによって、1781年の回顧録「Mémoire sur la théorie des déblais et des remblais」で紹介されました。大雑把に訳すと「土砂移動理論に関する回顧録」となります。Monge-Kantorovich問題を理解する一つの方法は、画面上でMと表される鉱山のリストと、Fと表される工場のリストを考えることです。鉱山は鉱石を生産し、工場はその鉱石を消費します。私たちが求めているのは、鉱山で生産されたすべての鉱石を、工場が必要とする消費量に対応付ける輸送計画Tを構築することです。
モンジュは、鉱山から工場へ全ての鉱石を輸送するためのコストを資本Cとして定義しました。このコストは、すべての鉱山からすべての工場への鉱石輸送の総和であり、当然ながら非効率な輸送方法も存在します。したがって、特定のコストがあると言うときには、それが最適な輸送計画を反映していることを意味します。この資本Cは、最適な輸送計画を考慮した場合に達成可能な最良のコストを表しているのです。
これは本質的には、何世紀にもわたって広範に研究されてきたサプライチェーンの問題です。完全な問題定式化では、Tに対する制約があります。簡潔さのために、すべての制約を画面に表示してはいません。たとえば、輸送計画が各鉱山の生産能力を超えないこと、そして各工場が要求に見合った割り当てを受けることで完全に満たされるという制約があります。制約は数多く存在しますが、その記述は非常に冗長なため、ここでは省略しています。
さて、輸送問題自体は興味深いものですが、鉱山のリストと工場のリストを2つの確率分布として解釈し始めると、点ごとの尺度を分布全体の尺度に変換する方法が得られます。これは、Monge-Kantorovichの視点を通じた高次元における形状マッチングの重要な洞察です。この視点はWasserstein距離とも呼ばれますが、主に非離散的な場合に関係し、我々にとっての関心はそれほど高くありません。
Monge-Kantorovichの視点では、2つの数値や数値ベクトル間の差を計算する点ごとの尺度を、同じ空間で動作する確率分布に適用できる尺度に変換することができます。これは非常に強力な仕組みですが、Monge-Kantorovich問題は解決が困難で、相当な処理能力を必要とします。講義の残りでは、より実装と実行が容易な手法に固執します。

ベイジアンの視点とは、一連の観測結果を先入観の観点から見ることです。ベイジアンの視点は、実際の観測に基づいて結果の頻度を推定するフリクエント主義の視点と対比して理解されることが多いです。フリクエント主義は先入観を持たないという考えに基づいています。そのため、ベイジアンの視点は、観測結果と特定のモデルを考慮した際の驚きの度合いを評価するための「尤度」として知られるツールを提供してくれます。このモデルは本質的に確率的予測モデルであり、我々の先入観の形式化を意味します。ベイジアンの視点は、確率的予測モデルに対してデータセットを評価する方法を提供してくれます。これがどのように行われるかを理解するために、まず単一のデータポイントに対する尤度から始めましょう。観測値xに対する尤度は、モデルに従ってxが観測される確率です。ここで、モデルはパラメータthetaによって完全に特徴付けられていると仮定されます。ベイジアンの視点では、通常、モデルが何らかのパラメトリックな形を持ち、thetaが全てのモデルパラメータの完全なベクトルであると仮定します。
thetaというとき、我々は暗黙のうちに、確率モデルを完全に特徴付け、その結果として各点に対する局所的な確率密度を与えるものだと仮定しています。したがって、尤度はこの1つのデータポイントが観測される確率となります。モデルthetaの尤度は、データセット内のすべてのデータポイントが観測される結合確率となります。これらの点を独立であると仮定するので、尤度は確率の積になります。
もし何千もの観測値がある場合、1未満の値が何千も掛け合わされる尤度は、数値的に極めて小さくなってしまいます。極小の値は、コンピュータの浮動小数点数の表現方法では表現が難しいのが通常です。そこで、直接扱いにくい尤度の代わりに、対数尤度を用いる傾向があります。対数尤度とは、単に尤度の対数であり、乗算を加算に変換するという素晴らしい性質を持っています。
モデルthetaの対数尤度は、画面の最終行に示されているように、すべてのデータポイント個々の尤度の対数の総和です。尤度は、与えられた確率的予測がどれほどデータに適合しているかを示す尺度です。これは、観測されるデータセットがそのモデルによって生成された可能性の高さを教えてくれます。2つの確率的予測が競合している場合、他のフィッティングの問題を一旦脇に置けば、最も高い尤度、または対数尤度を与えるモデルを選ぶべきです。尤度が高いほど良いのです。
尤度は非常に興味深いのは、Monge-Kantorovich法とは異なり、高次元でも問題なく動作するからです。局所的な確率密度を提供するモデルさえあれば、尤度、もしくは現実的には対数尤度を尺度として利用することができます。

さらに、一度適合度を表す尺度が手に入れば、その尺度に対して最適化を行うことが可能になります。必要なのは、自由度が少なくとも1つ、つまり最低1つのパラメータを持つモデルだけです。このモデルを尤度、すなわち適合度の尺度に対して最適化すれば、せめてまともな確率的予測を生成するように学習されたモデルが得られるはずです。これが、まさに画面上で実施されていることです。
1行目と2行目では、モックデータセットを生成します。2,000行のテーブルを作成し、続いて2行目で、平均が2のポアソン分布からの偏差、すなわち2,000の観測値を生成します。こうして、2,000の観測値が得られます。3行目では、自動微分ブロックを開始します。これは微分可能プログラミングパラダイムの一部です。このブロックは確率的勾配降下法を実行し、観測テーブル内のすべての観測値に対して何度も繰り返し処理を行います。ここで、観測テーブルはTというテーブルです。
4行目では、lambdaと呼ばれるモデルの1つのパラメータを宣言します。このパラメータが正の値のみであることを指定しています。このパラメータを、確率的勾配降下法によって再発見しようと試みます。5行目では、損失関数を定義します。これは単に対数尤度にマイナスをつけたものです。尤度を最大化したいのですが、自動微分ブロックは損失を最小化しようとするため、対数尤度を最大化するためにはその前にマイナス符号を付与する必要があり、これがまさに行われたことです。
学習されたlambdaパラメータは6行目に表示されます。当然ながら、得られた値は2に非常に近くなります。なぜなら、平均2のポアソン分布で開始したからです。パラメトリックで同じ形状の、つまりポアソン分布としての確率的予測モデルを作成しました。ポアソン分布の唯一のパラメータを再発見することが目的であり、結果としてほぼそれが実現されています。元の推定値から約1%以内のモデルを得たのです。
これで、最初の確率的予測モデルを学習しましたが、必要だったのは実質的に3行のコードだけでした。これは明らかに非常にシンプルなモデルですが、確率的予測自体に本質的な複雑さは伴わないことを示しています。通常の二乗平均誤差による予測ではありませんが、適切なツール、たとえば微分可能プログラミングを用いれば、古典的な点予測よりも複雑ではありません。
以前使用したlog_likelihood.poisson関数は、Envisionの標準ライブラリの一部です。しかし、何か魔法のようなものが使われているわけではありません。この関数が内部でどのように実装されているか見てみましょう。最初の2行は、ポアソン分布の対数尤度の実装を示しています。ポアソン分布は、その1つのパラメータであるlambdaによって完全に特徴付けられており、対数尤度関数は、ポアソン分布を完全に定義するパラメータと実際の観測値という2つの引数だけを取ります。ここで記述した数式は、まさに教科書通りの内容です。教科書のポアソン分布を特徴付ける数式を実装した結果と言え、特に派手な工夫はありません。
この関数がautodiffキーワードでマークされている点に注目してください。前回の講義で見たように、autodiffキーワードは自動微分がこの関数を通じて正しく流れることを保証します。ポアソン分布の対数尤度は、log_gammaという別の特殊な関数も利用しています。log_gamma関数は、ガンマ関数の対数であり、ガンマ関数は階乗関数を複素数に一般化したものです。ここでは、実数の正の数に対する階乗関数の一般化だけが必要です。
log_gamma関数の実装はやや冗長ですが、これもまた教科書通りの内容です。log_gamma関数には連分数近似が用いられています。ここでの素晴らしい点は、下層に至るまで自動微分が機能していることです。autodiffブロックから始まり、autodiff関数として実装されたlog_likelihood.poisson関数を呼び出し、この関数はさらにautodiffマーカー付きで実装されたlog_gamma関数を呼び出します。要するに、よく設計された標準ライブラリのおかげで、確率的予測方法を3行のコードで実現できるのです。
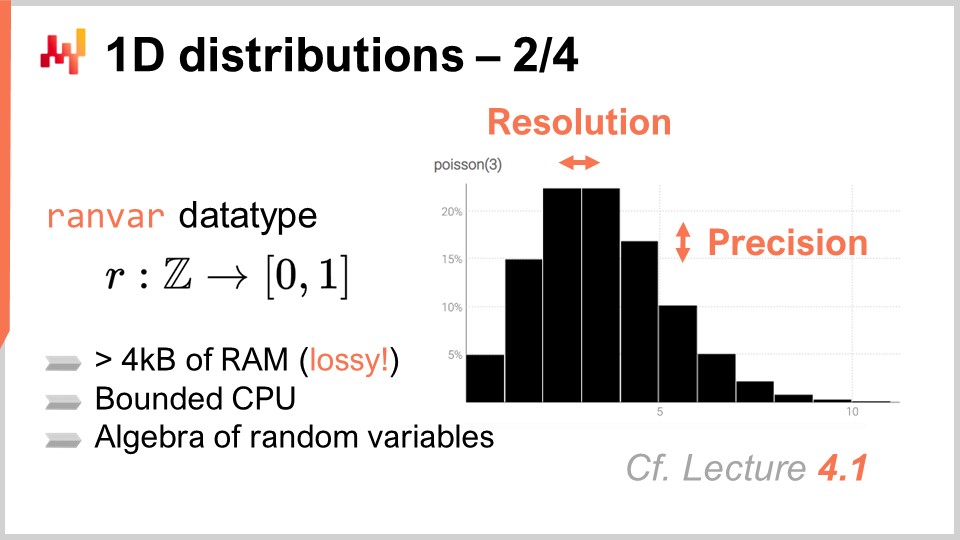
さて、1次元の離散分布という特別なケースに移りましょう。これらの分布はサプライチェーンのあらゆる場所に存在し、確率的予測への入り口を形成します。たとえば、日単位の粒度でリードタイムを予測する場合、1日のリードタイムとなる確率、2日のリードタイムとなる確率、3日、…といった具合に考えることができます。これらすべてが、リードタイムに対する確率のヒストグラムを構成します。同様に、ある日の特定のSKUの需要について考えると、需要が0ユニット、1ユニット、2ユニット…と観測される確率が存在すると言えます。
これらすべての確率をまとめると、それらを表すヒストグラムが得られます。同様に、SKUの在庫レベルについて考える場合、シーズン終了時にそのSKUがどれだけの在庫を残すかを評価することに関心があるかもしれません。確率的予測を用いて、シーズン終了時に在庫が0ユニット、1ユニット、2ユニット…となる確率を求めることができます。これらすべての状況は、対象となる現象の各離散的な結果に対応するバケットを持つヒストグラムで表現されるというパターンに収まります。
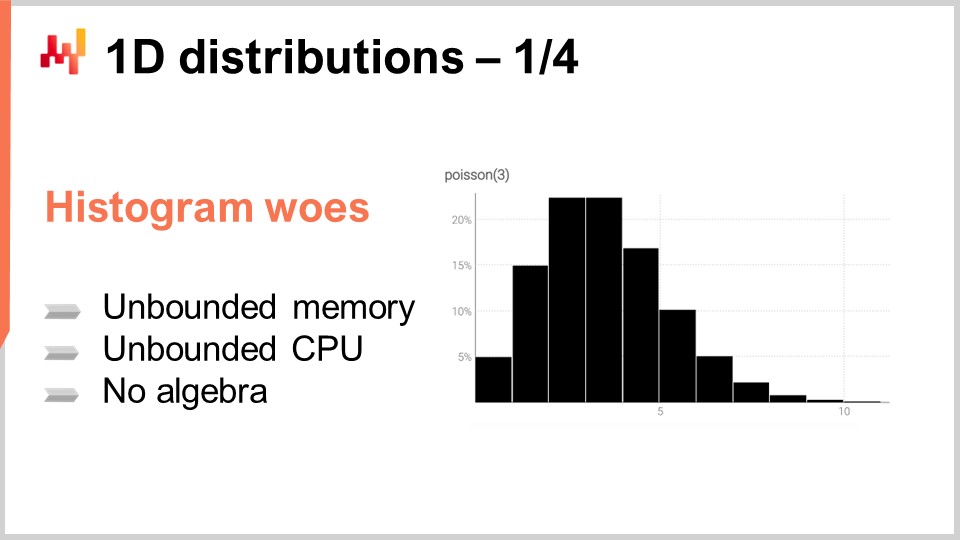
ヒストグラムは1次元の離散分布を表現する標準的な方法です。各バケットは、その離散的な結果に対する確率の質量と結びついています。しかし、データの可視化という用途を除けば、ヒストグラムは少々物足りないものです。実際、確率分布を単に可視化する以外の操作を行う際、ヒストグラムの取り扱いは多少の苦労を伴います。ヒストグラムには本質的に2つの問題があります。1つは計算資源に関するもので、もう1つはヒストグラム自体のプログラミング表現力に関するものです。
計算資源の観点からは、ヒストグラムに必要なメモリ量は本質的に無制限であることを考慮すべきです。ヒストグラムは、必要に応じて大きくなる配列と考えることができます。単一のヒストグラム、たとえサプライチェーンの視点で非常に大きなものであっても、現代のコンピュータにとっては必要なメモリ量は問題になりません。問題は、サプライチェーンの文脈で、1つのヒストグラムだけでなく、数百万のSKUに対して数百万ものヒストグラムが存在するときに生じます。各ヒストグラムがかなり大きくなる可能性がある場合、これらのヒストグラムの管理は、現代のコンピュータが非一様なメモリアクセスを提供する傾向があることを考えると、非常に困難になります。
逆に、これらのヒストグラムを処理するために必要なCPUの量も無制限です。ヒストグラムの操作は概ね線形ですが、非一様なメモリアクセスのためにメモリ量が増大すると処理時間も増加します。その結果、必要なメモリとCPUに明確な制限を設けることに大きな関心が寄せられています。
ヒストグラムに関する第2の問題は、付随する代数体系が存在しないことです。2つのヒストグラムに対して、各バケットごとに加算や乗算を行うことは可能ですが、それではヒストグラムを確率変数の表現として解釈した場合に意味を成すものにはなりません。たとえば、2つのヒストグラムを点ごとに乗算すると、全体の質量が1にならないヒストグラムが得られてしまいます。これは、確率変数の代数的観点からは正当な操作ではありません。実際のところ、ヒストグラムは加算も乗算も自由に行うことができないため、できることが限られてしまいます。
Lokadでは、これらの普遍的な1次元離散分布に対処する最も実用的なアプローチとして、専用のデータ型を導入することにしました。聴衆の皆さんは、整数、浮動小数点数、文字列など、ほとんどのプログラミング言語に存在する一般的なデータ型にはすでに馴染みがあることでしょう。これらはどこにでも見られる典型的な基本データ型です。しかし、サプライチェーンの要求に特に適したより専門的なデータ型を導入することを妨げるものはありません。これこそが、Lokadがranvarデータ型を採用した理由です。
ranvarデータ型は1次元離散分布に特化しており、その名称はランダム変数(random variable)の略です。技術的に言えば、形式的な観点からranvarは、全ての整数(正の整数および負の整数)の集合Zから、0から1の間の数値である確率への関数です。Z全体の質量は常に1であり、これは確率分布を表しています。
純粋な数学的見地からは、そのような関数に含められる情報量は任意に大きくなり得ると主張する人もいるでしょう。これは事実ですが、実際にはサプライチェーンの観点から、単一のranvarに含まれる関連情報の量には非常に明確な限界があるのです。理論上、表現にメガバイトを要する確率分布を考案することは可能ですが、サプライチェーンの目的にかなうそのような分布は存在しません。
ranvarデータ型に対して4キロバイトの上限を設計することは可能です。このranvarが使用できるメモリに制限を設けることで、すべての操作に対してCPU面での上限も決まり、これは非常に重要です。単純にバケツの上限を1,000に設定するのではなく、Lokadはranvarデータ型に圧縮方式を導入しています。この圧縮は本質的に元のデータの情報を損なう表現であり、分解能と精度が失われます。しかし、目標は、ヒストグラムを十分に正確に表現できる圧縮方式を設計し、供給チェーンの観点から見たときに導入される近似の度合いが無視できるものにすることです.
ranvarデータ型に関連する圧縮アルゴリズムの詳細は本講義の範囲外ですが、これはコンピュータ上の画像に用いられる圧縮アルゴリズムよりも桁違いにシンプルな非常に単純なアルゴリズムです。ranvarが使用できるメモリに上限を設けるという副次的効果により、すべての操作に対してCPU面での上限も決まり、これが非常に重要となります。最後に、ranvarデータ型の最も重要な点は、このデータ型上で実際に操作を行い、基本的なデータ型でできるようなすべてのことを行うための変数の代数が得られることであり、要件に合った形でそれらのプリミティブを組み合わせることが可能になる点です.
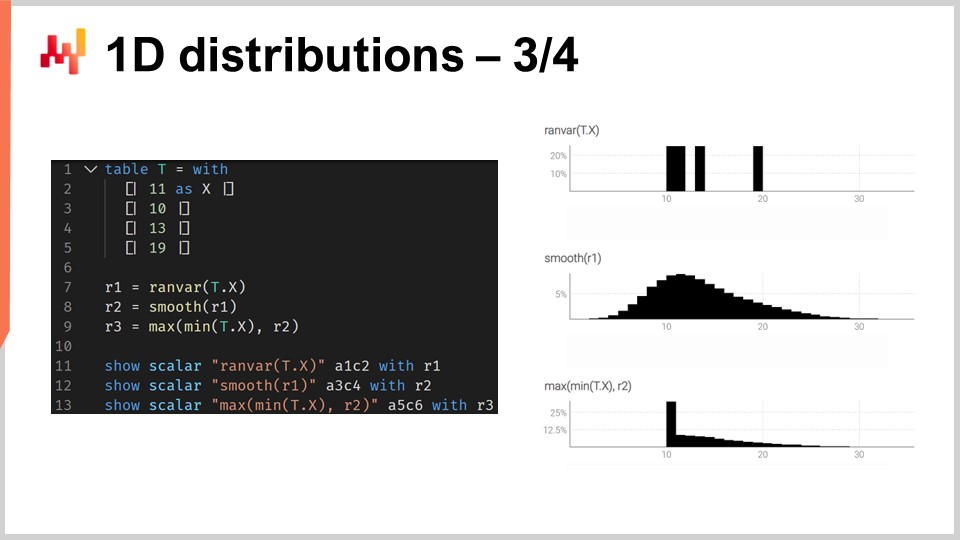
ranvarを用いる意味を説明するために、リードタイムの予測、より具体的にはリードタイムの確率的予測の状況を考えてみましょう。画面上には、そのような確率的予測を構築する方法を示す短いEnvisionスクリプトが表示されています。行1~5では、11日、10日、13日、90日という4つのリードタイムの変動値を含むテーブルTを導入します。4つの観測値は非常に少ないですが、リードタイムの観測においてはデータポイントが非常に限られているのが残念ながら一般的です。実際、年間に2件の注文を受ける海外サプライヤーの場合、これら4つのデータを集めるのに2年かかるため、非常に限られた観測セットでも動作する技術が重要となります.
行7では、4つの観測値を直接集計することでranvarを作成しています。ここで行7に現れる「ranvar」という用語は、一連の数値を入力として受け取り、ranvarデータ型の単一の値を返す集計器を指します。その結果は画面の右上に表示され、これは経験的ranvarです.
しかし、この経験的ranvarは実際の分布を現実的に表現しているとは言えません。例えば、11日のリードタイムや13日のリードタイムは観測できるのに、12日のリードタイムが観測されないのは非現実的に感じられます。このranvarを確率的予測として解釈すると、12日のリードタイムが観測される確率はゼロと示され、これは誤りと思われます。これは明らかに過剰適合の問題です.
この状況を改善するために、行8では「smooth」関数を呼び出して元のranvarを平滑化します。smooth関数は本質的に元のranvarを複数の分布の混合に置き換えます。元の分布の各バケットごとに、そのバケットを中心とする平均値のポアソン分布に置き換え、該当するバケットの確率に応じた重み付けを行います。この平滑化された分布を通じて、画面の右中央に表示されるヒストグラムが得られます。これにより、奇妙なギャップがなくなり、中央の確率がゼロになることもなくなりました。さらに、12日のリードタイムが観測される確率も非ゼロとなるため、ずっと現実味が増します。また、20日を超えるリードタイムについても非ゼロの確率が示され、4つのデータポイントしかなくすでに19日のリードタイムが観測されていることを考えると、20日というリードタイムがあり得るという考えも非常に妥当です。したがって、この確率的予測により、これらの事象に対する非ゼロの確率が示される良い分布が得られます.
しかし、左側には少し奇妙な点があります。この確率分布が右側に広がるのは問題ありませんが、左側については同じことが言えません。観測されたリードタイムが輸送時間の結果であり、truckの到着に9日かかることを考えると、3日のリードタイムが観測されるのはありそうにないと感じられます。この点で、モデルは非常に非現実的です.
そこで、行9では、これまでに観測された最小のリードタイムよりも大きいという条件付きで調整されたranvarを導入します。ここでは、テーブルTの数値の中から最小値を選ぶ"min_of(T, x)“を用い、次に"max"を使用して分布と数値間で大きい方を取ります。結果として得られる値は、この最小値よりも大きくなければなりません。調整後のranvarは画面の右下に表示され、これが最終的なリードタイム予測となります。4つのデータポイントという非常に限られたデータセットを考慮すると、この最終予測は非常に妥当な確率的リードタイム予測に感じられます。素晴らしい確率的予測とは言えないかもしれませんが、これは実運用レベルの予測であり、平均値による単純な予測では大幅に過小評価されるリードタイム変動のリスクを補う技術として、実際の運用でも十分に機能するものだと考えられます.
確率的予測の素晴らしさは、たとえそれが非常にcrudeであっても、観測データに基づく単純な平均予測の適用から生じる誤った判断に対して、ある程度のリスク軽減効果を既に備えている点にあります.
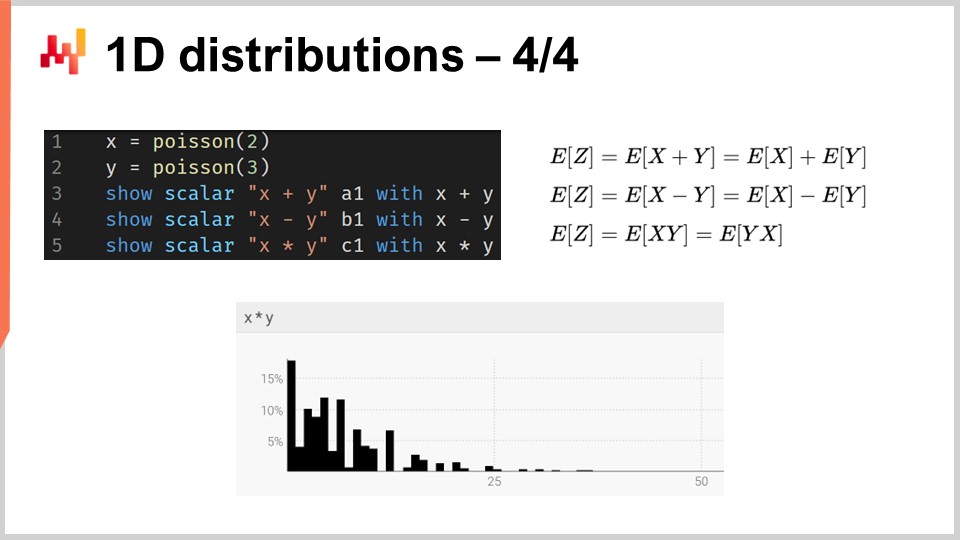
より一般的には、ranvarは加算、減算、乗算といった、整数と同様の操作をサポートしています。内部的には、意味論的に離散の確率変数を扱っているため、これらすべての操作は畳み込みとして実装されています。画面下部に表示されるヒストグラムは、平均がそれぞれ2と3の2つのポアソン分布の乗算によって得られたものです。供給チェーンにおいて、確率変数の乗算は直接畳み込みと呼ばれます。供給チェーンの文脈では、たとえば、顧客が同じ製品を求めながらも乗数が異なる場合に得られる結果を表現するために、2つの確率変数の乗算が意味を持ちます。例えば、2つの顧客層に対応する書店があるとします。一方は、来店時に1冊を購入する学生からなる第一の層、もう一方は、来店時に20冊を購入する教授からなる第二の層です.
モデリングの観点からは、学生または教授のいずれかによる書店への来店率を表す確率的予測を1つ持つことができます。これにより、その日の顧客数がゼロ、1人、2人…と観測される確率分布が得られ、特定の日にある特定の顧客数が観測される確率分布が明らかになります。第二の変数は、1冊を購入する(学生)場合と20冊を購入する(教授)場合のそれぞれの確率を示します。需要の表現を得るために、これら2つの確率変数を単に乗算すると、顧客層の消費パターンにおける乗数を反映した、一見ばらつきのあるヒストグラムが得られます.

モンテカルロ・ジェネレーター、または単にジェネレーターは、確率的予測に対する別のアプローチです。局所的な確率密度を示す分布を提示する代わりに、その名の通り、同じ局所確率分布に暗黙のうちに従うと期待される結果を生成するジェネレーターを提示することができます。ジェネレーターと確率密度の間には双対性が存在し、これは本質的に同じ視点の二面性であることを意味します.
ジェネレーターがあれば、そのジェネレーターから得られた結果を平均化して局所確率密度の推定値を再構築することが常に可能です。逆に、局所の確率密度があれば、この分布に従って偏差を抽出することは常に可能です。根本的には、これら2つの手法は、私たちがモデル化しようとしている現象の確率的または確率論的な性質を捉えるための異なる方法にすぎません.
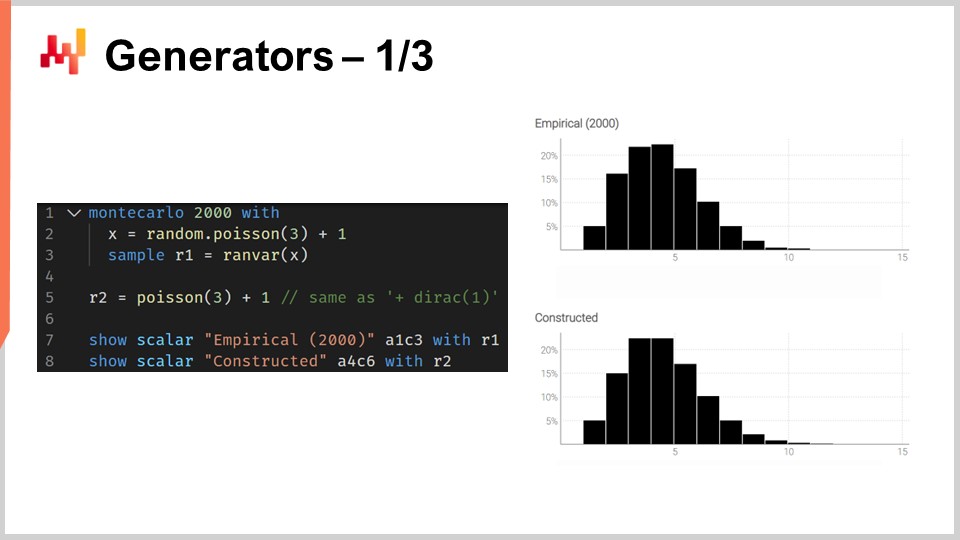
画面上のスクリプトはこの双対性を示しています。行1では、モンテカルロブロックを導入します。このブロックは、自動微分ブロックが確率的勾配降下法の多数のステップで反復されるのと同様に、システムによって反復実行されます。このモンテカルロブロックは2,000回実行され、そのブロックから2,000個の偏差が収集されます.
行2では、平均が3のポアソン分布から偏差を抽出し、その偏差に1を加えます。つまり、このポアソン分布からランダムな数値を得て1を加えます。行3では、この偏差を集計器ranvarのためのアキュムレータとして機能するL1に収集します。これは先にリードタイムの例で導入したものと全く同じ集計器です。ここでは、これらの観測値すべてをL1に集め、モンテカルロプロセスによって得られる一次元の分布を構築しています。行5では、全く同じ一次元の離散分布を構築しますが、今回はランダム変数の代数を用いて行います。つまり、ポアソンから3を引いて1を加えます。行5では、モンテカルロプロセスは行われず、純粋に離散確率と畳み込みの問題です.
行7と行8で2つの分布を視覚的に比較すると、ほぼ同じであることがわかります。『ほぼ』と言うのは、2,000回の反復という多くの試行を行っていますが、それが無限ではないためです。ranvarで得られる正確な確率と、モンテカルロプロセスで得られる近似的な確率との間には、わずかながらも依然として差異が存在します.
ジェネレーターはシミュレーターと呼ばれることもありますが、決して混同してはいけません。シミュレーターが存在すれば、それは確率的予測プロセスの背後に暗黙のうちに存在する生成プロセスがあることを意味します。シミュレーターやジェネレーターが関与している場合、頭に留めておくべき疑問は、「このシミュレーションの精度はどれほどか?」ということです。設計上、正確であるとは限らず、確率的であろうとなかろうと、全く不正確な予測が出る可能性は十分にあります。完全に不正確なシミュレーションが得られることも非常に容易です.
ジェネレーターを用いる場合、シミュレーションは確率的予測の見方の一つにすぎませんが、これは技術的な詳細に過ぎません。最終的に、予測によって特徴付けようとしているシステムを正確に描写する何かを持ちたいという事実は変わりません.
生成的アプローチは、すぐ後で具体例を見るように非常に有用であるだけでなく、確率密度を用いるアプローチと比較して概念的に把握しやすい面もあります。ただし、モンテカルロアプローチにも技術的な課題は存在します。実際のサプライチェーンにおいてこのアプローチを実用化するためには、いくつか必要な条件があります.
まず、ジェネレーターは高速でなければなりません。モンテカルロ法は、利用可能な計算資源を考慮して望む反復回数と実際に実行可能な反復回数との間の trade-off です。確かに現代のコンピュータは十分な処理能力を持っていますが、モンテカルロプロセスは非常に多くのリソースを消費する可能性があります。デフォルトで非常に高速なものが求められます。第4章第2講義で紹介された要素に戻ると、ExhaustShiftやWhiteHashといった非常に高速な関数があり、これらは超高速な基本ランダムジェネレーターを生成するためのプリミティブの構築に不可欠です。これらが必要であり、さもなければ苦労することになるでしょう。第二に、実行の分散化が必要です。モンテカルロプログラムの単純な実装は、逐次的に反復するループを持つに過ぎません。しかし、モンテカルロの要求に対して単一のCPUしか使用していないと、実質的に20年前のコンピュータの計算能力に戻ってしまいます。この点は第4章の最初の講義でも触れられました。過去20年でコンピュータはより強力になりましたが、それは主にCPUの増加と並列化の度合いの向上によるものです。したがって、ジェネレーターには分散実行の視点が必要です.
最後に、実行は決定論的でなければなりません。これはどういう意味でしょうか?同じコードを2回実行した場合、全く同じ結果が得られる必要があるということです。ランダム化手法を扱っているため、一見すると直感に反するかもしれません。しかし、決定論が必要であることは、1990年代に金融業界がモンテカルロジェネレーターを価格算定に使用し始めたとき、痛い目にあって初めて明らかになりました。金融業界はかなり前から確率的予測の道を歩み、モンテカルロジェネレーターを広範に利用していました。彼らが学んだことの一つは、決定論がなければ、バグやクラッシュを引き起こした条件を再現することがほぼ不可能になるということでした。供給チェーンの視点からも、発注計算のミスは非常に高額なコストを招く可能性があります.
サプライチェーンを管理するソフトウェアを実運用レベルに引き上げたいのであれば、モンテカルロを扱う際に必ずこの決定論的な特性を持たせる必要があります。多くのオープンソースソリューションは学界発であり、実運用レベルの完成度には全く配慮されていないことに注意してください。モンテカルロを扱う際は、プロセスが設計上非常に高速で、分散実行がなされ、決定論的であることを確認し、将来的に必然的に発生するバグの診断が可能な状態にしておく必要があります.
私たちは、ランダム変数で行われていた処理を複製するためにジェネレーターが導入された状況を見てきました。経験則として、モンテカルロ法を使わずにランダム変数の確率密度だけで済む場合は、それで十分です。より正確な結果が得られ、モンテカルロ法で常に少々複雑な数値的安定性の問題を心配する必要がなくなります。しかし、ランダム変数の代数は表現力に限界があり、そこでモンテカルロ法が本領を発揮するのです。これらのジェネレーターは、単なるランダム変数の代数だけでは解決できない状況を把握できるため、より表現力豊かなのです。
これをサプライチェーンの状況で例示してみましょう。初期在庫レベル、需要の確率的予測、そして3ヶ月にわたる関心期間を持つ単一SKUを考えます。この期間の途中で入荷があると仮定します。需要は、在庫から即時に対応されるか、あるいは永久に失われるかのどちらかです。このSKUの期間終了時の予想在庫レベルを知りたいのは、死蔵在庫のリスクをどの程度抱えているかを判断するのに役立つからです。
この状況は、期間の真ん中でストックアウトが発生する第3の可能性があるように設計されているため、非常に厄介です。素朴なアプローチでは、初期在庫レベルと期間全体の需要分布を用いて、在庫レベルから需要を差し引き、残りの在庫レベルを算出します。しかし、これは、入荷中の在庫-補充-定義が保留中に在庫切れが起こり、需要のかなりの部分が失われる可能性があるという事実を考慮していません。素朴な方法では、期間終了時の在庫量が過小評価され、対応される需要が過大評価される結果になります。
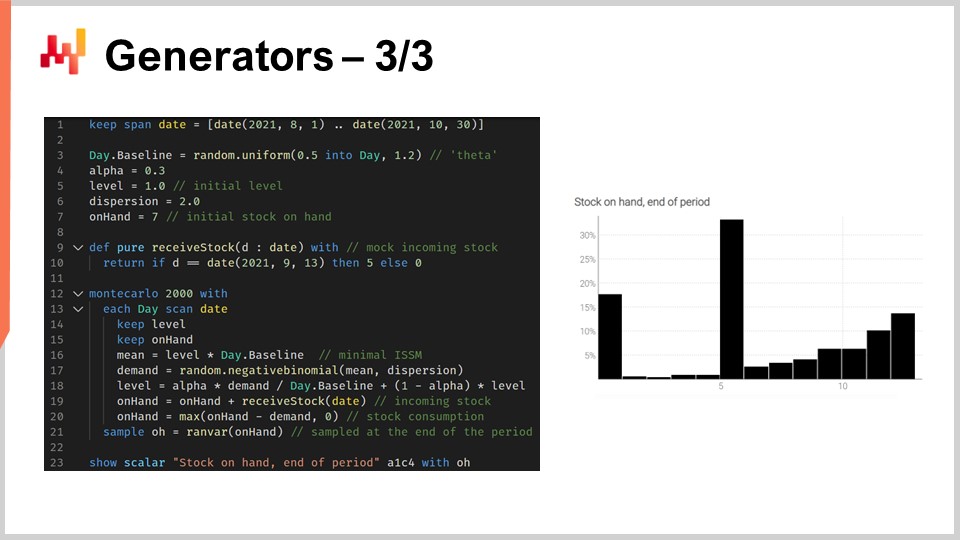
表示されているスクリプトは、在庫切れの発生をモデル化することで、このSKUの期間終了時の正確な在庫推定値を得るためのものです。1行目から10行目では、モデルを特徴づけるモックデータを定義しています。3行目から6行目にはISSMモデルのパラメーターが記載されています。すでにこの第5章の最初の講義でICSMモデルを見たことがあるでしょう。基本的に、このモデルは1日ごとに1つのデータポイントを持つ需要軌跡を生成します。関心期間は日テーブルで定義され、この軌跡のパラメーターは最初に設定されます。
前回の講義では、AICSMモデルと、微分可能なプログラミングを通じてこれらのパラメーターを学習するための手法を紹介しました。今日は、学ぶべきことはすべて学んだと仮定して、このモデルを使用します。7行目では、通常はERPまたはWMSから得られる初期手元在庫を定義しています。9行目と10行目では、補充の数量と日付を定義しています。これらのデータポイントは通常、サプライヤーから示される到着予定時刻としてERPに保存されます。配送日が完全に既知であると仮定していますが、この単一の日付を確率的なリードタイム予測に置き換えることは容易です。
12行目から21行目では、需要軌跡を生成するISSMモデルが示されています。ここではモンテカルロループ内にあり、モンテカルロの各反復ごとに関心期間の各日に対して処理を行います。日付の繰り返しは13行目から始まります。ESSMのメカニクスが稼働していますが、19行目と20行目で手元在庫変数を更新しています。この手元在庫変数はISSMモデルの一部ではなく、追加の要素です。19行目では、手元在庫は昨日の在庫に入荷分を加えたものであるとし、大部分の日はゼロですが、9月13日には5単位となります。次に20行目で、その日の需要によって一定数が消費され、在庫レベルが負にならないように最大値0の処理がされます。
最後に、21行目で最終的な手元在庫を収集し、23行目でこの最終在庫が表示されます。これが画面右側に表示されるヒストグラムです。ここでは非常に不規則な形状の分布が見られ、その形状は単なるランダム変数の代数では得ることができません。ジェネレーターは非常に表現力豊かですが、その表現力を精度と混同してはなりません。ジェネレーターは非常に表現力に富んでいますが、その精度を評価するのは容易ではありません。間違いなく、ジェネレーターやシミュレーターが稼働するたびに、確率予測が伴い、シミュレーションは、他の予測手法と同様に劇的に不正確になる可能性があります。

すでに長い講義となっていますが、本日はまだ触れていないトピックが多く存在します。例えば意思決定です。すべての未来があり得る場合、どのようにして何かを決定すればよいのでしょうか?この疑問にはまだ答えていませんが、次回の講義で取り上げる予定です。
高次元も考慮すべき重要な要素です。一次元の分布は出発点に過ぎませんが、サプライチェーンにはそれ以上の情報が必要です。例えば、特定のSKUで在庫切れが発生した場合、顧客が自然と代替品に流れるカニバリゼーションが起きる可能性があります。たとえ粗いモデルであっても、これをモデリングしたいと考えています。
また、高次の構造も役割を果たします。前述の通り、需要予測は惑星の運行予測のようなものではありません。各所に自己予知的な効果が存在します。いずれ、価格政策や在庫補充政策を考慮に入れる必要が出てきます。そのためには高次の構造が必要となり、つまり、ある政策を与えると、その結果の確率的予測が得られるが、その政策を高次の構造内に組み込む必要があるということです。
さらに、確率的予測をマスターするには、多くの数値手法と、特定の状況に最も適した分布が何であるかを見極めるための専門知識が必要です。この講義シリーズでは、後ほどさらに多くの例を紹介していきます。
最後に、変化という挑戦があります。確率的予測は、主流のサプライチェーン手法から根本的に逸脱しています。確率的予測に関連する技術的な詳細は、挑戦の一部に過ぎません。最も困難なのは、組織そのものを再構築し、本質的に希望的観測に過ぎないポイント予測に依存するのではなく、確率的予測を活用し始めることです。これらすべての要素は後の講義で取り上げますが、扱うべき内容が非常に多いため、時間がかかるでしょう。

結論として、確率的予測は、実現すべき唯一の未来に対するある種の合意を期待するポイント予測の視点からの根本的な逸脱を表しています。確率的予測は、未来の不確実性がどうしても解消できないという観察に基づいています。予測科学の1世紀の歴史は、いかなる試みも正確な予測に近づくことができなかったことを示しています。したがって、我々は多くの不定の未来に直面しているのです。しかし、確率的予測は、これらの未来を定量化・評価するための手法とツールを提供してくれます。確率的予測は大きな成果であり、経済予測が天文学のようなものでなかったという現実に至るまでにはほぼ1世紀を要しました。惑星の正確な位置を1世紀後に高精度で予測できる一方、サプライチェーンの領域で同様の成果を収める希望は全くありません。全てを支配する一つの予測という考えはもはや戻らないのです。しかし、多くの企業は、いつの日か真に正確な予測が実現すると未だに信じ続けています。1世紀にわたる試みの末、これは本質的に希望的観測に過ぎないのです。
現代のコンピューターを用いれば、この「一つの未来」という視点だけが唯一の見方ではなく、代替手段も存在します。確率的予測は90年代から存在しており、つまり30年前のことです。Lokadでは、10年以上にわたり、確率的予測を用いてサプライチェーンを実運用してきました。まだ主流ではないかもしれませんが、サイエンスフィクションの域には程遠く、金融業界では30年、サプライチェーンの分野では10年の実績があります。
確率的予測は威圧的で非常に技術的に見えるかもしれませんが、適切なツールを使えば、ほんの数行のコードで実装可能です。確率的予測は他の予測手法と比べて特に難解というわけではありません。確率的予測における最大の課題は、未来が完全に制御されているという幻想を捨てることです。未来は決して完全に制御されることはなく、むしろそれが最良の状態なのです。

これにて本日の講義は終了です。次回は4月6日に小売在庫配送における意思決定について講演し、本日提示した確率的予測が、基本的なサプライチェーンの意思決定、すなわち小売ネットワークでの在庫補充にどのように活用できるかを示します。講義は同じ曜日である水曜日、同じ時間帯の午後3時に行われ、4月の最初の水曜日となります。
質問: Envisionにおける精度の解像度とRAM容量の最適化は可能でしょうか?
はい、もちろん可能です。ただし、それはEnvision自体の中で行うのではなく、Envisionの設計に基づく選択です。私のアプローチは、サプライチェーン-サイエンティストを低レベルの技術的な細部から解放することにあります。Envisionの4キロバイトは、サプライチェーンの状況を正確に描写するには十分な容量であり、解像度や精度の点で失われる近似の誤差は重要ではありません。
もちろん、圧縮アルゴリズムの設計に関しては、考慮すべきトレードオフが数多く存在します。例えば、ほぼゼロに近い値のバケットは、完璧な解像度を持たなければなりません。需要がゼロである確率を正確に表現したい場合、ゼロ需要、1単位、2単位のバケットをまとめてしまってはなりません。しかし、1,000単位の需要の場合、1,000単位と1,001単位をまとめても問題ないでしょう。つまり、サプライチェーンの要件に本当に適した圧縮アルゴリズムを開発するための工夫は多数存在します。これは画像圧縮で行われていることと比べれば桁違いに単純です。私の見解では、適切に設計されたツールがあれば、この問題はサプライチェーン科学者にとって自動的に抽象化され、低レベルの微調整を行う必要がほとんどなくなるでしょう。もしウォルマートのように、100万SKUではなく数億SKUを扱う場合でなければ、完全な最適化が達成されていないことによる性能低下はほとんど問題にならないと考えています。
質問: これらのパラメーターを最適化する際、サプライチェーンの視点から考慮すべき実務上の点は何でしょうか?
サプライチェーンにおける確率的予測では、精度が10万分の1以上あっても、データが十分に存在しないため、通常は問題になりません。
質問: 確率的予測手法から最も恩恵を受ける業界はどこでしょうか?
簡単に答えると、パターンが不規則で予測が困難であればあるほど、その利点は大きくなります。間欠的な需要や不規則な需要変動がある場合、また、リードタイムが大きくばらつき、サプライチェーンに不規則なショックが頻発する場合に、最も大きな利益が得られます。一方、例えば水の供給チェーンのように、消費が極めて安定しており、大きなショックがほとんど発生しない場合、この確率的アプローチの恩恵はあまり期待できません。つまり、全ての製品の予測誤差が5%未満である状況では、確率的予測は不要であり、むしろ非常に正確な予測自体が機能するのです。しかし、SKUレベルや日次レベルという最も詳細なレベルで予測誤差が30%以上といった場合、確率的予測は大いに効果を発揮します。ちなみに、ここで言う30%の予測誤差とは、非常に細分化された予測のことを指しています。多くの企業は全体としては5%の精度だと主張しますが、集約するとその精度は誤解を招くものであり、実際に意思決定がなされるSKUレベルや日次レベルでの精度が重要なのです。もし、SKUや日次レベルでの予測が5%以内で収まるのであれば、確率的予測は必要ありません。しかし、パーセンテージで二桁の誤差が見られる場合、確率的予測は大いに役立つのです。
質問: リードタイムは季節変動があるため、マルチモーダルな分布を避けるために、各季節ごとに別々のリードタイム予測に分解するべきでしょうか?
これは良い質問です。ここでの考えは、通常、リードタイムのためにパラメトリックなモデルを構築し、そのモデルに季節性プロファイルを含めるということです。リードタイムの季節性に対処する方法は、前回の講義で需要に関して扱った他の周期性に対処する方法と根本的には大きく異なりません。通常の方法は複数のモデルを構築しないことであり、なぜならご指摘の通り、複数のモデルがあると、あるモダリティから次のモダリティへ移る際にあらゆる奇妙なジャンプが発生するためです。モデルの中央に季節性プロファイルを組み込んだ一つのモデルを持つのが一般的に良いアプローチです。これは、パラメトリックな分解のようなもので、年間の特定の週にリードタイムに影響を与える週ごとの効果を示すベクトルを持つことに相当します。後の講義で、より詳細な例を示す時間があるかもしれません。
質問: 断続的需要を予測する際、確率的予測は良いアプローチでしょうか?
その通りです。実際、断続的需要がある場合、確率的予測は単なる良い手法であるだけでなく、従来の一点予測は全く意味をなさないと私は考えています。従来の予測手法では、通常、無数のゼロの扱いに苦労します。これらのゼロをどう解釈しますか?結果として、とても低くかつ小数的な値が出てしまい、実際には意味をなさなくなります。断続的需要では、本当に答えたい問いは、「時折発生する需要の急増に対応するために、在庫は十分か?」ということになります。平均的な予測を用いると、その点は決して明らかにならないのです。
書店の例に戻ると、ある週に平均して1日あたり1ユニットの需要が観測された場合、高いサービス品質を維持するために書店には何冊の本を在庫すべきでしょうか? 書店が毎日補充されると仮定します。もしサービス対象が学生だけであれば、1日平均1ユニットの需要で在庫に3冊の本があれば非常に高いサービス品質を実現できます。しかし、時折教授が現れて一度に20冊を求める場合、書店に3冊しか在庫がなければ教授たちに全く対応できず、サービス品質はひどいものになってしまいます。これは断続的需要の場合に典型的な事例です––需要が断続的であるという事実だけでなく、需要の急増がその大きさにおいて大きく変動し得るからです。ここで確率的予測は、その平均値だけに依存して細かな構造が失われるのではなく、需要の微細な構造を捉えることができる点で真価を発揮するのです。
質問: リードタイムを分布で置き換えた場合、ジェネレーターの最初のスライドに示された滑らかなベルカーブが表すスパイクはそのまま現れるのでしょうか?
ある程度、よりランダムにすると物事は広がりやすくなります。ジェネレーターに関する最初のスライドでは、様々な設定で実験を行ってみなければ結果は分かりません。リードタイムを分布で置き換えたい理由は、リードタイムが変動しているという問題に対する洞察があるからです。もしサプライヤーを絶対に信頼でき、彼らが非常に信頼性の高い実績を持っているのであれば、ETA(到着予定時刻)はそれ自体であり、実際の値に対してほぼ完璧な推定値と考えても問題ありません。しかし、過去にサプライヤーが時折不規則であったり目標を外したりした経験がある場合は、リードタイムを分布で置き換える方が適切です。
リードタイムを分布で置き換えることは、最終的に得られる結果を必ずしも平滑化するわけではなく、観察している内容によって異なります。例えば、在庫過剰の最も極端なケースを考えると、変動するリードタイムがむしろ死蔵在庫のリスクを高める可能性さえあります。なぜなら、非常に季節性の強い製品でリードタイムが変動しており、製品がシーズン終了後に到着すると、その製品はシーズン外のものとなり、シーズン末に死蔵在庫のリスクが拡大するからです。したがって、これは一筋縄ではいかない問題です。変数をその確率的な置換に変えたからといって、観察される結果が自然に平滑化されるわけではなく、時には分布がさらに鋭くなることもあります。というわけで、答えは「場合による」ということになります。
素晴らしいですね、今日はこれで全てだと思います。また次回お会いしましょう。