Sparsity: quando la misura dell'accuratezza va male

Joannes Vermorel

Tre anni fa, pubblicavamo [Overfitting: quando la misura di accuracy non funziona](/blog/2009/4/22/overfitting-when-accuracy-measure-goes-wrong/), tuttavia overfitting è tutt’altro che l’unica situazione in cui le semplici misurazioni di accuratezza possono essere molto fuorvianti. Oggi, ci concentriamo su una situazione in cui gli errori sono molto frequenti: la domanda intermittente che si riscontra tipicamente nelle vendite a livello di negozio (o Ecommerce).

Riteniamo che questo singolo problema da solo abbia impedito alla maggior parte dei rivenditori di passare a sistemi avanzati di previsione a livello di negozio. Come per la maggior parte dei problemi di previsione, è sottile, è controintuitivo, e alcune aziende fanno pagare molto per offrire risposte scadenti alla questione.

Le metriche d’errore più popolari nelle previsioni delle vendite sono il Mean Absolute Error (MAE) e il Mean Absolute Percentage Error (MAPE). Come linea guida generale, suggeriamo di utilizzare il MAE poiché il MAPE si comporta molto male ogni volta che le serie temporali non sono regolari, ovvero, costantemente, per quanto riguarda i rivenditori. Tuttavia, ci sono situazioni in cui anche il MAE si comporta male. I bassi volumi di vendita rientrano in tali situazioni.

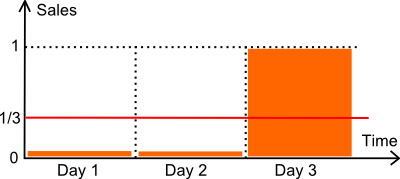
Rivediamo l’illustrazione qui sopra. Abbiamo un articolo venduto in 3 giorni. Il numero di unità vendute nei primi due giorni è zero. Nel terzo giorno, viene venduta un’unità. Supponiamo che la domanda sia, in effetti, esattamente di 1 unità ogni 3 giorni. Tecnicamente parlando, si tratta di una distribuzione di Poisson con λ=1/3.

Di seguito, confrontiamo due modelli di previsione:

• un modello costante M a 1/3 ogni giorno (la media).
• un modello costante Z a zero ogni giorno.

Per quanto riguarda l’ottimizzazione dell’inventario, il modello zero (Z) è davvero dannoso. Supponendo che l’analisi delle scorte di sicurezza venga utilizzata per calcolare un punto di riapprovvigionamento, una previsione zero molto probabilmente produrrà anche un punto di riapprovvigionamento pari a zero, causando frequenti rotture di stock. Una metrica di accuratezza che favorisse il modello zero rispetto a previsioni più ragionevoli si comporterebbe in modo piuttosto inadeguato.

Confrontiamo i nostri due modelli con il MAPE (*) e il MAE.

• M ha un MAPE del 44%.
• Z ha un MAPE del 33%.
• M ha un MAE di 0.44.
• Z ha un MAE di 0.33.

(*) La definizione classica di MAPE prevede una divisione per zero quando il valore reale è zero. Supponiamo qui che il valore reale venga sostituito da 1 quando è zero. In alternativa, avremmo potuto anche dividere per la previsione (invece che per il valore reale), oppure utilizzare lo sMAPE. Queste modifiche non fanno differenza: la conclusione della discussione rimane la stessa.

In conclusione, qui, secondo sia il MAPE che il MAE, il modello zero prevale.

Tuttavia, qualcuno potrebbe sostenere che questa sia una situazione troppo semplicistica e che non rifletta la complessità di un negozio reale. Questo non è del tutto vero. Abbiamo effettuato benchmark su decine di negozi al dettaglio, e di solito il modello vincente (secondo MAE o MAPE) è il modello zero - il modello che restituisce sempre zero. Inoltre, questo modello tipicamente vince con un margine confortevole rispetto a tutti gli altri modelli.

In pratica, a livello di punto vendita, basarsi su MAE o MAPE per valutare la qualità dei modelli di previsione equivale a cercarsi guai: la metrica favorisce i modelli che restituiscono zeri; più zeri, meglio è. Questa conclusione vale per quasi tutti i negozi che abbiamo analizzato finora (esclusi i pochi articoli ad alto volume che non soffrono di questo problema).

I lettori che hanno familiarità con le metriche di accuratezza potrebbero proporre di utilizzare invece il Mean Square Error (MSE), che non favorirà il modello zero. Questo è vero, tuttavia, il MSE, quando applicato a dati erratici - e le vendite a livello di negozio sono erratiche - non è numericamente stabile. In pratica, qualsiasi outlier nella storia delle vendite distorce immensamente i risultati finali. Questo genere di problema È LA ragione per cui gli statistici hanno lavorato così duramente sulle statistiche robuste fin dall’inizio. Nessun pranzo gratis qui.

Come valutare, allora, le previsioni a livello di negozio?

Ci è voluto un tempo lungo e interminabile per trovare una soluzione soddisfacente al problema di quantificare l’accuratezza delle previsioni a livello di negozio. Nel 2011 e prima, sostanzialmente baraventavamo. Invece di osservare i punti dati giornalieri, quando i dati di vendita erano troppo scarsi, passavamo tipicamente ad aggregati settimanali (o anche mensili per dati estremamente scarsi). Passando a periodi di aggregazione più lunghi, aumentavamo artificialmente i volumi di vendita per periodo, rendendo nuovamente utilizzabile il MAE.

La svolta è arrivata solo qualche mese fa grazie ai quantili. In sostanza, l’illuminazione è stata: dimentica le previsioni, contano solo i punti di riapprovvigionamento. Cercando di ottimizzare le nostre previsioni classiche contro metriche X, Y o Z, stavamo cercando di risolvere il problema sbagliato.

Aspetta! Dato che i punti di riordino vengono calcolati in base alle previsioni, come puoi affermare che le previsioni siano irrilevanti?

Non stiamo dicendo che le previsioni e la loro accuratezza siano irrilevanti. Tuttavia, affermiamo che conta solo l’accuratezza dei punti di riapprovvigionamento stessi. La previsione, o qualsiasi altra variabile usata per calcolare i punti di riapprovvigionamento, non può essere valutata da sola. Solo l’accuratezza dei punti di riapprovvigionamento deve essere valutata.

Risulta che esiste una metrica per valutare i punti di riapprovvigionamento: è la funzione di perdita pinball, una funzione conosciuta dagli statistici da decenni. La perdita pinball è enormemente superiore non a causa delle sue proprietà matematiche, ma semplicemente perché si adatta al compromesso di inventario: scorte eccessive contro troppe rotture di stock.