選択的経路自動微分:バックプロパゲーションドロップアウトにおける一様分布を超えて
確率的勾配降下法(SGD)の並外れた有効性は、おそらく2010年代最大の機械学習の発見です。SGDは、近年のほぼすべての機械学習におけるブレークスルーの原動力となっています。概念的には、SGDは極めてシンプルで、データセットを1データポイントずつ処理し、各ポイントに対してその示す方向へモデルのパラメータを微調整します。より技術的に言えば、その「方向」は勾配として与えられ、「微調整」には通常、_学習率_と呼ばれる小さなスケーリング係数が伴います。
SGD手法は1950年代にその起源を持ちますが、ディープラーニングの登場まではほとんど知られておらず、あまり用いられていない手法でした。この手法がなぜ機能するのか、その理由は明確ではなく、ある意味では今もなお不明な部分があります。モデル全体の誤差を最小化するという目標からすると、各ポイントを厳密に個別に選ぶだけでは、数値的なゴミ以外の何かが得られるとは考えにくいのです。
今日では、SGDの有効性、すなわち_なぜ機能するのか_は2つの要因によると広く理解されています。第一に、SGDで得られる勾配は非常にノイジーですが―各ステップが単一のデータポイントを考慮するため―その計算コストは極めて低いのです。与えられた計算資源の予算内では、低品質な勾配更新を多数適用することが、1回の高品質な勾配更新を行うよりもはるかに優れていることが判明しています。第二に、これらのノイジーな更新自体が、より高次元に存在する数値的無関心の広大なプラトーからモデルを脱出させる助けとなります。実際、高次元では、最適化の本質は、長らく考えられてきた局所最小値からの脱出ではなく、損失がほとんど変動しない局所プラトーからの脱出にあるのです。

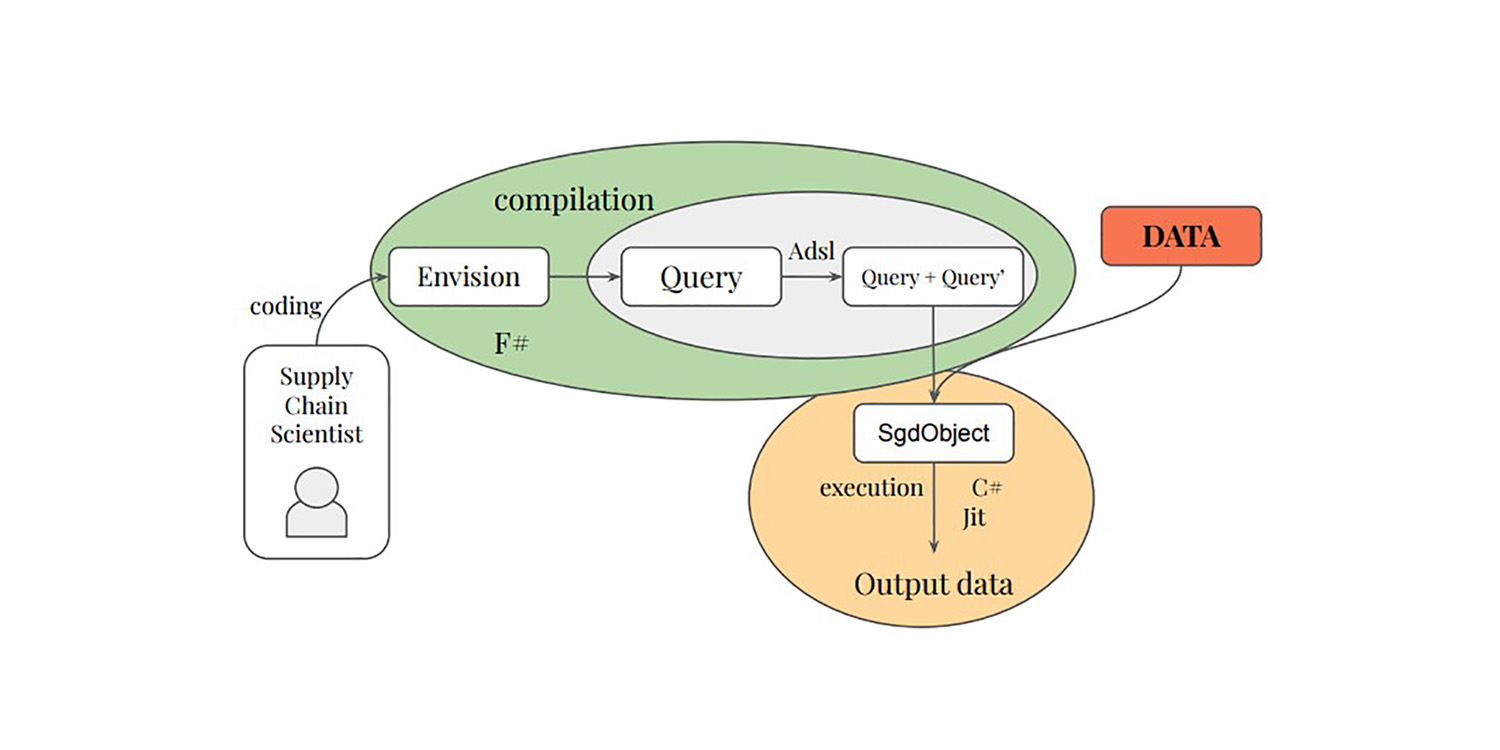
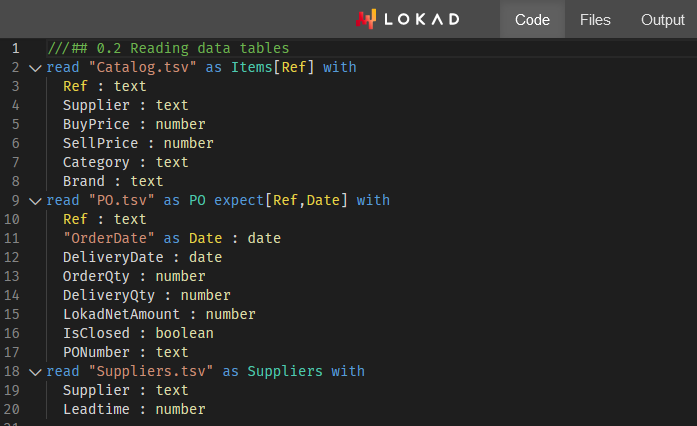
私たちの中には、Paul PeseuxやVictor Nicolletを含む者たちが、これらのアイデアをさらに発展させることに取り組みました。もしSGDが、勾配の質を犠牲にして計算効率を追求することで機能しているなら、この原則をさらに拡張することは如何でしょうか?たとえよりノイジーであっても、計算コストがさらに低いサブポイント勾配は如何でしょう?これがまさに、選択的経路自動微分(SPAD)で実現されたことです。SPADは、現代機械学習パラダイムの基盤の一つをひねりを加えて再検討します。つまり、データポイントはその評価経路によって勾配的に「分割」されうるのです。 以下の論文は、Paul Peseux(Lokad)、Victor Nicollet(Lokad)、Maxime Berar(Litis)、およびThierry Paquet(Litis)からの貢献を紹介しています。
Title: 選択的経路自動微分:バックプロパゲーションドロップアウトにおける一様分布を超えて
著者: Paul Peseux, Maxime Berar, Thierry Paquet, Victor Nicollet
要旨: 本稿では、埋め込み型人工知能向けの勾配ベースモデルにおけるメモリ消費の削減と過学習の緩和を目的とした新たな手法、選択的経路自動微分(SPAD)を紹介します。SPADは、Oktayらによって提案された、行列注入を伴いバックプロパゲーショングラフ上のランダムな経路を描く既存のランダム自動微分を拡張し、バックプロパゲーショングラフ上での代替確率分布の適用を可能にすることで、学習性能とメモリ管理を向上させます。特定の反復では、SPADはバックプロパゲーショングラフ内の複数の経路を評価し、ランキングを行います。以降の反復において、より高いランクの経路を優先的にたどります。本研究は、ディープモデルに限定されない様々なモデルアーキテクチャに対して普遍的な適用性を保証する、モデルに依存しないランダム経路へのアクセスを可能にするコンパイルベースの技術も提示します。各種最適化関数に対する実験評価により、SPADを採用することで最小化性能が向上することが示されました。さらに、SPADを用いたディープラーニング実験では、従来のドロップアウト手法と同様の利点を提供しながらもメモリ使用量の低減を実現し、過学習が著しく軽減されることが確認されました。 本研究では、我々の成果がもたらす独自の確率性の意味合いと、それが他の確率的手法をどのように補強し得るかについても議論します。