Mathematische Optimierung for supply chain - Vorlesung 4.3

00:18 Einführung
02:18 Hintergrund
12:08 Warum optimieren? 1/2: Prognose mit Holt-Winters
17:32 Warum optimieren? 2/2 – Fahrzeugroutingproblem
20:49 Bisherige Entwicklung
22:21 Hilfswissenschaften (Rückblick)
23:45 Probleme und Lösungen (Rückblick)
27:12 Mathematische Optimierung
28:09 Konvexität
34:42 Stochastizität
42:10 Multi-Objective
46:01 Solver-Design
50:46 Deep (Learning) Lektionen
01:10:35 Mathematische Optimierung
01:10:58 “Echtes” Programmieren
01:12:40 Lokale Suche
01:19:10 Stochastischer Gradientenabstieg
01:26:09 Automatische Differenzierung
01:31:54 Differentialprogrammierung (circa 2018)
01:35:36 Fazit
01:37:44 Bevorstehende Vorlesung und Fragen aus dem Publikum

Beschreibung

Mathematische Optimierung ist der Prozess, eine mathematische Funktion zu minimieren. Fast alle modernen statistischen Lerntechniken – d.h. Forecasting, wenn wir eine supply chain Perspektive einnehmen – basieren im Kern auf mathematischer Optimierung. Außerdem beruht, sobald die Prognosen erstellt wurden, die Identifizierung der profitabelsten Entscheidungen im Kern ebenfalls auf mathematischer Optimierung. Supply chain Probleme beinhalten häufig viele Variablen. Sie sind zudem meist stochastischer Natur. Mathematische Optimierung ist ein Eckpfeiler einer modernen supply chain Praxis.

Gesamtes Transkript

Willkommen zu dieser Reihe von supply chain Vorlesungen. Ich bin Joannes Vermorel, und heute präsentiere ich „Mathematical Optimization for Supply Chain.“ Mathematische Optimierung ist der klar definierte, formalisierte und rechnerisch handhabbare Weg, die beste Lösung für ein gegebenes Problem zu finden. Alle Forecasting-Probleme können als Probleme der mathematischen Optimierung betrachtet werden. Alle Entscheidungsfindungssituationen in supply chain und außerhalb von supply chains können ebenfalls als mathematische Optimierungsprobleme gesehen werden. Tatsächlich ist die Perspektive der mathematischen Optimierung so tief in unserer modernen Weltanschauung verankert, dass es sehr schwierig geworden ist, das Verb “to optimize” außerhalb des engen Rahmens zu definieren, den uns das Paradigma der mathematischen Optimierung bietet.

Nun, die Literatur zur mathematischen Optimierung ist immens, ebenso wie das Software-Ökosystem, das Werkzeuge für mathematische Optimierung bereitstellt. Leider ist der Großteil davon von sehr geringem Nutzen und kaum relevant, was supply chain betrifft. Das Ziel dieser Vorlesung ist zweifach: Zum einen möchten wir verstehen, wie man mathematische Optimierung so angeht, dass man aus supply chain Sicht etwas Wertvolles und Praktisch Nutztbares gewinnt. Zum anderen wollen wir in dieser weiten Landschaft einige der wertvollsten Elemente identifizieren.

Die formale Definition der mathematischen Optimierung ist einfach: Man stellt sich eine Funktion vor, die typischerweise als loss function bezeichnet wird, und diese Funktion liefert reellwertige Ergebnisse, also nur Zahlen. Ziel ist es, den Eingabewert (X0) zu finden, der den Verlust der Funktion minimiert. Das ist typischerweise das Paradigma der mathematischen Optimierung, das trügerisch einfach erscheint. Wir werden sehen, dass sich zu diesem allgemeinen Ansatz noch vieles sagen lässt.

Dieses Gebiet, so glaube ich, wurde – wenn man an angewandte mathematische Optimierung denkt – primär unter dem Namen Operational Research entwickelt, das wir genauer als das klassische Operational Research definieren, das von den 1940er Jahren bis in die späten 1970er Jahre des 20. Jahrhunderts praktiziert wurde. Die Idee ist, dass das klassische Operational Research, im Gegensatz zur mathematischen Optimierung, sich wirklich um Geschäftsprobleme kümmerte. Mathematische Optimierung befasst sich mit der allgemeinen Form des Optimierungsproblems und weniger damit, ob das Problem eine geschäftliche Relevanz besitzt. Im Gegenteil: Das klassische Operational Research führte im Wesentlichen Optimierungen durch – allerdings nur bei Problemen, die als für Unternehmen wichtig identifiziert wurden.

Interessanterweise sind wir vom Operational Research zur mathematischen Optimierung übergegangen, fast auf dieselbe Weise, wie wir vom Forecasting – das zu Beginn des 20. Jahrhunderts als Feld entstand, das sich mit der allgemeinen Vorhersage zukünftiger wirtschaftlicher Aktivitätsniveaus beschäftigte, typischerweise in Verbindung mit time series Prognosen – zum Machine Learning übergegangen sind. Dieses Gebiet wurde im Wesentlichen von Machine Learning abgelöst, das sich breiter darum bemühte, Vorhersagen für ein viel größeres Spektrum von Problemen zu treffen. Man könnte sagen, dass wir in etwa denselben Übergang vom Operational Research zur mathematischen Optimierung erlebt haben wie vom Forecasting zum Machine Learning. Als ich sagte, dass die klassische Ära des Operational Research bis in die späten 70er reichte, hatte ich ein ganz konkretes Datum im Kopf. Im Februar 1979 veröffentlichte Russell Ackoff ein beeindruckendes Papier mit dem Titel “The Future of Operational Research is Past.” Um dieses Papier zu verstehen, das ich als einen Meilenstein in der Geschichte der Optimierungswissenschaft betrachte, muss man wissen, dass Russell Ackoff im Grunde einer der Gründerväter des Operational Research war.

Als er dieses Papier veröffentlichte, war er nicht mehr jung; er war 60 Jahre alt. Ackoff wurde 1919 geboren und hatte nahezu seine gesamte Karriere im Bereich Operational Research verbracht. Mit der Veröffentlichung seines Papiers stellte er im Grunde fest, dass das Operational Research gescheitert sei. Es lieferte nicht nur keine Ergebnisse, sondern das Interesse an der Branche schwand, sodass Ende der 90er Jahre weniger Interesse bestand als noch vor 20 Jahren.

Was sehr interessant zu verstehen ist, ist, dass der Grund absolut nicht darin liegt, dass die damaligen Computer viel schwächer waren als die heutigen. Das Problem hat überhaupt nichts mit den damaligen Begrenzungen in der Rechenleistung zu tun. Ende der 70er Jahre waren Computer im Vergleich zu heutigen sehr bescheiden, konnten jedoch trotzdem Millionen arithmetische Operationen in einem angemessenen Zeitrahmen durchführen. Das Problem steht nicht im Zusammenhang mit der begrenzten Rechenleistung, vor allem in einer Zeit, in der diese unglaublich schnell voranschreitet.

Übrigens, dieses Papier ist hervorragend zu lesen. Ich empfehle dem Publikum dringend, einen Blick darauf zu werfen; es ist mit der bevorzugten Suchmaschine leicht zu finden. Das Papier ist sehr zugänglich und gut geschrieben. Obwohl die Art von Problemen, auf die Ackoff in diesem Papier hinweist, auch vier Jahrzehnte später noch stark nachhallt, ist es in vielerlei Hinsicht sehr vorausschauend in Bezug auf viele der Probleme, die heutige supply chains immer noch plagen.

Was ist also das Problem? Das Problem ist, dass dieses Paradigma – bei dem man eine Funktion nimmt und sie optimiert – zwar beweist, dass der Optimierungsprozess eine gute oder sogar optimale Lösung finden kann, jedoch nicht belegt, dass die tatsächlich optimierte Verlustfunktion von geschäftlichem Interesse ist. Das Problem besteht darin, dass, wenn ich sage, wir können ein gegebenes Problem oder eine gegebene Funktion optimieren, was, wenn das, was optimiert wird, eigentlich eine Fantasie ist? Was, wenn diese Funktion überhaupt nichts mit der Realität des Geschäfts, das man zu optimieren versucht, zu tun hat?

Hier liegt der springende Punkt des Problems, und hier liegt auch der Grund, warum jene frühen Versuche im Wesentlichen alle scheiterten. Es stellte sich nämlich heraus, dass, wenn man einen mathematischen Ausdruck konstruiert, der angeblich das Interesse eines Unternehmens repräsentieren soll, das Resultat eine mathematische Fantasie ist. Genau das weist Russell Ackoff in seinem Papier auf – und er befand sich an einem Punkt in seiner Karriere, an dem er dieses Spiel schon seit sehr langer Zeit spielte und erkannte, dass es im Grunde nirgendwohin führt. In seinem Papier vertritt er die Ansicht, dass dieses Forschungsfeld gescheitert ist, und stellt seine Diagnose, ohne jedoch wirklich eine Lösung anbieten zu können. Es ist bemerkenswert, dass einer der Gründerväter – ein hoch angesehener und anerkannter Forscher – behauptet, dass dieses gesamte Forschungsfeld ein toter Winkel sei. Den Rest seines noch recht langen Lebens wird er damit verbringen, sich vollständig von einer quantitativen Perspektive der Geschäftsoptimierung hin zu einer qualitativen Perspektive zu bewegen. Er wird die letzten drei Jahrzehnte seines Lebens auf qualitative Methoden setzen und dennoch sehr interessante Arbeiten im zweiten Teil seines Lebens nach diesem Wendepunkt hervorbringen.

Was diese Vorlesungsreihe betrifft, so: Was tun wir, da die von Russell Ackoff angesprochenen Punkte zum Operational Research auch heute noch sehr gültig sind? Tatsächlich habe ich bereits begonnen, die größten Probleme anzugehen, auf die Ackoff hingewiesen hat und für die er und seine Kollegen damals keine Lösungen anbieten konnten. Sie konnten das Problem diagnostizieren, hatten aber keine Lösung. In dieser Vorlesungsreihe basieren die von mir vorgeschlagenen Lösungen im Wesentlichen auf methodischen Ansätzen, ganz im Sinne dessen, dass Ackoff auf ein grundlegendes methodologisches Problem in der Operational-Research-Perspektive hinweist.

Die von mir vorgeschlagenen Methoden sind im Wesentlichen zweigeteilt: Einerseits das supply chain Personal und andererseits die Methode der experimentellen Optimierung, die sich als wirklich komplementär zur mathematischen Optimierung erweist. Zudem positioniere ich – im Gegensatz zum Operational Research, das beansprucht, von Geschäftsinteresse zu sein – die heutige Herangehensweise nicht aus der Perspektive des Operational Research, sondern durch die Linse der mathematischen Optimierung, die ich als reine Hilfswissenschaft für supply chain betrachte. Ich behaupte, dass an der mathematischen Optimierung for supply chain nichts von vornherein Fundamentales liegt; sie ist lediglich von grundlegender Bedeutung. Sie ist ein Mittel, kein Selbstzweck. Genau darin liegt der Unterschied. Der Punkt mag sehr simpel erscheinen, hat aber große Bedeutung, wenn es darum geht, tatsächlich prognosegerechte Ergebnisse zu erzielen.

Warum wollen wir überhaupt optimieren? Die meisten Forecasting-Algorithmen haben im Kern ein mathematisches Optimierungsproblem. Auf diesem Bildschirm sehen Sie den klassischen multiplikativen Holt-Winters-Zeitreihen-Prognosealgorithmus. Dieser Algorithmus ist vor allem von historischem Interesse; ich würde keiner heutigen supply chain empfehlen, diesen spezifischen Algorithmus tatsächlich zu nutzen. Aber der Einfachheit halber handelt es sich um eine sehr einfache parametrische Methode, die so prägnant ist, dass sie vollständig auf einem Bildschirm dargestellt werden kann. Sie ist nicht einmal besonders umfangreich.

Alle Variablen, die Sie auf dem Bildschirm sehen, sind einfache Zahlen; es kommen keine Vektoren zum Einsatz. Grundsätzlich ist Y(t) Ihre Schätzung; dies ist Ihre Zeitreihen-Prognose. Hier auf dem Bildschirm wird für H Perioden in die Zukunft prognostiziert, wobei H als Horizont dient. Man kann dabei an wöchentlich aggregierte Verkaufsdaten oder monatlich aggregierte Verkaufsdaten denken. Dieses Modell besteht im Wesentlichen aus drei Komponenten: Lt, das Niveau (Sie haben ein Niveau pro Periode), Bt, den Trend, und St, eine saisonale Komponente. Wenn Sie das Holt-Winters-Modell erlernen möchten, haben Sie drei Parameter: Alpha, Beta und Gamma. Diese drei Parameter sind im Wesentlichen Zahlen zwischen null und eins. Also haben Sie drei Parameter, alle Zahlen zwischen null und eins, und wenn Sie den Holt-Winters-Algorithmus anwenden, bedeutet das, dass Sie die optimalen Werte für diese drei Parameter ermitteln – und das war’s. Die Idee ist, dass diese Parameter – Alpha, Beta und Gamma – optimal sind, wenn sie den für Ihre Prognose festgelegten Fehler minimieren. Auf diesem Bildschirm sehen Sie einen mittleren quadratischen Fehler, was sehr klassisch ist.

Das Ziel der mathematischen Optimierung besteht darin, Algorithmen zu entwickeln, die angesichts eines bestimmten Umfangs an Rechenressourcen weitaus mehr leisten. Kann man eine deutlich bessere Lösung erzielen als mit reiner Brute-Force-Suche? Die Antwort ist ja, absolut.

Diese Auflösung ist jedoch ziemlich grob. 0,1 liefert etwa eine 10%-Auflösung auf der Skala, die Sie für Ihre Parameter haben. Vielleicht möchten Sie daher 0,01 wählen, was viel besser ist – das entspricht einer 1%-Auflösung. Allerdings führt dies zu einer Explosion der möglichen Kombinationen. Man wechselt von 1.000 Kombinationen zu einer Million Kombinationen, und das ist eben das Problem der Grid Search: sehr schnell stößt man an eine kombinatorische Grenze und sieht sich einer enormen Anzahl von Optionen gegenüber.

Mathematische Optimierung dreht sich darum, Algorithmen zu entwickeln, die mit einem gegebenen Rechenaufwand weitaus bessere Ergebnisse liefern. Kann man eine viel bessere Lösung erzielen als mit bloßer Brute-Force-Suche? Die Antwort lautet: Ja, ganz eindeutig.

Was können wir in diesem Fall tun, um tatsächlich eine bessere Lösung mit weniger investierten Rechenressourcen zu erhalten? Zunächst könnten wir eine Art Gradienten verwenden. Der gesamte Ausdruck für Holt-Winters ist vollständig differenzierbar, abgesehen von einer einzigen Division, die ein kleines Randproblem darstellt, das relativ leicht zu beheben ist. Somit ist dieser gesamte Ausdruck, einschließlich der Verlustfunktion, vollständig differenzierbar. Wir könnten einen Gradienten benutzen, um unsere Suche zu leiten; das wäre ein Ansatz.

Ein anderer Ansatz wäre, dass man in der supply chain in der Praxis vielleicht Tonnen von Zeitreihen hat. Statt jede einzelne Zeitreihe unabhängig zu behandeln, möchte man vielleicht eine Grid-Suche für die ersten 1.000 Zeitreihen durchführen, darin investieren und dann Kombinationen für alpha, beta und gamma identifizieren, die gut sind. Anschließend wählt man für alle anderen Zeitreihen aus dieser Vorauswahl an Kandidaten die beste Lösung aus.

Sehen Sie, es gibt viele einfache Ideen, wie man tatsächlich viel besser vorgehen kann, als nur einen reinen Grid-Search-Ansatz zu verfolgen, und das Wesentliche der mathematischen Optimierung sowie aller Arten von Entscheidungsproblemen kann typischerweise als mathematisches Optimierungsproblem betrachtet werden.

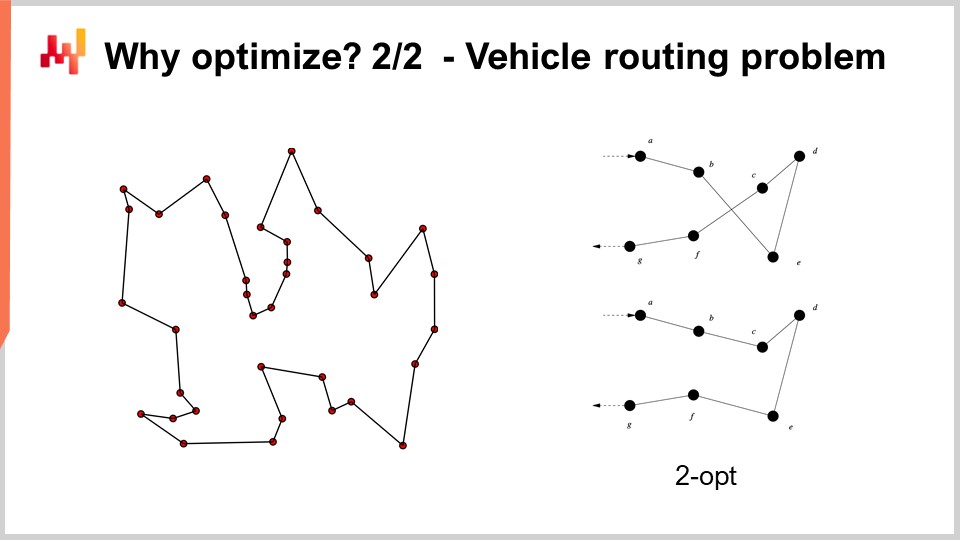
Zum Beispiel kann das Vehicle Routing Problem, das Sie auf dem Bildschirm sehen, als mathematisches Optimierungsproblem betrachtet werden. Es geht darum, eine Liste von Punkten auszuwählen. Ich habe die formale Version des Problems nicht niedergeschrieben, da sie relativ variabel ist und nicht viel Einsicht bietet. Aber wenn Sie darüber nachdenken möchten, können Sie sich einfach vorstellen: “Ich habe Punkte, ich kann jedem einzelnen Punkt eine Art Pseudo-Rang zuweisen, der einem Score entspricht, und dann habe ich einen Algorithmus, der alle Punkte nach Pseudo-Rängen in aufsteigender Reihenfolge sortiert, und das ist meine Route.” Das Ziel des Algorithmus wird es sein, die Werte für diese Pseudo-Ränge zu identifizieren, die Ihnen die besten Routen liefern.

Nun, mit diesem Problem sehen wir, dass wir ein Problem haben, bei dem eine Grid-Suche keine Option mehr ist. Wir haben Dutzende von Punkten, und wenn wir alle Kombinationen ausprobieren würden, wäre das viel zu aufwendig. Außerdem wird der Gradient uns nicht helfen, zumindest ist nicht offensichtlich, wie er uns helfen könnte, da das Problem von Natur aus sehr diskret ist und es kein offensichtliches Gradientenabstiegsverfahren für diese Art von Problem gibt.

Allerdings stellt sich heraus, dass es, wenn wir dieses Problem angehen wollen, sehr leistungsstarke Heuristiken gibt, die in der Literatur identifiziert wurden. Zum Beispiel bietet die Two-Opt-Heuristik, veröffentlicht von Croes im Jahr 1958, eine sehr einfache Heuristik. Sie beginnen mit einer zufälligen Route, und in dieser Route wenden Sie, wann immer sich die Route selbst kreuzt, eine Permutation an, um die Kreuzung zu entfernen. Also starten Sie mit einer zufälligen Route, und bei der ersten beobachteten Kreuzung führen Sie die Permutation durch, um die Kreuzung zu beseitigen, und wiederholen diesen Vorgang. Sie wiederholen den Prozess mit der Heuristik, bis keine Kreuzungen mehr vorhanden sind. Aus dieser sehr einfachen Heuristik erhalten Sie tatsächlich eine sehr gute Lösung. Sie mag im wahren mathematischen Sinne nicht optimal sein, also nicht unbedingt die perfekte Lösung; jedoch ist sie eine sehr gute Lösung, und das mit einem vergleichsweise geringen Einsatz an Rechenressourcen.

Das Problem bei der Two-Opt-Heuristik ist, dass sie zwar eine sehr gute Heuristik ist, aber unglaublich spezifisch für genau dieses Problem. Was für die mathematische Optimierung wirklich von Interesse ist, ist die Identifikation von Methoden, die auf große Klassen von Problemen anwendbar sind, anstatt nur eine Heuristik zu haben, die nur für eine spezifische Version eines Problems funktioniert. Deshalb wollen wir sehr allgemeine Methoden.

Nun, die bisherige Geschichte in dieser Vortragsreihe: Dieser Vortrag ist Teil einer Vortragsreihe, und dieses Kapitel widmet sich den Hilfswissenschaften der supply chain. Im ersten Kapitel stellte ich meine Ansichten zur supply chain sowohl als Studienfeld als auch in der Praxis vor. Das zweite Kapitel war der Methodik gewidmet, und insbesondere führten wir eine Methodik ein, die für den vorliegenden Vortrag von größter Relevanz ist, nämlich die experimentelle Optimierung. Das ist der Schlüssel zur Lösung des sehr relevanten Problems, das Russell Ackoff vor Jahrzehnten identifizierte. Das dritte Kapitel ist vollständig dem Personal der supply chain gewidmet. In diesem Vortrag konzentrieren wir uns darauf, das Problem zu identifizieren, das wir lösen wollen, anstatt Lösung und Problem zu vermischen. In diesem vierten Kapitel untersuchen wir alle Hilfswissenschaften der supply chain. Es gibt einen Fortschritt, beginnend auf der untersten Ebene der Hardware, hinauf zur Ebene der Algorithmen und dann zur mathematischen Optimierung. Wir schreiten in den Abstraktionsebenen im Laufe dieser Reihe voran.

Ein kurzer Rückblick auf die Hilfswissenschaften: Sie bieten eine Perspektive auf die supply chain selbst. Dieser Vortrag handelt nicht per se von der supply chain, sondern vielmehr von einer der Hilfswissenschaften der supply chain. Diese Perspektive macht einen erheblichen Unterschied zwischen der klassischen Perspektive des Operations Research, das als Selbstzweck betrachtet wurde, und der mathematischen Optimierung, die ein Mittel zum Zweck, aber kein Selbstzweck ist – zumindest was die supply chain betrifft. Die mathematische Optimierung kümmert sich nicht um geschäftliche Details, und die Beziehung zwischen mathematischer Optimierung und supply chain ist vergleichbar mit der Beziehung zwischen Chemie und Medizin. Aus moderner Sicht muss man kein brillanter Chemiker sein, um ein brillanter Arzt zu sein; allerdings würde es verdächtig erscheinen, wenn ein Arzt behauptet, nichts über Chemie zu wissen.

Die mathematische Optimierung setzt voraus, dass das Problem bekannt ist. Sie kümmert sich nicht um die Gültigkeit des Problems, sondern konzentriert sich darauf, das Beste aus einem gegebenen Problem in Bezug auf die Optimierung herauszuholen. In gewisser Weise ist sie wie ein Mikroskop – sehr leistungsstark, aber mit einem unglaublich engen Fokus. Die Gefahr, wenn wir zur Diskussion über die Zukunft des Operations Research zurückkehren, besteht darin, dass, wenn man das Mikroskop falsch ausrichtet, man sich von interessanten, aber letztlich irrelevanten intellektuellen Herausforderungen ablenken lassen könnte.

Deshalb muss die mathematische Optimierung in Verbindung mit der experimentellen Optimierung eingesetzt werden. Experimentelle Optimierung, die wir in der vorherigen Vorlesung behandelt haben, ist der Prozess, bei dem Sie mit Feedback aus der realen Welt iterieren, um zu besseren Versionen des Problems selbst zu gelangen. Experimentelle Optimierung ist ein Prozess, bei dem nicht die Lösung, sondern das Problem verändert wird, sodass man iterativ zu einem guten Problem konvergiert. Dies ist der entscheidende Punkt, und genau hier hatten Russell Ackoff und seine Zeitgenossen keine Lösung. Sie verfügten zwar über Werkzeuge, um ein gegebenes Problem zu optimieren, jedoch nicht über Werkzeuge, um das Problem so lange zu verändern, bis es gut war. Wenn Sie ein mathematisches Problem so betrachten, wie Sie es in Ihrem Elfenbeinturm niederschreiben können, ohne Feedback aus der realen Welt, erhalten Sie eine Fantasie. Ihr Ausgangspunkt, wenn Sie einen Prozess der experimentellen Optimierung beginnen, ist nur eine Fantasie. Es erfordert das Feedback der realen Welt, um es zum Funktionieren zu bringen. Die Idee ist, zwischen mathematischer Optimierung und experimenteller Optimierung hin und her zu wechseln. In jeder Phase Ihres experimentellen Optimierungsprozesses werden Sie Werkzeuge der mathematischen Optimierung einsetzen. Das Ziel ist es, sowohl die Rechenressourcen als auch den Ingenieuraufwand zu minimieren, sodass der Prozess zur nächsten Version des Problems iterieren kann.

In dieser Vorlesung werden wir zunächst unser Verständnis der Perspektive der mathematischen Optimierung verfeinern. Die formale Definition ist trügerisch einfach, aber es gibt Komplexitäten, derer wir uns bewusst sein müssen, um praktische Relevanz für die supply chain zu erreichen. Anschließend werden wir zwei breite Klassen von Solver untersuchen, die den Stand der Technik in der mathematischen Optimierung aus der Perspektive der supply chain repräsentieren.

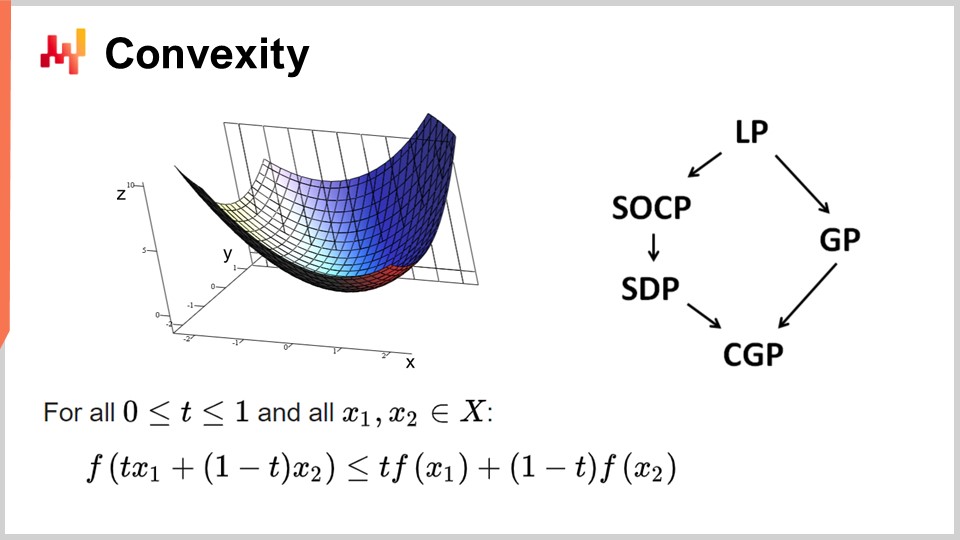
Zunächst wollen wir über Konvexität und frühe Arbeiten in der mathematischen Optimierung sprechen. Das Operations Research konzentrierte sich zunächst auf konvexe Verlustfunktionen. Eine Funktion gilt als konvex, wenn sie bestimmten Eigenschaften genügt. Intuitiv ist eine Funktion konvex, wenn für beliebige zwei Punkte auf der von der Funktion definierten Mannigfaltigkeit die gerade Linie, die diese Punkte verbindet, stets oberhalb der von der Funktion in den Zwischenräumen angenommenen Werte verläuft.

Die Konvexität ist der Schlüssel, um wahre mathematische Optimierung zu ermöglichen, bei der man Ergebnisse beweisen kann. Intuitiv bedeutet eine konvexe Funktion, dass man bei jedem Punkt der Funktion (jeder Kandidatenlösung) immer umsehen und eine Richtung finden kann, in die man absteigen kann. Egal, wo man startet, man kann immer absteigen, und Absteigen ist stets eine gute Bewegung. Der einzige Punkt, an dem man nicht weiter absteigen kann, ist im Wesentlichen der optimale Punkt. Ich vereinfache hier; es gibt Randfälle, in denen die Lösungen nicht eindeutig oder gar keine Lösungen vorhanden sind. Aber abgesehen von einigen Randfällen ist der einzige Punkt, an dem man mit einer konvexen Funktion nicht weiter optimieren kann, der optimale Punkt. Andernfalls kann man immer absteigen, und Absteigen ist eine sinnvolle Maßnahme.

Es wurde eine enorme Menge an Forschung zu konvexen Funktionen betrieben, und im Laufe der Jahre sind verschiedene Programmierparadigmen entstanden. LP steht für lineare Programmierung, und weitere Paradigmen umfassen die Second-Order-Conic-Programming, geometrische Programmierung (im Umgang mit Polynomen), semidefinite Programmierung (bei der es um Matrizen mit positiven Eigenwerten geht) sowie geometrische konische Programmierung. Diese Rahmenwerke haben gemeinsam, dass sie sich mit strukturierten konvexen Problemen befassen. Sie sind sowohl in ihrer Verlustfunktion als auch in den Beschränkungen konvex, die zulässige Lösungen einschränken.

Diese Rahmenwerke haben großes Interesse geweckt und es wurde eine umfangreiche wissenschaftliche Literatur dazu veröffentlicht. Trotz ihrer beeindruckend klingenden Namen besitzen diese Paradigmen jedoch sehr wenig Ausdruckskraft. Selbst einfache Probleme übersteigen die Fähigkeiten dieser Rahmenwerke. Zum Beispiel liegt die Optimierung der Holt-Winters-Parameter, ein grundlegendes Prognosemodell aus den 1960er Jahren, bereits über dem, was eines dieser Rahmenwerke leisten kann. Ebenso übersteigen das Vehicle Routing Problem und das Traveling Salesman Problem, beide einfache Probleme, die Fähigkeiten dieser Rahmenwerke.

Deshalb sagte ich bereits zu Beginn, dass es einen enormen Umfang an Literatur gibt, der jedoch nur wenig Nutzen bringt. Der einzige Punkt, an dem man nicht weiter absteigen kann, ist im Wesentlichen der optimale Punkt. Ich vereinfache hier; es gibt Randfälle, in denen die Lösungen nicht eindeutig oder gar keine Lösungen vorhanden sind. Aber abgesehen von einigen Randfällen ist der einzige Punkt, an dem man mit einer konvexen Funktion nicht weiter optimieren kann, der optimale Punkt. Andernfalls kann man immer absteigen, und Absteigen ist eine gute Maßnahme.

Es wurde eine enorme Menge an Forschung zu konvexen Funktionen betrieben, und im Laufe der Jahre sind verschiedene Programmierparadigmen entstanden. LP steht für lineare Programmierung, und weitere Paradigmen umfassen die Second-Order-Conic-Programming, geometrische Programmierung (im Umgang mit Polynomen), semidefinite Programmierung (bei der es um Matrizen mit positiven Eigenwerten geht) sowie geometrische konische Programmierung. Diese Rahmenwerke haben gemeinsam, dass sie sich mit strukturierten konvexen Problemen befassen. Sie sind sowohl in ihrer Verlustfunktion als auch in den Beschränkungen konvex, die zulässige Lösungen einschränken.

Diese Rahmenwerke haben großes Interesse geweckt und es wurde eine umfangreiche wissenschaftliche Literatur dazu veröffentlicht. Trotz ihrer beeindruckend klingenden Namen besitzen diese Paradigmen jedoch sehr wenig Ausdruckskraft. Selbst einfache Probleme übersteigen die Fähigkeiten dieser Rahmenwerke. Zum Beispiel liegt die Optimierung der Holt-Winters-Parameter, ein grundlegendes Prognosemodell aus den 1960er Jahren, bereits über dem, was eines dieser Rahmenwerke leisten kann. Ebenso übersteigen das Vehicle Routing Problem und das Traveling Salesman Problem, beide einfache Probleme, die Fähigkeiten dieser Rahmenwerke.

Deshalb sagte ich bereits zu Beginn, dass es einen enormen Umfang an Literatur gibt, der jedoch nur wenig Nutzen bringt. Ein Teil des Problems war der fehlgeleitete Fokus auf reine mathematische Optimierungs-Solver. Diese Solver sind aus mathematischer Sicht sehr interessant, weil man mathematische Beweise führen kann, jedoch können sie nur bei buchstäblich Spielzeugproblemen oder rein erfundenen Problemen eingesetzt werden. Sobald man in der realen Welt ist, versagen sie, und in diesen Bereichen gab es in den letzten Jahrzehnten nur sehr wenig Fortschritte. Was die supply chain betrifft, so ist fast nichts, abgesehen von einigen Nischen, für diese Solver relevant.

Ein weiterer Aspekt, der während der klassischen Ära des Operations Research völlig abgetan und ignoriert wurde, ist die Zufälligkeit. Zufälligkeit oder Stochastizität ist in zweierlei radikal unterschiedlicher Weise von entscheidender Bedeutung. Der erste Ansatz zur Zufälligkeit bezieht sich auf den Solver selbst. Heutzutage nutzen alle State-of-the-Art-Solver intern umfangreich stochastische Prozesse. Das ist sehr interessant im Vergleich zu einem vollständig deterministischen Prozess. Ich spreche hier von den inneren Mechanismen des Solvers, dem Softwaremodul, das die mathematischen Optimierungstechniken implementiert.

Der Grund, warum alle State-of-the-Art-Solver intern umfangreich stochastische Prozesse nutzen, hängt mit der Art und Weise zusammen, wie moderne Computerhardware funktioniert. Die Alternative zur Zufälligkeit bei der Erkundung von Lösungen besteht darin, sich daran zu erinnern, was man in der Vergangenheit getan hat, um nicht in derselben Schleife steckenzubleiben. Wenn man sich erinnern muss, verbraucht das Speicher. Das Problem liegt darin, dass zahlreiche Speicherzugriffe notwendig sind. Eine Möglichkeit, Zufälligkeit einzuführen, besteht üblicherweise darin, den Bedarf an zufälligen Speicherzugriffen weitgehend zu mindern.

Indem Sie Ihren Prozess stochastisch gestalten, können Sie vermeiden, Ihre eigene Datenbank danach zu durchsuchen, was Sie unter möglichen Lösungen für das zu optimierende Problem getestet oder nicht getestet haben. Sie machen es ein wenig zufällig, aber nicht völlig. Dies hat wesentliche Bedeutung bei praktisch allen modernen Solvern. Einer der etwas kontraintuitiven Aspekte eines stochastischen Prozesses ist, dass obwohl Sie einen stochastischen Solver haben können, das Ergebnis dennoch ziemlich deterministisch sein kann. Um dies zu verstehen, betrachten Sie die Analogie einer Reihe von Sieben. Ein Sieb ist im Wesentlichen ein physikalischer stochastischer Prozess, bei dem Sie zufällige Bewegungen anwenden und der Siebvorgang stattfindet. Obwohl der Prozess vollkommen stochastisch ist, ist das Ergebnis völlig deterministisch. Am Ende erhalten Sie ein völlig vorhersehbares Ergebnis aus dem Siebvorgang, obwohl Ihr Prozess grundlegend zufällig war. Genau dies geschieht bei gut konstruierten stochastischen Solvern. Dies ist eine der Schlüsselkomponenten moderner Solver.

Ein weiterer Aspekt, der in Bezug auf Zufälligkeit orthogonal ist, ist die stochastische Natur der Probleme selbst. Dies war in der klassischen Ära der Operations Research größtenteils abwesend – die Idee, dass Ihre Verlustfunktion verrauscht ist und jede Messung, die Sie davon erhalten, ein gewisses Maß an Rauschen aufweisen wird. Dies ist in der supply chain fast immer der Fall. Warum? Tatsache ist, dass in der supply chain, wann immer Sie eine Entscheidung treffen, dies deshalb geschieht, weil Sie irgendeine Art von zukünftigen Ereignissen erwarten. Wenn Sie sich entscheiden, etwas zu kaufen, dann, weil Sie erwarten, dass später in der Zukunft ein Bedarf dafür bestehen wird. Die Zukunft ist nicht vorgezeichnet, sodass Sie einige Einblicke in die Zukunft haben können, aber diese Einsicht ist nie perfekt. Wenn Sie sich entscheiden, jetzt ein Produkt zu produzieren, dann, weil Sie erwarten, dass später in der Zukunft eine Nachfrage nach diesem Produkt bestehen wird. Die Qualität Ihrer Entscheidung, also das heutige Produzieren, hängt von zukünftigen unsicheren Bedingungen ab, und somit wird jede Entscheidung, die Sie in der supply chain treffen, eine Verlustfunktion haben, die je nach diesen zukünftigen, nicht kontrollierbaren Bedingungen variiert. Die Art der Zufälligkeit, die mit zukünftigen Ereignissen einhergeht, ist irreduzibel, und das ist von zentralem Interesse, da es bedeutet, dass wir es grundsätzlich mit stochastischen Problemen zu tun haben.

Wenn wir jedoch zu den klassischen mathematischen Solvern zurückkehren, stellen wir fest, dass dieser Aspekt völlig fehlt, was ein großes Problem darstellt. Das bedeutet, dass wir Solver-Klassen haben, die nicht einmal die Art von Problemen erfassen können, denen wir begegnen werden, da die Probleme, an denen wir mathematische Optimierung anwenden möchten, stochastischer Natur sein werden. Ich spreche von dem Rauschen in der Verlustfunktion.

Es gibt den Einwand, dass wenn man ein stochastisches Problem hat, man es durch Sampling immer wieder in ein deterministisches Problem umwandeln kann. Wenn Sie Ihre verrauschte Verlustfunktion 10.000 Mal auswerten, können Sie eine annähernd deterministische Verlustfunktion erhalten. Dieser Ansatz ist jedoch unglaublich ineffizient, da er einen 10.000-fachen Overhead in Ihrem Optimierungsprozess einführt. Die Perspektive der mathematischen Optimierung zielt darauf ab, die besten Ergebnisse für Ihre begrenzten Rechenressourcen zu erzielen. Es geht nicht darum, unendlich große Rechenressourcen zu investieren, um das Problem zu lösen. Wir müssen mit einer endlichen Menge an Rechenressourcen arbeiten, auch wenn diese Menge ziemlich groß ist. Daher müssen wir bei der Betrachtung von Solvern später im Hinterkopf behalten, dass es von primärem Interesse ist, Solver zu haben, die stochastische Probleme nativ erfassen können, anstatt standardmäßig den deterministischen Ansatz zu verwenden.

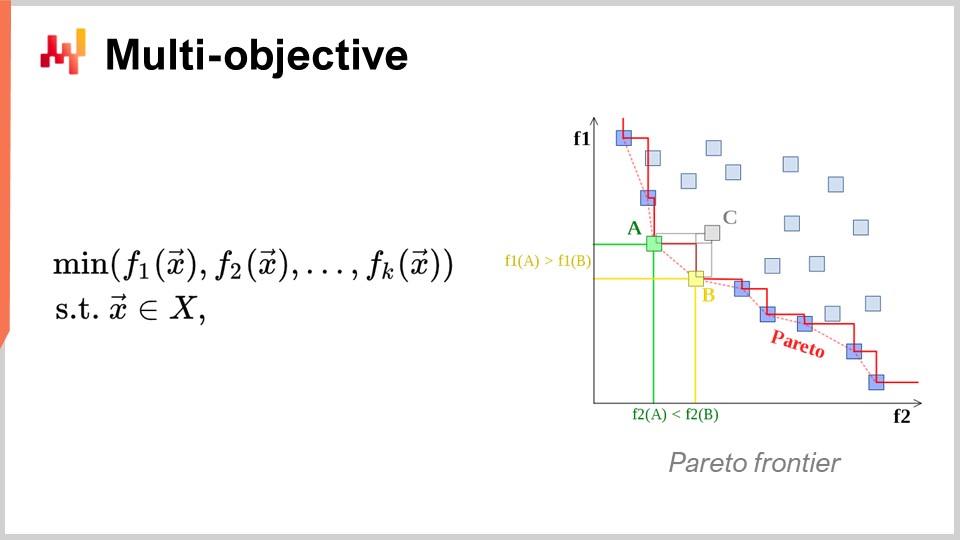
Ein weiterer Aspekt, der ebenfalls von primärem Interesse ist, ist die Multi-Objective-Optimierung. In der naiven Darstellung des mathematischen Optimierungsproblems sagte ich, dass die Verlustfunktion im Grunde eindimensional sei, sodass wir einen Wert minimieren wollten. Aber was, wenn wir einen Vektor von Werten haben und was wir tun wollen, ist die Lösung zu finden, die den niedrigsten Punkt gemäß der lexikografischen Ordnung aller Vektoren liefert, wie f1, f2, f3 usw.?

Warum ist das aus Sicht der supply chain überhaupt von Interesse? Tatsache ist, dass wenn Sie diese Multi-Objective-Perspektive übernehmen, Sie alle Ihre Nebenbedingungen als nur eine dedizierte Verlustfunktion ausdrücken können. Sie können zunächst eine Funktion haben, die Ihre Verletzungen von Nebenbedingungen zählt. Warum gibt es Nebenbedingungen in der supply chain? Nun, überall gibt es Nebenbedingungen. Beispielsweise, wenn Sie eine Bestellung aufgeben, müssen Sie sicherstellen, dass Sie genügend Platz in Ihrem warehouse haben, um die Waren bei ihrer Ankunft zu lagern. Also gibt es Beschränkungen bezüglich Lagerraum, Produktionskapazität und mehr. Die Idee ist, dass es interessanter ist, einen Solver zu haben, der mit Multi-Objective-Optimierung umgehen kann und bei dem Sie die Nebenbedingungen als eines der Ziele ausdrücken können, anstatt einen Solver zu haben, bei dem Sie die Nebenbedingungen speziell behandeln müssen. Sie zählen einfach die Anzahl der Nebenbedingungenverletzungen, und Sie wollen diese minimieren, sodass diese Anzahl von Verletzungen auf null reduziert wird.

Der Grund, warum diese Denkweise in der supply chain so relevant ist, liegt darin, dass die Optimierungsprobleme, mit denen supply chains konfrontiert sind, keine kryptographischen Rätsel sind. Es handelt sich nicht um super eng kombinatorische Probleme, bei denen entweder eine Lösung existiert und sie gut ist, oder man ist nur ein kleines Stück von der Lösung entfernt und hat nichts. In der supply chain ist es typischerweise völlig trivial, eine sogenannte machbare Lösung zu erhalten – eine Lösung, die alle Nebenbedingungen erfüllt. Eine einzige Lösung zu identifizieren, die die Nebenbedingungen erfüllt, ist keine große Herausforderung. Sehr schwierig ist es, unter allen Lösungen, die die Nebenbedingungen erfüllen, diejenige zu finden, die am profitabelsten für das Geschäft ist. Genau da wird es sehr schwierig. Eine Lösung zu finden, die die Nebenbedingungen nicht verletzt, ist sehr unkompliziert. Das ist in anderen Bereichen nicht der Fall, zum Beispiel in der mathematischen Optimierung für das Industriedesign, wo Sie Komponentenplatzierung innerhalb eines Mobiltelefons vornehmen möchten. Dies ist ein unglaublich streng eingeschränktes Problem, bei dem Sie nicht dadurch schummeln können, dass Sie auf eine Nebenbedingung verzichten und eine kleine Beule an Ihrem Mobiltelefon in Kauf nehmen. Es ist ein Problem, das unglaublich eng und kombinatorisch ist, und bei dem Sie Nebenbedingungen wirklich als erstklassige Bürger behandeln müssen. Ich glaube nicht, dass dies für die überwiegende Mehrheit der supply chain Probleme notwendig ist. Daher ist es erneut von hohem Interesse, Techniken zu haben, die nativerweise mit Multi-Objective-Optimierung umgehen können.

Nun wollen wir noch ein wenig mehr über das Design des Solvers sprechen. Aus einer sehr hochrangigen Perspektive, wie wir ein Softwarestück entwickeln wollen, das Lösungen für eine sehr breite Klasse von Problemen liefert, möchte ich zwei sehr bemerkenswerte Designaspekte hervorheben. Der erste Aspekt, der zu berücksichtigen ist, ist, ob wir aus einer White-Box- oder Black-Box-Perspektive arbeiten wollen. Die Idee der Black-Box-Perspektive ist, dass wir jedes beliebige Programm verarbeiten können, sodass die Verlustfunktion ein beliebiges Programm sein kann. Das interessiert uns nicht; wir behandeln das als eine vollständige Black Box. Das Einzige, was wir wollen, ist ein Programm, in dem wir das Programm auswerten und den Wert einer vorläufigen Lösung erhalten können. Im Gegensatz dazu betont ein White-Box-Ansatz die Tatsache, dass die Verlustfunktion selbst eine Struktur hat, die wir untersuchen und nutzen können. Wir können in die Verlustfunktion hineinschauen. Übrigens, als ich vor einigen Folien über Konvexität sprach, waren all diese Modelle und reinen mathematischen Solver tatsächlich White-Box-Ansätze. Sie sind der extreme Fall von White-Box-Ansätzen, bei dem man nicht nur in das Problem hineinsehen kann, sondern das Problem auch eine sehr starre Struktur hat, wie z. B. semi-definites Programmieren, bei dem die Form sehr eingeschränkt ist. Ohne zu einem so starren mathematischen Rahmenwerk zu greifen, kann man jedoch zum Beispiel sagen, dass als Teil der White Box etwas wie der Gradient vorliegt, der Ihnen helfen wird. Der Gradient der Verlustfunktion ist von entscheidender Bedeutung, weil Sie plötzlich wissen können, in welche Richtung Sie abwärts gehen wollen, selbst wenn Sie kein konvexes Problem haben, bei dem der einfache Gradientenabstieg ein gutes Ergebnis garantiert. Als Faustregel gilt, dass, wenn Sie Ihren Solver white box gestalten können, Sie einen Solver haben werden, der um Größenordnungen leistungsfähiger ist als ein Black-Box-Solver.

Nun, als zweiten Aspekt, haben wir Offline- versus Online-Solver. Der Offline-Solver arbeitet typischerweise in Stapeln, sodass ein Offline-Solver einfach das Problem aufnimmt, ausführt und Sie warten müssen, bis er abgeschlossen ist. Zu diesem Zeitpunkt, wenn der Solver abgeschlossen ist, liefert er Ihnen die beste Lösung oder etwas, das als die bestmögliche identifizierte Lösung gilt. Im Gegensatz dazu arbeitet ein Online-Solver viel mehr mit einem Best-Effort-Ansatz. Er wird eine passable Lösung identifizieren und dann Rechenressourcen investieren, um mit der Zeit und zunehmenden Investitionen in Rechenressourcen schrittweise zu besseren Lösungen zu iterieren. Was wirklich von zentralem Interesse ist, ist, dass wenn Sie sich einem Problem mit einem Online-Solver nähern, bedeutet das, dass Sie den Prozess praktisch jederzeit pausieren und eine frühzeitige Kandidatenlösung erhalten können. Sie können den Prozess sogar wieder aufnehmen. Wenn wir zu den mathematischen Solvern zurückkehren, handelt es sich typischerweise um Batch-Solver, bei denen Sie bis zum Ende des Prozesses warten müssen.

Leider kann das Arbeiten in der supply chain Welt sehr holprig sein, wie in einer der vorherigen Vorlesungen dieser Serie behandelt wurde. Es wird Situationen geben, in denen Sie normalerweise, sagen wir, drei Stunden aufwenden können, um diesen mathematischen Optimierungsprozess auszuführen. Aber manchmal kann es zu IT-Störungen, realen Problemen oder einem Notfall in Ihrer supply chain kommen. In solchen Fällen ist es lebensrettend, wenn das, was normalerweise drei Stunden dauern würde, nach fünf Minuten unterbrochen werden kann und eine Antwort liefert, selbst wenn sie schlecht ist, anstatt gar keiner Antwort. Es gibt ein Sprichwort im Militär, dass der schlechteste Plan kein Plan ist, also ist es besser, einen sehr groben Plan zu haben, als gar nichts. Genau das gibt Ihnen ein Online-Solver. Dies sind die Schlüsseldesign-Elemente, die wir in der folgenden Diskussion im Hinterkopf behalten werden.

Nun, um diesen ersten Abschnitt der Vorlesung zur Herangehensweise an die mathematische Optimierung abzuschließen, werfen wir einen Blick auf die deep learning Lektionen. Deep learning war eine vollständige Revolution im Bereich des maschinellen Lernens. Allerdings beinhaltet deep learning im Kern auch ein mathematisches Optimierungsproblem. Ich glaube, dass deep learning eine Revolution innerhalb der mathematischen Optimierung selbst ausgelöst hat und die Art und Weise, wie wir Optimierungsprobleme betrachten, vollständig verändert hat. Deep learning hat neu definiert, was wir als Stand der Technik in der mathematischen Optimierung betrachten.

Heutzutage beschäftigen sich die größten deep learning Modelle mit mehr als einer Billion Parametern, was tausend Milliarden entspricht. Um das in Perspektive zu setzen: Die meisten mathematischen Solver kämpfen bereits damit, mit nur 1.000 Variablen zurechtzukommen und stürzen typischerweise bei nur einigen Zehntausend Variablen ab, egal wie viel Rechenhardware man ihnen zur Verfügung stellt. Im Gegensatz dazu ist deep learning erfolgreich, wobei zwar eine große Menge an Rechenressourcen verwendet wird, aber dennoch ist es machbar. Es gibt deep learning Modelle in der Produktion, die über eine Billion Parameter haben, und all diese Parameter werden optimiert, was bedeutet, dass wir mathematische Optimierungsprozesse haben, die auf eine Billion Parameter skalieren können. Dies ist absolut erstaunlich und radikal anders als die Leistung, die wir bei klassischen Optimierungsperspektiven gesehen haben.

Das Interessante ist, dass selbst Probleme, die vollkommen deterministisch sind, wie zum Beispiel Go oder Schach spielen, die nicht-statistisch, diskret und kombinatorisch sind, am erfolgreichsten mit Methoden gelöst wurden, die vollkommen stochastisch und statistisch sind. Dies ist verwunderlich, denn Go oder Schach spielen kann man als diskrete Optimierungsprobleme ansehen, und dennoch werden sie heutzutage am effizientesten mit Methoden gelöst, die vollständig stochastisch und statistisch sind. Dies widerspricht der Intuition, die die wissenschaftliche Gemeinschaft vor zwei Jahrzehnten über diese Probleme hatte.

Lassen Sie uns das Verständnis, das durch deep learning in Bezug auf die mathematische Optimierung freigesetzt wurde, noch einmal überdenken. Das Erste ist, den Fluch der Dimensionalität vollständig neu zu betrachten. Ich glaube, dass dieses Konzept größtenteils fehlerhaft ist, und deep learning beweist, dass man nicht einmal über die Schwierigkeit eines Optimierungsproblems in dieser Weise nachdenken sollte. Es stellt sich heraus, dass, wenn man sich Klassen mathematischer Probleme ansieht, man mathematisch beweisen kann, dass bestimmte Probleme außerordentlich schwer perfekt zu lösen sind. Zum Beispiel haben Sie schon von NP-schweren Problemen gehört; Sie wissen, dass, je mehr Dimensionen dem Problem hinzugefügt werden, es exponentiell schwieriger wird, es zu lösen. Jede zusätzliche Dimension macht das Problem schwerer, und es gibt eine kumulative Hürde. Man kann beweisen, dass kein Algorithmus jemals hoffen kann, das Problem mit einer begrenzten Menge an Rechenressourcen perfekt zu lösen. Deep learning zeigte jedoch, dass diese Perspektive größtenteils fehlerhaft war.

Zunächst müssen wir zwischen der Repräsentationskomplexität des Problems und der intrinsischen Komplexität des Problems unterscheiden. Lassen Sie mich diese beiden Begriffe anhand eines Beispiels verdeutlichen. Werfen wir einen Blick auf das eingangs gegebene Beispiel der Zeitreihenprognose. Nehmen wir an, wir haben eine Verkaufshistorie, täglich über drei Jahre aggregiert, sodass wir einen Tages-Zeitvektor von etwa 1.000 Tagen haben. Dies ist die Repräsentation des Problems.

Was wäre nun, wenn ich zu einer Zeitreihenrepräsentation pro Sekunde übergehe? Dies ist dieselbe Verkaufshistorie, aber anstatt meine Verkaufsdaten in täglichen Aggregaten darzustellen, werde ich dieselbe Zeitreihe in Sekundensprüngen darstellen. Das bedeutet, dass es in jedem einzelnen Tag 86.400 Sekunden gibt, sodass ich die Größe und Dimension meiner Problemdarstellung um den Faktor 86.400 aufblähen werde.

Aber wenn wir anfangen, über die intrinsische Dimension nachzudenken, so liegt es nicht daran, dass ich eine Verkaufshistorie habe, und nicht daran, dass ich von einer täglichen Aggregation zu einer sekundären Aggregation übergehe, dass ich die Komplexität oder die dimensionale Komplexität des Problems um das Tausendfache erhöhe. Höchstwahrscheinlich wird, wenn ich zu pro Sekunde aggregierten Verkäufen übergehe, die Zeitreihe unglaublich spärlich sein, sodass sie in nahezu allen Intervallen hauptsächlich Nullen enthält. Ich erhöhe nicht die interessante Dimensionalität des Problems um den Faktor 100.000. Deep learning verdeutlicht, dass es nicht daran liegt, dass man eine Problemrepräsentation mit vielen Dimensionen hat, dass das Problem grundsätzlich schwer ist.

Ein weiterer Aspekt, der mit der Dimensionalität zusammenhängt, ist, dass obwohl man beweisen kann, dass bestimmte Probleme NP-vollständig sind – zum Beispiel das Traveling Salesman Problem (eine vereinfachte Version des zu Beginn dieser Vorlesung vorgestellten Vehicle Routing Problems) – der Traveling Salesman technisch gesehen als NP-schwer gilt. Also, es ist ein Problem, bei dem, wenn man im Allgemeinen die beste Lösung finden möchte, die Kosten exponentiell ansteigen, sobald man weitere Punkte zu seiner Karte hinzufügt. Aber die Realität ist, dass diese Probleme sehr einfach zu lösen sind, wie die Two-Opt-Heuristik veranschaulicht; man kann ausgezeichnete Lösungen mit minimalen Rechenressourcen erzielen. Seien Sie also gewarnt, dass mathematische Beweise, die zeigen, dass manche Probleme sehr schwer sind, täuschen können. Sie besagen nicht, dass, wenn man mit einer approximativen Lösung zufrieden ist, diese Annäherung exzellent sein kann – und manchmal ist es nicht einmal nur eine Annäherung; man bekommt die optimale Lösung. Es heißt nur, dass man nicht beweisen kann, dass sie optimal ist. Das sagt nichts darüber aus, ob man das Problem approximieren kann, und sehr häufig erweisen sich jene Probleme, die angeblich vom Fluch der Dimensionalität geplagt sind, als unkompliziert zu lösen, weil ihre interessanten Dimensionen gar nicht so hoch sind. Deep Learning hat erfolgreich gezeigt, dass viele Probleme, die als unglaublich schwierig galten, von vornherein gar nicht so schwierig waren.

Die zweite zentrale Erkenntnis waren die lokalen Minima. Die Mehrheit der Forscher, die an mathematischer Optimierung und Operations Research arbeiten, bevorzugte konvexe Funktionen, da es keine lokalen Minima gab. Lange Zeit dachten diejenigen, die nicht mit konvexen Funktionen arbeiteten, darüber nach, wie man vermeiden kann, in einem lokalen Minimum steckenzubleiben. Der Großteil der Bemühungen war darauf ausgerichtet, an Dingen wie Meta-Heuristiken zu arbeiten. Deep Learning hat ein erneuertes Verständnis vermittelt: Es ist uns egal, ob es lokale Minima gibt.

Wenn man eine sehr hohe Dimension hat, kann man zeigen, dass lokale Minima verschwinden, wenn die Dimension des Problems zunimmt. Lokale Minima kommen in niedrigdimensionalen Problemen sehr häufig vor, aber wenn man die Dimension der Probleme auf Hunderte oder Tausende erhöht, werden lokale Minima statistisch gesehen unglaublich unwahrscheinlich – so sehr, dass sie bei Dimensionen von Millionen komplett verschwinden.

Anstatt zu denken, dass eine höhere Dimension Ihr Feind ist, wie es mit dem Fluch der Dimensionalität assoziiert wurde, was wäre, wenn man genau das Gegenteil tun könnte und die Dimension des Problems so weit aufblähen könnte, bis es trivial ist, einen sauberen Abstieg ohne jegliche lokalen Minima zu erzielen? Es stellt sich heraus, dass genau dies in der Deep Learning Community und bei Modellen mit einer Billion Parametern gemacht wird. Dieser Ansatz bietet einen sehr sauberen Weg, sich mittels Gradientenabstieg vorwärts zu bewegen.

Im Wesentlichen hat die Deep Learning Community gezeigt, dass es unerheblich ist, einen Beweis über die Qualität des Abstiegs oder die endgültige Konvergenz zu erbringen. Was zählt, ist die Geschwindigkeit des Abstiegs. Man möchte iterieren und sehr rasch in Richtung einer sehr guten Lösung absteigen. Wenn man einen Prozess hat, der schneller absteigt, wird man letztlich in Bezug auf die Optimierung weiterkommen. Diese Erkenntnisse widersprechen dem allgemeinen Verständnis der mathematischen Optimierung oder dem, was vor zwei Jahrzehnten als Mainstream galt.

Es gibt noch weitere Lehren aus dem Deep Learning, da es ein sehr reichhaltiges Feld ist. Eine davon ist die Hardware-Sympathie. Das Problem bei mathematischen Solvern, wie der konischen Programmierung oder der geometrischen Programmierung, besteht darin, dass sie zuerst auf mathematische Intuition setzen und nicht auf die Rechenhardware. Wenn Sie einen Solver entwerfen, der prinzipiell Ihrer Rechenhardware entgegenwirkt, ganz gleich, wie klug Ihre Mathematik auch sein mag, dann werden Sie aufgrund der schlechten Ausnutzung der Hardware aller Wahrscheinlichkeit nach verzweifelt ineffizient arbeiten.

Eine der zentralen Erkenntnisse der Deep Learning Community ist, dass man gut mit der Rechenhardware zusammenarbeiten und einen Solver entwerfen muss, der sie einbezieht. Aus diesem Grund habe ich diese Vorlesungsreihe über Hilfswissenschaften für supply chain mit modernen Computern für supply chain begonnen. Es ist wichtig, die vorhandene Hardware zu verstehen und sie bestmöglich zu nutzen. Diese Hardware-Sympathie ermöglicht es, Modelle mit einer Billion Parametern zu realisieren – vorausgesetzt, man verfügt über einen großen Computercluster oder einen Supercomputer.

Eine weitere Lehre aus dem Deep Learning ist die Verwendung von Stellfunktionen. Traditionell zielten mathematische Solver darauf ab, das Problem so zu optimieren, wie es war, ohne davon abzuweichen. Deep Learning hat jedoch gezeigt, dass es manchmal besser ist, Stellfunktionen zu verwenden. So nutzen Deep Learning Modelle sehr häufig cross-entropy als Fehlermetrik statt des mittleren quadratischen Fehlers. In der Praxis interessiert sich nahezu niemand in der realen Welt für cross-entropy als Metrik, da sie ziemlich bizarr ist.

Warum verwenden die Leute also cross-entropy? Es liefert unglaublich steile Gradienten und, wie Deep Learning gezeigt hat, dreht sich alles um die Geschwindigkeit des Abstiegs. Wenn Sie sehr steile Gradienten haben, können Sie sehr schnell absteigen. Manche könnten einwenden: „Wenn ich den mittleren quadratischen Fehler optimieren möchte, warum sollte ich dann cross-entropy verwenden? Es ist nicht einmal dasselbe Ziel.“ Die Realität ist, dass Sie, wenn Sie cross-entropy optimieren, sehr steile Gradienten erhalten und am Ende, wenn Sie Ihre Lösung anhand des mittleren quadratischen Fehlers bewerten, sehr häufig – wenn nicht immer – auch eine bessere Lösung gemäß dem Kriterium des mittleren quadratischen Fehlers erzielen. Ich vereinfache hier nur, um das Konzept zu erklären. Die Idee der Stellfunktionen ist, dass das eigentliche Problem kein absolutes Ziel ist; es ist lediglich etwas, das Sie zur Kontrolle heranziehen, um die endgültige Gültigkeit Ihrer Lösung zu beurteilen. Es ist nicht notwendigerweise das, was Sie während der Ausführung des Solvers verwenden.

Schließlich gibt es die Bedeutung, in Paradigmen zu arbeiten. Bei der mathematischen Optimierung gibt es implizit eine Arbeitsteilung bei der Organisation Ihres Ingenieurteams. Die implizite Arbeitsteilung, die mit mathematischen Solvern einhergeht, sieht vor, dass Sie einerseits mathematische Ingenieure haben, die für die Entwicklung des Solvers verantwortlich sind, und andererseits Problemingenieure, deren Aufgabe es ist, das Problem in eine Form zu bringen, die von den mathematischen Solvern verarbeitet werden kann. Diese Arbeitsteilung war weit verbreitet, und die Idee war, es dem Problemingenieur so einfach wie möglich zu machen, indem er das Problem in der minimalistischsten und reinsten Form ausdrückt, während der Solver die eigentliche Arbeit übernimmt.

Deep Learning hat gezeigt, dass diese Perspektive zutiefst ineffizient war. Diese willkürliche Arbeitsteilung war keineswegs der beste Weg, das Problem anzugehen. Wenn man es so handhabt, entstehen Situationen, die unheimlich schwierig sind – weitaus über dem Stand der Technik dessen, was mathematische Ingenieure bei der Bearbeitung des Optimierungsproblems leisten können. Ein viel besserer Ansatz besteht darin, dass die Problemingenieure etwas mehr Aufwand betreiben, um die Probleme so umzuformulieren, dass sie für den mathematischen Optimierer wesentlich besser geeignet sind.

Deep Learning dreht sich um eine Reihe von Rezepten, die es ermöglichen, das Problem oberhalb des Solvers zu formulieren, sodass Sie das Optimum aus Ihrem Optimierer herausholen. Die meisten Entwicklungen in der Deep Learning Community konzentrierten sich darauf, diese Rezepte zu erarbeiten, die beim Lernen sehr effektiv sind und sich gut in das Paradigma der genutzten Solvers (z. B. TensorFlow, PyTorch, MXNet) einfügen. Das Fazit ist, dass man wirklich mit dem Problemingenieur zusammenarbeiten möchte – oder, in supply chain Terminologie, mit dem Supply Chain Scientist.

Nun wollen wir zum zweiten und letzten Abschnitt dieser Vorlesung über die wertvollsten Elemente der Literatur übergehen. Wir werden uns zwei breite Klassen von Solvern ansehen: lokale Suche und differentiable Programmierung.

Zunächst möchte ich noch einmal bei dem Begriff “programming” innehalten. Dieses Wort hat eine wesentliche Bedeutung, denn aus der Perspektive von supply chain wollen wir wirklich in der Lage sein, das Problem, dem wir gegenüberstehen – oder von dem wir glauben, dass wir es haben – auszudrücken. Wir wollen nicht irgendeine Art von super niedrigauflösender Version des Problems, die zufällig zu einer halb absurden mathematischen Hypothese passt, wie etwa, dass man sein Problem in einem Kegel ausdrücken muss oder dergleichen. Was uns wirklich interessiert, ist der Zugang zu einem echten Programmierparadigma.

Denken Sie daran, dass diese mathematischen Solvern wie lineare Programmierung, Second-Order Conic Programming und Geometric Programming alle mit einem “programming”-Schlüsselwort kamen. Allerdings haben sich unsere Erwartungen an ein Programmierparadigma in den letzten Jahrzehnten dramatisch verändert. Heutzutage wollen wir etwas, das es erlaubt, mit nahezu beliebigen Programmen umzugehen – Programmen, in denen Sie Schleifen, Verzweigungen und möglicherweise auch Speicherzuteilungen haben, usw. Man möchte wirklich etwas, das so nah wie möglich an einem beliebigen Programm ist und nicht irgendeine Art super eingeschränkte Spielzeugversion mit einigen interessanten mathematischen Eigenschaften. Im supply chain ist es besser, annähernd richtig zu sein, als genau falsch.

Um sich mit generischer Optimierung auseinanderzusetzen, beginnen wir mit der lokalen Suche. Lokale Suche ist eine trügerisch einfache mathematische Optimierungstechnik. Der Pseudocode sieht vor, mit einer zufälligen Lösung zu beginnen, die Sie als eine Ansammlung von Bits darstellen. Anschließend initialisieren Sie Ihre Lösung zufällig und beginnen, Bits zufällig umzuschalten, um die Umgebung der Lösung zu erkunden. Wenn Sie durch diese zufällige Erkundung eine Lösung finden, die zufällig besser ist, wird diese zu Ihrer neuen Referenzlösung.

Dieser überraschend leistungsstarke Ansatz kann mit buchstäblich jedem Programm funktionieren, indem man es als Black Box behandelt, und kann auch von jeder bekannten Lösung aus neu gestartet werden. Es gibt zahlreiche Möglichkeiten, diesen Ansatz zu verbessern. Eine davon ist die differentielle Berechnung, die nicht mit differentiable computation zu verwechseln ist. Differentielle Berechnung beruht auf der Idee, dass wenn Sie Ihr Programm an einer gegebenen Lösung ausführen und dann ein Bit umschalten, Sie das gleiche Programm mittels einer differentiellen Ausführung erneut ausführen können, ohne das gesamte Programm neu zu starten. Offensichtlich kann Ihr Nutzen variieren, und es hängt stark von der Struktur des Problems ab. Eine Möglichkeit, den Prozess zu beschleunigen, besteht darin, nicht irgendwelche zusätzlichen Informationen über das Black-Box-Programm auszunutzen, mit dem wir arbeiten, sondern schlicht das Programm selbst zu beschleunigen – wobei es größtenteils weiterhin als Black Box behandelt wird, weil man nicht jedes Mal das gesamte Programm neu ausführt.

Es gibt noch weitere Ansätze, um die lokale Suche zu verbessern. Man kann die Art der vorgenommenen Schritte optimieren. Die grundlegendste Strategie heißt k-Flips, bei der Sie k Bits umschalten, wobei k eine sehr kleine Zahl ist – etwa ein paar bis ein Dutzend. Anstatt einfach nur Bits umzuschalten, können Sie dem Problemingenieur erlauben, die Art der Mutationen festzulegen, die an der Lösung angewendet werden sollen. Zum Beispiel können Sie festlegen, dass eine bestimmte Permutation in Ihrem Problem angewendet wird. Die Idee dahinter ist, dass diese intelligenten Veränderungen oft dazu führen, dass gewisse Nebenbedingungen in Ihrem Problem erhalten bleiben, was den lokalen Suchprozess beschleunigen kann.

Eine weitere Möglichkeit, die lokale Suche zu verbessern, besteht darin, den Suchraum nicht völlig zufällig zu erkunden. Anstatt Bits willkürlich umzuschalten, können Sie versuchen, die richtigen Richtungen zu erlernen, um die vielversprechendsten Bereiche für Änderungen zu identifizieren. Einige neuere Arbeiten haben gezeigt, dass man ein kleines Deep Learning-Modul über die lokale Suche schalten kann, das als Generator fungiert. Dieser Ansatz kann jedoch in Bezug auf das Engineering knifflig sein, da Sie sicherstellen müssen, dass der durch den Machine-Learning-Prozess eingeführte Mehraufwand einen positiven Ertrag in Bezug auf die Rechenressourcen liefert.

Es gibt noch weitere bekannte Heuristiken, und wenn Sie einen sehr guten zusammenfattenden Überblick darüber wünschen, was es braucht, um eine moderne lokale Suchmaschine zu implementieren, können Sie das Papier “LocalSolver: A Black-Box Local-Search Solver for 0-1 Programs” lesen. Das Unternehmen, das LocalSolver betreibt, hat auch ein Produkt mit demselben Namen. In diesem Papier geben sie einen technisch orientierten Einblick in das, was unter der Haube ihres produktionsreifen Solvers vor sich geht. Sie verwenden Multi-Start und Simulated Annealing, um bessere Ergebnisse zu erzielen.

Ein Vorbehalt, den ich bezüglich der lokalen Suche hinzufügen möchte, ist, dass sie mit stochastischen Problemen nicht sehr gut bzw. nativ zurechtkommt. Bei stochastischen Problemen ist es nicht so einfach, lediglich zu sagen “Ich habe eine bessere Lösung” und sofort zu entscheiden, dass dies die beste Lösung ist. Es ist komplizierter, und Sie müssen etwas mehr Aufwand betreiben, bevor Sie von der als neu beste beurteilten Lösung springen.

Nun wollen wir uns der zweiten Klasse von Solvern zuwenden, über die wir heute sprechen werden, nämlich der differentiable Programmierung. Aber zuerst müssen wir, um differentiable Programmierung zu verstehen, den stochastischen Gradientenabstieg begreifen.

Der stochastische Gradientenabstieg geht davon aus, dass die Verlustfunktion additiv in eine Reihe von Komponenten zerlegt werden kann. In der Gleichung repräsentiert Q(W) die Verlustfunktion, die in eine Reihe von Teilfunktionen Qi zerlegt wird. Dies ist relevant, weil die meisten Lernprobleme darin bestehen, aus einer Serie von Beispielen eine Vorhersage zu erlernen. Die Idee ist, dass Sie Ihre Verlustfunktion als den durchschnittlichen Fehler, der über den gesamten Datensatz begangen wird, zerlegen können, mit einem lokalen Fehler für jeden Datenpunkt. Viele supply chain Probleme können auf diese Weise additiv zerlegt werden. Zum Beispiel können Sie Ihr supply chain Netzwerk in eine Reihe von Leistungen für jede einzelne SKU zerlegen, wobei an jeder SKU eine Verlustfunktion hängt. Die tatsächliche Verlustfunktion, die Sie optimieren möchten, ist die Gesamtsumme.

Wenn Sie diese Dekomposition eingerichtet haben, was bei Lernproblemen sehr selbstverständlich ist, können Sie mit dem stochastischen Gradientenabstiegsprozess (SGD) iterieren. Der Parametervektor W kann eine sehr große Reihe sein, da die größten Deep-Learning-Modelle eine Billion Parameter haben. Die Idee ist, dass Sie bei jedem Schritt des Prozesses Ihre Parameter aktualisieren, indem Sie eine kleine Menge des Gradienten anwenden. Eta ist die Lernrate, eine kleine Zahl, typischerweise zwischen 0 und 1, oft um 0,01. Nabla von Q ist der Gradient der partiellen Verlustfunktion Qi. Überraschenderweise funktioniert dieser Prozess gut.

SGD wird als stochastisch bezeichnet, weil Sie zufällig Ihr nächstes i-Element auswählen, durch Ihr Datenset springen und bei jedem einzelnen Schritt eine winzige Menge Gradienten auf Ihre Parameter anwenden. Das ist das Wesen des stochastischen Gradientenabstiegs.

Es blieb fast sechs Jahrzehnte lang relativ nischig und wurde von der breiten Gemeinschaft weitgehend ignoriert, da es durchaus überraschend ist, dass stochastischer Gradientenabstieg überhaupt funktioniert. Er funktioniert, weil er einen hervorragenden Trade-off zwischen dem Rauschen in der Verlustfunktion und den Rechenkosten für den Zugriff auf die Verlustfunktion selbst bietet. Anstatt eine Verlustfunktion zu haben, die gegen das gesamte Datenset bewertet werden muss, können wir mit stochastischem Gradientenabstieg einen Datenpunkt nach dem anderen verwenden und dennoch einen kleinen Gradienten anwenden. Diese Messung wird sehr fragmentarisch und verrauscht sein, doch dieses Rauschen ist tatsächlich in Ordnung, weil es sehr schnell ist. Sie können um Größenordnungen mehr winzige, verrauschte Optimierungen durchführen, als es das Verarbeiten des gesamten Datensets zulässt.

Überraschenderweise hilft das eingeführte Rauschen dem Gradientenabstieg. Eines der Probleme in hochdimensionalen Räumen ist, dass lokale Minima nahezu nicht existieren. Dennoch können Sie auf große Plateaubereiche stoßen, in denen der Gradient sehr klein ist und der Gradientenabstieg keine klare Absteigtrichtung hat. Das Rauschen liefert Ihnen steilere, verrauschte Gradienten, die beim Abstieg helfen.

Was am Gradientenabstieg ebenfalls interessant ist, ist, dass es ein stochastischer Prozess ist, der stochastische Probleme ohne zusätzlichen Aufwand bewältigen kann. Wenn Qi eine stochastische Funktion mit Rauschen ist und bei jeder Auswertung ein zufälliges, variierendes Ergebnis liefert, müssen Sie nicht einmal eine einzige Zeile des Algorithmus ändern. Der stochastische Gradientenabstieg ist von herausragendem Interesse, da er Ihnen etwas bietet, das vollständig im Einklang mit dem Paradigma steht, das für supply chain Zwecke relevant ist.

Die zweite Frage lautet: Woher kommt der Gradient? Wir haben ein Programm und nehmen einfach den Gradienten der partiellen Verlustfunktion, aber woher stammt dieser Gradient? Wie erhält man einen Gradienten für ein beliebiges Programm? Es stellt sich heraus, dass es eine sehr elegante, minimalistische Technik gibt, die bereits vor langer Zeit entdeckt wurde und als automatische Differenzierung bezeichnet wird.

Die automatische Differenzierung entstand in den 1960er Jahren und wurde im Laufe der Zeit verfeinert. Es gibt zwei Arten: den Vorwärtsmodus, der 1964 entdeckt wurde, und den Rückwärtsmodus, der 1980 entdeckt wurde. Die automatische Differenzierung kann als ein Kompilierungstrick betrachtet werden. Die Idee ist, dass Sie ein Programm zum Kompilieren haben, das Ihre Verlustfunktion darstellt. Sie können dieses Programm neu kompilieren, um ein zweites Programm zu erhalten, dessen Ausgabe nicht die Verlustfunktion, sondern die Gradienten aller an der Berechnung der Verlustfunktion beteiligten Parameter ist.

Darüber hinaus liefert die automatische Differenzierung Ihnen ein zweites Programm mit einer Rechenkomplexität, die im Grunde identisch mit der Ihres ursprünglichen Programms ist. Das bedeutet, dass Sie nicht nur einen Weg haben, ein zweites Programm zu erstellen, das die Gradienten berechnet, sondern dass auch dieses zweite Programm dieselben rechentechnischen Eigenschaften in Bezug auf die Leistung wie das erste besitzt. Es ist eine konstante Faktor-Inflation in Bezug auf die Rechenkosten. In Wirklichkeit hat das erhaltene zweite Programm jedoch nicht exakt die gleichen Speichereigenschaften wie das ursprüngliche Programm. Obwohl die Details den Rahmen dieser Vorlesung sprengen, können wir diese während der Fragen besprechen. Im Wesentlichen wird das zweite Programm, der sogenannte Rückwärtsmodus, mehr Speicher benötigen und in einigen pathologischen Situationen sogar erheblich mehr als das ursprüngliche Programm. Bedenken Sie, dass mehr Speicher Probleme bei der Rechenleistung verursacht, da ein einheitlicher Speicherzugriff nicht vorausgesetzt werden kann.

Um ein wenig zu veranschaulichen, wie die automatische Differenzierung aussieht, gibt es, wie erwähnt, zwei Modi: Vorwärts- und Rückwärtsmodus. Aus der Perspektive des Lernens oder der supply chain Optimierung ist für uns nur der Rückwärtsmodus von Interesse. Was Sie auf dem Bildschirm sehen, ist eine erfundene Verlustfunktion F. Sie erkennen die Vorwärtsspur, eine Abfolge von arithmetischen oder elementaren Operationen, die durchgeführt werden, um Ihre Funktion für zwei gegebene Eingabewerte, X1 und X2, zu berechnen. Dies zeigt alle grundlegenden Schritte, die zur Berechnung des Endwerts ausgeführt werden.

Die Idee ist, dass für jeden elementaren Schritt – und die meisten davon sind nur grundlegende arithmetische Operationen wie Multiplikation oder Addition – der Rückwärtsmodus ein Programm ist, das dieselben Schritte, aber in umgekehrter Reihenfolge ausführt. Anstatt der Vorwärtswerte erhalten Sie die Adjungierten. Für jede arithmetische Operation gibt es ein entsprechendes rückwärtiges Gegenstück. Der Übergang von der Vorwärtsoperation zu diesem Gegenstück ist sehr einfach.

Auch wenn es kompliziert aussieht, haben Sie eine Vorwärts- und eine Rückwärtsausführung, wobei Ihre Rückwärtsausführung nichts anderes als eine elementare Transformation ist, die auf jede einzelne Operation angewendet wird. Am Ende der Rückwärtsausführung erhalten Sie die Gradienten. Die automatische Differenzierung mag kompliziert erscheinen, ist es aber nicht. Unser erster implementierter Prototyp umfasste weniger als 100 Codezeilen, sodass er sehr einfach und im Wesentlichen ein kostengünstiger Transpilations-Trick ist.

Nun ist das interessant, denn wir haben den stochastischen Gradientenabstieg, einen fantastischen und leistungsstarken Optimierungsmechanismus. Er ist unglaublich skalierbar, online, whiteboardfähig und funktioniert nativ mit stochastischen Problemen. Das einzige verbleibende Problem war, wie man den Gradienten erhält, und mit der automatischen Differenzierung bekommen wir den Gradienten zu einem festen Overhead oder konstanten Faktor für praktisch jedes beliebige Programm. Am Ende erhalten wir das, was man differenzierbares Programmieren nennt.

Interessanterweise ist differenzierbares Programmieren eine Kombination aus stochastischem Gradientenabstieg und automatischer Differenzierung. Obwohl diese beiden Techniken – stochastischer Gradientenabstieg und automatische Differenzierung – Jahrzehnte alt sind, wurde differenzierbares Programmieren erst Anfang 2018 populär, als Yann LeCun, Head of AI bei Facebook, begann, über dieses Konzept zu sprechen. LeCun hat dieses Konzept nicht erfunden, war aber maßgeblich daran beteiligt, es populär zu machen.

Zum Beispiel verwendete die Deep-Learning-Community zunächst Backpropagation anstelle der automatischen Differenzierung. Für diejenigen, die mit neuronalen Netzen vertraut sind, ist Backpropagation ein komplexer Prozess, der um Größenordnungen komplizierter umzusetzen ist als die automatische Differenzierung. Diese ist in jeder Hinsicht überlegen. Mit diesem Wissen verfeinerte die Deep-Learning-Community ihr Verständnis dessen, was Lernen im Deep Learning ausmacht. Deep Learning kombinierte mathematische Optimierung mit verschiedenen Lerntechniken, und differenzierbares Programmieren entstand als ein klares Konzept, das die nicht-lernenden Teile des Deep Learning isoliert.

Moderne Deep-Learning-Techniken, wie das Transformer-Modell, setzen eine differenzierbare Programmierumgebung zugrunde voraus. Dies ermöglicht es den Forschern, sich auf die Lernaspekte zu konzentrieren, die darauf aufbauen. Differenzierbares Programmieren, obwohl es die Grundlage des Deep Learning bildet, ist auch hochrelevant für die supply chain Optimierung und die Unterstützung supply chain Lernprozesse, wie statistische Prognosen.

Genau wie im Deep Learning gibt es zwei Bestandteile des Problems: differenzierbares Programmieren als Basisschicht und Optimierungs- oder Lerntechniken darauf aufbauend. Die Deep-Learning-Community strebt danach, Architekturen zu identifizieren, die gut mit differenzierbarem Programmieren funktionieren, wie etwa Transformer. Ebenso muss man die Architekturen finden, die für Optimierungszwecke gut geeignet sind. Genau das wurde gemacht, um zu lernen, wie man Go oder Schach in hoch kombinatorischen Umgebungen spielt. In späteren Vorlesungen werden wir Techniken besprechen, die speziell für supply chain Optimierung funktionieren.

Aber nun ist es Zeit, zum Schluss zu kommen. Ein erheblicher Teil der supply chain Literatur und selbst die meisten Softwareimplementierungen sind sehr verwirrt, wenn es um mathematische Optimierung geht. Dieser Aspekt wird meist nicht einmal korrekt als solcher identifiziert, und infolgedessen vermischen Praktiker, Forscher und sogar Softwareingenieure, die für enterprise software Unternehmen arbeiten, mathematische Optimierung oft ziemlich willkürlich in ihre numerischen Rezepte. Sie haben ein großes Problem, denn eine Komponente wird nicht als Teil der mathematischen Optimierung erkannt, und da die Menschen gar nicht wissen, was in der Literatur zur Verfügung steht, greifen sie oft zu groben Gittersuchen oder übereilten Heuristiken, die zu unregelmäßigen und inkonsistenten Ergebnissen führen. Als Fazit dieser Vorlesung: Wann immer Sie zukünftig auf eine supply chain numerische Methode oder supply chain Software stoßen, die irgendeine Art analytischer Funktion verspricht, müssen Sie sich fragen, was in Bezug auf mathematische Optimierung geschieht und was getan wird. Wenn Sie feststellen, dass die Anbieter keine kristallklare Sicht auf diese Perspektive bieten, stehen die Chancen gut, dass Sie sich auf der linken Seite der Darstellung befinden – und das ist nicht der Platz, an dem Sie sein möchten.

Nun schauen wir uns die Fragen an.

Frage: Ist der Übergang zu computergestützten Methoden eine notwendige Fähigkeit im operativen Bereich, und würden operative Rollen obsolet werden, oder umgekehrt?

Zunächst möchte ich ein paar Dinge klarstellen. Ich glaube, es ist ein Fehler, solche Bedenken auf den CIO zu schieben. Die Leute erwarten viel zu viel von ihren CIOs. Als Chief Information Officer müssen Sie sich bereits mit der Basis Ihrer Softwareinfrastruktur befassen – wie Rechenressourcen, Transaktionssystemen auf niedriger Ebene, Netzwerkintegrität und Cybersicherheit. Von einem CIO wird nicht erwartet, dass er versteht, was es wirklich braucht, um etwas Wertvolles für Ihre supply chain zu leisten.

Das Problem ist, dass in vielen Unternehmen die Menschen so verzweifelt unwissend in Bezug auf alles Computergestützte sind, dass der CIO zur Anlaufstelle für alles wird. Die Realität ist, dass sich der CIO um die Basisschicht der Infrastruktur kümmern sollte, und dann ist es Aufgabe des jeweiligen Spezialisten, seine spezifischen Bedürfnisse mit den verfügbaren Rechenressourcen und Softwarewerkzeugen zu adressieren.

Bezüglich des Auslaufens operativer Rollen: Wenn Ihre Aufgabe darin besteht, den ganzen Tag manuell Excel Tabellenkalkulationen durchzugehen, wird Ihre Rolle sehr wahrscheinlich obsolet. Dies ist ein bekanntes Problem seit 1979, als Russell Ackoff sein Papier veröffentlichte. Das Problem ist, dass die Menschen wussten, dass diese Methode der Entscheidungsfindung nicht die Zukunft war, sie jedoch lange Zeit Status quo blieb. Der Kern des Problems ist, dass Unternehmen den experimentellen Prozess verstehen müssen. Ich glaube, es wird einen Übergang geben, in dem Unternehmen diese Fähigkeiten wieder erwerben. Viele große nordamerikanische Unternehmen verfügten nach dem Zweiten Weltkrieg unter ihren Führungskräften über Kenntnisse im Bereich Operations Research. Es war ein brandaktuelles Thema, und die Vorstände großer Unternehmen waren mit Operations Research vertraut. Wie Russell Ackoff feststellte, wurden diese Ideen aufgrund mangelnder Ergebnisse immer weiter in der Unternehmenshierarchie nach unten gedrängt, bis sie schließlich sogar komplett ausgelagert wurden, da sie größtenteils irrelevant waren und keine greifbaren Ergebnisse lieferten. Ich glaube, dass Operations Research nur dann zurückkehren wird, wenn die Menschen die Lehren daraus ziehen, warum die klassische Ära des Operations Research keine Ergebnisse lieferte. Der CIO wird in diesem Unterfangen nur einen bescheidenen Beitrag leisten; es geht hauptsächlich darum, den Mehrwert der Menschen im Unternehmen neu zu überdenken.

Sie möchten einen kapitalistischen Beitrag leisten, und das führt zurück zu einer meiner früheren Vorlesungen über produktorientierte Lieferung im Sinne von Softwareprodukten für supply chains. Der Kern ist: Welchen kapitalistischen Mehrwert liefern Sie Ihrem Unternehmen? Wenn die Antwort „keinen“ Mehrwert darstellt, dann gehören Sie möglicherweise nicht zu dem, was Ihr Unternehmen in Zukunft sein sollte und wird.

Frage: Was ist mit der Verwendung des Excel-Solvers, um den MRMSC-Wert zu minimieren und den optimalen Wert für Alpha, Beta und Gamma zu finden?

Ich glaube, dass diese Frage im Holt-Winters-Fall relevant ist, bei dem Sie mithilfe einer Gittersuche tatsächlich eine Lösung finden können. Aber was passiert in diesem Excel-Solver? Handelt es sich um einen Gradientenabstieg oder etwas anderes? Wenn Sie sich auf den linearen Solver von Excel beziehen, so handelt es sich nicht um ein lineares Problem, sodass Excel in diesem Fall nichts für Sie tun kann. Falls Sie andere Solver in Excel oder Add-ins haben, ja, diese können arbeiten – aber diese Perspektive ist sehr veraltet. Sie greift nicht eine stochastischere Sichtweise auf; die Art von Prognose, die Sie erhalten, ist eine nicht-probabilistische Prognose, was ein veralteter Ansatz ist.

Ich sage nicht, dass Excel nicht verwendet werden kann, aber die Frage ist, welche Programmierfähigkeiten in Excel freigeschaltet werden. Können Sie in Excel stochastischen Gradientenabstieg durchführen? Wahrscheinlich, wenn Sie ein dediziertes Add-in hinzufügen. Excel erlaubt es Ihnen, beliebige Programme darauf zu installieren. Könnten Sie potenziell differenzierbares Programmieren in Excel umsetzen? Ja. Ist es eine gute Idee, dies in Excel zu tun? Nein. Um zu verstehen, warum, müssen Sie zum Konzept der produktorientierten Softwarelieferung zurückkehren, das detailliert, was mit Excel schief läuft. Es läuft letztlich auf das Programmiermodell hinaus und darauf, ob Sie Ihre Arbeit langfristig im Team tatsächlich aufrechterhalten können.

Frage: Optimierungsprobleme neigen typischerweise in Richtung Fahrzeugrouting oder Prognosen. Warum sollte man nicht auch die gesamte supply chain optimieren? Würde das nicht die Kosten senken, verglichen mit dem isolierten Blick auf einzelne Bereiche?

Ich stimme völlig zu. Der Fluch der supply chain Optimierung liegt darin, dass, wenn man eine lokale Optimierung an einem Teilproblem durchführt, man höchstwahrscheinlich das Problem verlagert, statt es für die gesamte supply chain zu lösen. Ich stimme völlig zu, und sobald man beginnt, sich ein komplexeres Problem anzusehen, handelt es sich um ein hybrides Problem – zum Beispiel ein Fahrzeug-Routing-Problem kombiniert mit einer Auffüllung Strategie. Das Problem ist, dass man einen sehr generischen Solver benötigt, um sich diesem zu nähern, weil man nicht eingeschränkt werden möchte. Wenn man einen sehr generischen Solver besitzt, muss man sehr generische Mechanismen haben, anstatt sich auf clevere Heuristiken wie das Zwei-Opt zu verlassen, das nur gut beim Fahrzeug-Routing funktioniert und nicht für etwas, das gleichzeitig ein Hybrid aus Auffüllung und Fahrzeug-Routing ist.

Um zu dieser ganzheitlichen Perspektive überzugehen, darf man sich nicht vor dem Fluch der Dimensionalität fürchten. Vor zwanzig Jahren sagte man, dass diese Probleme bereits extrem schwer und NP-vollständig sind – wie das Problem des Handlungsreisenden –, und man möchte ein noch schwierigeres Problem lösen, indem man es mit einem anderen verknüpft. Die Antwort lautet ja; man will dazu in der Lage sein, und deshalb ist es essenziell, einen Solver zu haben, der es ermöglicht, mit beliebigen Programmen umzugehen, weil Ihre Lösung möglicherweise die Konsolidierung vieler verwobener und ineinandergreifender Probleme darstellt.

Tatsächlich ist die Idee, diese Probleme isoliert zu lösen, viel schwächer, als alles zusammen anzugehen. Es ist besser, annähernd korrekt zu sein, als exakt falsch. Es ist viel besser, einen sehr schwachen Solver zu haben, der die gesamte supply chain als ein System, als einen Block angeht, anstatt fortschrittliche lokale Optimierungen vorzunehmen, die lediglich an anderer Stelle Probleme verursachen, während man lokal mikro-optimiert. Die wahre Optimierung des Systems ist nicht zwangsläufig die optimale Optimierung jedes einzelnen Teils, weshalb es natürlich ist, dass, wenn Sie im Interesse des gesamten Unternehmens und seiner gesamten supply chain optimieren, dies nicht lokal optimal sein wird, da Sie auch die anderen Aspekte des Unternehmens und seiner supply chain berücksichtigen.

Frage: Nach Durchführung einer Optimierungsübung, wann sollten wir das Szenario erneut betrachten, wenn jederzeit neue Einschränkungen auftreten können? Die Antwort lautet, dass Sie die Optimierung regelmäßig überprüfen sollten. Dies ist die Rolle des Supply Chain Scientist, den ich in der zweiten Vorlesung dieser Reihe vorgestellt habe. Der Supply Chain Scientist wird die Optimierung so oft wie nötig wiederholen. Wenn eine neue Einschränkung auftritt, wie ein gigantisches Schiff, das den Suezkanal blockiert – etwas Unerwartetes –, müssen Sie mit dieser Störung in Ihrer supply chain umgehen. Sie haben keine andere Option, als diese Probleme anzugehen; andernfalls wird das von Ihnen eingerichtete System unsinnige Ergebnisse erzeugen, weil es unter falschen Bedingungen arbeitet. Selbst wenn kein Notfall vorliegt, möchten Sie dennoch Ihre Zeit investieren, um den Ansatz zu finden, der mit hoher Wahrscheinlichkeit den größten Ertrag für das Unternehmen bringt. Dies ist im Grunde Forschung und Entwicklung. Sie haben das System eingerichtet, es arbeitet, und Sie versuchen lediglich, Bereiche zu identifizieren, in denen Sie das System verbessern können. Es wird zu einem angewandten Forschungsprozess, der stark kapitalistisch und unbeständig verläuft. Als Supply Chain Scientist gibt es Tage, an denen Sie den ganzen Tag numerische Methoden testen, von denen keine bessere Ergebnisse liefern als das, was Sie bereits haben. An manchen Tagen nehmen Sie eine winzige Anpassung vor und haben großes Glück, wodurch das Unternehmen Millionen spart. Es ist ein unbeständiger Prozess, aber im Durchschnitt kann das Ergebnis enorm sein.

Frage: Was wären die Anwendungsfälle für Optimierungsprobleme außer der linearen Programmierung, der ganzzahligen Programmierung, der gemischten Programmierung und im Fall von Weber und Kosten der Güter?

Ich würde die Frage umdrehen: Wo sehen Sie, dass lineare Programmierung irgendeine Relevanz für ein supply chain Problem hat? Es gibt praktisch kein supply chain Problem, das linear ist. Mein Einwand ist, dass diese Rahmenwerke sehr simpel sind und nicht einmal an Spielzeugprobleme herankommen. Wie ich bereits sagte, können diese mathematischen Rahmenwerke, wie die lineare Programmierung, nicht einmal an ein Spielzeugproblem wie die harte Winteroptimierung für ein altes, niedrigdimensionales parametrisches Prognosemodell herankommen. Sie können nicht einmal mit dem Problem des Handlungsreisenden oder so ziemlich irgendetwas anderem umgehen.

Ganzzahlige Programmierung oder gemischt-ganzzahlige Programmierung ist nur ein generischer Begriff dafür, dass einige der Variablen ganze Zahlen sein werden, aber das ändert nichts daran, dass diese Programmier-Rahmenwerke lediglich mathematische Spielereien sind, die bei weitem nicht die Ausdruckskraft besitzen, die benötigt wird, um supply chain Probleme zu bewältigen.

Wenn Sie nach den Anwendungsfällen von Optimierungsproblemen fragen, lade ich Sie ein, sich alle meine Vorlesungen über supply chain personas anzusehen. Wir haben bereits eine Reihe von supply chain personas, und ich liste buchstäblich Unmengen von Problemen auf, die mit mathematischer Optimierung angegangen werden können. In den Vorlesungen über die supply chain personas haben wir Paris, Miami, Amsterdam und eine World Series, und es kommen noch weitere hinzu. Wir haben viele Probleme, die angegangen werden müssen und es verdienen, aus einer ordentlichen mathematischen Optimierungsperspektive betrachtet zu werden. Allerdings werden Sie feststellen, dass Sie keines dieser Probleme in die super engen und meist bizarren Einschränkungen einrahmen können, die sich aus diesen mathematischen Rahmenwerken ergeben. Nochmals: Diese Rahmenwerke drehen sich größtenteils um Konvexität, und das ist nicht die richtige Perspektive für supply chain. Die meisten der von uns behandelten Punkte sind nicht-konvex. Aber das ist in Ordnung; es ist nicht so, dass sie wegen ihrer Nichtkonvexität unmöglich schwer sind. Es ist einfach so, dass Sie am Ende des Tages keinen mathematischen Beweis vorlegen können. Aber Ihr Chef oder Ihr Unternehmen interessiert sich für den Profit, nicht dafür, ob Sie einen mathematischen Beweis zur Unterstützung Ihrer Entscheidung haben. Es geht darum, dass Sie die richtige Entscheidung in Bezug auf Produktion, Auffüllung, Preise, Sortimente und Ähnliches treffen – nicht darum, dass Sie einen math. Beweis an diese Entscheidungen knüpfen.

Frage: Wie lange sollten die Daten des Lernalgorithmus gespeichert werden, um beim Lernen zu unterstützen?

Nun, ich würde sagen, wenn man bedenkt, dass die Datenspeicherung heutzutage unglaublich günstig ist, warum sollte man sie nicht für immer behalten? Datenspeicherung ist so preiswert; gehen Sie zum Beispiel in einen Supermarkt, und Sie werden feststellen, dass der Preis für eine Festplatte mit einem Terabyte ungefähr bei 60 liegt oder so ähnlich. Also, sie ist unglaublich günstig.

Natürlich gibt es das separate Anliegen, dass, wenn in Ihren Daten persönliche Informationen enthalten sind, die gespeicherten Daten zu einer Belastung werden. Aber aus der Perspektive der supply chain, wenn wir davon ausgehen, dass Sie zuerst alle persönlichen Daten entfernt haben – da Sie diese in der Regel gar nicht benötigen – müssen Sie weder Kreditkartennummern noch die Namen Ihrer Kunden aufbewahren. Sie benötigen lediglich Kundenkennungen und Ähnliches. Entfernen Sie also alle persönlichen Daten aus Ihren Daten, und ich würde sagen: Wie lange? Nun, behalten Sie sie für immer.

Einer der Punkte in der supply chain ist, dass Sie nur begrenzte Daten haben. Es ist nicht wie bei Deep-Learning-Problemen wie der Bilderkennung, bei denen Sie fast unendlich viele Bilder aus dem Web verarbeiten und auf riesige Datenbanken zugreifen können. In der supply chain sind Ihre Daten immer begrenzt. Tatsächlich gibt es nur sehr wenige Branchen, in denen es statistisch relevant ist, mehr als ein Jahrzehnt in die Vergangenheit zu blicken, um die Nachfrage fürs nächste Quartal vorherzusagen. Dennoch würde ich sagen, dass es immer einfacher ist, die Daten zu kürzen, wenn Sie sie benötigen, als festzustellen, dass Sie Daten verworfen haben, die nun fehlen. Daher mein Vorschlag: Bewahren Sie alles auf, entfernen Sie die persönlichen Daten, und ganz am Ende Ihrer data pipeline werden Sie sehen, ob es besser ist, die sehr alten Daten herauszufiltern. Es könnte sinnvoll sein, muss es aber nicht – es hängt von der Branche ab, in der Sie tätig sind. Zum Beispiel in der Luft- und Raumfahrt, wo Sie Teile und Flugzeuge mit einer Betriebsdauer von vier Jahrzehnten haben, sind Daten der letzten vier Jahrzehnte in Ihrem System von Relevanz.

Frage: Ist die Mehrzielprogrammierung eine Funktion von zwei oder mehr Zielvorgaben, wie etwa der Summe oder der Minimierung mehrerer Funktionen in einem Ziel?

Es gibt mehrere Varianten, wie man Mehrzielsetzungen angehen kann. Es geht nicht darum, eine Funktion als Summe zu haben, denn wenn Sie die Summe haben, dann handelt es sich lediglich um eine Frage der Zerlegung und Struktur der Verlustfunktion. Nein, es geht vielmehr darum, einen Vektor zu haben. Tatsächlich gibt es im Wesentlichen mehrere Ausprägungen der Mehrzielprogrammierung. Die interessanteste Variante ist diejenige, bei der man eine lexikographische Ordnung anstrebt. Was die supply chain betrifft, könnte die Minimierung – wenn man beispielsweise den Mittelwert oder das Maximum der vielen Funktionen betrachtet – von Interesse sein, aber ich bin mir nicht ganz sicher. Ich glaube, dass der mehrzielige Ansatz, bei dem Sie tatsächlich Einschränkungen einbringen und diese als Teil Ihrer regulären Optimierung behandeln können, von großem Interesse für supply chain Zwecke ist. Die anderen Varianten könnten ebenfalls interessant sein, aber ich bin mir nicht so sicher. Ich sage nicht, dass sie es nicht sind; ich sage nur, dass ich mir nicht sicher bin.

Frage: Wie würden Sie entscheiden, wann man eine approximative Lösung gegenüber der optimierten Lösung einsetzt?

Ich bin mir nicht ganz sicher, ob ich die Frage richtig verstehe. Die Idee ist, dass, wenn es eine Lehre aus dem Deep Learning gibt, es keine optimale Lösung gibt. Alles ist bis zu einem gewissen Grad eine Approximation. Selbst wenn Sie Zahlen haben, kommen diese in Computern nicht mit unendlicher, sondern mit endlicher Präzision, und diese endliche Präzision kann unter Umständen zu Problemen führen. Die Antwort lautet also, dass alles immer approximativ ist. Ich würde sagen, die wichtigste Erkenntnis ist, dass es eine Illusion ist zu denken, dass es überhaupt eine perfekte Lösung gibt. Eine perfekte, optimale Lösung existiert nicht. Alle Lösungen, die Sie haben, sind Approximationen, von denen einige, würde ich sagen, etwas weniger oder mehr approximativ sind. Ich bin mir zwar nicht ganz sicher, worauf Ihre Frage abzielt, aber aus der Perspektive der mathematischen Optimierung heißt das, dass Sie eine Verlustfunktion haben, um die Qualität zu bewerten, und am Ende, wenn Sie zwei konkurrierende Lösungen haben, verwenden Sie Ihre Verlustfunktion, um zu beurteilen, welche die beste ist. So funktioniert es.

Frage: Warum wurde die Zeitreihe, bezogen auf historische Daten, ursprünglich durch 86.400 geteilt?

Das wurde nicht so gemacht. Es war ein Beispiel. Ich wollte lediglich die Situation skizzieren und ins Absurde führen, indem ich zeige, dass, wenn Sie sich einer Zeitreihe zuwenden – einem klassischen Algorithmus zur Zeitreihenprognose – Sie das anwenden, was als äquidistante Zeitreihe bekannt ist. Es gibt viele Möglichkeiten, Zeitreihen darzustellen, und die typischste Art ist die äquidistante Variante, bei der Sie in gleich lange Intervalle aggregieren. Das ist typischerweise das, was Sie bei täglichen oder wöchentlichen Aggregationen erhalten: Intervalle gleicher Länge und eine schön vektorartige Struktur der Reihe.

Aber was ich hervorheben möchte, ist, dass dies in großem Maße willkürlich ist. Sie können sich entscheiden, Daten als Tagesdaten darzustellen, Sie könnten aber auch Daten sekundenweise darstellen. Ergäbe es jemals Sinn, Daten sekundenweise darzustellen? Die Antwort ist ja; es hängt von der Art der Probleme ab. Zum Beispiel, wenn Sie ein Stromanbieter sind und ein Netz verwalten möchten, müssen Sie die Leistung in jeder Sekunde steuern, damit Sie genau das Gleichgewicht zwischen der Stromversorgung in Ihrem Netz und dem Verbrauch erreichen. Und dieses Gleichgewicht wird tatsächlich sekündlich abgestimmt. Es mag also Situationen geben, in denen es sinnvoll ist, Daten sekundenweise darzustellen. Für den Verkauf in Ihrem lokalen Geschäft mag das jedoch wenig sinnvoll sein. Was ich mit den 86.400 – übrigens: 24 Stunden mal 60 Minuten mal 60 Sekunden – betonen wollte, ist, dass Sie immer eine Darstellung Ihrer Daten haben, und dass Sie die Darstellung Ihrer Daten, die eine bestimmte Dimensionalität aufweist, nicht mit der intrinsischen Dimension Ihrer Daten verwechseln sollten, die völlig anders sein kann. Die Darstellung ist weitgehend willkürlich und konstruiert. Sie liefert Ihnen einen numerischen Indikator, wie etwa drei Jahre Daten, sodass Sie einen Vektor der Dimension eintausend erhalten. Aber dieses „eintausend“ ist weitgehend willkürlich, da es auf der Entscheidung beruht, Daten täglich zu aggregieren. Würden Sie eine andere Aggregationsperiode wählen, bekämen Sie eine andere Dimension. Das ist der Punkt, den ich machen wollte, und das hat Deep Learning wirklich richtig erkannt: Solche Ansätze, bei denen man nicht von willkürlichen Darstellungsentscheidungen der Daten getäuscht wird. Man möchte gewissermaßen darstellungsagnostisch sein.

Frage: Indem wir die probabilistische Vorhersage einführen, wechseln wir zu einer Kostenfunktion und zu Einschränkungen, die ihrer Natur nach probabilistisch sind. Welche Auswirkungen hat das auf den Prozess der Lösungsfindung?

Nun, das bringt eine sehr grundlegende und fundamentale Einschränkung mit sich. Wenn Sie einen Solver haben, der Probleme nicht verarbeiten kann – und denken Sie daran, dass Sie immer von einem stochastischen Problem zu einem deterministischen zurückgehen können, indem Sie Ihre Ergebnisse über eine sehr große Anzahl von Stichproben mitteln – dann geraten Sie in Bezug auf die Rechenkosten in Schwierigkeiten. Das bedeutet, dass Sie etwa 10.000-mal mehr Rechenleistung aufwenden müssen, um zu einer zufriedenstellenden Lösung zu gelangen, im Vergleich zu einer alternativen Methode. Die Konsequenz ist, dass Sie wirklich sicherstellen müssen, dass Ihre mathematische Optimierungs-Infrastruktur, Ihr Tooling, von vornherein in der Lage ist, mit stochastischen Problemen umzugehen. Genau das erhalten Sie mit differentiable programming, weniger mit lokaler Suche, die Sie aber so erweitern oder anpassen können, dass sie in solchen Situationen flüssiger arbeitet.

Grundsätzlich, wenn man probabilistische Prognosen verfolgt, fordert es nicht nur die Art und Weise heraus, wie man in die Zukunft blickt; es fordert auch in tiefgreifender Weise die Art von Werkzeugen und Instrumentierung heraus, die man benötigt, um mit diesen Prognosen zu arbeiten. Genau diese Art von Werkzeugen hat Lokad im letzten Jahrzehnt entwickelt. Der Grund ist, dass wir Werkzeuge benötigen, die gut mit den stochastischen Problemen umgehen können, die zwangsläufig in der supply chain auftreten, denn nahezu alle Probleme in supply chains enthalten ein Element der Unsicherheit und befassen sich somit alle in gewissem Maße mit einem stochastischen Problem.

Ausgezeichnet. Also, die nächste Vorlesung wird am gleichen Wochentag stattfinden, an einem Mittwoch. Zwischen jetzt und dann wird es etwas Urlaub geben. Die nächste Vorlesung findet am 22. September statt, und ich hoffe, euch alle zu sehen. Dieses Mal werden wir maschinelles Lernen für die supply chain besprechen. Bis dann.

Referenzen

• Die Zukunft der Operationsforschung ist Vergangenheit, Russell L. Ackoff, Februar 1979
• LocalSolver 1.x: Ein Black-Box-Local-Search-Solver für 0-1-Programmierung, Thierry Benoist, Bertrand Estellon, Frédéric Gardi, Romain Megel, Karim Nouioua , September 2011
• Automatische Differenzierung im maschinellen Lernen: eine Übersicht, Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind, zuletzt überarbeitet im Februar 2018