Strukturierte prädiktive Modellierung für Supply Chain - Vorlesung 5.1

00:01 Einführung
02:44 Überblick über prädiktive Bedürfnisse
05:57 Modelle vs. Modellierung
12:26 Bisherige Geschichte
15:50 Etwas Theorie und etwas Praxis
17:41 Differenzierbares Programmieren, SGD 1/6
24:56 Differenzierbares Programmieren, Autodiff 2/6
31:07 Differenzierbares Programmieren, Funktionen 3/6
35:35 Differenzierbares Programmieren, Meta-Parameter 4/6
37:59 Differenzierbares Programmieren, Parameter 5/6
40:55 Differenzierbares Programmieren, Eigenheiten 6/6
43:41 Durchgang, Einzelhandels-Nachfrageprognose
45:49 Durchgang, Parameteranpassung 1/6
53:14 Durchgang, Parameterteilung 2/6
01:04:16 Durchgang, Verlustmaskierung 3/6
01:09:34 Durchgang, Kovariablenintegration 4/6
01:14:09 Durchgang, spärliche Zerlegung 5/6
01:21:17 Durchgang, freie Skalierung 6/6
01:25:14 Whiteboxing
01:33:22 Zurück zur experimentellen Optimierung
01:39:53 Fazit
01:44:40 Anstehende Vorlesung und Fragen des Publikums

Beschreibung

Differentiable Programming (DP) ist ein generatives Paradigma, das zur Entwicklung einer breiten Klasse statistischer Modelle eingesetzt wird, die sich hervorragend für prädiktive supply chain challenges eignen. DP setzte fast alle „klassischen“ Prognoseansätze, die auf parametrischen Modellen basieren, außer Kraft. DP ist auch den „klassischen“ machine learning Algorithmen – bis Ende der 2010er Jahre – in nahezu jeder Dimension, die für den praktischen Einsatz im supply chain wichtig ist, überlegen, einschließlich der einfachen Übernahme durch Praktiker.

Vollständiges Transkript

Willkommen zu dieser Reihe von supply chain Vorlesungen. Ich bin Joannes Vermorel, und heute präsentiere ich „Strukturierte prädiktive Modellierung mit Differenzierbarem Programmieren in Supply Chain.” Die Wahl der richtigen Handlungsstrategie erfordert detaillierte quantitative Einsichten in die Zukunft. Tatsächlich spiegelt jede Entscheidung – mehr zu kaufen, mehr zu produzieren – eine gewisse Erwartung der Zukunft wider. Unweigerlich betont die Mainstream supply chain Theorie den Begriff der Prognose zur Bewältigung genau dieses Problems. Allerdings ist die Prognoseperspektive, zumindest in ihrer klassischen Form, in zweierlei Hinsicht unzureichend.

Erstens legt sie einen engen Fokus auf Zeitreihenprognosen, der leider die Vielfalt der Herausforderungen in realen supply chains nicht abbildet. Zweitens konzentriert sie sich zu eng auf die Prognosegenauigkeit von Zeitreihen, was weitgehend an der eigentlichen Problematik vorbeigeht. Einige Prozentpunkte höhere Genauigkeit führen nicht automatisch zu einem zusätzlichen finanziellen Ertrag im supply chain.

Ziel der vorliegenden Vorlesung ist es, einen alternativen Ansatz zur Prognose zu entdecken, der teilweise eine Technologie und teilweise eine Methodik darstellt. Die Technologie wird differentiable programming (Differenzierbares Programmieren) sein, und die Methodik strukturierte prädiktive Modelle. Am Ende dieser Vorlesung sollten Sie in der Lage sein, diesen Ansatz auf eine supply chain Situation anzuwenden. Dieser Ansatz ist nicht theoretisch; er ist seit einigen Jahren der bewährte Standardansatz von Lokad. Falls Sie die vorherigen Vorlesungen nicht gesehen haben, sollte die vorliegende Vorlesung dennoch nicht völlig unverständlich sein. Allerdings kommen wir in dieser Vorlesungsreihe an den Punkt, an dem es sehr hilfreich ist, die Vorlesungen in ihrer Reihenfolge anzusehen. In der vorliegenden Vorlesung werden wir mehrere Elemente wieder aufgreifen, die in früheren Vorlesungen eingeführt wurden.

Die Prognose der zukünftigen Nachfrage ist der offensichtliche Kandidat, wenn es darum geht, den Überblick über die prädiktiven Bedürfnisse unserer supply chain zu gewinnen. Tatsächlich ist eine bessere Vorwegnahme der Nachfrage ein entscheidender Faktor für sehr grundlegende Entscheidungen wie mehr zu kaufen und mehr zu produzieren. Allerdings haben wir anhand der supply chain Prinzipien, die wir im Laufe des dritten Kapitels dieser Vorlesungsreihe eingeführt haben, gesehen, dass es eine ziemlich vielfältige Palette an Erwartungen in Bezug auf prädiktive Anforderungen gibt, um Ihre supply chain anzutreiben.

Insbesondere variieren zum Beispiel die Durchlaufzeiten und weisen saisonale Muster auf. Praktisch jede einzel inventory-bezogene Entscheidung erfordert eine Vorwegnahme sowohl der zukünftigen Nachfrage als auch der zukünftigen Durchlaufzeit. Daher müssen die Durchlaufzeiten prognostiziert werden. Retouren machen manchmal bis zur Hälfte des Volumens aus. Dies ist beispielsweise im Fashion-E-Commerce in Deutschland der Fall. In solchen Situationen wird das Vorhersagen der Retouren kritisch, und diese Retouren variieren erheblich von einem Produkt zum anderen. Daher müssen auch die Retouren prognostiziert werden.

Auf der Angebotsseite kann die Produktion selbst variieren, und das nicht nur aufgrund zusätzlicher Verzögerungen oder variierender Durchlaufzeiten. Beispielsweise kann die Produktion mit einem gewissen Maß an Unsicherheit verbunden sein. Dies tritt in Low-Tech-Bereichen wie der Landwirtschaft auf, aber auch in High-Tech-Sektoren wie der Pharmaindustrie kann es vorkommen. Daher müssen auch die Produktionsausbeuten prognostiziert werden. Schließlich spielt auch das Verhalten der Kunden eine große Rolle. So ist es zum Beispiel sehr wichtig, die Nachfrage durch Produkte anzukurbeln, die für die Kundengewinnung sorgen, und umgekehrt ist es von Bedeutung, Stockouts bei Produkten zu begegnen, die zu einem erheblichen Kundenverlust führen, wenn diese Produkte gerade aufgrund von Stockouts fehlen. Daher erfordern solche Verhaltensweisen Analyse und Vorhersage – mit anderen Worten, sie müssen prognostiziert werden. Das Wesentliche hier ist, dass die Zeitreihenprognose nur ein Teil des Puzzles ist. Wir brauchen einen prädiktiven Ansatz, der all diese Situationen und mehr abdecken kann, da dies eine Notwendigkeit ist, wenn wir einen Ansatz haben wollen, der auch bei all den Herausforderungen in realen supply chains eine Chance auf Erfolg hat.

Der bewährte Ansatz zur Lösung des prädiktiven Problems besteht darin, ein Modell zu präsentieren. Dieser Ansatz hat die Literatur zur Zeitreihenprognose seit Jahrzehnten dominiert und ist meiner Meinung nach immer noch der Mainstream in den Kreisen des machine learning. Dieser modellzentrierte Ansatz – darum werde ich diesen Ansatz nennen – ist so allgegenwärtig, dass es selbst schwierig sein kann, einen Moment innezuhalten, um zu beurteilen, was aus der modellzentrierten Perspektive wirklich geschieht.

Mein Vorschlag für diese Vorlesung ist, dass supply chain eine Modellierungstechnik, also eine modellzentrierte Perspektive, erfordert, und dass eine Reihe von Modellen, so umfangreich sie auch sein mögen, niemals ausreichen wird, um alle unsere Anforderungen, wie sie in realen supply chains vorkommen, zu erfüllen. Lassen Sie uns diesen Unterschied zwischen dem modellzentrierten Ansatz und dem modellierungzentrierten Ansatz klarstellen.

Der modellzentrierte Ansatz legt in erster Linie Wert auf ein Modell. Das Modell wird als Paket geliefert, als ein Satz von numerical recipes, die typischerweise in Form eines Stücks Software vorliegen, das Sie tatsächlich ausführen können. Selbst wenn eine solche Software nicht verfügbar ist, wird erwartet, dass das Modell mit mathematischer Präzision beschrieben wird, sodass eine vollständige Neuentwicklung des Modells möglich ist. Dieses Paket, das modellgemachte Software, soll das Endziel sein.

Aus einer idealisierten Perspektive soll sich dieses Modell genau wie eine mathematische Funktion verhalten: Eingaben rein, Ergebnisse raus. Falls das Modell noch konfigurierbare Elemente aufweist, werden diese als offene Fragen behandelt, als Probleme, die noch nicht vollständig gelöst sind. Tatsächlich schwächt jede Konfigurationsmöglichkeit die Aussagekraft des Modells. Wenn es zu viele Konfigurationsmöglichkeiten aus der modellzentrierten Perspektive gibt, neigt das Modell dazu, sich in einen Raum von Modellen aufzulösen, und plötzlich können wir gar nichts mehr vergleichbar machen, weil es so etwas wie ein einziges Modell nicht mehr gibt.

Der modellierungzentrierte Ansatz betrachtet die Konfigurationsmöglichkeiten völlig anders. Die Maximierung der Ausdruckskraft des Modells wird zum Endziel. Dies ist kein Fehler, sondern wird zur Eigenschaft. Die Situation kann ziemlich verwirrend sein, wenn wir eine modellierungzentrierte Perspektive betrachten, denn was wir sehen, ist eine Präsentation von Modellen. Diese Modelle verfolgen jedoch eine ganz andere Intention.

Wenn Sie die modellierungzentrierte Perspektive einnehmen, ist das präsentierte Modell nur eine Veranschaulichung. Es soll weder vollständig noch die endgültige Lösung des Problems darstellen. Es ist lediglich ein Schritt auf dem Weg, die Modellierungstechnik an sich zu veranschaulichen. Die größte Herausforderung bei der Modellierungstechnik besteht darin, dass es plötzlich sehr schwierig wird, den Ansatz zu beurteilen. Tatsächlich verlieren wir die naive Benchmarking-Option, denn in dieser modellierungzentrierten Perspektive haben wir Potenziale von Modellen. Wir konzentrieren uns nicht speziell auf ein Modell gegenüber einem anderen; das ist nicht einmal die richtige Denkweise. Was wir haben, ist eine fundierte Meinung.

Ich möchte jedoch sofort darauf hinweisen, dass es nicht schon deshalb, weil man einen Benchmark und Zahlen hat, die an diesen Benchmark gebunden sind, automatisch als Wissenschaft gilt. Die Zahlen könnten schlichtweg unsinnig sein, und umgekehrt: Nur weil es sich um eine fundierte Meinung handelt, ist es nicht weniger wissenschaftlich. In gewisser Weise ist es einfach ein anderer Ansatz, und die Realität ist, dass diese beiden Ansätze in verschiedenen Gemeinschaften koexistieren.

Zum Beispiel: Wenn wir uns das Paper “Forecasting at Scale” ansehen, das 2017 von einem Team bei Facebook veröffentlicht wurde, haben wir ein typisches Beispiel für den modellzentrierten Ansatz. In diesem Paper wird das Facebook Prophet Modell vorgestellt. Und in einem weiteren Paper, “Tensor Comprehension”, das 2018 von einem anderen Team bei Facebook veröffentlicht wurde, haben wir im Wesentlichen eine Modellierungstechnik. Dieses Paper kann als Archetyp des modellierungzentrierten Ansatzes angesehen werden. So können Sie sehen, dass selbst Forschungsteams im selben Unternehmen, fast zeitgleich, das Problem je nach Situation aus unterschiedlichen Perspektiven angehen.

Diese Vorlesung ist Teil einer Reihe von supply chain Vorlesungen. Im ersten Kapitel habe ich meine Ansichten über supply chain sowohl als Studienfach als auch als Praxis dargestellt. Bereits in der allerersten Vorlesung habe ich argumentiert, dass die Mainstream supply chain Theorie nicht den Erwartungen entspricht. Es stellt sich heraus, dass die Mainstream supply chain Theorie stark auf den modellzentrierten Ansatz setzt, und ich glaube, dass genau dieser Aspekt einer der Hauptgründe für Reibungen zwischen der Mainstream supply chain Theorie und den Anforderungen realer supply chains ist.

Im zweiten Kapitel dieser Vorlesungsreihe habe ich eine Reihe von Methodologien vorgestellt. Tatsächlich werden naive Methodologien typischerweise von der episodischen und häufig adversarialen Natur von supply chain Situationen überwältigt. Insbesondere die Vorlesung mit dem Titel “Empirical Experimental Optimization”, die Teil des zweiten Kapitels war, entspricht genau der Perspektive, die ich heute in dieser Vorlesung einnehme.

Im dritten Kapitel habe ich eine Reihe von supply chain personae vorgestellt. Die Personae repräsentieren einen ausschließlichen Fokus auf die Probleme, die wir zu lösen versuchen, und vernachlässigen dabei jede potenzielle Lösung. Diese Personae sind entscheidend, um die Vielfalt der prädiktiven Herausforderungen, denen reale supply chains gegenüberstehen, zu verstehen. Ich glaube, dass diese Personae unerlässlich sind, um zu vermeiden, in der engen Zeitreihenperspektive gefangen zu werden, die ein Kennzeichen einer supply chain Theorie ist, die wenig Wert auf die Details realer supply chains legt.

Im vierten Kapitel habe ich eine Reihe von Hilfswissenschaften vorgestellt. Diese Wissenschaften unterscheiden sich von supply chain, aber ein grundlegendes Verständnis dieser Disziplinen ist essenziell für die moderne supply chain Praxis. Im vierten Kapitel haben wir bereits kurz das Thema differentiable programming angesprochen, aber ich werde dieses Programmierparadigma in wenigen Minuten noch einmal ausführlicher vorstellen.

Abschließend haben wir in der ersten Vorlesung dieses fünften Kapitels ein einfaches, manche würden sogar sagen simples, Modell gesehen, das bei einem weltweiten forecasting competition im Jahr 2020 eine state-of-the-art Prognosegenauigkeit erzielte. Heute präsentiere ich eine Reihe von Techniken, mit denen die Parameter dieses Modells, das ich in der vorangegangenen Vorlesung vorgestellt habe, erlernt werden können.

Der Rest dieser Vorlesung lässt sich grob in zwei Blöcke unterteilen, gefolgt von einigen abschließenden Gedanken. Der erste Block widmet sich dem differentiable programming. Wir haben dieses Thema bereits im vierten Kapitel angesprochen; heute werden wir jedoch einen viel genaueren Blick darauf werfen. Am Ende dieser Vorlesung sollten Sie fast in der Lage sein, Ihre eigene Implementation von differentiable programming zu erstellen. Ich sage “fast”, weil dies je nach verwendeter Technologie variieren kann. Außerdem ist differentiable programming eine eigenständige Spezialität; es bedarf etwas Erfahrung, um es in der Praxis reibungslos zum Laufen zu bringen.

Der zweite Block dieser Vorlesung ist eine Schritt-für-Schritt-Anleitung für eine Einzelhandels-Nachfrageprognosesituation. Diese Anleitung baut auf der vorangegangenen Vorlesung auf, in der wir das Modell vorgestellt haben, das bei der M5 forecasting competition 2020 den ersten Platz erreichte. In dieser vorangegangenen Präsentation haben wir jedoch nicht im Detail dargelegt, wie die Parameter des Modells effektiv berechnet wurden. Diese Anleitung wird genau das vermitteln, und wir werden auch wichtige Elemente wie stockouts und promotions behandeln, die in der vorangegangenen Vorlesung unberücksichtigt blieben. Abschließend werde ich auf Grundlage all dieser Elemente meine Ansichten zur Eignung von differentiable programming für supply chain Zwecke darlegen.

Der stochastische Gradientenabstieg (SGD) ist eine der beiden Säulen der differenzierbaren Programmierung. Der SGD ist trügerisch einfach, und doch ist noch nicht vollständig klar, warum er so gut funktioniert. Es ist absolut klar, warum er funktioniert; was nicht sehr klar ist, ist, warum er so gut funktioniert.

Die Geschichte des stochastischen Gradientenabstiegs lässt sich bis in die 1950er Jahre zurückverfolgen, sodass er eine ziemlich lange Historie hat. Diese Technik erlangte jedoch erst im letzten Jahrzehnt mit dem Aufkommen von deep learning breite Anerkennung. Der stochastische Gradientenabstieg ist tief in der mathematischen Optimierung verwurzelt. Wir haben eine Verlustfunktion Q, die wir minimieren wollen, und einen Satz realer Parameter, bezeichnet als W, die alle möglichen Lösungen repräsentieren. Was wir finden möchten, ist die Kombination der Parameter W, die die Verlustfunktion Q minimiert.

Die Verlustfunktion Q soll eine grundlegende Eigenschaft wahren: Sie kann additiv in eine Reihe von Termen zerlegt werden. Das Vorhandensein dieser additiven Zerlegung ermöglicht erst überhaupt das Funktionieren des stochastischen Gradientenabstiegs. Wenn Ihre Verlustfunktion nicht auf diese Weise additiv zerlegt werden kann, dann ist der stochastische Gradientenabstieg als Technik nicht anwendbar. Aus dieser Perspektive repräsentiert X die Menge aller Terme, die zur Verlustfunktion beitragen, und Qx steht für einen partiellen Verlust, der den Verlust für einen der Terme in dieser Sichtweise, die die Verlustfunktion als Summe partieller Terme darstellt, ausdrückt.

Obwohl der stochastische Gradientenabstieg nicht spezifisch für Lernkontexte ist, passt er sehr gut zu allen Anwendungsfällen des Lernens – und wenn ich von Lernen spreche, meine ich das Lernen im Sinne von maschinellen Lernanwendungen. Tatsächlich, wenn wir einen Trainingsdatensatz haben, wird dieser Datensatz die Form einer Liste von Beobachtungen annehmen, wobei jede Beobachtung ein Paar von Merkmalen darstellt, welches den Eingang des Modells repräsentiert, und Labels, die die Ausgaben darstellen. Im Wesentlichen wollen wir aus lernerischer Perspektive ein Modell entwerfen, das beim empirischen Fehler und weiteren Kennzahlen, wie sie in diesem Trainingsdatensatz zu beobachten sind, am besten abschneidet. Aus dieser Perspektive wäre X tatsächlich die Liste der Beobachtungen, und die Parameter wären jene eines maschinellen Lernmodells, die wir optimieren, um diesen Datensatz bestmöglich anzupassen.

Der stochastische Gradientenabstieg ist im Grunde ein iterativer Prozess, der zufällig die Beobachtungen durchläuft – eine Beobachtung nach der anderen. Wir wählen jeweils eine Beobachtung, ein kleines X, und berechnen für diese Beobachtung einen lokalen Gradienten, dargestellt als nabla von Qx. Es handelt sich lediglich um einen lokalen Gradienten, der nur für einen Term der Verlustfunktion gilt. Dies ist nicht der Gradient der gesamten Verlustfunktion selbst, sondern ein lokaler Gradient, der nur für einen Term der Verlustfunktion gilt – man kann ihn als partiellen Gradienten betrachten.

Ein Schritt des stochastischen Gradientenabstiegs besteht darin, diesen lokalen Gradienten zu nutzen und die Parameter W ein wenig basierend auf dieser partiellen Beobachtung des Gradienten anzupassen. Genau das geschieht hier, wobei W mit W minus eta mal nabla QxW aktualisiert wird. Das bedeutet in aller Kürze, dass der W-Parameter in die Richtung des lokalen Gradienten verschoben wird, wie er mit X ermittelt wurde – wobei X nur eine der Beobachtungen Ihres Datensatzes darstellt, wenn wir ein Problem aus einer lernerischen Perspektive angehen. Anschließend fahren wir zufällig fort, wenden diesen lokalen Gradienten an und iterieren.

Intuitiv funktioniert der stochastische Gradientenabstieg so gut, weil er einen Trade-off zwischen schnelleren Iterationen und rauschigeren Gradienten aufzeigt, was zu feineren und somit schnelleren Iterationen führt. Das Wesentliche am stochastischen Gradientenabstieg ist, dass es uns nicht stört, sehr ungenaue Messungen unserer Gradienten zu haben, solange wir diese ungenauen Messungen super schnell erhalten können. Wenn wir den Trade-off hin zu schnelleren Iterationen verschieben können, selbst wenn dies auf Kosten rauschigerer Gradienten geht, dann machen wir es so. Deshalb ist der stochastische Gradientenabstieg so effektiv darin, den benötigten Rechenaufwand zu minimieren, um eine bestimmte Lösungsgüte für den Parameter W zu erreichen.

Schließlich haben wir die Variable eta, die als Lernrate bezeichnet wird. In der Praxis ist die Lernrate kein konstanter Wert; diese Variable variiert, während der stochastische Gradientenabstieg fortschreitet. Bei Lokad verwenden wir den Adam-Algorithmus, um die Entwicklung dieses eta-Parameters für die Lernrate zu steuern. Adam ist eine Methode, die 2014 veröffentlicht wurde, und sie ist in Machine-Learning-Kreisen sehr beliebt, wann immer der stochastische Gradientenabstieg zum Einsatz kommt.

Die zweite Säule der differenzierbaren Programmierung ist die automatische Differenzierung. Wir haben dieses Konzept bereits in einer früheren Vorlesung gesehen. Lassen Sie uns dieses Konzept anhand eines Codebeispiels erneut betrachten. Dieser Code ist in Envision geschrieben, einer domänenspezifischen Programmiersprache, die von Lokad für die prädiktive Optimierung von supply chains entwickelt wurde. Ich wähle Envision, weil, wie Sie sehen werden, die Beispiele viel prägnanter und hoffentlich auch viel klarer sind als alternative Darstellungen, falls ich Python, Java oder C# verwenden würde. Allerdings möchte ich darauf hinweisen, dass, auch wenn ich Envision benutze, keine geheime Zutat beteiligt ist. Sie könnten all diese Beispiele auch komplett in anderen Programmiersprachen implementieren. Dies würde höchstwahrscheinlich die Anzahl der Codezeilen um den Faktor 10 vervielfachen, aber im großen und ganzen ist das ein Detail. Hier, in einer Vorlesung, bietet uns Envision eine sehr klare und prägnante Darstellung.

Schauen wir, wie differenzierbare Programmierung verwendet werden kann, um eine lineare Regression anzugehen. Dies ist ein Spielzeugproblem; für eine lineare Regression benötigen wir keine differenzierbare Programmierung. Ziel ist es lediglich, sich mit der Syntax der differenzierbaren Programmierung vertraut zu machen. In den Zeilen 1 bis 6 deklarieren wir die Tabelle T, die die Beobachtungstabelle darstellt. Wenn ich von Beobachtungstabelle spreche, denken Sie einfach an die Menge X des stochastischen Gradientenabstiegs. Das ist exakt dasselbe. Diese Tabelle hat zwei Spalten, ein Merkmal bezeichnet als X und ein Label bezeichnet als Y. Was wir wollen, ist, X als Eingabe zu verwenden und Y mithilfe eines linearen Modells, beziehungsweise genauer gesagt, eines affinen Modells, vorherzusagen. Offensichtlich haben wir in dieser Tabelle T nur vier Datenpunkte. Dies ist ein lächerlich kleiner Datensatz; er dient einzig der Veranschaulichung.

In Zeile 8 führen wir den autodiff-Block ein. Der autodiff-Block kann in Envision als Schleife gesehen werden. Es ist eine Schleife, die über eine Tabelle iteriert – in diesem Fall über die Tabelle T. Diese Iterationen spiegeln die Schritte des stochastischen Gradientenabstiegs wider. Das heißt, wenn die Ausführung von Envision in diesen autodiff-Block eintritt, erfolgt eine Serie wiederholter Durchläufe, in denen wir Zeilen aus der Beobachtungstabelle auswählen und dann Schritte des stochastischen Gradientenabstiegs anwenden. Dazu benötigen wir die Gradienten.

Woher kommen die Gradienten? Hier haben wir ein Programm geschrieben, einen kleinen Ausdruck unseres Modells: Ax + B. Wir führen die Verlustfunktion ein, welche der mittlere quadratische Fehler ist. Wir möchten den Gradienten erhalten. Für eine Situation, die so einfach ist wie diese, könnten wir den Gradienten manuell berechnen. Allerdings ist die automatische Differenzierung eine Technik, mit der Sie ein Programm in zwei Formen kompilieren können: die erste Form ist die Vorwärtsausführung des Programms, und die zweite Form ist die umgekehrte Ausführung, die die Gradienten aller im Programm vorhandenen Parameter berechnet.

In den Zeilen 9 und 10 deklarieren wir zwei Parameter, A und B, mit dem Schlüsselwort “auto”, das Envision anweist, die Werte dieser beiden Parameter automatisch zu initialisieren. A und B sind skalare Werte. Die automatische Differenzierung erfolgt für alle Programme, die in diesem autodiff-Block enthalten sind. Im Wesentlichen handelt es sich um eine Technik auf Compiler-Ebene, um dieses Programm zweimal zu kompilieren: einmal für den Vorwärtsdurchlauf und ein zweites Mal für ein Programm, das die Werte der Gradienten liefert. Die Schönheit der automatischen Differenzierungstechnik besteht darin, dass garantiert wird, dass der für die Berechnung des normalen Programms benötigte CPU-Aufwand dem für die Berechnung des Gradienten im Rückwärtsdurchlauf nahezu entspricht. Das ist eine sehr wichtige Eigenschaft. Schließlich drucken wir in Zeile 14 die Parameter aus, die wir eben mit dem oben genannten autodiff-Block gelernt haben.

Die differenzierbare Programmierung glänzt wirklich als Programmierparadigma. Es ist möglich, ein beliebig komplexes Programm zu erstellen und dessen automatische Differenzierung zu erhalten. Dieses Programm kann beispielsweise Verzweigungen und Funktionsaufrufe enthalten. Dieses Codebeispiel greift die pinball Verlustfunktion wieder auf, die wir in der vorherigen Vorlesung eingeführt haben. Die pinball-Verlustfunktion kann verwendet werden, um Quantilschätzungen abzuleiten, wenn wir Abweichungen von einer empirischen Wahrscheinlichkeitsverteilung beobachten. Minimiert man den mittleren quadratischen Fehler mit seiner Schätzung, erhält man eine Schätzung des Mittelwerts der empirischen Verteilung. Minimiert man hingegen die pinball-Verlustfunktion, erhält man eine Schätzung für ein Quantilziel. Wenn Sie auf ein 90. Quantil abzielen, bedeutet das, dass es der Wert in Ihrer Wahrscheinlichkeitsverteilung ist, bei dem der zukünftige zu beobachtende Wert zu 90 % unter Ihrer Schätzung liegt – oder zu 10 % darüber. Dies erinnert an die Service Levels Analyse, die in supply chain existiert.

In den Zeilen 1 und 2 führen wir eine Beobachtungstabelle ein, die mit zufällig aus einer Poisson-Verteilung gezogenen Abweichungen gefüllt wird. Die Werte der Poisson-Verteilung werden mit einem Mittelwert von 3 gezogen, und wir erhalten 10.000 Abweichungen. In den Zeilen 4 und 5 stellen wir unsere maßgeschneiderte Implementierung der pinball-Verlustfunktion vor. Diese Implementierung ist nahezu identisch mit dem Code, den ich in der vorherigen Vorlesung vorgestellt habe. Allerdings wird dem Funktionsdeklaration nun das Schlüsselwort “autodiff” hinzugefügt. Dieses Schlüsselwort, wenn es an die Funktionsdeklaration angehängt wird, stellt sicher, dass der Envision-Compiler diese Funktion automatisch differenzieren kann. Während in der Theorie die automatische Differenzierung auf jedes Programm angewendet werden kann, gibt es in der Praxis viele Programme, bei denen es keinen Sinn macht, sie zu differenzieren, bzw. viele Funktionen, bei denen es nicht sinnvoll wäre. Betrachten Sie beispielsweise eine Funktion, die zwei Textwerte entgegennimmt und diese miteinander verkettet. Aus der Perspektive der automatischen Differenzierung ergibt es keinen Sinn, diese Art von Operation zu differenzieren. Automatische Differenzierung setzt voraus, dass in den Eingabe- und Ausgabewerten der Funktionen Zahlen vorhanden sind, die differenziert werden sollen.

In den Zeilen 7 bis 9 befindet sich der autodiff-Block, der die Ziel-Quantilschätzung für die über die Beobachtungstabelle erhaltene empirische Verteilung berechnet. Im Hintergrund handelt es sich tatsächlich um eine Poisson-Verteilung. Die Quantilschätzung wird in Zeile 8 als Parameter namens “quantile” deklariert, und in Zeile 9 rufen wir unsere eigene Implementierung der pinball-Verlustfunktion auf. Das Quantilziel ist auf 0,5 gesetzt, sodass wir tatsächlich eine Median-Schätzung der Verteilung anstreben. Schließlich drucken wir in Zeile 11 die Ergebnisse für den Wert aus, den wir durch die Ausführung des autodiff-Blocks gelernt haben. Dieses Codebeispiel zeigt, wie ein Programm, das wir automatisch differenzieren wollen, sowohl einen Funktionsaufruf als auch eine Verzweigung enthalten kann – und all dies völlig automatisch abläuft.

Ich habe erwähnt, dass die autodiff-Blöcke als eine Schleife interpretiert werden können, die eine Reihe von Schritten des stochastischen Gradientenabstiegs über die Beobachtungstabelle ausführt, wobei jeweils eine Zeile aus dieser Beobachtungstabelle ausgewählt wird. Allerdings bin ich hinsichtlich der Abbruchbedingung für diese Situation etwas vage geblieben. Wann stoppt der stochastische Gradientenabstieg in Envision? Standardmäßig stoppt der stochastische Gradientenabstieg nach 10 Epochen. Eine Epoche, in der Terminologie des maschinellen Lernens, stellt einen kompletten Durchlauf durch die Beobachtungstabelle dar. In Zeile 7 kann den autodiff-Blöcken ein Attribut namens “epochs” zugeordnet werden. Dieses Attribut ist optional; standardmäßig beträgt der Wert 10, aber wenn Sie dieses Attribut angeben, können Sie eine andere Anzahl wählen. Hier geben wir 100 Epochen an. Bedenken Sie, dass die Gesamtzeit für die Berechnung nahezu linear zur Anzahl der Epochen ist. Wenn Sie also doppelt so viele Epochen haben, dauert die Berechnungszeit doppelt so lange.

Dennoch führen wir in Zeile 7 auch ein zweites Attribut namens “learning_rate” ein. Dieses Attribut ist ebenfalls optional und standardmäßig mit dem Wert 0,01 versehen, der dem autodiff-Block zugeordnet ist. Diese Lernrate ist ein Faktor, der verwendet wird, um den Adam-Algorithmus zu initialisieren, der die Entwicklung der Lernrate steuert. Dies ist der eta-Parameter, den wir im Schritt des stochastischen Gradientenabstiegs gesehen haben. Er steuert den Adam-Algorithmus. Im Wesentlichen handelt es sich um einen Parameter, den Sie nicht häufig anpassen müssen, aber manchmal kann das Justieren dieses Parameters einen erheblichen Teil der Prozessorleistung einsparen. Es ist nicht überraschend, dass durch Feinabstimmung dieser Lernrate etwa 20 % der Gesamtrechenzeit für Ihren stochastischen Gradientenabstieg eingespart werden können.

Die Initialisierung der im autodiff-Block gelernten Parameter erfordert ebenfalls eine genauere Betrachtung. Bisher haben wir das Schlüsselwort “auto” verwendet, und in Envision bedeutet dies einfach, dass Envision den Parameter durch zufälliges Ziehen eines Wertes aus einer Gaußschen Verteilung mit einem Mittelwert von 1 und einer Standardabweichung von 0,1 initialisiert. Diese Initialisierung weicht von der üblichen Praxis im Deep Learning ab, bei der die Parameter zufällig mit Gaußen initialisiert werden, die um Null zentriert sind. Der Grund, warum Lokad diesen anderen Ansatz wählte, wird später in dieser Vorlesung deutlicher, wenn wir auf eine tatsächliche Prognosesituation für den Einzelhandelsbedarf eingehen.

In Envision ist es möglich, die Initialisierung der Parameter zu überschreiben und zu kontrollieren. Der Parameter “quantile” beispielsweise wird in Zeile 9 deklariert, muss aber nicht initialisiert werden. Tatsächlich haben wir in Zeile 7, direkt oberhalb des autodiff-Blocks, eine Variable “quantile”, der der Wert 4.2 zugewiesen wird, und somit ist die Variable bereits mit einem bestimmten Wert initialisiert. Eine automatische Initialisierung ist daher nicht mehr erforderlich. Es ist auch möglich, einen Wertebereich festzulegen, in dem sich die Parameter befinden dürfen, und dies geschieht mit dem Schlüsselwort “in” in Zeile 9. Im Grunde definieren wir, dass “quantile” zwischen 1 und 10 liegen soll, inklusive. Mit diesen Grenzen, wenn ein Update vom Adam-Algorithmus erfolgt, das den Parameterwert aus dem zulässigen Bereich hinauszuschieben droht, begrenzen wir die Änderung von Adam, sodass der Parameterwert innerhalb dieses Bereichs bleibt. Außerdem setzen wir auch die Impulswerte, die üblicherweise intern beim Adam-Algorithmus verwendet werden, auf Null. Das Erzwingen von Parametergrenzen weicht von der klassischen Deep-Learning-Praxis ab; jedoch werden die Vorteile dieser Funktion offensichtlich, sobald wir ein tatsächliches Beispiel zur Prognose der Einzelhandelsnachfrage besprechen.

Differenzierbares Programmieren stützt sich stark auf stochastischen Gradientenabstieg. Der stochastische Aspekt ist buchstäblich das, was den Abstieg so schnell funktionieren lässt. Es ist ein zweischneidiges Schwert; das Rauschen, das durch die partiellen Verluste entsteht, ist nicht nur ein Fehler, sondern auch ein Feature. Mit etwas Rauschen kann der Abstieg vermeiden, in Zonen mit sehr flachen Gradienten stecken zu bleiben. So bewirkt der verrauschte Gradient nicht nur eine wesentlich schnellere Iteration, sondern hilft auch, die Iteration aus Bereichen zu drängen, in denen der Gradient so flach ist, dass der Abstieg verlangsamt wird. Es ist jedoch zu beachten, dass beim Einsatz von stochastischem Gradientenabstieg die Summe der Gradienten nicht dem Gradienten der Summe entspricht. Folglich geht der stochastische Gradientenabstieg mit geringfügigen statistischen Verzerrungen einher, vor allem wenn es um Schwanzverteilungen geht. Dennoch ist es in solchen Fällen relativ unkompliziert, die numerischen Rezepte provisorisch zu fixieren, auch wenn die Theorie etwas trüb bleibt.

Differenzierbares Programmieren (DP) darf nicht mit einem beliebigen mathematischen Optimierungslöser verwechselt werden. Der Gradient muss durch das Programm fließen, damit differenzierbares Programmieren überhaupt funktioniert. Differenzierbares Programmieren kann mit beliebig komplexen Programmen arbeiten, aber diese Programme müssen mit differenzierbarem Programmieren im Hinterkopf entworfen werden. Außerdem ist differenzierbares Programmieren eine Kultur; es ist eine Sammlung von Tipps und Tricks, die gut mit stochastischem Gradientenabstieg harmonieren. Alles in allem liegt differenzierbares Programmieren auf der leichten Seite des Machine-Learning-Spektrums. Es ist als Technik sehr zugänglich. Dennoch erfordert es etwas handwerkliches Geschick, um dieses Paradigma zu meistern und reibungslos in der Produktion einzusetzen.

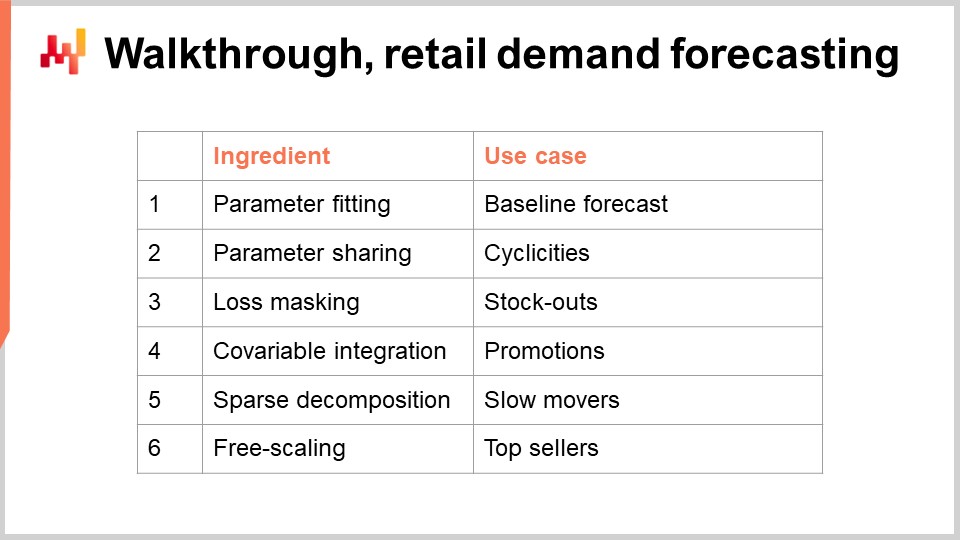
Wir sind nun bereit, mit dem zweiten Block dieser Vorlesung zu beginnen: dem Walkthrough. Wir werden einen Walkthrough für unsere Einzelhandelsnachfrageprognose-Aufgabe durchführen. Diese Modellierungsübung steht im Einklang mit der Prognose-Herausforderung, die wir in der vorherigen Vorlesung vorgestellt haben. Kurz gesagt wollen wir die tägliche Nachfrage auf SKU-Ebene in einem Einzelhandelsnetz prognostizieren. Eine SKU oder stock-keeping unit ist technisch das kartesische Produkt aus Produkten und Geschäften, gefiltert nach den Einträgen des Sortiments. Zum Beispiel, wenn wir 100 Geschäfte und 10.000 Produkte haben und jedes einzelne Produkt in jedem Geschäft vorhanden ist, kommen wir auf 1 Million SKUs.

Es gibt Werkzeuge, um eine deterministische Schätzung in eine probabilistische umzuwandeln. Eines dieser Werkzeuge haben wir in der vorherigen Vorlesung mit der ESSM-Technik gesehen. Dieses spezielle Anliegen – die Umwandlung von Schätzungen in probabilistische Schätzungen – werden wir in der nächsten Vorlesung ausführlicher behandeln. Heute befassen wir uns jedoch nur mit der Schätzung von Durchschnitten, und alle anderen Arten von Schätzungen (Quantile, probabilistisch) werden später als natürliche Erweiterungen des Kernbeispiels folgen, das ich heute präsentiere. In diesem Walkthrough werden wir die Parameter eines einfachen Nachfrageprognosemodells erlernen. Die Einfachheit dieses Modells ist trügerisch, denn diese Modellklasse erreicht tatsächlich den Stand der Technik in der Prognose, wie der M5-Prognosewettbewerb im Jahr 2020 gezeigt hat.

Für unser parametrisches Nachfrage-Modell führen wir für jede einzelne SKU einen einzelnen Parameter ein. Dies ist eine absolut vereinfachte Form eines Modells; die Nachfrage wird für jede SKU als Konstantwert modelliert. Allerdings ist es nicht derselbe konstante Wert für jede SKU. Sobald wir diesen konstanten Tagesdurchschnitt haben, wird er an allen Tagen des gesamten Lebenszyklus der SKU gleich sein.

Schauen wir uns an, wie dies mit differenzierbarem Programmieren umgesetzt wird. In den Zeilen 1 bis 4 führen wir den Mock-Daten-Block ein. In der Praxis würde dieses Modell und alle seine Varianten von Eingaben abhängen, die aus den Geschäftssystemen stammen: dem ERP, WMS, TMS etc. Eine Vorlesung zu präsentieren, in der ich ein mathematisches Modell in eine realistische Datenrepräsentation einfüge, wie sie aus dem ERP gewonnen wird, würde sämtliche zufälligen Komplikationen einführen, die für das aktuelle Thema der Vorlesung irrelevant sind. Was ich hier mache, ist, einen Mock-Daten-Block einzuführen, der in keiner Weise vorgibt, realistisch zu sein, oder die Art von Daten darstellt, die man in einer tatsächlichen Einzelhandelssituation beobachten kann. Das einzige Ziel dieses Mock-Daten-Blocks besteht darin, die Tabellen und die Beziehungen zwischen den Tabellen zu etablieren und sicherzustellen, dass das bereitgestellte Code-Beispiel vollständig, kompilierbar und ausführbar ist. Alle bisherigen Code-Beispiele sind vollständig eigenständig; es gibt keine versteckten Anteile davor oder danach. Der alleinige Zweck des Mock-Daten-Blocks besteht darin, sicherzustellen, dass wir ein in sich geschlossenes Code-Stück haben.

In jedem Beispiel dieses Walkthroughs beginnen wir mit diesem Mock-Daten-Block. In Zeile 1 führen wir die Datumstabelle mit “dates” als Primärschlüssel ein. Hier haben wir einen Datumsbereich, der grundsätzlich zwei Jahre und einen Monat umfasst. Dann, in Zeile 2, führen wir die SKUs-Tabelle ein, welche die Liste der SKUs darstellt. In diesem minimalistischen Beispiel haben wir lediglich drei SKUs. In einer realen Einzelhandelssituation für ein großes Einzelhandelsnetz hätten wir Millionen, wenn nicht zig Millionen SKUs. Aber hier, der Einfachheit halber, wähle ich eine sehr kleine Anzahl. In Zeile 3 haben wir die Tabelle “T”, welche das kartesische Produkt aus den SKUs und dem Datum darstellt. Im Grunde ergibt diese Tabelle “T” eine Matrix, in der jede einzelne SKU und jeder einzelne Tag vertreten ist. Diese Matrix hat zwei Dimensionen.

In Zeile 6 führen wir unseren eigentlichen autodiff-Block ein. Die Beobachtungstabelle ist die SKUs-Tabelle, und der stochastische Gradientenabstieg wählt hier jeweils eine SKU aus. In Zeile 7 führen wir das “level” ein, welches unser einziger Parameter sein wird. Es handelt sich um einen Vektorparameter, und bislang haben wir in unseren autodiff-Blöcken nur skalare Parameter eingeführt. Die bisherigen Parameter waren lediglich Zahlen; hier ist “SKU.level” tatsächlich ein Vektor. Es ist ein Vektor, der für jede SKU einen Wert enthält – und das stellt buchstäblich unsere als konstant modellierte Nachfrage auf SKU-Ebene dar. Wir spezifizieren einen Wertebereich, dessen Bedeutung wir gleich erläutern werden. Er muss mindestens 0,01 betragen, und wir setzen 1.000 als obere Grenze für die durchschnittliche Tagesnachfrage dieses Parameters fest. Dieser Parameter wird automatisch mit einem Wert initialisiert, der nahe bei eins liegt, was einen vernünftigen Ausgangspunkt darstellt. In diesem Modell verfügen wir pro SKU über einen einzigen Freiheitsgrad. Schließlich implementieren wir in den Zeilen 8 und 9 das Modell an sich. In Zeile 8 berechnen wir “dot.delta”, das heißt, die vom Modell prognostizierte Nachfrage abzüglich der beobachteten, nämlich “T.sold”.

Um zu verstehen, was hier vor sich geht, beobachten wir einige Broadcasting-Verhalten. Die Tabelle “T” ist eine Kreuztabelle zwischen SKU und Datum. Der autodiff-Block ist eine Iteration, die über die Zeilen der Beobachtungstabelle läuft. In Zeile 9 befinden wir uns innerhalb des autodiff-Blocks, weshalb wir eine Zeile aus der SKUs-Tabelle ausgewählt haben. Der Wert “SKUs.level” ist hier kein Vektor mehr, sondern ein Skalar, da nur eine Zeile der Beobachtungstabelle betrachtet wird. Gleichzeitig ist “T.sold” keine Matrix mehr, nachdem bereits eine SKU ausgewählt wurde. Was übrig bleibt, ist, dass “T.sold” tatsächlich ein Vektor ist, dessen Dimension dem Datum entspricht. Wenn wir die Subtraktion “SKUs.level - T.sold” durchführen, erhalten wir einen Vektor, der mit der Datumstabelle ausgerichtet ist, und wir weisen ihn “D.delta” zu – ein Vektor, der je einen Eintrag pro Tag, über zwei Jahre und einen Monat, enthält. Schließlich berechnen wir in Zeile 9 die Verlustfunktion, die einfach den mittleren quadratischen Fehler darstellt. Dieses Modell ist äußerst simpel. Sehen wir uns nun an, was bezüglich Kalendermustern möglich ist.

Parameter-Sharing ist wahrscheinlich eine der einfachsten und nützlichsten Techniken im differenzierbaren Programmieren. Ein Parameter gilt als geteilt, wenn er zu mehreren Beobachtungszeilen beiträgt. Durch das Teilen von Parametern über Beobachtungen hinweg können wir den Gradientenabstieg stabilisieren und Problemen des Overfitting entgegenwirken. Betrachten wir das Muster des Wochentags. Man könnte sieben Parameter einführen, die die verschiedenen Gewichtungen für jede einzelne SKU repräsentieren. Bisher hat eine SKU nur einen Parameter, nämlich die konstante Nachfrage. Möchte man die Betrachtung der Nachfrage erweitern, könnte man sagen, dass jeder Tag der Woche sein eigenes Gewicht hat, und da es sieben Wochentage gibt, können wir sieben Gewichte festlegen und diese multiplikativ anwenden.

Es ist jedoch unwahrscheinlich, dass jede einzelne SKU ihr eigenes, einzigartiges Wochentagsmuster besitzt. Vielmehr ist es vernünftiger anzunehmen, dass es eine Kategorie oder irgendeine Art von Hierarchie gibt – wie etwa eine Produktfamilie, Produktkategorie, Produktunterkategorie oder sogar eine Abteilung im Geschäft –, die dieses Wochentagsmuster korrekt abbildet. Die Idee besteht darin, nicht sieben Parameter pro SKU einzuführen, sondern sieben Parameter pro Kategorie, also auf der Gruppierungsebene, auf der von einem homogenen Verhalten in Bezug auf Wochentagsmuster ausgegangen wird.

Wenn wir uns dafür entscheiden, diese sieben Parameter mit einem multiplikativen Effekt auf das Level einzuführen, entspricht dies genau dem Ansatz, der in der vorherigen Vorlesung für dieses Modell gewählt wurde, welches auf SKU-Ebene im M5-Wettbewerb den ersten Platz belegte. Wir haben ein Level und einen multiplikativen Effekt in Form des Wochentagsmusters.

Im Code, in den Zeilen 1 bis 5, befindet sich der Mock-Daten-Block wie zuvor, und wir führen eine zusätzliche Tabelle namens “category” ein. Diese Tabelle ist eine Gruppierungstabelle der SKUs, und konzeptionell entspricht für jede Zeile in der SKUs-Tabelle genau eine Zeile in der category-Tabelle. In der Envision-Sprache sagen wir, dass die Kategorie stromaufwärts der Tabelle SKUs liegt. Zeile 7 führt die Wochentagstabelle ein. Diese Tabelle ist essenziell, und wir führen sie in einer spezifischen Form ein, die das zyklische Muster widerspiegelt, das wir erfassen möchten. In Zeile 7 erstellen wir die Wochentagstabelle, indem wir Daten nach ihrem Wert modulo sieben aggregieren. Wir erstellen eine Tabelle, die exakt sieben Zeilen besitzt, und diese sieben Zeilen repräsentieren die sieben Wochentage. Für jede Zeile der Datumstabelle hat jede Zeile in der Datenbank genau ein entsprechendes Gegenstück in der Wochentagstabelle. Somit ist in der Envision-Sprache die Wochentagstabelle stromaufwärts der Tabelle “date”.

Nun haben wir die Tabelle “CD”, welche ein kartesisches Produkt zwischen Kategorie und Wochentag darstellt. Hinsichtlich der Zeilenanzahl wird diese Tabelle so viele Zeilen enthalten, wie es Kategorien mal sieben gibt, da der Wochentag sieben Zeilen umfasst. In Zeile 12 führen wir einen neuen Parameter namens “CD.DOW” ein (DOW steht für day of the week), der ein weiterer Vektorparameter der Tabelle CD ist. Was die Freiheitsgrade betrifft, haben wir genau sieben Parameterwerte mal der Anzahl der Kategorien – exakt das, was wir beabsichtigen. Wir wollen ein Modell, das in der Lage ist, dieses Wochentagsmuster zu erfassen, jedoch mit nur einem Muster pro Kategorie und nicht einem pro SKU.

Wir deklarieren diesen Parameter und verwenden das Schlüsselwort “in”, um festzulegen, dass der Wert für “CD.DOW” zwischen 0.1 und 100 liegen soll. In Zeile 13 formulieren wir die durch das Modell ausgedrückte Nachfrage. Die Nachfrage lautet “SKUs.level * CD.DOW”, was die Nachfrage repräsentiert. Wir berechnen die Differenz zwischen dieser modellierten Nachfrage und dem Beobachteten “T.sold”, was uns das Delta liefert. Anschließend berechnen wir den mittleren quadratischen Fehler.

In Zeile 13 findet eine Menge Broadcasting-Magie statt. “CD.DOW” ist eine Kreuztabelle zwischen Kategorie und Wochentag. Da wir uns innerhalb des autodiff-Blocks befinden, stellt die Tabelle CD eine Kreuztabelle zwischen Kategorie und Wochentag dar. Da der autodiff-Block über die SKUs-Tabelle iteriert, bedeutet das im Wesentlichen: Wenn wir eine SKU auswählen, haben wir effektiv eine Kategorie ausgewählt, da die category-Tabelle stromaufwärts liegt. Das bedeutet, dass CD.DOW hier nicht mehr als Matrix, sondern als Vektor der Dimension sieben vorliegt. Allerdings ist sie stromaufwärts der Tabelle “date”, sodass diese sieben Zeilen in der Datumstabelle gebroadcastet werden können. Es gibt nur einen Weg, dieses Broadcasting durchzuführen, da jede Zeile der Wochentagstabelle einer bestimmten Zeile der Datumstabelle entspricht. Wir haben ein doppeltes Broadcasting, und letztlich erhalten wir eine Nachfrage, die als Reihe von Werten zyklisch auf der Ebene des Wochentags für die SKU erscheint. Das ist unser Modell zu diesem Zeitpunkt, und der Rest der Verlustfunktion bleibt unverändert.

Wir sehen einen sehr eleganten Ansatz, zyklische Muster zu erfassen, indem wir die Broadcasting-Verhalten, die sich aus der relationalen Natur von Envision ergeben, mit dessen differenzierbaren Programmierfähigkeiten kombinieren. Wir können Kalendersyklizitäten in nur drei Zeilen Code ausdrücken. Dieser Ansatz funktioniert gut, selbst wenn wir es mit sehr spärlichen Daten zu tun haben. Er würde ebenso gut funktionieren, wenn wir Produkte betrachten würden, die im Durchschnitt nur eine Einheit pro Monat verkaufen. In solchen Fällen wäre es ratsam, eine Kategorie zu haben, die Dutzende, wenn nicht Hunderte von Produkten umfasst. Diese Technik kann auch genutzt werden, um andere zyklische Muster, wie beispielsweise den Monat des Jahres oder den Tag des Monats, abzubilden.

Das in der vorherigen Vorlesung vorgestellte Modell, das state-of-the-art Ergebnisse beim M5-Wettbewerb erzielte, war eine multiplikative Kombination aus drei Zyklen: Wochentag, Monat des Jahres und Tag des Monats. Alle diese Muster wurden als Multiplikation verknüpft. Die Implementierung der beiden anderen Varianten wird dem aufmerksamen Publikum überlassen, aber es handelt sich lediglich um ein paar Codezeilen pro zyklischem Muster, wodurch es sehr prägnant ist.

In der vorherigen Vorlesung haben wir ein Verkaufsprognosemodell vorgestellt. Allerdings interessiert uns nicht der Verkauf, sondern die Nachfrage. Wir sollten null Verkäufe nicht mit null Nachfrage verwechseln. Wenn an einem bestimmten Tag keine Ware mehr im Laden für den Kunden verfügbar war, wird bei Lokad die Verlustmaskierungstechnik eingesetzt, um mit Lagerausfällen umzugehen. Dies ist die einfachste Technik, um mit Lagerausfällen umzugehen, aber sie ist nicht die einzige. Soweit ich weiß, haben wir mindestens zwei weitere Techniken, die in der Produktion verwendet werden, jede mit ihren eigenen Vor- und Nachteilen. Diese anderen Techniken werden heute nicht behandelt, sondern in späteren Vorlesungen angesprochen.

Zurück zum Codebeispiel: Die Zeilen 1 bis 3 bleiben unverändert. Schauen wir uns an, was folgt. In Zeile 6 erweitern wir die Mock-Daten um das In-Stock-Boolesche Flag. Für jede einzelne SKU und jeden einzelnen Tag haben wir einen Booleschen Wert, der angibt, ob am Ende des Tages im Laden ein Lagerausfall auftrat. In Zeile 15 modifizieren wir die Verlustfunktion, um die Tage auszuschließen, an denen am Ende des Tages ein Lagerausfall beobachtet wurde, indem wir diese auf Null setzen. Durch das Nullsetzen dieser Tage stellen wir sicher, dass in Situationen, die einen Bias aufgrund des Auftretens des Lagerausfalls aufweisen, kein Gradient zurückpropagiert wird.

Der verwirrendste Aspekt der Verlustmaskierungstechnik ist, dass sie das Modell nicht einmal verändert. Tatsächlich ist, wenn man sich das in Zeile 14 ausgedrückte Modell ansieht, es genau dasselbe; es wurde nicht verändert. Es wird nur die Verlustfunktion selbst modifiziert. Diese Technik mag einfach sein, weicht jedoch fundamental von einer modellzentrierten Perspektive ab. Im Kern ist es eine modellierungszentrierte Technik. Wir verbessern die Situation, indem wir den durch Lagerausfälle verursachten Bias anerkennen und dies in unseren Modellierungsbemühungen widerspiegeln. Allerdings tun wir dies, indem wir die Genauigkeitsmetrik ändern, nicht das Modell selbst. Mit anderen Worten, wir ändern den Verlust, den wir optimieren, wodurch dieses Modell in Bezug auf den reinen numerischen Fehler mit anderen Modellen nicht vergleichbar ist.

Für eine Situation wie Walmart, wie in der vorherigen Vorlesung besprochen, ist die Verlustmaskierungstechnik für die meisten Produkte geeignet. Als Faustregel funktioniert diese Technik gut, wenn die Nachfrage nicht so spärlich ist, dass man die meiste Zeit nur eine Einheit auf Lager hat. Außerdem sollte man Produkte vermeiden, bei denen häufig Lagerausfälle auftreten, da es die ausdrückliche Strategie des Einzelhändlers ist, am Ende des Tages einen Lagerausfall zu erreichen. Dies passiert typischerweise bei einigen ultrafrischen Produkten, bei denen der Einzelhändler darauf abzielt, bis Tagesende eine ausverkaufte Situation zu erreichen. Alternative Techniken beheben diese Einschränkungen, aber wir haben heute keine Zeit, sie zu behandeln.

Promotionen sind ein wichtiger Aspekt im Einzelhandel. Allgemeiner gibt es zahlreiche Möglichkeiten für den Einzelhändler, die Nachfrage zu beeinflussen und zu gestalten, wie zum Beispiel durch Preisgestaltung oder das Platzieren von Waren in einer Gondel. Die Variablen, die zusätzliche Informationen für Vorhersagezwecke liefern, werden in supply chain Kreisen typischerweise als Kovariaten bezeichnet. Es gibt viele Wunschvorstellungen über komplexe Kovariaten wie Wetterdaten oder Social-Media-Daten. Bevor wir uns jedoch in fortgeschrittene Themen vertiefen, müssen wir das offensichtliche Problem ansprechen, wie beispielsweise Preisinformationen, die offensichtlich einen signifikanten Einfluss auf die zu beobachtende Nachfrage haben. Daher führen wir in Zeile 7 in diesem Codebeispiel für jeden einzelnen Tag in Zeile 14 “category.ed” ein, wobei “ed” für die Elastizität der Nachfrage steht. Dies ist ein geteilter Vektorparameter mit einem Freiheitsgrad pro Kategorie, der als Darstellung der Elastizität der Nachfrage gedacht ist. In Zeile 16 führen wir eine exponentielle Form der price elasticity ein, nämlich das Exponenzial von (-category.ed * t.price). Intuitiv führt diese Form dazu, dass bei steigenden Preisen die Nachfrage aufgrund der Anwesenheit der Exponentialfunktion rasch gegen Null konvergiert. Umgekehrt steigt die Nachfrage explosiv, wenn der Preis gegen Null konvergiert.

Diese exponentielle Form der Preisreaktion ist simplistisch, und das Teilen der Parameter gewährleistet selbst mit dieser Exponentialfunktion im Modell ein hohes Maß an numerischer Stabilität. In realen Anwendungen, insbesondere in Situationen wie bei Walmart, hätten wir mehrere Preisinformationen, wie zum Beispiel Rabatte, die Differenz zum Normalpreis, Kovariaten, die Marketingaktionen des Lieferanten repräsentieren, oder kategoriale Variablen, die etwa Gondeln einführen. Mit differentiable programming ist es einfach, beliebig komplexe Preisreaktionen zu entwerfen, die exakt zur Situation passen. Die Integration von Kovariaten nahezu jeder Art ist mit differentiable programming sehr unkompliziert.

Langsame Verkaufsartikel sind eine Tatsache im Einzelhandel und in vielen anderen Branchen. Das bisher vorgestellte Modell hat einen Parameter, einen Freiheitsgrad pro SKU, bzw. mehr, wenn man die gemeinsamen Parameter mitzählt. Dies könnte jedoch bereits zu viel sein, insbesondere für SKUs, die sich nur einmal im Jahr oder nur wenige Male im Jahr drehen. In solchen Situationen können wir uns nicht einmal einen Freiheitsgrad pro SKU leisten, sodass die Lösung darin besteht, sich ausschließlich auf gemeinsame Parameter zu stützen und alle Parameter mit Freiheitsgraden auf der SKU-Ebene zu entfernen.

In den Zeilen 2 und 4 führen wir zwei Tabellen namens “products” und “stores” ein, und die Tabelle “SKUs” wird als gefilterte Subtabelle des kartesischen Produkts zwischen products und stores konstruiert, was der eigentlichen Definition von Sortiment entspricht. In den Zeilen 15 und 16 führten wir zwei gemeinsame Vektorparameter ein: ein Level mit einer Affinität zur Tabelle products und ein weiteres Level, das eine Affinität zu den Tabellen stores aufweist. Diese Parameter sind ebenfalls in einem spezifischen Bereich definiert, von 0,01 bis 100, was der Maximalwert ist.

Nun, in Zeile 18 wird das Level pro SKU als Multiplikation des Produktlevels und des Storelevels gebildet. Der Rest des Skripts bleibt unverändert. Also, wie funktioniert es? In Zeile 19 ist SKU.level ein Skalar. Wir haben den autodesk-Block, der über die SKUs-Tabelle iteriert, welche die Beobachtungstabelle ist. Somit ist SKUs.level in Zeile 18 einfach ein Skalarwert. Dann haben wir products.level. Da die Tabelle products stromaufwärts der SKUs-Tabelle liegt, gibt es für jede einzelne SKU genau eine products-Tabelle. Somit ist products.level einfach eine skalare Zahl. Dasselbe gilt für die Tabelle stores, die ebenfalls stromaufwärts der SKUs-Tabelle liegt. In Zeile 18 ist nur ein Store an diese spezifische SKU angehängt. Daher haben wir die Multiplikation von zwei Skalarwerten, was uns das SKU.level ergibt. Der Rest des Modells bleibt unverändert.

Diese Techniken werfen ein völlig neues Licht auf die Behauptung, dass manchmal nicht genügend Daten vorhanden sind oder dass die Daten zu spärlich seien. Tatsächlich, aus der Perspektive von differentiable programming, machen diese Behauptungen nicht einmal wirklich Sinn. Es gibt so etwas wie zu wenig Daten oder zu spärliche Daten zumindest nicht in absoluten Begriffen. Es gibt lediglich Modelle, die auf Sparsity und möglicherweise extreme Sparsity hin modifiziert werden können. Die auferlegte Struktur ist wie Führungsschienen, die den Lernprozess nicht nur ermöglichen, sondern auch numerisch stabil machen.

Im Vergleich zu anderen Machine-Learning-Techniken, die versuchen, das Machine-Learning-Modell alle Muster ex nihilo entdecken zu lassen, etabliert dieser strukturierte Ansatz die eigentliche Struktur, die wir lernen müssen. Der hier wirkende statistische Mechanismus hat somit nur einen begrenzten Spielraum dessen, was er lernen soll. Folglich kann er in Bezug auf Dateneffizienz unglaublich effizient sein. Natürlich beruht all das darauf, dass wir die richtige Struktur gewählt haben.

Wie Sie sehen können, ist es sehr einfach, Experimente durchzuführen. Wir machen bereits etwas sehr Kompliziertes, und in weniger als 50 Zeilen könnten wir eine ziemlich komplexe Walmart-ähnliche Situation bewältigen. Das ist wirklich eine Leistung. Es gibt einen gewissen empirischen Prozess, aber in Wirklichkeit ist es nicht viel. Wir sprechen hier von ein paar Dutzend Zeilen. Bedenken Sie, dass ein ERP-System, wie es in einem Unternehmen oder einem großen Einzelhandelsnetzwerk betrieben wird, typischerweise tausend Tabellen und 100 Felder pro Tabelle hat. Die Komplexität der Geschäftssysteme ist also im Vergleich zur Komplexität dieses strukturierten Vorhersagemodells absolut gigantisch. Wenn wir ein wenig Zeit mit Iterationen verbringen müssen, ist das fast nichts.

Zudem zeigt der M5 Forecasting Wettbewerb, dass supply chain Praktiker die Muster bereits kennen. Als das M5-Team drei Kalender-Muster verwendete – nämlich Wochentag, Monat des Jahres und Tag des Monats – waren all diese Muster für jeden erfahrenen supply chain Praktiker selbstverständlich. Die Realität in supply chain ist, dass wir nicht versuchen, ein verborgenes Muster zu entdecken. Die Tatsache, dass beispielsweise ein massiver Preisnachlass die Nachfrage massiv erhöhen wird, wird niemanden überraschen. Die einzige verbleibende Frage ist, wie groß der Effekt genau ist und wie die genaue Form der Reaktion aussieht. Das sind relativ technische Details, und wenn man sich die Möglichkeit gibt, ein wenig zu experimentieren, kann man diese Probleme relativ leicht angehen.

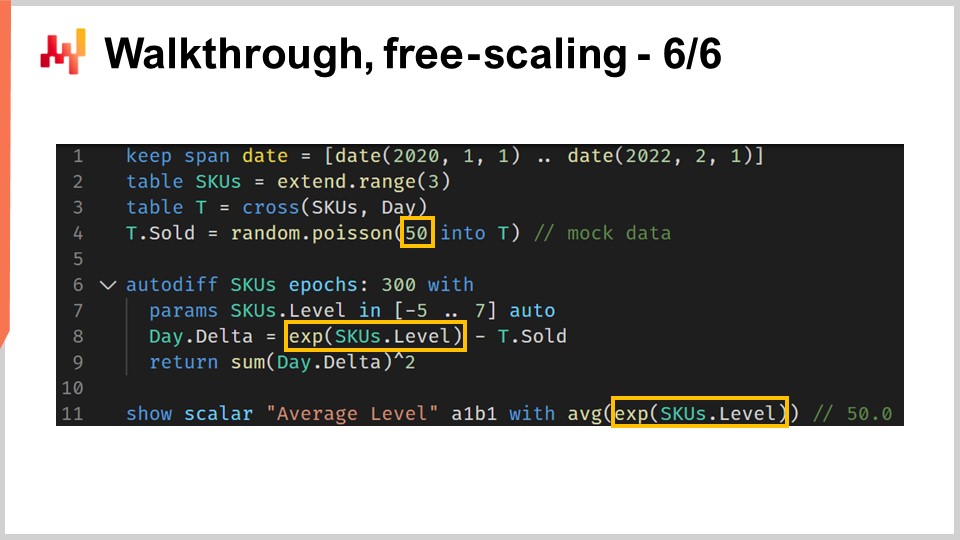
Als letzter Schritt dieser Durchsicht möchte ich auf eine kleine Besonderheit von differentiable programming hinweisen. differentiable programming sollte nicht mit einem generischen mathematischen Optimierungslöser verwechselt werden. Wir müssen im Hinterkopf behalten, dass ein Gradientabstieg stattfindet. Genauer gesagt hat der Algorithmus, der zur Optimierung und Aktualisierung der Parameter verwendet wird, eine maximale Abstiegsgeschwindigkeit, die der Lernrate entspricht, die mit dem ADAM-Algorithmus einhergeht. In Envision beträgt die Standard-Lernrate 0,01.

Wenn wir uns den Code ansehen, haben wir in Zeile 4 eine Initialisierung eingeführt, bei der die verkauften Mengen aus einer Poisson-Verteilung mit einem Mittelwert von 50 gezogen werden. Wenn wir ein Level lernen möchten, müssten wir technisch gesehen ein Level von der Größenordnung 50 haben. Allerdings starten wir bei einer automatischen Initialisierung des Parameters mit einem Wert, der ungefähr bei eins liegt, und wir können nur in Schritten von 0,01 vorgehen. Es würde etwa 5.000 Epochen dauern, um diesen Wert von 50 tatsächlich zu erreichen. Da wir einen nicht geteilten Parameter, SKU.level, haben, wird dieser Parameter pro Epoche nur einmal berührt. Daher bräuchten wir 5.000 Epochen, was die Berechnung unnötig verlangsamen würde.

Man könnte die Lernrate erhöhen, um den Abstieg zu beschleunigen, was eine Lösung wäre. Ich würde jedoch nicht empfehlen, die Lernrate aufzublähen, da dies typischerweise nicht der richtige Ansatz ist. In einer realen Situation hätten wir zusätzlich zu diesem nicht geteilten Parameter gemeinsame Parameter. Diese gemeinsamen Parameter werden durch den stochastischen Gradientenabstieg in jeder Epoche viele Male berührt. Wenn man die Lernrate stark erhöht, riskiert man, numerische Instabilitäten für die gemeinsamen Parameter zu erzeugen. Man könnte die Bewegungsgeschwindigkeit des SKU-Levels erhöhen, würde aber für die anderen Parameter numerische Stabilitätsprobleme schaffen.

Eine bessere Technik wäre, einen Rescaling-Trick zu verwenden und den Parameter in eine Exponentialfunktion einzubetten, was genau in Zeile 8 gemacht wird. Mit diesem Wrapper können wir nun Parameterwerte für das Level erreichen, die entweder sehr niedrig oder sehr hoch sein können, und das mit deutlich weniger Epochen. Diese Besonderheit ist im Grunde die einzige, die ich einführen müsste, um ein realistisches Beispiel für diese Durchsicht der Einzelhandelsnachfrageprognose-Situation zu bieten. Alles in allem ist es eine kleine Besonderheit. Dennoch erinnert es daran, dass differentiable programming Aufmerksamkeit auf den Fluss der Gradienten erfordert. differentiable programming bietet insgesamt ein flüssiges Design-Erlebnis, aber es ist kein Zaubertrick.

Einige abschließende Gedanken: Strukturierte Modelle erreichen tatsächlich state-of-the-art Vorhersagegenauigkeit. Dieser Punkt wurde in der vorherigen Vorlesung ausführlich behandelt. Allerdings würde ich basierend auf den heute vorgestellten Elementen argumentieren, dass Genauigkeit nicht einmal der entscheidende Faktor zugunsten von differentiable programming mit einem strukturierten parametrischen Modell ist. Was wir erhalten, ist Verständnis; wir bekommen nicht nur ein Stück Software, das in der Lage ist, Vorhersagen zu treffen, sondern auch direkte Einblicke in die Muster, die wir zu erfassen versuchen. Zum Beispiel würde uns das heute vorgestellte Modell direkt eine Nachfrageprognose liefern, die mit expliziten Wochentagsgewichten und einer expliziten Elastizität der Nachfrage einhergeht. Wenn wir diese Nachfrage beispielsweise erweitern wollten, um einen Uplift in Verbindung mit Black Friday einzuführen, ein quasi-saisonales Ereignis, das nicht jedes Jahr zur gleichen Zeit stattfindet, könnten wir das tun. Wir würden einfach einen Faktor hinzufügen, und dann hätten wir eine Schätzung für den Black Friday Uplift isoliert von allen anderen Mustern, wie dem Wochentagsmuster. Dies ist von größtem Interesse.

Was wir durch den strukturierten Ansatz erhalten, ist Verständnis, und es ist weit mehr als nur das rohe Modell. Zum Beispiel, wenn wir mit einer negativen Elastizität enden – einer Situation, in der das Modell uns sagt, dass wenn man den Preis erhöht, die Nachfrage steigt – in einer Walmart-ähnlichen Situation, ist dies ein sehr zweifelhaftes Ergebnis. Höchstwahrscheinlich spiegelt es wider, dass Ihre Modellimplementierung fehlerhaft ist oder dass tiefgreifende Probleme vorliegen. Unabhängig davon, was die Genauigkeitsmetrik aussagt, sollten Sie Ihre gesamte Datenpipeline hinterfragen, wenn Sie in einer Walmart-Situation etwas erhalten, das besagt, dass durch eine Preiserhöhung mehr Produkte gekauft werden, denn höchstwahrscheinlich stimmt etwas nicht. Darum geht es beim Verständnis.

Außerdem ist das Modell veränderbar. Differenzierbares Programmieren ist unglaublich ausdrucksstark. Das Modell, das wir haben, ist nur eine Iteration auf einer Reise. Wenn sich der Markt wandelt oder sich das Unternehmen selbst wandelt, können wir uns sicher sein, dass das Modell, das wir haben, diese Entwicklung auf natürliche Weise erfassen wird. Es gibt so etwas wie eine automatische Evolution nicht; es bedarf der Anstrengung eines supply chain scientist, um diese Evolution einzufangen. Dieser Aufwand kann jedoch als relativ minimal angesehen werden. Letztlich läuft es darauf hinaus, dass wenn man ein sehr kleines, übersichtliches Modell hat, dann wird es, wenn man dieses Modell später erneut überprüfen muss, um seine Struktur anzupassen, eine relativ kleine Aufgabe sein im Vergleich zu einer Situation, in der das Modell ein technisches Ungetüm wäre.

Wenn Modelle, die mittels differenzierbarem Programmieren erstellt wurden, sorgfältig entwickelt werden, sind sie sehr stabil. Die Stabilität beruht auf der Wahl der Struktur. Stabilität ist nicht selbstverständlich für ein Programm, das man durch differenzierbares Programmieren optimiert; sie entsteht, wenn man eine sehr klare Struktur hat, in der die Parameter eine spezifische Bedeutung haben. Zum Beispiel, wenn Sie ein Modell haben, bei dem Sie, wann immer Sie es neu trainieren, komplett unterschiedliche Gewichte für den Wochentag erhalten, dann ändert sich die Realität in Ihrem Geschäft nicht so schnell. Wenn Sie Ihr Modell zweimal ausführen, sollten Sie relativ stabile Werte für den Wochentag erhalten. Wenn das nicht der Fall ist, dann stimmt etwas grundlegend mit der Art und Weise, wie Sie Ihre Nachfrage modelliert haben, nicht. Folglich, wenn Sie eine kluge Wahl für die Struktur Ihres Modells treffen, können Sie unglaublich stabile numerische Ergebnisse erzielen. Damit vermeiden wir Fallstricke, die dazu neigen, komplexe Machine-Learning-Modelle zu behindern, wenn wir versuchen, sie im supply chain-Kontext einzusetzen. Tatsächlich sind aus supply chain-Perspektive numerische Instabilitäten tödlich, weil wir überall Sperreffekte haben. Wenn Sie eine Schätzung der Nachfrage haben, die schwankt, bedeutet das, dass Sie zufällig eine Bestellung oder einen Produktionsauftrag auslösen, ohne dass es notwendig wäre. Sobald Sie Ihren Produktionsauftrag ausgelöst haben, können Sie nicht in der nächsten Woche entscheiden, dass es ein Fehler war und dass Sie es nicht hätten tun sollen. Sie stecken mit der getroffenen Entscheidung fest. Wenn Sie einen Schätzer für die zukünftige Nachfrage haben, der weiterhin schwankt, werden Sie am Ende mit aufgeblähten replenishment und aufgeblähten Produktionsaufträgen dastehen. Dieses Problem lässt sich durch Sicherstellung der Stabilität lösen, was eine Frage des Designs ist.

Eine der größten Hürden, Machine Learning in die Produktion zu bringen, ist Vertrauen. Wenn man mit Millionen von Euro oder Dollar operiert, ist es entscheidend, zu verstehen, was in Ihrem numerischen Rezept vor sich geht. Fehlentscheidungen im supply chain können extrem kostspielig sein, und es gibt zahlreiche Beispiele für supply chain disasters, die durch die mangelhafte Anwendung schlecht verstandener Algorithmen verursacht wurden. Obwohl differenzierbares Programmieren sehr leistungsfähig ist, sind die Modelle, die entwickelt werden können, unglaublich einfach. Diese Modelle könnten tatsächlich in einem Excel-spreadsheet ausgeführt werden, da es sich in der Regel um einfache multiplikative Modelle mit Verzweigungen und Funktionen handelt. Der einzige Aspekt, der nicht in einem Excel-Spreadsheet ausgeführt werden könnte, ist die automatische Differentiation, und offensichtlich – wenn Sie Millionen von SKUs haben – sollten Sie nicht versuchen, dies in einer Tabelle zu tun. Einfachheitshalber ist es jedoch sehr kompatibel mit etwas, das man in eine Tabelle einfügen könnte. Diese Einfachheit trägt maßgeblich dazu bei, Vertrauen zu schaffen und Machine Learning in die Produktion zu bringen, anstatt sie als ausgefallene Prototypen zu belassen, denen man nie ganz vertrauen kann.

Schließlich, wenn wir all diese Eigenschaften zusammenbringen, erhalten wir ein sehr präzises Stück Technologie. Dieser Aspekt wurde im allerersten Kapitel dieser Vortragsreihe diskutiert. Wir möchten alle in die supply chain investierten Bemühungen in kapitalistische Investitionen umwandeln, anstatt supply chain-Experten und Praktiker als Verbrauchsmaterialien zu behandeln, die immer wieder dasselbe tun müssen. Mit diesem Ansatz können wir all diese Bemühungen als Investitionen betrachten, die über die Zeit einen Return on Investment erzeugen und weiterhin generieren. Differenzierbares Programmieren passt sehr gut zu dieser kapitalistischen Perspektive auf supply chain.

Im zweiten Kapitel haben wir einen wichtigen Vortrag mit dem Titel “Experimental Optimization” vorgestellt, der eine mögliche Antwort auf die einfache, aber grundlegende Frage lieferte: Was bedeutet es eigentlich, sich in einer supply chain zu verbessern oder besser zu sein? Die Perspektive des differenzierbaren Programmierens bietet einen sehr spezifischen Einblick in viele Herausforderungen, denen supply chain-Praktiker gegenüberstehen. Unternehmens-software vendors geben häufig schlechten Daten die Schuld an ihren supply chain-Fehlern. Ich glaube jedoch, dass dies einfach der falsche Ansatz ist, um das Problem zu betrachten. Die Daten sind, was sie sind. Ihr ERP-System wurde nie für Data Science entwickelt, aber es funktioniert seit Jahren, wenn nicht Jahrzehnten reibungslos, und die Mitarbeiter im Unternehmen schaffen es trotzdem, die supply chain zu betreiben. Selbst wenn Ihr ERP, das Daten über Ihre supply chain erfasst, nicht perfekt ist, ist das in Ordnung. Wenn Sie erwarten, dass perfekte Daten zur Verfügung stehen, ist das nur Wunschdenken. Wir sprechen hier von supply chain; die Welt ist sehr komplex, sodass Systeme unvollkommen sind. Realistischerweise haben Sie nicht ein einziges Geschäftssystem; Sie haben etwa ein halbes Dutzend, und sie stimmen nicht vollständig überein. Das ist einfach eine Tatsache des Lebens. Wenn Unternehmensanbieter jedoch schlechten Daten die Schuld geben, liegt die Realität darin, dass ein sehr spezifisches Prognosemodell vom Anbieter verwendet wird, und dieses Modell wurde mit einem bestimmten Satz von Annahmen über das Unternehmen entwickelt. Das Problem ist, dass, wenn Ihr Unternehmen zufällig eine dieser Annahmen verletzt, die Technologie völlig zusammenbricht. In dieser Situation haben Sie ein Prognosemodell, das mit unrealistischen Annahmen arbeitet, Sie füttern es mit den nicht perfekten Daten, und so bricht die Technologie zusammen. Es ist völlig unangemessen zu sagen, dass das Unternehmen schuld sei. Die fehlerhafte Technologie ist diejenige, die vom Anbieter vorangetrieben wird und völlig unrealistische Annahmen darüber trifft, welche Daten in einem supply chain-Kontext überhaupt möglich sind.

Ich habe heute keinen Benchmark für irgendeine Genauigkeitsmetrik vorgestellt. Meine These ist jedoch, dass diese Genauigkeitsmetriken größtenteils unerheblich sind. Ein Prognosemodell ist ein Werkzeug, um Entscheidungen zu treffen. Was zählt, ist, ob diese Entscheidungen – was gekauft werden soll, was produziert werden soll, ob der Preis erhöht oder gesenkt wird – gut oder schlecht sind. Schlechte Entscheidungen können auf das Prognosemodell zurückgeführt werden, das stimmt. Aber meistens ist es kein Genauigkeitsproblem. Zum Beispiel hatten wir ein Verkaufsprognosemodell und haben den Aspekt des Lagerfehlbestandes behoben, der nicht angemessen gemanagt wurde. Als wir jedoch den Lagerfehlbestand bereinigt haben, haben wir im Grunde genommen die Genauigkeitsmetrik selbst korrigiert. Das Beheben des Prognosemodells bedeutet also nicht, die Genauigkeit zu verbessern; sehr häufig bedeutet es, buchstäblich das zugrunde liegende Problem und die Perspektive, in der Sie arbeiten, zu überdenken und dadurch die Genauigkeitsmetrik oder etwas noch Grundlegenderes zu verändern. Das Problem bei der klassischen Perspektive ist, dass sie davon ausgeht, dass die Genauigkeitsmetrik ein erstrebenswertes Ziel ist. Das ist nicht ganz der Fall.

supply chain operieren in der realen Welt, und es gibt zahlreiche unerwartete und sogar außergewöhnliche Ereignisse. Zum Beispiel kann es zu einer Blockade des Suezkanals durch ein Schiff kommen; dies ist ein völlig außergewöhnliches Ereignis. In solch einer Situation würde jedes existierende Prognosemodell für die Durchlaufzeit, das sich mit diesem Teil der Welt befasst, sofort ungültig werden. Offensichtlich war so etwas bisher noch nie passiert, sodass wir in solch einer Situation nichts wirklich rücktesten können. Selbst wenn wir diese völlig außergewöhnliche Situation mit einem Schiff, das den Suezkanal blockiert, haben, können wir das Modell trotzdem anpassen – zumindest, wenn wir einen solchen White-Box-Ansatz haben, den ich heute vorstelle. Diese Anpassung wird ein gewisses Maß an Schätzarbeit beinhalten, was in Ordnung ist. Es ist besser, ungefähr richtig zu liegen, als genau falsch. Zum Beispiel, wenn wir davon ausgehen, dass der Suezkanal blockiert ist, können Sie einfach sagen: “Fügen wir der Durchlaufzeit für alle Lieferungen, die über diese Route gehen sollten, einen Monat hinzu.” Das ist sehr ungenau, aber es ist besser, anzunehmen, dass es überhaupt keine Verzögerung geben wird, obwohl Sie bereits die Information haben. Außerdem kommt Veränderung häufig von innen. Betrachten wir zum Beispiel ein Einzelhandelsnetzwerk, das ein altes Distributionszentrum und ein neues Distributionszentrum hat, das einige Dutzend Filialen beliefert. Nehmen wir an, es findet eine Migration statt, bei der im Grunde genommen die Lieferungen für die Filialen vom alten zum neuen Distributionszentrum verlagert werden. Diese Situation tritt fast nur einmal in der Geschichte dieses spezifischen Einzelhändlers auf und kann nicht wirklich rückgetestet werden. Dennoch ist es mit einem Ansatz wie dem differenzierbaren Programmieren völlig unkompliziert, ein Modell zu implementieren, das dieser allmählichen Migration gerecht wird.

Zusammenfassend ist differenzierbares Programmieren eine Technologie, die uns einen Ansatz bietet, unsere Einsichten über die Zukunft zu strukturieren. Differenzierbares Programmieren ermöglicht es uns, buchstäblich die Art und Weise zu gestalten, wie wir in die Zukunft blicken. Es befindet sich auf der Wahrnehmungsseite dieses Bildes. Basierend auf dieser Wahrnehmung können wir bessere Entscheidungen für supply chain treffen, und diese Entscheidungen treiben die Maßnahmen an, die auf der anderen Seite stehen. Eines der größten Missverständnisse der gängigen supply chain-Theorie ist, dass man Wahrnehmung und Handlung isoliert als streng getrennte Komponenten behandeln könne. Das äußert sich beispielsweise darin, dass ein Team für die Planung (das ist Wahrnehmung) und ein unabhängiges Team für [replenishment] (das ist Handlung) zuständig ist.

Der Feedbackkreis zwischen Wahrnehmung und Handlung ist jedoch von äußerster Wichtigkeit. Dies ist buchstäblich der Mechanismus, der Sie zu einer korrekten Form der Wahrnehmung führt. Wenn Sie diesen Feedbackkreis nicht haben, ist nicht einmal klar, ob Sie das Richtige betrachten oder ob das, was Sie betrachten, wirklich dem entspricht, was Sie zu glauben meinen. Sie benötigen diesen Feedbackmechanismus, und durch diesen Feedbackkreis können Sie Ihre Modelle tatsächlich zu einer korrekten quantitativen Bewertung der Zukunft lenken, die für die Handlungsoptionen Ihrer supply chain relevant ist. Die gängigen supply chain-Ansätze verwerfen diesen Fall nahezu vollständig, weil ich im Wesentlichen glaube, dass sie an eine sehr starre Form der Prognose gebunden sind. Diese modellzentrierte Form der Prognose kann ein altes Modell sein, wie das Holt-Winters-Prognosemodell, oder ein aktuelles, wie Facebook Prophet. Die Situation bleibt gleich: Wenn Sie an einem einzigen Prognosemodell festhängen, dann ist sämtliches Feedback, das Sie von der Handlungsseite erhalten, hinfällig, weil Sie nichts an diesem Feedback ändern können, außer es völlig zu ignorieren.

Wenn Sie an einem bestimmten Prognosemodell festhängen, können Sie Ihr Modell nicht umformatieren oder umstrukturieren, sobald Sie Informationen von der Handlungsseite erhalten. Differenzierbares Programmieren hingegen, mit seinem strukturierten Modellierungsansatz, bietet Ihnen ein völlig anderes Paradigma. Das Prognosemodell ist vollständig austauschbar – das gesamte Modell. Wenn das Feedback, das Sie von Ihrer Handlung erhalten, radikale Änderungen in Ihrer prognostischen Perspektive erfordert, dann setzen Sie diese radikalen Änderungen einfach um. Es besteht keine besondere Bindung an eine bestimmte Iteration des Modells. Ein sehr einfaches Modell zu behalten, trägt maßgeblich dazu bei, sicherzustellen, dass Sie, sobald Sie in der Produktion sind, die Möglichkeit bewahren, dieses Modell weiter zu verändern. Denn wenn das, was Sie entwickelt haben, einem Ungeheuer, einem technischen Monster gleicht, wird es, sobald Sie in der Produktion sind, unglaublich schwierig, es zu ändern. Einer der Schlüsselaspekte ist, dass, wenn Sie kontinuierlich Änderungen vornehmen wollen, Sie ein Modell benötigen, das in Bezug auf den Codeumfang und die interne Komplexität sehr sparsam ist. Hier glänzt das differenzierbare Programmieren. Es geht nicht darum, eine höhere Genauigkeit zu erreichen; es geht darum, eine höhere Relevanz zu erzielen. Ohne Relevanz sind alle Genauigkeitsmetriken völlig hinfällig. Differenzierbares Programmieren und strukturierte Modellierung bieten Ihnen den Weg, Relevanz zu erreichen und diese über die Zeit aufrechtzuerhalten.

Dies schließt den heutigen Vortrag ab. Nächstes Mal, am zweiten März, zur gleichen Tageszeit, 15 Uhr Pariser Zeit, werde ich probabilistisches Modellieren für supply chain präsentieren. Wir werden einen genaueren Blick auf die technischen Implikationen werfen, alle möglichen Zukünfte zu betrachten, anstatt lediglich eine Zukunft auszuwählen und sie als richtig zu deklarieren. Tatsächlich ist es sehr wichtig, alle möglichen Zukünfte in Betracht zu ziehen, wenn Sie möchten, dass Ihre supply chain effektiv widerstandsfähig gegen Risiken ist. Wenn Sie sich nur auf eine Zukunft festlegen, führt das fast zwangsläufig dazu, dass Sie etwas erhalten, das unglaublich fragil ist, falls Ihre Prognose nicht perfekt korrekt ist. Und wissen Sie was, die Prognose ist niemals vollständig korrekt. Deshalb ist es sehr wichtig, den Gedanken zu verinnerlichen, dass Sie alle möglichen Zukünfte betrachten müssen, und wir werden uns anschauen, wie man das mit modernen numerischen Rezepten umsetzt.

Question: Stochastisches Rauschen wird hinzugefügt, um lokale Minima zu vermeiden, aber wie wird es genutzt oder skaliert, um große Abweichungen zu vermeiden, damit der Gradientabstieg nicht weit von seinem Ziel abgeworfen wird?

Das ist eine sehr interessante Frage, und diese Antwort hat zwei Teile.

Zunächst einmal ist dies der Grund, warum der Adam-Algorithmus in Bezug auf die Größe der Bewegungen sehr konservativ ist. Der Gradient ist grundsätzlich unbegrenzt; man kann einen Gradient haben, der tausende oder Millionen wert ist. Mit Adam ist der maximale Schritt jedoch tatsächlich durch die Lernrate nach oben begrenzt. Somit bietet Adam effektiv ein numerisches Rezept, das buchstäblich einen maximalen Schritt erzwingt und hoffentlich dadurch massive numerische Instabilität vermeidet.

Nun, wenn zufällig – ungeachtet der Tatsache, dass wir diese Lernrate haben – man sagen könnte, dass wir rein aufgrund reiner Schwankungen iterativ, einen Schritt nach dem anderen voranschreiten werden, allerdings häufig in eine falsche Richtung, dann ist das eine Möglichkeit. Deshalb sage ich, dass der stochastische Gradientenabstieg noch nicht vollständig verstanden ist. Er funktioniert in der Praxis unglaublich gut, aber warum er so gut funktioniert, warum er so schnell konvergiert und warum wir nicht auf mehr der möglichen Probleme stoßen, ist nicht vollständig geklärt, vor allem wenn man bedenkt, dass der stochastische Gradientenabstieg in hohen Dimensionen stattfindet. Typischerweise berühren buchstäblich Dutzende, wenn nicht Hunderte von Parametern jeden Schritt. Die Art von Intuition, die man in zwei oder drei Dimensionen haben kann, ist sehr irreführend; in höheren Dimensionen verhalten sich die Dinge völlig anders.

Also, der Punkt in dieser Frage ist: Es ist sehr relevant. Es gibt einen Teil, in dem es um den Adam-Zauber geht, der sehr konservativ mit dem Ausmaß der Gradienten-Schritte umgeht, und einen anderen Teil, der zwar wenig verstanden wird, in der Praxis aber sehr gut funktioniert. Übrigens glaube ich, dass gerade die Tatsache, dass der stochastische Gradientenabstieg nicht völlig intuitiv ist, auch der Grund dafür ist, dass diese Technik fast 70 Jahre lang bekannt war, aber nicht als effektiv anerkannt wurde. Fast 70 Jahre lang wussten die Leute, dass sie existierte, waren aber sehr skeptisch. Der massive Erfolg des Deep Learnings war nötig, damit die Community erkannte und zugab, dass sie tatsächlich sehr gut funktioniert, auch wenn wir nicht wirklich verstehen, warum.

Frage: Wie erkennt man, wann ein bestimmtes Muster schwach ist und daher aus dem Modell entfernt werden sollte?

Nochmals, eine sehr gute Frage. Es gibt keine strikten Kriterien; es ist buchstäblich eine Entscheidung des Supply Chain Scientist. Der Grund ist, dass, wenn das eingeführte Muster nur minimale Vorteile bietet, in Bezug auf das Modellieren nur zwei Codezeilen benötigt und der Einfluss auf die erforderliche Rechenzeit unbedeutend ist, und falls man das Muster später entfernen möchte, dies halbwegs trivial ist, man sagen könnte: “Nun, ich kann es einfach behalten. Es scheint keinen Schaden anzurichten, es bringt auch nicht viel Gutes. Ich sehe Situationen, in denen dieses Muster, das jetzt schwach ist, tatsächlich stark werden könnte.” Hinsichtlich der Wartbarkeit ist das in Ordnung.

Allerdings kann man auch die Kehrseite betrachten, bei der ein Muster nicht viel erfasst und dem Modell erheblich Rechenleistung hinzufügt. Es ist also nicht umsonst; jedes Mal, wenn man einen Parameter oder eine Logik hinzufügt, erhöht man die benötigten Rechenressourcen des Modells, wodurch es langsamer und unhandlicher wird. Wenn Sie glauben, dass dieses schwache Muster tatsächlich stark werden könnte, aber auf eine ungünstige Weise, Instabilität erzeugt und in der prädiktiven Modellierung Chaos anrichtet, ist dies typischerweise die Situation, in der Sie denken: “Nein, ich sollte es wahrscheinlich entfernen.”

Sehen Sie, es ist letztlich eine Frage der Entscheidungsfindung. Differentiable Programming ist eine Kultur; man ist nicht auf sich allein gestellt. Man hat Kollegen und Gleichgesinnte, die bei Lokad vielleicht verschiedene Dinge ausprobiert haben. Diese Art von Kultur versuchen wir zu pflegen. Ich weiß, dass es im Vergleich zur allmächtigen KI-Perspektive – der Vorstellung, dass eine allmächtige künstliche Intelligenz all diese Probleme für uns lösen könnte – etwas enttäuschend sein mag. Aber die Realität ist, dass supply chains so komplex sind und unsere Techniken der künstlichen Intelligenz so grob, dass es keinen realistischen Ersatz für menschliche Intelligenz gibt. Wenn ich von einer Entscheidungsfindung spreche, meine ich damit, dass man eine gesunde Portion angewandter, sehr menschlicher Intelligenz benötigt, denn all die algorithmischen Tricks kommen nicht annähernd an eine zufriedenstellende Antwort heran.

Nichtsdestotrotz heißt das nicht, dass man keine Art von Werkzeugen entwerfen kann. Das wäre ein anderes Thema; ich werde sehen, ob ich tatsächlich auf die Art von Tools eingehe, die wir bei Lokad bereitstellen, um das Design zu erleichtern. Ein angrenzendes Muster wäre, wenn wir einen Entscheidungsprozess treffen müssen, dass wir versuchen, sämtliche Instrumentierung bereitzustellen, damit dieser Entscheidungsprozess sehr zügig durchgeführt werden kann, wodurch der mit dieser Art von Unentschlossenheit einhergehende Schmerz – bei der der Supply Chain Scientist über das Schicksal des aktuellen Zustands des Modells entscheiden muss – minimiert wird.

Frage: Was ist die Komplexitätsschwelle einer supply chain, ab der maschinelles Lernen und Differentiable Programming deutlich bessere Ergebnisse liefern?

Bei Lokad erzielen wir in der Regel beachtliche Ergebnisse für Unternehmen, die einen Jahresumsatz von 10 Millionen Dollar und mehr haben. Ich würde sagen, es beginnt wirklich zu glänzen, wenn man ein Unternehmen mit einem Jahresumsatz von 50 Millionen Dollar und mehr hat.

Der Grund liegt darin, dass man grundsätzlich eine sehr zuverlässige Daten-Pipeline einrichten muss. Man muss in der Lage sein, alle relevanten Daten täglich aus dem ERP zu extrahieren. Ich meine nicht, dass es sich um gute oder schlechte Daten handelt, allein die vorhandenen Daten können viele Mängel aufweisen. Nichtsdestotrotz bedeutet das, dass viel Installationsarbeit nötig ist, um allein die grundlegendsten Transaktionen täglich extrahieren zu können. Wenn das Unternehmen zu klein ist, haben sie in der Regel nicht einmal eine eigene IT-Abteilung, und sie schaffen es nicht, eine zuverlässige tägliche Extraktion sicherzustellen, was die Ergebnisse erheblich beeinträchtigt.

Nun, was Branchen oder Komplexität betrifft, liegt der Punkt darin, dass in den meisten Unternehmen und in den meisten supply chains meiner Meinung nach noch nicht einmal mit der Optimierung begonnen wurde. Wie bereits gesagt, betont die Mainstream-supply chain-Theorie, dass man genauere Prognosen anstreben sollte. Ein reduzierter Prozentsatz an Prognosefehlern ist ein Ziel, und viele Unternehmen gehen das zum Beispiel mit einem Planungsteam oder einem Prognoseteam an. Meiner Meinung nach fügt all das dem Geschäft keinen echten Mehrwert hinzu, da es grundsätzlich sehr ausgeklügelte Antworten auf die falschen Fragen liefert.

Es mag überraschen, aber Differentiable Programming glänzt nicht, weil es im Grunde genommen super mächtig ist – was es ja ist – sondern weil es in der Regel das erste Mal ist, dass etwas wirklich Relevantes für das Geschäft im Unternehmen implementiert wird. Wenn man nur ein Beispiel anführen möchte: Das meiste, was in supply chain implementiert wird, sind typischerweise Modelle wie das safety stock-Modell, die keinerlei Relevanz für irgendeine reale supply chain haben. Zum Beispiel geht man im safety stock-Modell davon aus, dass es möglich sei, eine negative Durchlaufzeit zu haben, was bedeutet, dass man jetzt bestellt und gestern beliefert wird. Das ergibt keinen Sinn, und folglich sind die operativen Ergebnisse für safety stocks in der Regel unbefriedigend.

Differentiable Programming glänzt, indem es Relevanz schafft – nicht dadurch, dass es irgendeine Art von grandioser numerischer Überlegenheit erreicht oder besser ist als andere alternative maschinelle Lerntechniken. Es geht im Grunde darum, in einer Welt, die sehr komplex, chaotisch, adversarial und ständig im Wandel ist und in der man es mit einer nahezu alptraumhaften Anwendungslandschaft zu tun hat, die die zu verarbeitenden Daten repräsentiert, Relevanz zu erzielen.

Es scheint, als gäbe es keine weiteren Fragen. In diesem Fall, denke ich, sehen wir uns nächsten Monat zur Vorlesung über probabilistisches Modellieren für die supply chain.