Différentiation Automatique par Chemins Sélectifs: Au-delà de la Distribution Uniforme sur le Dropout en Rétropropagation
L’efficacité démesurée de la Stochastic Gradient Descent (SGD) est sans doute la plus grande découverte du machine learning des années 2010. SGD alimente presque toutes les percées récentes en machine learning. Conceptuellement, SGD est remarquablement simple : traiter votre ensemble de données un point à la fois et, pour chaque point, ajuster les paramètres du modèle dans la direction indiquée par ce point. D’un point de vue plus technique, la « direction » est donnée sous forme de gradient, et l’« ajustement » implique un petit coefficient d’échelle habituellement désigné sous le nom de taux d’apprentissage.
Bien que la technique SGD remonte aux années 1950, elle est restée en grande partie une méthode obscure et peu utilisée jusqu’à ce qu’elle gagne en importance avec l’avènement du deep learning. Les raisons pour lesquelles cette technique fonctionne n’étaient pas claires et, dans une certaine mesure, le restent encore. Puisque l’objectif est de minimiser l’erreur globale du modèle sur l’ensemble des données, il n’est pas évident que choisir des points de manière strictement isolée produise autre chose que du non-sens numérique.
Aujourd’hui, il est généralement admis que l’efficacité de SGD – c’est-à-dire, pourquoi cela fonctionne – tient à deux facteurs. Premièrement, bien que le gradient obtenu par SGD soit très bruité – chaque étape ne considérant qu’un seul point de données – ce gradient est très peu coûteux. Il s’avère que, pour un budget donné de ressources informatiques, l’application de nombreuses mises à jour de gradient de faible qualité surpasse de loin l’application d’une seule mise à jour de gradient de haute qualité. Deuxièmement, ces mises à jour bruitées aident le modèle à sortir des vastes plateaux d’indifférence numérique qui existent dans les dimensions supérieures. En effet, dans ces dimensions, le cœur de l’optimisation n’est pas, comme on l’a longtemps cru, de fuir les minima locaux, mais de s’échapper des plateaux locaux – des zones où la perte varie très peu.

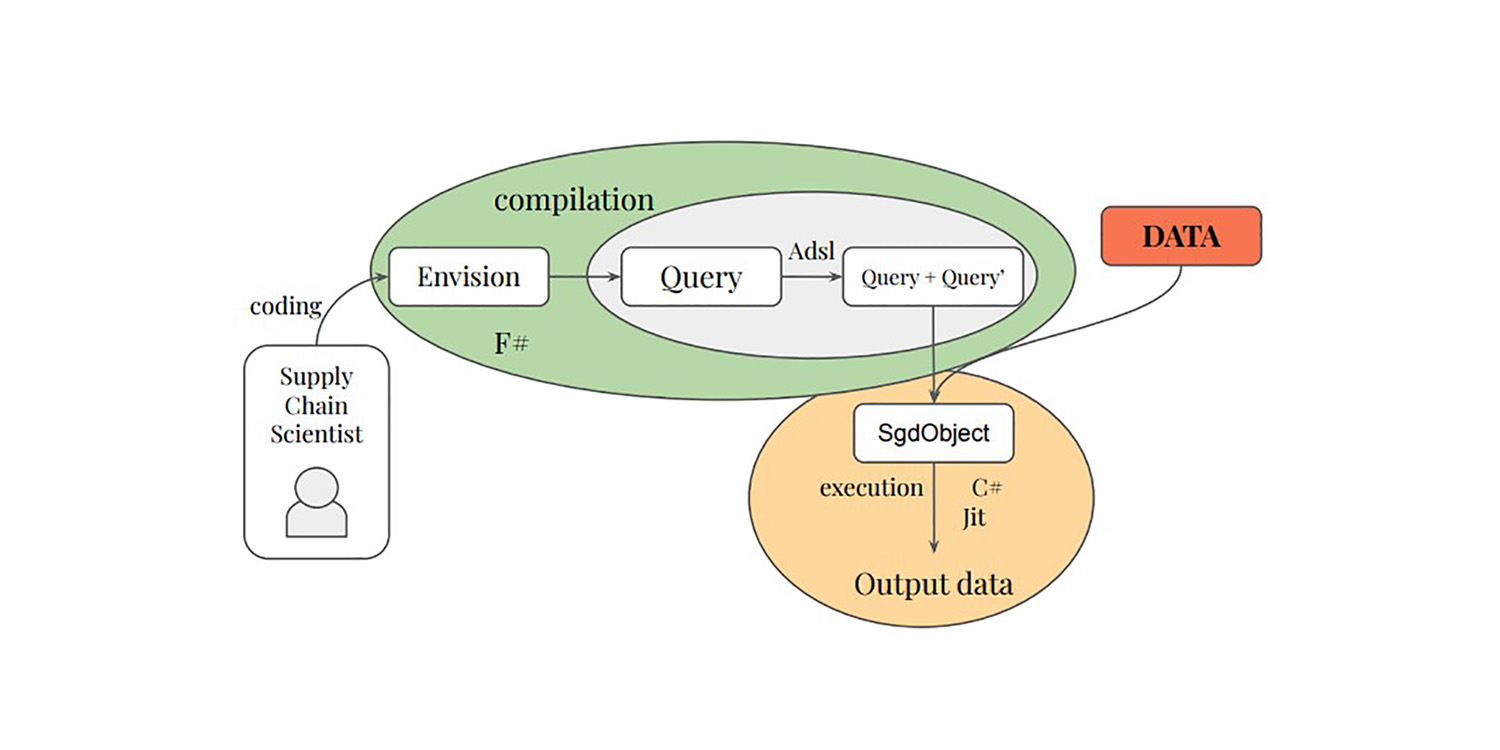
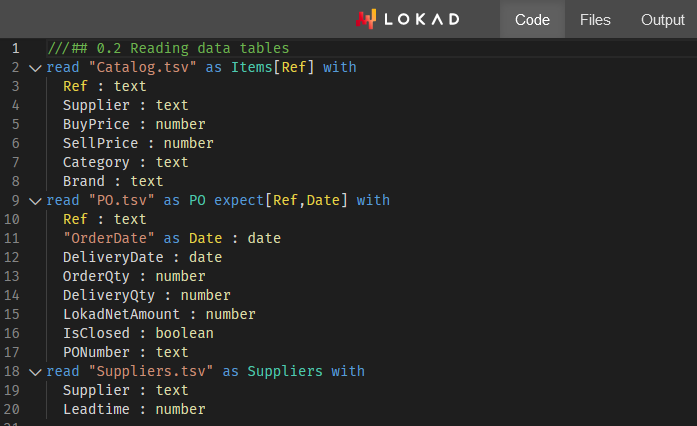
Certains d’entre nous, y compris Paul Peseux et Victor Nicollet, ont décidé de pousser ces idées plus loin. Si SGD fonctionne en sacrifiant la qualité du gradient au profit de l’efficacité informatique, que diriez-vous d’étendre encore ce principe ? Qu’en est-il d’un gradient sous-point, encore moins coûteux à calculer, quoique encore plus bruité ? C’est exactement ce qui a été réalisé avec la Différentiation Automatique par Chemins Sélectifs (SPAD). SPAD revisite l’un des piliers du paradigme moderne du machine learning avec une nuance : un point de données peut être « divisé » sur le plan des gradients selon ses chemins d’évaluation.
L’article ci-dessous présente une contribution de Paul Peseux (Lokad), Victor Nicollet (Lokad), Maxime Berar (Litis) et Thierry Paquet (Litis).
Title: Différentiation Automatique par Chemins Sélectifs: Au-delà de la Distribution Uniforme sur le Dropout en Rétropropagation
Authors: Paul Peseux, Maxime Berar, Thierry Paquet, Victor Nicollet
Abstract: Cet article présente la Différentiation Automatique par Chemins Sélectifs (SPAD), une approche novatrice visant à réduire la consommation de mémoire et à atténuer le overfitting dans les modèles basés sur les gradients pour l’intelligence artificielle embarquée. SPAD étend la méthode existante de Différentiation Automatique Randomisée, proposée par Oktay et al. et qui trace des chemins aléatoires à travers le graphe de rétropropagation avec injection de matrices, en permettant des distributions de probabilité alternatives sur le graphe de rétropropagation, améliorant ainsi les performances d’apprentissage et la gestion de la mémoire. Dans une itération spécifique, SPAD évalue et classe plusieurs chemins au sein du graphe de rétropropagation. Au fil des itérations suivantes, il suit de manière préférentielle ces chemins les mieux classés. Ce travail présente également une technique basée sur la compilation permettant un accès non dépendant du modèle aux chemins aléatoires, garantissant ainsi une généralisabilité à travers diverses architectures de modèles, et non limitée aux modèles deep learning. Des évaluations expérimentales menées sur diverses fonctions d’optimisation démontrent une performance de minimisation accrue lors de l’utilisation de SPAD. De plus, les expériences en deep learning avec SPAD atténuent notablement le surapprentissage, offrant des avantages similaires à ceux des méthodes traditionnelles de dropout, mais avec une diminution concomitante de l’utilisation de la mémoire. Nous concluons en discutant des implications uniques de la stochasticité dans notre travail et du potentiel qu’il offre pour augmenter d’autres techniques dans le domaine.