00:18 Введение
02:18 Предыстория
12:08 Зачем оптимизировать? 1/2 Прогнозирование по методу Холта-Винтса
17:32 Зачем оптимизировать? 2/2 - Задача маршрутизации транспортных средств
20:49 Что было до сихего момента
22:21 Вспомогательные науки (повторение)
23:45 Проблемы и решения (повторение)
27:12 Математическая оптимизация
28:09 Выпуклость
34:42 Стохастичность
42:10 Многоцелевая оптимизация
46:01 Проектирование решателя
50:46 Уроки глубокого обучения
01:10:35 Математическая оптимизация
01:10:58 “Настоящее” программирование
01:12:40 Локальный поиск
01:19:10 Стохастический градиентный спуск
01:26:09 Автоматическое дифференцирование
01:31:54 Дифференцируемое программирование (примерно 2018)
01:35:36 Заключение
01:37:44 Предстоящая лекция и вопросы аудитории
Описание
Математическая оптимизация — это процесс минимизации математической функции. Почти все современные методы статистического обучения — то есть прогнозирование, если рассматривать его с точки зрения управления цепями поставок — в своей основе опираются на математическую оптимизацию. Более того, как только прогнозы построены, определение наиболее прибыльных решений также базируется на математической оптимизации. Задачи в области цепей поставок часто включают множество переменных. Они, как правило, обладают стохастическим характером. Математическая оптимизация является краеугольным камнем современной практики управления цепями поставок.
Полная стенограмма

Добро пожаловать в эту серию лекций по управлению цепями поставок. Я — Жоаннес Вермо́рел, и сегодня я представлю «Математическую оптимизацию для цепей поставок». Математическая оптимизация — это чётко определённый, формализованный, вычислительно реализуемый способ нахождения наилучшего решения для данной задачи. Все задачи прогнозирования можно рассматривать как задачи математической оптимизации. Все ситуации, связанные с принятием решений, как в цепях поставок, так и вне их, также можно рассматривать как задачи математической оптимизации. На самом деле, перспектива математической оптимизации настолько глубоко укоренилась в нашем современном мировоззрении, что стало чрезвычайно сложно определить глагол “оптимизировать” вне тесных рамок, задаваемых парадигмой математической оптимизации.
Литература по математической оптимизации и экосистема программного обеспечения, предоставляющая инструменты для её реализации, чрезвычайно обширны. К сожалению, большая их часть мало полезна и практически неактуальна с точки зрения управления цепями поставок. Цель этой лекции двояка: во-первых, мы хотим понять, как подойти к математической оптимизации, чтобы получить нечто ценное и практически применимое с точки зрения цепей поставок. Во-вторых, необходимо выделить в этом обширном ландшафте некоторые из самых ценных элементов.

Формальное определение математической оптимизации достаточно простое: вы рассматриваете функцию, которая обычно называется функцией потерь, и эта функция принимает действительные значения, то есть выдаёт лишь числа. Ваша задача — определить такой входной параметр (X0), который обеспечивает наилучшее значение, минимизирующее функцию потерь. Это и есть парадигма математической оптимизации, которая на первый взгляд выглядит обманчиво простой. Мы увидим, что об этой общей перспективе можно сказать многое.
Эта область, как мне кажется, в терминах прикладной математической оптимизации была в первую очередь разработана под названием операционных исследований, что мы определяем более конкретно как классические операционные исследования, проводимые с 1940-х до конца 1970-х годов XX века. Идея заключается в том, что классические операционные исследования, в отличие от математической оптимизации, действительно ориентировались на бизнес-задачи. Математическая оптимизация же заботится о общей форме задачи оптимизации и намного меньше о том, имеет ли задача какое-либо бизнес-значение. Напротив, классические операционные исследования по сути занимались оптимизацией, но не на любых задачах – только на тех, которые признаны важными для бизнеса.
Что примечательно, мы перешли от операционных исследований к математической оптимизации практически так же, как произошёл переход от прогнозирования, возникшего в начале XX века как области, занимающейся общим прогнозированием будущих уровней экономической активности, обычно ассоциируемого с прогнозами временных рядов. Эта область была в значительной степени вытеснена машинным обучением, которое занимается предсказаниями в гораздо более широком спектре задач. Можно сказать, что процесс перехода от операционных исследований к математической оптимизации схож с переходом от прогнозирования к машинному обучению. Когда я говорил, что классическая эра операционных исследований длилась до конца 70-х, я имел в виду очень конкретную дату. В феврале 1979 года Рассел Аков опубликовал поразительную статью под названием “The Future of Operational Research is Past”. Чтобы понять эту статью, которая, как мне кажется, стала вехой в истории науки об оптимизации, нужно осознать, что Рассел Аков фактически является одним из основателей операционных исследований.
Когда он опубликовал эту статью, он уже не был молод: ему было 60 лет. Аков родился в 1919 году и почти всю свою карьеру посвятил операционным исследованиям. Опубликовав свою статью, он фактически заявил, что операционные исследования потерпели неудачу. Они не только не приносили результатов, но и интерес к отрасли уменьшался, так что к концу 90-х годов интерес к этой области был ниже, чем 20 лет назад.
Интересно отметить, что причиной этого вовсе не было то, что компьютеры того времени были намного слабее, чем современные. Проблема не заключается в ограничениях вычислительной мощности. Это конец 70-х: компьютеры были довольно скромными по сравнению с нынешними, но они всё же могли выполнять миллионы арифметических операций за разумное время. Проблема не связана с ограничением вычислительной мощности, особенно в эпоху, когда она прогрессирует с невероятной скоростью.
Кстати, эту статью читать просто потрясающе. Я настоятельно рекомендую аудитории ознакомиться с ней; вы легко найдёте её через любой любимый поисковик. Статья очень доступна и хорошо написана. Хотя проблемы, на которые указывает Аков в этой статье, по-прежнему актуальны спустя четыре десятилетия, во многом она предвидела многие проблемы, которые до сих пор преследуют современные цепи поставок.
Так в чём же тогда заключается проблема? Проблема в том, что в этой парадигме, где вы берёте функцию и оптимизируете её, можно доказать, что ваш процесс оптимизации находит хорошее или, возможно, оптимальное решение. Однако как доказать, что функция потерь, которую вы оптимизируете, имеет значение для бизнеса? Проблема в том, что если мы можем оптимизировать задачу или функцию, то что делать, если оптимизируемое нами явление — всего лишь фантазия? Что если это вовсе не соответствует реальности бизнеса, который вы пытаетесь оптимизировать?
Вот в чём суть проблемы, и вот причина, по которой все ранние попытки, по сути, потерпели неудачу. Дело в том, что когда вы создаёте математическое выражение, которое должно отражать интересы бизнеса, вы получаете математическую фантазию. Именно это и указывает Рассел Аков в своей статье, и он находится на таком этапе карьеры, когда, играя эту игру очень долго, он понял, что она в основном ни к чему не приводит. В своей статье он утверждает, что данная область потерпела неудачу, и предлагает свой диагноз, но практически не имеет решения. Это особенно интересно, так как один из отцов-основателей, очень уважаемый и признанный исследователь, говорит, что вся эта область исследований находится в тупике. Он проведёт остаток своей жизни, которая всё ещё довольно длинна, полностью переходя от количественного подхода к оптимизации бизнеса к качественному. Он проведёт последние три десятилетия своей жизни, занимаясь качественными методами, и при этом продолжит создавать весьма интересные работы во второй части своей жизни после этого переломного момента.
Теперь, что касается этой серии лекций, что же мы делаем, поскольку замечания Рассела Акоба об операционных исследованиях остаются актуальными и сегодня? На самом деле, я уже начал решать те самые большие проблемы, на которые указывал Аков, и в своё время у него и его коллег не было решений. Они могли диагностировать проблему, но не имели способа её решить. В этой серии лекций предлагаемые мной решения носят методологический характер, как и тот факт, что Аков указывал на глубокую методологическую проблему в подходе операционных исследований.
Предлагаемые мной методы по существу двояки: с одной стороны — персонал цепей поставок, а с другой — метод, именуемый экспериментальной оптимизацией, который оказывается действительно дополнением к математической оптимизации. Кроме того, в отличие от операционных исследований, претендующих на бизнес-значимость и актуальность, мой подход сегодня не исходит из угла зрения операционных исследований. Я рассматриваю проблему через призму математической оптимизации, которую позиционирую как чистую вспомогательную науку для цепей поставок. Я утверждаю, что в математической оптимизации для цепей поставок нет ничего по своей сути фундаментального; она имеет лишь основополагающее значение. Это всего лишь средство, а не цель. Вот в чем разница. Смысл может показаться очень простым, но он имеет огромное значение для достижения результатов уровня прогноза.

Итак, зачем же нам вообще нужна оптимизация? Большинство алгоритмов прогнозирования имеют в своей основе задачу математической оптимизации. На этом экране вы видите классический мультипликативный алгоритм прогнозирования временных рядов по Холту-Винтсу. Этот алгоритм имеет, прежде всего, историческое значение; я не рекомендовал бы использовать его в современных цепях поставок. Но для простоты это очень простой параметрический метод, который настолько лаконичен, что его можно полностью разместить на одном экране. Он даже не так многословен.
Все переменные, которые вы видите на экране, — это просто числа; никаких векторов здесь нет. По сути, Y(t) представляет собой вашу оценку; это ваш прогноз временного ряда. На этом экране прогнозируется на H периодов вперёд, где H является горизонтом. Можно считать, что вы работаете с Y(t), который, по существу, представляет собой ваш временной ряд. Это могут быть агрегированные данные по продажам за неделю или за месяц. Модель состоит, по существу, из трёх компонентов: Lt — уровень (один уровень на период), Bt — тренд и St — сезонная составляющая. Когда вы говорите, что хотите изучить модель Холта-Винтса, у вас есть три параметра: альфа, бета и гамма. Эти три параметра по сути являются числами от нуля до единицы. То есть у вас есть три параметра, все числа от нуля до единицы, и когда вы хотите применить алгоритм Холта-Винтса, вы просто определяете соответствующие значения для этих параметров, и всё. Идея в том, что параметры альфа, бета и гамма будут оптимальными, если они минимизируют ошибку, заданную для прогноза. На экране вы видите среднеквадратичную ошибку, что является классическим показателем.
Суть математической оптимизации заключается в разработке алгоритмов, которые позволяют определить правильные значения параметров альфа, бета и гамма. Что мы можем сделать? Самый простой и наивный метод — перебор по сетке (grid search). Grid search предполагает, что мы просто перебираем все возможные значения. Поскольку это дробные числа, их бесконечно много, поэтому мы выбираем определённое разрешение, скажем, шаги по 0.1, и будем увеличивать значения на 0.1. Поскольку у нас есть три переменные от 0 до 1, при шагах по 0.1 получается около 1000 итераций для определения наилучшего значения с выбранным разрешением.
Однако такое разрешение довольно слабое. Шаг 0.1 даёт примерно 10%-ное разрешение для масштабов, характерных для ваших параметров. Поэтому, возможно, вы захотите использовать шаг 0.01, что гораздо лучше — 1%-ное разрешение. Однако если сделать это, число комбинаций действительно взлетает: вы переходите от 1000 комбинаций к миллиону, и вот в чём проблема grid search — очень быстро вы сталкиваетесь с комбинаторным взрывом и огромным количеством вариантов.
Математическая оптимизация заключается в разработке алгоритмов, которые обеспечивают максимальную отдачу от заданного объёма вычислительных ресурсов, которые вы готовы вложить в решение задачи. Можно ли получить значительно лучшее решение, чем при простом переборе? Ответ — да, абсолютно.
Итак, что мы можем сделать в этом случае, чтобы на самом деле получить лучшее решение, затрачивая меньше вычислительных ресурсов? Во-первых, мы могли бы использовать некий градиент. Всё выражение метода Холта-Уинтерса полностью дифференцируемо, за исключением одной небольшой операции деления, которая представляет собой незначительный крайний случай и относительно легко устраняется. Таким образом, всё это выражение, включая функцию потерь, полностью дифференцируемо. Мы могли бы использовать градиент, чтобы направлять наш поиск; это был бы один из подходов.
Другой подход заключается в том, что на практике в цепочках поставок у вас может быть огромное количество временных рядов. Поэтому вместо того, чтобы рассматривать каждый временной ряд отдельно, вы можете провести перебор по сетке для первых 1000 временных рядов, вложить средства, а затем определить комбинации параметров альфа, бета и гамма, которые являются хорошими. Затем для всех остальных временных рядов вы просто выберете оптимальное решение из этого краткого списка кандидатов.
Видите ли, существует множество простых идей, как можно добиться гораздо лучших результатов, чем просто полагаться на перебор по сетке, и суть математической оптимизации, а также всевозможные задачи принятия решений, обычно можно рассматривать как задачи математической оптимизации.
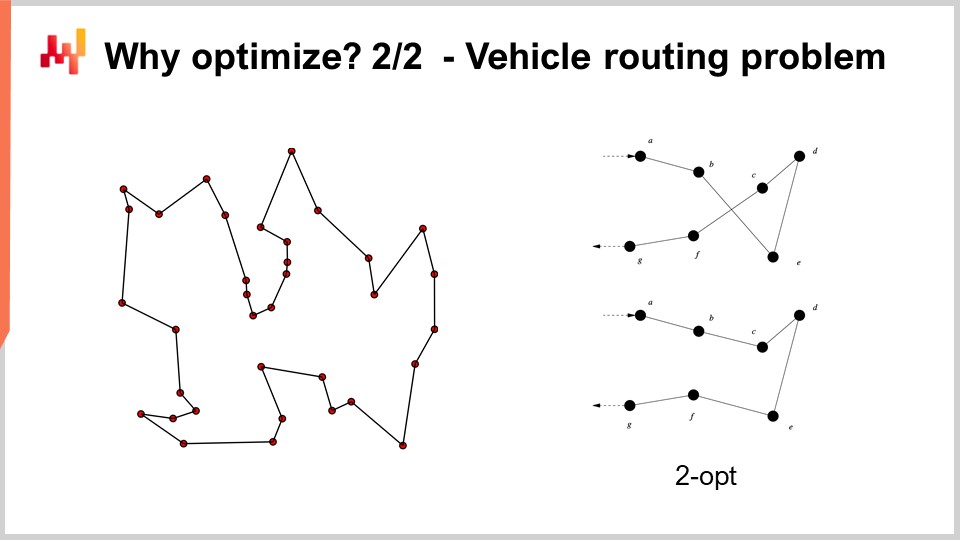
Например, задача маршрутизации транспортных средств, которую вы видите на экране, может рассматриваться как задача математической оптимизации. Суть её заключается в выборе списка точек. Я не записал формальную версию задачи, поскольку она достаточно изменчива и не даёт значительного понимания. Но если задуматься, можно просто представить: «У меня есть точки, я могу назначить каждой из них своего рода псевдранж, который представляет собой просто оценку, а затем у меня есть алгоритм, который сортирует все точки по псевродранжу в порядке возрастания, и это составляет мой маршрут». Цель алгоритма — определить такие значения псевродранжей, которые дадут наилучшие маршруты.
Теперь, в этой задаче мы видим, что перебор по сетке даже отдалённо не является вариантом. У нас десятки точек, и если попробовать все комбинации, их число будет слишком велико. Кроме того, градиент нам не поможет, по крайней мере, не очевидно, как он может помочь, потому что задача имеет явно дискретную природу, и нет чего-то вроде очевидного градиентного спуска для такой задачи.
Однако оказывается, что если мы хотим подойти к такой задаче, в литературе были выявлены весьма мощные эвристики. Например, эвристика two-opt, опубликованная Кроэсом в 1958 году, предлагает очень прямолинейный подход. Вы начинаете со случайного маршрута, и всякий раз, когда маршрут сам пересекается, вы применяете перестановку для устранения пересечения. То есть, вы начинаете со случайного маршрута, и при первом обнаружении пересечения вы меняете порядок, чтобы убрать пересечение, а затем повторяете процесс. Вы продолжаете применять эту эвристику до тех пор, пока пересечений не останется. Результатом этой очень простой эвристики становится на самом деле весьма хорошее решение. Оно может быть не оптимальным в строгом математическом смысле, то есть не обязательно идеальным, однако это всё же очень хорошее решение, которое можно получить с относительно малыми вычислительными ресурсами.
Проблема эвристики two-opt заключается в том, что, хотя она и является отличной, она невероятно специфична именно для этой задачи. Что действительно важно для математической оптимизации — это разработка методов, работающих для широкого класса задач, а не одной эвристики, которая сработает только для одной конкретной версии задачи. Поэтому нам нужны весьма универсальные методы.
Теперь, обзор текущей серии лекций: эта лекция является частью серии лекций, и текущая глава посвящена вспомогательным наукам управления цепочками поставок. В первой главе я представил свои взгляды на цепочку поставок как на область исследования и как на практику. Вторая глава была посвящена методологии, и, в частности, мы представили одну методологию, имеющую первостепенное значение для данной лекции, а именно экспериментальную оптимизацию. Это ключ к решению очень актуальной проблемы, обозначенной Расселом Аккаффом десятилетия назад. Третья глава полностью посвящена персоналу цепочки поставок. В этой лекции мы сосредотачиваемся на определении проблемы, которую собираемся решать, а не на смешении решения и самой проблемы. В четвертой главе мы изучаем все вспомогательные науки цепочки поставок. Здесь наблюдается прогрессия от самого низкого уровня в плане аппаратного обеспечения, через уровень алгоритмов, до математической оптимизации. Мы продвигаемся по уровням абстракции на протяжении всей этой серии.

Краткий обзор вспомогательных наук: они предлагают особую перспективу на саму цепочку поставок. Настоящая лекция не о самой цепочке поставок, а о одной из вспомогательных наук, связанных с ней. Эта перспектива создаёт существенную разницу между классическим взглядом операционных исследований, где оптимизация считалась конечной целью, и математической оптимизацией, которая является средством для достижения цели, а не целью сама по себе, по крайней мере, в контексте цепочек поставок. Математическая оптимизация не заботится о специфике бизнеса, и её отношение к цепочкам поставок схоже с отношением между химией и медициной. С современной точки зрения, чтобы быть отличным врачом, не обязательно быть блестящим химиком; однако врач, утверждающий, что он ничего не знает о химии, вызывает подозрения.

Математическая оптимизация исходит из того, что проблема известна. Ей не важна корректность самой проблемы, а важен максимальный выжим из возможностей данной задачи с точки зрения оптимизации. В некотором смысле она подобна микроскопу — очень мощному, но с чрезвычайно узким полем зрения. Опасность, как мы уже упоминали в обсуждении будущего операционных исследований, заключается в том, что если нацелить микроскоп не в ту область, можно отвлечься на интересные, но в конечном итоге несущественные интеллектуальные задачи.
Вот почему математическую оптимизацию необходимо применять в сочетании с экспериментальной оптимизацией. Экспериментальная оптимизация, которую мы рассмотрели в предыдущей лекции, — это процесс итеративного улучшения постановки проблемы с помощью обратной связи из реального мира. Экспериментальная оптимизация — это процесс изменения не решения, а самой задачи, чтобы итеративно прийти к хорошей постановке проблемы. В этом и заключается суть вопроса, и здесь у Рассела Аккаффа и его современников не было решения. У них были инструменты для оптимизации данной задачи, но не для изменения задачи до тех пор, пока она не станет хорошей. Если вы формулируете математическую задачу так, как её можно записать в башне из слоновой кости, без обратной связи из реального мира, вы получаете фантазию. Ваша отправная точка при начале процесса экспериментальной оптимизации — всего лишь фантазия. Для того чтобы это сработало, необходима обратная связь из реального мира. Идея заключается в том, чтобы чередовать математическую оптимизацию и экспериментальную оптимизацию. На каждом этапе процесса экспериментальной оптимизации вы будете использовать инструменты математической оптимизации. Цель состоит в минимизации как вычислительных ресурсов, так и инженерных затрат, что позволяет процессу итеративно переходить к следующей версии задачи.

В этой лекции мы сначала уточним наше понимание перспективы математической оптимизации. Формальное определение кажется обманчиво простым, но существуют сложности, о которых нужно знать, чтобы добиться практической применимости в цепочках поставок. Затем мы рассмотрим два широких класса решателей, представляющих современное состояние математической оптимизации с точки зрения цепочек поставок.
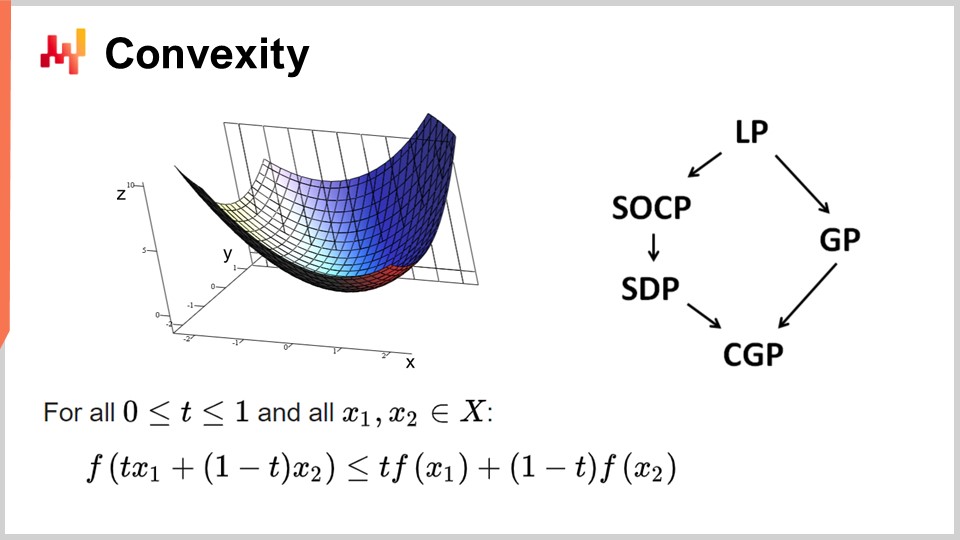
Во-первых, давайте обсудим выпуклость и ранние работы в области математической оптимизации. Операционные исследования изначально фокусировались на выпуклых функциях потерь. Функция называется выпуклой, если она удовлетворяет определённым свойствам. Интуитивно, функция является выпуклой, если для любых двух точек на многообразии, определяемом функцией, прямая, соединяющая эти точки, всегда находится выше значений функции между ними.
Выпуклость — ключ к настоящей математической оптимизации, где можно доказать результаты. Интуитивно, если у вас есть выпуклая функция, это означает, что для любой точки функции (для любого кандидатного решения) вы всегда можете осмотреться и найти направление, по которому можно двигаться вниз. Независимо от того, с какой точки вы начинаете, всегда можно двигаться вниз, а движение вниз всегда является хорошим шагом. Единственная точка, где дальнейшее снижение невозможно, — это по сути оптимальная точка. Я упрощаю; существуют крайние случаи, когда решений несколько или вовсе нет. Но отбросив несколько исключений, единственная точка, где нельзя дальше оптимизировать выпуклой функцией, — это оптимальная точка. В противном случае, всегда можно двигаться вниз, и это правильное решение.
Проводилось огромное количество исследований по выпуклым функциям, и за эти годы появилось множество парадигм программирования. LP означает линейное программирование, а другие парадигмы включают программирование на вторых конусах, геометрическое программирование (работающее с полиномами), полусемидефинитное программирование (с матрицами с положительными собственными значениями) и геометрическое конусное программирование. Все эти подходы имеют общее то, что они занимаются структурированными выпуклыми задачами. Они выпуклы как по функции потерь, так и по ограничениям, определяющим допустимые решения.
Эти подходы вызвали огромный интерес, и по ним было создано обширное научное наследие. Однако, несмотря на их впечатляющие названия, эти парадигмы обладают очень ограниченной выразительностью. Даже простые задачи превосходят их возможности. Например, оптимизация параметров метода Холта-Уинтерса, базовой модели прогнозирования 1960-х годов, уже выходит за рамки возможностей этих подходов. Точно так же задачи маршрутизации транспортных средств и задачи коммивояжёра, обе являющиеся достаточно простыми, превосходят возможности этих методов.
Вот почему я говорил с самого начала, что существует огромное количество литературы, но практически не к чему её применить. Единственная точка, где уже не получается двигаться дальше, — это по сути оптимальная точка. Я упрощаю; бывают крайние случаи, когда решений несколько или вовсе нет. Но отбросив несколько исключений, единственная точка, где нельзя дальше оптимизировать выпуклой функцией, — это оптимальная точка. В противном случае, всегда можно двигаться вниз, и это правильное решение.
Проводилось огромное количество исследований по выпуклым функциям, и за эти годы появилось множество парадигм программирования. LP означает линейное программирование, а другие парадигмы включают программирование на вторых конусах, геометрическое программирование (работающее с полиномами), полусемидефинитное программирование (с матрицами с положительными собственными значениями) и геометрическое конусное программирование. Все эти подходы имеют общее то, что они занимаются структурированными выпуклыми задачами. Они выпуклы как по функции потерь, так и по ограничениям, определяющим допустимые решения.
Эти подходы вызвали огромный интерес, и по ним было создано обширное научное наследие. Однако, несмотря на их впечатляющие названия, эти парадигмы обладают очень ограниченной выразительностью. Даже простые задачи превосходят их возможности. Например, оптимизация параметров метода Холта-Уинтерса, базовой модели прогнозирования 1960-х годов, уже выходит за рамки возможностей этих подходов. Точно так же задачи маршрутизации транспортных средств и задачи коммивояжёра, хотя и достаточно простые, превосходят возможности этих методов.
Вот почему я говорил с самого начала, что существует огромное количество литературы, но практически не к чему её применить. Одна из проблем заключалась в ошибочном упоре на чистые решатели математической оптимизации. Эти решатели весьма интересны с математической точки зрения, поскольку позволяют строить математические доказательства, но их можно применять только к буквально игрушечным или полностью выдуманным задачам. Как только вы переходите в реальный мир, они оказываются неэффективными, и в этих областях за последние десятилетия практически не было прогресса. Что касается цепочек поставок, то почти ничто, за исключением нескольких нишевых областей, не имеет отношения к этим решателям.

Еще один аспект, который полностью игнорировался в классическую эпоху операционных исследований, — это случайность. Случайность или стохастичность имеет критическое значение в двух радикально разных аспектах. Первый аспект, который необходимо учитывать, — это сам решатель. В наши дни все современные решатели в значительной степени используют стохастические процессы внутри себя. Это очень интересно по сравнению с полностью детерминированным процессом. Я говорю о внутренних механизмах решателя, о части программного обеспечения, которая реализует методы математической оптимизации.
Причина, по которой все современные решатели в значительной степени используют стохастические процессы, кроется в устройстве современного компьютерного оборудования. Альтернатива случайности при поиске решений — хранить в памяти то, что уже было сделано ранее, чтобы не застревать в одном и том же цикле. Если вам необходимо запоминать, это потребляет память. Проблема в том, что требуется много обращений к памяти. Один из способов внедрения случайности обычно позволяет значительно сократить необходимость случайного доступа к памяти.
Сделав ваш процесс стохастическим, вы можете избежать обращения к собственной базе данных того, что вы уже протестировали или не протестировали среди возможных решений проблемы, которую вы хотите оптимизировать. Вы делаете это немного случайным образом, но не полностью. Это имеет ключевое значение практически для всех современных решателей. Один из несколько контринтуитивных аспектов стохастического процесса заключается в том, что, хотя у вас может быть стохастический решатель, результат всё же может оказаться достаточно детерминированным. Чтобы это понять, представьте аналогию с серией сит. Сито — по своей сути физический стохастический процесс, в котором вы применяете случайные движения, и происходит процесс просеивания. Хотя процесс полностью случайный, его итог абсолютно детерминирован. В конце вы получаете полностью предсказуемый результат процесса просеивания, даже если ваш процесс изначально был случайным. Именно это происходит с хорошо спроектированными стохастическими решателями. Это один из ключевых ингредиентов современных решателей.
Другой аспект, который является ортогональным по отношению к случайности, — это стохастическая природа самих задач. Этот аспект был почти полностью отсутствующим в классическую эпоху операционных исследований — идея о том, что ваша функция потерь зашумлена и любое измерение, которое вы от неё получите, будет иметь некоторую степень шума. Это почти всегда так в цепочке поставок. Почему? Дело в том, что в цепочке поставок, когда вы принимаете решение, оно основано на ожидании будущих событий. Если вы решаете что-то купить, это потому, что вы ожидаете, что в будущем возникнет потребность в этом. Будущее не записано заранее, поэтому вы можете иметь некоторое представление о будущем, но это представление никогда не бывает идеальным. Если вы решаете приступить к производству продукта сейчас, это потому, что вы ожидаете, что позднее появится спрос на этот продукт. Качество вашего сегодняшнего решения зависит от неопределённых будущих условий, и, следовательно, любое решение в цепочке поставок будет обладать функцией потерь, которая изменяется в зависимости от этих неконтролируемых будущих условий. Такая случайность, связанная с будущими событиями, неустранима, и именно поэтому мы имеем дело со стохастическими задачами.
Однако, если мы вернёмся к классическим математическим решателям, мы увидим, что этот аспект полностью отсутствует, что является большой проблемой. Это означает, что существуют классы решателей, которые даже не способны понять те задачи, с которыми мы столкнёмся, потому что задачи, представляющие интерес, когда мы хотим применить математическую оптимизацию, будут стохастической природы. Я говорю о шуме в функции потерь.
Существует возражение, что если у вас стохастическая задача, вы всегда можете преобразовать её обратно в детерминированную посредством сэмплинга. Если вы оцените свою зашумлённую функцию потерь 10 000 раз, вы получите примерно детерминированную функцию потерь. Однако такой подход невероятно неэффективен, так как он вносит 10 000-кратное увеличение вычислительной нагрузки вашего процесса оптимизации. Перспектива математической оптимизации заключается в получении наилучших результатов при ограниченных вычислительных ресурсах. Речь не идёт о том, чтобы инвестировать бесконечно большое количество ресурсов для решения задачи. Нам приходится иметь дело с конечным количеством вычислительных ресурсов, даже если это количество довольно велико. Поэтому при выборе решателей важно, чтобы они нативно могли обрабатывать стохастические задачи, а не прибегали по умолчанию к детерминированному подходу.
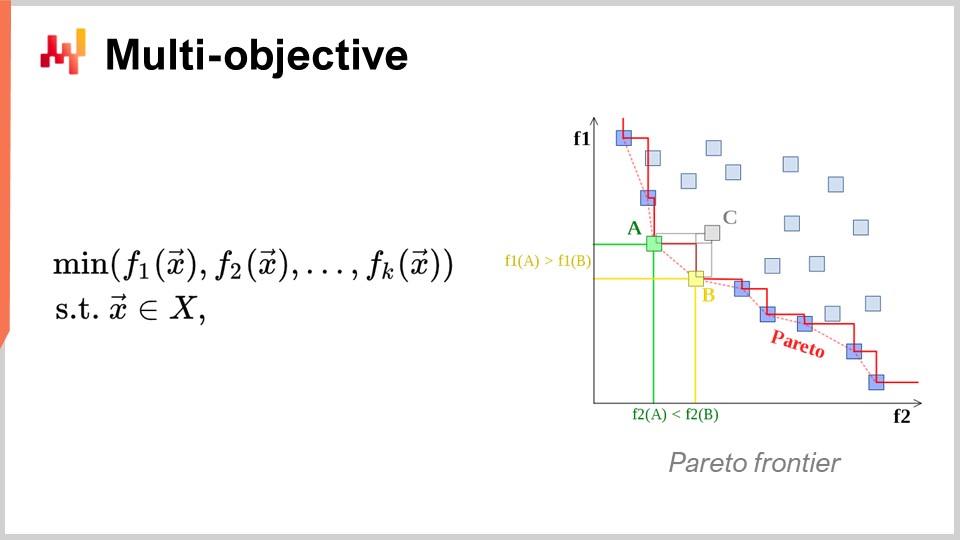
Ещё один аспект, имеющий первостепенное значение, — это многокритериальная оптимизация. В наивном изложении задачи математической оптимизации я утверждал, что функция потерь по сути однозначна, то есть существует одно значение, которое мы хотим минимизировать. Но что, если у нас есть вектор значений, и мы хотим найти решение, которое даёт минимальную точку согласно лексикографическому порядку всех векторов, таких как f1, f2, f3 и так далее?
Почему это вообще интересно с точки зрения цепочки поставок? Дело в том, что если использовать многокритериальный подход, можно представить все ограничения в виде единой специальной функции потерь. Сначала можно создать функцию, которая подсчитывает нарушения ограничений. Зачем вам ограничения в цепочке поставок? Они встречаются повсюду. Например, если вы размещаете заказ на покупку, вы должны убедиться, что на складе достаточно места для хранения товаров по прибытии. То есть у вас есть ограничения по месту для хранения, производственной мощности и многим другим параметрам. Идея в том, что вместо использования решателя с особыми случаями для ограничений, гораздо интереснее иметь решатель, который может нативно обрабатывать многокритериальную оптимизацию и где ограничения выражаются как одна из целей. Вы просто подсчитываете количество нарушений ограничений и стремитесь минимизировать это значение, доводя число нарушений до нуля.
Причина, по которой такой подход особенно актуален для цепочки поставок, заключается в том, что оптимизационные задачи, с которыми сталкиваются цепочки поставок, не являются криптографическими головоломками. Это не суперсложные комбинаторные задачи, где либо у вас есть решение, и оно абсолютно правильное, либо вы чуть не попали в решение, и у вас ничего не выходит. В цепочке поставок получение того, что обычно называется допустимым решением — решением, удовлетворяющим всем ограничениям — обычно является абсолютно тривиальной задачей. Найти решение, удовлетворяющее ограничениям, не представляет большой сложности. Что же по-настоящему сложно, так это среди всех допустимых решений определить то, которое является наиболее выгодным для бизнеса. В этом и заключается основная сложность. Найти решение, не нарушающее ограничения, довольно просто. Это не то, что происходит в других областях, например, в математической оптимизации для промышленного дизайна, когда требуется разместить компоненты внутри сотового телефона. Это невероятно строго ограниченная задача, и вы не можете обойтись без одного из ограничений, получив небольшое отступление в дизайне телефона. Это задача, которая чрезвычайно жёстко ограничена и комбинаторна, и где ограничения необходимо рассматривать как важнейший компонент. Я считаю, что для подавляющего большинства задач цепочки поставок это не требуется. Таким образом, наличие методов нативной многокритериальной оптимизации имеет чрезвычайно высокое значение.
Теперь давайте немного подробнее обсудим дизайн решателя. С точки зрения высокого уровня, если рассматривать, как мы хотим спроектировать программное обеспечение, которое будет генерировать решения для очень широкого класса задач, существуют два заметных конструктивных аспекта, которые я хотел бы выделить. Первый аспект, который следует принять во внимание, — это то, будем ли мы работать по принципу «белого ящика» или «чёрного ящика». Идея подхода «чёрного ящика» заключается в том, что мы можем обрабатывать любую произвольную программу, так что функция потерь может быть абсолютно любой программой. Нам всё равно; мы рассматриваем это как полностью чёрный ящик. Единственное, что нам нужно — это программа, в которой можно оценить предлагаемые решения и получить их значение. Напротив, подход «белого ящика» подчеркивает тот факт, что сама функция потерь имеет структуру, которую можно проанализировать и использовать. Мы можем заглянуть внутрь функции потерь. Кстати, когда я говорил о выпуклости несколько слайдов назад, все эти модели и чисто математические решатели действительно представляли собой подходы «белого ящика». Это крайний случай, когда не только можно заглянуть внутрь задачи, но и сама задача имеет очень жёсткую структуру, например, в полусемидефинитивном программировании, где форма задачи строго фиксирована. Однако, не прибегая к такому жёсткому математическому аппарату, можно, например, сказать, что в рамках подхода «белого ящика» у вас есть нечто вроде градиента, который поможет вам. Градиент функции потерь имеет первостепенное значение, потому что он позволяет определить направление, в котором нужно двигаться для уменьшения потерь, даже если задача не является выпуклой, где простой градиентный спуск гарантирует хороший результат. Как правило, если вы можете работать с решателем «белого ящика», его производительность будет на порядки выше, чем у решателя «чёрного ящика».
Теперь, в качестве второго аспекта, рассмотрим офлайн и онлайн решатели. Офлайн-решатель обычно работает пакетно: он принимает задачу, выполняется, и вам приходится ждать его завершения. По окончании процесса решатель выдаёт наилучшее решение или нечто, что является наилучшим найденным решением. В отличие от этого, онлайн-решатель работает по принципу наилучших усилий. Он находит решение, которое является приемлемым, а затем использует вычислительные ресурсы для постепенного улучшения решения по мере того, как проходит время и добавляются вычислительные ресурсы. Главным преимуществом онлайн-решателя является то, что вы можете практически в любой момент приостановить процесс и получить предварительное кандидатское решение. Вы даже можете возобновить процесс. Если вернуться к математическим решателям, то они обычно являются пакетными, и вы ждёте завершения всего процесса.
К сожалению, работа в мире цепочки поставок может быть весьма тернистой, как обсуждалось в одной из предыдущих лекций этой серии. Бывают ситуации, когда обычно можно позволить себе потратить, скажем, три часа на выполнение процесса математической оптимизации. Но иногда могут возникнуть IT-сбои, реальные проблемы или чрезвычайная ситуация в цепочке поставок. В таких случаях будет настоящим спасением, если процесс, который обычно занимает три часа, можно будет прервать через пять минут и получить ответ, пусть даже не идеальный, вместо того чтобы не получить ответа вовсе. Существует поговорка в армии, что худший план — это отсутствие плана, поэтому лучше иметь очень грубый план, чем вообще ничего. Именно это и даёт онлайн-решатель. Это ключевые конструктивные элементы, которые мы будем учитывать в дальнейшем обсуждении.
Теперь, чтобы завершить этот первый раздел лекции об оптимизации, давайте обратим внимание на уроки по глубокому обучению. Глубокое обучение стало настоящей революцией в области машинного обучения. Однако, в своей основе глубокое обучение также представляет собой задачу математической оптимизации. Я считаю, что глубокое обучение вызвало революцию в самой математической оптимизации и полностью изменило наш взгляд на оптимизационные задачи.
На сегодняшний день крупнейшие модели глубокого обучения работают с более чем триллионом параметров, то есть с тысячей миллиардов. Чтобы оценить масштаб, большинство математических решателей с трудом справляются даже с 1 000 переменными и обычно не могут работать с десятками тысяч переменных, независимо от того, сколько вычислительных мощностей им предоставить. В отличие от этого, глубокое обучение успешно, пусть и с использованием большого количества вычислительных ресурсов, остаётся осуществимым. Существуют модели глубокого обучения, эксплуатируемые в промышленности, с более чем триллионом параметров, и все эти параметры оптимизируются, что означает, что у нас есть процессы математической оптимизации, способные масштабироваться до триллиона параметров. Это поразительно и радикально отличается по производительности от классических подходов к оптимизации.
Интересно, что даже задачи, которые являются полностью детерминированными, такие как игра в Го или шахматы — задачи, не основанные на статистике, дискретные и комбинаторные, — наиболее успешно решаются методами, которые совершенно стохастичны и статистичны. Это удивительно, ведь игру в Го или шахматы можно рассматривать как задачу дискретной оптимизации, однако в настоящее время они решаются наиболее эффективно методами, которые являются полностью стохастическими и статистическими. Это идёт вразрез с интуицией, которой научное сообщество обладало два десятилетия назад.
Давайте пересмотрим понимание, которое открыло глубокое обучение в отношении математической оптимизации. Первое — полностью переосмыслить проклятие размерности. Я считаю, что эта концепция в основном ошибочна, и глубокое обучение доказывает, что не стоит думать о сложности задачи оптимизации лишь исходя из количества измерений.
Во-первых, необходимо различать представительную сложность задачи и её внутреннюю сложность. Позвольте пояснить эти два понятия на примере. Рассмотрим пример прогнозирования временных рядов, приведённый в начале. Допустим, у нас есть история продаж, агрегированная по дням за три года, то есть у нас есть временной вектор с дневными данными примерно за 1 000 дней. Это представление задачи.
А теперь, что если я перейду к представлению временного ряда по секундам? Это та же история продаж, но вместо того чтобы представлять данные о продажах в виде дневных агрегатов, я буду представлять их в агрегатах по секундам. Это означает, что в каждом дне 86 400 секунд, таким образом, я увеличу размерность и масштаб представления задачи примерно в 86 000 раз.
Но если задуматься о внутренней размерности, не то чтобы наличие истории продаж или переход от дневной к секундной агрегации увеличивало сложность задачи в 1 000 раз, на самом деле, при переходе к секундной агрегации временной ряд, скорее всего, окажется невероятно разреженным, почти все ячейки будут заполнены нулями. Я не увеличиваю интересную размерность задачи в 100 000 раз. Глубокое обучение показывает, что не из-за большого количества измерений в представлении задачи она становится принципиально сложной.
Еще один аспект, связанный с размерностью, заключается в том, что, хотя можно доказать, что некоторые задачи являются NP-полными, например, задача коммивояжера (упрощенная версия проблемы маршрутизации транспортных средств, представленной в начале этой лекции), коммивояжер технически является NP-трудной задачей. То есть это задача, для которой поиск наилучшего решения в общем случае будет стоить экспоненциально дороже с добавлением новых точек на карту. Но реальность такова, что эти задачи очень легко решаются, как демонстрирует эвристика two-opt; можно получить отличные решения с минимальными вычислительными ресурсами. Так что будьте осторожны: математические доказательства, показывающие, что некоторые задачи очень сложны, могут быть обманчивыми. Они не говорят вам, что если вас устраивает приближённое решение, то приближение может оказаться отличным, а иногда это даже не приближение; вы получите оптимальное решение. Просто доказать его оптимальность нельзя. Это не говорит о том, что задачу нельзя приблизить, и очень часто те задачи, якобы страдающие от проклятия размерности, на самом деле просты для решения, поскольку их важные размеры не так велики. Глубокое обучение успешно показало, что многие задачи, считавшиеся невероятно сложными, изначально вовсе не были таковы.
Второе ключевое наблюдение — локальные минимумы. Большинство исследователей, занимающихся математической оптимизацией и операционными исследованиями, выбирали выпуклые функции, поскольку в них не было локальных минимумов. Долгое время те, кто не работал с выпуклыми функциями, размышляли о том, как избежать застревания в локальном минимуме. Большая часть усилий была направлена на разработку таких методов, как метаэвристики. Глубокое обучение дало новое понимание: нас не волнуют локальные минимумы. Это понимание основано на последних исследованиях учёных в области глубокого обучения.
Если размерность задачи очень высока, можно показать, что локальные минимумы исчезают по мере увеличения размерности. Локальные минимумы очень часто встречаются в низкоразмерных задачах, но если увеличить размерность до сотен или тысяч, с точки зрения статистики локальные минимумы становятся невероятно маловероятными. До такой степени, что при рассмотрении очень больших размерностей, например, миллионов, они полностью исчезают.
Вместо того чтобы считать, что высокая размерность — ваш враг, как это связано с проклятием размерности, что если можно сделать прямо наоборот и раздувать размерность задачи до такой степени, что спуск по градиенту становится тривиальным и без каких-либо локальных минимумов? Оказывается, именно это и происходит в сообществе глубокого обучения и в моделях, содержащих триллион параметров. Такой подход обеспечивает чистейший способ продвижения по градиенту.
По сути, сообщество глубокого обучения показало, что доказательство качества спуска или окончательной сходимости не имеет значения. Важно скорость спуска. Вы хотите быстро итеративно приближаться к очень хорошему решению. Если у вас есть процесс, который спускается быстрее, в конечном итоге вы достигнете большего в оптимизации. Эти идеи противоречат общепринятому пониманию математической оптимизации, каким оно было два десятилетия назад.
Из глубокого обучения можно извлечь и другие уроки, так как эта область чрезвычайно богата. Один из них — симпатия к аппаратному обеспечению. Проблема математических решателей, таких как коническое программирование или геометрическое программирование, заключается в том, что они в первую очередь опираются на математическую интуицию, а не на вычислительное оборудование. Если вы разрабатываете решатель, который принципиально конфликтует с вашим аппаратным обеспечением, то, как бы умны ни были ваши математические методы, вы, скорее всего, будете крайне неэффективны из-за плохого использования вычислительных ресурсов.
Одно из ключевых наблюдений сообщества глубокого обучения заключается в том, что нужно работать в гармонии с вычислительным оборудованием и проектировать решатель, который его использует. Именно поэтому я начал этот цикл лекций по вспомогательным наукам для цепей поставок с современными компьютерами для цепей поставок. Важно понимать, какое оборудование у вас есть, и как максимально эффективно его использовать. Такая симпатия к аппаратному обеспечению позволяет достигать моделей с триллионом параметров, хотя для этого требуется большой кластер компьютеров или суперкомпьютер.
Еще один урок глубокого обучения — использование суррогатных функций. Традиционно математические решатели стремились оптимизировать задачу такой, какая она есть, не отклоняясь от неё. Однако глубокое обучение показало, что иногда лучше использовать суррогатные функции. Например, очень часто для предсказаний модели глубокого обучения используют кросс-энтропию в качестве метрики ошибки вместо среднеквадратичной ошибки. Практически никого в реальном мире не интересует кросс-энтропия как метрика, поскольку она довольно странная.
Так почему же люди используют кросс-энтропию? Она обеспечивает невероятно крутые градиенты, и, как показало глубокое обучение, всё сводится к скорости спуска. Если градиенты очень крутые, вы можете спускаться очень быстро. Некоторые могут возразить: «Если я хочу оптимизировать среднеквадратичную ошибку, зачем мне использовать кросс-энтропию? Это даже не та же самая цель». Но на деле, если оптимизировать кросс-энтропию, вы получите очень крутые градиенты, и в итоге, если оценивать решение по среднеквадратичному критерию, оно окажется лучше, очень часто, если не всегда. Я упрощаю для ясности. Идея суррогатных функций в том, что истинная задача не является абсолютной; это просто инструмент контроля для оценки окончательной достоверности вашего решения. И не обязательно то, что вы будете использовать во время работы решателя. Это полностью противоречит идеям, лежащим в основе математических решателей, популярных в последние десятилетия.
Наконец, важна работа в рамках парадигм. В математической оптимизации существует неявное разделение труда при организации инженерного коллектива. Это разделение труда предполагает, что с одной стороны работают математические инженеры, отвечающие за разработку решателя, а с другой — инженеры по постановке задач, чья задача состоит в выражении проблемы в форме, пригодной для обработки математическими решателями. Такое разделение труда было распространено, и его суть заключалась в том, чтобы максимально упростить задачу инженера по постановке задач, чтобы ему нужно было лишь минималистично и чисто выразить проблему, оставив основную работу решателю.
Глубокое обучение показало, что такой подход оказывается крайне неэффективным. Это произвольное разделение труда вовсе не является наилучшим способом подхода к решению задачи. Если так поступать, то возникают ситуации, которые становятся невероятно сложными, значительно превосходящими современные достижения математических инженеров, работающих над задачей оптимизации. Гораздо лучше, чтобы инженеры по постановке задач приложили дополнительные усилия по переосмыслению задачи таким образом, чтобы она стала гораздо более пригодной для оптимизации математическим оптимизатором.
Глубокое обучение — это набор рецептов, позволяющих формулировать задачу поверх вашего решателя, чтобы извлечь максимум из оптимизатора. Большинство разработок в сообществе глубокого обучения было направлено на создание таких рецептов, которые отлично обучаются, оставаясь в рамках парадигмы имеющихся решателей (например, TensorFlow, PyTorch, MXNet). Вывод таков: вам действительно нужно сотрудничать с инженером по постановке задач или, в терминологии цепей поставок, с специалистом по цепям поставок.

Теперь перейдем ко второй и последней части этой лекции, посвященной самым ценным элементам литературы. Мы рассмотрим два широких класса решателей: локальный поиск и дифференцируемое программирование.

Сначала позвольте снова остановиться на термине “программирование”. Это слово имеет критическое значение, потому что, с точки зрения цепей поставок, нам действительно нужно уметь формулировать проблему, с которой мы сталкиваемся, или ту, с которой, как мы полагаем, сталкиваемся. Мы не хотим какую-то супернизкокачественную версию проблемы, которая случайно соответствует какой-то полусмешной математической гипотезе, например, необходимости выразить задачу в форме конуса или чего-то подобного. Нас же действительно интересует доступ к настоящей парадигме программирования.
Помните, что такие математические решатели, как линейное программирование, программирование второй порядка конусов и геометрическое программирование, все основаны на ключевом слове “программирование”. Однако за последние несколько десятилетий наши ожидания от парадигмы программирования кардинально изменились. Сегодня нам нужно нечто, что позволяет работать практически с произвольными программами, в которых есть циклы, ветвления и, возможно, выделение памяти и т.д. Вам действительно нужно что-то максимально приближенное к произвольной программе, а не какая-то суперограниченная игрушечная версия с несколькими интересными математическими свойствами. В цепях поставок лучше быть примерно правым, чем абсолютно неправильным.

Чтобы справиться с общей оптимизацией, начнем с локального поиска. Локальный поиск — это обманчиво простая техника математической оптимизации. Псевдокод предполагает начало с случайного решения, которое вы представляете в виде набора битов. Затем вы инициализируете своё решение случайным образом и начинаете случайно переключать биты, чтобы исследовать окрестность решения. Если в ходе этого случайного исследования вы находите решение, которое оказывается лучше, оно становится вашим новым опорным решением.
Этот удивительно мощный подход может работать с буквально любой программой, рассматривая её как черный ящик, и может также перезапускаться с любого известного решения. Существует множество способов улучшить этот подход. Один из них — дифференциальные вычисления, не путайте с дифференцируемыми вычислениями. Дифференциальные вычисления — это идея о том, что если вы запускаете программу на данном решении, а затем переключаете один бит, вы можете выполнить ту же программу с дифференциальным запуском, не перезапуская всю программу. Конечно, результаты могут варьироваться, и это в значительной степени зависит от структуры задачи. Один из способов ускорить процесс — не использовать какую-то дополнительную информацию о черном ящике программы, а просто ускорить саму программу, оставаясь в основном с ней в роли черного ящика, поскольку вы не выполняете всю программу каждый раз.
Существуют и другие подходы к улучшению локального поиска. Вы можете совершенствовать виды ходов, которые вы предпринимаете. Самая базовая стратегия называется k-переключениями, при которой вы переключаете k битов, где k — очень маленькое число, что-то вроде пары или дюжины. Вместо того чтобы просто переключать биты, вы можете позволить инженеру по постановке задач определить тип мутаций, применяемых к решению. Например, вы можете указать, что хотите применить некоторую перестановку в задаче. Идея в том, что такие продуманные ходы часто сохраняют выполнение некоторых ограничений в задаче, что может помочь локальному поиску сходиться быстрее.
Другой способ улучшить локальный поиск — не исследовать пространство полностью случайным образом. Вместо случайного переключения битов вы можете попытаться научиться определять правильные направления, выявляя наиболее перспективные области для переключений. Некоторые недавние исследования показали, что можно подключить небольшой модуль глубокого обучения поверх локального поиска, действующий как генератор. Однако этот подход может быть сложным с инженерной точки зрения, так как необходимо обеспечить, чтобы накладные расходы, введенные процессом машинного обучения, окупались с точки зрения вычислительных ресурсов.
Существуют и другие широко известные эвристики, и если вы хотите получить очень хорошее общее представление о том, что требуется для реализации современного движка локального поиска, вы можете прочитать статью “LocalSolver: A Black-Box Local-Search Solver for 0-1 Programs.” Компания, разрабатывающая LocalSolver, также имеет продукт с тем же названием. В этой статье они представляют инженерный взгляд на то, что происходит под капотом их промышленного решателя. Для достижения лучших результатов они используют многократный запуск и имитацию отжига.
Одна оговорка, которую я хотел бы добавить по поводу локального поиска, заключается в том, что он не очень хорошо или нативно справляется со стохастическими задачами. В стохастических задачах не так просто сказать “У меня есть лучшее решение” и сразу же признать его наилучшим. Это гораздо сложнее, и необходимо приложить дополнительные усилия, прежде чем перейти к решению, оцененному как новое лучшее.

Теперь перейдем ко второму классу решателей, который мы сегодня обсудим, а именно — дифференцируемому программированию. Но прежде, чтобы понять дифференцируемое программирование, нам нужно разобраться в стохастическом градиентном спуске. Стохастический градиентный спуск — это итеративная, основанная на градиенте техника оптимизации. Он появился как серия методов, разработанных в начале 1950-х годов, ему уже почти 70 лет. Долгое время он оставался довольно нишевым методом почти шесть десятилетий, и нам пришлось ждать развития глубокого обучения, чтобы осознать истинный потенциал и силу стохастического градиентного спуска.
Стохастический градиентный спуск предполагает, что функция потерь может быть аддитивно разложена на ряд компонентов. В уравнении Q(W) представляет функцию потерь, которая разлагается на ряд частичных функций Qi. Это важно, потому что большинство задач обучения рассматриваются как необходимость научиться делать предсказания на основе серии примеров. Идея заключается в том, что вы можете представить функцию потерь в виде средней ошибки, допущенной по всему набору данных, с локальной ошибкой для каждой точки данных. Многие задачи цепей поставок также можно аддитивно разложить таким образом. Например, вы можете разложить свою сеть цепей поставок на ряд показателей для каждой отдельной SKU, при этом к каждой SKU привязана своя функция потерь. Истинная функция потерь, которую вы хотите оптимизировать, — это их сумма.
Когда вы настроили это разложение, что очень естественно для задач обучения, вы можете начать итерации методом стохастического градиентного спуска (SGD). Вектор параметров W может содержать очень много элементов, ведь самые крупные модели глубокого обучения имеют триллион параметров. Идея состоит в том, что на каждом шаге процесса вы обновляете параметры, применяя небольшую долю градиента. Эту долю обозначают как η, скорость обучения — небольшое число, обычно находящееся между 0 и 1, часто около 0.01. Nabla функции Q представляет собой градиент для частичной функции потерь Qi. Удивительно, но этот процесс работает хорошо.
Говорят, что SGD является стохастическим, потому что вы случайным образом выбираете следующий элемент i, переходя по вашему набору данных и на каждом шаге применяя к параметрам крошечное количество градиента. Это и есть суть стохастического градиентного спуска.
Он оставался относительно нишевым и в значительной мере игнорировался широким сообществом почти шесть десятилетий, поскольку довольно удивительно, что стохастический градиентный спуск вообще работает. Он работает, поскольку обеспечивает отличный компромисс между шумом в функции потерь и вычислительными затратами на доступ к самой функции потерь. Вместо того чтобы оценивать функцию потерь на всем наборе данных, при использовании стохастического градиентного спуска мы можем брать по одной точке данных и всё равно применять немного градиента. Это измерение будет весьма фрагментарным и шумным, однако такой шум допустим, потому что процесс очень быстрый. Вы можете выполнить на порядки больше мелких, шумных оптимизаций по сравнению с обработкой всего набора данных.
Удивительно, но внесённый шум помогает градиентному спуску. Одна из проблем в высокоразмерных пространствах заключается в том, что локальные минимумы практически отсутствуют. Однако вы всё равно можете столкнуться с большими участками плато, где градиент очень мал, и градиентный спуск не имеет направления для спуска. Шум даёт возможность получить более крутые, но шумные градиенты, которые способствуют спуску.
Еще интересным в градиентном спуске является то, что, будучи стохастическим процессом, он может справляться со стохастическими задачами без дополнительных усилий. Если Qi — это стохастическая функция с шумом, дающая случайный результат, который меняется при каждом её вычислении, то вам даже не нужно изменять ни одной строки алгоритма. Стохастический градиентный спуск представляет особый интерес, поскольку он полностью соответствует парадигме, актуальной для задач цепочки поставок.

Второй вопрос: откуда берется градиент? У нас есть программа, и мы просто берем градиент частичной функции потерь, но откуда появляется этот градиент? Как получить градиент для произвольной программы? Оказывается, существует очень элегантная, минималистичная техника, открытая давно, называемая автоматическим дифференцированием.
Автоматическое дифференцирование появилось в 1960-х годах и со временем было усовершенствовано. Существует два типа: прямой режим, открытый в 1964 году, и обратный режим, открытый в 1980 году. Автоматическое дифференцирование можно рассматривать как трюк компиляции. Идея заключается в том, что у вас есть программа, которую нужно скомпилировать, представляющая функцию потерь. Вы можете перекомпилировать эту программу, получив вторую программу, вывод которой представляет не функцию потерь, а градиенты всех параметров, участвующих в вычислении этой функции.
Кроме того, автоматическое дифференцирование дает вторую программу со сложностью вычислений, по сути, идентичной исходной программе. Это означает, что вы не только получаете способ создать вторую программу для вычисления градиентов, но и эта программа обладает такими же вычислительными характеристиками, как и первая. Это приводит к постоянному коэффициенту увеличения вычислительных затрат. Однако на практике вторая программа не имеет точно таких же характеристик использования памяти, как исходная. Хотя детали этого вопроса выходят за рамки данной лекции, мы можем обсудить их во время вопросов. По сути, вторая программа, называемая обратной, будет требовать больше памяти, а в некоторых патологических случаях может требовать значительно больше памяти, чем исходная. Помните, что увеличение памяти создаёт проблемы с производительностью вычислений, так как нельзя предполагать равномерный доступ к памяти.
Чтобы немного проиллюстрировать, как выглядит автоматическое дифференцирование, как я уже упоминал, существуют два режима: прямой и обратный. С точки зрения обучения или оптимизации цепочки поставок нас интересует только обратный режим. То, что вы видите на экране, — это функция потерь F, полностью вымышленная. Вы видите прямую трассировку — последовательность арифметических или элементарных операций, выполняемых для вычисления функции для двух заданных входных значений, X1 и X2. Это демонстрирует все элементарные шаги, используемые для получения окончательного значения.
Идея состоит в том, что для каждого элементарного шага, большинство из которых представляют собой базовые арифметические операции, такие как умножение или сложение, обратный режим представляет собой программу, которая выполняет те же шаги, но в обратном порядке. Вместо прямых значений вы получаете сопряженные значения. Для каждой арифметической операции существует обратное соответствие. Переход от прямой операции к обратной чрезвычайно прост.
Даже если это выглядит сложно, у вас есть прямая последовательность выполнения и обратная последовательность, где обратное выполнение представляет собой элементарное преобразование, применяемое к каждой операции. В конце обратного прохода вы получаете градиенты. Автоматическое дифференцирование может показаться сложным, но это не так. Первый прототип, который мы реализовали, состоял из менее чем 100 строк кода, поэтому он очень прямолинеен и по сути представляет собой дешевый трюк трансляции.
Теперь это интересно, поскольку у нас есть стохастический градиентный спуск — фантастически мощный оптимизационный механизм. Он невероятно масштабируем, работает в режиме онлайн, «с чистого листа» и изначально предназначен для стохастических задач. Единственная оставшаяся проблема заключалась в том, как получить градиент, и с помощью автоматического дифференцирования мы получаем градиент при фиксированных накладных расходах или постоянном коэффициенте для практически любой произвольной программы. В итоге мы получаем дифференцируемое программирование.
Интересно, что дифференцируемое программирование представляет собой сочетание стохастического градиентного спуска и автоматического дифференцирования. Хотя эти две техники — стохастический градиентный спуск и автоматическое дифференцирование — существуют уже десятки лет, дифференцируемое программирование вышло на первый план только в начале 2018 года, когда Янн Лекун, глава отдела искусственного интеллекта в Facebook, начал рассказывать об этой концепции. Лекун не изобретал эту концепцию, но сыграл ключевую роль в её популяризации.
Например, сообщество глубокого обучения изначально использовало обратное распространение ошибки, а не автоматическое дифференцирование. Для тех, кто знаком с нейронными сетями, обратное распространение ошибки — это сложный процесс, реализация которого в несколько раз сложнее, чем автоматическое дифференцирование. Автоматическое дифференцирование превосходит его во всех аспектах. Благодаря этому пониманию сообщество глубокого обучения уточнило свое представление о том, что такое обучение в глубоких нейронных сетях. Глубокое обучение сочетало математическую оптимизацию с различными методами обучения, и дифференцируемое программирование возникло как чистая концепция, выделяющая те части глубокого обучения, которые не связаны с обучением.
Современные методы глубокого обучения, такие как модель трансформера, предполагают наличие подлежащей среды дифференцируемого программирования. Это позволяет исследователям сосредоточиться на аспектах обучения, построенных поверх этой основы. Дифференцируемое программирование, будучи фундаментальным для глубокого обучения, также имеет высокую актуальность для оптимизации цепочки поставок и поддержки процессов обучения в цепочке поставок, таких как статистическое прогнозирование.
Как и в случае с глубоким обучением, существует две составляющие проблемы: дифференцируемое программирование как базовый уровень и методы оптимизации или обучения, работающие поверх него. Сообщество глубокого обучения стремится определить архитектуры, хорошо сочетающиеся с дифференцируемым программированием, такие как трансформеры. Аналогичным образом необходимо выявить архитектуры, подходящие для оптимизационных целей. Именно это было сделано для обучения игре в Го или шахматы в условиях высокой комбинаторики. Мы обсудим техники, хорошо работающие для оптимизации, специфичной для цепочки поставок, в последующих лекциях.

Но теперь пришло время подвести итоги. Значительная часть литературы по цепочке поставок и даже большинство программных реализаций в этой области весьма запутаны, когда речь идет о математической оптимизации. Этот аспект обычно даже не определяется должным образом, и в результате практики, исследователи и даже инженеры-программисты, работающие в компаниях enterprise software, зачастую небрежно смешивают свои численные методы, связанные с математической оптимизацией. У них возникает серьезная проблема, поскольку один из компонентов не был определен как относящийся к математической оптимизации, а поскольку люди даже не знают, что доступно в литературе, они часто прибегают к грубым переборам или поспешным эвристикам, которые дают нестабильные и непоследовательные результаты. В заключение этой лекции, с этого момента, когда вы сталкиваетесь с численным методом в цепочке поставок или программным обеспечением, претендующим на наличие аналитических возможностей, вам следует задать себе вопрос, что происходит с точки зрения математической оптимизации и какие меры предпринимаются. Если вы понимаете, что поставщики не предлагают абсолютно ясного взгляда с этой точки зрения, скорее всего, вы находитесь не по адресу.
Теперь давайте посмотрим на вопросы.

Вопрос: Является ли переход к вычислительным методам обязательным навыком в операционной деятельности, и утратят ли операционные роли своё значение, или наоборот?
Прежде всего, позвольте уточнить несколько моментов. Я считаю ошибочным возлагать подобные заботы на плечи CIO. От CIO ожидают слишком многого. В качестве директора по информационным технологиям вам уже приходится заниматься базовым уровнем программной инфраструктуры, таким как вычислительные ресурсы, низкоуровневые транзакционные системы, целостность сети и кибербезопасность. Не следует ожидать, что CIO будет понимать, что необходимо для создания чего-то действительно ценного для вашей цепочки поставок.
Проблема в том, что во многих компаниях люди настолько слабо разбираются во всем, что связано с компьютерами, что CIO становится универсальным специалистом по всем вопросам. На самом деле, CIO должен заниматься базовым уровнем инфраструктуры, а дальнейшими вопросами должны заниматься соответствующие специалисты, используя доступные вычислительные ресурсы и программные инструменты.
Что касается устаревания операционных ролей, если ваша задача заключается в том, чтобы вручную просматривать Excel таблицы весь день, то, да, велика вероятность, что ваша роль утратит свою актуальность. Эта проблема известна с 1979 года, когда Расселл Аков опубликовал свою статью. Суть в том, что люди знали, что такой способ принятия решений не является будущим, но он долго оставался нормой. Главная проблема в том, что компаниям необходимо понимать экспериментальный процесс. Я считаю, что наступит период, когда компании вновь начнут осваивать эти навыки. Многие крупные североамериканские компании после Второй мировой войны имели некоторое представление об операционных исследованиях среди своих руководителей. Это была горячая тема, и советы директоров крупных компаний разбирались в операционных исследованиях. Как отмечает Расселл Аков, из-за отсутствия ощутимых результатов эти идеи были отодвинуты вниз по иерархии компании до их полной аутсорсинговой передачи, поскольку они в основном не приносили конкретных результатов. Я полагаю, что операционные исследования вернутся только тогда, когда люди извлекут уроки из того, почему классическая эпоха операционных исследований не принесла результатов. В этом процессе вклад CIO будет скромным; все сводится к переосмыслению добавленной ценности сотрудников компании.
Вы стремитесь внести капиталистический вклад, и это возвращает нас к одной из моих предыдущих лекций о продуктовой ориентированности поставок программного обеспечения для цепочек поставок. Суть в следующем: какой капиталистический добавленный вклад вы вносите в свою компанию? Если ответа нет, возможно, вы не являетесь частью того, чем ваша компания должна и станет в будущем.
Вопрос: А как насчет использования Excel Solver для минимизации значения MRMSC и нахождения оптимальных значений для alpha, beta и gamma?
Я считаю, что этот вопрос актуален для случая Holt-Winters, где решение можно действительно найти методом перебора по сетке. Однако что происходит в этом Excel Solver? Это градиентный спуск или что-то иное? Если речь идет о линейном решателе Excel, то проблема не является линейной, и Excel в этом случае вам ничем не поможет. Если у вас есть другие решатели в Excel или надстройки, то да, они могут работать, но такой подход весьма устарел. Он не учитывает стохастическую природу; прогноз, который вы получаете, является не вероятностным, что является устаревшим методом.
Я не утверждаю, что Excel нельзя использовать, но вопрос в том, какие возможности программирования открываются в Excel? Можно ли в Excel выполнять стохастический градиентный спуск? Вероятно, если добавить специализированную надстройку. Excel позволяет интегрировать любую произвольную программу. Можно ли потенциально реализовать дифференцируемое программирование в Excel? Да. Но хорошая ли это идея — делать это в Excel? Нет. Чтобы понять почему, нужно вернуться к концепции поставки программного обеспечения, ориентированной на продукт, которая описывает проблемы Excel. Всё сводится к модели программирования и тому, сможете ли вы действительно поддерживать свою работу с течением времени в условиях командной работы.
Вопрос: Обычно задачи оптимизации сосредоточены на маршрутизации транспортных средств или прогнозировании. Почему бы не рассмотреть оптимизацию всей цепочки поставок? Разве это не снизило бы затраты по сравнению с подходом, ориентированным на отдельные области?
Я полностью согласен. Проклятие оптимизации цепочки поставок заключается в том, что при выполнении локальной оптимизации для подзадачи вы, скорее всего, лишь сместите проблему, а не решите её для всей цепочки поставок. Я полностью согласен, и как только вы начинаете рассматривать более сложную проблему, вы сталкиваетесь с гибридной задачей – например, задачей маршрутизации транспортных средств в сочетании со стратегией пополнения запасов. Проблема в том, что нужен очень универсальный решатель для решения этой задачи, потому что вы не хотите быть ограниченными. Если у вас есть очень универсальный решатель, вам потребуются универсальные механизмы, а не полагаться на искусные эвристики, такие как алгоритм two-opt, который хорошо работает только для маршрутизации транспортных средств и не подходит для гибридных задач пополнения запасов и маршрутизации одновременно.
Чтобы перейти к этому целостному взгляду, не стоит бояться проклятия размерности. Двадцать лет назад люди говорили бы, что эти задачи уже чрезвычайно сложны и являются NP-полными, как задача коммивояжера, и вы пытаетесь решить ещё более сложную задачу, совмещая её с другой проблемой. Ответ – да; вы должны иметь возможность это делать, и именно поэтому крайне важно иметь решатель, который позволяет работать с произвольными программами, потому что ваше решение может быть консолидацией множества взаимосвязанных и переплетённых задач.
Действительно, идея решения этих задач поодиночке намного слабее, чем решение их в совокупности. Лучше быть примерно правильным, чем точно ошибочным. Гораздо предпочтительнее иметь очень слабый решатель, который решает всю цепочку поставок как единую систему, как единое целое, чем применять передовые локальные оптимизации, которые лишь создают проблемы в других местах при микроподстройке на локальном уровне. Истинная оптимизация системы не обязательно означает оптимизацию каждой её части, поэтому естественно, что если вы оптимизируете с учётом интересов всей компании и её цепочки поставок, результат не будет локально оптимальным, поскольку вы учитываете и другие аспекты компании и её цепи поставок.
Вопрос: После проведения оптимизационного мероприятия, когда нам следует пересмотреть сценарий, учитывая, что новые ограничения могут появляться в любой момент? Ответ заключается в том, что оптимизацию следует пересматривать часто. Это роль учёного по цепочке поставок, о которой я рассказывал во второй лекции этой серии. Учёный по цепочке поставок будет пересматривать оптимизацию так часто, как это необходимо. Если появится новое ограничение, например, гигантское судно, блокирующее Суэцкий канал, – это было неожиданно, но с этим срывом в вашей цепочке поставок придется считаться. Вам не остается другого выбора, кроме как решать эти проблемы; иначе система, которую вы внедрили, будет давать бессмысленные результаты, поскольку будет работать в ложных условиях. Даже если экстренных ситуаций нет, вы все равно хотите тратить время на анализ того направления, которое, скорее всего, принесёт компании наибольшую прибыль. По своей сути это исследовательская и опытно-конструкторская работа. Система у вас уже налажена, она работает, а вы просто пытаетесь определить области, где можно улучшить систему. Это превращается в прикладной исследовательский процесс, который является весьма капиталистичным и непредсказуемым. Как учёный по цепочке поставок, бывают дни, когда вы проводите весь день, тестируя численные методы, ни один из которых не даёт лучших результатов, чем то, что у вас уже есть. В некоторые дни вы делаете небольшую корректировку, и вам удаётся спасти для компании миллионы. Это непредсказуемый процесс, но в среднем его результат может быть колоссальным.
Вопрос: Какие существуют варианты применения задач оптимизации, помимо линейного программирования, целочисленного программирования, смешанного программирования и, в случае Вебера, затрат на товары?
Я бы переформулировал вопрос: где, по вашему мнению, линейное программирование может иметь отношение к задачам цепочки поставок? Практически не существует задач в цепочке поставок, которые были бы линейными. Моё возражение состоит в том, что эти математические модели слишком упрощённые и не способны даже решить игрушечные задачи. Как я уже говорил, такие математические модели, как линейное программирование, не в состоянии даже справиться с игрушечной задачей, например, с оптимизацией сложной зимней периферии для древней, низкоразмерной параметрической модели прогнозирования. Они не могут справиться даже с задачей коммивояжера или практически с любой другой задачей.
Целочисленное программирование или смешанное целочисленное программирование – это всего лишь общее название для обозначения того, что некоторые переменные должны принимать целочисленные значения, но это не меняет того факта, что эти модели – всего лишь игрушечные математические конструкции, далекие от выразительности, необходимой для решения задач цепочки поставок.
Когда вы спрашиваете об областях применения задач оптимизации, я приглашаю вас ознакомиться со всеми моими лекциями о персонажах цепочки поставок personas. У нас уже есть целая серия персонажей цепочки поставок, и я буквально перечисляю тонны задач, которые можно решать с помощью математической оптимизации. В лекциях о персонажах цепочки поставок у нас есть Париж, Майами, Амстердам и Мировая серия, и это только начало. У нас масса задач, которые нуждаются в решении и заслуживают подхода с использованием настоящей математической оптимизации. Однако вы увидите, что для каждой из этих задач не получится задать рамки в рамках строго ограниченных и зачастую странных условий, вытекающих из этих математических моделей. Опять же, эти модели в основном касаются выпуклости, и это не тот подход, который подходит для цепочки поставок. Большинство задач, с которыми мы сталкиваемся, являются невыпуклыми. Но это не значит, что они непреодолимо сложны. Дело не в том, чтобы иметь математическое доказательство в конце. Ваш начальник или компания ценят прибыль, а не наличие математического доказательства, подтверждающего решение. Их интересует то, чтобы вы могли принять правильное решение в отношении производства, пополнения запасов, цен, ассортимента и тому подобное, а не наличие математического обоснования для этих решений.
Вопрос: Как долго следует хранить данные алгоритма обучения для поддержки процесса обучения?
Ну, я бы сказал, что учитывая, насколько сегодня дёшево хранение данных, почему бы не хранить их вечно? Хранение данных настолько недорого; например, достаточно зайти в супермаркет, и вы увидите, что цена за жесткий диск ёмкостью один терабайт составляет примерно 60 долларов или около того. То есть, это невероятно дёшево.
Конечно, существует ещё одна проблема: если в данных содержатся персональные данные, то их хранение превращается в обузу. Но с точки зрения цепочки поставок, если предположить, что вы сначала удалили все персональные данные, ведь обычно вам они и не нужны. Вам не нужно хранить номера кредитных карт или имена ваших клиентов. Достаточно иметь идентификаторы клиентов и подобную информацию. Если вы просто очистите данные от всей личной информации, я бы сказал: как долго? Храните их вечно.
Один из аспектов цепочки поставок заключается в том, что у вас ограниченное количество данных. Это не такие задачи глубокого обучения, как распознавание изображений, где можно обработать все изображения в интернете и получить доступ к практически бесконечным базам данных. В цепочке поставок данные всегда ограничены. Действительно, если вы хотите прогнозировать будущий спрос, существует очень мало отраслей, где рассмотрение данных более чем за десятилетие назад действительно имеет статистическую значимость для прогнозирования спроса на следующий квартал. Но, тем не менее, я бы сказал, что всегда проще обрезать данные, если это необходимо, чем потом понять, что вы их утратили. Поэтому мой совет – храните всё, удаляйте персональные данные, а на завершающем этапе вашего конвейера извлечения данных вы сможете решить, стоит ли отфильтровать самые старые данные. Возможно, это сработает, а возможно нет; всё зависит от отрасли, в которой вы работаете. Например, в аэрокосмической отрасли, где у вас есть детали и самолёты со сроком эксплуатации в четыре десятилетия, наличие данных за последние четыре десятилетия имеет значение.
Вопрос: Является ли многоцелевое программирование функцией двух или более целей, например, суммированием или минимизацией нескольких функций в одной задаче?
Существует несколько вариантов того, как можно подходить к многоцелевым задачам. Речь идет не о том, чтобы иметь функцию, являющуюся суммой, потому что если у вас есть сумма, то это просто вопрос декомпозиции и структуры функции потерь. Нет, дело в том, чтобы иметь вектор. И действительно, существует по существу несколько вариантов многоцелевого программирования. Самый интересный вариант – это тот, где вы стремитесь к лексикографическому порядку. Что касается цепочки поставок, минимизация, когда вы берёте среднее или максимум из множества функций, может быть интересна, но я не слишком уверен. Я считаю, что подход, основанный на многоцелевой оптимизации, где вы можете внедрять ограничения и рассматривать их как часть общей оптимизации, представляет значительный интерес для задач цепочки поставок. Другие варианты также могут быть интересны, но я не настолько уверен. Я не говорю, что они бесполезны; я лишь выражаю сомнение.
Вопрос: Как вы определяете, когда использовать приблизительное решение вместо оптимизированного?
То есть, я не до конца понимаю вопрос. Суть в том, что, если есть один урок, который можно извлечь из глубокого обучения, так это урок о том, что не существует единственного оптимального решения. Всё является приближением в той или иной степени. Даже если вы работаете с числами, в компьютерах числа не обладают бесконечной точностью, а имеют конечную точность. И эта конечная точность иногда может сыграть с вас злую шутку. Так что ответ таков: всё всегда приблизительно. Я бы сказал, что главный урок состоит в том, что иллюзия существования совершенного решения – ошибочна. Идеального оптимального решения не существует. Все решения, которые у вас есть, являются приближениями, одни из которых, я бы сказал, чуть менее или более точны. Поэтому я не совсем понимаю суть вашего вопроса, но с точки зрения математической оптимизации это означает, что у вас есть функция потерь для оценки качества, и в конце концов, если у вас есть два конкурирующих решения, функция потерь поможет определить, какое из них лучше. Вот как это работает.
Вопрос: Почему временной ряд, в терминах исторических данных, изначально делили на 86 400?
Это не так. Это был просто пример. Я хотел показать и довести ситуацию до абсурда, когда вы берётесь за временной ряд, и классический алгоритм прогнозирования временных рядов предполагает равномерное распределение данных во времени. Существует множество способов представления временных рядов, и наиболее типичным является равномерное распределение, когда вы агрегируете данные в корзинах равной длины. Именно это обычно и происходит при дневной или недельной агрегации. У вас есть корзины одинаковой длины, и ваш ряд имеет приятную вектороподобную структуру.
Но я хочу подчеркнуть, что это во многом произвольно. Вы можете представить данные как ежедневные, но вы также можете представлять данные по секундам. Имеет ли смысл представлять данные по секундам? Ответ – да; это зависит от типа задачи. Например, если вы поставщик электроэнергии и хотите управлять сетью, то вам нужно регулировать подачу электроэнергии каждую секунду, чтобы точно уравновесить поступление электроэнергии и её потребление в сети. И это равновесие настраивается поминутно, если не каждую секунду. Так что могут быть ситуации, когда представление данных по секундам имеет смысл. Для продаж в местном магазине это может быть излишним. Число 86 400, кстати, означает 24 часа × 60 минут × 60 секунд, и я хотел подчеркнуть, что у вас всегда есть представление ваших данных, и не стоит путать способ представления данных, который имеет определённую размерность, с intrinsic-измерением самих данных, которое может быть совершенно иного рода. Представление в значительной степени вымышлено и произвольно. Оно даёт числовой индикатор, например, наличие трёх лет данных, что соответствует вектору размерностью тысяча. Но это число в значительной степени выбрано произвольно, так как оно основано на решении агрегировать данные ежедневно. Если бы вы выбрали иной период, размерность была бы иной. Вот в чём заключается суть, которую я хотел донести, и именно это глубокое обучение правильно поняло: не стоит увлекаться произвольными выборами представления данных.
Вопрос: При введении вероятностного прогнозирования мы переходим к функции затрат и ограничениям, которые по своей природе являются вероятностными. Как это влияет на процесс поиска решения?
Что же, это действительно накладывает одно очень основополагающее ограничение. Если у вас есть решатель, который не может обрабатывать такие задачи, и, повторюсь, помните, что вы всегда можете свести стохастическую задачу к детерминированной, просто усреднив результаты по огромному числу выборок, тогда вы фактически столкнётесь с проблемой вычислительных затрат. Это означает, что вам придётся затратить примерно в 10 000 раз больше вычислительной мощности для получения удовлетворительного решения по сравнению с альтернативными методами. Следовательно, важно убедиться, что ваши инструменты математической оптимизации и инфраструктура изначально способны работать со стохастическими задачами. Именно это вы получаете с дифференцируемым программированием, в отличие от локального поиска, хотя локальный поиск можно усовершенствовать так, чтобы он работал более эффективно в подобных ситуациях.
В принципе, когда вы прибегаете к вероятностному прогнозированию, это не только бросает вызов вашему взгляду на будущее; оно также глубоко ставит под сомнение тип инструментов и измерительных приборов, с которыми вам приходится работать для этих прогнозов. Именно такой инструментарий Lokad разрабатывал в течение последнего десятилетия. Причина в том, что нам нужен инструментарий, способный эффективно работать с теми стохастическими проблемами, которые неизбежно возникают в цепочке поставок, поскольку практически все проблемы в цепочках поставок содержат элемент неопределенности, и, следовательно, они в той или иной степени связаны со стохастическими задачами.
Отлично. Итак, следующая лекция состоится в тот же день недели, в среду. Между этим и тем временем будет небольшой отпуск. Следующая лекция состоится 22 сентября, и я надеюсь увидеть вас всех. На этот раз мы обсудим машинное обучение для цепочки поставок. До встречи.
Ссылки
- Будущее операционных исследований уже прошло, Рассел Л. Аков, февраль 1979
- LocalSolver 1.x: черный ящик для локального поиска в задачах 0-1 программирования, Тьерри Беноа, Бертран Эстеллон, Фредерик Гарди, Ромен Мегель, Карим Нуиуа, сентябрь 2011
- Автоматическое дифференцирование в машинном обучении: обзор, Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind, последний раз обновлено в феврале 2018


