00:54 Introduction
02:25 On the nature of progress
05:26 The story so far
06:10 A few quantitative principles: observational principles
07:27 Solving “needle in a haystack” via entropy
14:58 SC populations are Zipf-distributed
22:41 Small numbers prevail in SC decisions
29:44 Patterns are everywhere in SC
36:11 A few quantitative principles: optimization principles
37:20 5 to 10 rounds are needed to fix any SC issue
44:44 Aged SCs are unidirectionally quasi-optimal
49:06 Local SC optimizations only displace problems
52:56 Better problems trump better solutions
01:00:08 Conclusion
01:02:24 Upcoming lecture and audience questions
Description
While supply chains can’t be characterized by definitive quantitative laws - unlike electromagnetism - general quantitative principles can still be observed. By “general”, we mean applicable to (almost) all supply chains. Uncovering such principles is of prime interest because they can be used to facilitate the engineering of numerical recipes intended for the predictive optimization of supply chains, but they can also be used to make those numerical recipes more powerful overall. We review two short lists of principles: a few observational principles and a few optimization principles.
Full transcript

Hi everyone, welcome to this series of supply chain lectures. I’m Joannes Vermorel, and today I will be presenting a few “Quantitative Principles for Supply Chains.” For those of you who are watching the lecture live on YouTube, you can ask your questions at any point of time via the YouTube chat. However, I will not be reading your questions during the lectures. I will be coming back to the chat at the end of the lecture and do my best to answer at least most of the questions.
Quantitative principles are of high interest because, in supply chains, as we have seen during the first lectures, they involve the mastery of optionality. Most of these options are quantitative in nature. You have to decide how much to buy, how much to produce, how much inventory to move, and potentially the price point – whether you want to move the price point up or down. So, a quantitative principle that can drive improvements in the numerical recipes for supply chains is of high interest.
However, if I were to ask most supply chain authorities or experts nowadays what their core quantitative principles for supply chains are, I suspect that frequently, I would get an answer along the lines of a series of techniques for better time series forecasting or something equivalent. My personal reaction is that although this is interesting and relevant, it is also missing the point. I believe at the core, the misunderstanding lies in the very nature of progress itself – what is progress and how can you implement something like progress as far as supply chains are concerned? Let me start with an illustrating example.

Six thousand years ago, the wheel was invented, and six thousand years later, the wheeled suitcase was invented. The invention is dated from 1949, as illustrated by this patent. By the time the wheeled suitcase was invented, we had already harnessed atomic power and even detonated the first few atomic bombs.
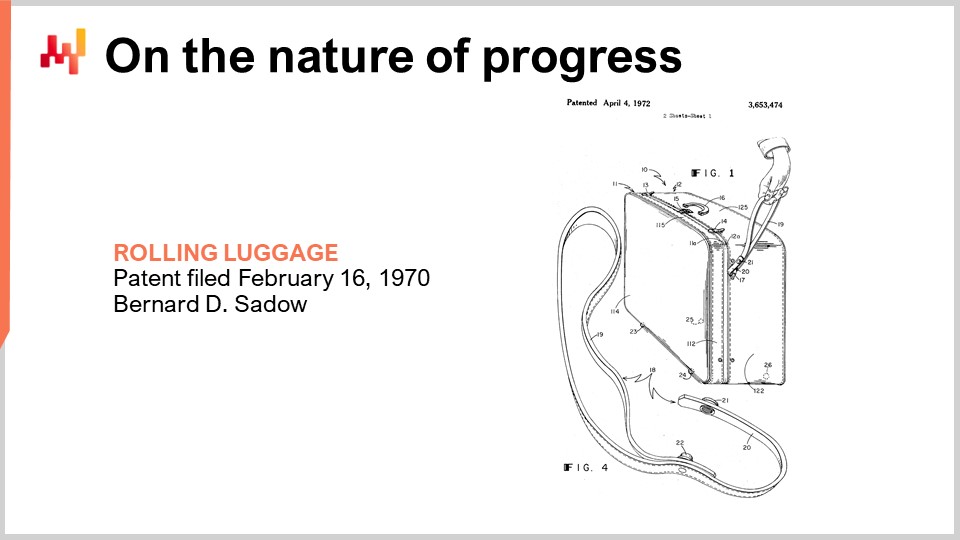
Fast forward 20 years later, in 1969, mankind sent the first people on the moon. The next year, the wheeled suitcase is improved with a slightly better handle, which looks like a leash, as illustrated by this patent. It’s still not very good.

Then, 20 years later, by that time, we already have the GPS global positioning system that has been serving civilians for almost a decade, and the proper handle for the wheeled suitcase is finally invented.
There are at least two lessons of interest here. First, there is no such thing as an obvious arrow of time as far as progress is concerned. Progress happens in a highly chaotic, non-linear manner, and it’s very hard to assess the progress that should happen in one field based on what is happening in other fields. This is one element that we need to keep in mind today.
The second thing is that progress should not be confused with sophistication. You can have something that is vastly superior but also vastly simpler. If I take the example of the suitcase, once you’ve seen one, the design looks completely obvious and self-evident. But was it an easy problem to solve? I would say absolutely not. The simple proof that supply chain management was a difficult problem to solve is that it took an advanced industrial civilization a bit more than four decades to address this issue. Progress is deceptive in the sense that it doesn’t abide by the rule of sophistication. It’s very hard to identify what the world was like before progress happened because it’s literally changing your view of the world as it occurs.

Now, back to our supply chain discussion. This is the sixth and last lecture in this prologue. There is a comprehensive plan that you can check online on the Lokad website about the entire series of supply chain lectures. Two weeks ago, I presented the 20th-century trends for supply chains, adopting a purely qualitative perspective on the problem. Today, I’m taking the opposite approach by adopting a fairly quantitative perspective on this set of problems as a counterpoint.

Today, we will be reviewing a set of principles. By principle, I mean something that can be used to improve the design of numerical recipes in general for all supply chains. We have an ambition of generalization here, and that’s where it’s quite difficult to find things that are of prime relevance for all supply chains and all the numerical methods to improve them. We will review two shortlists of principles: observational principles and optimization principles.
Observational principles apply in the way you can gain knowledge and information quantitatively about supply chains. Optimization principles relate to how you act once you’ve acquired qualitative knowledge about your supply chain, specifically, how to use these principles to improve your optimization processes.
Let’s get started with observing a supply chain. It’s puzzling to me when people speak about supply chains as if they could observe them directly with their own eyes. For me, this is a very distorted perception of the reality of supply chains. Supply chains cannot be humanly observed directly, at least not from a quantitative perspective. This is because supply chains, by design, are geographically distributed, involving potentially thousands of SKUs and tens of thousands of units. With your human eyes, you could only observe the supply chain as it is today and not how it was in the past. You can’t remember more than a few numbers or a tiny fraction of the numbers associated with your supply chain.
Whenever you want to observe a supply chain, you’re going to perform such observations indirectly via enterprise software. This is a very specific way to look at supply chains. All the observations that can be made quantitatively about supply chains happen via this specific medium: enterprise software.
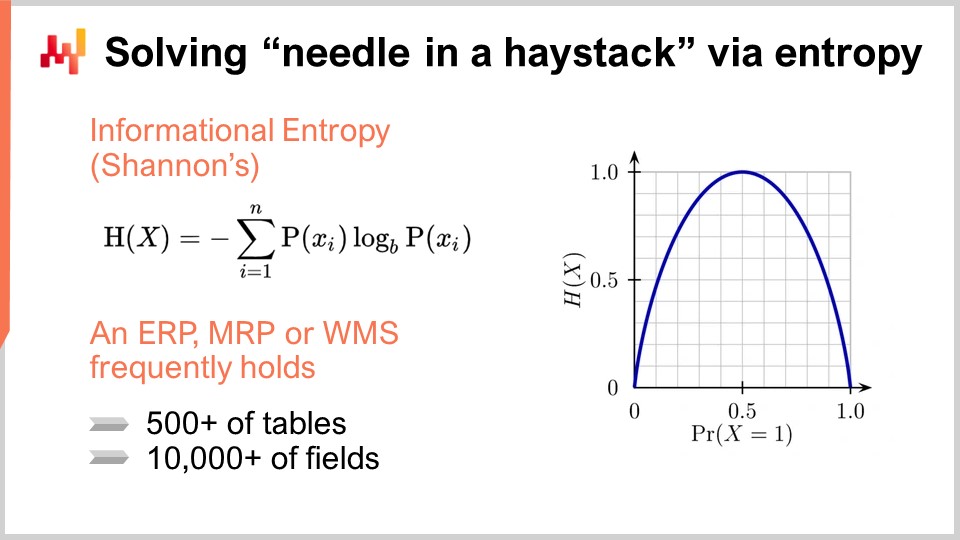
Let’s characterize a typical piece of enterprise software. It’s going to contain a database, as the vast majority of such software is designed that way. The software is likely to have around 500 tables and 10,000 fields (a field is essentially a column in a table). As an entry point, we have a system that potentially contains a massive amount of information. However, in most situations, only a tiny fraction of this software complexity is actually relevant for the supply chain of interest.
Software vendors design enterprise software taking into account very diverse situations across the board. When looking at one specific client, odds are that only a tiny fraction of the software’s capabilities are actually used. This means that while there may be 10,000 fields to explore in theory, in reality, companies are only using a small fraction of those fields.
The challenge is how to sort out the relevant information from the non-existent or irrelevant data. We can only observe supply chains via enterprise software, and there may be more than one piece of software involved. In some cases, a field has never been used, and the data is constant, containing only zeros or nulls. In this situation, it’s easy to eliminate the field because it doesn’t contain any information. However, in practice, the number of fields that can be eliminated using this method may only be around 10%, as many features in the software have been used over the years, even if only accidentally.
To identify fields that have never been put to any meaningful use, we can turn to a tool called informational entropy. For those unfamiliar with Shannon’s theory of information, the term may seem intimidating, but it’s actually more straightforward than it appears. Informational entropy is about quantifying the amount of information in a signal, with a signal being defined as a sequence of symbols. For example, if we have a field that contains only two types of values, true or false, and the column randomly oscillates between these values, the column contains a lot of data. In contrast, if there’s only one line out of a million where the value is true and all the other lines are false, the field in the database contains almost no information whatsoever.
Informational entropy is very interesting because it allows you to quantify, in bits, the amount of information present in each field of your database. By conducting an analysis, you can rank these fields from the richest to the poorest in terms of information and eliminate those that barely contain any relevant information for supply chain optimization purposes. Informational entropy may seem complicated at first, but it is not difficult to understand.

For example, envisioning a domain-specific programming language, we have implemented informational entropy as an aggregator. By taking a table, such as data from a flat file called data.csv with three columns, we can plot the summary of how much entropy is present in each column. This process allows you to easily determine which fields contain the least amount of information and eliminate them. Using entropy as a guide, you can quickly start a project instead of taking years to do so.
Moving on to the next stage, we make our first observations about supply chains and consider what to expect. In natural sciences, the default expectation is normal distributions, also known as bell-shaped curves or Gaussians. For example, the height of a 20-year-old human male or his weight will have a normal distribution. In the realm of living things, many measurements follow this pattern. However, when it comes to supply chain, this is not the case. There is practically nothing of interest that is normally distributed in supply chains.
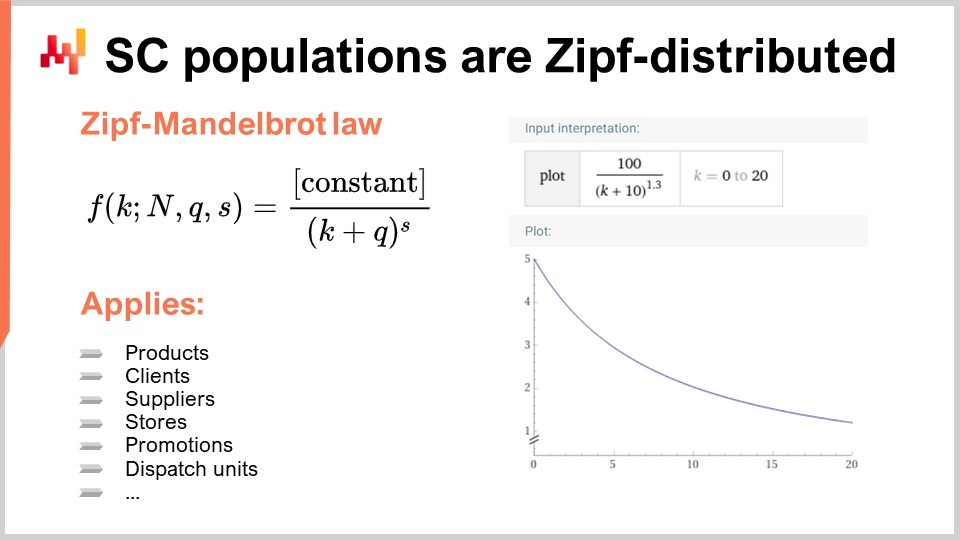
Instead, nearly all distributions of interest in supply chains are Zipf distributed. The Zipf distribution is illustrated in the given formula. To understand this concept, consider a population of products, with the measurement of interest being sales volume for each product. You would rank the products from the highest to the lowest sales volume over a given time period, such as a year. The question then becomes whether there is a model that predicts the shape of the curve, and if given the rank, will provide the expected sales volume. This is precisely what the Zipf distribution is about. Here, f represents the form of a Zipf-Mandelbrot law, and k refers to the kth biggest element. There are two parameters, q and s, which are essentially learned, just as you have mu (the mean) and sigma (the variance) for a normal distribution. These parameters can be used to fit the distribution to a population of interest. The Zipf-Mandelbrot law encompasses these parameters.
It’s important to note that virtually every single population of interest in supply chain follows a Zipf distribution. This is true for products, clients, suppliers, promotions, and even dispatch units. The Zipf distribution is essentially a descendant of the Pareto principle, but it is more tractable and, in my opinion, more interesting, as it provides an explicit model of what to expect for any population of interest in the supply chain. If you encounter a population that is not Zipf-distributed, it is more likely that there is an issue with the data, rather than a true deviation from the principle.

To exploit the concept of Zipf distribution in the real world, you can use Envision. If we look at this code snippet, you’ll see that it only takes a few lines of code to apply this model to a real dataset. Here, I assume that there is a population of interest in a flat file called “data.csv” with one column representing the quantity. Normally, you would have a product identifier and the quantity. On line 4, I’m computing the ranks using the rank aggregator and sorting against the quantity. Then, between lines 6 to 11, I enter a differentiable programming block, made explicit by Autodev, where I declare three scalar parameters: c, q, and s, just like in the formula on the left of the screen. I then compute the Zipf model predictions and use a mean square error between the observed quantity and the model’s prediction. You can literally regress the Zipf distribution with just a few lines of code. Even if it sounds sophisticated, it’s quite simple with the proper tools.

This brings me to another observational aspect of supply chains: the numbers that you would expect at any level of the supply chain are small, usually less than 20. Not only will you have few observations, but the numbers you observe will also be small. Of course, this principle depends on the units used, but when I say “numbers,” I mean those that make canonical sense from a supply chain perspective, which are what you are trying to observe and optimize.
The reason why we only have small numbers is due to economies of scale. Let’s take t-shirts in a store as an example. The store might have thousands of t-shirts in stock, which seems like a large number, but in reality, they have hundreds of different types of t-shirts with variations in size, color, and design. When you start looking at the t-shirts at the granularity of relevance for a supply chain perspective, which is the SKU, the store won’t have thousands of units of t-shirts for a given SKU; instead, they will have only a handful.
If you have a larger number of t-shirts, you’re not going to have thousands of t-shirts lying around, as it would be a nightmare in terms of processing and moving them. Instead, you’ll package those t-shirts into convenient boxes, which is precisely what happens in practice. If you have a distribution center that deals with a lot of t-shirts, because you’re shipping them to stores, then the odds are that those t-shirts are actually in boxes. You might even have a box containing a full assortment of t-shirts with varying sizes and colors, making it easier to process along the chain. If you have many boxes lying around, you’re not going to have thousands of boxes like that. Instead, if you have dozens of boxes, you’re going to organize them neatly on pallets. One pallet can hold several dozen boxes. If you have many pallets, you’re not going to have them organized as individual pallets; most likely, you’re going to have them organized as containers. And if you have many containers, you’re going to use a cargo ship or something similar.
My point is that when it comes to numbers in supply chain, the truly relevant number is always a small number. This situation cannot be escaped by just moving upward to a higher aggregated level because, as you move to a higher level of aggregation, some kind of economies of scale kicks in, and you want to introduce a mechanism of batching to lower your operating costs. This happens multiple times, so no matter which scale you’re looking at, whether it’s the final product sold by the unit in a store or a mass-produced item, it’s always a game of small numbers.
Even if you have a factory that produces millions of t-shirts, chances are you have gigantic batches, and the numbers that are of interest to you are not the number of t-shirts but the number of batches, which is going to be a much smaller number.
Where am I getting at with this principle? First, you have to look at what most methods in scientific computing or statistics look like. It turns out that in most other fields that are not supply chain-related, the opposite is prevalent: large numbers of observations and large numbers where precision matters. In supply chain, however, the numbers are small and discrete.
My proposition is that we need tools based on this principle that deeply accommodate and embrace the fact that we are going to have small numbers instead of large numbers. If you have tools that have only been designed with the law of large numbers in mind, either because of many observations or because of large numbers themselves, you have a complete misfit when it comes to supply chain.
By the way, this has profound software implications. If you have small numbers, there are many ways to make the software layers take advantage of this observation. For example, if you look at the dataset of transaction lines for a hypermarket, you will notice that, based on my experience and observation, 80% of the lines have a quantity that is being sold to a final client in a hypermarket that is exactly one. So, do you need 64 bits of information to represent this information? No, that’s a complete waste of space and processing time. Embracing this concept can result in one or two orders of magnitude operational gain. This is not just wishful thinking; there are real operational gains. You might think that computers nowadays are very powerful, and they are, but if you have more processing power at your disposal, you can have more advanced algorithms that do things that are even better for your supply chain. It’s pointless to waste this processing power just because you have a paradigm that expects large numbers when small numbers prevail.
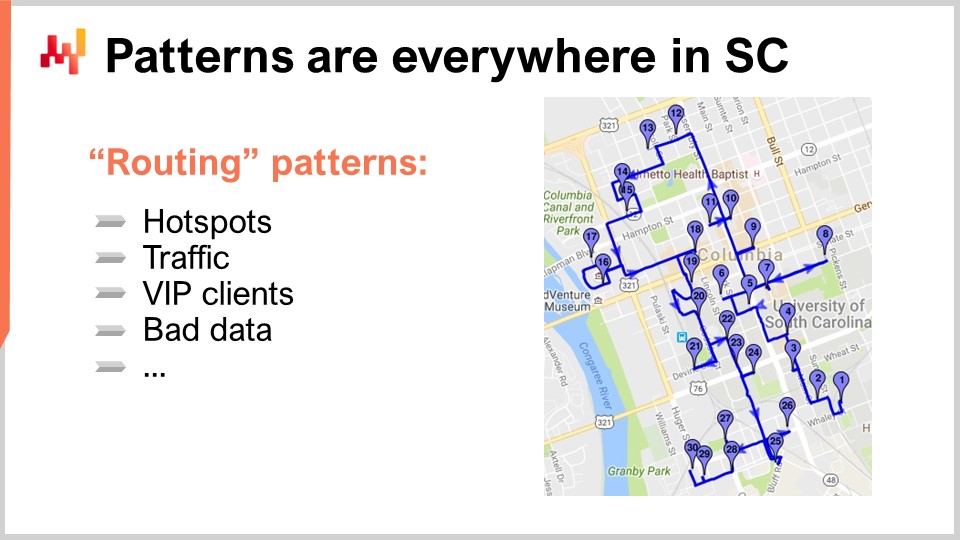
That brings me to my last observational principle for today: patterns are everywhere in supply chain. To understand this, let’s have a look at a classic supply chain problem where patterns are usually considered absent: route optimization. The classic problem of route optimization involves a list of deliveries to be made. You can place deliveries on a map, and you want to find the route that minimizes transportation time. You want to establish a route that goes through every single delivery point while minimizing the total transportation time. At first glance, this problem appears to be a completely geometric problem with no patterns involved in its resolution.
However, I propose that this perspective is entirely wrong. By approaching the problem from this angle, you’re looking at the mathematical problem, not the supply chain problem. Supply chains are iterated games where problems manifest themselves repeatedly. If you are in the business of organizing deliveries, the odds are that you’re doing deliveries every single day. It’s not just one route; it’s literally one route per day, at least.
Moreover, if you’re in the business of doing deliveries, you likely have an entire fleet of vehicles and drivers. The problem isn’t just optimizing one route; it’s optimizing a whole fleet, and this game repeats itself every single day. That’s where all the patterns appear.
First, the points are not randomly distributed on the map. You have hot spots, or geographical areas with a high density of deliveries. You may have addresses that receive deliveries almost every day, like the headquarters of a large company in a big city. If you’re a large e-commerce company, you’re probably delivering packages to this address every single business day. These hotspots are not immutable; they have their seasonality. Some neighborhoods might be very quiet during the summer or winter. There are patterns, and if you want to be very good at playing the game of route optimization, you have to take into account not only where these hotspots are going to happen, but also how they are going to displace themselves during the course of the year. Additionally, you have traffic to consider. You shouldn’t think only about the geometric distance, as traffic is time-dependent. If a driver starts at a certain point in time during the day, as they progress through their route, the traffic will change. To play this game well, you need to take into account traffic patterns, which change and can be reliably predicted in advance. For example, in Paris, at 9:00 AM and 6:00 PM, the entire city is completely jammed, and you don’t have to be an expert in forecasting to know that.
There are also things that happen on the spot, like accidents that disturb the usual patterns of traffic. If we look at deliveries from a mathematical perspective, it assumes that all delivery points are the same, but they are not. You might have VIP clients, or specific addresses where you have to deliver half of your shipment. These key milestones in your route need to be taken into account for effective route optimization.
You also need to be aware of the context, and it’s common to have imperfect data about the world. For example, if a bridge is closed and the software doesn’t know about it, the problem isn’t not knowing the bridge was closed the first time, but rather that the software never learns from the issue and always proposes a route that is supposed to be optimal but ends up being nonsensical. People then fight against the system, which is not a good practical route optimization solution from a supply chain perspective.
The point is that when we look at supply chain situations, there are plenty of patterns all over the place. We have to be careful not to be distracted by elegant mathematical structures and remember that these considerations apply to time series forecasting as well. I took the route optimization problem as an example because it was more manifest in this case.
In conclusion, we need to observe the supply chain from all the dimensions that are observable, not just the ones that are obvious or where the solution presents itself in an elegant way.

This brings me to the second series of principles related to how we should look at our supply chain. So far, we have seen four principles related to how we should look at our supply chain: indirect observation, enterprise software, sorting out the mess to determine what is relevant and what is not, and entropy. We have observed that distributions often follow Zipf’s law, and even with small numbers, we can still see patterns emerge. The question now is, how do we act? Mathematically speaking, when we want to decide the best course of action, we perform an optimization of some kind, which is the quantitative perspective.

The first thing to note is that as soon as we have a piece of optimization logic in production for supply chains, issues will arise, such as bugs. Enterprise software is a very complex beast and is often full of bugs. As you craft your own optimization logic for your supply chain, there will be plenty of issues. However, if a piece of logic is good enough to be put into production, any issues we face now are probably edge cases. If it wasn’t an edge case and the software or logic was malfunctioning every single time, it would never have made its way to production.
The idea of this principle is that it takes five to ten rounds to fix any issue. When I say five to ten rounds, I mean you’re going to face an issue, look at it, understand the root cause, and then try to apply a fix. But most of the time, the fix is not going to solve the problem. You will discover that there was a problem hidden inside the problem, or the problem you thought you fixed was not the actual cause, or that the situation has revealed a broader class of problems. You might have fixed a small instance of a broader class of problems, but other issues will keep occurring that are variants of the one you thought you solved.
Supply chains are complex, ever-changing beasts that operate in the real world, making it difficult to have a design that is properly correct against all situations. In most cases, you do a best-effort attempt to fix a problem, and then you have to put your revised logic to the test of real-world experience to see if it works or if it doesn’t. You will have to iterate to get the problem fixed. With the principle that it takes between five and ten iterations to get a problem fixed, there are profound consequences on the velocity of adaptations and the frequency at which you refresh or recompute your supply chain optimization logic. For example, if you have a piece of logic that is producing a quarterly forecast for the next two years and you only run this logic once per quarter, it will take between one and two years to fix any problems that you face with this forecasting logic, which is an incredibly long time.
Even if you have a piece of logic that runs every month, like in the case of an S&OP (Sales and Operations Planning) process, it could still take up to a year to fix a problem. This is why it’s important to increase the frequency of running your supply chain optimization logic. At Lokad, for instance, every bit of logic runs on a daily basis, even for forecasts five years ahead. These forecasts are refreshed daily, even if they don’t change much from one day to the next. The goal is not to gain statistical accuracy, but to ensure that the logic is run frequently enough to fix any issues or bugs within a reasonable time frame.
This observation is not unique to supply chain management. Smart engineering teams at companies like Netflix have popularized the idea of chaos engineering. They realized that edge cases were rare and the only way to fix these problems was to repeat the experience more frequently. As a result, they created a piece of software called the Chaos Monkey, which adds chaos to their software infrastructure by creating network disruptions and random crashes. The purpose of the Chaos Monkey is to make edge cases manifest themselves faster, allowing the engineering team to fix them more quickly.
While it may seem counterintuitive to introduce an extra level of chaos into your operations, this approach has proven effective for Netflix, which is known for its excellent reliability. They understand that when they face a software-driven problem, it takes many iterations to resolve it, and the only way to get to the bottom of the problem is to iterate rapidly. The Chaos Monkey is just one way to increase the speed of iteration.
From a supply chain perspective, the Chaos Monkey may not be directly applicable, but the concept of increasing the frequency of running your supply chain optimization logic is still very relevant. Whatever logic you have to optimize your supply chain, it needs to run at high velocity and high frequency; otherwise, you will never fix any of the problems that you face.

Now, aged supply chains are quasi-optimal, and when I say aged, I mean supply chains that have been in operation for two decades or more. Another way to state this principle is that your supply chain predecessors were not all incompetent. When you look at supply chain optimization initiatives, too frequently, there are grand ambitions like cutting stock levels by half, increasing service levels from 95% to 99%, eliminating stockouts, or dividing lead times by two. These are big, unidirectional moves where you focus on one KPI and attempt to massively improve it. However, I’ve observed that these initiatives almost always fail for a very blunt reason: when you take a supply chain that has been in operation for decades, there is usually some latent wisdom in the way things have been done.
For example, if service levels are at 95%, chances are that if you try to raise them to 99%, you will vastly increase stock levels and create a massive amount of dead stock in the process. Similarly, if you have a certain amount of stock and launch a massive initiative to slash it by half, you will likely create significant quality of service problems that are unsustainable.
What I’ve observed is that many supply chain practitioners who don’t understand the principle that aged supply chains are unidirectionally quasi-optimal tend to have oscillations around the local optimum. Keep in mind that I’m not saying aged supply chains are optimal, but they are unidirectionally quasi-optimal. If you look at the analogy of the Grand Canyon, the river carves the optimal path due to the unidirectional force of gravity. If you were to apply a force that was ten times stronger, the river would still undergo many convolutions.
The point is that with aged supply chains, if you want to bring sizable improvements, you need to tweak many variables at once. Focusing on just one variable will not yield the desired results, especially if your company has been operating for decades with the status quo. Your predecessors probably did a few things right in their own time, so the odds that you stumble upon a vastly dysfunctional supply chain that nobody ever paid attention to are minimal. Supply chains are wicked problems, and while it’s possible to engineer completely dysfunctional situations at scale, it’s going to be very infrequent at best.

Another aspect to consider is that local optimization only displaces problems instead of solving them. To understand this, you have to recognize that supply chains are systems, and when thinking in terms of supply chain performance, it’s only the system-wide performance that is of interest. Local performance is relevant, but it’s only a part of the picture.
A common way of thinking is that you can apply the divide-and-conquer strategy to address problems in general, not just supply chain problems. For example, in a retail network with many stores, you might want to optimize stock levels in each store. However, the problem is that if you have a network of stores and distribution centers, each serving many stores, it’s completely trivial to micro-optimize one store and achieve excellent quality of service for that store at the expense of all the other stores.
The correct perspective is to think that when you have one unit available in the distribution center, the question you should ask yourself is: where is this unit most needed? What is the most profitable move for me? The problem of optimizing the dispatch of inventory, or the inventory allocation problem, is one that only makes sense at the system level, not at the store level. If you optimize what happens in one store, you’re likely to create problems in another store.
When I say “local,” this principle should not just be understood from a geographical perspective; it can also be a purely logical matter within the supply chain. For example, if you are an e-commerce company with many product categories, you may want to allocate varying budgets for the various categories. This is another type of divide-and-conquer strategy. However, if you partition your budget and allocate a fixed amount at the beginning of the year for each category, what happens if the demand for products in one category doubles while the demand for products in another category is halved? In this case, you end up with a problem of incorrect allocation of funds between those two categories. The challenge here is that you cannot apply any kind of divide-and-conquer logic. If you use local optimization techniques, you may end up creating problems as you create your supposedly optimized solution.

That brings me to the last principle, which is probably the most tricky among all the principles I have presented today: better problems trump better solutions. This can be exceedingly confusing, especially among certain academic circles. The typical way things are presented through a classic education is that a well-defined problem is presented to you, and then you start looking for solutions to these problems. In a mathematical problem, for example, one student may come up with a more concise, more elegant solution, and that’s considered the best solution.
However, in reality, things do not happen that way in supply chain management. To illustrate this, let’s go back 60 years and look at the problem of cooking, a very time-consuming activity. People in the past imagined that robots could be used in the future to perform cooking tasks, thereby significantly increasing productivity for the person in charge of cooking. This sort of thinking was prevalent in the 1950s and 1960s.
Fast forward to today, and it’s obvious that this is not how things have evolved. To minimize cooking efforts, people now buy pre-cooked meals. This is another example of problem displacement. Providing supermarkets with pre-cooked meals is more challenging from a supply chain perspective than providing them with raw products, due to the increased number of references and shorter expiration dates. The problem was solved through a superior supply chain solution, not by providing a better cooking solution. The cooking problem was removed entirely and redefined as providing a halfway decent meal with minimal effort.
In terms of supply chains, the academic perspective often focuses on finding better solutions to existing problems. One good example would be Kaggle competitions, where you have a dataset, a problem, and potentially hundreds or thousands of teams competing to get the best prediction on these datasets. You have a well-defined problem and thousands of solutions competing against each other. The issue with this mindset is that it gives you the impression that if you want to deliver improvement for your supply chain, what you need is a better solution.
The essence of the principle is that a better solution might help marginally, but only marginally. Usually, what really helps is when you redefine the problem, and that is surprisingly difficult. This applies to quantitative problems as well. You need to rethink your actual supply chain strategy and the key problem you should be optimizing.
In many circles, people think of problems as if they are static and immutable, looking for better solutions. I don’t deny that having a better time series forecasting algorithm can be of help, but time series forecasting belongs to the realm of statistical forecasting, not the mastery of supply chain management. If we go back to my initial example of the travel suitcase, the key improvement for a wheeled suitcase was not about the wheels, but about the handle. It was something that had nothing to do with the wheels at first glance, and that’s why it took 40 years to come up with a solution – you have to think outside the box to let the better problem emerge.
This quantitative principle is about challenging the problems you face. Maybe you’re not thinking hard enough about the problem, and there is a tendency to fall in love with the solution while you should be focused on the problem and the things you don’t understand about it. As soon as you have a well-defined problem, having a good solution is usually just a mundane matter of execution, which is not that difficult.

In conclusion, supply chain as a field of study has plenty of impressive and authoritative perspectives. These can be sophisticated, but the question I would like to ask this audience is: could it be that all of that might be severely misguided? Are we really confident that elements like time series forecasting and operational research are the proper perspectives on the problem? No matter the amount of sophistication and decades of engineering and effort invested in pursuing those directions, are we really on the right track?
Today, I’m presenting a series of principles that I believe to be of prime relevance for supply chain management. However, they might seem weird to most of you. We have two worlds here – the proven and the weird – and the question is what will happen a few decades from now.

Progress tends to unfold in chaotic, nonlinear fashion. The idea with these principles is to let you embrace a world that is highly chaotic, where there is room for the unexpected. These principles can help you develop faster, more reliable, and more efficient solutions that will bring improvement to your supply chains from a quantitative perspective.

Now, let’s move on to some questions.
Question: How do Zipf distributions compare to the Pareto law?
The Pareto law is the rule of thumb of the 80-20, but from a quantitative perspective, the Zipf distribution is an explicit predictive model. It has predictive capabilities that can be challenged against datasets in a very straightforward manner.
Question: Wouldn’t the Zipf-Mandelbrot distribution be better viewed as a logarithmic curve to see supply chain fluctuations, like epidemiologists do with reporting cases and deaths?
Absolutely. At a philosophical level, the question is whether you live in Mediocrity-land or Extreme-land. Supply chains and most human affairs exist in the world of extremes. Logarithmic curves are indeed useful if you want to visualize the amplitude of promotions. For example, if you want to see the amplitudes of all past promotions for large retail networks over the last 10 years, using a regular scale might make everything else invisible, simply because the biggest promotion ever was so much larger than the others. So, using a logarithmic scale can help you see the variations more clearly. With the Zipf-Mandelbrot distribution, I’m giving you a model that you can literally roll out with a few lines of code, which is more than just a logarithmic view of the data. However, I agree that the core intuition is the same. For a high-level philosophical perspective, I recommend reading Nassim Taleb’s work on Mediocristan versus Extremistan in his book “Antifragile.”
Question: On the topic of local supply chain optimization, are you relating to underlying data which supports supply chain network collaboration and SNLP?
My issue with local optimization is that large companies that operate major supply chains usually have matrix organizations. This organizational structure, with its divide-and-conquer mindset, results in local optimization by design. For example, consider two different teams – one responsible for demand forecasting and the other for purchasing decisions. These two problems – demand forecasting and purchasing optimization – are entirely entangled. You cannot perform local optimization by focusing only on the percentage of error in demand forecasting and then separately optimize purchasing based on processing efficiency. There are systemic effects, and you need to consider all of them together.
The biggest challenge for most large, established companies driving significant supply chains today is that when aiming for quantitative optimization, you have to think system-wide and company-wide. This goes against decades of matrix organization sedimentation within the company, where people have become focused solely on their well-defined boundaries, forgetting the bigger picture.
Another example of this problem would be store inventory. Stock serves two purposes: on one hand, it fulfills customer demand, and on the other, it acts as merchandise. To have the right amount of stock, you need to embrace the problem of quality of service and the problem of store appeal. Store appeal is about making the store look attractive and interesting to clients, which is more of a marketing problem. In a company, you have a marketing division and a supply chain division, and they don’t naturally work together when it comes to supply chain optimization. My point is that if you don’t bring all of these aspects together, the optimization will not work.
Regarding your SNLP concern, the problem is that people come together only to have meetings, which is not very efficient. We have published a Lokad TV episode about SNLP a few months ago, so you can refer to that if you want to have a specific discussion on SNLP.
Question: How should we distribute the time and energy between supply chain strategy and quantitative execution?
That’s a great question. The answer, as I mentioned in my second lecture, is that you need complete robotization of mundane tasks. This allows you to devote all your time and energy to the continuous strategic improvement of your numerical recipes. If you spend more than 10% of your time dealing with mundane aspects of supply chain execution, you have a problem with your methodology. Supply chain experts are too valuable to waste their time and energy on mundane execution problems that should be automated in the first place.
You need to follow a methodology that lets you devote almost all your energy to strategic thinking, which then gets immediately implemented as superior numerical recipes that drive day-to-day supply chain execution. This relates to my third lecture on product-oriented delivery, where I mean software product-oriented delivery.
Question: Is it possible to hypothesize a sort of ceiling analysis, the best improvement possible for supply chain problems given their systemic formulation?
I would say no, absolutely not. Thinking that there is some kind of optimum or ceiling is equivalent to saying that there is a limit to human ingenuity. While I don’t have any proof that there is no limit to human ingenuity, it is one of my core beliefs. Supply chains are wicked problems. You can transform the problem, and even turn what appears to be a big problem into a big solution and a potential for growth for the company. For example, look at Amazon. Jeff Bezos, in the early 2000s, understood that to be a successful retailer, he would need a massive, rock-solid software infrastructure. But this massive, industrial production-grade infrastructure that he needed to run Amazon’s e-commerce was incredibly costly, costing the company billions. So, the teams at Amazon decided to turn this cloud computing infrastructure, which was a huge investment, into a commercial product. Nowadays, this large-scale computing infrastructure is actually one of the primary sources of profit for Amazon.
When you start thinking about wicked problems, you can always redefine the problem in a superior way. That’s why I think it’s misguided to believe that there is some kind of optimal solution. When you think in terms of ceiling analysis, you’re looking at a fixed problem, and from a fixed problem perspective, you may have a solution that is probably quasi-optimal. For instance, if you look at the wheels on modern suitcases, they are probably quasi-optimal. But is there something that is completely obvious that we’re missing? Maybe there is a way to make the wheels much better, an invention that hasn’t been made yet. As soon as we see it, it will appear to be completely self-evident.
That’s why we need to think that there is no such thing as a ceiling for these problems because the problems are arbitrary. You can redefine the problem and decide that the game is to be played according to completely different rules. This is puzzling because people like to think that they have a neatly designed problem and can find solutions. The modern western education system emphasizes a solution-finding mindset, where we give you a problem and assess the quality of your solution. However, a much more interesting question is the quality of the problem itself.
Question: The best solutions will solve the problems, but sometimes finding the best solution can cost both time and money. Are there workarounds for this?
Absolutely. Again, if you have a solution that is theoretically correct but takes forever to implement, it’s not a good solution. This sort of thinking tends to be prevalent in certain academic circles, where they focus on finding the perfect solution according to narrow-minded mathematical criteria that have nothing to do with the real world. That’s exactly what I was talking about when I mentioned the right optimization problem.
Every quarter or so, there is a professor that comes to me and asks if I could review their online algorithm to solve the route optimization problem. Most of the papers I review nowadays are focused on online flavors. My response is always the same: you are not solving the right problem. I don’t care about your solution because you’re not even thinking correctly about the problem itself.
Progress should not be confused with sophistication. It’s a misguided perception that progress goes from something simple to something sophisticated. In reality, progress is often achieved by starting with something impossibly convoluted and, through superior thinking and technology, achieving simplicity. For example, if you look at my last lecture on supply chain trends for the 21st century, you will see the Machine of Marly, which brought water to the Palace of Versailles. It was an insanely complicated system, whereas modern electric pumps are much simpler and more efficient.
Progress is not necessarily found in extra sophistication. Sometimes it’s required, but it’s not an essential ingredient of progress.
Question: Large retail networks are driving their stock level, but need to fulfill orders almost immediately. Sometimes they decide to make a promo on their own that has not been initiated by the supplier. What would be the approach to predict and prepare accordingly on the supplier level?
First, we have to look at the problem from a different perspective. You’re assuming a forecasting perspective, where your client, a large retailer, is doing a big promotion that comes out of the blue. First, is it such a bad thing? If they promote your products without informing you, that’s just a fact of life. If you look at your history, they usually do that on a regular basis, and there are even patterns.
If I go back to my principles, patterns are everywhere. First, you need to embrace a perspective that you cannot forecast the future; instead, you need probabilistic forecasts. Even if you cannot perfectly anticipate fluctuations, they may not be entirely unexpected either. Perhaps you need to change the rules of the game instead of letting the supplier surprise you entirely. Maybe you need to negotiate commitments that bind the retailer, the retail network, and the supplier. If the retail network starts doing a big push without giving a heads up to the supplier, the supplier cannot realistically be held responsible for not maintaining the quality of service.
Perhaps the solution is something more collaborative. Maybe the supplier should have a better risk assessment. If the materials sold by the supplier are not perishable, it might be more profitable to have a couple of months of stock. People often think of having zero delay, zero stock, and zero everything, but is that really what your customers expect from you? Maybe what your customers expect is added value in the form of plentiful stock. Again, the answer depends on various factors.
You need to look at the problem from many angles, and there is no trivial solution. You need to think really hard about the problem and consider all the options available to you. Maybe the issue is not more stock but more production capacity. If there is a big surge of demand and it’s not too expensive to have a massive spike, and the suppliers of the suppliers can provide the materials fast enough, maybe all you need is more versatile production capacity. This would allow you to redirect your production capacity to whatever is spiking now.
By the way, this does exist in certain industries. For example, the packaging industry has massive capacities. Most of the machines in the packaging industry are industrial printers, which are relatively inexpensive. People in the packaging business typically have many printers that are not used most of the time. However, when there is a big event or a big brand wants to do a massive push, they have the capacity to print tons of new packages that fit the new marketing push of the brand.
So, it really depends on various factors, and I apologize for not having a definitive answer. But what I can definitively say is that you have to think really hard about the problem you’re facing.
This concludes today’s lecture, the sixth and last of the prologue. Two weeks from now, at the same day and hour, I will be presenting on supply chain personalities. See you next time.


