Estacionalidad (Supply Chain)

En supply chain, se dice que la demanda - o las ventas - de un producto dado exhibe estacionalidad cuando la serie de tiempo subyacente sufre una variación cíclica predecible dependiendo del momento del año. La estacionalidad es uno de los patrones estadísticos más frecuentemente usados para mejorar la precisión de los forecasts de demanda.

Ilustración de series de tiempo estacionales

El siguiente gráfico ilustra 4 series de tiempo estacionales (haz clic para agrandar). Las series de tiempo están agregadas a nivel semanal durante un período de 159 semanas (aproximadamente 3 años). Los datos representan envíos semanales de 4 productos distintos desde el almacén de un gran minorista europeo.

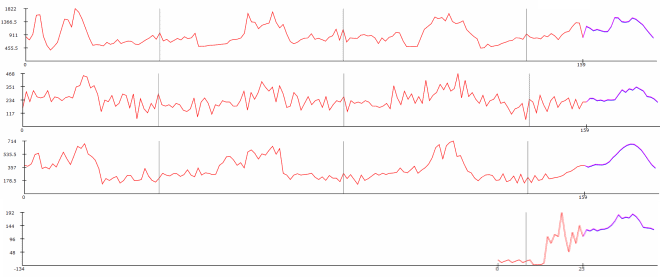
El primer día del año (1 de enero) está marcado con un marcador vertical gris. Los datos históricos aparecen en rojo mientras que el forecast de Lokad se muestra en púrpura. La estacionalidad puede ser observada visualmente como una semejanza de los patrones de un año a otro; usa los marcadores grises como referencia.

Modelo básico para la descomposición estacional

Sea Y(t) la demanda en el tiempo t. Descomponemos la demanda Y(t) en dos componentes: S(t), una función estrictamente cíclica, y Z(t), el complemento no estacional. Esto da:

Y(t) = S(t) * Z(t) where S(t + 1 year) = S(t)

Si se puede estimar tal función S(t), entonces el proceso de forecast típicamente sigue tres etapas:

• Calcular la serie de tiempo desestacionalizada como Z(t) = Y(t) / S(t).
• Producir el forecast sobre la serie de tiempo Z(t), posiblemente a través de un promedio móvil.
• Reaplicar los índices de estacionalidad al forecast posteriormente.

Volviendo al problema inicial de estimar los índices estacionales S(t), asumiendo que no existe tendencia (entre otras cosas), S(t) se puede estimar con:

S(t) = AVERAGE( Y(t-1)/MA(t-1) + Y(t-2)/MA(t-2) + Y(t-3)/MA(t-3) + ... )

donde Y(t-1) es la abreviatura de Y(t - 1 year) y MA(t) es el promedio móvil de 1 año de Y(t).

El enfoque propuesto en esta sección es naive, pero se puede implementar fácilmente en Excel. Muchos modelos estadísticos se pueden encontrar en la literatura para abordar la estacionalidad con métodos más complicados. Ej: Box-Jenkins, ARMA, ARIMA, Holt-Winters…

Desafíos en la estimación de índices de estacionalidad

El modelo de estacionalidad ilustrado anteriormente es un enfoque bastante naive que funciona para series de tiempo estacionales largas y suaves. Sin embargo, existen múltiples dificultades prácticas al estimar la estacionalidad:

1. Las series de tiempo son cortas. La vida útil de la mayoría de los bienes de consumo no excede los 3 o 4 años. Como resultado, para un producto dado, el historial de ventas ofrece en promedio muy pocos puntos en el pasado para estimar cada índice estacional (es decir, los valores de S(t) a lo largo del año, cf. la sección anterior).
2. Las series de tiempo son ruidosas. Las fluctuaciones aleatorias del mercado impactan las ventas y hacen que la estacionalidad sea más difícil de aislar.
3. Se involucran múltiples estacionalidades. Al analizar las ventas a nivel de tienda, la estacionalidad del producto en sí suele estar entrelazada con la estacionalidad de la tienda.
4. Otros patrones, como la tendencia o el ciclo de vida del producto, también impactan las series de tiempo, introduciendo diversos tipos de sesgo en la estimación.

Un método simple - aunque intensivo en mano de obra - para abordar esos problemas consiste en crear manualmente perfiles de estacionalidad a partir de agregados de productos conocidos por tener el mismo comportamiento estacional. La vida útil del agregado de productos es típicamente mucho mayor que la de los productos individuales, lo que mitiga esos problemas de estimación.

Cuasi-estacionalidad

Existen muchos patrones que ocurren una vez al año pero no siempre en la misma fecha. En Lokad, llamamos a esos patrones quasi-seasonal. Por ejemplo, el Día de la Madre (que cae en diferentes fechas dependiendo del año y también varía entre países) y otros días festivos como Ramadan, Easter y Hanukkah (que caen en diferentes fechas según el año) son quasi-seasonal.

Esos eventos quasi-seasonal quedan fuera del alcance de los modelos de forecast cíclicos clásicos que asumen que el período del ciclo es estrictamente constante. Para lidiar con esos eventos quasi-seasonal, se requiere una lógica quasi-cíclica más compleja.

La trampa de Lokad

En nuestra experiencia, la estacionalidad impacta la gran mayoría de las actividades humanas. En particular, en series de tiempo que representan las ventas de bienes de consumo (tanto alimenticios como no alimenticios), casi siempre está presente un factor estacional. Sin embargo, sucede con frecuencia que, debido a la cantidad de ruido del mercado, la calidad de la estimación de los índices estacionales termina siendo demasiado baja para ser de utilidad práctica en el refinamiento de los forecasts.

La tecnología de forecast de Lokad maneja de forma nativa tanto la estacionalidad como la quasi-seasonal, por lo que no tienes que informar a Lokad sobre ellos, ya está solucionado.

Para superar los problemas derivados de la limitada profundidad histórica disponible para la mayoría de las series de tiempo en el comercio minorista o la manufactura, Lokad utiliza análisis de múltiples series de tiempo y la estacionalidad se evalúa no en un solo producto sino observando muchos productos. Al hacer esto, reducimos el ruido en nuestra estimación de la estacionalidad, pero también introducimos estacionalidad en los forecasts incluso cuando los productos se han vendido por menos de un año.