Puntuación de Probabilidad Clasificada Continua (CRPS)

Originalmente escrito por Joannes Vermorel, junio de 2016. Actualizado por Alexey Tikhonov, mayo de 2024.

Los forecast probabilísticos asignan una probabilidad a cada futuro posible. Sin embargo, no todos los forecast probabilísticos son igual de precisos, y se requieren métricas para evaluar la precisión respectiva de distintos forecast probabilísticos. Métricas simples de métricas de precisión como MAE (Error Absoluto Medio) o MAPE (Error Porcentual Medio Absoluto) no son directamente aplicables a los forecast probabilísticos. La Continuous Ranked Probability Score (CRPS) generaliza el MAE al caso de los forecast probabilísticos. Junto con la cross entropy, la CRPS es una de las métricas de precisión más utilizadas cuando se involucran forecast probabilísticos.

Visión general

El CRPS se utiliza frecuentemente para evaluar la precisión respectiva de dos modelos de forecast probabilístico. En particular, esta métrica puede combinarse con un proceso de backtesting para estabilizar la evaluación de la precisión aprovechando múltiples mediciones sobre el mismo conjunto de datos.

Esta métrica se diferencia notablemente de métricas más simples como el MAE debido a su expresión asimétrica: mientras que los forecast son probabilísticos, las observaciones son deterministas. A diferencia de la función de pérdida pinball, el CRPS no se centra en ningún punto específico de la distribución de probabilidad, sino que considera la distribución de los forecast en su conjunto.

Definición formal

Sea $${X}$$ una variable aleatoria.

Sea $${F}$$ la función de distribución acumulativa (CDF) de $${X}$$, tal que $${F(y)=\mathbf{P}\left[X \leq y\right]}$$.

Sea $${x}$$ la observación, y $${F}$$ la CDF asociada a un forecast probabilístico empírico.

El CRPS entre $${x}$$ y $${F}$$ se define como:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^{\infty}\Big(F(y)- 𝟙(y - x)\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \qquad \tag{1}$$

donde $${𝟙}$$ es la función escalón de Heaviside y denota una función escalón a lo largo de la recta real que toma:

el valor de 1 si el argumento real es positivo o cero,
el valor de 0 en caso contrario.

El CRPS se expresa en la misma unidad que la variable observada (por ejemplo, si la demanda de un producto fue forecasted en unidades, el CRPS también se expresará en unidades).

El CRPS generaliza el error absoluto medio (MAE). De hecho, se reduce al MAE si el forecast es determinista. Este punto se ilustra en el gráfico D a continuación.

Propiedades conocidas

Gneiting y Raftery (2004) demuestran que el CRPS puede escribirse de manera equivalente como:

$$\qquad \qquad \qquad \qquad {CRPS(F,x) = \mathbf{E}\Big[|X-x|\Big]-\frac{1}{2}\mathbf{E}\Big[|X-X^*|\Big]} \qquad \qquad \qquad \qquad \qquad \qquad \tag{2}$$

donde

$${X}$$ y $${X^*}$$ son copias independientes de una variable aleatoria lineal,
$${X}$$ es la variable aleatoria asociada con la función de distribución acumulativa $${F}$$,
$${\mathbf{E} }$$ es el valor esperado de $${X}$$.

Evaluación numérica

Desde una perspectiva numérica, una forma sencilla de calcular el CRPS consiste en descomponer la integral original en dos integrales con límites bien elegidos para simplificar la función escalón de Heaviside, lo que da:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^x F(y)^2dy + \int_x^{\infty}\Big(F(y)- 1\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \tag{3}$$

En la práctica, dado que $$F$$ es una distribución empírica obtenida a través de un modelo de forecast, la variable aleatoria correspondiente $${X}$$ tiene un soporte compacto, lo que significa que solo existe un número finito de puntos donde $${\mathbf{P}[X = x] > 0}$$. Además, todos los valores de $$x$$ son números discretos. Así, las integrales pueden transformarse en sumas finitas discretas, como se ilustra en la fórmula a continuación y en el gráfico B de la siguiente sección.

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \sum_{k=0}^x F(y_k)^2 + \sum_{x+1}^{n} (F(y_k) - 1)^2} \qquad \qquad \qquad \qquad \qquad \qquad \tag{4}$$

En la fórmula (4), un índice $$n$$ representa el último elemento de la cola derecha de una distribución de probabilidad (por ejemplo, el valor máximo de la demanda con una probabilidad diferente de cero).

Finalmente, dado que el cálculo del CRPS se realiza para un único punto en el tiempo, para computar el CRPS sobre un cierto período de evaluación de interés (por ejemplo, para la ventana de responsabilidad, que es la suma del lead time del proveedor y el período de reorder) se debe tomar un promedio de los respectivos valores de CRPS calculados para ese período.

$$\qquad \qquad \qquad \qquad \qquad \qquad {CRPS = \frac{1}{T} \sum_{t=1}^{T} CRPS_t} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \tag{5}$$

Intuición visual

Para ilustrar el cálculo del CRPS, considere el siguiente ejemplo (consulte los gráficos a continuación):

A: Inicialmente, creamos un forecast de demanda probabilístico utilizando una distribución binomial negativa y truncando sus colas con probabilidades inferiores al 0.1% (lo que representa eventos extremadamente improbables, como aquellos que ocurren aproximadamente cada tres años). Los valores de demanda predichos con probabilidades diferentes de cero abarcaban un rango de 1 a 26 unidades. Más tarde, resultó que la demanda real fue de 15 unidades (tal como se muestra con la línea discontinua roja vertical).

B: Calculamos el CRPS según la 4ª fórmula anterior (véase “Evaluación numérica”). El valor resultante del CRPS representa la suma de dos áreas llenas de color rojo claro.

C: Igual que el gráfico A pero con un forecast puntual añadido para comparación.

D: El cálculo del CRPS aplicado al forecast puntual demuestra que, cuando se aplica el CRPS a un forecast puntual, el resultado es una métrica de precisión MAE. De hecho, los forecast puntuales son formas triviales de forecast probabilísticos en los que asignamos implícitamente un 100% de probabilidad a un único valor. Entonces, un gráfico de probabilidad acumulada para el CRPS estará representado por dos funciones escalonadas: una para los forecast puntuales y otra para la demanda real. Esto significa que, dependiendo de las posiciones relativas del forecast puntual y el valor real, una de las dos sumas en la fórmula (4) se reducirá a cero: la primera suma para sobrepredicciones y la segunda suma para subpredicciones.

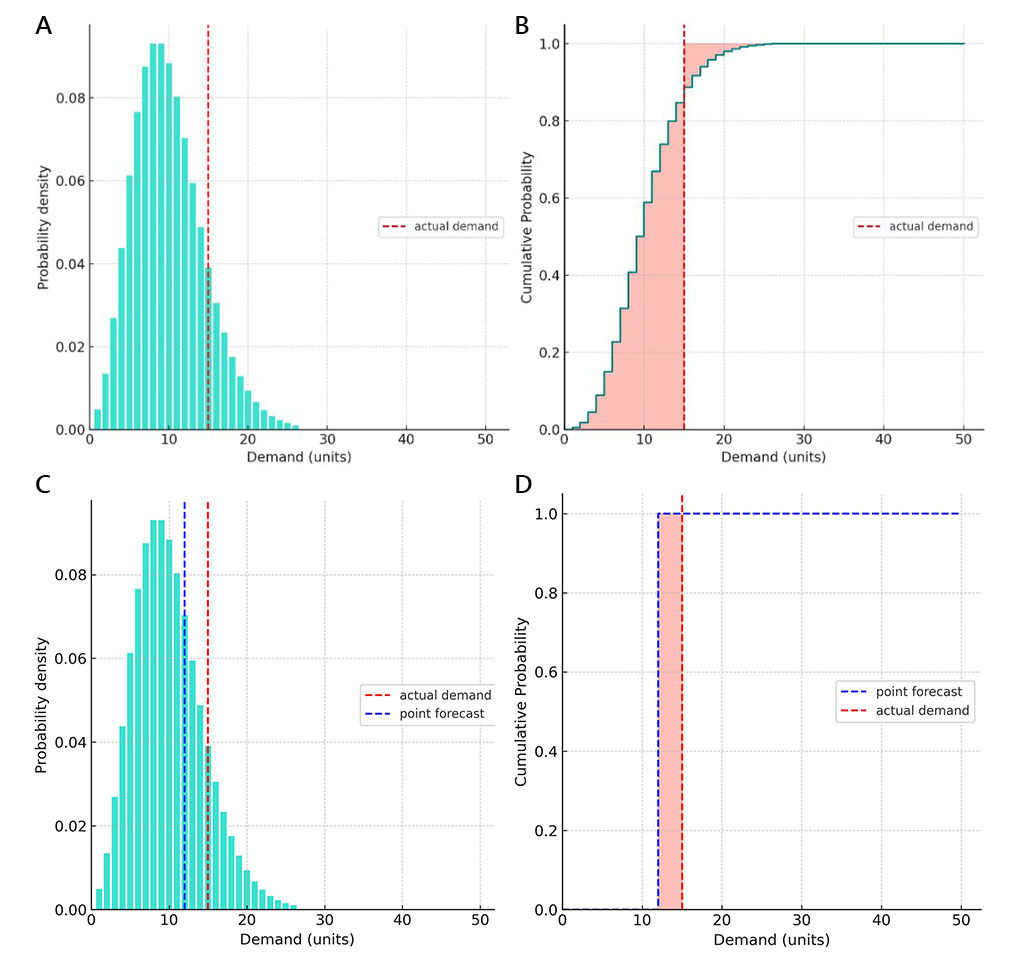
A chart illustrating probabilistic forecast and CRPS metric for evaluating its accuracy.

A: Forecast probabilístico. B: CRPS. C: Forecast probabilístico vs. forecast puntual. D: El CRPS del forecast puntual es MAE.

Para el ejemplo proporcionado a través de estos 4 gráficos, los valores resultantes del CRPS para el forecast probabilístico y para el forecast puntual son 3.32 y 3, respectivamente. Al observar los números, uno podría concluir que el forecast puntual es más preciso porque su métrica de precisión es menor (mejor) que la del forecast probabilístico. Sin embargo, esta conclusión es errónea.

En el ejemplo anterior solo consideramos un valor de la demanda real; sin embargo, cuando el forecast probabilístico se aprende utilizando datos históricos, las probabilidades se ajustan de acuerdo con las frecuencias de ocurrencia de los respectivos valores de demanda (considerando los valores disponibles en el conjunto de datos de aprendizaje). Si se eligen apropiadamente, entonces el valor promedio del CRPS para el conjunto de prueba será comparable al del conjunto de entrenamiento/validación, ya que el forecast representará adecuadamente las frecuencias de ocurrencia de diferentes valores de demanda en los datos de prueba.

El gráfico a continuación demuestra la superioridad de los forecast probabilísticos en comparación con los forecast puntuales.

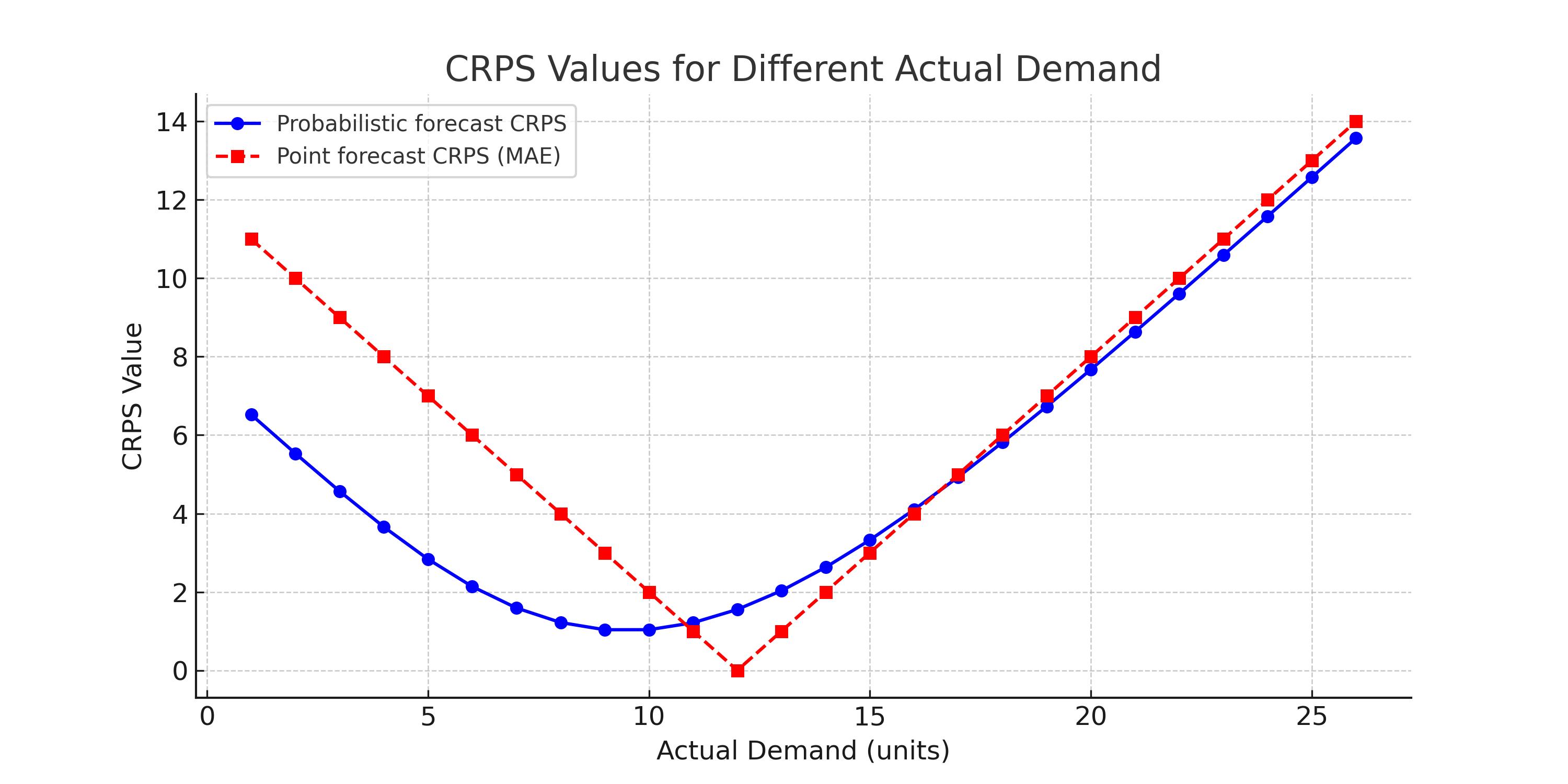
A chart illustrating how CRPS changes depending on the actual values for both probabilistic and point forecasts.

Observe qué tan suavemente varía el CRPS en función de los diferentes valores reales. Además, observe que, aparte de una pequeña región (donde el forecast puntual está muy cerca del real), en todas las demás áreas el CRPS para los forecast probabilísticos es menor que el del forecast puntual.

Si tuviéramos múltiples forecast puntuales diferentes, esta observación seguiría siendo válida. Uno tendría que desplazar mentalmente la curva roja hacia la izquierda o la derecha dependiendo de la predicción puntual, pero la superioridad del forecast probabilístico continuaría siendo válida.

Referencias

Gneiting, T. y Raftery, A. E. (2004). Strictly proper scoring rules, prediction, and estimation. Informe técnico n.º 463, Departamento de Estadística, Universidad de Washington, Seattle, Washington, USA.