Función de pérdida pinball

learn menu
Por Joannès Vermorel, febrero 2012

La función de pérdida pinball, también conocida como quantile loss, es una métrica utilizada para evaluar la precisión de un quantile forecast.

Evaluar la precisión de un quantile forecast es un problema sutil. De hecho, a diferencia de los forecasts clásicos donde el objetivo es que el forecast esté lo más cercano posible a los valores observados, la situación es intencionalmente sesgada cuando se trata de quantile forecasts. Por ello, la comparación ingenua observado vs forecasts no es satisfactoria. La función de pérdida pinball devuelve un valor que puede interpretarse como la precisión de un modelo de forecast cuantil.

Fórmula

Sea $${\tau}$$ el cuantil objetivo, $${y}$$ el valor real y $${z}$$ el quantile forecast, entonces $${L_\tau}$$, la función de pérdida pinball, se puede escribir:

$${ \begin{eqnarray} L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ si } y \geq z \\\ & = & (z - y) (1 - \tau) & \textrm{ si } z > y \end{eqnarray} }$$

Descarga: pinball-loss-function.xlsx

La hoja de cálculo ilustra cómo calcular la función de pérdida pinball en Microsoft Excel. La fórmula real no es más complicada que la de la mayoría de indicadores de precisión, como el MAPE.

Ilustración

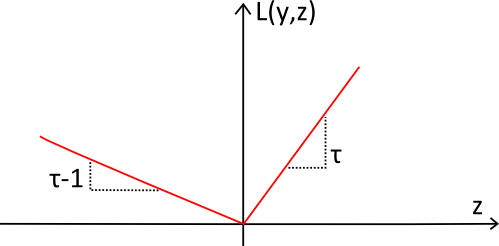
/pinball-loss-function

La función de pérdida pinball (en rojo) ha sido denominada así por su forma, que se asemeja a la trayectoria de una bola en un pinball. La función es siempre positiva y, cuanto más se aleja del objetivo $${y}$$, mayor es el valor de $${L_\tau(y,z)}$$. La pendiente se utiliza para reflejar el desequilibrio deseado en el quantile forecast.

El mejor modelo cuantil tiene la función de pérdida pinball más baja

El resultado más importante asociado con la función de pérdida pinball es que cuanto menor es la función de pérdida pinball, más precisa es el quantile forecast.

Se puede demostrar que la función que minimiza la función de pérdida pinball también entrega el cuantil óptimo. Sin embargo, el formalismo requerido para la demostración va más allá del alcance de este artículo.

Por lo tanto, para comparar la respectiva precisión de dos modelos cuantiles (por ejemplo, Lokad vs otros), es suficiente calcular el promedio de la función de pérdida pinball de cada modelo sobre un número de series de tiempo lo suficientemente grande como para asegurarse de que la diferencia observada es estadísticamente significativa. En la práctica, unos pocos cientos de series de tiempo son suficientes para evaluar cuál modelo cuantil es el más preciso.

La trampa de Lokad

La supuesta simplicidad de la noción de precisión para un forecast clásico (es decir, forecast de la media) está, en nuestra opinión, sobrevalorada. Los forecasts, tanto la media como los cuantiles, están sujetos a overfitting, lo que complica enormemente la comparación de modelos de forecast. Sin embargo, la función de pérdida pinball constituye una forma muy sencilla de evaluar la precisión relativa de dos modelos de forecast cuantil.

Lecturas adicionales