00:18 Introduction
02:18 Background
12:08 Why optimize? 1/2 Forecasting with Holt-Winters
17:32 Why optimize? 2/2 - Vehicle routing problem
20:49 The story so far
22:21 Auxiliary Sciences (recap)
23:45 Problems and solutions (recap)
27:12 Mathematical optimization
28:09 Convexity
34:42 Stochasticity
42:10 Multi-objective
46:01 Solver design
50:46 Deep (Learning) lessons
01:10:35 Mathematical optimization
01:10:58 “True” programming
01:12:40 Local search
01:19:10 Stochastic gradient descent
01:26:09 Automatic differentiation
01:31:54 Differential programming (circa 2018)
01:35:36 Conclusion
01:37:44 Upcoming lecture and audience questions
Descripción
Optimización matemática es el proceso de minimizar una función matemática. Casi todas las modernas técnicas de aprendizaje estadístico - es decir, forecast si adoptamos una perspectiva de supply chain - se basan en la optimización matemática en su núcleo. Además, una vez que se establecen los forecast, la identificación de las decisiones más rentables también se basa, en esencia, en la optimización matemática. Los problemas de supply chain frecuentemente involucran muchas variables. También son usualmente de naturaleza estocástica. La optimización matemática es una piedra angular de la práctica moderna de supply chain.
Transcripción completa

Bienvenidos a esta serie de conferencias de supply chain. Soy Joannes Vermorel, y hoy presentaré “Optimización matemática para supply chain.” La optimización matemática es la forma bien definida, formalizada y computacionalmente factible de identificar la mejor solución para un problema dado. Todos los problemas de forecast pueden verse como problemas de optimización matemática. Todas las situaciones de toma de decisiones tanto en supply chain como fuera de supply chain también pueden verse como problemas de optimización matemática. De hecho, la perspectiva de la optimización matemática está tan arraigada en nuestra visión moderna del mundo que se ha vuelto muy difícil definir el verbo “optimizar” fuera del pequeño recuadro que nos proporciona el paradigma de la optimización matemática.
Ahora, la literatura científica sobre la optimización matemática es vasta, y lo es también el ecosistema de software que ofrece herramientas para la optimización matemática. Desafortunadamente, la mayor parte de ella es de muy poco uso y relevancia en lo que respecta a supply chain. El objetivo de esta conferencia será doble: primero, queremos entender cómo abordar la optimización matemática para obtener algo que sea valioso y de utilidad práctica desde una perspectiva de supply chain. El segundo elemento será identificar, en este vasto panorama, algunos de los elementos más valiosos que se pueden encontrar.

La definición formal de la optimización matemática es sencilla: piensas en una función que normalmente se llamará la función de pérdida, y esta función será de valores reales, es decir, produce simplemente números. Lo que se busca es identificar la entrada (X0) que representa el mejor valor que minimiza la función de pérdida. Este es, típicamente, el paradigma de la optimización matemática, y es engañosamente simple. Veremos que hay muchas cosas que se pueden decir sobre esta perspectiva general.
Este campo, creo, cuando pensamos en términos de optimización matemática aplicada, se desarrolló principalmente bajo el nombre de investigación operativa, que definimos de manera más específica como la investigación operativa clásica que abarcó desde la década de 1940 hasta finales de los años 70 del siglo XX. La idea es que la investigación operativa clásica, en comparación con la optimización matemática, se preocupaba realmente por los problemas de negocio. La optimización matemática se ocupa de la forma general del problema de optimización, mucho menos de si el problema tiene alguna significación comercial. Por el contrario, la investigación operativa clásica esencialmente realizaba optimización, pero no en cualquier tipo de problema – sino en problemas que se identificaban como importantes para las empresas.
Curiosamente, pasamos de la investigación operativa a la optimización matemática de manera muy similar a como pasamos del forecast, que surgió a principios del siglo XX como un campo preocupado por el forecast general de los niveles de actividad económica futura, típicamente asociado con los forecast de series de tiempo. Este dominio fue esencialmente reemplazado por machine learning, que se ocupa de hacer predicciones en un ámbito mucho más amplio de problemas. Podríamos decir que hemos tenido, de manera general, la misma transición de la investigación operativa a la optimización matemática que ocurrió del forecast al machine learning. Ahora, cuando dije que la era clásica de la investigación operativa se extendió hasta finales de los años 70, tenía una fecha muy específica en mente. En febrero de 1979, Russell Ackoff publicó un impresionante artículo titulado “The Future of Operational Research is Past.” Para entender este artículo, que considero realmente un hito en la historia de la ciencia de optimización, hay que entender que Russell Ackoff es, esencialmente, uno de los padres fundadores de la investigación operativa.
Cuando publicó este artículo, ya no era un hombre joven; tenía 60 años. Ackoff nació en 1919 y había pasado prácticamente toda su carrera trabajando en investigación operativa. Cuando publicó su artículo, básicamente afirmó que la investigación operativa había fracasado. No solo no entregó resultados, sino que el interés en la industria se estaba reduciendo, de modo que había menos interés a finales de los 90 que en el campo hace 20 años.
Lo que es muy interesante de entender es que la causa no es en absoluto el hecho de que las computadoras de esa época fueran mucho más débiles que las que tenemos hoy. El problema no tiene nada que ver con la limitación en términos de capacidad de procesamiento. Estamos a finales de los años 70; las computadoras son muy modestas en comparación con lo que tenemos hoy en día, pero aún pueden realizar millones de operaciones aritméticas en un plazo razonable. El problema no está relacionado con la limitación de la capacidad de procesamiento, especialmente en una época en la que esta progresa a una velocidad increíble.
Por cierto, este artículo es una lectura fantástica. Realmente sugiero a la audiencia que lo consulte; se puede encontrar fácilmente con su motor de búsqueda favorito. Este artículo es muy accesible y está bien escrito. Aunque los tipos de problemas que Ackoff señala en este artículo aún resuenan con mucha fuerza cuatro décadas después, de muchas maneras, el artículo es muy previsor respecto a muchos de los problemas que aún aquejan a los supply chains actuales.
Entonces, ¿cuál es el problema? El problema es que este paradigma, en el que tomas una función y la optimizas, puede demostrar que tu proceso de optimización identifica alguna solución buena o quizá óptima. Sin embargo, ¿cómo demuestras que la función de pérdida que realmente estás optimizando tiene algún interés para el negocio? El problema es que cuando digo que podemos optimizar un problema o una función dada, ¿qué pasa si lo que estás optimizando es en realidad una fantasía? ¿Y si esto no tiene nada que ver con la realidad del negocio que intentas optimizar?
Aquí radica el meollo del problema, y aquí se encuentra la razón por la que todos esos primeros intentos fracasaron esencialmente. Es porque resulta que cuando se inventa algún tipo de expresión matemática que se supone debe representar el interés del negocio, lo que se obtiene es una fantasía matemática. Eso es literalmente lo que Russell Ackoff señala en este artículo, y se encuentra en un punto de su carrera en el que ha jugado este juego durante mucho tiempo y reconoce que esencialmente no conduce a nada. En su artículo, comparte la opinión de que el campo ha fracasado, y propone su diagnóstico, pero no tiene mucha solución que ofrecer. Es muy interesante porque uno de los padres fundadores, un investigador muy respetado y reconocido, dice que este campo de investigación es una calle sin salida. Pasará el resto de su vida, que aún es bastante larga, transitando completamente de una perspectiva cuantitativa de la optimización del negocio hacia una perspectiva cualitativa. Pasará las últimas tres décadas de su vida apostando por métodos cualitativos y aún así producirá trabajos muy interesantes en la segunda parte de su vida tras este punto de inflexión.
Ahora, en lo que respecta a esta serie de conferencias, ¿qué hacemos, dado que los puntos que Russell Ackoff plantea sobre la investigación operativa siguen siendo muy válidos en la actualidad? De hecho, ya he comenzado a abordar los mayores problemas que Ackoff señalaba, y en ese entonces, él y sus colegas no tenían soluciones que ofrecer. Podían diagnosticar el problema, pero no tenían una solución. En esta serie de conferencias, las soluciones que propongo son de naturaleza metodológica, al igual que el hecho de que Ackoff señala que existe un profundo problema metodológico con esta perspectiva de investigación operativa.
Los métodos que propongo son esencialmente dos: por un lado, el personal de supply chain, y por otro lado, el método titulado optimización experimental, que resulta ser realmente complementario a la optimización matemática. Además, me posiciono, a diferencia de la investigación operativa que afirma tener interés o relevancia para el negocio, en que la forma en que abordo el problema hoy no es a través del ángulo o de la perspectiva de la investigación operativa. Abordo el problema desde la óptica de la optimización matemática, que posiciono como una ciencia auxiliar pura para supply chain. Digo que no hay nada intrínsecamente fundamental en la optimización matemática para supply chain; es solo de interés fundamental. Es solo un medio, no un fin. Ahí es donde se diferencia. El punto puede ser muy simple, pero tiene una gran importancia a la hora de lograr resultados de grado predictivo con todo esto.

Ahora, ¿por qué queremos incluso optimizar en primer lugar? La mayoría de los algoritmos de forecast tienen un problema de optimización matemática en su núcleo. En esta pantalla, lo que puedes ver es el clásico algoritmo de forecast de series de tiempo multiplicativo Holt-Winters. Este algoritmo es, principalmente, de interés histórico; no recomendaría a ningún supply chain actual que aproveche este algoritmo específico. Pero por simplicidad, este es un método paramétrico muy simple, y es tan conciso que en realidad se puede poner completamente en una sola pantalla. Ni siquiera es tan verboso.
Todas las variables que puedes ver en la pantalla son simplemente números; no hay vectores involucrados. Esencialmente, Y(t) es tu estimación; este es tu forecast de series de tiempo. Aquí en la pantalla, se va a hacer forecast de H periodos hacia adelante, por lo que H es como el horizonte. Y puedes pensar que en realidad estás trabajando sobre Y(t), que es esencialmente tu serie de tiempo. Puedes pensar en datos de ventas agregados semanalmente o datos de ventas agregados mensualmente. Este modelo tiene esencialmente tres componentes: Lt, que es el nivel (tienes un nivel por periodo), Bt, que es la tendencia, y St, que es un componente estacional. Cuando dices que quieres aprender el modelo Holt-Winters, tienes tres parámetros: alpha, beta y gamma. Estos tres parámetros son esencialmente solo números entre cero y uno. Entonces, tienes tres parámetros, todos números entre cero y uno, y cuando dices que quieres aplicar el algoritmo Holt-Winters, simplemente significa que identificarás los valores adecuados para esos tres parámetros, y eso es todo. La idea es que estos parámetros, alpha, beta y gamma, serán los mejores si minimizan el tipo de error que has especificado para tu forecast. En esta pantalla, puedes ver un error cuadrático medio, lo cual es muy clásico.
El objetivo de la optimización matemática es idear un método para hacer esta identificación de los valores correctos de los parámetros para alpha, beta y gamma. ¿Qué podemos hacer? Bueno, el método más fácil y simple es algo como la búsqueda en cuadrícula (grid search). La búsqueda en cuadrícula diría que simplemente vamos a explorar todos los valores. Debido a que estos son números fraccionarios, hay un número infinito de valores, así que en realidad vamos a elegir una resolución, digamos pasos de 0.1, e iremos en incrementos de 0.1. Dado que tenemos tres variables entre 0 y 1, avanzamos en incrementos de 0.1; son aproximadamente 1,000 iteraciones para pasar y encontrar el mejor valor, considerando esta resolución.
Sin embargo, esta resolución es bastante débil. 0.1 te da aproximadamente una resolución del 10% en la escala que tienes para tus parámetros. Así que tal vez quieras optar por 0.01, que es mucho mejor; es una resolución del 1%. Sin embargo, si haces eso, el número de combinaciones realmente explota. Pasas de 1,000 combinaciones a un millón de combinaciones, y ves que ese es el problema con la búsqueda en cuadrícula: muy rápidamente, te topas con un muro combinatorio y tienes un número enorme de opciones.
La optimización matemática consiste en idear algoritmos que te den más rendimiento por el esfuerzo por una cantidad dada de recursos informáticos que quieras dedicar al problema. ¿Puedes obtener una solución mucho mejor que una búsqueda exhaustiva? La respuesta es sí, absolutamente.
Entonces, ¿qué podemos hacer en este caso para obtener una mejor solución invirtiendo menos recursos computacionales? Primero, podríamos usar algún tipo de gradiente. La expresión completa para Holt-Winters es completamente diferenciable, salvo por una única división que es un pequeño caso marginal relativamente fácil de solucionar. Así, toda esta expresión, incluida la función de pérdida, es enteramente diferenciable. Podríamos usar un gradiente para guiar nuestra búsqueda; ese sería un enfoque.
Otro enfoque diría que, en la práctica, en supply chain, tal vez tengas toneladas de series de tiempo. Así que, en lugar de tratar cada serie de tiempo de forma independiente, lo que quieres hacer es una búsqueda en cuadrícula para las primeras 1,000 series de tiempo, en la que vas a invertir, y luego identificarás combinaciones para alpha, beta y gamma que sean buenas. Luego, para todas las demás series de tiempo, simplemente elegirás de esta lista corta de candidatos para identificar la mejor solución.
Verás, hay muchas ideas simples sobre cómo puedes hacer mucho mejor que simplemente optar por un enfoque de búsqueda en cuadrícula puro, y la esencia de la optimización matemática, así como todo tipo de problemas de toma de decisiones, puede verse típicamente como problemas de optimización matemática.
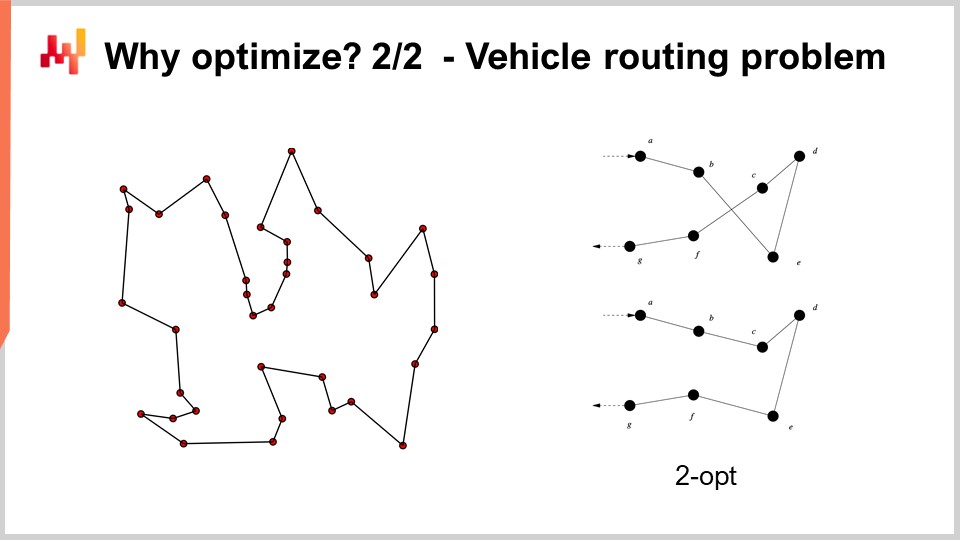
Por ejemplo, el problema de ruteo de vehículos que puedes ver en la pantalla puede considerarse un problema de optimización matemática. Se trata de seleccionar la lista de puntos. No escribí la versión formal del problema porque es relativamente variable y no aporta mucha claridad. Pero si quieres pensarlo, puedes simplemente pensar: “Tengo puntos, puedo asignar una especie de pseudo-ranking, que es simplemente una puntuación a cada punto, y luego tengo un algoritmo que ordena todos los puntos por pseudo-ranking en orden ascendente, y esa es mi ruta.” El objetivo del algoritmo será identificar los valores para esos pseudo-rankings que te proporcionen las mejores rutas.
Ahora, con este problema, vemos que nos enfrentamos a una situación en la que, de repente, la búsqueda en cuadrícula ni remotamente es una opción. Tenemos docenas de puntos, y si intentáramos probar todas las combinaciones, sería demasiado. Además, el gradiente no nos va a ayudar, al menos no es obvio cómo lo haría, porque el problema es muy discreto por naturaleza, y no existe algo que se parezca a un descenso por gradiente obvio para este tipo de problema.
Sin embargo, resulta que si queremos abordar este tipo de problema, existen heurísticas muy potentes que se han identificado en la literatura. Por ejemplo, la heurística two-opt, publicada por Croes en 1958, te ofrece una heurística muy directa. Comienzas con una ruta aleatoria, y en esta ruta, cada vez que la ruta se cruza consigo misma, aplicas una permutación para eliminar el cruce. Así, comienzas con una ruta aleatoria, y en el primer cruce que observes, realizas la permutación para eliminarlo, y luego repites el proceso. Repetirás el proceso con la heurística hasta que no quede ningún cruce. Lo que obtendrás de esta heurística tan simple es, en realidad, una muy buena solución. Puede que no sea óptima en el verdadero sentido matemático, por lo que no es necesariamente la solución perfecta; sin embargo, es una muy buena solución, y la puedes obtener con una cantidad de recursos computacionales relativamente mínima.
El problema con la heurística two-opt es que es una heurística muy refinada, pero es increíblemente específica para este único problema. Lo que realmente interesa en la optimización matemática es identificar métodos que funcionen en grandes clases de problemas en lugar de contar con una heurística que solo funcione para una versión específica de un problema. Así, queremos tener métodos muy generales.
Ahora, la historia hasta ahora en esta serie de conferencias: esta conferencia forma parte de una serie de conferencias, y el presente capítulo está dedicado a las ciencias auxiliares de supply chain. En el primer capítulo, presenté mis puntos de vista sobre supply chain tanto como campo de estudio como práctica. El segundo capítulo se dedicó a la metodología, y en particular, introdujimos una metodología que es de suma relevancia para la presente conferencia, que es la optimización experimental. Esa es la clave para abordar el problema tan válido identificado por Russell Ackoff hace décadas. El tercer capítulo está completamente dedicado al personal de supply chain. En esta conferencia, nos centramos en identificar el problema que estamos a punto de resolver, en lugar de mezclar la solución y el problema. En este cuarto capítulo, estamos investigando todas las ciencias auxiliares de supply chain. Hay una progresión desde el nivel más bajo en términos de hardware, subiendo al nivel de algoritmos, y luego a la optimización matemática. Estamos avanzando en términos de niveles de abstracción a lo largo de esta serie.

Un breve repaso de las ciencias auxiliares: ofrecen una perspectiva sobre el propio supply chain. La presente conferencia no trata de supply chain per se, sino más bien de una de las ciencias auxiliares de supply chain. Esta perspectiva marca una diferencia significativa entre la perspectiva clásica de la investigación operativa, que se suponía que era un fin, y la optimización matemática, que es un medio para un fin, pero no un fin en sí mismo, al menos en lo que respecta a supply chain. La optimización matemática no se preocupa por los detalles específicos del negocio, y la relación entre la optimización matemática y supply chain es similar a la relación entre la química y la medicina. Desde una perspectiva moderna, no necesitas ser un químico brillante para ser un médico brillante; sin embargo, un médico que afirme no saber nada de química parecería sospechoso.

La optimización matemática asume que el problema es conocido. No se preocupa por la validez del problema, sino que se centra en sacar el máximo provecho de lo que se puede hacer para un problema dado en términos de optimización. De alguna manera, es como un microscopio: muy poderoso pero con un enfoque increíblemente estrecho. El peligro, al volver a la discusión sobre el futuro de la investigación operativa, es que si apuntas tu microscopio en el lugar equivocado, podrías distraerte con desafíos intelectuales interesantes pero, en última instancia, irrelevantes.
Por eso, la optimización matemática debe usarse en conjunto con la optimización experimental. La optimización experimental, que cubrimos en la conferencia anterior, es el proceso mediante el cual puedes iterar con retroalimentación del mundo real hacia versiones mejores del propio problema. La optimización experimental es un proceso para mutar no la solución, sino el problema, de modo que, de forma iterativa, puedas converger hacia un buen problema. Este es el meollo del asunto, y en donde Russell Ackoff y sus colegas de aquella época no tenían una solución. Ellos tenían las herramientas para optimizar un problema dado, pero no las herramientas para mutar el problema hasta que fuera bueno. Si tomas un problema matemático tal como lo puedes escribir en tu torre de marfil, sin la retroalimentación del mundo real, lo que obtienes es una fantasía. Tu punto de partida, cuando comienzas un proceso de optimización experimental, es simplemente una fantasía. Se necesita la retroalimentación del mundo real para que funcione. La idea es alternar entre la optimización matemática y la optimización experimental. En cada etapa de tu proceso de optimización experimental, utilizarás herramientas de optimización matemática. El objetivo es minimizar tanto los recursos computacionales como los esfuerzos de ingeniería, permitiendo que el proceso itere hacia la siguiente versión del problema.

En esta conferencia, primero refinaremos nuestra comprensión de la perspectiva de la optimización matemática. La definición formal es engañosamente simple, pero hay complejidades de las que debemos ser conscientes para lograr una relevancia práctica para supply chain. Luego, exploraremos dos amplias clases de solucionadores que representan el estado del arte en optimización matemática desde una perspectiva de supply chain.
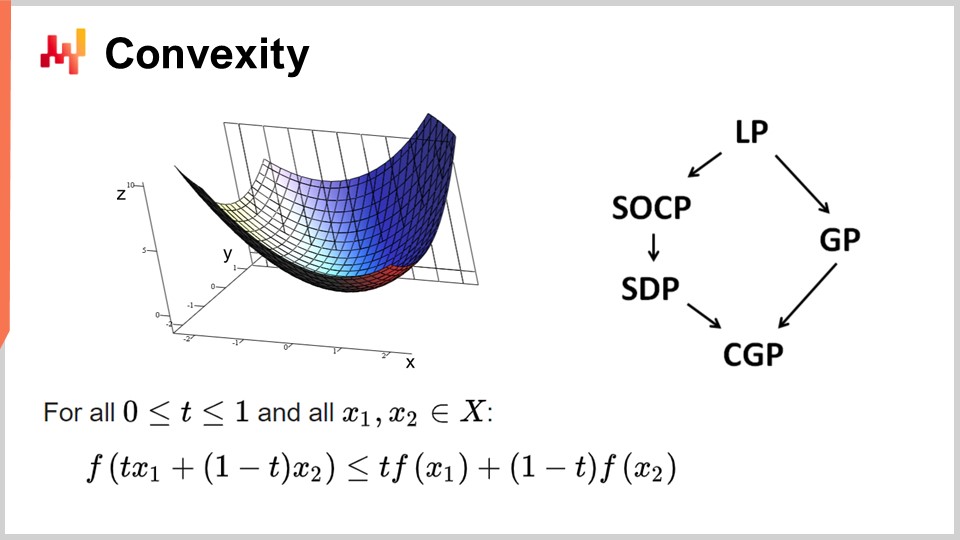
Primero, hablemos de la convexidad y de los primeros trabajos en optimización matemática. La investigación operativa se centró inicialmente en funciones de pérdida convexas. Se dice que una función es convexa si cumple con ciertas propiedades. Intuitivamente, una función es convexa si, para dos puntos cualesquiera en la variedad definida por la función, la línea recta que conecta esos puntos siempre estará por encima de los valores que toma la función entre ellos.
La convexidad es clave para permitir una verdadera optimización matemática, donde puedes demostrar resultados. Intuitivamente, cuando tienes una función convexa, significa que para cualquier punto de la función (cualquier solución candidata), siempre puedes mirar a tu alrededor y encontrar una dirección en la que puedas descender. No importa por dónde comiences, siempre puedes descender, y descender es siempre una buena jugada. El único punto donde esencialmente no puedes descender más es el punto óptimo. Estoy simplificando aquí; hay casos excepcionales en los que existen soluciones no únicas o ninguna solución. Pero dejando a un lado algunos casos excepcionales, el único punto en el que no puedes optimizar más con una función convexa es el punto óptimo. De lo contrario, siempre puedes descender, y descender es una buena jugada.
Se ha realizado una enorme cantidad de investigación sobre funciones convexas, y han surgido diversos paradigmas de programación a lo largo de los años. LP significa programación lineal, y otros paradigmas incluyen la programación cónica de segundo orden, la programación geométrica (tratando con polinomios), la programación semidefinida (involucrando matrices con valores propios positivos) y la programación cónica geométrica. Estos marcos tienen en común que abordan problemas convexos estructurados. Son convexos tanto en su función de pérdida como en las restricciones que limitan las soluciones elegibles.
Estos marcos han sido de muy alto interés, con una intensa literatura científica producida. Sin embargo, a pesar de sus nombres impresionantes, estos paradigmas tienen muy poca expresividad. Incluso problemas simples exceden las capacidades de estos marcos. Por ejemplo, la optimización de los parámetros de Holt-Winters, un modelo básico de forecast de los años 60, ya excede lo que cualquiera de estos marcos puede hacer. De manera similar, el problema de ruteo de vehículos y el problema del viajante, ambos simples, exceden las capacidades de estos marcos.
Por eso dije al principio que ha habido un enorme cuerpo de literatura, pero hay muy poco uso. Estoy simplificando aquí; hay casos excepcionales en los que existen soluciones no únicas o ninguna solución. Pero dejando a un lado algunos casos excepcionales, el único punto en el que no puedes optimizar más con una función convexa es el punto óptimo. De lo contrario, siempre puedes descender, y descender es una buena jugada.
Se ha realizado una enorme cantidad de investigación sobre funciones convexas, y han surgido diversos paradigmas de programación a lo largo de los años. LP significa programación lineal, y otros paradigmas incluyen la programación cónica de segundo orden, la programación geométrica (tratando con polinomios), la programación semidefinida (involucrando matrices con valores propios positivos) y la programación cónica geométrica. Estos marcos tienen en común que abordan problemas convexos estructurados. Son convexos tanto en su función de pérdida como en las restricciones que limitan las soluciones elegibles.
Estos marcos han sido de muy alto interés, con una intensa literatura científica producida. Sin embargo, a pesar de sus nombres impresionantes, estos paradigmas tienen muy poca expresividad. Incluso problemas simples exceden las capacidades de estos marcos. Por ejemplo, la optimización de los parámetros de Holt-Winters, un modelo básico de forecast de los años 60, ya excede lo que cualquiera de estos marcos puede hacer. De manera similar, el problema de ruteo de vehículos y el problema del viajante, ambos simples, exceden las capacidades de estos marcos.
Por eso dije al principio que ha existido un enorme cuerpo de literatura, pero hay muy poco uso. Una parte del problema fue un enfoque equivocado en los solucionadores de optimización matemática pura. Estos solucionadores son muy interesantes desde una perspectiva matemática porque puedes producir pruebas matemáticas, pero solo pueden usarse con problemas de juguete literalmente o con problemas completamente inventados. Una vez que estás en el mundo real, fallan, y ha habido muy poco progreso en estos campos en las últimas décadas. En lo que respecta a supply chain, casi nada, excepto algunos nichos, tiene relevancia para estos solucionadores.

Otro aspecto, que fue completamente desestimado e ignorado durante la era clásica de la investigación operativa, es la aleatoriedad. La aleatoriedad o estocasticidad es de importancia crítica en dos formas radicalmente diferentes. La primera forma en que debemos abordar la aleatoriedad es en el propio solucionador. Hoy en día, todos los solucionadores de última generación aprovechan extensamente los procesos estocásticos internamente. Esto es muy interesante en contraposición a tener un proceso completamente determinista. Estoy hablando del funcionamiento interno del solucionador, el fragmento de software que implementa las técnicas de optimización matemática.
La razón por la que todos los solucionadores de última generación aprovechan extensamente los procesos estocásticos tiene que ver con la forma en que existe el hardware de computación moderno. La alternativa a la aleatoriedad al explorar soluciones es recordar lo que has hecho en el pasado, para no quedarte atrapado en el mismo bucle. Si tienes que recordar, consumirás memoria. El problema radica en el hecho de que necesitamos realizar muchos accesos a la memoria. Una forma de introducir aleatoriedad suele ser una manera de aliviar en gran medida la necesidad de acceso aleatorio a la memoria.
Al hacer que tu proceso sea estocástico, puedes evitar sondear tu propia base de datos sobre lo que has probado o no probado entre las posibles soluciones para el problema que deseas optimizar. Lo haces un poco al azar, pero no completamente. Esto tiene una importancia clave en prácticamente todos los solucionadores modernos. Uno de los aspectos algo contraintuitivos de tener un proceso estocástico es que, aunque puedes tener un solucionador estocástico, la salida aún puede ser bastante determinista. Para entender esto, considera la analogía de una serie de tamices. Un tamiz es, fundamentalmente, un proceso físico estocástico, en el que aplicas movimientos aleatorios y se lleva a cabo el proceso de tamizado. Aunque el proceso es completamente estocástico, el resultado es completamente determinista. Al final, obtienes un resultado completamente predecible del proceso de tamizado, a pesar de que tu proceso fue, en esencia, aleatorio. Esto es exactamente lo que sucede con solucionadores estocásticos bien diseñados. Este es uno de los ingredientes clave de los solucionadores modernos.
Otro aspecto, que es ortogonal en lo que respecta al azar, es la naturaleza estocástica de los propios problemas. Esto estuvo mayormente ausente en la era clásica de la investigación operativa – la idea de que tu función de pérdida es ruidosa y que cualquier medición que obtengas de ella tendrá cierto grado de ruido. Esto es casi siempre el caso en supply chain. ¿Por qué? La realidad es que en supply chain, cada vez que tomas una decisión, es porque anticipas algún tipo de evento futuro. Si decides comprar algo, es porque anticipas que habrá necesidad de ello más adelante. El futuro no está escrito, por lo que puedes tener algunas ideas sobre lo que vendrá, pero la intuición nunca es perfecta. Si decides producir un producto ahora, es porque esperas que más adelante haya demanda para este producto. La calidad de tu decisión, que es producir hoy, depende de condiciones futuras inciertas, y por lo tanto, cualquier decisión que tomes en supply chain tendrá una función de pérdida que varía dependiendo de estas condiciones futuras que no pueden ser controladas. Ese tipo de aleatoriedad debida a tratar con eventos futuros es irreducible, y eso es de interés clave porque significa que, en esencia, estamos lidiando con problemas estocásticos.
Sin embargo, si volvemos a los solucionadores matemáticos clásicos, vemos que este aspecto está completamente ausente, lo cual es un gran problema. Esto significa que existen clases de solucionadores que ni siquiera pueden comprender el tipo de problemas que enfrentaremos, porque los problemas que serán de interés, donde queremos aplicar la optimización matemática, serán de naturaleza estocástica. Estoy hablando del ruido en la función de pérdida.
Existe una objeción de que si tienes un problema estocástico, siempre puedes transformarlo de nuevo en un problema determinista mediante el muestreo. Si evalúas tu función de pérdida ruidosa 10,000 veces, puedes obtener una función de pérdida aproximadamente determinista. Sin embargo, este enfoque es increíblemente ineficiente porque introduce una sobrecarga 10,000 veces mayor en tu proceso de optimización. La perspectiva de la optimización matemática consiste en obtener los mejores resultados para tus recursos computacionales limitados. No se trata de invertir una cantidad infinitamente grande de recursos computacionales para resolver el problema. Tenemos que lidiar con una cantidad finita de recursos computacionales, incluso si esta cantidad es bastante grande. Por lo tanto, al analizar solucionadores más adelante, debemos tener en cuenta que es de interés primordial contar con solucionadores que puedan comprender nativamente los problemas estocásticos en lugar de recurrir por defecto al enfoque determinista.
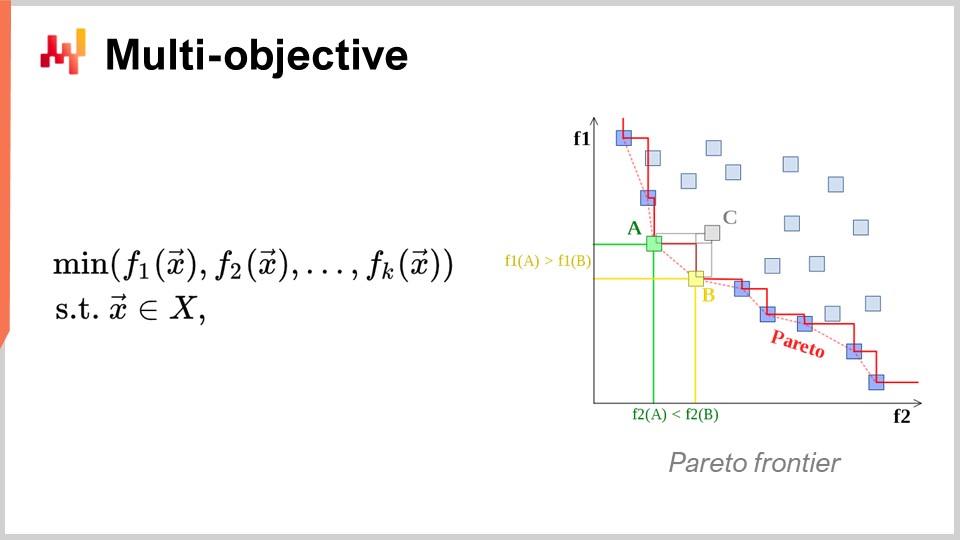
Otro enfoque, que también es de interés primordial, es la optimización multiobjetivo. En la expresión ingenua del problema de optimización matemática, dije que la función de pérdida era, esencialmente, de un solo valor, por lo que teníamos un valor que queríamos minimizar. Pero, ¿qué sucede si tenemos un vector de valores, y lo que queremos hacer es encontrar la solución que ofrezca el punto más bajo según el orden lexicográfico de todos los vectores, como f1, f2, f3, etc.?
¿Por qué es esto de interés desde la perspectiva de supply chain? La realidad es que si adoptas esta perspectiva multiobjetivo, puedes expresar todas tus restricciones como una única función de pérdida dedicada. Primero, puedes tener una función que cuente las violaciones de tus restricciones. ¿Por qué hay restricciones en supply chain? Bueno, hay restricciones por todas partes. Por ejemplo, si realizas una orden de compra, debes asegurarte de tener suficiente espacio en tu almacén para almacenar las mercancías cuando lleguen. Así, tienes restricciones de espacio de almacenamiento, capacidad de producción y más. La idea es que, en lugar de tener un solucionador en el que trates las restricciones como casos especiales, es más interesante tener un solucionador que pueda abordar la optimización multiobjetivo y en el que puedas expresar las restricciones como uno de los objetivos. Simplemente cuentas el número de violaciones y deseas minimizarlo, llevando ese número de infracciones a cero.
La razón por la que este enfoque es tan relevante para supply chain es que los problemas de optimización que enfrentan las supply chains no son rompecabezas criptográficos. No se trata de los problemas combinatorios súper restrictivos en los que o tienes una solución y es buena, o estás a un pelo de distancia de la solución y no tienes nada. En supply chain, obtener lo que típicamente se llama una solución factible – una solución que satisface todas las restricciones – es generalmente algo completamente trivial. Identificar una solución que cumpla con las restricciones no es una gran tarea. Lo que es muy difícil es, entre todas las soluciones que satisfacen las restricciones, identificar la que resulta más rentable para el negocio. Aquí es donde se complica. Encontrar una solución que no viole las restricciones es muy sencillo. Esto no es el caso en otros campos, por ejemplo, en la optimización matemática para el diseño industrial, donde quieres colocar componentes dentro de un teléfono móvil. Ese es un problema increíblemente restringido y combinatorio, y no puedes hacer trampa renunciando a una restricción y obteniendo un pequeño fallo en tu teléfono. Es un problema extremadamente estricto y combinatorio, y donde realmente necesitas tratar las restricciones como una prioridad. Esto no es necesario, creo, para la gran mayoría de los problemas de supply chain. Por lo tanto, es nuevamente de muy alto interés contar con técnicas que puedan abordar nativamente la optimización multiobjetivo.
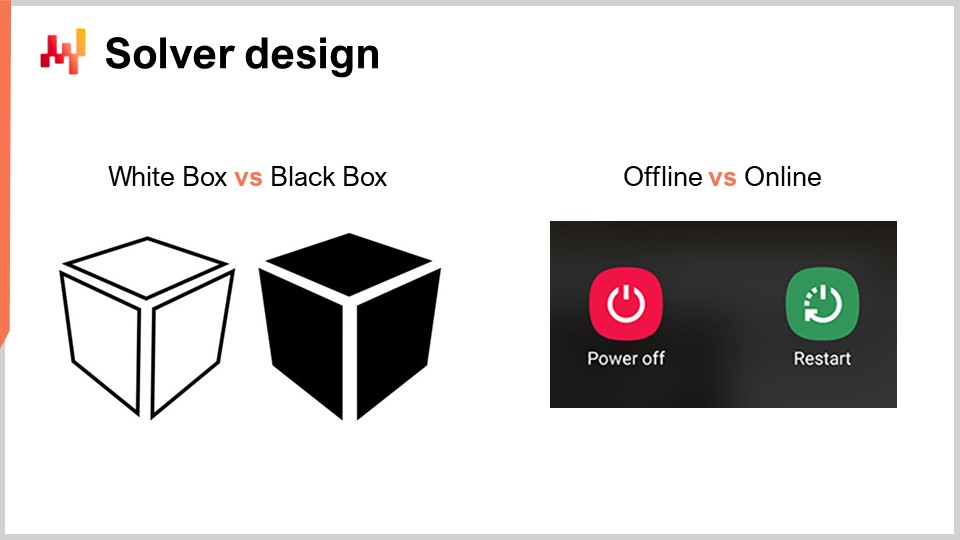
Ahora, hablemos un poco más sobre el diseño del solucionador. Desde una perspectiva de muy alto nivel sobre cómo queremos diseñar una pieza de software que vaya a producir soluciones para una clase muy amplia de problemas, hay dos aspectos de diseño muy notables que me gustaría destacar. El primer aspecto a considerar es si vamos a operar desde una perspectiva de caja blanca o de caja negra. La idea de una perspectiva de caja negra es que podemos procesar cualquier programa arbitrario, de modo que la función de pérdida puede ser cualquier programa arbitrario. No nos importa; lo tratamos como una caja negra completa. Lo único que queremos es un programa en el que podamos evaluarlo y obtener el valor de una solución tentativa. Por el contrario, un enfoque de caja blanca enfatiza el hecho de que la función de pérdida en sí tiene una estructura que podemos inspeccionar y aprovechar. Podemos ver dentro de la función de pérdida. Por cierto, cuando estaba discutiendo la convexidad unos slides antes, todos esos modelos y solucionadores matemáticos puros eran realmente enfoques de caja blanca. Son el caso extremo de los enfoques de caja blanca, en los que no solo puedes ver dentro del problema, sino que el problema tiene una estructura muy rígida, como la programación semidefinida, donde la forma es muy estrecha. Sin embargo, sin recurrir a algo tan rígido como un marco matemático, puedes, por ejemplo, decir que como parte de la caja blanca, cuentas con algo como el gradiente que te ayudará. Un gradiente de la función de pérdida es de interés clave porque, de repente, puedes saber en qué dirección quieres ir para descender, incluso si no cuentas con un problema convexo en el que el simple descenso por gradiente garantice un buen resultado. Como regla general, si puedes aplicar un enfoque de caja blanca a tu solucionador, tendrás uno que es órdenes de magnitud más eficiente en comparación con un solucionador de caja negra.
Ahora, como segundo aspecto, tenemos solucionadores offline versus online. El solucionador offline opera, típicamente, en lote, de modo que un solucionador offline simplemente toma el problema, lo ejecuta y tendrás que esperar hasta que se complete. En ese momento, cuando el solucionador finaliza, te da la mejor solución o algo que sea la mejor solución identificada. Por el contrario, un solucionador online funciona con un enfoque de mejor esfuerzo. Va a identificar una solución que sea aceptable y luego invertir recursos computacionales para iterar hacia soluciones cada vez mejores a medida que pasa el tiempo y se invierten más recursos computacionales. Lo que realmente es de interés clave es que, cuando abordas un problema con un solucionador online, significa que prácticamente puedes pausar el proceso en cualquier momento y obtener una solución candidata temprana. Incluso puedes reanudar el proceso. Si volvemos a los solucionadores matemáticos, estos son típicamente solucionadores en lote en los que debes esperar hasta el final del proceso.
Desafortunadamente, operar en el mundo de supply chain puede ser un camino muy accidentado, como se mencionó en una de las conferencias previas de esta serie. Habrá situaciones en las que, normalmente, podrías permitirte gastar, digamos, tres horas para ejecutar este proceso de optimización matemática. Pero, a veces, pueden ocurrir fallos de TI, problemas del mundo real o una emergencia en tu supply chain. En tales casos, será un salvavidas si lo que usualmente toma tres horas puede ser interrumpido después de cinco minutos y proporcionar una respuesta, incluso si es una respuesta deficiente, en lugar de no dar ninguna respuesta. Existe un dicho en el ejército que dice que el peor plan es no tener plan, por lo que es mejor tener un plan muy rudimentario que nada en absoluto. Esto es exactamente lo que te ofrece un solucionador online. Estos son los elementos clave de diseño que tendremos en cuenta en la siguiente discusión.
Ahora, para concluir esta primera sección de la conferencia sobre cómo abordar la optimización matemática, echemos un vistazo a las lecciones de deep learning. Deep learning ha sido una revolución total para el campo del machine learning. Sin embargo, en esencia, deep learning también tiene un problema de optimización matemática. Creo que deep learning generó una revolución dentro de la optimización matemática misma y cambió por completo la forma en que vemos los problemas de optimización. Deep learning redefinió lo que consideramos el estado del arte de la optimización matemática.
Hoy en día, los modelos de deep learning más grandes manejan más de un billón de parámetros, lo que equivale a mil mil millones. Solo para ponerlo en perspectiva, la mayoría de los solucionadores matemáticos luchan incluso para manejar 1,000 variables y, típicamente, colapsan con apenas algunas decenas de miles de variables, sin importar cuánta potencia de hardware les asignes. En contraste, deep learning tiene éxito, indiscutiblemente usando una gran cantidad de recursos computacionales, pero, aun así, resulta factible. Existen modelos de deep learning en producción que tienen más de un billón de parámetros, y todos esos parámetros se optimizan, lo que significa que contamos con procesos de optimización matemática que pueden escalar a un billón de parámetros. Esto es absolutamente asombroso y radicalmente diferente al rendimiento que vimos con las perspectivas clásicas de optimización.
Lo interesante es que incluso problemas que son completamente deterministas, como jugar Go o ajedrez, que son no estadísticos, discretos y combinatorios, han sido resueltos con mayor éxito mediante métodos que son completamente estocásticos y estadísticos. Esto resulta desconcertante, porque jugar Go o ajedrez puede verse como problemas de optimización discretos, sin embargo, hoy en día se resuelven de manera más eficiente con métodos que son completamente estocásticos y estadísticos. Esto va en contra de la intuición que la comunidad científica tenía sobre estos problemas hace dos décadas.
Revisemos la comprensión que deep learning ha desbloqueado en lo que concierne a la optimización matemática. Lo primero es reconsiderar por completo la maldición de la dimensionalidad. Creo que este concepto es, en gran medida, defectuoso, y deep learning está demostrando que no es de esa manera como se debe pensar siquiera en la dificultad de un problema de optimización. Resulta que, al observar clases de problemas matemáticos, puedes probar, desde un punto de vista matemático, que ciertos problemas son extremadamente difíciles de resolver a la perfección. Por ejemplo, habrás oído hablar de problemas NP-hard; sabes que a medida que añades dimensiones al problema, se vuelve exponencialmente más difícil de resolver. Cada dimensión extra hace el problema más complicado, y existe una barrera acumulativa. Se puede probar que ningún algoritmo puede esperar resolver el problema perfectamente con una cantidad limitada de recursos computacionales. Sin embargo, deep learning demostró que esta perspectiva era, en gran medida, defectuosa.
Primero, tenemos que diferenciar entre la complejidad representacional del problema y la complejidad intrínseca del mismo. Permíteme clarificar estos dos términos con un ejemplo. Echemos un vistazo al ejemplo de forecast de series temporales dado inicialmente. Digamos que tenemos un historial de ventas, agregado diariamente durante tres años, por lo que contamos con un vector temporal diario de aproximadamente 1,000 días. Esta es la representación del problema.
Ahora, ¿y si cambio a una representación de la serie temporal por segundo? Este es el mismo historial de ventas, pero en lugar de representar mis datos de ventas en agregados diarios, voy a representar esta serie temporal –la misma serie– en agregados por segundo. Esto significa que hay 86,400 segundos en cada día, de modo que voy a inflar el tamaño y la dimensión de mi representación del problema por 86,000.
Pero si empezamos a pensar en la dimensión intrínseca, no es porque tenga un historial de ventas, ni porque pase de una agregación diaria a una por segundo, que estoy incrementando la complejidad o la complejidad dimensional del problema en 1,000. Muy probablemente, si me adentro en ventas agregadas por segundo, la serie temporal será increíblemente dispersa, por lo que estará compuesta en su mayoría por ceros en prácticamente todos los intervalos. No estoy aumentando la dimensionalidad interesante del problema por un factor de 100,000. Deep learning aclara que no es porque tengas una representación del problema con muchas dimensiones que el problema sea, en esencia, difícil.
Otro ángulo asociado con la dimensionalidad es que, aunque puedes demostrar que ciertos problemas son NP-completos, por ejemplo, el problema del viajante (una versión simplificada del problema de enrutamiento de vehículos presentado al comienzo de esta conferencia), el viajante es técnicamente lo que se conoce como un problema NP-hard. Entonces, es un problema en el que, si deseas encontrar la mejor solución en el caso general, tendrá un costo exponencial a medida que añades puntos a tu mapa. Pero la realidad es que estos problemas son muy fáciles de resolver, como lo ilustra la heurística two-opt; puedes obtener soluciones excelentes con una cantidad mínima de recursos computacionales. Así que, ten cuidado, porque las pruebas matemáticas que demuestran que algunos problemas son muy difíciles pueden ser engañosas. No te indican que, si estás de acuerdo con obtener una solución aproximada, la aproximación puede ser excelente, y a veces ni siquiera es una aproximación; vas a obtener la solución óptima. Simplemente, no puedes probar que es óptima. Esto no dice nada acerca de si puedes aproximar el problema y, con mucha frecuencia, esos problemas supuestamente plagados por la maldición de la dimensionalidad son sencillos de resolver porque sus dimensiones interesantes no son tan altas. Deep learning ha demostrado con éxito que muchos problemas que se pensaba que eran increíblemente difíciles no lo eran tanto en primer lugar.
La segunda idea clave fue los mínimos locales. La mayoría de los investigadores que trabajaban en optimización matemática e investigación operativa optaron por funciones convexas porque no existían mínimos locales. Durante mucho tiempo, quienes no trabajaban con funciones convexas pensaban en cómo evitar quedar atrapados en un mínimo local. La mayor parte de los esfuerzos se dedicaron a trabajar en cosas como meta-heurísticas. Deep learning ha proporcionado una comprensión renovada: no nos importan los mínimos locales. Esta comprensión proviene de trabajos recientes originados en la comunidad de deep learning.
Si tienes una dimensión muy alta, puedes demostrar que los mínimos locales desaparecen a medida que aumenta la dimensión del problema. Los mínimos locales son muy frecuentes en problemas de baja dimensión, pero si aumentas la dimensión de los problemas a cientos o miles, hablando estadísticamente, los mínimos locales se vuelven increíblemente improbables. Hasta el punto de que, al observar dimensiones muy grandes como millones, desaparecen por completo.
En lugar de pensar que una dimensión más alta es tu enemiga, como se asociaba con la maldición de la dimensionalidad, ¿qué pasaría si pudieras hacer exactamente lo contrario e inflar la dimensión del problema hasta que se vuelva tan grande que resulte trivial tener un descenso limpio sin mínimos locales en absoluto? Resulta que esto es exactamente lo que se está haciendo en la comunidad de deep learning y con modelos que tienen un billón de parámetros. Este enfoque te brinda una manera muy clara de avanzar mediante gradientes.
Esencialmente, la comunidad de deep learning demostró que era irrelevante tener una demostración sobre la calidad del descenso o la convergencia final. Lo que importa es la velocidad del descenso. Quieres iterar y descender muy rápidamente hacia una solución muy buena. Si puedes tener un proceso que descienda más rápido, en última instancia avanzarás más en términos de optimización. Estas ideas van en contra de la comprensión general de la optimización matemática, o de lo que era la comprensión dominante hace dos décadas.
Hay otras lecciones que se pueden aprender del deep learning, ya que es un campo muy rico. Una de ellas es la simpatía con el hardware. El problema con los solucionadores matemáticos, como la programación cónica o la programación geométrica, es que se centran primero en la intuición matemática y no en el hardware de cómputo. Si diseñas un solucionador que de manera fundamental antagoniza tu hardware de cómputo, no importa lo inteligente que sea tu matemática, es probable que termines siendo desesperadamente ineficiente debido al mal uso de los recursos computacionales.
Una de las ideas clave de la comunidad de deep learning es que tienes que llevarte bien con el hardware de cómputo y diseñar un solucionador que lo aproveche. Por eso comencé esta serie de conferencias sobre ciencias auxiliares para supply chain con computadoras modernas para supply chain. Es importante entender el hardware que tienes y cómo aprovecharlo al máximo. Esta simpatía con el hardware es la forma en que puedes lograr modelos con un billón de parámetros, aunque requiere un gran clúster de computadoras o un supercomputador.
Otra lección del deep learning es el uso de funciones sustitutas. Tradicionalmente, los solucionadores matemáticos se enfocaban en optimizar el problema tal como era, sin desviarse de él. Sin embargo, el deep learning demostró que, a veces, es mejor utilizar funciones sustitutas. Por ejemplo, con mucha frecuencia para predicciones, los modelos de deep learning utilizan cross-entropy como métrica de error en lugar del error cuadrático medio. Prácticamente nadie en el mundo real está interesado en la cross-entropy como métrica, ya que es bastante extraña.
Entonces, ¿por qué la gente utiliza cross-entropy? Proporciona gradientes increíblemente pronunciados, y como demostró el deep learning, todo se trata de la velocidad del descenso. Si tienes gradientes muy pronunciados, puedes descender muy rápidamente. Algunas personas podrían objetar y decir, “Si quiero optimizar el error cuadrático medio, ¿por qué debería usar cross-entropy? Ni siquiera es el mismo objetivo.” La realidad es que, si optimizas cross-entropy, obtendrás gradientes muy pronunciados y, al final, si evalúas tu solución con respecto al error cuadrático medio, obtendrás una mejor solución según ese mismo criterio, con mucha frecuencia, si no siempre. Estoy simplificando solo para efectos de esta explicación. La idea de las funciones sustitutas es que el problema real no es absoluto; es simplemente algo que utilizarás para el control y para evaluar la validez final de tu solución. No es necesariamente algo que utilizarás mientras el solucionador está en progreso. Esto va completamente en contra de las ideas asociadas a los solucionadores matemáticos que fueron populares durante las últimas décadas.
Finalmente, existe la importancia de trabajar en paradigmas. Con la optimización matemática, existe implícitamente una división del trabajo en la organización de tu equipo de ingeniería. La división del trabajo implícita asociada a los solucionadores matemáticos es que tendrás ingenieros matemáticos por un lado, que son responsables de desarrollar el solucionador, e ingenieros de problemas por el otro, cuya responsabilidad es expresar el problema en una forma adecuada para ser procesado por los solucionadores matemáticos. Esta división del trabajo era prevalente, y la idea era hacerla lo más sencilla posible para el ingeniero de problemas, de modo que solo tuviera que expresar el problema de la manera más minimalista y pura, dejando que el solucionador hiciera el trabajo.
El deep learning demostró que esta perspectiva era profundamente ineficiente. Esta división arbitraria del trabajo no era, en absoluto, la mejor manera de abordar el problema. Si haces eso, terminas con situaciones increíblemente difíciles, superando con creces el estado del arte para cualquiera que sean los ingenieros matemáticos trabajando en el problema de optimización. Una forma mucho mejor es que los ingenieros de problemas hagan un esfuerzo extra para replantear los problemas de manera que sean mucho más adecuados para la optimización por parte del optimizador matemático.
Deep learning se trata de un conjunto de recetas que te permiten plantear el problema sobre tu solucionador, para que puedas aprovechar al máximo tu optimizador. La mayoría de los desarrollos en la comunidad de deep learning se han centrado en elaborar estas recetas que son muy buenas para aprender mientras se desempeñan bien dentro del paradigma de los solucionadores que tienen (por ejemplo, TensorFlow, PyTorch, MXNet). La conclusión es que realmente quieres colaborar con el ingeniero de problemas, o en terminología de supply chain, el supply chain scientist.

Ahora pasemos a la segunda y última sección de esta conferencia sobre los elementos más valiosos de la literatura. Echaremos un vistazo a dos amplias clases de solucionadores: la búsqueda local y la programación diferenciable.

Primero, permíteme detenerme de nuevo en el término “programming.” Esta palabra tiene una importancia crítica porque, desde una perspectiva de supply chain, realmente queremos poder expresar el problema al que nos enfrentamos, o el problema que creemos que estamos enfrentando. No queremos algún tipo de versión de muy baja resolución del problema que simplemente encaje con alguna hipótesis matemática semi-absurda, como la necesidad de expresar tu problema en un cono o algo por el estilo. Lo que realmente nos interesa es tener acceso a un verdadero paradigma de programming.
Recuerda, aquellos solucionadores matemáticos como la programación lineal, la programación cónica de segundo orden y la programación geométrica venían todos con una palabra clave de programming. Sin embargo, en las últimas décadas, lo que esperamos de un paradigma de programming ha evolucionado drásticamente. Hoy en día, queremos algo que te permita lidiar con programas casi arbitrarios, programas en los que tienes bucles, ramas y, posiblemente, asignaciones de memoria, etc. Realmente quieres algo lo más cercano posible a un programa arbitrario, y no algún tipo de versión de juguete súper limitada que tenga algunas propiedades matemáticas interesantes. En supply chain, es mejor estar aproximadamente correcto que exactamente equivocado.

Para abordar la optimización genérica, comencemos con la búsqueda local. La búsqueda local es una técnica de optimización matemática engañosamente simple. El pseudocódigo implica comenzar con una solución aleatoria, que representas como un conjunto de bits. Luego, inicializas tu solución de forma aleatoria y comienzas a cambiar bits al azar para explorar el vecindario de la solución. Si, a través de esta exploración aleatoria, encuentras una solución que resulta ser mejor, esta se convierte en tu nueva solución de referencia.
Este enfoque sorprendentemente poderoso puede funcionar con literalmente cualquier programa, tratándolo como una caja negra, y también puede reiniciarse desde cualquier solución conocida. Hay muchas formas de mejorar este enfoque. Una forma es la computación diferencial, que no debe confundirse con la computación diferenciable. La computación diferencial es la idea de que, si ejecutas tu programa en una solución dada y luego cambias un bit, puedes reejecutar el mismo programa con una ejecución diferencial, sin tener que reejecutar todo el programa. Obviamente, tus resultados pueden variar, y depende mucho de la estructura del problema. Una forma de acelerar el proceso no es aprovechar algún tipo de información extra sobre el programa caja negra con el que operamos, sino simplemente poder acelerar el programa en sí, tratándolo aún en gran parte como una caja negra, porque no vuelves a ejecutar todo el programa cada vez.
Existen otros enfoques para mejorar la búsqueda local. Puedes mejorar el tipo de movimientos que realizas. La estrategia más básica se llama los k-flips, en la que cambias k bits, siendo k un número muy pequeño, algo como un par hasta una docena. En lugar de simplemente cambiar bits, puedes permitir que el ingeniero de problemas indique el tipo de mutaciones a aplicar a la solución. Por ejemplo, puedes expresar que deseas aplicar algún tipo de permutación en tu problema. La idea es que estos movimientos inteligentes a menudo preservan el cumplimiento de algunas restricciones en tu problema, lo cual puede ayudar a que el proceso de búsqueda local converja más rápidamente.
Otra manera de mejorar la búsqueda local es no explorar el espacio completamente al azar. En lugar de cambiar bits de forma aleatoria, puedes intentar aprender las direcciones correctas, identificando las áreas más prometedoras para realizar los flips. Algunos artículos recientes han demostrado que puedes conectar un pequeño módulo de deep learning sobre la búsqueda local, actuando como generador. Sin embargo, este enfoque puede ser complicado en términos de ingeniería, ya que tienes que asegurarte de que la sobrecarga introducida por el proceso de aprendizaje automático proporcione un retorno positivo en términos de recursos computacionales.
Existen otras heurísticas bien conocidas, y si deseas una visión sintética muy buena de lo que se necesita para implementar un motor de búsqueda local moderno, puedes leer el artículo “LocalSolver: A Black-Box Local-Search Solver for 0-1 Programs.” La empresa que opera LocalSolver también cuenta con un producto con el mismo nombre. En este artículo, ofrecen una perspectiva de ingeniería sobre lo que ocurre tras bastidores en su solucionador de grado de producción. Utilizan multi-start y recocido simulado para obtener mejores resultados.
Una advertencia que agregaría sobre la búsqueda local es que no maneja muy bien, ni de forma nativa, los problemas estocásticos. Con los problemas estocásticos, no es tan fácil como simplemente decir “Tengo una solución mejor,” y decidir de inmediato que se convierta en la mejor solución. Es más complicado que eso, y necesitas hacer un esfuerzo adicional antes de lanzarte a la solución evaluada como la nueva mejor.

Ahora, pasemos a la segunda clase de solucionadores que discutiremos hoy, que es la programación diferenciable. Pero primero, para entender la programación diferenciable, necesitamos comprender el descenso de gradiente estocástico. El descenso de gradiente estocástico es una técnica de optimización iterativa basada en gradientes. Surgió como una serie de técnicas pioneras a principios de la década de 1950, lo que lo hace tener casi 70 años de antigüedad. Permaneció bastante de nicho durante casi seis décadas, y tuvimos que esperar el avance del deep learning para darnos cuenta del verdadero potencial y poder del descenso de gradiente estocástico.
El descenso de gradiente estocástico asume que la función de pérdida se puede descomponer de forma aditiva en una serie de componentes. En la ecuación, Q(W) representa la función de pérdida, que se descompone en una serie de funciones parciales, Qi. Esto es relevante porque la mayoría de los problemas de aprendizaje pueden verse como el tener que aprender una predicción basada en una serie de ejemplos. La idea es que puedes descomponer tu función de pérdida como el error promedio cometido sobre todo el conjunto de datos, con un error local para cada punto de datos. Muchos problemas de supply chain también se pueden descomponer de forma aditiva de esta manera. Por ejemplo, puedes descomponer tu red de supply chain en una serie de desempeños para cada SKU, con una función de pérdida asociada a cada SKU. La verdadera función de pérdida que deseas optimizar es el total.
Cuando tienes esta descomposición en su lugar, que es muy natural para problemas de aprendizaje, puedes iterar con el proceso de descenso del gradiente estocástico (SGD). El vector de parámetros W puede ser una serie muy grande, ya que los modelos de deep learning más grandes tienen un billón de parámetros. La idea es que en cada paso del proceso, actualizas tus parámetros aplicando una pequeña cantidad de gradiente. Eta es la tasa de aprendizaje, un pequeño número típicamente entre 0 y 1, a menudo alrededor de 0.01. Nabla de Q es el gradiente para una función de pérdida parcial Qi. Sorprendentemente, este proceso funciona bien.
Se dice que SGD es estocástico porque aleatoriamente eliges el siguiente elemento i, saltando a través de tu conjunto de datos y aplicando un pequeño trozo de gradiente a tus parámetros en cada paso. Esta es la esencia del descenso del gradiente estocástico.
Permaneció relativamente de nicho y en gran medida ignorado por la comunidad en general durante casi seis décadas, porque es bastante sorprendente que el descenso del gradiente estocástico funcione en absoluto. Funciona porque proporciona un excelente trade-off entre el ruido en la función de pérdida y el costo computacional de acceder a la misma función de pérdida. En lugar de tener una función de pérdida que debe evaluarse contra todo el conjunto de datos, con el descenso del gradiente estocástico, podemos tomar un punto de datos a la vez y aún así aplicar un poco de gradiente. Esta medición será muy fragmentaria y ruidosa, aunque este ruido en realidad es aceptable porque es muy rápido. Puedes realizar órdenes de magnitud más optimizaciones diminutas y ruidosas en comparación con procesar todo el conjunto de datos.
Sorprendentemente, el ruido introducido ayuda al descenso del gradiente. Uno de los problemas en espacios de alta dimensión es que los mínimos locales se vuelven relativamente inexistentes. Sin embargo, aún puedes enfrentar grandes áreas de mesetas donde el gradiente es muy pequeño, y el descenso del gradiente no tiene una dirección definida para descender. El ruido te proporciona gradientes más pronunciados y ruidosos que ayudan con el descenso.
Lo que también es interesante del descenso del gradiente es que es un proceso estocástico, pero puede manejar problemas estocásticos de forma gratuita. Si Qi es una función estocástica con ruido y da un resultado aleatorio que varía cada vez que la evalúas, ni siquiera necesitas cambiar una sola línea del algoritmo. El descenso del gradiente estocástico es de gran interés porque te brinda algo que está completamente alineado con el paradigma que es relevante para supply chain.

La segunda pregunta es: ¿de dónde proviene el gradiente? Tenemos un programa, y simplemente tomamos el gradiente de la función de pérdida parcial, pero ¿de dónde proviene este gradiente? ¿Cómo obtienes un gradiente para un programa arbitrario? Resulta que existe una técnica muy elegante y minimalista descubierta hace mucho tiempo llamada diferenciación automática.
La diferenciación automática surgió en la década de 1960 y se ha refinado con el tiempo. Hay dos tipos: el modo forward, descubierto en 1964, y el modo reverse, descubierto en 1980. La diferenciación automática puede verse como un truco de compilación. La idea es que tienes un programa para compilar, y con la diferenciación automática, tienes tu programa que representa la función de pérdida. Puedes recompilar este programa para obtener un segundo programa, y la salida del segundo programa no es la función de pérdida, sino los gradientes de todos los parámetros involucrados en el cálculo de la función de pérdida.
Además, la diferenciación automática te proporciona un segundo programa con una complejidad computacional básicamente idéntica a la de tu programa inicial. Esto significa que no solo tienes una forma de crear un segundo programa que compute los gradientes, sino que también el segundo programa tiene las mismas características computacionales en términos de rendimiento que el primer programa. Es una inflación de costo computacional por un factor constante. La realidad, sin embargo, es que el segundo programa obtenido no tiene exactamente las mismas características de memoria que el programa inicial. Aunque los detalles finos van más allá del alcance de esta conferencia, podemos discutirlos durante las preguntas. Esencialmente, el segundo programa, llamado el reverse, requerirá más memoria, y en algunas situaciones patológicas, puede requerir mucha más memoria que el programa inicial. Recuerda que más memoria crea problemas con el rendimiento computacional, ya que no se puede asumir un acceso uniforme a la memoria.
Para ilustrar un poco cómo se ve la diferenciación automática, como mencioné, hay dos modos: forward y reverse. Desde una perspectiva de aprendizaje o de optimización de supply chain, el único modo de interés para nosotros es el modo reverse. Lo que puedes ver en la pantalla es una función de pérdida F, completamente inventada. Puedes ver el rastro forward, una secuencia de operaciones aritméticas o elementales que se realizan para calcular tu función para dos valores de entrada dados, X1 y X2. Esto te proporciona todos los pasos elementales realizados para calcular el valor final.
La idea es que para cada paso elemental, y la mayoría de ellos son simplemente operaciones aritméticas básicas como la multiplicación o la suma, el modo reverse es un programa que ejecuta los mismos pasos pero en orden inverso. En lugar de tener los valores forward, vas a tener los adjuntos. Para cada operación aritmética, tendrás su contraparte en reverse. La transición de la operación forward a su contraparte es muy directa.
Aunque parezca complicado, tienes una ejecución forward y una ejecución reverse, donde tu ejecución reverse no es más que una transformación elemental aplicada a cada operación. Al final del reverse, obtienes los gradientes. La diferenciación automática puede parecer complicada, pero no lo es. El primer prototipo que implementamos tenía menos de 100 líneas de código, por lo que es muy directo y, esencialmente, un truco de transpilation barato.
Ahora, esto es interesante porque tenemos el descenso del gradiente estocástico, que es un mecanismo de optimización increíblemente poderoso. Es increíblemente escalable, en línea, de pizarra blanca, y funciona nativamente con problemas estocásticos. El único problema que quedaba era cómo obtener el gradiente, y con la diferenciación automática, tenemos el gradiente con un costo fijo o un factor constante, para prácticamente cualquier programa arbitrario. Lo que obtenemos al final es la programación diferenciable.
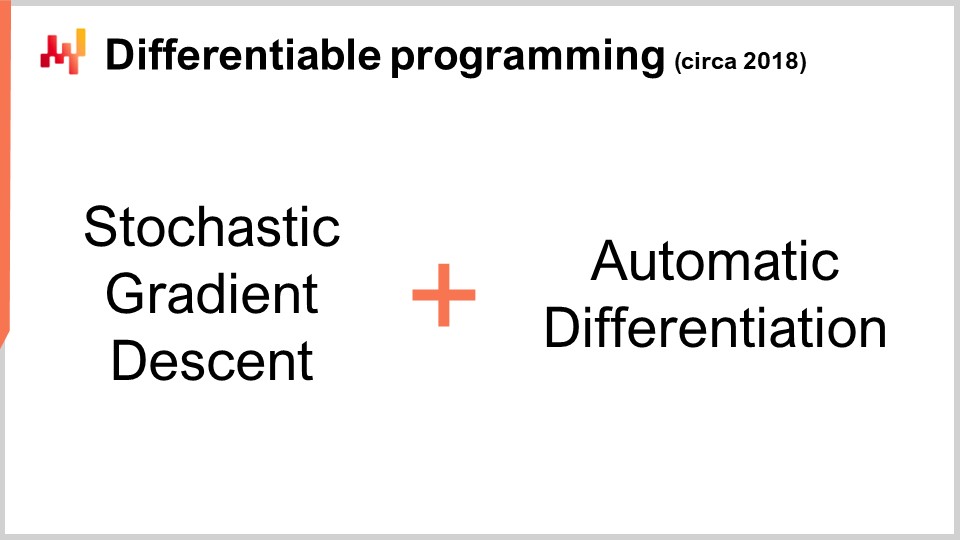
Curiosamente, la programación diferenciable es una combinación del descenso del gradiente estocástico y la diferenciación automática. Aunque estas dos técnicas, el descenso del gradiente estocástico y la diferenciación automática, tienen décadas de antigüedad, la programación diferenciable solo alcanzó prominencia a principios de 2018 cuando Yann LeCun, el Head of AI at Facebook, comenzó a comunicar sobre este concepto. LeCun no inventó este concepto, pero fue fundamental para hacerlo popular.
Por ejemplo, la comunidad de deep learning inicialmente utilizó la retropropagación en lugar de la diferenciación automática. Para aquellos familiarizados con las redes neuronales, la retropropagación es un proceso complejo que es órdenes de magnitud más complicado de implementar que la diferenciación automática. La diferenciación automática es superior en todos los aspectos. Con este conocimiento, la comunidad de deep learning refinó su visión de lo que constituye el aprendizaje en deep learning. Deep learning combinó la optimización matemática con varias técnicas de aprendizaje, y la programación diferenciable emergió como un concepto limpio que aisló las partes no dedicadas al aprendizaje del deep learning.
Las modernas técnicas de deep learning, como el modelo transformer, asumen un entorno de programación diferenciable que opera en la parte inferior. Esto permite a los investigadores centrarse en los aspectos de aprendizaje que se construyen en la parte superior. La programación diferenciable, aunque es fundamental para el deep learning, también es muy relevante para la optimización de supply chain y para apoyar los procesos de aprendizaje de supply chain, tales como statistical forecasting.
Al igual que con el deep learning, hay dos partes en el problema: la programación diferenciable como capa base y las técnicas de optimización o aprendizaje en la parte superior. La comunidad de deep learning busca identificar arquitecturas que funcionen bien con la programación diferenciable, como los transformers. De manera similar, se deben identificar las arquitecturas que funcionen bien para fines de optimización. Esto es lo que se ha hecho para aprender a jugar Go o ajedrez en entornos altamente combinatorios. Discutiremos técnicas que funcionan bien para la optimización específica de supply chain en conferencias posteriores.

Pero ahora, es momento de concluir. Una buena parte de la literatura de supply chain e incluso la mayoría de sus implementaciones de software están bastante confundidas cuando se trata de optimización matemática. Este aspecto usualmente ni siquiera se identifica correctamente como tal, y como resultado, los profesionales, investigadores e incluso los ingenieros de software que trabajan para enterprise software a menudo mezclan sus recetas numéricas de manera bastante desordenada cuando se trata de optimización matemática. Tienen un gran problema, ya que uno de los componentes no se ha identificado como de naturaleza de optimización matemática, y debido a que las personas ni siquiera son conscientes de lo que está disponible en la literatura, a menudo recurren a búsquedas en rejilla toscas o heurísticas apresuradas que producen un rendimiento errático e inconsistente. Como conclusión a esta conferencia, de ahora en adelante, cada vez que te encuentres con un método numérico de supply chain o software de supply chain que afirme ofrecer algún tipo de característica analítica, debes preguntarte qué está pasando en términos de optimización matemática y qué se está haciendo. Si te das cuenta de que los proveedores no ofrecen una visión clara al respecto, lo más probable es que estés en el lado izquierdo de la ilustración, y este no es el lugar en el que quieres estar.
Ahora, echemos un vistazo a las preguntas.

Pregunta: ¿Es la transición hacia métodos computacionales una habilidad previa en operaciones, y los roles operativos se volverían obsoletos, o viceversa?
Primero, permíteme aclarar algunas cosas. Creo que es un error dirigir este tipo de inquietudes hacia el CIO. La gente espera demasiado de sus CIOs. Como Chief Information Officer, ya debes lidiar con la capa base de tu infraestructura de software, tales como recursos computacionales, sistemas transaccionales de bajo nivel, integridad de la red y ciberseguridad. No se debe esperar que el CIO tenga una comprensión de lo que se necesita para realmente hacer algo de valor para tu supply chain.
El problema es que en muchas empresas, la gente es tan desesperadamente ignorante en lo relacionado con lo informático que el CIO se convierte en la persona a la que se recurre para todo. La realidad es que el CIO debería ocuparse de la capa base de la infraestructura, y luego corresponde a cada especialista abordar sus necesidades específicas con los recursos computacionales y las herramientas de software disponibles para ellos.
En cuanto a los roles operativos volviéndose obsoletos, si tu rol consiste en revisar manualmente hojas de cálculo de Excel spreadsheets todo el día, entonces sí, es muy probable que tu rol se vuelva obsoleto. Este ha sido un problema conocido desde 1979, cuando Russell Ackoff publicó su artículo. El problema es que la gente sabía que este método para tomar decisiones no era el futuro, pero se mantuvo como el status quo durante mucho tiempo. La esencia del problema es que las empresas necesitan entender el proceso experimental. Creo que habrá una transición en la que las empresas comiencen a readquirir estas habilidades. Muchas grandes empresas norteamericanas después de la Segunda Guerra Mundial tenían cierto conocimiento de investigación operativa entre sus ejecutivos. Era un tema novedoso, y los consejos de administración de las grandes empresas sabían algo sobre investigación operativa. Como señala Russell Ackoff, debido a la falta de resultados, estas ideas fueron empujadas hacia abajo en la jerarquía de la empresa hasta que incluso se externalizaron por completo, ya que en su mayoría eran irrelevantes y no ofrecían resultados tangibles. Creo que la investigación operativa solo regresará si la gente aprende las lecciones de por qué la era clásica de la investigación operativa no entregó resultados. El CIO tendrá solo una contribución modesta en esta empresa; es principalmente una cuestión de repensar el valor agregado de las personas dentro de la empresa.
Quieres hacer una contribución capitalista, y eso remonta a una de mis conferencias previas sobre la entrega orientada a productos, en el sentido de productos de software para supply chain. La cuestión es: ¿qué tipo de valor agregado capitalista entregas a tu empresa? Si la respuesta es ninguna, entonces es posible que no formes parte de lo que tu empresa debería y será en el futuro.
Pregunta: ¿Qué hay de usar el solucionador de Excel para minimizar el valor MRMSC y encontrar el valor óptimo para alpha, beta y gamma?
Creo que esta pregunta es relevante para el caso de Holt-Winters, donde en realidad se puede encontrar una solución con búsqueda en rejilla. Sin embargo, ¿qué está pasando en este solucionador de Excel? ¿Se trata de un descenso por gradiente o de algo más? Si te refieres al solucionador lineal de Excel, no es un problema lineal, por lo que Excel no puede hacer nada por ti en ese caso. Si tienes otros solucionadores en Excel o complementos, sí, pueden operar, pero esta es una perspectiva muy anticuada. No adopta una visión más estocástica; el tipo de forecast que obtienes es un forecast no probabilístico, que es un enfoque anticuado.
No estoy diciendo que no se pueda usar Excel, pero la cuestión es, ¿qué tipo de capacidades de programación se están desbloqueando en Excel? ¿Puedes hacer un descenso por gradiente estocástico en Excel? Probablemente, si añades algún complemento dedicado. Excel te permite integrar cualquier programa arbitrario sobre él. ¿Podrías potencialmente hacer programación diferenciable en Excel? Sí. ¿Es una buena idea hacerlo en Excel? No. Para entender por qué, tienes que volver al concepto de entrega orientada a productos de software, que detalla lo que está fallando con Excel. Se reduce al modelo de programación y a si realmente puedes mantener tu trabajo a lo largo del tiempo con un esfuerzo en equipo.
Pregunta: Los problemas de optimización suelen estar sesgados hacia el enrutamiento de vehículos o forecast. ¿Por qué no considerar optimizar toda la supply chain también? ¿No reduciría eso los costos en comparación con analizar áreas aisladas?
Estoy completamente de acuerdo. La maldición de la optimización de la supply chain es que cuando realizas una optimización local en un subproblema, lo más probable es que desplazarás el problema, en lugar de resolverlo para toda la supply chain. Estoy completamente de acuerdo, y en cuanto empiezas a abordar un problema más complejo, te enfrentas a un problema híbrido – por ejemplo, un problema de ruteo de vehículos combinado con una estrategia de replenishment. El problema es que necesitas un solver muy genérico para abordarlo, porque no quieres estar restringido. Si tienes un solver muy genérico, necesitas tener mecanismos muy genéricos en lugar de confiar en heurísticas inteligentes como el two-opt, que solo funciona bien para el ruteo de vehículos y no para algo que es un híbrido de replenishment y ruteo de vehículos al mismo tiempo.
Para transitar hacia esta perspectiva holística, no debes tener miedo de la maldición de la dimensionalidad. Hace veinte años, la gente decía que estos problemas ya eran extremadamente difíciles y NP-completos, como el problema del viajante, y quieres resolver un problema aún más difícil al entrelazarlo con otro problema. La respuesta es sí; quieres poder hacer eso, y por eso es fundamental contar con un solver que te permita lidiar con programas arbitrarios, ya que tu resolución puede ser la consolidación de muchos problemas entrelazados e intercalados.
En efecto, la idea de resolver estos problemas de forma aislada es mucho más débil comparada con resolver todo. Es mejor estar aproximadamente correcto que exactamente equivocado. Es mucho mejor tener un solver muy débil que aborde toda la supply chain como un sistema, como un bloque, en lugar de tener optimizaciones locales avanzadas que simplemente crean problemas en otros lugares mientras micro-optimizas localmente. La verdadera optimización del sistema no es necesariamente la mejor optimización para cada parte, por lo que es natural que, si optimizas para el interés de toda la empresa y de su supply chain, no sea óptimo a nivel local, ya que tomas en cuenta otros aspectos de la empresa y de su supply chain.
Pregunta: Después de realizar un ejercicio de optimización, ¿cuándo deberíamos revisar el scenario considerando que pueden aparecer nuevas restricciones en cualquier momento? La respuesta es que deberías revisar la optimización con frecuencia. Este es el rol del Supply Chain Scientist que presenté en la segunda conferencia de esta serie. El Supply Chain Scientist revisará la optimización tan a menudo como sea necesario. Si surge una nueva restricción, como un barco gigantesco bloqueando el Canal de Suez, fue inesperado, pero tienes que lidiar con esta disruption en tu supply chain. No tienes otra opción que abordar estos problemas; de lo contrario, el sistema que has implementado generará resultados sin sentido porque operará bajo condiciones falsas. Incluso si no tienes una emergencia que atender, aún deseas invertir tu tiempo en pensar en el ángulo que probablemente genere el mayor retorno para la empresa. Esto es fundamentalmente investigación y desarrollo. Tienes el sistema en funcionamiento, opera, y solo intentas identificar áreas donde puedes mejorar el sistema. Se convierte en un proceso de investigación aplicada que es altamente capitalista y errático. Como Supply Chain Scientist, hay días en los que pasas todo el día probando métodos numéricos, ninguno de los cuales ofrece resultados mejores que lo que ya tienes. En algunos días, realizas una pequeña modificación, y tienes muchísima suerte, ahorrándole a la empresa millones. Es un proceso errático, pero en promedio, el resultado puede ser masivo.
Pregunta: ¿Cuáles serían los casos de uso para problemas de optimización, aparte de la programación lineal, la programación entera, la programación mixta, y en el caso de Weber y el costo de los bienes?
Yo revertiría la pregunta: ¿dónde ves que la programación lineal tiene alguna relevancia para algún problema de supply chain? Prácticamente no existe ningún problema de supply chain que sea lineal. Mi objeción es que estos marcos son muy simplistas y ni siquiera pueden abordar problemas de juguete. Como dije, estos marcos matemáticos, como la programación lineal, ni siquiera pueden abordar un problema de juguete como la optimización de un duro invierno para un antiguo modelo paramétrico de forecast de baja dimensión. Ni siquiera pueden lidiar con el problema del viajante o prácticamente cualquier otra cosa.
La programación entera o la programación entera mixta es solo un término genérico para añadir que algunas de las variables serán enteros, pero eso no cambia el hecho de que estos marcos de programación son simplemente marcos matemáticos de juguete que están lejos de tener la expresividad necesaria para abordar problemas de supply chain.
Cuando preguntas acerca de los casos de uso de problemas de optimización, te invito a que veas todas mis conferencias sobre personas de supply chain. Ya tenemos una serie de personas de supply chain, y estoy enumerando literalmente toneladas de problemas que se pueden abordar mediante optimización matemática. En las conferencias sobre las personas de supply chain, tenemos a París, Miami, Ámsterdam y una serie mundial, y vendrán más. Tenemos muchos problemas que necesitan ser abordados y que merecerían ser tratados con una perspectiva adecuada de optimización matemática. Sin embargo, verás que para cada uno de esos problemas, no podrás enmarcarlos dentro de las restricciones super estrechas y mayormente extrañas que emergen de estos marcos matemáticos. De nuevo, esos marcos matemáticos se centran mayormente en la convexidad, y esta no es la perspectiva adecuada para la supply chain. La mayoría de los puntos con los que lidiamos son no convexos. Pero está bien; no es porque sean no convexos que sean imposiblemente difíciles. Verás, es solo que al final del día no podrás tener una prueba matemática. Pero a tu jefe o a tu empresa les importa el beneficio, no si tienes una prueba matemática que respalde la decisión. Les importa el hecho de que puedas tomar la decisión correcta en términos de producción, replenishment, precios, assortments, y demás, y no que tengas una prueba matemática adjunta a esas decisiones.
Pregunta: ¿Cuánto tiempo se deben almacenar los datos del algoritmo de aprendizaje para favorecer el aprendizaje?
Bueno, yo diría que, considerando que el almacenamiento de datos hoy en día es increíblemente barato, ¿por qué no conservarlo para siempre? El almacenamiento de datos es tan económico; por ejemplo, solo ve a un supermercado y puedes ver que el precio de un disco duro de un terabyte ronda los 60 o algo así. Así que es increíblemente barato.
Ahora, obviamente, existe una preocupación aparte de que si tienes datos personales en tus datos, entonces los datos que guardes se convierten en una responsabilidad. Pero desde la perspectiva de supply chain, si asumimos que has eliminado primero todos los datos personales, porque normalmente no necesitas tener datos personales en primer lugar. No necesitas conservar números de tarjetas de crédito o los nombres de tus clientes. Solo necesitas tener identificadores de clientes y demás. Si simplemente eliminas todos los datos personales de tus datos, yo diría, ¿por cuánto tiempo? Bueno, conservalo para siempre.
Uno de los puntos en la supply chain es que tienes datos limitados. No es como en los problemas de deep learning, tales como el reconocimiento de imágenes, donde puedes procesar todas las imágenes de la web y tener acceso a bases de datos casi infinitas para analizar. En supply chain, tus datos siempre son limitados. De hecho, si quieres forecast la demanda futura, hay muy pocas industrias en las que mirar más de una década en el pasado sea realmente relevante, estadísticamente hablando, para forecast la demanda del próximo trimestre. Pero, sin embargo, yo diría que siempre es más fácil truncar los datos si los necesitas, en lugar de darte cuenta de que has descartado datos y ahora faltan. Así que mi sugerencia es conservar todo, eliminar los datos personales, y al final de tu data pipeline, verás si es mejor filtrar los datos muy antiguos. Podría ser, o podría no ser; depende de la industria en la que operas. Por ejemplo, en aeroespacial, cuando tienes partes y aeronaves con una vida operativa de cuatro décadas, tener datos en tu sistema de las últimas cuatro décadas es relevante.
Pregunta: ¿Es la programación multiobjetivo una función de dos o más objetivos, como la suma o la minimización de múltiples funciones en un mismo objetivo?
Existen múltiples variantes de cómo abordar los multiobjetivos. No se trata de tener una función que sea una suma porque, si tienes la suma, entonces es solo cuestión de descomposición y estructura de la función de pérdida. No, se trata realmente de tener un vector. Y, de hecho, existen esencialmente múltiples sabores de programación multiobjetivo. El sabor más interesante es aquel en el que optas por un orden lexicográfico. En lo que respecta a la supply chain, la minimización, cuando quieres decir que tomas la media o el máximo de las muchas funciones, puede ser de interés, pero no estoy muy seguro. Creo que el enfoque multiobjetivo, en el que en realidad puedes inyectar restricciones y tratar las restricciones como parte de tu optimización regular, es de gran interés para fines de supply chain. Las otras variantes también podrían ser interesantes, pero no estoy tan seguro. No estoy diciendo que no lo sean; solo digo que no estoy seguro.
Pregunta: ¿Cómo decidirías cuándo usar una solución aproximada contra la solución optimizada?
Quiero decir, no estoy muy seguro de entender la pregunta. La idea es que, si hay una lección que aprender del deep learning, es que no existe una solución óptima única. Todo es una aproximación en cierto grado. Incluso cuando dices que tienes números, en las computadoras, los números no vienen con precisión infinita; vienen con precisión finita. Y esta precisión finita puede, en algunas circunstancias, volver y picarte. Así que la respuesta es que siempre es aproximado. Diría que la mayor lección es que es una ilusión pensar que existe una solución perfecta. No hay tal cosa como una solución perfecta u óptima. Todas las soluciones que tienes son aproximaciones, y algunas de ellas son, diría yo, algo menos o más aproximadas. Así que, no estoy muy seguro del sentido de tu pregunta, pero desde la perspectiva de la optimización matemática, significa que tienes una función de pérdida para evaluar la calidad, y al final del día, si tienes dos soluciones en competencia, cuentas con tu función de pérdida para evaluar cuál es la mejor. Así es como opera.
Pregunta: ¿Por qué se dividió la serie de tiempo, en términos de datos históricos, por 86,400 en primer lugar?
No fue así. Fue un ejemplo. Solo quería esbozar y llevar la situación a un estado absurdo donde ves que, cuando optas por una serie de tiempo, un algoritmo clásico de forecast de series de tiempo, adoptas lo que se conoce como una serie de tiempo equidistante. Hay muchas formas de representar series de tiempo, y la forma más típica de representar la serie de tiempo es la modalidad equidistante, donde optas por la agregación en intervalos de igual longitud. Típicamente, eso es lo que obtienes con la agregación diaria o semanal. Tienes intervalos que tienen la misma longitud, y tu serie tiene una bonita estructura de vector.
Pero lo que estoy señalando es que, en gran medida, es arbitrario. Puedes decidir representar los datos como datos diarios, pero también podrías decidir representarlos por segundo. ¿Tendría algún sentido representar los datos por segundo? La respuesta es sí; depende del tipo de problemas. Por ejemplo, si eres un proveedor de electricidad y deseas gestionar una red, entonces tienes que gestionar la energía en cada segundo para que tengas exactamente el balance entre el suministro de electricidad en tu red y el consumo de energía. Y este balance se ajusta, de hecho, por segundo. Así que, podrían haber situaciones en las que tenga sentido representar los datos por segundo. Para la venta en tu tienda local, podría no tener sentido. Lo que quise señalar con esos 86,400, por cierto, es simplemente 24 horas por 60 minutos por 60 segundos, y quería aclarar el hecho de que siempre tienes una representación de tus datos, y no debes confundir la representación de tus datos, que viene con cierta dimensionalidad, con la dimensión intrínseca de tus datos, que puede tener una dimensión completamente diferente. La representación es, en gran medida, completamente inventada y arbitraria. Te proporciona un indicator numérico, como tener datos de tres años, de modo que cuentas con un vector de dimensión mil. Pero ese mil es algo que, en gran parte, es inventado porque se basa en la decisión de agregar datos de forma diaria. Si eligieras cualquier otro periodo alternativo, obtendrías una dimensión diferente. Ese es el punto que quería hacer, y eso es lo que el deep learning entendió realmente bien: tener otras cosas en las que no te engañen al confundirte con elecciones arbitrarias de representación de los datos. Quieres ser, en cierto modo, agnóstico a la representación.
Pregunta: Al introducir el forecast probabilístico, transitamos hacia una función de costo y restricciones que son probabilísticas por naturaleza. ¿Qué implicación tiene esto en el proceso de encontrar una solución?
Bueno, sí tiene una restricción muy básica y fundamental. Si tienes un solver que no puede procesar problemas, y nuevamente, recuerda que siempre puedes volver de un problema estocástico a uno determinista simplemente promediando tu resultado sobre un número muy grande de muestras, entonces estarás en problemas en términos de costos computacionales. Esto significa que tendrás que gastar 10,000 veces o más en poder de procesamiento para llegar a una solución satisfactoria en comparación con una solución alternativa. La implicación es que realmente quieres asegurarte de que tus herramientas de optimización matemática, la infraestructura que tienes, sean capaces nativamente de manejar problemas estocásticos. Eso es exactamente lo que obtienes con differentiable programming, no tanto con local search, pero puedes mejorar o revisar el local search para que opere de manera más fluida en ese tipo de situaciones también.
Fundamentalmente, cuando optas por forecast probabilístico, no solo cuestiona la forma en que miras el futuro; sino que también desafía profundamente el tipo de herramientas e instrumentación con las que tienes que trabajar esos forecast. Eso es exactamente el tipo de herramientas que Lokad ha estado desarrollando durante la última década. La razón es que necesitamos herramientas que puedan trabajar bien con el tipo de problemas estocásticos que invariablemente surgen en supply chain porque casi todos los problemas en supply chain tienen un componente de incertidumbre, y por lo tanto, en cierto modo, todos tratan con un problema estocástico.
Excelente. Entonces, la próxima clase será el mismo día de la semana, un miércoles. Habrá unas vacaciones entre ahora y entonces. La próxima clase será el 22 de septiembre, y espero verlos a todos. Esta vez, discutiremos machine learning para supply chain. Nos vemos entonces.
Referencias
- El futuro de la Investigación Operativa es pasado, Russell L. Ackoff, febrero 1979
- LocalSolver 1.x: Un solver de búsqueda local de caja negra para programación 0-1, Thierry Benoist, Bertrand Estellon, Frédéric Gardi, Romain Megel, Karim Nouioua , septiembre 2011
- Diferenciación automática en machine learning: una encuesta, Atilim Gunes Baydin, Barak A. Pearlmutter, Alexey Andreyevich Radul, Jeffrey Mark Siskind, última revisión en febrero 2018


