Sparsité : quand la mesure d'exactitude se trompe
Il y a trois ans, nous publiions [Surapprentissage : quand la mesure d’exactitude se trompe](/blog/2009/4/22/overfitting-when-accuracy-measure-goes-wrong/), cependant le surapprentissage est loin d’être la seule situation où des mesures simples de l’exactitude peuvent être très trompeuses. Aujourd’hui, nous nous concentrons sur une situation particulièrement sujette aux erreurs : la demande intermittente qui est typiquement rencontrée lorsqu’on observe les ventes au niveau du magasin (ou le e-commerce).
Nous croyons que ce problème unique a empêché la plupart des détaillants de passer à des systèmes de prévision avancée au niveau du magasin. Comme pour la plupart des problèmes de prévision, c’est subtil, c’est contre-intuitif et certaines entreprises qui font payer cher pour apporter des réponses médiocres à la question.
Les métriques d’erreur les plus populaires dans la prévision des ventes sont l’Erreur Moyenne Absolue (MAE) et l’Erreur Moyenne Absolue en Pourcentage (MAPE). En règle générale, nous suggérons de s’en tenir au MAE car le MAPE se comporte très mal dès que les séries temporelles ne sont pas régulières, c’est-à-dire, tout le temps, du point de vue des détaillants. Cependant, il existe des situations où le MAE se comporte aussi mal. Les faibles volumes de vente entrent dans ces cas.
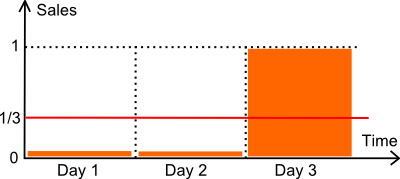
Passons en revue l’illustration ci-dessus. Nous avons un article vendu sur 3 jours. Le nombre d’unités vendues durant les deux premiers jours est nul. Le troisième jour, une unité est vendue. Supposons que la demande soit, en fait, exactement de 1 unité tous les 3 jours. Techniquement parlant, il s’agit d’une distribution de Poisson avec λ=1/3.
Dans ce qui suit, nous comparons deux modèles de prévision :
- un modèle constant M à 1/3 chaque jour (la moyenne).
- un modèle constant Z à zéro chaque jour.
En ce qui concerne l’optimisation de stocks, le modèle zéro (Z) est vraiment nuisible. En supposant que l’analyse des stocks de sécurité sera utilisée pour calculer un point de réapprovisionnement, une prévision de zéro est très susceptible de produire lui aussi un point de réapprovisionnement à zéro, entraînant des ruptures de stock fréquentes. Une métrique d’exactitude qui favoriserait le modèle zéro au détriment de prévisions plus raisonnables se comporterait de manière assez médiocre.
Examinons nos deux modèles en regard du MAPE (*) et du MAE.
- M a un MAPE de 44%.
- Z a un MAPE de 33%.
- M a un MAE de 0.44.
- Z a un MAE de 0.33.
(*) La définition classique du MAPE implique une division par zéro lorsque la valeur réelle est nulle. Nous supposons ici que la valeur réelle est remplacée par 1 lorsqu’elle est à zéro. Alternativement, nous aurions pu diviser par la prévision (au lieu de la valeur réelle), ou utiliser le sMAPE. Ces modifications ne font aucune différence : la conclusion de la discussion reste la même.
En conclusion, ici, selon le MAPE et le MAE, le modèle zéro l’emporte.
Cependant, on pourrait soutenir que c’est une situation simpliste, et qu’elle ne reflète pas la complexité d’un véritable magasin. Ce n’est pas tout à fait vrai. Nous avons effectué des benchmarks sur des dizaines de magasins de détail, et généralement le modèle gagnant (selon le MAE ou le MAPE) est le modèle zéro - le modèle qui renvoie toujours zéro. De plus, ce modèle gagne typiquement par une marge confortable sur tous les autres modèles.
En pratique, au niveau du magasin, se fier soit au MAE soit au MAPE pour évaluer la qualité des modèles de prévision, c’est inviter le désastre : la métrique favorise les modèles qui renvoient des zéros ; plus il y a de zéros, mieux c’est. Cette conclusion s’applique à presque tous les magasins que nous avons analysés jusqu’à présent (à l’exception des quelques articles à fort volume qui ne souffrent pas de ce problème).
Les lecteurs familiers avec les métriques d’exactitude pourraient proposer de se tourner plutôt vers l’Erreur Quadratique Moyenne (MSE) qui ne favorisera pas le modèle zéro. C’est vrai, cependant, le MSE appliqué à des données erratiques - et les ventes au niveau du magasin sont erratiques - n’est pas numériquement stable. En pratique, toute valeur aberrante dans l’historique des ventes faussera largement les résultats finaux. Ce genre de problème est LA raison pour laquelle les statisticiens ont travaillé si dur sur les statistiques robustes dès le départ. Il n’y a pas de repas gratuit ici.
Comment évaluer alors les prévisions au niveau du magasin ?
Il nous a fallu un long, long moment pour trouver une solution satisfaisante au problème de quantifier l’exactitude des prévisions au niveau du magasin. En 2011 et auparavant, nous trichions essentiellement. Au lieu de regarder les données journalières, lorsque les données de ventes étaient trop éparses, nous passions généralement à des agrégats hebdomadaires (ou même à des agrégats mensuels pour des données extrêmement éparses). En passant à des périodes d’agrégation plus longues, nous augmentions artificiellement les volumes de vente par période, rendant ainsi le MAE à nouveau utilisable.
La percée est survenue il y a seulement quelques mois grâce aux quantiles. Essentiellement, la révélation a été : oubliez les prévisions, seuls les points de réapprovisionnement comptent. En essayant d’optimiser nos prévisions classiques selon les métriques X, Y ou Z, nous essayions de résoudre le mauvais problème.
Attendez ! Puisque les points de réapprovisionnement sont calculés à partir des prévisions, comment pouvez-vous dire que les prévisions sont sans importance ?
Nous ne disons pas que les prévisions et l’exactitude des prévisions sont sans importance. Cependant, nous affirmons que seule l’exactitude des points de réapprovisionnement eux-mêmes compte. La prévision, ou toute autre variable utilisée pour calculer les points de réapprovisionnement, ne peut être évaluée isolément. Seule l’exactitude des points de réapprovisionnement doit et devrait être évaluée.
Il se trouve que une métrique pour évaluer les points de réapprovisionnement existe : c’est la fonction de perte pinball, une fonction connue des statisticiens depuis des décennies. La perte pinball est largement supérieure non pas à cause de ses propriétés mathématiques, mais simplement parce qu’elle correspond au compromis de stocks : trop de stocks contre trop de ruptures de stock.


