Scarsità vs. Stock, l'accuratezza delle previsioni conta

Joannes Vermorel

La previsione della domanda è un pilastro dell’ottimizzazione dell’inventario. Tuttavia, la relazione esatta tra:

• il livello di servizio (probabilità di non avere una scarsità),
• le scorte di sicurezza (quantità di inventario oltre la domanda prevista),
• e l’accuratezza delle previsioni

è talvolta un po’ confusa. Quindi, cerchiamo di chiarire la situazione.

Le scarsità costano soldi: i clienti sono insoddisfatti e meno propensi a tornare, il denaro investito nell’acquisizione dei clienti viene sprecato, anche le vendite indirette possono andare perse, …

Eppure i costi di inventario costano soldi: maggiori scorte significano più capitale circolante, maggiore obsolescenza dei prodotti, costi di magazzino più elevati; un inventario in eccesso comporta costi pubblicitari più elevati e prezzi di vendita inferiori, …

Pertanto, servire i clienti è un compromesso finanziario tra la quantità di inventario e quella delle scarsità.

Stiamo implicitamente considerando una situazione al dettaglio qui, ma un ragionamento quasi identico vale anche per i produttori.

A questo punto, non è ancora chiaro come l’accuratezza delle previsioni entri in gioco. In particolare, per alcune aziende, potrebbe sembrare che non vengano prodotte previsioni in primo luogo. Esempio: solo politiche min-max di riapprovvigionamento, e nessuna previsione.

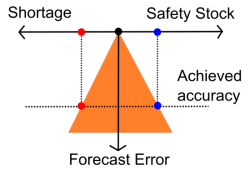
In effetti, anche se nessuno nella tua azienda produce esplicitamente previsioni, il tuo inventario possiede comunque un’accuratezza implicita delle previsioni (illustrazione qui sopra, il triangolo arancione che rappresenta il vincolo). Infatti, è possibile - sebbene un po’ complicato - calcolare l’accuratezza implicita considerando i livelli di scorte di sicurezza insieme alle frequenze di scarsità.

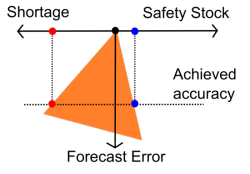
A****dattare il compromesso sia a favore del livello di servizio, sia a favore della riduzione dell’inventario, non migliora l’accuratezza implicita, poiché un costo viene scambiato con un altro (illustrazione a destra, il vincolo viene ruotato, non ridotto). Le previsioni potrebbero essere nascoste dai tuoi processi, ma ciò non impedirà alla tua azienda di subire perdite finanziarie se tali previsioni dovessero essere errate.

A meno che non vi sia una profonda mancanza di analisi nelle tue politiche di inventario, ci si aspetta che il miglioramento apportato dall’adattamento del compromesso scarsità vs. stock sia marginale (che tuttavia potrebbe rappresentare notevoli risparmi, soprattutto se il margine è sottile).

Per migliorare entrambi i lati dell’equazione, hai bisogno di previsioni migliori.

L’impatto di un’accuratezza migliorata è illustrato nel grafico a sinistra. Rispetto alle situazioni precedenti, vediamo che una maggiore accuratezza ti permette di ridurre sia la frequenza delle scarsità sia la quantità di scorte di sicurezza.

La teoria afferma approssimativamente che riducendo l’errore delle previsioni dell'1% (relativo) si può ridurre sia la frequenza delle scarsità dell'1% (relativo) sia la quantità di scorte di sicurezza dell'1% (relativo).

In pratica, potrebbero esserci ostacoli a sfruttare appieno il miglioramento apportato dall’ulteriore accuratezza, come i livelli di servizio offerti dai tuoi fornitori. Tuttavia, adottando una posizione conservativa, possiamo comunque stimare che un extra dell'1% di accuratezza comporti una riduzione della frequenza delle scarsità dello 0,5% oppure una riduzione della quantità di scorte di sicurezza dello 0,5%.

Ancora, il compromesso scarsità vs. stock può essere riequilibrato mantenendo la nuova accuratezza migliorata.

Commenti dei Lettori (6)

Ciao Benhard, La maggior parte delle formule per le scorte di sicurezza si basa sulla varianza delle previsioni, ma, poiché questo valore è più difficile da calcolare, una tipica euristica consiste nel sostituire le varianze delle previsioni con la varianza dei dati storici, anche se si tratta di un’approssimazione. Pertanto, se desideri integrare l’errore delle previsioni nel calcolo delle scorte di sicurezza, basta sostituire il coefficiente ‘sigma’ della varianza storica con la varianza attesa delle previsioni stesse. Spero sia d’aiuto. Joannes Vermorel (7 years ago)

Ciao Joannes, Trovo questo articolo davvero interessante. Sono nel bel mezzo della definizione di politica dell’inventario basata sulla previsione della domanda anziché sulla sua storia. La maggior parte dei siti mostra come determinare la politica dell’inventario basandosi sulla varianza dei dati storici. Mi chiedo come inserire l’errore delle previsioni nell’equazione delle scorte di sicurezza. Mi dispiace se la mia domanda esula dall’argomento sopra. Qualsiasi tipo di aiuto sarà apprezzato. Grazie, Jo. ben Benhard Adolf (7 years ago)

In realtà, non è il triangolo a essere importante ma i suoi due lati (destro e sinistro). Intuitivamente, l’angolo principale è una costante che non può essere modificata, quindi se sposti un lato, anche l’altro si muove. La forma in qualche modo assomiglia a un triangolo, ma in realtà sono solo due lati e un angolo a contare. Joannes Vermorel (8 years ago)

Caro Joannes, Trovo la tua spiegazione molto chiara, ma non capisco il triangolo arancione. Rappresenta il vincolo. Ma non lo comprendo nel disegno. Hai qualche ulteriore spiegazione? Grazie Piet Buyck (8 years ago)

Ciao Achyut, nel modello classico delle scorte di sicurezza, solitamente assumiamo una distribuzione normale (distribuzione gaussiana) della domanda. La distribuzione normale è definita da due parametri: la sua media e la sua varianza. La quantità di scorte di sicurezza (cioè lo stock extra sopra il livello medio della domanda), per un dato livello di servizio, è linearmente proporzionale alla varianza. Pertanto, se riduci la varianza (cioè l’errore delle previsioni) dell'1%, riduci anche le scorte di sicurezza dell'1% in questo modello ideale. Inoltre, l’altra parte, relativa alla riduzione della frequenza delle scarsità mantenendo la stessa quantità di scorte di sicurezza, è più complicata e richiederebbe un post apposito. Cercherò di affrontare questo argomento appena avrò tempo. Joannes Vermorel (8 years ago)

Ciao Joannes, È un articolo molto utile. Ho solo bisogno di maggiore chiarezza su una delle cose che hai menzionato in questo articolo. Hai detto che “La teoria afferma approssimativamente che riducendo l’errore delle previsioni dell'1% (relativo) si può ridurre sia la frequenza delle scarsità dell'1% (relativo) sia la quantità di scorte di sicurezza dell'1% (relativo).” Potresti elaborare ulteriormente sul concetto su cui si basa? Capisco che una previsione migliore ridurrebbe i livelli di inventario, ma trovo difficile quantificarlo. Grazie in anticipo Achyut Koushik A (8 years ago)