Дефицит против запасов, точность прогнозирования имеет значение

Joannes Vermorel

Прогнозирование спроса является краеугольным камнем оптимизации запасов. Однако точная взаимосвязь между:

• уровень сервиса (вероятность отсутствия дефицита),
• резервный запас (количество запасов сверх ожидаемого спроса),
• и точностью прогнозирования

иногда оказывается немного расплывчатой. Поэтому давайте попробуем прояснить ситуацию.

Дефицит товаров стоит денег: клиенты остаются недовольны и с меньшей вероятностью вернутся, деньги, вложенные в привлечение клиентов, теряются, а косвенные продажи могут также быть упущены, …

Однако запасы тоже стоят денег: больше запасов означает больший оборотный капитал, большее устаревание продуктов, увеличенные расходы на складирование; избыток запасов приводит к увеличению затрат на рекламу и снижению цен продажи, …

Таким образом, обслуживание клиентов представляет собой финансовый компромисс между объёмом запасов и уровнем дефицита.

Здесь мы подразумеваем ситуацию в розничной торговле, но почти такая же логика применима и к производителям.

На данный момент всё ещё неясно, как точность прогнозирования влияет на ситуацию. В частности, для некоторых компаний может показаться, что прогнозы вообще не составляются. Например: только политики min-max пополнения запасов, и никаких прогнозов.

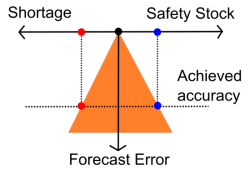
На самом деле, даже если никто в вашей компании явно не составляет прогнозы, ваши запасы всё равно обладают неявной точностью прогнозирования (иллюстрация выше, оранжевый треугольник, представляющий ограничение). Действительно, возможно — хоть и несколько сложно - вычислить неявную точность для компаний по вашим уровням резервных запасов с учетом частоты дефицита.

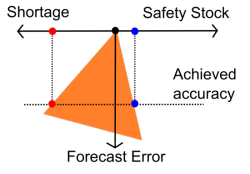
Корректировка компромисса либо в пользу уровня сервиса, либо в пользу сокращения запасов не улучшает неявную точность, так как одна стоимость заменяется другой (иллюстрация справа, ограничение повернуто, а не уменьшено). Прогнозы могут быть скрытыми из-за ваших процессов, это не помешает вашей компании понести финансовые потери, если эти прогнозы окажутся неверными.

Если только в ваших запасных политиках не наблюдается крайний недостаток анализа, ожидается, что улучшение, достигнутое за счет корректировки компромисса дефицита против запасов, будет незначительным (хотя это все равно может привести к существенной экономии, особенно если маржа невысока).

Чтобы улучшить обе стороны уравнения, вам нужны лучшие прогнозы.

Влияние повышения точности показано на графике слева. По сравнению с предыдущими ситуациями, мы видим, что снижение ошибки прогноза позволяет уменьшить как частоту дефицита, так и объем резервных запасов.

Теория примерно такова: снижение ошибки прогноза на 1% (относительно) может быть использовано либо для сокращения частоты дефицита на 1% (относительно), либо для уменьшения объема резервных запасов на 1% (относительно).

На практике могут возникнуть препятствия на пути полного использования преимуществ, принесенных дополнительной точностью, такие как уровни сервиса, предлагаемые вашими поставщиками. Тем не менее, занимая консервативную позицию, мы все еще можем оценить, что 1% дополнительной точности приводит либо к снижению дефицита на 0.5%, либо к уменьшению резервных запасов на 0.5%.

С другой стороны, компромисс дефицит против запасов может быть пересмотрен с учетом новой улучшенной точности.

Комментарии читателей (6)

Привет, Бенхард, Большинство формул расчета резервных запасов основываются на дисперсии прогнозов, однако, поскольку эту величину сложнее вычислить, типичная эвристика состоит в замене дисперсии прогнозов на дисперсию исторических данных, но это приближение. Таким образом, если вы хотите учесть ошибку прогноза в расчете резервных запасов, просто замените коэффициент ‘сигма’ исторической дисперсии на ожидаемую дисперсию самих прогнозов. Надеюсь, это поможет. Joannes Vermorel (7 лет назад)

Привет, Joannes, Мне действительно интересна эта статья. Я нахожусь в процессе определения политики запасов на основе прогнозирования спроса, а не истории спроса. Большинство сайтов показывает, как определить политику запасов, исходя из дисперсии исторических данных. Мне интересно, как включить ошибку прогноза в уравнение расчета резервных запасов. Извините, если мой вопрос не по теме. Любая помощь будет оценена. Спасибо, Jo. ben Benhard Adolf (7 лет назад)

На самом деле, не столько важен сам треугольник, сколько его две стороны (правая и левая). Интуитивно, основной угол является неизменной величиной, поэтому если сдвинуть одну сторону, другая изменится тоже. Фигура как-то напоминает треугольник, но на самом деле важны только две стороны и один угол. Joannes Vermorel (8 лет назад)

Дорогой Joannes, Ваше объяснение мне кажется очень ясным, но я не понимаю оранжевый треугольник. Он представляет ограничение. Но я не до конца понимаю это на рисунке. Можете дать дополнительное объяснение? Спасибо Piet Buyck (8 лет назад)

Привет, Achyut, в классической модели резервных запасов мы обычно предполагаем нормальное распределение (распределение Гаусса) спроса. Нормальное распределение определяется двумя параметрами: средним значением и дисперсией. Объем резервного запаса (то есть дополнительный запас сверх среднего уровня спроса) для заданного уровня сервиса линейно пропорционален дисперсии. Таким образом, если вы снижаете дисперсию (то есть ошибку прогноза) на 1%, то в этой идеальной модели и резервный запас уменьшается на 1%. А что касается сокращения частоты дефицита при сохранении того же объема резервных запасов, это более сложный вопрос, который требует отдельного блога. Я постараюсь вернуться к этой теме, когда у меня появится время. Joannes Vermorel (8 лет назад)

Привет, Joannes, Это очень полезная статья. Мне нужно немного больше ясности по одному из моментов, который вы упомянули в статье. Вы сказали: “Теория примерно такова: снижение ошибки прогноза на 1% (относительно) может быть использовано либо для сокращения частоты дефицита на 1% (относительно), либо для уменьшения объема резервных запасов на 1% (относительно)”. Можете, пожалуйста, подробнее пояснить, на каком концепте это основано? Я понимаю, что лучший прогноз позволит снизить уровни запасов, но мне трудно это точно количественно оценить. Заранее благодарю Achyut Koushik A (8 лет назад)