Stock de sécurité
Le stock de sécurité est une méthode d’optimisation de stocks qui indique la quantité de stocks à conserver au-delà de la demande prévue afin d’atteindre un taux de service donné. Le stock supplémentaire agit comme une marge « de sécurité » – d’où son nom – pour protéger l’entreprise contre les fluctuations futures anticipées. La formule du stock de sécurité dépend à la fois de la demande future prévue et du délai de livraison attendu. L’incertitude est supposée suivre une distribution normale pour les deux facteurs. La formule du stock de sécurité se retrouve dans la plupart des systèmes de gestion des stocks, y compris dans les ERPs et les MRPs.
Mise à jour juillet 2020 : L’approche détaillée ci-dessous relève de la supply chain « classique » (textbook), malheureusement, elle se révèle également largement dysfonctionnelle. En particulier, ni la demande future ni le délai de livraison futur ne suivent une distribution normale (c’est-à-dire, elles ne sont pas gaussiennes). De plus, cette approche passe entièrement à côté du fait que tous les SKU pouvant être commandés ou produits par l’entreprise sont en concurrence pour les mêmes ressources. Nous recommandons fortement de ne pas utiliser de modèle de stock de sécurité pour les véritables supply chains.
Public visé : Ce document est principalement destiné aux professionnels de la supply chain dans le commerce de détail ou la fabrication. Cependant, il est également utile pour les éditeurs de logiciels de comptabilité / ERP / le e-commerce qui souhaiteraient étendre leurs applications avec des fonctionnalités de gestion des stocks.
Nous avons essayé de garder les exigences mathématiques aussi faibles que possible, toutefois nous ne pouvons pas totalement éviter les formules puisque le but précis de ce document est d’être un guide pratique expliquant comment calculer le stock de sécurité.
Télécharger : calculate-safety-stocks.xls (tableur Microsoft Excel)
Introduction
La gestion des stocks représente un compromis financier entre les coûts des stocks et les coûts liés aux ruptures de stock. Plus il y a de stocks, plus le besoin en fonds de roulement est élevé et plus la dépréciation des stocks est importante. En revanche, en l’absence de stocks suffisants, vous risquez des ruptures de stocks, des ventes potentielles manquées et même des interruptions de l’ensemble du processus de production.
Les stocks dépendent essentiellement de deux facteurs
- demande: la quantité d’articles qui sera consommée ou achetée.
- délai de livraison: le délai entre la décision de point de commande et la disponibilité renouvelée.
Cependant, ces deux facteurs sont soumis à des incertitudes
- variations de la demande : les comportements des clients peuvent évoluer de manière assez imprévisible.
- variations du délai de livraison : les fournisseurs ou les transporteurs peuvent rencontrer des difficultés imprévues.
Déterminer le niveau de stock de sécurité revient implicitement à établir un compromis entre ces coûts en tenant compte des incertitudes.
L’équilibre entre les coûts des stocks et les coûts des ruptures de stock dépend beaucoup de l’entreprise. Ainsi, au lieu de considérer directement ces coûts, nous allons maintenant introduire la notion classique de taux de service.
La notion de taux de service exprime la probabilité qu’un certain niveau de stock de sécurité ne conduise pas à une rupture de stock. Naturellement, lorsque les stocks de sécurité sont augmentés, le taux de service augmente également. Lorsque les stocks de sécurité deviennent très importants, le taux de service tend vers 100 % (c’est-à-dire, zéro probabilité de rencontrer une rupture de stock).
Le choix du taux de service, c’est-à-dire la probabilité acceptable de rupture de stock, dépasse le cadre de ce guide, mais nous disposons d’un guide distinct sur le calcul de taux de service optimal.
Modèle de réapprovisionnement des stocks
Le point de commande est la quantité de stocks qui devrait déclencher une commande. En l’absence d’incertitude (c’est-à-dire, si la demande future était parfaitement connue et l’approvisionnement parfaitement fiable), le point de commande serait simplement égal à la demande prévisionnelle totale pendant le délai de livraison, également appelée demande pendant le délai.
En pratique, en raison des incertitudes, nous avons
point de commande = demande pendant le délai + stock de sécurité
Si nous supposons que les prévisions ne sont pas biaisées (au sens statistique), l’absence de stock de sécurité conduirait à un taux de service de 50 %. En effet, des prévisions non biaisées signifient qu’il y a autant de chances que la demande future soit supérieure ou inférieure à la demande pendant le délai (rappelons que la demande pendant le délai n’est qu’une valeur prévisionnelle).
Attention : les prévisions peuvent être non biaisées sans être exactes. Le biais indique une erreur systématique du modèle de prévision (ex : surestimer systématiquement la demande de 20 %).
Distribution normale de l’erreur
À ce stade, nous avons besoin d’une méthode pour représenter l’incertitude dans la demande pendant le délai. Dans ce qui suit, nous supposerons que l’erreur est distribuée normalement, voir l’image ci-dessous.
Notes statistiques : cette hypothèse de distribution normale n’est pas totalement arbitraire. Dans certaines situations, les estimateurs statistiques convergent vers une distribution normale comme l’explique le théorème de la limite centrale. Mais ces considérations dépassent le cadre de ce guide.
Une distribution normale est définie uniquement par deux paramètres : sa moyenne et sa variance. Puisque nous supposons que les prévisions ne sont pas biaisées, nous considérons la moyenne de la distribution des erreurs comme nulle, ce qui ne signifie pas que nous supposons une erreur nulle.
La détermination de la variance de l’erreur de prévision est une tâche plus délicate. Lokad, comme la plupart des ensembles d’outils de prévision, fournit des estimations MAPE (erreur absolue en pourcentage moyen) associées à ses prévisions. Pour être exhaustifs, nous expliquerons comment des heuristiques simples peuvent être utilisées pour surmonter ce problème.
En particulier, la variance des données historiques peut être utilisée comme une bonne heuristique pour estimer la variance de l’erreur de prévision. David Piasecki suggère également d’utiliser la demande prévisionnelle au lieu de la demande moyenne dans l’expression de la variance, à savoir
où $$E$$ est l’opérateur moyenne, $$y_t$$ est la demande historique pour la période $$t$$ (typiquement la quantité de ventes) et $$y’$$ est la demande prévisionnelle.
L’idée principale derrière cette hypothèse est que l’erreur de prévision est très souvent corrélée à l’ampleur des variations attendues : plus les variations à venir sont importantes, plus l’erreur dans les prévisions est élevée.
En réalité, le calcul de cette variance d’erreur comporte quelques subtilités qui seront traitées plus en détail ci-dessous.
Expression du stock de sécurité
À ce stade, nous avons déterminé à la fois la moyenne et la variance, ainsi la distribution des erreurs est connue. Nous devons maintenant calculer le niveau d’erreur acceptable au sein de cette distribution. Ci-dessus, nous avons introduit la notion de taux de service (un pourcentage) pour ce faire.
Remarques : Nous supposons un délai de livraison statique. Toutefois, une approche très similaire peut être utilisée pour un délai variable. Voir
Pour convertir le taux de service en un niveau d’erreur, également appelé facteur de service, nous devons utiliser la fonction de répartition normale inverse (parfois appelée distribution normale inverse) (voir NORMSINV pour la fonction Excel correspondante). Bien que cela puisse sembler compliqué, ne l’est pas vraiment ; nous vous suggérons de jeter un œil à cette applet de distribution normale pour obtenir une vue plus visuelle. Comme vous pouvez le constater, la fonction de répartition transforme le pourcentage en une aire sous la courbe, l’axe des X correspondant au seuil du facteur de service.
Intuitivement, nous calculons
stock de sécurité = écart-type de l'erreur * facteur de service
De manière plus formelle, soit $$S$$ le stock de sécurité, nous avons
où $$\sigma$$ est l’écart-type (c’est-à-dire la racine carrée de $$\sigma^2$$, la variance définie ci-dessus), $$cdf$$ est la fonction de répartition normale normalisée (de moyenne zéro et de variance égale à un) et $$P$$ le taux de service.
En rappelant que
point de commande = demande pendant le délai + stock de sécurité
Soit $$R$$ le point de commande, nous avons
Faire correspondre le délai de livraison et la période de prévision
Jusqu’à présent, nous avons simplement supposé que pour un délai de livraison donné, nous pouvions directement produire la prévision de la demande future correspondante. En pratique, cela ne fonctionne pas exactement ainsi. L’analyse des données historiques commence généralement par une agrégation des données en périodes (typiquement des semaines ou des mois).
Or, la période choisie ne correspond pas exactement au délai de livraison ; ainsi, des calculs supplémentaires sont nécessaires pour exprimer la demande pendant le délai et sa variance associée (en considérant que nous supposons toujours une distribution normale pour l’erreur de prévision, comme détaillé dans la section précédente).
Intuitivement, la demande pendant le délai peut être calculée comme la somme des valeurs prévisionnelles pour les périodes futures qui se chevauchent avec le segment du délai de livraison. Il faut prendre soin d’ajuster correctement la dernière période prévisionnelle.
Formellement, soit $$T$$ la période et $$L$$ le délai de livraison. Nous écrivons
où $$k$$ est un entier et $$0 ≤ α < 1$$. Soit $$D$$ la demande pendant le délai. Alors, nous obtenons l’expression finale de la demande pendant le délai
où $$y’_n$$ est la demande prévisionnelle pour la $$n^{ième}$$ période future.
En considérant les mêmes hypothèses de distribution normale, nous pouvons calculer la variance de l’erreur de prévision comme
où $$y’$$ est la prévision moyenne par période
Or, $$\sigma^2$$ est calculée ici comme une variance par période alors que nous aurions besoin d’une variance correspondant au délai de livraison. Soit $$\sigma_{L}^2$$ la variance ajustée pour le délai de livraison, nous avons
Enfin, nous pouvons réexprimer le point de commande comme
Utilisation d’Excel pour calculer le point de commande
Cette section détaille comment calculer le point de commande avec Microsoft Excel. Nous vous suggérons de consulter le tableur Excel d’exemple fourni.
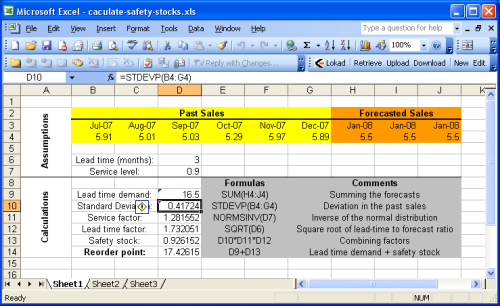
La feuille d’exemple est essentiellement divisée en deux sections : les hypothèses en haut et les calculs en bas. Les prévisions sont supposées faire partie des hypothèses car la prévision des ventes (ou de la demande) dépasse le cadre de ce guide. Vous pouvez consulter notre tutoriel sur la prévision des ventes avec Microsoft Excel pour plus de détails.
La plupart des formules présentées dans la section précédente sont des opérations très simples (additions, multiplications) qui sont très faciles à réaliser avec Microsoft Excel. Toutefois, deux fonctions se distinguent
- NORMSINV (Microsoft KB) : estime la fonction de répartition normale cumulative, notée cdf ci-dessus.
- STDEV (Microsoft KB) : estime l’écart-type, noté $$σ$$ ci-dessus. Nous rappelons que l’écart-type $$σ$$ est la racine carrée de la variance $${σ^2}$$.
Pour simplifier, la première feuille n’implémente pas l’heuristique $${σ^2 = E[ (y_t - y’)^2 ]}$$ lors du calcul du facteur de service. Cette approche est mise en œuvre dans Sheet2 (la deuxième feuille du document Excel). Comme nous avons supposé des prévisions stationnaires dans l’exemple, le point de commande reste identique avec ou sans cette heuristique.
Ressources
Inventory Management and Production Planning and Scheduling, Edward A. Silver, David F. Pyke, Rein Peterson, Wiley ; 3e édition, 1998