Score de probabilité classée continue (CRPS)

Les prévisions probabilistes attribuent une probabilité à chaque futur possible. Pourtant, toutes les prévisions probabilistes ne sont pas également précises, et des métriques sont nécessaires pour évaluer la précision respective de prévisions probabilistes distinctes. Des métriques de précision simples telles que le MAE (Erreur Absolue Moyenne) ou le MAPE (Erreur en Pourcentage Moyenne Absolue) ne sont pas directement applicables aux prévisions probabilistes. Le Continuous Ranked Probability Score (CRPS) généralise le MAE au cas des prévisions probabilistes. Avec l’entropie croisée, le CRPS est l’une des métriques de précision les plus utilisées lorsque des prévisions probabilistes sont impliquées.

Aperçu

Le CRPS est fréquemment utilisé pour évaluer la précision respective de deux modèles de prévisions probabilistes. En particulier, cette métrique peut être combinée avec un processus de backtesting afin de stabiliser l’évaluation de la précision en tirant parti de multiples mesures sur le même ensemble de données.

Cette métrique diffère notamment des métriques plus simples telles que le MAE en raison de son expression asymétrique : alors que les prévisions sont probabilistes, les observations sont déterministes. Contrairement à la fonction de perte pinball, le CRPS ne se concentre pas sur un point spécifique de la distribution de probabilité, mais considère la distribution des prévisions dans sa globalité.

Définition formelle

Soit $${X}$$ une variable aléatoire.

Soit $${F}$$ la fonction de répartition (CDF) de $${X}$$, telle que $${F(y)=\mathbf{P}\left[X \leq y\right]}$$.

Soit $${x}$$ l’observation, et $${F}$$ la CDF associée à une prévision probabiliste empirique.

Le CRPS entre $${x}$$ et $${F}$$ est défini comme :

où $${𝟙}$$ est la fonction échelon de Heaviside et désigne une fonction échelon sur la droite réelle qui prend :

• la valeur 1 si l’argument réel est positif ou nul,
• la valeur 0 sinon.

Le CRPS est exprimé dans la même unité que la variable observée (par exemple, si la demande d’un produit a été prévisible en unités, le CRPS sera également exprimé en unités).

Le CRPS généralise l’erreur absolue moyenne (MAE). En effet, il se réduit au MAE si la prévision est déterministe. Ce point est illustré dans le graphique D ci-dessous.

Propriétés connues

Gneiting et Raftery (2004) montrent que le continuous ranked probability score peut être écrit de manière équivalente comme :

où

• $${X}$$ et $${X^*}$$ sont des copies indépendantes d’une variable aléatoire linéaire,
• $${X}$$ est la variable aléatoire associée à la fonction de répartition $${F}$$,
• $${\mathbf{E} }$$ est la valeur attendue de $${X}$$.

Évaluation numérique

Du point de vue numérique, une façon simple de calculer le CRPS consiste à décomposer l’intégrale originale en deux intégrales sur des bornes judicieusement choisies pour simplifier la fonction échelon de Heaviside, ce qui donne :

En pratique, puisque $$F$$ est une distribution empirique obtenue par un modèle de prévisions, la variable aléatoire correspondante $${X}$$ a un support compact, ce qui signifie qu’il n’y a qu’un nombre fini de points pour lesquels $${\mathbf{P}[X = x] \gt 0}$$. De plus, toutes les valeurs de $$x$$ sont des nombres discrets. Ainsi, les intégrales peuvent être transformées en sommes finies discrètes, comme illustré par la formule ci-dessous et le graphique B dans la section suivante.

Dans la formule (4), un indice $$n$$ représente le dernier élément de la queue droite d’une distribution de probabilité (par exemple, la valeur de demande la plus élevée ayant une probabilité non nulle).

Enfin, comme le calcul du CRPS est effectué pour un point dans le temps, pour calculer le CRPS sur une certaine période d’évaluation d’intérêt (par exemple, pour la fenêtre de responsabilité, qui est la somme du lead time du fournisseur et de la période de reorder) nous devons prendre une moyenne des valeurs de CRPS respectives calculées pour cette période.

Intuition visuelle

Pour illustrer le calcul du CRPS, considérez l’exemple suivant (consultez les graphiques ci-dessous) :

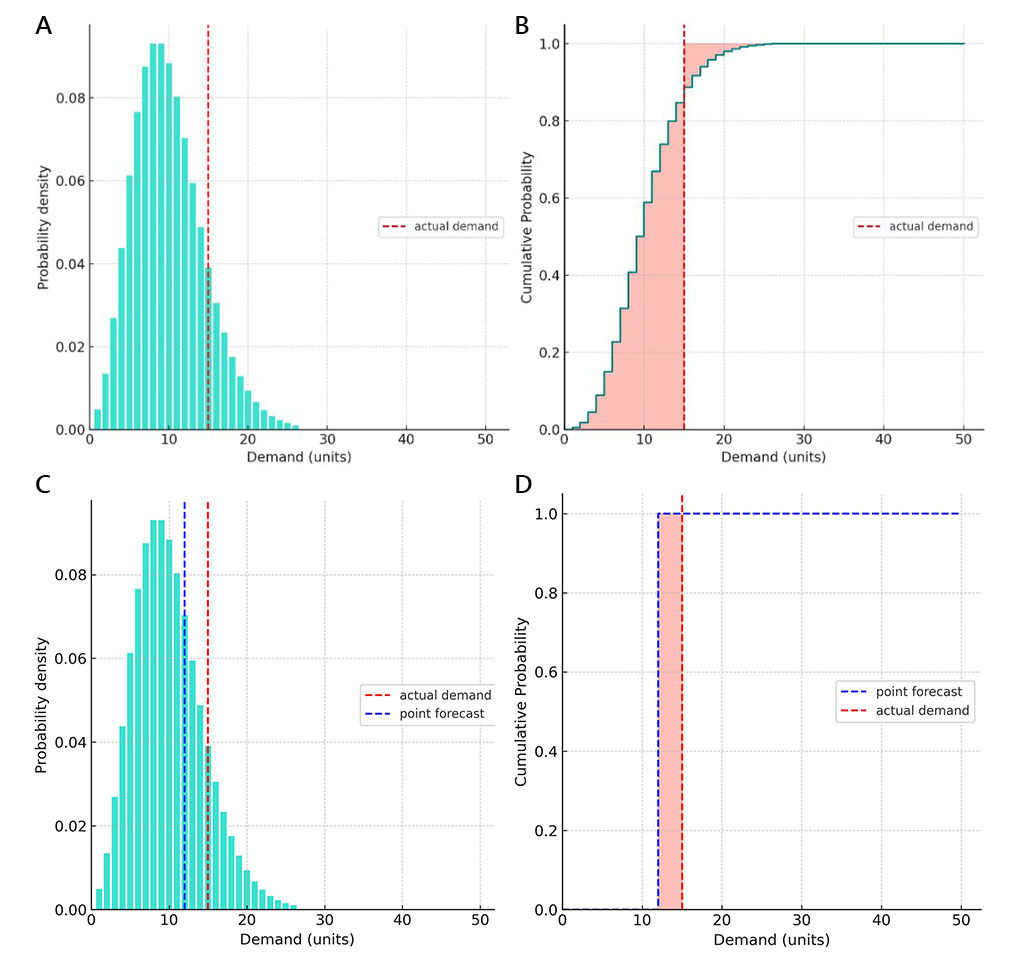
A: Initialement, nous avons construit une prévision probabiliste de la demande en utilisant une distribution binomiale négative et en tronquant ses queues avec des probabilités inférieures à 0,1 % (ce qui représente des événements extrêmement improbables, tels que ceux qui se produisent environ une fois tous les trois ans). Les valeurs de demande prédites avec des probabilités non nulles s’étendaient de 1 à 26 unités. Par la suite, il s’est avéré que la demande réelle était de 15 unités (comme illustré par la ligne verticale rouge en pointillés).

B: Nous avons calculé le CRPS selon la 4ème formule ci-dessus (voir « Évaluation numérique »). La valeur de CRPS obtenue représente la somme de deux zones remplies de couleur rouge clair.

C: Identique au graphique A, mais avec une prévision ponctuelle ajoutée à titre de comparaison.

D: Le calcul du CRPS appliqué à la prévision ponctuelle démontre que lorsque le CRPS est appliqué à une prévision ponctuelle, le résultat est une métrique de précision MAE. En effet, les prévisions ponctuelles sont des formes triviales de prévisions probabilistes où nous attribuons implicitement une probabilité de 100 % à une seule valeur. Ainsi, un graphique de probabilité cumulée pour le CRPS sera représenté par deux fonctions échelonnées - une pour les prévisions ponctuelles et une pour la demande réelle. Cela signifie que, selon les positions relatives de la prévision ponctuelle par rapport à la valeur réelle, l’une des deux sommes dans la formule (4) passera à zéro : la première somme pour les sur-prévisions et la deuxième somme pour les sous-prévisions.

Pour l’exemple fourni à travers ces 4 graphiques, les valeurs de CRPS obtenues pour la prévision probabiliste et pour la prévision ponctuelle sont respectivement de 3,32 et 3. En regardant les chiffres, on pourrait conclure que la prévision ponctuelle est plus précise parce que sa métrique de précision est plus faible (meilleure) que celle de la prévision probabiliste. Cependant, cette conclusion est erronée.

Dans l’exemple ci-dessus, nous n’avons considéré qu’une seule valeur de la demande réelle ; toutefois, lorsque la prévision probabiliste est apprise à l’aide de données historiques, les probabilités sont ajustées en fonction de la fréquence d’occurrence respective des valeurs de demande (en tenant compte des valeurs disponibles dans l’ensemble de données d’apprentissage). Si elles sont choisies de manière appropriée, alors la valeur moyenne du CRPS pour l’ensemble de données de test sera comparable à celle de l’ensemble de données d’entraînement/validation, car la prévision représentera adéquatement les fréquences d’occurrence des différentes valeurs de demande dans les données de test.

Le graphique ci-dessous démontre la supériorité des prévisions probabilistes par rapport aux prévisions ponctuelles.

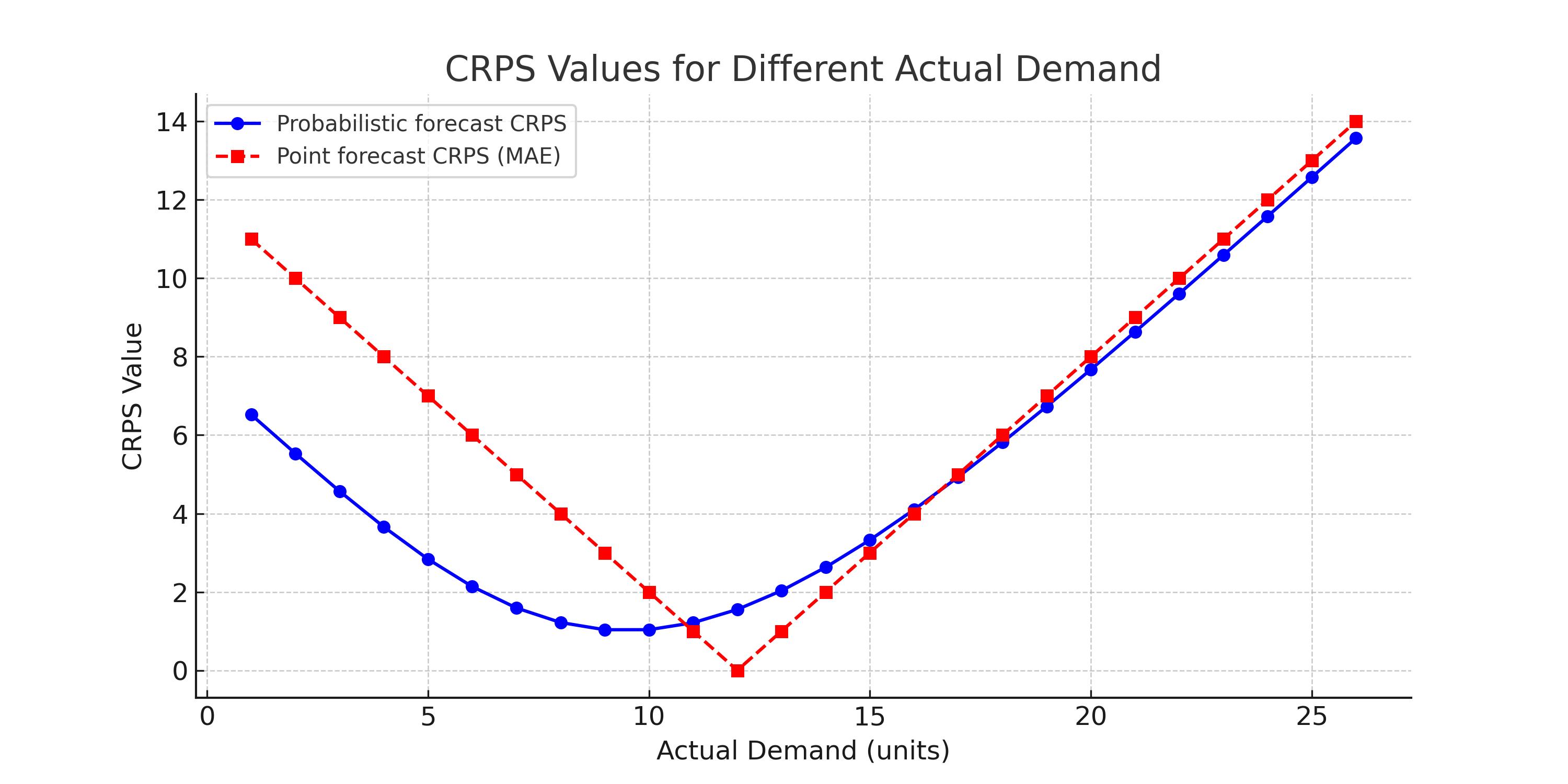
Notez à quel point le CRPS varie de manière fluide en fonction des différentes valeurs réelles. Notez également qu’en dehors d’une infime région (où la prévision ponctuelle est très proche de la valeur réelle), dans toutes les autres zones, le CRPS des prévisions probabilistes est inférieur à celui de la prévision ponctuelle.

Si nous avions plusieurs prévisions ponctuelles différentes, cette observation resterait valable. Il faudrait déplacer mentalement la courbe rouge vers la gauche ou la droite en fonction de la prévision ponctuelle, mais la supériorité des prévisions probabilistes resterait incontestable.

Références

Gneiting, T. et Raftery, A. E. (2004). Strictly proper scoring rules, prediction, and estimation. Rapport technique n° 463, Département de Statistiques, University of Washington, Seattle, Washington, USA.