安全在庫
安全在庫とは、所定のサービスレベル目標を達成するために、予想需要を上回る在庫量をどれだけ保持するかを示す在庫最適化手法です。追加在庫は「安全」のバッファとして機能し、将来の変動から企業を保護します。安全在庫の数式は、将来の需要予測とリードタイムの推定の両方に依存します。両要因ともに不確実性が正規分布であると仮定されています。安全在庫の数式は、特に有名な在庫管理システムやERPs、MRPに遍在しています.
2020年7月更新: 以下に詳述する手法は「教科書通り」のサプライチェーンですが、残念ながら極めて機能不全に陥る場合があります。特に、将来需要もリードタイムも正規分布(すなわちガウス分布)ではありません。さらに、全SKUが同一リソースを競合するという視点を全く考慮していません。実際のサプライチェーンに関しては、いかなる安全在庫モデルも使用しないことを強く推奨します.
対象読者: 本文書は主に小売または製造業のサプライチェーン専門家を対象としています。しかし、在庫管理機能を拡張したい会計/ERP/eコマースソフトウェアの編集者にも有用です.
数学的な要件をできるだけ低く抑えようと努めましたが、安全在庫の計算方法を実用的に解説する本稿の性質上、完全に数式を排除することはできませんでした.
ダウンロード: calculate-safety-stocks.xls (Microsoft Excel スプレッドシート)
はじめに
在庫管理は、トレードオフとしての在庫コストとストックアウトコストとのバランスを取るものです。在庫が多いほど必要な運転資本が増加し、在庫の減価償却も大きくなります。一方、在庫が不足すれば品切れが発生し、潜在的な売上を逃す可能性や生産プロセスの中断につながります.
在庫は本質的に2つの要因に依存します
しかし、これら2つの要因は不確実性の影響を受けます
- 需要の変動: 顧客行動は予測困難な方法で変化する可能性があります.
- リードタイムの変動: 仕入先や運送業者が予期せぬ困難に直面することがあります.
安全在庫のレベルを決定することは、これらの不確実性を考慮した上でのコスト間のトレードオフを意味します.
在庫コストと品切れコストのバランスは企業ごとに大きく異なります。そこで、これらのコストを直接考慮する代わりに、古典的な概念であるサービスレベルを導入します.
サービスレベルは、一定の安全在庫量で品切れが発生しない確率を示します。当然、安全在庫を増やせばサービスレベルも向上し、安全在庫が非常に大きくなるとサービスレベルは100%(すなわち品切れ発生確率ゼロ)に近づきます.
サービスレベル、すなわち許容される品切れ確率の選定は本ガイドの範疇外ですが、最適なサービスレベルの計算に関する別冊をご参照ください.
在庫補充モデル
リオーダー・ポイントとは発注を促す在庫量のことです。不確実性がなければ(すなわち将来需要が完全に既知で、供給が完全に信頼できる場合)、リオーダー・ポイントは単にリードタイム中の総予測需要、すなわちリードタイム需要と同じになります.
実際には、不確実性のために次のようになります:
reorder point = lead time demand + safety stock
予測が_偏りがない_(統計的に言えば)と仮定すると、安全在庫がゼロの場合、サービスレベルは50%となります。つまり、偏りのない予測は将来需要がリードタイム需要より大きくなる確率と小さくなる確率が同等であることを意味します(リードタイム需要はあくまで予測値です).
注意: 予測は必ずしも正確ではありませんが、偏りがなければ問題ありません。偏りとは、予測モデルが体系的な誤差(例:需要を常に20%過大評価する)を起こすことを示します.
誤差の正規分布
ここで、リードタイム需要の不確実性を表現する方法が求められます。以下では、誤差が正規分布に従うと仮定します(下図参照).
統計ノート: この正規分布の仮定は全く恣意的なものではありません。特定の状況下では、統計的推定量は中心極限定理により正規分布に収束しますが、そうした考察は本ガイドの範疇外です.
正規分布はその平均と分散という2つのパラメータによって定義されます。予測が偏りのないと仮定しているため、誤差分布の平均はゼロと仮定しますが、これは誤差がゼロであることを意味しません.
予測誤差の分散を求めるのはより微妙な課題です。Lokadは他の多くの予測ツールキットと同様に、予測に伴うMAPE推定(平均絶対誤差率)を提供します。ここでは、単純なヒューリスティックを用いてこの問題に対処する方法を説明します.
特に、過去データ内の分散は予測誤差の分散推定に有用なヒューリスティックとなります。David Piaseckiは、分散の表現において平均需要の代わりに予測需要を用いることも提案しています。すなわち、
ここで、$$E$$は_平均_演算子、$$y_t$$は期間$$t$$の過去需要(通常は販売量)、そして$$y’$$は予測需要を表します.
この仮定の背景にある基本的な考えは、予測誤差が将来の変動量に大きく依存する点にあります。すなわち、将来の変動が大きければ予測誤差も大きくなるということです.
実際、この予測誤差分散の計算には以下で詳述するいくつかの微妙な点が含まれます.
安全在庫の数式
ここまでで平均と分散が求まったため、誤差分布が既知となりました。次に、この分布内で_許容される誤差レベル_、すなわちサービスファクターを計算する必要があります。ここまででサービスレベル(パーセンテージ)という概念を導入しました.
注記: ここでは_静的_リードタイムを仮定しています。しかし、非常に類似した手法が変動リードタイムにも適用可能です。参照:
サービスレベルを_誤差レベル_、すなわちサービスファクターに変換するには、逆累積正規分布(逆正規分布とも呼ばれる)を利用する必要があります(対応するExcel関数についてはNORMSINVを参照)。複雑に感じられるかもしれませんが、そうではありません。normal distribution appletで視覚的に確認することをお勧めします.
直感的には、次のように計算します:
safety stock = standard deviation of error * service factor
より正式には、$$S$$を安全在庫とすると、次のようになります:
ここで、$$\sigma$$は標準偏差(すなわち、前述の分散$$σ^2$$の平方根)、$$cdf$$は_正規化された_累積正規分布(平均0、分散1)、および$$P$$はサービスレベルを表します.
次を思い出してください:
reorder point = lead time demand + safety stock
$$R$$をリオーダー・ポイントとすると、次のようになります:
マッチング:リードタイムと予測期間の一致
ここまで、ある_リードタイム_に対して対応する将来需要予測を直接得られると単純に仮定してきました。しかし実際には、歴史的データの分析は通常、週や月などの期間に集計して行います.
しかし、選択された期間がリードタイムと完全に一致するとは限らないため、リードタイム需要およびそれに伴う分散を表現するための追加計算が必要となります(ここでも、予測誤差が正規分布に従うと仮定しています).
直感的には、リードタイム需要は、リードタイム区間に重なる将来期間の予測値の合計として計算されます。最後の期間については適切な調整が必要です.
形式的には、$$T$$を期間、$$L$$をリードタイムとすると、次のように表せます:
ここで、$$k$$は整数、$$0 ≤ α < 1$$です。$$D$$をリードタイム需要とすると、最終的なリードタイム需要の表現は以下の通りです:
ここで、$$y’_n$$は将来$$n^{th}$$期間の予測需要です.
同じ正規分布の仮定に基づき、予測誤差の分散は次のように計算できます:
ここで、$$y’$$は期間ごとの平均予測です.
しかし、ここで計算される$$\sigma^2$$は期間ごとの分散であり、リードタイムに対応する分散が必要です。調整されたリードタイムごとの分散を$$\sigma_{L}^2$$とすると、次のようになります:
最後に、リオーダー・ポイントは次のように再表現できます:
エクセルを用いたリオーダー・ポイントの計算
このセクションでは、Microsoft Excelでリオーダー・ポイントを計算する方法について詳述します。提供されているサンプルのExcelスプレッドシートをご覧ください.
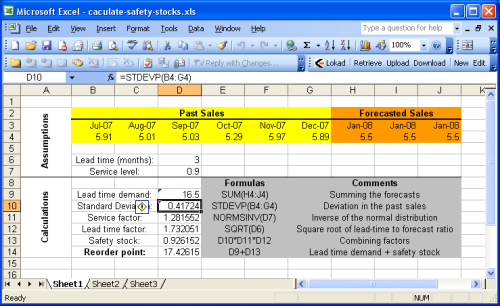
サンプルシートは基本的に、上部の前提条件と下部の計算の2つのセクションに分かれています。予測は前提条件の一部とされており、売上(または需要)予測は本ガイドの範疇外です。詳細については、Microsoft Excelを用いた売上予測のチュートリアルを参照してください.
前節で紹介した多くの数式は非常に単純な演算(加算、乗算)ですが、Microsoft Excelで簡単に実施できます。しかし、特に注目すべき2つの関数があります:
- NORMSINV (Microsoft KB): 上記の累積正規分布(cdf)を推定します.
- STDEV (Microsoft KB): ここでの$$σ$$、すなわち分散$${σ^2}$$の平方根を推定します.
簡略化のため、最初のシートでは、サービスファクターの計算において$${σ^2 = E[ (y_t - y’)^2 ]}$$というヒューリスティックは実装されていません。この手法はExcelドキュメントの2番目のシート(Sheet2)で実装されています。例では定常的な予測を仮定しているため、リオーダー・ポイントはこのヒューリスティックの有無にかかわらず同一です.
リソース
Inventory Management and Production Planning and Scheduling, Edward A. Silver, David F. Pyke, Rein Peterson, Wiley; 3版, 1998