Fehlbestand vs. Lagerbestand, die Prognosegenauigkeit zählt

Joannes Vermorel

Die Nachfrageprognose ist ein Eckpfeiler der Bestandsoptimierung. Dennoch bleibt die exakte Beziehung zwischen:

• dem Servicelevel (Wahrscheinlichkeit, keinen Fehlbestand zu haben),
• dem Sicherheitsbestand (Menge an Lagerbestand über der erwarteten Nachfrage),
• und der Prognosegenauigkeit

ist manchmal etwas unklar. Daher wollen wir die Situation klären.

Fehlbestände kosten Geld: Kunden sind unzufrieden und kehren seltener zurück, in die Kundenakquise investiertes Geld wird verschwendet, indirekte Umsätze gehen möglicherweise auch verloren, …

Doch Lagerhaltungskosten kosten ebenfalls Geld: Mehr Lagerbestände bedeuten mehr Umlaufvermögen, mehr Produktveralterung, höhere Lagerkosten; überschüssiger Lagerbestand bedeutet höhere Werbekosten und niedrigere Verkaufspreise, …

Daher ist das Bedienen von Kunden ein finanzieller Zielkonflikt zwischen der Menge an Lagerbestand und der Anzahl an Fehlbeständen.

Wir betrachten hier implizit eine Situation im Einzelhandel, aber nahezu dieselbe Argumentation gilt auch für Hersteller.

An diesem Punkt ist noch unklar, wie die Prognosegenauigkeit ins Spiel kommt. Insbesondere scheint es bei einigen Unternehmen, als ob überhaupt keine Prognosen erstellt würden. Beispiel: lediglich min-max Nachfüll Richtlinien und keine Prognose.

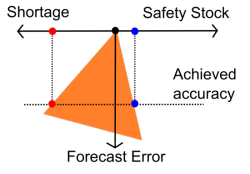
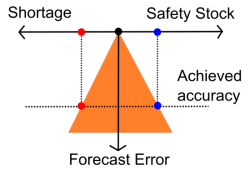
Tatsächlich, selbst wenn in Ihrem Unternehmen niemand explizit Prognosen erstellt, erhält Ihr Lagerbestand dennoch eine implizite Prognosegenauigkeit (Abbildung oben, das orangefarbene Dreieck stellt die Einschränkung dar). Tatsächlich ist es möglich - wenn auch ein wenig kompliziert - die implizite Genauigkeit anhand der Sicherheits-Bestandsniveaus und Ihrer Fehlbestandshäufigkeiten zu berechnen.

Die Anpassung des Zielkonflikts zugunsten des Servicelevels oder zugunsten der Bestandsreduzierung verbessert nicht die implizite Genauigkeit, da eine Kostenart gegen eine andere eingetauscht wird (Abbildung rechts, die Einschränkung wird gedreht, nicht reduziert). Prognosen könnten von Ihren Prozessen verdeckt werden, was Ihr Unternehmen nicht daran hindert, finanzielle Verluste zu erleiden, falls diese Prognosen unzutreffend sein sollten.

Sofern in Ihren Bestandsrichtlinien keine gravierenden Analysefehler vorliegen, wird die Verbesserung durch die Anpassung des Fehlbestand vs. Lagerbestand Zielkonflikts als marginal erwartet (was dennoch erhebliche Einsparungen bedeuten könnte, insbesondere wenn die Marge eng ist).

Um beide Seiten der Gleichung zu verbessern, benötigen Sie bessere Prognosen.

Die Auswirkungen einer verbesserten Genauigkeit werden in der Grafik links veranschaulicht. Im Vergleich zu den vorigen Situationen sehen wir, dass eine verbesserte Genauigkeit sowohl die Häufigkeit von Fehlbeständen als auch die Menge des Sicherheitsbestands verringert.

Die Theorie besagt grob, dass eine Verringerung des Prognosefehlers um 1% (relativ) entweder dazu verwendet werden kann, die Fehlbestandshäufigkeit um 1% (relativ) zu senken oder die Menge des Sicherheitsbestands um 1% (relativ) zu reduzieren.

In der Praxis kann es Hindernisse geben, den durch die zusätzliche Genauigkeit erzielten Verbesserungen voll auszuschöpfen, wie zum Beispiel die Servicelevels, die von Ihren Lieferanten angeboten werden. Doch mit einer konservativen Annahme können wir dennoch schätzen, dass 1% zusätzliche Genauigkeit entweder zu einer Reduzierung der Fehlbestandshäufigkeit um 0,5% oder zu einer Verringerung des Sicherheitsbestands um 0,5% führt.

Der Zielkonflikt Fehlbestand vs. Lagerbestand kann dann mit der neuen verbesserten Genauigkeit neu ausbalanciert werden.

Kommentare der Leser (6)

Hi Benhard, Die meisten Sicherheitsbestandsformeln beruhen auf der Varianz der Prognosen, jedoch, da dieser Wert schwerer zu berechnen ist, besteht eine typische Heuristik darin, die Varianzen der Prognosen durch die Varianz der historischen Daten zu ersetzen, was jedoch nur eine Näherung ist. Daher, wenn Sie den Prognosefehler in Ihre Sicherheitsbestandsberechnung integrieren möchten, ersetzen Sie einfach den ‘Sigma’-Faktor der historischen Varianz durch die erwartete Varianz der Prognosen selbst. Ich hoffe, es hilft. Joannes Vermorel (vor 7 Jahren)

Hi Joannes, Ich finde diesen Artikel wirklich interessant. Ich bin gerade dabei, eine Bestandsrichtlinie basierend auf der Nachfrageprognose anstelle der Nachfragehistorie zu bestimmen. Die meisten Webseiten zeigen, wie man die Bestandsrichtlinie anhand der Varianz historischer Daten ermittelt. Ich frage mich, wie man den Prognosefehler in die Sicherheitsbestandsrechnung einbeziehen kann. Entschuldigung, falls meine Frage vom obigen Thema abweicht. Jede Art von Hilfe wäre sehr willkommen. Danke, Jo. ben Benhard Adolf (vor 7 Jahren)

Eigentlich ist es nicht das Dreieck, das wirklich zählt, sondern seine beiden Seiten (rechts und links). Intuitiv ist der Hauptwinkel eine Konstante, die nicht verändert werden kann, sodass wenn man eine Seite verschiebt, sich auch die andere bewegt. Die Form sieht irgendwie wie ein Dreieck aus, aber letztlich zählen nur die beiden Seiten und ein Winkel. Joannes Vermorel (vor 8 Jahren)

Lieber Joannes, Ich finde Ihre Erklärung sehr klar, aber ich verstehe das orangefarbene Dreieck nicht. Es stellt die Einschränkung dar. Aber ich sehe es nicht im Diagramm. Haben Sie eine zusätzliche Erklärung? Vielen Dank Piet Buyck (vor 8 Jahren)

Hi Achyut, im klassischen Sicherheitsbestandsmodell nehmen wir typischerweise eine Normalverteilung (Gaußsche Verteilung) der Nachfrage an. Die Normalverteilung wird durch zwei Parameter definiert: ihren Mittelwert und ihre Varianz. Die Menge des Sicherheitsbestands (alias der zusätzliche Bestand oberhalb des durchschnittlichen Nachfrageniveaus) ist für ein gegebenes Servicelevel linear proportional zur Varianz. Daher, wenn Sie die Varianz (alias den Prognosefehler) um 1% reduzieren, senken Sie in diesem idealen Modell auch den Sicherheitsbestand um 1%. Der andere Teil, der die Reduzierung der Fehlbestandshäufigkeit bei gleichbleibendem Sicherheitsbestand betrifft, ist komplizierter und würde einen eigenen Blogbeitrag erfordern. Ich werde versuchen, darauf zurückzukommen, sobald ich Zeit habe. Joannes Vermorel (vor 8 Jahren)

Hi Joannes, Das ist ein sehr nützlicher Artikel. Ich benötige jedoch noch etwas mehr Klarheit in einem Punkt, den Sie in diesem Artikel erwähnt haben. Sie sagten, dass “die Theorie grob besagt, dass eine Verringerung des Prognosefehlers um 1% (relativ) entweder dazu verwendet werden kann, die Fehlbestandshäufigkeit um 1% (relativ) zu senken oder die Menge des Sicherheitsbestands um 1% (relativ) zu reduzieren.” Können Sie bitte das zugrunde liegende Konzept näher erläutern? Ich verstehe, dass eine bessere Prognose die Lagerbestände reduzieren würde, aber ich finde es schwierig, dies zu quantifizieren. Vielen Dank im Voraus Achyut Koushik A (vor 8 Jahren)