00:00 Einführung
02:55 Der Fall der Durchlaufzeiten
09:25 Reale Durchlaufzeiten (1/3)
12:13 Reale Durchlaufzeiten (2/3)
13:44 Reale Durchlaufzeiten (3/3)
16:12 Bisherige Entwicklung
19:31 ETA: 1 Stunde ab jetzt
22:16 CPRS (Zusammenfassung) (1/2)
23:44 CPRS (Zusammenfassung) (2/2)
24:52 Kreuzvalidierung (1/2)
27:00 Kreuzvalidierung (2/2)
27:40 Glättung der Durchlaufzeiten (1/2)
31:29 Glättung der Durchlaufzeiten (2/2)
40:51 Zusammensetzen der Durchlaufzeiten (1/2)
44:19 Zusammensetzen der Durchlaufzeiten (2/2)
47:52 Quasi-saisonale Durchlaufzeit
54:45 Log-logistisches Durchlaufzeitmodell (1/4)
57:03 Log-logistisches Durchlaufzeitmodell (2/4)
01:00:08 Log-logistisches Durchlaufzeitmodell (3/4)
01:03:22 Log-logistisches Durchlaufzeitmodell (4/4)
01:05:12 Unvollständiges Durchlaufzeitmodell (1/4)
01:08:04 Unvollständiges Durchlaufzeitmodell (2/4)
01:09:30 Unvollständiges Durchlaufzeitmodell (3/4)
01:11:38 Unvollständiges Durchlaufzeitmodell (4/4)
01:14:33 Nachfrage über die Durchlaufzeit (1/3)
01:17:35 Nachfrage über die Durchlaufzeit (2/3)
01:24:49 Nachfrage über die Durchlaufzeit (3/3)
01:28:27 Modularität prädiktiver Techniken
01:31:22 Fazit
01:32:52 Bevorstehende Vorlesung und Fragen aus dem Publikum
Beschreibung
Durchlaufzeiten sind ein grundlegender Aspekt der meisten supply chain-Situationen. Durchlaufzeiten können – wie die Nachfrage – prognostiziert werden. Probabilistische Vorhersage Modelle, die den Durchlaufzeiten gewidmet sind, können verwendet werden. Es wird eine Reihe von Techniken vorgestellt, um probabilistische Durchlaufzeitprognosen für supply chain-Zwecke zu erstellen. Die Zusammenführung dieser Prognosen – Durchlaufzeit und Nachfrage – ist ein Eckpfeiler der prädiktiven Modellierung in supply chain.
Vollständiges Transkript

Willkommen zu dieser Reihe von supply chain-Vorlesungen. Ich bin Joannes Vermorel, und heute werde ich “Forecasting Lead Times” präsentieren. Durchlaufzeiten, und allgemein alle relevanten Verzögerungen, sind ein grundlegender Aspekt in supply chain, wenn es darum geht, Angebot und Nachfrage ins Gleichgewicht zu bringen. Man muss die dabei auftretenden Verzögerungen berücksichtigen. Nehmen wir zum Beispiel die Nachfrage nach einem Spielzeug. Die richtige Antizipation des saisonalen Nachfragespitzen vor Weihnachten ist sinnlos, wenn die Ware erst im Januar eintreffen würde. Die Durchlaufzeiten bestimmen – ebenso wie die Nachfrage – das Kleingedruckte der Planung.
Durchlaufzeiten variieren; sie variieren sehr stark. Das ist eine Tatsache, und ich werde in Kürze einige Belege dafür präsentieren. Auf den ersten Blick ist diese Aussage jedoch rätselhaft. Es ist nicht klar, warum die Durchlaufzeit überhaupt so stark variieren sollte. Wir haben Fertigungsprozesse, die mit einer Toleranz von weniger als einem Mikrometer arbeiten können. Darüber hinaus können wir als Teil des Fertigungsprozesses einen Effekt, wie etwa die Anwendung einer Lichtquelle, bis auf eine Mikrosekunde genau steuern. Wenn wir die Umwandlung von Materie bis auf Mikrometer- und Mikrosekundenebene mit ausreichendem Engagement kontrollieren können, sollten wir auch in der Lage sein, den Fluss der Nachfrage mit einem vergleichbaren Grad an Präzision zu steuern. Oder vielleicht nicht.
Diese Denkweise könnte erklären, warum Durchlaufzeiten in der supply chain-Literatur scheinbar so wenig wertgeschätzt werden. Supply chain-Bücher und folglich supply chain software erkennen die Existenz von Durchlaufzeiten kaum an, abgesehen davon, dass sie als Eingangsparameter für ihr Inventurmodell eingeführt werden. Für diese Vorlesung wird es drei Ziele geben:
Wir wollen die Bedeutung und die Natur der Durchlaufzeiten verstehen. Wir wollen nachvollziehen, wie Durchlaufzeiten prognostiziert werden können, mit speziellem Augenmerk auf probabilistische Modelle, die es uns ermöglichen, die Unsicherheit zu berücksichtigen. Wir wollen Durchlaufzeitprognosen mit Nachfrageprognosen auf eine Weise kombinieren, die für supply chain-Zwecke von Interesse ist.

Nach der vorherrschenden supply chain-Literatur sind Durchlaufzeiten kaum mehr als ein paar Fußnoten wert. Diese Aussage mag als extravagante Übertreibung erscheinen, aber leider ist dem nicht so. Laut Google Scholar, einer spezialisierten Suchmaschine für wissenschaftliche Literatur, liefert die Suchanfrage “demand forecasting” für das Jahr 2021 10.500 Arbeiten. Ein flüchtiger Blick auf die Ergebnisse zeigt, dass tatsächlich die überwiegende Mehrheit dieser Einträge die Prognose der Nachfrage in unterschiedlichsten Situationen und Märkten behandelt. Dieselbe Suchanfrage, ebenfalls für das Jahr 2021, auf Google Scholar für “lead time forecasting” liefert 71 Ergebnisse. Die Resultate der Suchanfrage zur Durchlaufzeitprognose sind so begrenzt, dass es nur wenige Minuten dauert, einen kompletten Jahresbestand an Forschung zu überblicken.
Es stellt sich heraus, dass es nur etwa ein Dutzend Einträge gibt, die sich wirklich mit der Prognose von Durchlaufzeiten beschäftigen. Tatsächlich finden sich die meisten Treffer bei Formulierungen wie “long lead time forecast” oder “short lead time forecast”, die sich auf die Prognose der Nachfrage und nicht auf die Prognose der Durchlaufzeit beziehen. Diese Übung kann auch mit “demand prediction” und “lead time prediction” sowie anderen ähnlichen Bezeichnungen und für weitere Jahre wiederholt werden. Ich überlasse dies als Übung dem Publikum.
Somit haben wir, grob geschätzt, etwa tausendmal mehr Arbeiten über die Prognose der Nachfrage als über die Prognose von Durchlaufzeiten. Supply chain-Bücher und supply chain software ziehen nach, indem sie die Durchlaufzeit als Bürger zweiter Klasse und als unbedeutende technische Kleinigkeit behandeln. Allerdings erzählen die supply chain-Akteure, die in dieser Vorlesungsreihe vorgestellt wurden, eine andere Geschichte. Diese Akteure mögen fiktive Unternehmen repräsentieren, spiegeln jedoch typische supply chain-Archetypen wider. Sie geben uns Aufschluss über die Art von Situation, die als typisch angesehen werden sollte. Schauen wir, was diese Akteure in Bezug auf Durchlaufzeiten zu sagen haben.
Paris ist eine fiktive Modemarke, die ein eigenes Einzelhandelsnetz betreibt. Paris bestellt bei ausländischen Lieferanten, wobei die Durchlaufzeiten lang sind und manchmal länger als sechs Monate betragen. Diese Durchlaufzeiten sind nur unvollständig bekannt, und dennoch muss die neue Kollektion zum vorgegebenen Zeitpunkt im Geschäft eintreffen, wie es die damit verbundene Marketingkampagne vorschreibt. Die Durchlaufzeiten der Lieferanten erfordern eine angemessene Vorwegnahme; mit anderen Worten, sie bedürfen einer Prognose.
Amsterdam ist ein fiktives FMCG-Unternehmen, das sich auf die Produktion von Käse, Cremes und Butter spezialisiert hat. Der Reifungsprozess von Käse ist bekannt und kontrolliert, variiert jedoch mit Abweichungen von einigen Tagen. Dennoch entspricht genau diese Dauer von wenigen Tagen der Intensität der Werbeaktionen, die von den retail chains ausgelöst werden und den primären Vertriebskanal von Amsterdam darstellen. Diese Herstellungsdurchlaufzeiten erfordern eine Prognose.
Miami ist ein fiktives aviation MRO. MRO steht für Wartung, Reparatur und Überholung. Jeder Jet benötigt jährlich Tausende von Teilen, um weiterfliegen zu können. Ein einzelnes fehlendes Teil kann das Flugzeug am Boden halten. Die Reparaturdauer für ein reparierbares Teil, auch als TAT (Turnaround Time) bezeichnet, bestimmt, wann das drehbare Teil wieder einsatzfähig wird. Dennoch variiert die TAT von Tagen bis zu Monaten, abhängig vom Umfang der Reparaturen, die zum Zeitpunkt der Demontage nicht bekannt sind. Diese TATs erfordern eine Prognose.
San Jose ist ein fiktives E-Commerce-Unternehmen, das ein breites Sortiment an Möbeln und Accessoires vertreibt. Im Rahmen seines Serviceversprechens gibt San Jose für jede Transaktion ein Lieferdatum an. Die Lieferung selbst hängt jedoch von Drittunternehmen ab, die alles andere als zuverlässig sind. Daher erfordert San Jose eine fundierte Schätzung des Lieferdatums, das für jede Transaktion zugesagt werden kann. Diese fundierte Schätzung ist implizit eine Durchlaufzeitprognose.
Schließlich ist Stuttgart ein fiktives Unternehmen im automobilen Aftermarket. Es betreibt Niederlassungen, die Autoreparaturen durchführen. Der niedrigste Anschaffungspreis für die Autoteile kann von Großhändlern bezogen werden, die lange und etwas unregelmäßige Durchlaufzeiten bieten. Es gibt zuverlässigere Lieferanten, die teurer und näher liegen. Die Auswahl des richtigen Lieferanten für jedes Teil erfordert eine sorgfältige Vergleichsanalyse der jeweiligen Durchlaufzeiten der verschiedenen Lieferanten.
Wie wir sehen können, erfordert jeder einzelne bisher vorgestellte supply chain-Akteur die Vorwegnahme von mindestens einer, und häufig mehreren, Durchlaufzeiten. Zwar könnte man argumentieren, dass die Prognose der Nachfrage mehr Aufmerksamkeit und Aufwand erfordert als die Prognose der Durchlaufzeiten, letztlich werden jedoch beide für nahezu alle supply chain-Situationen benötigt.
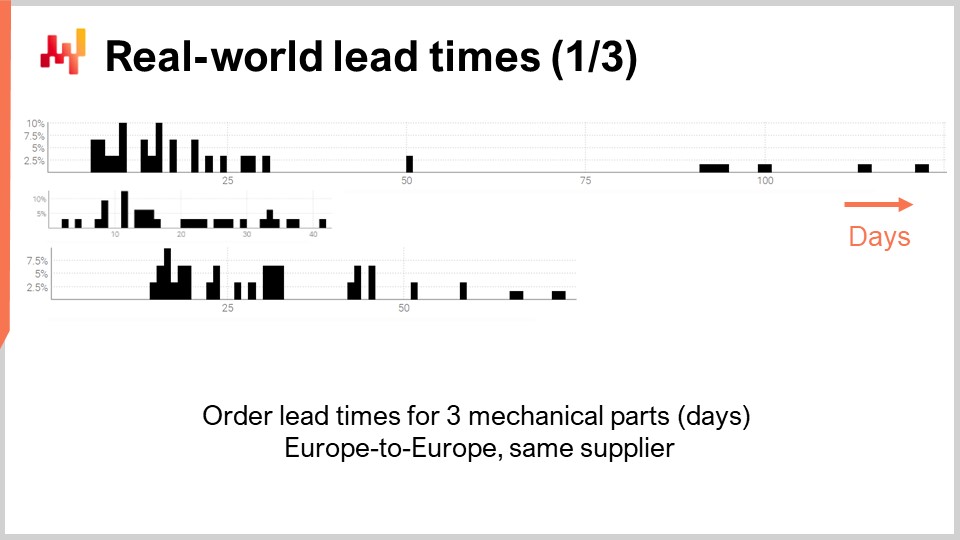
Schauen wir uns also einige tatsächliche reale Durchlaufzeiten an. Auf dem Bildschirm sind drei Histogramme zu sehen, die durch die Zusammenstellung beobachteter Durchlaufzeiten in Verbindung mit drei mechanischen Teilen erstellt wurden. Diese Teile werden von demselben Lieferanten aus Westeuropa bezogen. Die Bestellungen stammen von einem ebenfalls in Westeuropa ansässigen Unternehmen. Die x-Achse zeigt die Dauer der beobachteten Durchlaufzeiten in Tagen, und die y-Achse gibt die Anzahl der Beobachtungen in Prozent an. Im Folgenden werden alle Histogramme die gleichen Konventionen übernehmen, wobei die x-Achse mit in Tagen ausgedrückten Dauern und die y-Achse die Häufigkeit widerspiegelt. Aus diesen drei Verteilungen können wir bereits einige Beobachtungen ableiten.
Erstens, die Daten sind spärlich. Wir haben nur wenige Dutzend Datenpunkte, und diese Beobachtungen wurden über mehrere Jahre gesammelt. Diese Situation ist typisch; wenn das Unternehmen nur einmal im Monat bestellt, dauert es fast ein Jahrzehnt, über 100 Beobachtungen der Durchlaufzeiten zu sammeln. Daher sollte, was auch immer wir in statistischer Hinsicht tun, es auf kleine Zahlen statt auf große Zahlen ausgerichtet sein. Tatsächlich werden wir selten den Luxus haben, mit großen Datenmengen zu arbeiten.
Zweitens, sind die Durchlaufzeiten unbeständig. Wir haben Beobachtungen, die von wenigen Tagen bis zu einem Quartal reichen. Zwar ist es immer möglich, eine durchschnittliche Durchlaufzeit zu berechnen, doch sich auf irgendeinen Durchschnittswert für eines dieser Teile zu verlassen, wäre unklug. Es ist auch offensichtlich, dass keine dieser Verteilungen auch nur annähernd normal ist.
Drittens, wir haben drei Teile, die in Größe und Preis etwas vergleichbar sind, und dennoch variieren die Durchlaufzeiten stark. Auch wenn es verlockend sein könnte, diese Beobachtungen zusammenzufassen, um die Daten weniger spärlich erscheinen zu lassen, ist dies offensichtlich unklug, da dabei Verteilungen vermischt würden, die hochgradig unähnlich sind. Diese Verteilungen besitzen nicht denselben Mittelwert, Median oder sogar dasselbe Minimum bzw. Maximum.
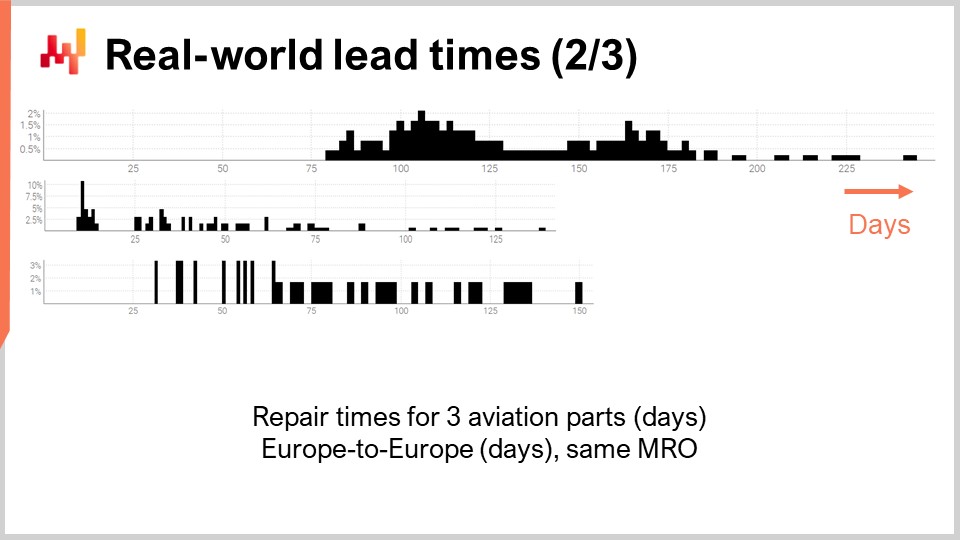
Schauen wir uns eine zweite Gruppe von Durchlaufzeiten an. Diese Dauern spiegeln die Zeit wider, die benötigt wird, um drei unterschiedliche Flugzeugteile zu reparieren. Die erste Verteilung scheint zwei Modi plus einen Auslauf zu haben. Wenn eine Verteilung zwei Modi aufweist, deutet dies in der Regel auf das Vorhandensein einer versteckten Variable hin, die diese beiden Modi erklärt. Zum Beispiel könnte es zwei verschiedene Arten von Reparaturvorgängen geben, von denen jede mit einer eigenen Durchlaufzeit verbunden ist. Die zweite Verteilung erscheint mit einem Modus plus einem Auslauf. Dieser Modus entspricht einer relativ kurzen Dauer, etwa zwei Wochen. Er könnte einen Prozess widerspiegeln, bei dem das Teil zunächst inspiziert wird und manchmal als einsatzfähig ohne weitere Intervention eingestuft wird, was zu einer wesentlich kürzeren Durchlaufzeit führt. Die dritte Verteilung scheint sich vollständig auszubreiten, ohne einen offensichtlichen Modus oder Auslauf. Möglicherweise sind hier mehrere Reparaturprozesse im Spiel, die zusammengefasst werden. Die Spärlichkeit der Daten, mit nur drei Dutzend Beobachtungen, erschwert weitere Aussagen. Wir werden diese dritte Verteilung später in dieser Vorlesung erneut betrachten.
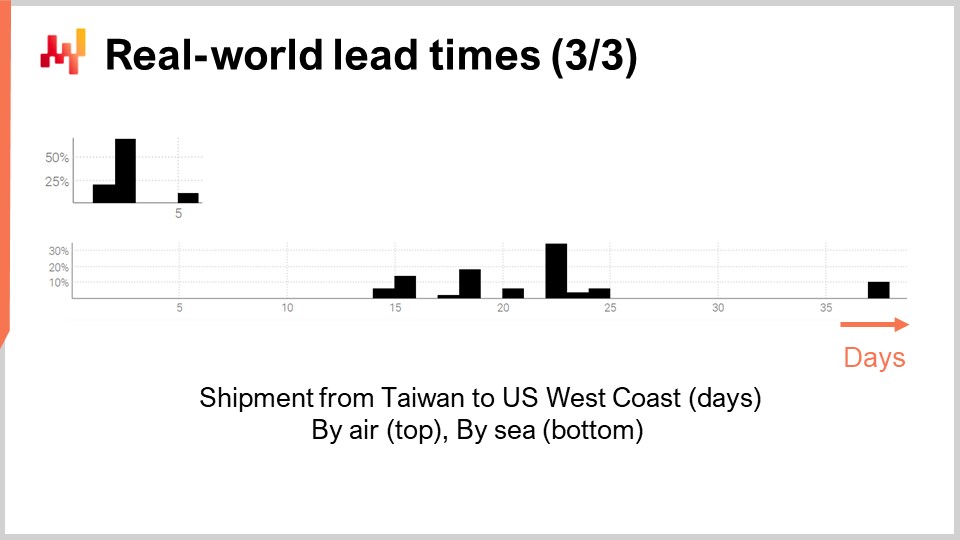
Abschließend betrachten wir zwei Durchlaufzeiten, die die Versandverzögerungen von Taiwan zur US-Westküste widerspiegeln, sei es per Luft oder per See. Nicht überraschend sind Frachflugzeuge schneller als Frachtschiffe. Die zweite Verteilung deutet darauf hin, dass manchmal eine Seefracht ihr ursprüngliches Schiff verpasst und dann mit dem nächsten Schiff verschifft wird, wodurch sich die Verzögerung fast verdoppelt. Dasselbe Phänomen könnte auch bei der Luftfracht auftreten, obwohl die Daten so begrenzt sind, dass es nur eine wilde Vermutung ist. Es sei darauf hingewiesen, dass der Zugang zu nur wenigen Beobachtungen bei Durchlaufzeiten keineswegs ungewöhnlich ist. Diese Situationen kommen häufig vor. Es ist wichtig zu bedenken, dass wir in dieser Vorlesung Werkzeuge und Instrumente suchen, die es uns ermöglichen, mit den vorhandenen Durchlaufzeitdaten – auch wenn es nur eine Handvoll Beobachtungen sind – zu arbeiten und nicht mit den Durchlaufzeitdaten, die wir uns wünschen würden, etwa Tausende von Beobachtungen. Die kurzen Lücken in beiden Verteilungen deuten auch auf ein wöchentliches zyklisches Muster hin, obwohl die vorliegende Histogrammvisualisierung nicht geeignet ist, diese Hypothese zu validieren.
Aus dieser kurzen Übersicht der realen Durchlaufzeiten können wir bereits einige der zugrunde liegenden Phänomene erkennen. In der Tat sind Durchlaufzeiten hoch strukturiert; Verzögerungen treten nicht ohne Grund auf, und diese Gründe können identifiziert, zerlegt und quantifiziert werden. Allerdings wird das Kleingedruckte der Durchlaufzeitzerlegung häufig noch nicht in den IT-Systemen erfasst. Selbst wenn eine umfassende Zerlegung der beobachteten Durchlaufzeit vorliegt, wie es in bestimmten Branchen, beispielsweise der Luftfahrt, der Fall sein könnte, impliziert dies nicht, dass Durchlaufzeiten perfekt vorausgesagt werden können. Teilsegmente oder Phasen innerhalb der Durchlaufzeit weisen wahrscheinlich ihre eigene, irreduzible Unsicherheit auf.
Diese Reihe von supply chain-Vorlesungen präsentiert meine Ansichten und Einsichten sowohl in Bezug auf das Studium als auch auf die Praxis von supply chain. Ich versuche, diese Vorlesungen einigermaßen unabhängig zu halten, aber sie ergeben im Gesamtkontext mehr Sinn, wenn man sie in Folge anschaut. Der Rest dieser Vorlesung baut auf Elementen auf, die in dieser Reihe bereits eingeführt wurden, obwohl ich in Kürze eine Auffrischung geben werde.
Das erste Kapitel ist eine allgemeine Einführung in das Gebiet und das Studium von supply chain. Es verdeutlicht die Perspektive, der diese Vorlesungsreihe zugrunde liegt. Wie Sie vielleicht bereits vermutet haben, weicht diese Perspektive erheblich von derjenigen ab, die als Mainstream-Perspektive auf supply chain betrachtet wird.
Das zweite Kapitel führt eine Reihe von Methoden ein. Tatsächlich besiegt supply chain naive Methoden. Supply chains bestehen aus Menschen, die ihre eigenen Agenden verfolgen; es gibt keine neutrale Partei in supply chain. Dieses Kapitel behandelt diese Komplikationen, einschließlich meines eigenen Interessenkonflikts als CEO von Lokad, einem Unternehmenssoftwareunternehmen, das sich auf prädiktive supply chain optimization spezialisiert hat.
Das dritte Kapitel gibt einen Überblick über eine Reihe von supply chain “Personas”. Diese Personas sind fiktive Unternehmen, die wir heute kurz betrachtet haben, und sie sollen archetypische supply chain-Situationen darstellen. Der Zweck dieser Personas besteht darin, sich ausschließlich auf die Probleme zu konzentrieren und die Präsentation der Lösungen aufzuschieben.
Das vierte Kapitel behandelt die Hilfswissenschaften der supply chain. Diese Wissenschaften befassen sich nicht direkt mit supply chain, sollten aber als unverzichtbar für eine moderne Praxis von supply chain betrachtet werden. Dieses Kapitel beinhaltet einen Fortschritt durch die Abstraktionsebenen, beginnend mit Computerhardware bis hin zu Fragestellungen der Cybersicherheit.
Das fünfte und aktuelle Kapitel widmet sich dem prädiktiven Modellieren. Prädiktives Modellieren ist eine allgemeinere Perspektive als die Prognose; es geht nicht nur darum, die Nachfrage vorherzusagen. Es geht um die Gestaltung von Modellen, die dazu verwendet werden können, zukünftige Faktoren der interessierenden supply chain zu schätzen und zu quantifizieren. Heute tauchen wir in die Durchlaufzeiten ein, aber allgemein gilt in supply chain: Alles, was nicht mit hinreichender Sicherheit bekannt ist, verdient eine Prognose.
Das sechste Kapitel erklärt, wie optimierte Entscheidungen berechnet werden können, indem prädiktive Modelle genutzt werden, genauer gesagt probabilistische Modelle, die im fünften Kapitel eingeführt wurden. Das siebte Kapitel kehrt zu einer weitgehend nicht-technischen Perspektive zurück, um die tatsächliche unternehmerische Umsetzung einer die Quantitative Supply Chain Initiative zu erörtern.

Heute konzentrieren wir uns auf Durchlaufzeiten. Wir haben gerade gesehen, warum Durchlaufzeiten wichtig sind, und wir haben eine kurze Reihe realer Durchlaufzeiten betrachtet. Daher werden wir mit Elementen des Durchlaufzeit-Modellings fortfahren. Da ich eine probabilistische Perspektive einnehmen werde, werde ich den Continuous Rank Probability Score (CRPS) kurz wieder einführen – eine Metrik zur Bewertung der Güte einer probabilistischen Vorhersage. Außerdem werde ich Cross-Validation und eine Variante der Cross-Validation vorstellen, die für unsere probabilistische Perspektive geeignet ist. Mit diesen Werkzeugen werden wir unser erstes nicht-naives probabilistisches Modell für Durchlaufzeiten einführen und bewerten. Durchlaufzeitdaten sind spärlich, und der erste Punkt auf unserer Agenda ist, diese Verteilungen zu glätten. Durchlaufzeiten können in eine Reihe von Zwischenphasen zerlegt werden. Angesichts dessen, dass einige zerlegte Durchlaufzeitdaten vorliegen, benötigen wir ein Verfahren, um diese Durchlaufzeiten wieder zusammenzusetzen, während der probabilistische Ansatz erhalten bleibt.
Anschließend werden wir differenzierbares Programmieren wieder einführen. Differenzierbares Programmieren wurde in dieser Vorlesungsreihe bereits verwendet, um die Nachfrage vorherzusagen, kann aber auch zur Vorhersage von Durchlaufzeiten eingesetzt werden. Wir werden dies anhand eines einfachen Beispiels tun, das darauf abzielt, die Auswirkungen des chinesischen Neujahrs auf die Durchlaufzeiten zu erfassen – ein typisches Muster, das beim Import von Waren aus Asien beobachtet wird.
Anschließend werden wir mit einem parametrischen probabilistischen Modell für Durchlaufzeiten fortfahren, bei dem wir die log-logistische Verteilung nutzen. Wiederum wird differentiables Programmieren dabei eine wesentliche Rolle beim Erlernen der Modellparameter spielen. Dieses Modell werden wir dann erweitern, indem wir unvollständige Durchlaufzeitbeobachtungen berücksichtigen. Tatsächlich liefern selbst noch nicht abgeschlossene Bestellungen gewisse Informationen über die Durchlaufzeit.
Abschließend vereinen wir eine probabilistische Durchlaufzeitprognose und eine probabilistische Nachfrageprognose in einer einzigen Inventar-replenishment-Situation. Dies bietet die Gelegenheit zu demonstrieren, warum Modularität eine entscheidende Anforderung im Bereich des prädiktiven Modellierens darstellt – sogar wichtiger als das Kleingedruckte der Modelle selbst.

In der Vorlesung 5.2 über probabilistische Vorhersagen haben wir bereits einige Werkzeuge zur Beurteilung der Güte einer probabilistischen Vorhersage eingeführt. Tatsächlich gelten die üblichen Genauigkeitsmetriken, wie der mittlere quadratische Fehler oder der mittlere absolute Fehler, nur für Punktvorhersagen, nicht für probabilistische Vorhersagen. Dennoch bedeutet es nicht, dass Genauigkeit im allgemeinen Sinne irrelevant wird, nur weil unsere Vorhersagen probabilistisch sind. Wir benötigen lediglich ein statistisches Instrument, das mit der probabilistischen Perspektive kompatibel ist.
Zu diesen Instrumenten gehört der Continuous Rank Probability Score (CRPS). Die Formel wird auf dem Bildschirm angezeigt. Der CRPS ist eine Verallgemeinerung der L1-Metrik, also des absoluten Fehlers, jedoch für Wahrscheinlichkeitsverteilungen. Die gebräuchliche Variante des CRPS vergleicht eine Verteilung, hier F genannt, mit einer Beobachtung, hier X genannt. Der mit der CRPS-Funktion ermittelte Wert ist homogen zur Beobachtung. Zum Beispiel, wenn X eine in Tagen ausgedrückte Durchlaufzeit ist, wird der CRPS-Wert ebenfalls in Tagen angegeben.

Der CRPS kann verallgemeinert werden, um zwei Verteilungen zu vergleichen. Genau das wird auf dem Bildschirm gezeigt. Es handelt sich dabei nur um eine geringfügige Abwandlung der vorherigen Formel. Das Wesentliche dieser Metrik bleibt unverändert. Wenn F die tatsächliche Durchlaufzeitverteilung und F_hat eine Schätzung der Durchlaufzeitverteilung ist, wird der CRPS in Tagen angegeben. Der CRPS spiegelt den Grad der Differenz zwischen den beiden Verteilungen wider. Er kann auch als die minimale Energiemenge interpretiert werden, die benötigt wird, um die gesamte Masse der ersten Verteilung so zu transportieren, dass sie exakt die Form der zweiten Verteilung annimmt.
Wir verfügen nun über ein Instrument, um zwei eindimensionale Wahrscheinlichkeitsverteilungen zu vergleichen. Dies wird in Kürze von Interesse sein, wenn wir unser erstes probabilistisches Modell für Durchlaufzeiten vorstellen.
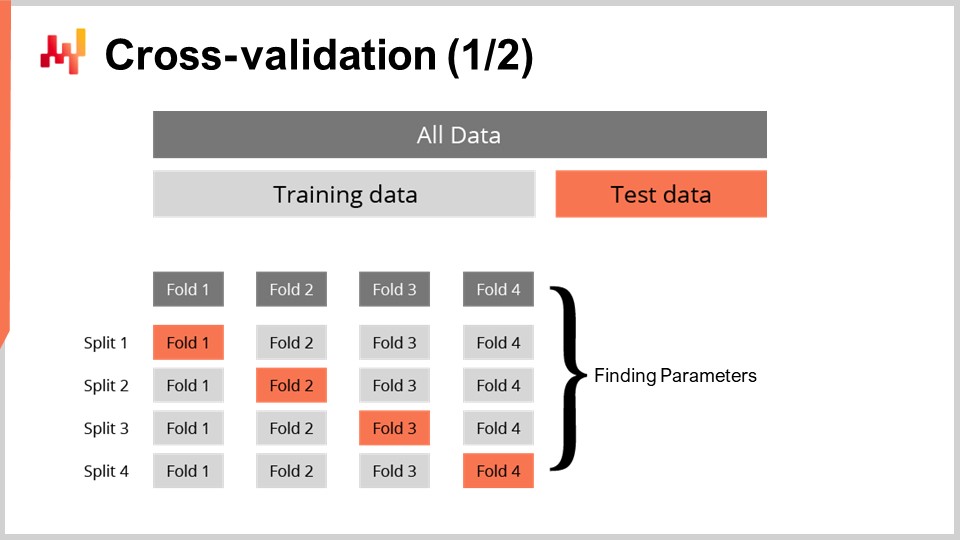
Allein eine Metrik zur Messung der Güte einer probabilistischen Vorhersage zu haben, ist nicht ausreichend. Die Metrik misst die Güte anhand der vorliegenden Daten; was wir jedoch wirklich wollen, ist, die Güte unserer Vorhersage auch für Daten beurteilen zu können, die uns nicht vorliegen. Schließlich interessieren uns die zukünftigen Durchlaufzeiten, nicht jene, die bereits in der Vergangenheit beobachtet wurden. Unsere Fähigkeit, ein Modell so zu gestalten, dass es auch bei unbekannten Daten gut funktioniert, bezeichnet man als Generalisierung. Cross-Validation ist eine allgemeine Technik zur Modellvalidierung, die genau darauf abzielt, die Generalisierungsfähigkeit eines Modells zu bewerten.
In ihrer einfachsten Form besteht Cross-Validation darin, die Beobachtungen in eine kleine Anzahl von Teilmengen aufzuteilen. Bei jeder Iteration wird eine Teilmenge beiseitegelegt und als Test-Teilmenge bezeichnet. Das Modell wird dann auf Basis der übrigen Datensätze, den Trainings-Teilmenge(n), erstellt oder trainiert. Nach dem Training wird das Modell an der Test-Teilmenge validiert. Dieser Prozess wird eine bestimmte Anzahl von Malen wiederholt, und der durchschnittliche Gütewert, der über alle Iterationen hinweg erzielt wird, stellt das endgültige cross-validierte Ergebnis dar.
Cross-Validation wird im Kontext der time series Vorhersage selten verwendet, da zwischen den Beobachtungen zeitliche Abhängigkeiten bestehen. Tatsächlich setzt die hier vorgestellte Cross-Validation voraus, dass die Beobachtungen unabhängig sind. Bei Zeitreihen kommt stattdessen Backtesting zum Einsatz. Backtesting kann als eine Form der Cross-Validation betrachtet werden, die zeitliche Abhängigkeiten berücksichtigt.
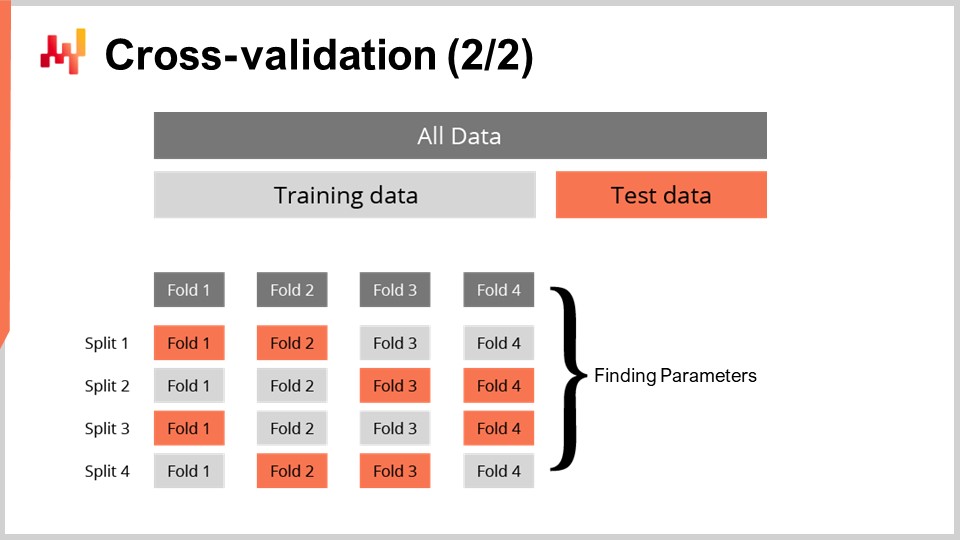
Die Cross-Validation-Technik existiert in zahlreichen Varianten, die eine Vielzahl potenzieller Blickwinkel widerspiegeln, die berücksichtigt werden müssen. Diese Varianten werden wir im Rahmen dieser Vorlesung nicht durchgehen. Ich werde eine spezifische Variante verwenden, bei der bei jeder Aufteilung die Trainings- und die Test-Teilmenge in etwa gleich groß sind. Diese Variante wurde eingeführt, um die Validierung eines probabilistischen Modells zu handhaben, wie wir in Kürze anhand von etwas Code sehen werden.
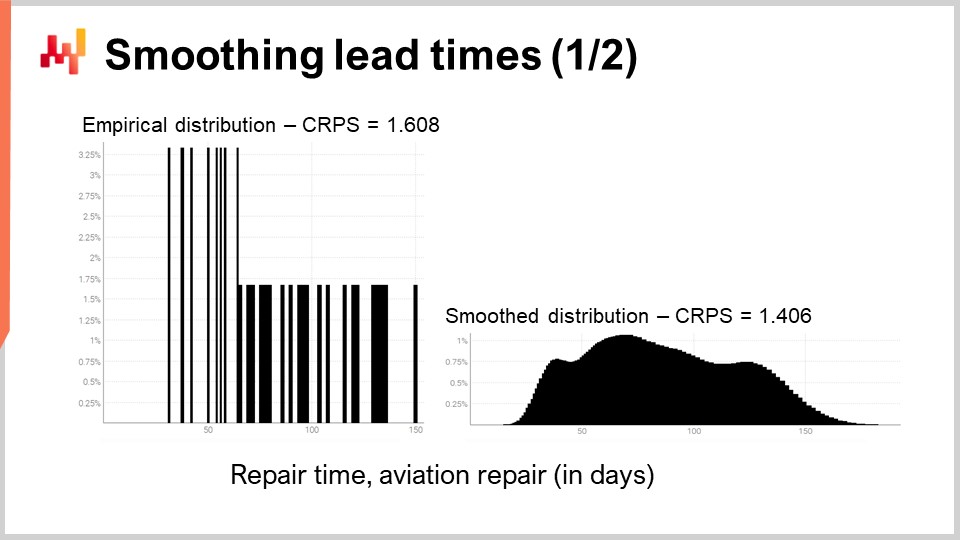
Betrachten wir noch einmal eine der realen Durchlaufzeiten, die wir zuvor auf dem Bildschirm gesehen haben. Links ist das Histogramm mit den dritten Reparaturzeitverteilungen der Luftfahrt verknüpft. Es handelt sich um dieselben Beobachtungen wie zuvor, und das Histogramm wurde lediglich vertikal gestreckt. Dadurch weisen die beiden Histogramme links und rechts die gleiche Skala auf. Für das linke Histogramm haben wir etwa 30 Beobachtungen. Das ist zwar nicht viel, aber bereits mehr, als wir häufig vorfinden.
Das Histogramm links wird als empirische Verteilung bezeichnet. Es ist buchstäblich das rohe Histogramm, wie es aus den Beobachtungen gewonnen wurde. Das Histogramm hat einen Behälter für jede in ganzen Tagen ausgedrückte Dauer. Für jeden Behälter wird die Anzahl der beobachteten Durchlaufzeiten ermittelt. Aufgrund der Spärlichkeit sieht die empirische Verteilung aus wie ein Barcode.
Hier liegt ein Problem vor. Wenn wir zwei beobachtete Durchlaufzeiten von genau 50 Tagen haben, macht es Sinn zu behaupten, dass die Wahrscheinlichkeit, entweder 49 oder 51 Tage zu beobachten, exakt null ist? Das tut sie nicht. Offensichtlich gibt es ein Spektrum an Dauern; wir haben schlichtweg nicht genügend Datenpunkte, um die tatsächliche zugrunde liegende Verteilung zu erfassen, die höchstwahrscheinlich wesentlich glatter ist als diese barcodeähnliche Verteilung.
Daher gibt es beim Glätten dieser Verteilung unzählige Möglichkeiten, diesen Vorgang durchzuführen. Einige Glättungsmethoden mögen vielversprechend erscheinen, sind jedoch statistisch nicht fundiert. Als guter Ausgangspunkt möchten wir sicherstellen, dass ein geglättetes Modell genauer ist als das empirische. Es stellt sich heraus, dass wir bereits zwei Instrumente eingeführt haben – den CRPS und die Cross-Validation –, mit denen wir dies erreichen können.
Gleich werden die Ergebnisse angezeigt. Der CRPS-Fehler, der mit der barcodeähnlichen Verteilung assoziiert ist, beträgt 1,6 Tage, während der CRPS-Fehler der geglätteten Verteilung 1,4 Tage beträgt. Diese beiden Werte wurden mittels Cross-Validation ermittelt. Der geringere Fehler zeigt, dass im Sinne des CRPS die Verteilung rechts die genauere der beiden ist. Der Unterschied von 0,2 zwischen 1,4 und 1,6 ist nicht groß; entscheidend ist jedoch, dass wir eine geglättete Verteilung haben, die nicht willkürlich bestimmte Zwischenwerte mit einer Wahrscheinlichkeit von null belässt. Dies ist plausibel, da unser Verständnis der Reparaturen uns wissen lässt, dass diese Dauern sehr wahrscheinlich eintreten würden, wenn die Reparaturen wiederholt werden. Der CRPS spiegelt nicht die tatsächliche Tiefe der Verbesserung wieder, die wir durch das Glätten der Verteilung erzielt haben. Zumindest bestätigt die Verringerung des CRPS jedoch, dass diese Transformation aus statistischer Sicht gerechtfertigt ist.
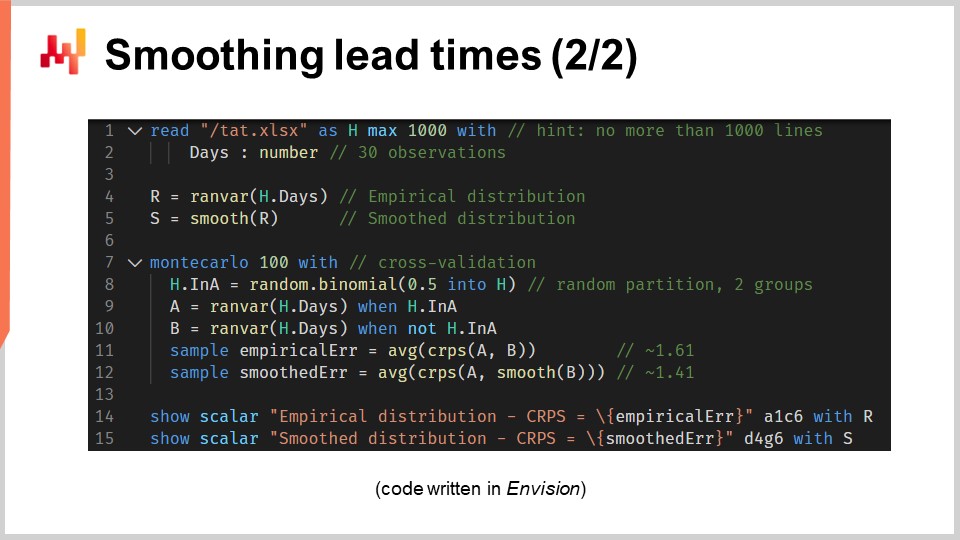
Werfen wir nun einen Blick auf den Quellcode, der diese beiden Modelle erzeugt und die beiden Histogramme anzeigt. Insgesamt wird dies in 12 Codezeilen erreicht, wenn wir die Leerzeilen auslassen. Wie üblich in dieser Vorlesungsreihe ist der Code in Envision geschrieben, der domänenspezifischen Programmiersprache von Lokad, die der prädiktiven Optimierung von supply chains gewidmet ist. Es liegt jedoch keine Magie zugrunde; diese Logik hätte auch in Python verfasst werden können. Für die Art von Problemen, die wir in dieser Vorlesung betrachten, ist Envision allerdings prägnanter und in sich geschlossen.
Schauen wir uns diese 12 Codezeilen im Detail an. In den Zeilen 1 und 2 lesen wir eine Excel-Tabelle ein, die eine einzige Datenspalte enthält. Die Tabelle umfasst 30 Beobachtungen. Diese Daten werden in einer Tabelle namens “H” zusammengefasst, die eine einzige Spalte namens “days” aufweist. In Zeile 4 erstellen wir eine empirische Verteilung. Die Variable “R” hat den Datentyp “ranvar”, und auf der rechten Seite der Zuweisung fungiert die Funktion “ranvar” als Aggregator, der Beobachtungen als Eingabe nimmt und das Histogramm in Form eines “ranvar”-Datentyps zurückgibt. Damit ist der Datentyp “ranvar” speziell für eindimensionale ganzzahlige Verteilungen vorgesehen. Wir haben den Datentyp “ranvar” bereits in einer früheren Vorlesung dieses Kapitels eingeführt. Dieser Datentyp garantiert einen konstanten Speicherverbrauch sowie konstante Rechenzeit für jede Operation. Der Nachteil des Datentyps “ranvar” besteht darin, dass eine verlustbehaftete Kompression erfolgt, wobei der dabei entstehende Datenverlust für supply chain-Zwecke so konzipiert wurde, dass er unbedeutend ist.
In Zeile 5 glätten wir die Verteilung mit der eingebauten Funktion namens “smooth”. Im Hintergrund ersetzt diese Funktion die ursprüngliche Verteilung durch eine Mischung von Poisson-Verteilungen. Jeder Behälter des Histogramms wird in eine Poisson-Verteilung umgewandelt, deren Mittelwert der ganzzahligen Position dieses Behälters entspricht, und schließlich weist die Mischung jeder Poisson-Verteilung ein Gewicht zu, das proportional zum Gewicht des Behälters ist. Eine alternative Sichtweise auf die Arbeitsweise der “smooth”-Funktion besteht darin, dass sie äquivalent dazu ist, jede einzelne Beobachtung durch eine Poisson-Verteilung zu ersetzen, deren Mittelwert der Beobachtung selbst entspricht. All diese Poisson-Verteilungen – eine pro Beobachtung – werden dann gemischt. Beim Mischen werden die jeweiligen Histogramm-Behälterwerte gemittelt. Die “ranvar”-Variablen “R” und “S” werden vor Zeile 14 und 15, in denen sie angezeigt werden, nicht weiter verwendet.
Zeile 7 starten wir einen Monte Carlo-Block. Dieser Block ist eine Art Schleife und wird 100 Mal ausgeführt, wie durch die 100 Werte, die unmittelbar nach dem Schlüsselwort Monte Carlo erscheinen, festgelegt. Der Monte Carlo-Block soll unabhängige Beobachtungen sammeln, die gemäß einem Prozess mit einem gewissen Grad an Zufälligkeit erzeugt werden. Sie fragen sich vielleicht, warum es in Envision ein spezielles Monte Carlo-Konstrukt gibt, anstatt einfach eine Schleife zu verwenden, wie es bei herkömmlichen Programmiersprachen häufig der Fall ist. Es stellt sich heraus, dass ein dediziertes Konstrukt erhebliche Vorteile mit sich bringt. Erstens gewährleistet es, dass die Iterationen tatsächlich unabhängig sind, bis hin zu den Seeds, die zur Ableitung der Pseudozufälligkeit verwendet werden. Zweitens bietet es ein explizites Ziel für die automatisierte Verteilung der Arbeitslast auf mehrere CPU-Kerne oder sogar auf mehrere Maschinen.
In Zeile 8 erstellen wir einen Zufallsvektor von booleschen Werten innerhalb der Tabelle “H.” Mit dieser Zeile erzeugen wir unabhängige Zufallswerte, sogenannte Abweichungen (true oder false), für jede Zeile der Tabelle “H.” Wie üblich bei Envision werden die Schleifen durch Array-Programmierung abstrahiert. Mit diesen booleschen Werten teilen wir die Tabelle “H” in zwei Gruppen auf. Diese zufällige Aufteilung wird für den Cross-Validierungsprozess verwendet.
In den Zeilen 9 und 10 erstellen wir zwei “ranvars” namens “A” bzw. “B.” Wir verwenden erneut den “ranvar”-Aggregator, wenden diesmal jedoch direkt nach dem Aggregator-Aufruf einen Filter mit dem Schlüsselwort “when” an. “A” wird nur aus den Zeilen generiert, in denen der Wert in “a” true ist; bei “B” ist es umgekehrt. “B” wird nur aus den Zeilen generiert, in denen der Wert in “a” false ist.
In den Zeilen 11 und 12 sammeln wir die interessanten Kennzahlen aus dem Monte Carlo-Block. In Envision kann das Schlüsselwort “sample” nur innerhalb eines Monte Carlo-Blocks verwendet werden. Es dient dazu, die Beobachtungen zu sammeln, die während der vielfachen Durchläufe des Monte Carlo-Prozesses gemacht werden. In Zeile 11 berechnen wir den durchschnittlichen Fehler, ausgedrückt in CRPS-Begriffen, zwischen zwei empirischen Verteilungen: einer Teilstichprobe der ursprünglichen Durchlaufzeiten. Das Schlüsselwort “sample” spezifiziert, dass die während der Monte Carlo-Iterationen gesammelten Werte verwendet werden. Der “AVG”-Aggregator, der auf der rechten Seite der Zuweisung für “average” steht, wird genutzt, um am Ende des Blocks einen einzelnen Schätzwert zu erzeugen.
In Zeile 12 machen wir etwas fast Identisches wie in Zeile 11. Dieses Mal wenden wir jedoch die “smooth”-Funktion auf den “ranvar” “B” an. Wir möchten überprüfen, wie nah die geglättete Variante an der naiven empirischen Verteilung liegt. Es stellt sich heraus, dass sie – zumindest in CRPS-Begriffen – näher liegt als ihre ursprünglichen empirischen Gegenstücke.
In den Zeilen 14 und 15 stellen wir die Histogramme und die CRPS-Werte dar. Diese Zeilen erzeugen die Abbildungen, die wir in der vorherigen Folie gesehen haben. Dieses Skript liefert uns die Grundlage für die Qualität der empirischen Verteilung unseres Modells. Zwar ist dieses Modell, das “barcode”-Modell, durchaus als naiv anzusehen, dennoch ist es ein Modell und zudem ein probabilistisches. Somit liefert uns dieses Skript auch ein besseres Modell, zumindest im Sinne des CRPS, durch eine geglättete Variante der ursprünglichen empirischen Verteilung.
Je nachdem, wie vertraut Sie mit Programmiersprachen sind, mag es im Moment viel erscheinen. Ich möchte jedoch darauf hinweisen, wie einfach es ist, eine vernünftige Wahrscheinlichkeitsverteilung zu erzeugen, selbst wenn wir nicht mehr als einige Beobachtungen haben. Obwohl wir 12 Codezeilen haben, stellen nur die Zeilen 4 und 5 den eigentlichen Modellierungsteil der Aufgabe dar. Wenn wir ausschließlich an der geglätteten Variante interessiert wären, könnte der “ranvar” “S” in nur einer Codezeile geschrieben werden. Es ist also buchstäblich ein Einzeiler im Code: Zuerst eine ranvar-Aggregation anwenden, und danach einen Glättungsoperator – und fertig. Der Rest besteht nur aus Instrumentierung und Darstellung. Mit den richtigen Werkzeugen kann probabilistisches Modellieren – sei es bei Durchlaufzeiten oder etwas anderem – äußerst unkompliziert gestaltet werden. Es erfordert keine hochtrabende Mathematik, keinen komplexen Algorithmus, keine aufwändigen Softwarekomponenten. Es ist einfach und bemerkenswert unkompliziert.

Wie bekommt man eine Lieferung, die sechs Monate zu spät ist? Die Antwort ist offensichtlich: einen Tag nach dem anderen. Ernsthaft betrachtet, können Durchlaufzeiten üblicherweise in eine Reihe von Verzögerungen zerlegt werden. Beispielsweise kann eine Lieferanten-Durchlaufzeit in eine Warteverzögerung, während die Bestellung in eine Rückstandswarteschlange gestellt wird, eine Produktionsverzögerung, während Waren hergestellt werden, und schließlich eine Transitverzögerung, während die Waren versandt werden, aufgeteilt werden. Wenn Durchlaufzeiten also zerlegbar sind, ist es auch interessant, sie wieder zusammenzusetzen.
Würden wir in einer hochdeterministischen Welt leben, in der die Zukunft präzise vorausgesagt werden könnte, dann wäre das Zusammenfügen von Durchlaufzeiten lediglich eine Frage des Addierens. Zurück zu dem Beispiel, das ich gerade erwähnt habe: Die Bestell-Durchlaufzeit wäre die Summe der Warteschlangenverzögerung in Tagen, der Produktionsverzögerung in Tagen und der Transitverzögerung in Tagen. Doch wir leben nicht in einer Welt, in der die Zukunft exakt vorhersagbar ist. Die realen Durchlaufzeitverteilungen, die wir zu Beginn dieser Vorlesung präsentiert haben, untermauern diese Annahme. Durchlaufzeiten sind unbeständig, und es gibt wenig Grund zu der Annahme, dass sich dies in den kommenden Jahrzehnten grundlegend ändern wird.
Daher sollten zukünftige Durchlaufzeiten als Zufallsvariablen betrachtet werden. Diese Zufallsvariablen fassen die Unsicherheit auf und quantifizieren sie, anstatt sie zu ignorieren. Genauer gesagt bedeutet dies, dass jede Komponente der Durchlaufzeit ebenfalls einzeln als Zufallsvariable modelliert werden sollte. Zurück zu unserem Beispiel: Die Bestell-Durchlaufzeit ist eine Zufallsvariable, die als Summe von drei Zufallsvariablen erhalten wird, die jeweils der Warteschlangenverzögerung, der Produktionsverzögerung und der Transitverzögerung zugeordnet sind.
Die Formel für die Summe von zwei unabhängigen, eindimensionalen, ganzzahligen Zufallsvariablen wird auf dem Bildschirm dargestellt. Diese Formel besagt lediglich, dass wenn wir eine Gesamtdauer von Z Tagen erhalten und die erste Zufallsvariable X K Tage beisteuert, dann muss die zweite Zufallsvariable Y Z minus K Tage betragen. Diese Art der Summation ist in der Mathematik allgemein als Faltung bekannt.
Obwohl es scheint, als gäbe es unendlich viele Terme in dieser Faltung, interessieren wir uns in der Praxis nur für eine endliche Anzahl. Erstens haben alle negativen Dauern eine Wahrscheinlichkeit von Null; tatsächlich würden negative Verzögerungen bedeuten, in der Zeit zurückzureisen. Zweitens werden bei großen Verzögerungen die Wahrscheinlichkeiten so klein, dass sie für praktische supply chain Zwecke zuverlässig als Null angenähert werden können.
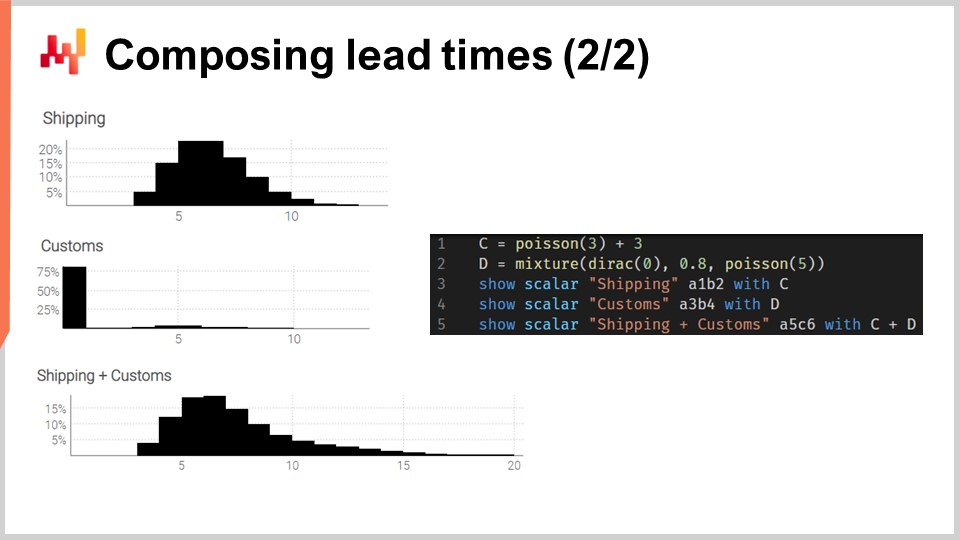
Lassen Sie uns diese Faltungen in die Praxis umsetzen. Betrachten wir eine Transitzeit, die in zwei Phasen zerlegt werden kann: eine Versandverzögerung, gefolgt von einer Verzögerung bei der Zollabfertigung. Wir möchten diese beiden Phasen mit zwei unabhängigen Zufallsvariablen modellieren und die Transitzeit durch Addition dieser beiden Zufallsvariablen rekonstruieren.
Auf dem Bildschirm werden die Histogramme links durch das Skript rechts erzeugt. In Zeile 1 wird die Versandverzögerung als Faltung einer Poisson-Verteilung plus einer Konstante modelliert. Die Poisson-Funktion liefert einen “ranvar”-Datentyp; das Hinzufügen von drei bewirkt eine Verschiebung der Verteilung nach rechts. Der resultierende “ranvar” wird der Variable “C” zugewiesen. Dieser “ranvar” wird in Zeile 3 angezeigt und ist links als oberstes Histogramm zu erkennen. Wir erkennen die Form einer Poisson-Verteilung, die in diesem Fall um drei Einheiten nach rechts verschoben wurde. In Zeile 2 wird die Zollabfertigung als Mischung aus einem Dirac bei Null und einer Poisson bei fünf modelliert. Der Dirac bei Null tritt achtzig Prozent der Zeit auf; das ist es, was diese Konstante 0.8 bedeutet. Sie spiegelt Situationen wider, in denen die Waren meistens gar nicht vom Zoll inspiziert werden und ohne nennenswerte Verzögerung passieren. Alternativ werden zwanzig Prozent der Zeit die Waren beim Zoll inspiziert, und die Verzögerung wird als Poisson-Verteilung mit einem Mittelwert von fünf modelliert. Der resultierende ranvar wird einer Variablen namens D zugewiesen. Dieser ranvar wird in Zeile 4 angezeigt und ist links als mittleres Histogramm zu erkennen. Dieser asymmetrische Aspekt verdeutlicht, dass der Zoll in den meisten Fällen keine zusätzliche Verzögerung verursacht.
Schließlich berechnen wir in Zeile 5 C plus D. Diese Addition ist eine Faltung, da sowohl C als auch D ranvars und keine Zahlen sind. Dies ist die zweite Faltung in diesem Skript, da bereits in Zeile 1 eine Faltung stattgefunden hat. Der resultierende ranvar wird angezeigt und ist links als das dritte und unterste Histogramm sichtbar. Dieses dritte Histogramm ähnelt dem ersten, nur dass der Schwanz sich viel weiter nach rechts erstreckt. Erneut zeigt sich, dass wir mit wenigen Codezeilen nicht-triviale Effekte der realen Welt, wie Verzögerungen bei der Zollabfertigung, modellieren können.
Allerdings lassen sich zu diesem Beispiel zwei Kritikpunkte anbringen. Erstens wird nicht erklärt, woher die Konstanten stammen; in der Praxis möchten wir diese Konstanten aus historischen Daten erlernen. Zweitens, obwohl die Poisson-Verteilung den Vorteil der Einfachheit besitzt, könnte sie – insbesondere in Fat-Tail-Situationen – für die Modellierung von Durchlaufzeiten nicht sehr realistisch sein. Daher werden wir diese beiden Punkte der Reihe nach angehen.
Um Parameter aus Daten zu lernen, werden wir ein Programmierparadigma wieder aufgreifen, das wir in dieser Vorlesungsreihe bereits vorgestellt haben, nämlich das differentiable programming. Wenn Sie die vorherigen Vorlesungen in diesem Kapitel noch nicht gesehen haben, lade ich Sie ein, diese nach Ende der vorliegenden Vorlesung anzusehen. Differentiable programming wird in diesen Vorlesungen ausführlicher behandelt.
Differentiable programming ist eine Kombination aus zwei Techniken: stochastischem Gradientenabstieg und automatischer Differentiation. Der stochastische Gradientenabstieg ist eine Optimierungstechnik, die die Parameter bei jeder Beobachtung schrittweise in die entgegengesetzte Richtung der Gradienten verschiebt. Die automatische Differentiation ist eine Kompilierungstechnik, ähnlich dem Compiler einer Programmiersprache; sie berechnet die Gradienten für alle Parameter, die in einem allgemeinen Programm vorkommen.
Lassen Sie uns differentiable programming anhand eines Durchlaufzeitproblems veranschaulichen. Dies dient entweder als Auffrischung oder als Einführung, je nachdem, wie vertraut Sie mit diesem Paradigma sind. Wir wollen den Einfluss des Chinesischen Neujahrs auf die Durchlaufzeiten bei Importen aus China modellieren. Tatsächlich verlängern sich die Durchlaufzeiten, da die Fabriken für zwei oder drei Wochen wegen des Chinesischen Neujahrs schließen. Das Chinesische Neujahr ist zyklisch; es findet jedes Jahr statt. Allerdings ist es nicht streng saisonal, zumindest nicht im Sinne des gregorianischen Kalenders.
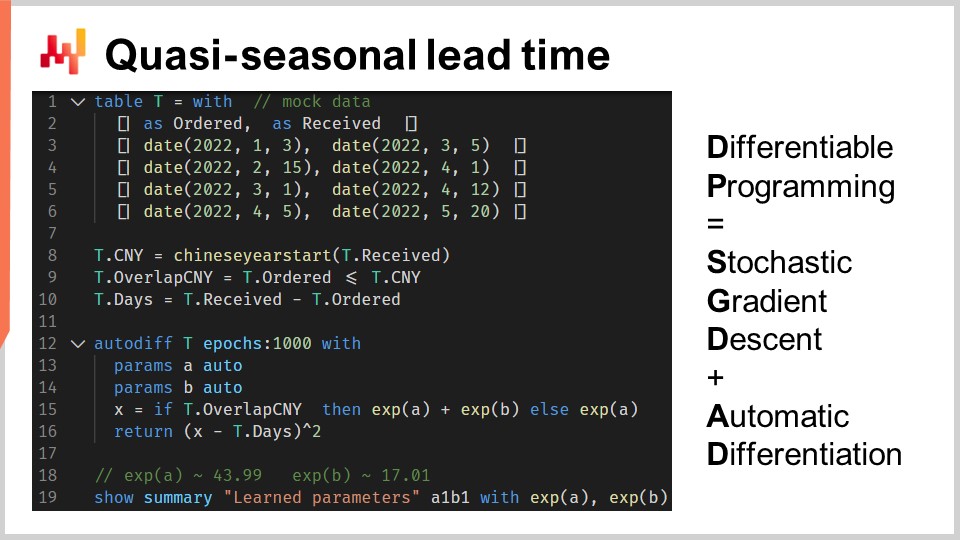
In den Zeilen eins bis sechs führen wir einige Beispielsbestellungen mit vier Beobachtungen ein, wobei sowohl ein Bestelldatum als auch ein Eingangsdatum vorliegen. In der Praxis würden diese Daten nicht fest codiert, sondern aus den Systemen des Unternehmens geladen werden. In den Zeilen acht und neun berechnen wir, ob sich die Durchlaufzeit mit dem Chinesischen Neujahr überschneidet. Die Variable “T.overlap_CNY” ist ein boolescher Vektor, der angibt, ob die Beobachtung vom Chinesischen Neujahr beeinflusst wird oder nicht.
In Zeile 12 führen wir einen “autodiff”-Block ein. Die Tabelle T wird als Beobachtungstabelle verwendet, und es gibt 1000 Epochen. Das bedeutet, dass jede Beobachtung, also jede Zeile in der Tabelle T, tausendmal besucht wird. Ein Schritt des stochastischen Gradientenabstiegs entspricht einer Ausführung der Logik innerhalb des “autodiff”-Blocks.
In den Zeilen 13 und 14 werden zwei skalare Parameter deklariert. Der “autodiff”-Block wird diese Parameter erlernen. Der Parameter A spiegelt die Basis-Durchlaufzeit ohne den Effekt des Chinesischen Neujahrs wider, und der Parameter B repräsentiert die zusätzliche Verzögerung, die mit dem Chinesischen Neujahr verbunden ist. In Zeile 15 berechnen wir X, die Durchlaufzeitvorhersage unseres Modells. Dies ist ein deterministisches Modell, kein probabilistisches; X ist eine punktuelle Prognose der Durchlaufzeit. Die rechte Seite der Zuweisung ist klar: Überlappt die Beobachtung mit dem Chinesischen Neujahr, so geben wir die Basis plus die Neujahrs-Komponente zurück; andernfalls nur die Basis. Da der “autodiff”-Block jeweils nur eine Beobachtung verarbeitet, bezieht sich in Zeile 15 die Variable T.overlap_CNY auf einen Skalar und nicht auf einen Vektor. Dieser Wert entspricht der einen Zeile, die als Beobachtungszeile innerhalb der Tabelle T ausgewählt wurde.
Die Parameter A und B werden in die Exponentialfunktion “exp” eingebettet, was ein kleiner Trick im differentiable programming ist. Tatsächlich tendiert der Algorithmus, der den stochastischen Gradientenabstieg steuert, dazu, relativ konservativ in Bezug auf die inkrementellen Veränderungen der Parameter zu sein. Möchten wir also einen positiven Parameter erlernen, der möglicherweise größer als beispielsweise 10 werden kann, beschleunigt das Einhüllen dieses Parameters in einen exponentiellen Prozess die Konvergenz.
In Zeile 16 geben wir den mittleren quadratischen Fehler zwischen unserer Vorhersage X und der beobachteten Dauer, ausgedrückt in Tagen (T.days), zurück. Auch hier ist T.days innerhalb des “autodiff”-Blocks ein Skalar und kein Vektor. Da die Tabelle T als Beobachtungstabelle verwendet wird, wird der Rückgabewert als Verlustfunktion behandelt, die durch den stochastischen Gradientenabstieg minimiert wird. Die automatische Differentiation leitet die Gradienten vom Verlust zurück zu den Parametern A und B. Schließlich zeigen wir in Zeile 19 die beiden Werte an, die wir für A und B erlernt haben, welche die Basis und die Neujahrs-Komponente unserer Durchlaufzeit darstellen.
Damit schließen wir unsere erneute Einführung in das differentiable programming als vielseitiges Werkzeug zur Erkennung statistischer Muster ab. Von hier aus werden wir die “autodiff”-Blöcke in komplexeren Situationen erneut betrachten. Lassen Sie uns jedoch noch einmal darauf hinweisen, dass, auch wenn es etwas überwältigend erscheinen mag, hier nichts wirklich Kompliziertes vor sich geht. Man könnte argumentieren, dass das komplexeste Codefragment in diesem Skript die zugrunde liegende Implementierung der Funktion “ChineseYearStart” ist, die in Zeile 8 aufgerufen wird und Teil der Envision-Standardbibliothek ist. Innerhalb weniger Codezeilen führen wir ein Modell mit zwei Parametern ein und erlernen diese Parameter. Noch einmal: Diese Einfachheit ist bemerkenswert.
Lieferzeiten weisen häufig fette Schwänze auf; das heißt, wenn eine Lieferzeit abweicht, weicht sie stark ab. Um Lieferzeiten zu modellieren, ist es daher interessant, Verteilungen zu verwenden, die diese fat-tail Verhaltensweisen reproduzieren können. Die mathematische Literatur bietet eine umfangreiche Liste solcher Verteilungen, und viele davon würden unserem Zweck genügen. Allerdings würde es Stunden dauern, die mathematische Landschaft nur zu überblicken. Lassen Sie uns einfach feststellen, dass die Poisson-Verteilung keinen fetten Schwanz hat. Deshalb werde ich heute die log-logistische Verteilung auswählen, die zufällig eine Verteilung mit fettem Schwanz ist. Die Hauptbegründung für diese Wahl ist, dass die Lokad-Teams Lieferzeiten für mehrere Kunden mittels log-logistischer Verteilungen modellieren. Es funktioniert mit minimalen Komplikationen. Bedenken Sie jedoch, dass die log-logistische Verteilung keinesfalls ein Allheilmittel ist und es zahlreiche Situationen gibt, in denen Lokad Lieferzeiten anders modelliert.
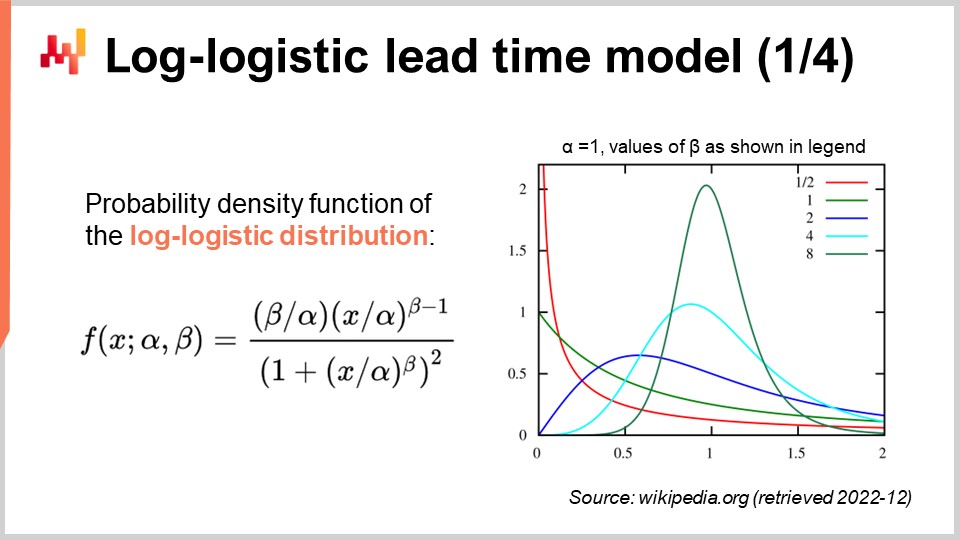
Auf dem Bildschirm sehen wir die Wahrscheinlichkeitsdichtefunktion der log-logistischen Verteilung. Dies ist eine parametrische Verteilung, die von zwei Parametern, alpha und beta, abhängt. Der Alpha-Parameter entspricht dem Median der Verteilung, und der Beta-Parameter bestimmt deren Form. Rechts kann man durch verschiedene Beta-Werte eine kurze Reihe von Formen erzeugen. Auch wenn diese Dichteformel einschüchternd wirkt, ist sie buchstäblich Lehrbuchmaterial, genauso wie die Formel zur Berechnung des Volumens einer Kugel. Sie können versuchen, diese Formel zu entschlüsseln und auswendig zu lernen, aber das ist nicht einmal notwendig; Sie müssen nur wissen, dass es eine analytische Formel gibt. Sobald Sie wissen, dass die Formel existiert, dauert es weniger als eine Minute, sie online wiederzufinden.

Unser Ziel ist es, die log-logistische Verteilung zu nutzen, um ein probabilistisches Modell für Lieferzeiten zu erlernen. Dazu werden wir die Log-Likelihood minimieren. Tatsächlich haben wir in der vorherigen Vorlesung dieses fünften Kapitels gesehen, dass es mehrere Metriken gibt, die für die probabilistische Perspektive geeignet sind. Vor kurzem haben wir den CRPS (Continuous Ranked Probability Score) erneut betrachtet. Hier widmen wir uns der Log-Likelihood, die eine bayessche Perspektive einnimmt.
Kurz gesagt, bei gegebenen zwei Parametern gibt die log-logistische Verteilung an, mit welcher Wahrscheinlichkeit jede Beobachtung im empirischen Datensatz vorkommt. Wir wollen die Parameter erlernen, die diese Wahrscheinlichkeit maximieren. Der Logarithmus – und damit die Log-Likelihood anstelle der bloßen Likelihood – wird eingeführt, um numerische Unterläufe zu vermeiden. Numerische Unterläufe treten auf, wenn wir mit sehr kleinen Zahlen arbeiten, die nahe bei Null liegen; diese winzigen Zahlen kommen mit der in moderner Computerhardware üblichen Gleitkommadarstellung nicht gut zurecht.
Um die Log-Likelihood der log-logistischen Verteilung zu berechnen, wenden wir daher den Logarithmus auf ihre Wahrscheinlichkeitsdichtefunktion an. Der analytische Ausdruck wird auf dem Bildschirm dargestellt. Dieser Ausdruck kann implementiert werden, und genau das wird in den drei Codezeilen unten gemacht.
In Zeile eins wird die Funktion “L4” eingeführt. L4 steht für “log-likelihood of log-logistic” – ja, das sind viele L’s und viele Logs. Diese Funktion nimmt drei Argumente entgegen: die beiden Parameter alpha und beta sowie die Beobachtung x. Sie gibt den Logarithmus der Likelihood zurück. Die Funktion L4 ist mit dem Schlüsselwort “autodiff” versehen; dieses weist darauf hin, dass die Funktion mittels automatischer Differenzierung differenziert werden soll. Mit anderen Worten, Gradienten können vom Rückgabewert dieser Funktion rückwärts zu ihren Argumenten, den Parametern alpha und beta, fließen. Technisch gesehen fließt der Gradient auch rückwärts durch die Beobachtung x; da wir die Beobachtungen während des Lernprozesses jedoch unveränderlich halten, haben die Gradienten keine Auswirkungen auf diese. In Zeile drei erhalten wir die wörtliche Transkription der mathematischen Formel, die sich direkt über dem Skript befindet.
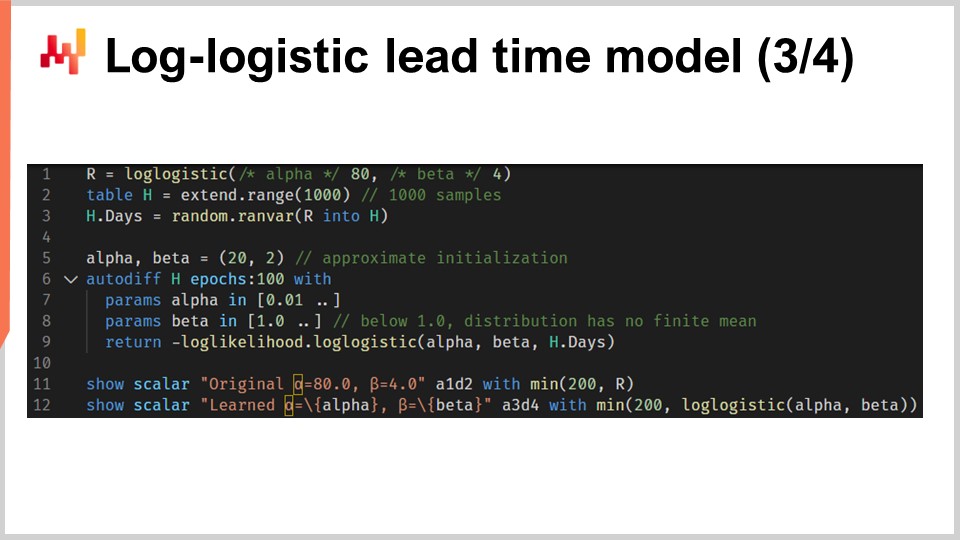
Lassen Sie uns nun alles zusammenführen mit einem Skript, das die Parameter eines probabilistischen Lieferzeitmodells auf Basis der log-logistischen Verteilung erlernt. In den Zeilen eins und drei generieren wir unseren simulierten Trainingsdatensatz. Im realen Einsatz würden wir historische Daten verwenden, anstatt simulierte Daten zu erzeugen. In Zeile eins erstellen wir eine “ranvar”, die die ursprüngliche Verteilung repräsentiert. Im Interesse der Übung wollen wir die Parameter alpha und beta wieder erlernen. Die log-logistische Funktion ist Teil der Standardbibliothek von Envision und gibt eine “ranvar” zurück. In Zeile zwei erstellen wir die Tabelle “H”, die 1.000 Einträge enthält. In Zeile drei ziehen wir 1.000 Stichproben, die zufällig aus der ursprünglichen Verteilung “R” entnommen wurden. Dieser Vektor “H.days” stellt den Trainingsdatensatz dar.
In Zeile sechs befindet sich ein “autodiff”-Block; hier findet das Lernen statt. In den Zeilen sieben und acht deklarieren wir zwei Parameter, alpha und beta, und um numerische Probleme wie eine Division durch Null zu vermeiden, werden diesen Parametern Grenzen gesetzt. Alpha muss größer als 0,01 bleiben und beta größer als 1,0. In Zeile neun geben wir den Verlust zurück, der das Gegenteil der Log-Likelihood darstellt. Tatsächlich minimieren “autodiff”-Blöcke per Konvention die Verlustfunktion, weshalb wir die Likelihood maximieren wollen – daher das Minuszeichen. Die Funktion “log_likelihood.logistic” ist Teil der Standardbibliothek von Envision, aber im Hintergrund handelt es sich einfach um die Funktion “L4”, die wir auf der vorherigen Folie implementiert haben. Es geschieht also kein Zauber, sondern alles basiert auf automatischer Differenzierung, die den Gradienten vom Verlust zu den Parametern alpha und beta rückwärts leitet.
In den Zeilen 11 und 12 werden die ursprüngliche Verteilung und die erlernte Verteilung dargestellt. Die Histogramme werden bei 200 begrenzt; diese Begrenzung macht das Histogramm etwas lesbarer. Wir werden gleich darauf zurückkommen. Falls Sie sich über die Performance des “autodiff”-Teils dieses Skripts wundern: Die Ausführung dauert weniger als 80 Millisekunden auf einem einzelnen CPU-Kern. Differenzierbares Programmieren ist nicht nur vielseitig, sondern nutzt auch die Rechenressourcen moderner Hardware optimal.
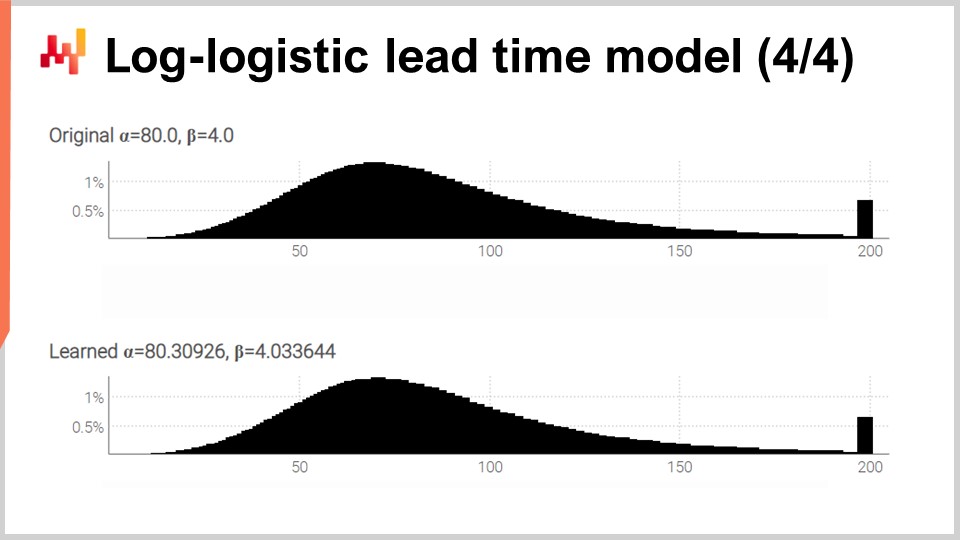
Auf dem Bildschirm sehen wir die beiden Histogramme, die von unserem soeben betrachteten Skript erzeugt wurden. Oben ist die ursprüngliche Verteilung mit ihren zwei ursprünglichen Parametern, alpha und beta, jeweils 80 und 4, dargestellt. Unten befindet sich die erlernte Verteilung, bei der die beiden Parameter durch differenzierbares Programmieren ermittelt wurden. Die beiden Spitzen ganz rechts gehören zu den abgeschnittenen Schwänzen, da diese sich sehr weit erstrecken. Übrigens kommt es, wenn auch selten, vor, dass bestimmte Waren mehr als ein Jahr nach der Bestellung eintreffen. Dies ist nicht in jedem Bereich der Fall, sicherlich nicht bei Milchprodukten, aber bei Maschinenteilen oder Elektronik passiert es gelegentlich.
Auch wenn der Lernprozess nicht exakt ist, erzielen wir Ergebnisse, die innerhalb von einem Prozent der ursprünglichen Parameterwerte liegen. Das zeigt zumindest, dass die Maximierung der Log-Likelihood durch differenzierbares Programmieren in der Praxis funktioniert. Die log-logistische Verteilung mag geeignet sein oder auch nicht – es hängt von der Form der Lieferzeitverteilung ab, mit der Sie konfrontiert sind. Allerdings könnten wir prinzipiell jede alternative parametrische Verteilung wählen. Alles, was es braucht, ist ein analytischer Ausdruck der Wahrscheinlichkeitsdichtefunktion. Es gibt eine riesige Auswahl solcher Verteilungen. Sobald Sie eine Lehrbuchformel haben, erledigt eine direkte Implementierung mittels differenzierbarem Programmieren normalerweise den Rest.
Lieferzeiten werden nicht erst beobachtet, wenn die Transaktion abgeschlossen ist. Während die Transaktion noch läuft, wissen Sie bereits etwas; Sie haben schon eine unvollständige Beobachtung der Lieferzeit. Nehmen wir an, Sie haben vor 100 Tagen eine Bestellung aufgegeben. Die Waren sind noch nicht eingetroffen; dennoch wissen Sie schon, dass die Lieferzeit mindestens 100 Tage beträgt. Diese Dauer von 100 Tagen stellt die Untergrenze für eine Lieferzeit dar, die noch nicht vollständig beobachtet wurde. Diese unvollständigen Lieferzeiten sind oft sehr wichtig. Wie ich zu Beginn dieser Vorlesung erwähnte, sind Lieferzeitdatensätze häufig spärlich. Es ist nicht ungewöhnlich, einen Datensatz zu haben, der nur ein halbes Dutzend Beobachtungen enthält. In solchen Fällen ist es wichtig, jede Beobachtung optimal zu nutzen – auch die, die noch andauern.
Betrachten wir folgendes Beispiel: Wir haben insgesamt fünf Bestellungen. Drei Bestellungen wurden bereits geliefert, und die Lieferzeiten lagen sehr nahe bei 30 Tagen. Allerdings sind die letzten beiden Bestellungen seit 40 bzw. 50 Tagen offen. Den ersten drei Beobachtungen zufolge sollte die durchschnittliche Lieferzeit etwa 30 Tage betragen. Doch die beiden noch unvollständigen Bestellungen widersprechen dieser Annahme. Die beiden offenen Bestellungen bei 40 und 50 Tagen deuten auf eine deutlich längere Lieferzeit hin. Deshalb sollten wir die letzten Bestellungen nicht verwerfen, nur weil sie unvollständig sind. Wir sollten diese Information nutzen und unsere Annahme in Richtung längerer Lieferzeiten, vielleicht 60 Tage, anpassen.
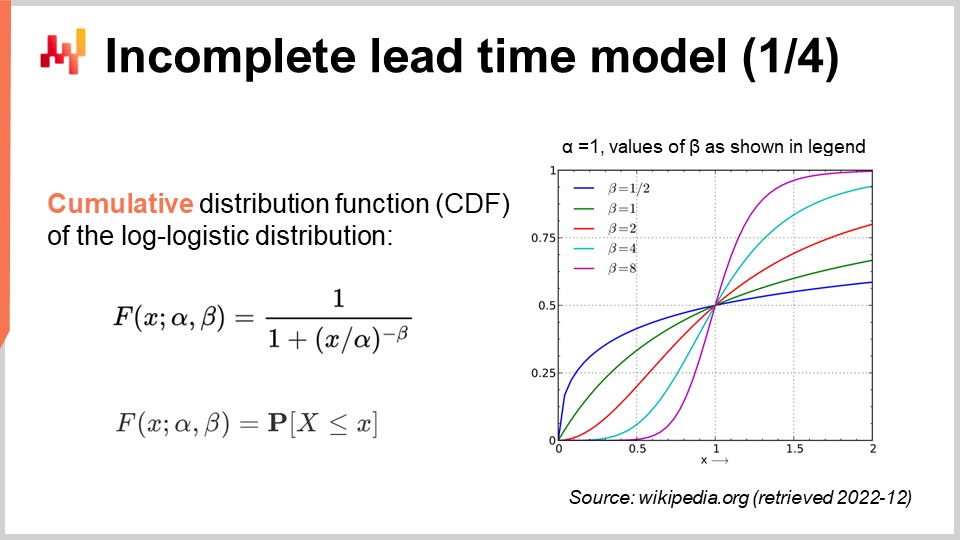
Lassen Sie uns unser probabilistisches Lieferzeitmodell erneut betrachten, diesmal jedoch unter Einbeziehung unvollständiger Beobachtungen. Mit anderen Worten, wir wollen auch mit Beobachtungen umgehen, die manchmal nur eine Untergrenze für die endgültige Lieferzeit darstellen. Dafür können wir die kumulative Verteilungsfunktion (CDF) der log-logistischen Verteilung verwenden. Diese Formel ist auf dem Bildschirm zu sehen; auch sie ist Lehrbuchmaterial. Die CDF der log-logistischen Verteilung profitiert von einem einfachen analytischen Ausdruck. Im Folgenden werde ich diese Methode als “conditional probability technique” bezeichnen, um mit zensierten Daten umzugehen.

Auf Basis dieses analytischen Ausdrucks der CDF können wir die Log-Likelihood der log-logistischen Verteilung erneut betrachten. Das auf dem Bildschirm gezeigte Skript bietet eine überarbeitete Implementierung unserer vorherigen L4-Funktion. In Zeile eins haben wir weitgehend dieselbe Funktionsdeklaration. Diese Funktion nimmt ein zusätzliches viertes Argument entgegen, einen Boolean-Wert namens “is_incomplete”, der – wie der Name schon sagt – angibt, ob die Beobachtung unvollständig ist oder nicht. In den Zeilen zwei und drei greifen wir, falls die Beobachtung vollständig ist, auf die vorherige Situation mit der regulären log-logistischen Verteilung zurück. So rufen wir die Log-Likelihood-Funktion auf, die Teil der Standardbibliothek ist. Ich hätte den Code der vorherigen L4-Implementierung wiederholen können, aber diese Version ist prägnanter. In den Zeilen vier und fünf drücken wir die Log-Likelihood dafür aus, letztendlich eine Lieferzeit zu beobachten, die größer ist als die aktuelle unvollständige Beobachtung “X”. Dies wird durch die CDF und genauer gesagt durch den Logarithmus der CDF erreicht.
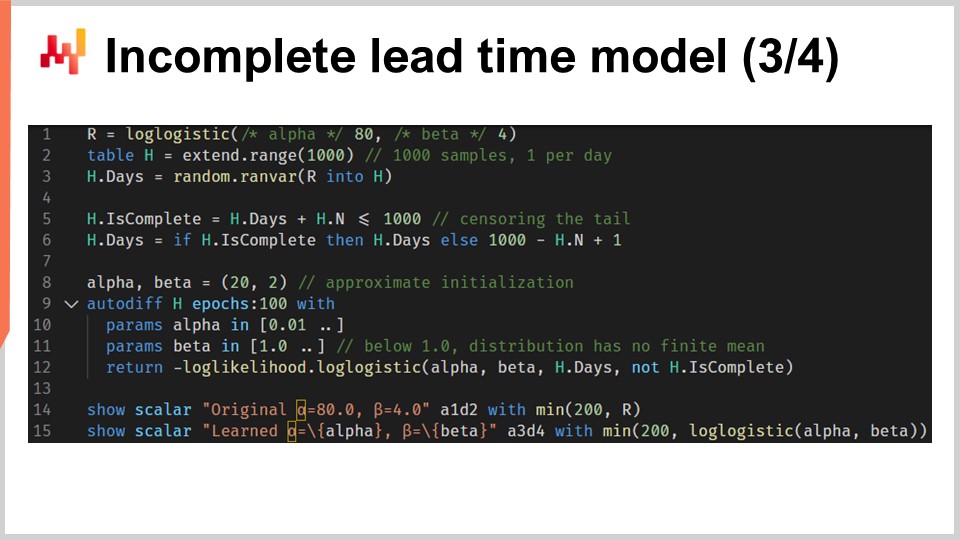
Nun können wir unser Setup mit einem Skript wiederholen, das die Parameter der log-logistischen Verteilung erlernt, diesmal jedoch in Anwesenheit unvollständiger Lieferzeiten. Das Skript auf dem Bildschirm ist fast identisch mit dem vorherigen. In den Zeilen eins bis drei generieren wir die Daten; diese Zeilen haben sich nicht verändert. Beachten Sie, dass H.N ein automatisch erzeugter Vektor ist, der implizit in Zeile zwei erstellt wird. Dieser Vektor nummeriert die generierten Zeilen, beginnend bei eins. Die vorherige Version dieses Skripts nutzte diesen automatisch erzeugten Vektor nicht, aber momentan erscheint der H.N-Vektor am Ende von Zeile sechs.
Die Zeilen fünf und sechs sind in der Tat die wichtigen. Hier zensieren wir die Lieferzeiten. Es ist, als würden wir pro Tag eine Lieferzeitbeobachtung machen und diejenigen Beobachtungen abschneiden, die zu aktuell sind, um vollständig ausgewertet zu werden. Das bedeutet zum Beispiel, dass eine 20-tägige Lieferzeit, die vor sieben Tagen begonnen hat, als eine sieben-tägige unvollständige Lieferzeit erscheint. Am Ende von Zeile sechs haben wir eine Liste von Lieferzeiten erzeugt, bei denen einige der jüngsten Beobachtungen (diejenigen, die nach dem heutigen Datum enden würden) unvollständig sind. Der Rest des Skripts bleibt unverändert, mit Ausnahme von Zeile 12, in der der Vektor H.is_complete als viertes Argument der Log-Likelihood-Funktion übergeben wird. Somit rufen wir in Zeile 12 die Funktion des differenzierbaren Programmierens auf, die wir vor einer Minute eingeführt haben.
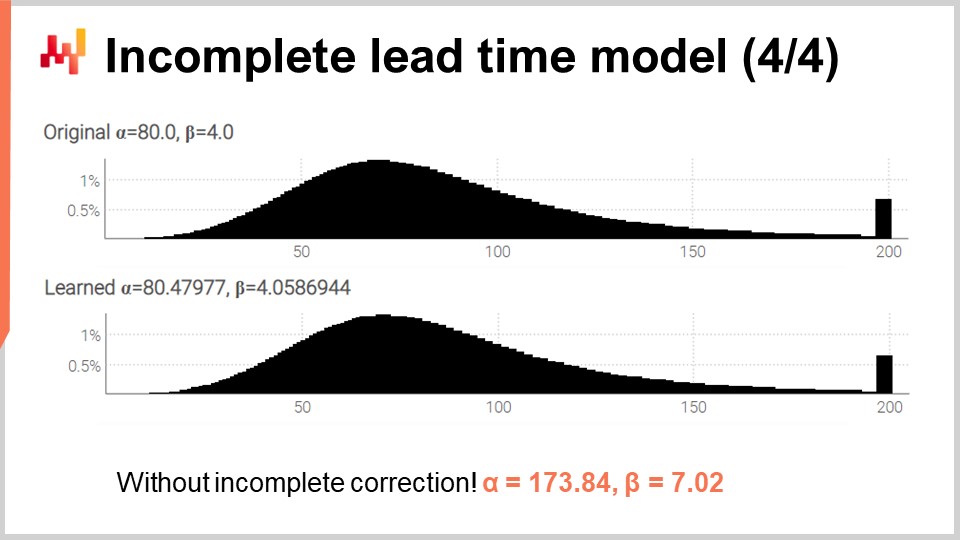
Abschließend werden auf dem Bildschirm die beiden Histogramme dieses überarbeiteten Skripts dargestellt. Die Parameter werden weiterhin mit hoher Genauigkeit erlernt, obwohl nun zahlreiche unvollständige Lieferzeiten vorliegen. Um zu überprüfen, dass der Umgang mit unvollständigen Zeiten keine unnötige Komplikation darstellt, habe ich das Skript erneut ausgeführt – diesmal mit einer modifizierten Variante, die die dreistellige Überladung der Log-Likelihood-Funktion verwendet (diejenige, die wir zuerst nutzten und davon ausgingen, dass alle Beobachtungen vollständig sind). Für alpha und beta erhalten wir die Werte, die am unteren Bildschirmrand angezeigt werden. Wie erwartet stimmen diese Werte überhaupt nicht mit den ursprünglichen Werten von alpha und beta überein.
In dieser Vorlesungsreihe wird nicht zum ersten Mal eine Methode eingeführt, um mit zensierten Daten umzugehen. In der zweiten Vorlesung dieses Kapitels wurde die Verlustmaskierungstechnik vorgestellt, um mit Fehlbeständen umzugehen. Tatsächlich möchten wir in der Regel die zukünftige Nachfrage vorhersagen, nicht den zukünftigen Verkauf. Fehlbestände führen zu einer Verzerrung nach unten, da wir nicht alle Verkäufe beobachten können, die stattgefunden hätten, wenn kein Fehlbestand eingetreten wäre. Die “conditional probability technique” kann verwendet werden, um mit zensierter Nachfrage umzugehen, wie es bei Fehlbeständen der Fall ist. Die “conditional probability technique” ist etwas komplexer als die Verlustmaskierung, weshalb sie wahrscheinlich nur dann eingesetzt werden sollte, wenn die Verlustmaskierung nicht ausreicht.
Im Fall von Lieferzeiten ist die Knappheit der Daten der Hauptmotivator. Es kann vorkommen, dass so wenig Daten vorhanden sind, dass es entscheidend ist, jede einzelne Beobachtung – auch die unvollständigen – optimal zu nutzen. Tatsächlich ist die “conditional probability technique” leistungsfähiger als die Verlustmaskierung, weil sie unvollständige Beobachtungen einbezieht, anstatt sie einfach zu verwerfen. Beispielsweise, wenn genau eine Lagerhaltungseinheit vorhanden ist und diese Einheit verkauft wird, dann – was auf einen Fehlbestand hindeutet – nutzt die “conditional probability technique” dennoch die Information, dass die Nachfrage größer oder gleich eins war.
Hier entdecken wir einen überraschenden Vorteil der probabilistischen Modellierung: Sie bietet einen eleganten Weg, mit Zensur umzugehen – ein Effekt, der in zahlreichen supply chain Situationen auftritt. Durch bedingte Wahrscheinlichkeit können wir ganze Klassen systematischer Verzerrungen eliminieren.
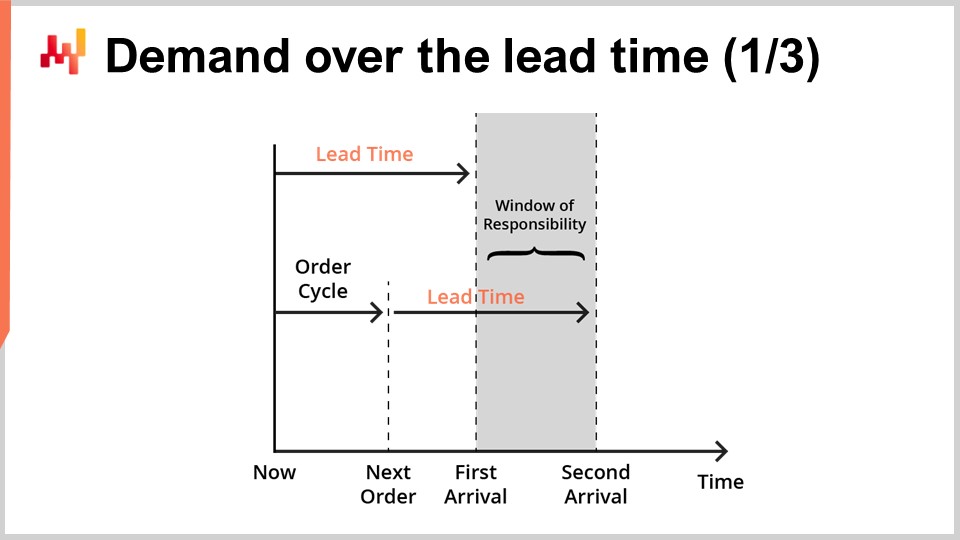
Lieferzeitprognosen sind typischerweise dazu gedacht, mit Nachfrageprognosen kombiniert zu werden. Tatsächlich betrachten wir nun eine einfache Situation der Lagerauffüllung, wie auf dem Bildschirm dargestellt.
Wir bedienen ein einzelnes Produkt, und der Lagerbestand kann durch eine Nachbestellung bei einem einzelnen Lieferanten aufgefüllt werden. Wir suchen eine Prognose, die unsere Entscheidung unterstützt, ob wir beim Lieferanten nachbestellen sollen oder nicht. Wir können jetzt nachbestellen, und wenn wir dies tun, werden die Waren zum als “erste Ankunft” markierten Zeitpunkt eintreffen. Später werden wir eine weitere Möglichkeit zum Nachbestellen haben. Diese spätere Möglichkeit tritt zu einem Zeitpunkt ein, der als “nächste Bestellung” bezeichnet wird, und in diesem Fall werden die Waren zum als “zweite Ankunft” bezeichneten Zeitpunkt eintreffen. Der als “Verantwortungsfenster” bezeichnete Zeitraum ist der Zeitraum, der für unsere Nachbestellentscheidung von Bedeutung ist.
Tatsächlich wird alles, was wir nachbestellen, nicht vor der ersten Lieferzeit eintreffen. Somit haben wir bereits die Kontrolle über die Bedienung der Nachfrage für alles, was vor der ersten Ankunft geschieht, verloren. Da wir später eine weitere Möglichkeit zum Nachbestellen erhalten, liegt die Bedienung der Nachfrage nach der zweiten Ankunft nicht mehr in unserer Verantwortung; sie ist die Verantwortung der nächsten Nachbestellung. Daher sollte eine Nachbestellung, die darauf abzielt, die Nachfrage über die zweite Ankunft hinaus zu bedienen, bis zur nächsten Nachbestellmöglichkeit verschoben werden.
Um die Nachbestellentscheidung zu unterstützen, gibt es zwei Faktoren, die prognostiziert werden sollten. Erstens sollten wir den erwarteten Lagerbestand zum Zeitpunkt der ersten Ankunft vorhersagen. Tatsächlich, wenn zum Zeitpunkt der ersten Ankunft noch ausreichend Lagerbestand vorhanden ist, gibt es keinen Grund, jetzt nachzubestellen. Zweitens sollten wir die erwartete Nachfrage während der Dauer des Verantwortungsfensters prognostizieren. In einem realen Setup müssten wir auch die Nachfrage über das Verantwortungsfenster hinaus vorhersagen, um die Lagerhaltungskosten der Waren, die wir jetzt bestellen, zu bewerten, da möglicherweise Restbestände in spätere Perioden übergehen. Allerdings werden wir der Kürze und dem Timing halber heute den erwarteten Lagerbestand und die erwartete Nachfrage insofern betrachten, als dass es das Verantwortungsfenster betrifft.
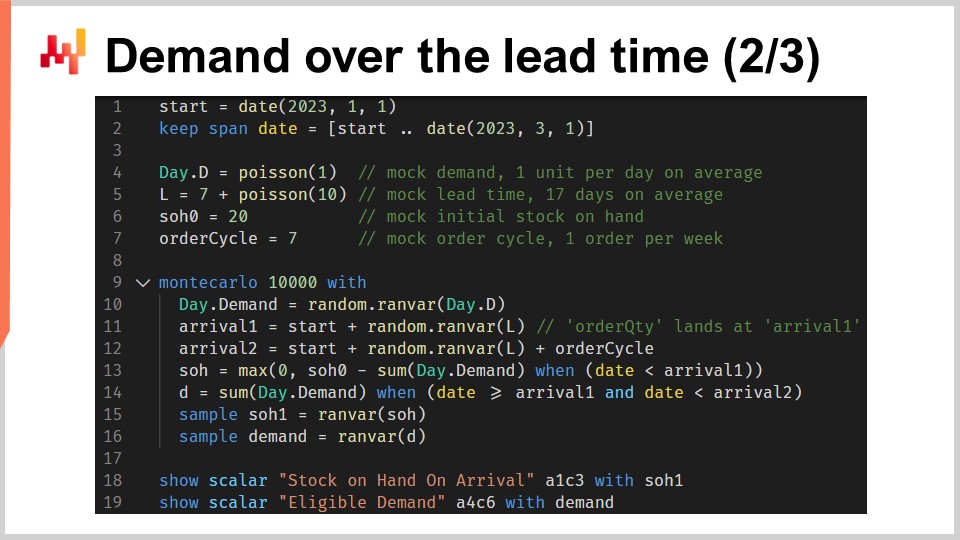
Dieses Skript implementiert die Faktoren bzw. Prognosen des Verantwortungsfensters, die wir gerade besprochen haben. Es nimmt als Eingabe eine probabilistische Lieferzeitprognose und eine probabilistische Nachfrageprognose. Es gibt zwei Wahrscheinlichkeitsverteilungen zurück, nämlich den Lagerbestand bei Ankunft und die berechtigte Nachfrage, wie sie durch das Verantwortungsfenster definiert ist.
In den Zeilen eins und zwei richten wir die Zeitpläne ein, die am 1. Januar beginnen und am 1. März enden. In einem Vorhersageszenario wäre dieser Zeitplan nicht fest codiert. In Zeile vier wird ein vereinfachtes probabilistisches Nachfragemodell eingeführt: eine Poisson-Verteilung, die Tag für Tag über die gesamte Dauer dieses Zeitplans wiederholt wird. Die Nachfrage beträgt im Durchschnitt eine Einheit pro Tag. Zur Klarheit verwende ich hier ein vereinfachtes Modell für die Nachfrage. In einem realen Setup würden wir beispielsweise ein ESSM (Ensemble State Space Model) verwenden. Zustandsraummodelle sind probabilistische Modelle, und sie wurden bereits in der allerersten Vorlesung dieses Kapitels eingeführt.
In Zeile fünf wird ein weiteres vereinfachtes probabilistisches Modell eingeführt. Dieses zweite Modell ist für Lieferzeiten gedacht. Es handelt sich um eine Poisson-Verteilung, die um sieben Tage nach rechts verschoben ist. Die Verschiebung erfolgt durch eine Faltung. In Zeile sechs definieren wir den anfänglichen Lagerbestand. In Zeile sieben legen wir den Bestellzyklus fest. Dieser Wert wird in Tagen angegeben und charakterisiert, wann die nächste Nachbestellung erfolgen wird.
Von Zeile 9 bis 16 haben wir einen Monte-Carlo-Block, der die Kernlogik des Skripts darstellt. Bereits früher in dieser Vorlesung haben wir einen weiteren Monte-Carlo-Block zur Unterstützung unserer Cross-Validierungslogik eingeführt. Hier verwenden wir diesen Konstrukt erneut, jedoch für einen anderen Zweck. Wir möchten zwei Zufallsvariablen berechnen, die jeweils den Lagerbestand bei Ankunft und die berechtigte Nachfrage widerspiegeln. Allerdings ist die Algebra der Zufallsvariablen nicht ausdrucksstark genug, um diese Berechnung durchzuführen. Daher verwenden wir stattdessen einen Monte-Carlo-Block.
In der dritten Vorlesung dieses Kapitels habe ich darauf hingewiesen, dass es eine Dualität zwischen probabilistischer Prognose und Simulationen gibt. Der Monte-Carlo-Block veranschaulicht diese Dualität. Wir beginnen mit einer probabilistischen Prognose, wandeln sie in eine Simulation um und konvertieren schließlich die Ergebnisse der Simulation zurück in eine weitere probabilistische Prognose.
Sehen wir uns die Details an. In Zeile 10 erzeugen wir eine Trajektorie für die Nachfrage. In Zeile 11 generieren wir das Ankunftsdatum für die erste Bestellung, unter der Annahme, dass wir heute bestellen. In Zeile 12 erzeugen wir das Ankunftsdatum für die zweite Bestellung, unter der Annahme, dass wir in einem Bestellzyklus von jetzt an bestellen. In Zeile 13 berechnen wir, was als Lagerbestand bei der ersten Ankunft übrig bleibt. Es ist der anfängliche Lagerbestand abzüglich der im Verlauf der ersten Lieferzeit beobachteten Nachfrage. Das „max zero“ besagt, dass der Lagerbestand nicht ins Negative fallen kann. Anders ausgedrückt, wir gehen davon aus, dass wir keine Rückstände übernehmen. Diese Annahme, keine Rückstände zuzulassen, kann modifiziert werden. Der Fall von Rückständen bleibt als Übung für das Publikum. Als Hinweis: Differenzierbares Programmieren kann verwendet werden, um den Prozentsatz der unerfüllten Nachfrage zu bewerten, der erfolgreich in Rückstände umgewandelt wird, abhängig davon, wie viele Tage es bis zur erneuten Verfügbarkeit des Lagerbestands dauert.
Zurück zum Skript: In Zeile 14 berechnen wir die berechtigte Nachfrage, also die Nachfrage, die während des Verantwortungsfensters auftritt. In den Zeilen 15 und 16 sammeln wir zwei Zufallsvariablen von Interesse mithilfe des Schlüsselworts “sample”. Im Gegensatz zum ersten Envision-Skript dieser Vorlesung, das sich mit Cross-Validation befasste, wollen wir hier Wahrscheinlichkeitsverteilungen aus diesem Monte-Carlo-Block sammeln, nicht nur Durchschnittswerte. In beiden Zeilen, 15 und 16, erscheint die Zufallsvariable auf der rechten Seite der Zuweisung als Aggregator. In Zeile 15 erhalten wir eine Zufallsvariable für den Lagerbestand bei Ankunft. In Zeile 16 erhalten wir eine weitere Zufallsvariable für die Nachfrage, die innerhalb des Verantwortungsfensters auftritt.
In den Zeilen 18 und 19 werden diese beiden Zufallsvariablen angezeigt. Halten wir nun einen Moment inne und betrachten das gesamte Skript noch einmal. Die Zeilen eins bis sieben dienen lediglich der Einrichtung der Testdaten. Die Zeilen 18 und 19 zeigen nur die Ergebnisse an. Die eigentliche Logik findet in den acht Zeilen zwischen Zeile 9 und 16 statt. Tatsächlich befindet sich die gesamte eigentliche Logik gewissermaßen in den Zeilen 13 und 14.
Mit nur wenigen Zeilen Code, weniger als 10, ganz gleich wie man es zählt, kombinieren wir eine probabilistische Lieferzeitprognose mit einer probabilistischen Nachfrageprognose, um eine Art hybrider probabilistischer Prognose von tatsächlicher supply chain Bedeutung zu erstellen. Beachten wir, dass hier nichts wirklich von den Details entweder der Lieferzeitprognose oder der Nachfrageprognose abhängt. Es wurden einfache Modelle verwendet, aber auch anspruchsvollere Modelle hätten genutzt werden können. Das hätte nichts geändert. Die einzige Voraussetzung ist, zwei probabilistische Modelle zu haben, sodass es möglich wird, diese Trajektorien zu generieren.
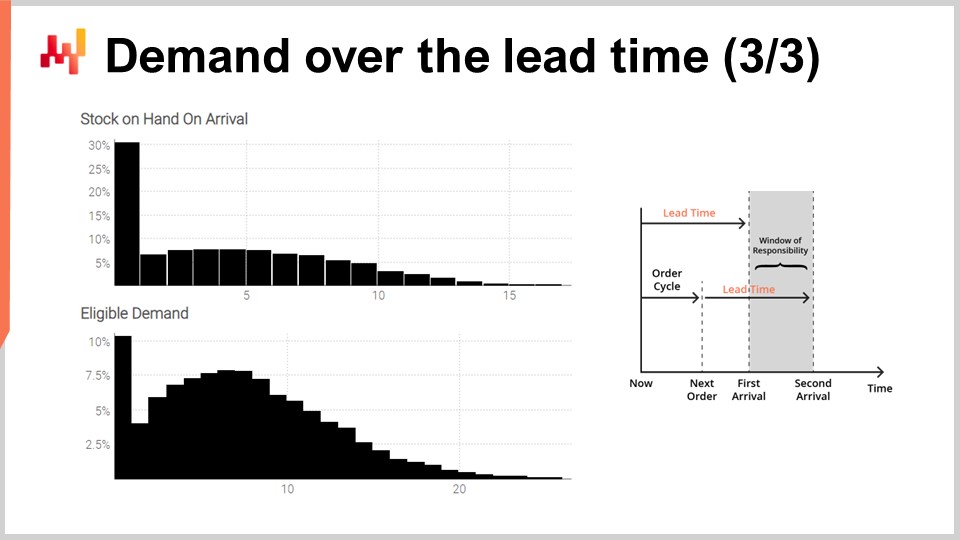
Schließlich werden auf dem Bildschirm die Histogramme angezeigt, wie sie vom Skript erzeugt wurden. Das obere Histogramm repräsentiert den Lagerbestand bei Ankunft. Es besteht ungefähr eine 30%-ige Chance, dass ein anfänglicher Lagerbestand von null vorliegt. Anders ausgedrückt, es besteht eine 30%-Chance, dass ein Lagerengpass spätestens am letzten Tag vor dem ersten Ankunftsdatum aufgetreten ist. Der durchschnittliche Lagerwert könnte etwa fünf Einheiten betragen. Würden wir diese Situation jedoch allein anhand des Durchschnitts beurteilen, würden wir die Situation ernsthaft falsch interpretieren. Eine probabilistische Prognose ist unerlässlich, um die anfängliche Lagersituation richtig abzubilden.
Das untere Histogramm repräsentiert die Nachfrage, die mit dem Verantwortungsfenster verbunden ist. Es besteht ungefähr eine 10%-Chance, dass keine Nachfrage auftritt. Dieses Ergebnis mag ebenfalls überraschend erscheinen. Tatsächlich sind wir mit einer stationären Poisson-Nachfrage von durchschnittlich einer Einheit pro Tag in diese Übung gestartet. Wir haben sieben Tage zwischen Bestellungen. Wäre die Lieferzeit nicht variabel, gäbe es weniger als eine 0,1%-Chance, dass über sieben Tage keine Nachfrage auftritt. Das Skript zeigt jedoch, dass dieses Ereignis viel häufiger vorkommt. Der Grund ist, dass ein kleines Verantwortungsfenster auftreten kann, wenn die erste Lieferzeit länger als gewöhnlich und die zweite Lieferzeit kürzer als gewöhnlich ist.
Keine Nachfrage im Verantwortungsfenster zu verzeichnen, bedeutet, dass der Bestand bei Ankunft zu einem bestimmten Zeitpunkt vermutlich sehr hoch werden wird. Je nach Situation kann dies kritisch sein oder auch nicht, beispielsweise wenn es eine Begrenzung der Lagerkapazität gibt oder wenn der Bestand verderblich ist. Noch einmal: Die durchschnittliche Nachfrage, vermutlich etwa acht, gibt keinen verlässlichen Einblick in die tatsächliche Nachfrage. Denken Sie daran, dass wir diese stark asymmetrische Verteilung aus einer anfänglichen stationären Nachfrage von durchschnittlich einer Einheit pro Tag erhalten haben. Dies ist der Effekt der variierenden Lieferzeit in Aktion.
Dieses einfache Setup zeigt die Bedeutung von Lieferzeiten in Situationen der Lagerauffüllung. Aus supply chain Sicht ist es bestenfalls eine praktische Abstraktion, Lieferzeitprognosen von Nachfrageprognosen zu isolieren. Die tägliche Nachfrage ist nicht das, woran wir wirklich interessiert sind. Von echtem Interesse ist die Zusammensetzung der Nachfrage mit der Lieferzeit. Wären weitere stochastische Faktoren vorhanden, wie Rückstände oder Retouren, so wären diese Faktoren ebenfalls Teil des Modells gewesen.

Das vorliegende Kapitel in dieser Vorlesungsreihe trägt den Titel “Predictive Modeling” anstelle von “Demand Forecasting”, wie es typischerweise in herkömmlichen supply chain Lehrbüchern der Fall wäre. Der Grund für diesen Kapiteltitel sollte im Laufe der Vorlesung zunehmend offensichtlich geworden sein. Tatsächlich wollen wir aus supply chain Sicht die Entwicklung des supply chain Systems prognostizieren. Die Nachfrage ist sicherlich ein wichtiger Faktor, aber nicht der einzige. Andere variable Faktoren wie die Lieferzeit müssen prognostiziert werden. Noch wichtiger ist, dass letztlich all diese Faktoren zusammen prognostiziert werden müssen.
In der Tat müssen wir diese prädiktiven Komponenten zusammenführen, um einen entscheidungsbasierte-Optimierung Prozess zu unterstützen. Daher geht es nicht darum, irgendein Endspiel-Nachfrageprognosemodell zu suchen. Diese Aufgabe ist letztlich größtenteils ein Narrenspiel, da die zusätzliche Genauigkeit auf Weisen erreicht wird, die dem besten Interesse des Unternehmens entgegenstehen. Mehr Komplexität bedeutet mehr Undurchsichtigkeit, mehr Fehler, mehr Rechenressourcen. Als Faustregel gilt: Je anspruchsvoller das Modell ist, desto schwerer wird es, dieses Modell erfolgreich operativ mit einem anderen Modell zu kombinieren. Wichtig ist, eine Sammlung prädiktiver Techniken zusammenzustellen, die beliebig kombinierbar sind. Darum geht es bei der Modularität aus der Perspektive des Predictive Modeling. In dieser Vorlesung wurden ein halbes Dutzend Techniken vorgestellt. Diese Techniken sind nützlich, da sie kritische realweltliche Aspekte wie unvollständige Beobachtungen adressieren. Sie sind auch einfach; keines der heute präsentierten Codebeispiele überschritt 10 Zeilen eigentliche Logik. Am wichtigsten ist, dass diese Techniken modular sind, wie Lego-Steine. Sie funktionieren gut zusammen und können fast endlos wieder kombiniert werden.
Das Endziel des Predictive Modeling für supply chain, so wie es verstanden werden sollte, ist die Identifizierung solcher Techniken. Jede Technik sollte für sich genommen eine Gelegenheit bieten, ein bereits bestehendes prädiktives Modell zu überdenken, um dieses zu vereinfachen oder zu verbessern.

Zusammenfassend lässt sich sagen, dass, obwohl die Lieferzeit von der akademischen Gemeinschaft weitgehend ignoriert wird, die Lieferzeit prognostiziert werden kann und sollte. Durch die Betrachtung einer kurzen Reihe realer Lieferzeitverteilungen haben wir zwei Herausforderungen identifiziert: Erstens, Lieferzeiten variieren; zweitens, Lieferzeiten sind spärlich. Daher haben wir Modellierungstechniken eingeführt, die geeignet sind, mit Lieferzeitbeobachtungen umzugehen, die sowohl spärlich als auch unregelmäßig sind.
Diese Lieferzeitmodelle sind probabilistisch und stellen weitgehend die Fortführung der Modelle dar, die in diesem Kapitel schrittweise eingeführt wurden. Wir haben auch gesehen, dass die Wahrscheinlichkeitsbetrachtung eine elegante Lösung für das Problem der unvollständigen Beobachtung bietet, ein nahezu allgegenwärtiger Aspekt in supply chain. Dieses Problem tritt auf, wenn es zu Lagerengpässen kommt und wenn Bestellungen offen sind. Schließlich haben wir gesehen, wie man eine probabilistische Lieferzeitprognose mit einer probabilistischen Nachfrageprognose kombiniert, um das prädiktive Modell zu erstellen, das wir zur Unterstützung eines späteren Entscheidungsprozesses benötigen.

Die nächste Vorlesung findet am 8. März statt. Sie wird an einem Mittwoch zur gleichen Tageszeit um 15 Uhr Pariser Zeit stattfinden. Die heutige Vorlesung war technisch, aber die nächste wird weitgehend nicht-technisch sein, und ich werde den Fall des supply chain scientist besprechen. Tatsächlich gehen herkömmliche supply chain Lehrbücher supply chain so an, als würden Prognosemodelle und Optimierungsmodelle aus dem Nichts entstehen und operieren, wobei sie ihre “wetware” Komponente – also die verantwortlichen Personen – völlig ignorieren. Daher werden wir einen genaueren Blick auf die Rollen und Verantwortlichkeiten des supply chain scientist werfen, einer Person, von der erwartet wird, dass sie die Quantitative Supply Chain Initiative vorantreibt.
Nun werde ich mit den Fragen fortfahren.
Frage: Was ist, wenn jemand seinen Lagerbestand für weitere Innovationen oder aus anderen Gründen als just in time oder andere Konzepte behalten möchte?
Dies ist in der Tat eine sehr wichtige Frage. Das Konzept wird typischerweise durch die wirtschaftliche Modellierung der supply chain behandelt, die wir in dieser Vorlesungsreihe technisch als die “economic drivers” bezeichnen. Was Sie fragen, ist, ob es besser ist, heute einen Kunden nicht zu bedienen, weil es zu einem späteren Zeitpunkt die Möglichkeit geben wird, dieselbe Einheit an eine andere, aus welchen Gründen auch immer wichtigere Person zu liefern. Im Wesentlichen sagen Sie, dass durch die Bedienung eines anderen Kunden später, vielleicht eines VIP-Kunden, mehr Wert geschaffen werden kann als durch die Bedienung eines Kunden heute.
Das könnte der Fall sein, und es kommt tatsächlich vor. Nehmen wir als Beispiel die Luftfahrtindustrie: Angenommen, Sie sind ein MRO (Wartung, Reparatur und Überholung) Anbieter. Sie haben Ihre üblichen VIP-Kunden – die Fluggesellschaften, denen Sie routinemäßig mit langfristigen Verträgen dienen, und diese sind sehr wichtig. Wenn dies geschieht, möchten Sie sicherstellen, dass Sie diesen Kunden immer dienen können. Aber was, wenn eine andere Fluggesellschaft anruft und nach einer Einheit fragt? In diesem Fall könnten Sie dieser Person zwar helfen, aber Sie haben keinen langfristigen Vertrag mit ihr. Was Sie also tun, ist Ihren Preis so anzupassen, dass er sehr hoch ist, um sicherzustellen, dass Sie genügend Wert erhalten, um den potenziellen Lagerausfall, dem Sie später möglicherweise gegenüberstehen, auszugleichen. Zusammenfassend bin ich der Meinung, dass es bei dieser ersten Frage nicht wirklich um Prognosen geht, sondern vielmehr um das korrekte Modellieren der wirtschaftlichen Treiber. Wenn Sie den Bestand erhalten wollen, möchten Sie ein Modell – ein Optimierungsmodell – erstellen, bei dem die rationale Reaktion nicht darin besteht, dem Kunden, der nach einer Einheit fragt, zu dienen, während Sie noch Reserven haben.
Übrigens ist eine weitere typische Situation, wenn Sie Kits verkaufen. Ein Kit ist eine Zusammenstellung vieler Teile, die zusammen verkauft werden, und es bleibt nur ein Teil übrig, das nur einen kleinen Bruchteil des Gesamtwerts des Kits ausmacht. Das Problem ist, dass wenn Sie diese letzte Einheit verkaufen, Sie Ihr Kit nicht mehr zusammenstellen und zu seinem vollen Preis verkaufen können. Somit könnten Sie sich in einer Situation befinden, in der Sie die Einheit lieber vorrätig halten, um das Kit zu einem späteren Zeitpunkt – möglicherweise mit ein wenig Unsicherheit – verkaufen zu können. Aber auch hier hängt alles von den wirtschaftlichen Treibern ab, und so würde ich diese Situation angehen.
Frage: In den letzten Jahren traten die meisten Verzögerungen in der supply chain aufgrund von Krieg oder Pandemie auf, was sehr schwer vorherzusagen ist, da wir bisher keine derartigen Situationen hatten. Wie beurteilen Sie das?
Meiner Meinung nach haben sich die Durchlaufzeiten schon immer verändert. Ich bin seit 2008 in der supply chain-Welt tätig, und meine Eltern arbeiteten in der supply chain schon 30 Jahre vor mir. Soweit wir uns erinnern können, waren die Durchlaufzeiten unbeständig und wechselhaft. Es passiert immer etwas, sei es ein Protest, ein Krieg oder eine Änderung der Zölle. Ja, in den letzten Jahren war es äußerst unbeständig, aber die Durchlaufzeiten variierten bereits sehr stark.
Ich stimme zu, dass niemand so tun kann, als könnte er den nächsten Krieg oder die nächste Pandemie vorhersagen. Wenn es möglich wäre, diese Ereignisse mathematisch zu prognostizieren, würden die Menschen keine Kriege führen oder in die supply chain investieren; sie würden stattdessen einfach mit dem Aktienmarkt spielen und reich werden, indem sie Marktbewegungen voraussehen.
Das Fazit ist, dass Sie für das Unerwartete planen müssen. Wenn Sie der Zukunft nicht zuversichtlich entgegensehen, können Sie die Variationen in Ihren Prognosen tatsächlich aufblähen. Es ist das Gegenteil davon, zu versuchen, Ihre Prognose genauer zu machen – Sie bewahren Ihre durchschnittlichen Erwartungen, blähen aber nur das Ausreißerende auf, sodass die Entscheidungen, die Sie auf Basis dieser probabilistischen Prognosen treffen, wider resilient gegen Schwankungen sind. Sie haben Ihre erwarteten Schwankungen so gestaltet, dass sie größer sind als das, was Sie momentan beobachten. Letztlich kommt die Vorstellung, dass Vorhersagen leicht oder schwer möglich seien, aus einer punktuellen Prognoseperspektive, in der man so tun würde, als wäre es möglich, die Zukunft präzise vorherzusehen. Das ist nicht der Fall – eine präzise Vorahnung der Zukunft gibt es nicht. Das Einzige, was Sie tun können, ist, mit Wahrscheinlichkeitsverteilungen mit großer Streuung zu arbeiten, die Ihre Unwissenheit über die Zukunft manifestieren und quantifizieren.
Anstatt Entscheidungen, die in hohem Maße von der genauen Ausführung des exakten Plans abhängen, fein abzustimmen, berücksichtigen und planen Sie für ein interessantes Maß an Variation, wodurch Ihre Entscheidungen robuster gegen diese Schwankungen werden. Dies gilt jedoch nur für die Art von Variation, die Ihre supply chain nicht auf allzu brutale Weise beeinträchtigt. Zum Beispiel können Sie mit längeren Lieferzeiten der Lieferanten umgehen, aber wenn Ihr warehouse bombardiert wurde, wird keine Prognose Sie in dieser Situation retten.
Frage: Können wir diese Histogramme erstellen und den CRPS in Microsoft Excel berechnen, zum Beispiel durch die Verwendung von Excel-Add-ins wie itsastat oder solchen, die viele Verteilungen enthalten?
Ja, das können Sie. Einer von uns bei Lokad hat tatsächlich eine Excel-Tabelle erstellt, die ein probabilistisches Modell für eine Situation der Bestandsauffüllung darstellt. Der springende Punkt des Problems ist, dass Excel keinen eigenen Datentyp für Histogramme hat, sodass Ihnen in Excel nur Zahlen zur Verfügung stehen – eine Zelle, eine Zahl. Es wäre elegant und einfach, einen Wert zu haben, der ein Histogramm darstellt, in dem ein vollständiges Histogramm in einer Zelle verpackt ist. Soweit ich weiß, ist das in Excel jedoch nicht möglich. Wenn Sie jedoch bereit sind, etwa 100 Zeilen zu verwenden, um das Histogramm darzustellen – auch wenn es nicht so kompakt und praktisch ist – können Sie in Excel eine Verteilung implementieren und probabilistisches Modellieren durchführen. Den Link zum Beispiel werden wir im Kommentarbereich posten.
Bedenken Sie, dass es ein relativ mühsames Unterfangen ist, da Excel für diese Aufgabe nicht ideal geeignet ist. Excel ist eine Programmiersprache, und Sie können damit alles machen, sodass Sie nicht einmal ein Add-in benötigen, um dies zu erreichen. Es wird jedoch etwas umständlich sein, also erwarten Sie nichts allzu Ordentliches.
Frage: Die Durchlaufzeit kann in Komponenten wie Bestellzeit, Produktionszeit, Transportzeit usw. unterteilt werden. Wenn man eine detailliertere Kontrolle über die Durchlaufzeiten wünscht, wie würde sich dieser Ansatz ändern?
Zunächst müssen wir überlegen, was es bedeutet, mehr Kontrolle über die Durchlaufzeit zu haben. Möchten Sie die durchschnittliche Durchlaufzeit reduzieren oder die Variabilität der Durchlaufzeit verringern? Interessanterweise habe ich viele Unternehmen gesehen, die es geschafft haben, die durchschnittliche Durchlaufzeit zu verkürzen, allerdings auf Kosten einer zusätzlichen Variation der Durchlaufzeit. Im Durchschnitt ist die Durchlaufzeit kürzer, aber gelegentlich ist sie deutlich länger.
In dieser Vorlesung führen wir eine Modellierungsübung durch. Für sich genommen gibt es keine Handlung; es geht lediglich um Beobachten, Analysieren und Vorhersagen. Wenn wir die Durchlaufzeit jedoch zerlegen und die zugrunde liegende Verteilung analysieren können, nutzen wir probabilistisches Modellieren, um einzuschätzen, welche Komponenten am stärksten variieren und welche den signifikantesten negativen Einfluss auf unsere supply chain haben. Mit diesen Informationen können wir „Was-wäre-wenn“-Szenarien durchspielen. Nehmen Sie beispielsweise einen Teil Ihrer Durchlaufzeit und fragen Sie: „Was wäre, wenn das Ausreißerende dieser Durchlaufzeit ein wenig kürzer wäre, oder wenn der Durchschnitt ein wenig kürzer wäre?“ Sie können dann alles neu zusammensetzen, Ihr prädiktives Modell für Ihre gesamte supply chain erneut ausführen und den Einfluss bewerten.
Dieser Ansatz ermöglicht es Ihnen, stückweise über bestimmte Phänomene zu argumentieren, einschließlich unregelmäßiger. Es wäre nicht so sehr ein geänderter Ansatz, sondern eine Fortsetzung dessen, was wir bereits getan haben, und führt in Kapitel 6, das sich mit der Optimierung tatsächlicher Entscheidungen auf Basis dieser probabilistischen Modelle befasst.
Frage: Ich glaube, das bietet die Möglichkeit, unsere Durchlaufzeiten in SAP neu zu berechnen, um einen realistischeren Zeitrahmen zu schaffen und unser System Pull-in und Pull-out zu minimieren. Ist das möglich?
Haftungsausschluss: SAP ist ein Wettbewerber von Lokad im Bereich der supply chain-Optimierung. Meine erste Antwort lautet nein, SAP kann das nicht. Tatsache ist, dass SAP vier unterschiedliche Lösungen für die supply chain-Optimierung hat, und es hängt davon ab, über welchen Technologie-Stack Sie sprechen. Allerdings haben all diese Stacks gemeinsam, dass sie auf punktuellen Prognosen basieren. Alles in SAP wurde mit der Prämisse entwickelt, dass die Prognosen genau sein werden.
Ja, SAP bietet einige Parameter zum Einstellen, wie beispielsweise die Normalverteilung, die ich zu Beginn dieser Vorlesung erwähnt habe. Allerdings waren die von uns beobachteten Durchlaufzeitverteilungen nicht normalverteilt. Meines Wissens nutzen die gängigen SAP-Konfigurationen für die supply chain-Optimierung eine Normalverteilung für Durchlaufzeiten. Das Problem ist, dass die Software im Kern eine weit verbreitete falsche mathematische Annahme trifft. Man kann sich nicht von einer so gravierend falschen Annahme, die direkt in den Kern Ihrer Softwarearchitektur geht, durch das Abstimmen eines Parameters erholen. Vielleicht können Sie durch verrücktes Reverse Engineering einen Parameter finden, der letztlich die richtige Entscheidung hervorbringt. Theoretisch ist das möglich, aber in der Praxis stellt es so viele Probleme dar, dass die Frage lautet, warum sollten Sie das überhaupt tun wollen?
Um eine probabilistische Perspektive einzunehmen, müssen Sie vollständig darauf setzen, dass Ihre Prognosen probabilistisch sind und Ihre Optimierungsmodelle ebenfalls probabilistische Modelle nutzen. Das Problem hierbei ist, dass selbst wenn wir das probabilistische Modellieren für etwas bessere Durchlaufzeiten abstimmen könnten, der restliche SAP-Stack wieder auf punktuelle Prognosen zurückfallen wird. Egal, was passiert, wir werden diese Verteilungen zu Punkten zusammenführen. Die Vorstellung, dass man dies durch einen Durchschnitt approximieren könnte, ist beunruhigend und schlichtweg falsch. Technisch gesehen könnten Sie die Durchlaufzeiten anpassen, aber danach würden Sie auf so viele Probleme stoßen, dass es den Aufwand möglicherweise nicht wert ist.
Frage: Es gibt Situationen, in denen Sie dieselben Teile von verschiedenen Lieferanten bestellen. Dies ist eine wichtige Information für die Verarbeitung in der Durchlaufzeit-Prognose. Machen Sie die Durchlaufzeitprognose nach Artikel oder gibt es Situationen, in denen Sie von der Gruppierung von Artikeln in Familien profitieren?
Das ist eine bemerkenswert interessante Frage. Wir haben zwei Lieferanten für denselben Artikel. Die Frage wird sein, wie viel Ähnlichkeit es zwischen den Artikeln und den Lieferanten gibt. Zunächst müssen wir die Situation betrachten. Wenn ein Lieferant zufällig in der Nähe ist und der andere auf der anderen Seite der Welt liegt, müssen Sie diese Aspekte wirklich getrennt betrachten. Aber nehmen wir einmal an, es handelt sich um eine interessante Situation, in der die beiden Lieferanten ziemlich ähnlich sind und es derselbe Artikel ist. Sollten Sie diese Beobachtungen zusammenfassen oder nicht?
Das Interessante daran ist, dass Sie durch differenzierbares Programmieren ein Modell zusammenstellen können, das dem Lieferanten und dem Artikel jeweils ein Gewicht zuweist und die Lernmagie ihre Wirkung entfalten lässt. Es wird ermitteln, ob wir dem Artikelanteil der Durchlaufzeit oder dem Lieferantenanteil mehr Gewicht verleihen sollten. Es könnte sein, dass zwei Lieferanten, die im Grunde ähnliche Produkte bedienen, eine gewisse Voreingenommenheit haben, wobei ein Lieferant im Durchschnitt etwas schneller ist als der andere. Aber es gibt Artikel, die definitiv mehr Zeit erfordern, und wenn Sie diese selektiv betrachten, ist es nicht eindeutig, dass ein Lieferant schneller ist als der andere, weil es wirklich darauf ankommt, welche Artikel Sie betrachten. Wahrscheinlich haben Sie sehr wenige Daten, wenn Sie alles nach jedem Lieferanten und jedem Artikel aufgliedern. Daher wäre das Interessante – und was ich hier empfehlen würde – die Anwendung des differenzierbaren Programmierens. Wir könnten in einer späteren Vorlesung versuchen, diese Situation noch einmal zu beleuchten, eine Situation, in der Sie einige Parameter auf Artikelebene und einige Parameter auf Lieferantenebene einsetzen. So erhalten Sie eine Gesamtzahl von Parametern, die nicht der Anzahl der Artikel multipliziert mit der Anzahl der Lieferanten entspricht; vielmehr wäre es die Anzahl der Artikel plus die Anzahl der Lieferanten oder vielleicht plus die Anzahl der Lieferanten mal Kategorien oder etwas Ähnliches. Sie lassen Ihre Parameteranzahl nicht explodieren; Sie fügen lediglich einen Parameter hinzu, ein Element, das eine Affinität zum Lieferanten besitzt und Ihnen eine Art dynamische Mischung ermöglicht, die von Ihren historischen Daten gesteuert wird.
Frage: Ich glaube, dass die bestellte Menge und welche Produkte zusammen bestellt werden, letztendlich auch die Durchlaufzeit beeinflussen könnten. Könnten Sie die Komplexität erläutern, alle Variablen in diese Art von Problem einzubeziehen?
Im letzten Beispiel hatten wir zwei Arten von Dauer: den Bestellzyklus und die eigentliche Durchlaufzeit. Der Bestellzyklus ist interessant, weil er nur insoweit unsicher ist, als wir die Entscheidung noch nicht getroffen haben. Im Grunde genommen ist es etwas, das Sie nahezu jederzeit entscheiden können, sodass der Bestellzyklus vollständig intern und selbst bestimmt ist. Das ist nicht das einzige Element in der supply chain; auch Preise verhalten sich ähnlich. Sie haben eine Nachfrage, Sie beobachten die Nachfrage, aber Sie können tatsächlich den Preis wählen, den Sie möchten. Einige Preise sind offensichtlich unklug, aber es ist dasselbe – er liegt in Ihrer eigenen Hand.
Der Bestellzyklus liegt in Ihrer eigenen Hand. Was Sie nun sagen, ist, dass es eine Unsicherheit darüber gibt, zu welchem genauen Zeitpunkt die nächste Durchlaufzeit für eine Bestellung eintritt, da Sie nicht genau wissen, wann Sie bestellen werden. In der Tat haben Sie völlig recht. Was passiert, ist, dass wenn Sie die Kapazität haben, dieses probabilistische Modell umzusetzen – wie im sechsten Kapitel dieser Vorlesungsreihe besprochen – Sie nicht sagen möchten, dass der Bestellzyklus schlichtweg sieben Tage beträgt. Stattdessen wollen Sie eine Nachbestellpolitik einführen, die die Kapitalrendite Ihres Unternehmens maximiert. Das heißt, Sie können die Zukunft so planen, dass, wenn Sie jetzt nachbestellen, Sie eine Entscheidung treffen und dann Ihre Politik Tag für Tag anwenden. Irgendwann in der Zukunft tätigen Sie eine Nachbestellung, und dann entsteht eine Art „Schlange, die ihren eigenen Schwanz frisst“, denn die beste Bestellentscheidung für heute hängt von der Entscheidung der nächsten Bestellung ab, die Sie noch nicht getroffen haben. Dieses Problem ist als Politikproblem bekannt und ein sequentielles Entscheidungsproblem. Im Hintergrund möchten Sie im Grunde genommen eine Art Richtlinie entwerfen – ein mathematisches Konstrukt, das Ihren Entscheidungsfindungsprozess steuert.
Das Problem der Politikoptimierung ist ziemlich kompliziert, und ich beabsichtige, dies im sechsten Kapitel zu behandeln. Aber das Fazit ist, dass wir – wenn wir auf Ihre Frage zurückkommen – zwei unterschiedliche Komponenten haben. Wir haben die Komponente, die unabhängig von Ihrem Handeln variiert, nämlich die Durchlaufzeit, die Ihre Lieferantendurchlaufzeit darstellt, und dann haben Sie die Bestellzeit, die wirklich intern durch Ihren Prozess gesteuert wird und als Optimierungsfrage behandelt werden sollte.
Abschließend erkennen wir, dass sich Optimierung und prädiktives Modellieren annähern. Letztendlich enden beide ziemlich damit, dass sie im Wesentlichen dasselbe sind, weil es Wechselwirkungen zwischen den Entscheidungen, die Sie treffen, und dem, was in der Zukunft geschieht, gibt.
Das war’s für heute. Vergessen Sie nicht, der 8. März, zur gleichen Tageszeit, wird ein Mittwoch sein, 15:00 Uhr. Vielen Dank und bis zum nächsten Mal.


