00:19 Introducción
04:33 Dos definiciones para “algoritmo”
08:09 Big-O
13:10 La historia hasta ahora
15:11 Ciencias auxiliares (resumen)
17:26 Algoritmos modernos
19:36 Superando la “optimalidad”
22:23 Estructuras de datos - 1/4 - Lista
25:50 Estructuras de datos - 2/4 - Árbol
27:39 Estructuras de datos - 3/4 - Grafo
29:55 Estructuras de datos - 4/4 - Tabla hash
31:30 Recetas mágicas - 1/2
37:06 Recetas mágicas - 2/2
39:17 Comprensiones de tensores - 1/3 - La notación “Einstein”
42:53 Comprensiones de tensores - 2/3 - El avance del equipo de Facebook
46:52 Comprensiones de tensores - 3/3 - Perspectiva de supply chain
52:20 Meta técnicas - 1/3 - Compresión
56:11 Meta técnicas - 2/3 - Memoización
58:44 Meta técnicas - 3/3 - inmutabilidad
01:03:46 Conclusión
01:06:41 Próxima lección y preguntas de la audiencia
Descripción
La optimización de supply chain depende de resolver numerosos problemas numéricos. Los algoritmos son recetas numéricas altamente codificadas destinadas a resolver problemas computacionales precisos. Los algoritmos superiores implican que se pueden lograr resultados superiores con menos recursos de cómputo. Al centrarse en lo específico de supply chain, el rendimiento algorítmico puede mejorar enormemente, a veces por órdenes de magnitud. Los algoritmos de supply chain también necesitan adoptar el diseño de las computadoras modernas, que han evolucionado significativamente en las últimas décadas.
Transcripción completa

Bienvenidos a esta serie de conferencias de supply chain. Soy Joannes Vermorel, y hoy presentaré “Modern Algorithms for Supply Chain.” Las capacidades superiores de cómputo son fundamentales para lograr un rendimiento de supply chain. Más accurate forecasts precisos, más optimización pormenorizada y optimizaciones más frecuentes son todas deseables para lograr un rendimiento superior de supply chain. Siempre hay un método numérico superior justo un poco más allá de los recursos de cómputo que puedas permitirte.
Los algoritmos, para simplificar, hacen que las computadoras funcionen más rápido. Los algoritmos son una rama de las matemáticas, y este es un campo de investigación muy activo. El progreso en este campo de investigación supera frecuentemente el avance del hardware de cómputo en sí. El objetivo de esta lección es comprender de qué tratan los algoritmos modernos y, más específicamente desde una perspectiva de supply chain, cómo abordar los problemas para que puedas sacar el máximo provecho de esos algoritmos modernos para tu supply chain.

En términos de algoritmos, hay un libro que es una referencia absoluta: Introduction to Algorithms, publicado por primera vez en 1990. Es un libro imprescindible. La calidad de la presentación y la redacción es simplemente excepcional. Este libro vendió más de medio millón de copias durante sus primeros 20 años y ha inspirado a toda una generación de escritores académicos. De hecho, la mayoría de los libros recientes de supply chain que tratan sobre teoría de supply chain, que se han publicado en la última década, han estado fuertemente inspirados en el estilo y la presentación de este libro.
Personalmente, leí este libro en 1997, y en realidad era una traducción al francés de la primera edición. Tuvo una influencia profunda en toda mi carrera. Después de leer este libro, nunca volví a ver el software de la misma manera. Una palabra de precaución, sin embargo, es que este libro adopta una perspectiva sobre el hardware de cómputo que era prevalente a finales de los años 80 y principios de los 90. Como hemos visto en las conferencias anteriores de esta serie, el hardware de cómputo ha progresado de manera bastante dramática durante las últimas décadas, y por lo tanto, algunas de las suposiciones hechas en este libro parecen estar relativamente desactualizadas. Por ejemplo, el libro asume que los accesos a la memoria tienen un tiempo constante, sin importar cuánta memoria se desee direccionar. Así ya no es así como funcionan las computadoras modernas.
No obstante, creo que hay ciertas situaciones en las que ser simplista es una proposición razonable si lo que se gana a cambio es un grado mucho mayor de claridad y sencillez en la exposición. Este libro hace un trabajo asombroso en este sentido. Aunque recomiendo tener en cuenta que algunas de las suposiciones clave hechas a lo largo del libro están desfasadas, sigue siendo una referencia absoluta que recomendaría a toda la audiencia.

Aclararemos el término “algoritmo” para la audiencia que quizá no esté tan familiarizada con la noción. Existe la definición clásica, en la que es una secuencia finita de instrucciones informáticas bien definidas. Es el tipo de definición que encontrarás en libros de texto o en Wikipedia. Aunque la definición clásica de un algoritmo tiene sus méritos, creo que resulta insuficiente, ya que no aclara la intención asociada a los algoritmos. No se trata de cualquier secuencia de instrucciones de interés; es una secuencia muy específica de instrucciones informáticas. Así, propongo una definición personal del término algoritmo: un algoritmo es, esencialmente, un método de software orientado al rendimiento, con gran nivel de detalle, para la resolución de problemas.
Desglosemos esta definición, ¿de acuerdo? Primero, la parte de la resolución de problemas: un algoritmo se caracteriza completamente por el problema que intenta resolver. En esta pantalla, lo que puedes ver es el pseudocódigo del algoritmo Quicksort, que es un algoritmo popular y bien conocido. Quicksort intenta resolver el problema de ordenamiento, que se plantea de la siguiente manera: tienes un arreglo que contiene entradas de datos, y deseas un algoritmo que devuelva el mismo arreglo pero con todas las entradas ordenadas en orden creciente. Los algoritmos se enfocan completamente en un problema específico y bien definido.
El segundo aspecto es cómo evaluar que se tiene un algoritmo superior. Un algoritmo superior es aquel que te permite resolver el mismo problema con menos recursos de cómputo, lo cual en la práctica significa mayor velocidad. Finalmente, está la parte de alto nivel de detalle. Cuando decimos el término “algoritmos”, conlleva la idea de abordar problemas muy elementales que son modulares y pueden componerse infinitamente para resolver problemas mucho más complicados. De eso se tratan realmente los algoritmos.
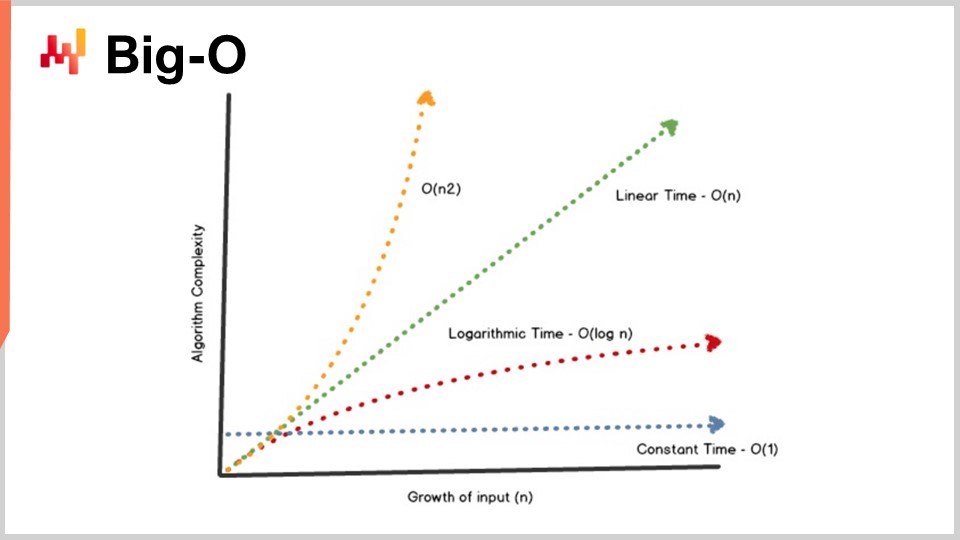
Un logro clave de la teoría de algoritmos es proporcionar una caracterización del rendimiento de los algoritmos de manera bastante abstracta. Hoy no tendré tiempo para profundizar en los detalles de esta caracterización y el marco matemático. La idea es que, para caracterizar el algoritmo, queremos observar el comportamiento asintótico. Tenemos un problema que depende de una o varias dimensiones clave que actúan como cuellos de botella y que caracterizan el problema. Por ejemplo, en el problema de ordenamiento que presenté anteriormente, la dimensión característica suele ser el número de elementos a ordenar. La pregunta es, ¿qué sucede cuando el arreglo de elementos a ordenar se vuelve muy grande? Voy a referirme a esta dimensión característica con el número “n” por convención.
Ahora, tengo esta notación, la notación Big O, que quizá hayas visto al tratar con algoritmos. Solo voy a esbozar algunos elementos para darte una intuición de lo que está sucediendo. Primero, digamos, por ejemplo, que tenemos un conjunto de datos, y queremos extraer un indicador estadístico simple, como un promedio. Si digo que tengo un algoritmo Big O de 1, significa que soy capaz de devolver una solución a este problema (calcular el promedio) en tiempo constante, sin importar si el conjunto de datos es pequeño o grande. El tiempo constante, o Big O de 1, es un requisito absoluto siempre que desees hacer algo en tiempo real en el sentido de comunicación máquina a máquina. Si no dispones de algo que sea en tiempo constante, es muy difícil, a veces imposible, lograr un rendimiento en tiempo real.
Típicamente, otro aspecto clave del rendimiento es Big O de N. Big O de N significa que la complejidad del algoritmo es estrictamente lineal al tamaño del conjunto de datos de interés. Esto es lo que obtienes cuando tienes una implementación eficiente que es capaz de resolver el problema leyendo los datos una sola vez o un número fijo de veces. La complejidad Big O de N suele ser solo compatible con la ejecución por lotes. Si deseas tener algo en línea y en tiempo real, no puedes tener algo que recorra todo el conjunto de datos, a menos que sepas que tu conjunto de datos tiene un tamaño fijo.
Más allá de la linealidad, tenemos Big O de N al cuadrado. Big O de N al cuadrado es un caso muy interesante porque es el punto álgido de la explosión en producción. Esto significa que la complejidad crece de manera cuadrática con respecto al tamaño del conjunto de datos, lo que implica que si tienes 10 veces más datos, tu rendimiento será 100 veces peor. Este es típicamente el tipo de rendimiento en el que no verás ningún problema en el prototipo, ya que se trabaja con conjuntos de datos pequeños. No observarás ningún problema en la fase de pruebas porque, de nuevo, se trata de conjuntos de datos pequeños. Tan pronto como pasas a producción, tienes un software completamente lento. Muy frecuentemente, en el mundo del enterprise software, especialmente en el mundo del software empresarial de supply chain, la mayoría de los problemas de rendimiento abismal que se pueden observar en el campo son causados por algoritmos cuadráticos que no habían sido identificados. Como resultado, se observa el comportamiento cuadrático que es realmente muy lento. Este problema no fue identificado a tiempo porque las computadoras modernas son bastante rápidas, y N al cuadrado no es tan malo siempre que N sea bastante pequeño. Sin embargo, tan pronto como se trata de un conjunto de datos a escala de producción grande, duele mucho.
Esta conferencia es, en realidad, la segunda conferencia de mi cuarto capítulo en esta serie de conferencias de supply chain. En el primer capítulo, el prólogo, presenté mis puntos de vista sobre supply chain tanto como campo de estudio como de práctica. Lo que hemos visto es que supply chain es una gran colección de problemas complejos, en contraposición a problemas sencillos. Los problemas complejos no pueden abordarse mediante metodologías ingenuas porque se encuentran comportamientos adversarios por doquier, y por lo tanto es necesario prestar mucha atención a la metodología en sí. La mayoría de los métodos ingenuos fracasan de manera bastante espectacular. Eso es exactamente lo que he hecho en el segundo capítulo, que está completamente dedicado a metodologías adecuadas para estudiar supply chain y mejorar la práctica de la gestión de supply chain. El tercer capítulo, que aún no está completo, es esencialmente un acercamiento a lo que llamo “supply chain personnel,” una metodología muy específica en la que nos centramos en los problemas mismos en lugar de en las soluciones que podemos idear para abordar el problema. En el futuro, alternaré entre el capítulo número tres y el presente capítulo, que trata sobre las ciencias auxiliares de supply chain.
Durante la última conferencia, vimos que podemos obtener más capacidades de cómputo para nuestro supply chain a través de un hardware de cómputo mejor y más moderno. Hoy, abordamos el problema desde otro ángulo: buscamos más capacidades de cómputo porque contamos con un mejor software. De eso tratan los algoritmos.

Un breve resumen: Las ciencias auxiliares son, esencialmente, una perspectiva sobre el propio supply chain. La conferencia de hoy no trata estrictamente sobre supply chain; trata sobre algoritmos. Sin embargo, creo que es de importancia fundamental para supply chain. Supply chain no es una isla; el progreso que se puede lograr en supply chain depende en gran medida del progreso que ya se ha alcanzado en otros campos adyacentes. Me refiero a esos campos como las ciencias auxiliares de supply chain.
Creo que la situación es bastante similar a la relación entre las ciencias médicas y la química durante el siglo XIX. Al comienzo del siglo XIX, a las ciencias médicas no les preocupaba en absoluto la química. La química aún era la novata y no se consideraba una propuesta válida para un paciente real. Avanzando rápidamente hasta el siglo XXI, la idea de que puedas ser un excelente médico sin saber nada de química se consideraría completamente disparatada. Se acepta que ser un excelente químico no te convierte en un excelente médico, pero se reconoce en general que, si no sabes nada de la química del cuerpo, no puedes ser competente en lo que respecta a las ciencias médicas modernas. Mi perspectiva para el futuro es que, durante el siglo XXI, el campo de supply chain comenzará a considerar el campo de los algoritmos de manera muy similar a como el campo de las ciencias médicas comenzó a ver la química a lo largo del siglo XIX.

Los algoritmos son un vasto campo de investigación, una rama de las matemáticas, y hoy solo rozaremos la superficie de este campo. En particular, este campo de investigación ha acumulado resultados asombrosos tras resultados asombrosos durante décadas. Puede ser un campo de investigación bastante teórico, pero eso no significa que sea solo teoría. En realidad, es un campo de investigación que, aunque es bastante teórico, ha arrojado numerosos hallazgos que han llegado a la producción.
De hecho, cualquier tipo de smartphone o computadora que estés usando hoy en día está utilizando literalmente decenas de miles de algoritmos que fueron publicados originalmente en algún lugar. Este historial es, en realidad, mucho más impresionante en comparación con la teoría de supply chain, donde la gran mayoría de los supply chains aún no están funcionando basados en los hallazgos de la teoría de supply chain. En lo que respecta a las computadoras modernas y a los algoritmos modernos, prácticamente todo lo relacionado con el software está completamente impulsado por todas esas décadas de hallazgos en la investigación algorítmica. Esto está, en esencia, en el corazón de prácticamente cada computadora que usamos hoy en día.
Para la clase de hoy, he seleccionado una lista de temas que creo que son bastante ilustrativos de lo que deberías saber para abordar el tema de los algoritmos modernos. Primero, discutiremos cómo podemos, de hecho, superar a los algoritmos supuestamente óptimos, especialmente para supply chain. Luego, echaremos un vistazo rápido a las estructuras de datos, seguido de recetas mágicas, compresión de tensores, y finalmente, técnicas meta.
Primero, me gustaría aclarar que cuando digo “algorithms for supply chain”, no me refiero a algoritmos destinados a resolver problemas específicos de supply chain. La perspectiva correcta es observar los algoritmos clásicos para problemas clásicos y reconsiderar esos problemas clásicos desde una perspectiva de supply chain para ver si realmente podemos hacer algo mejor. La respuesta es que sí, podemos.
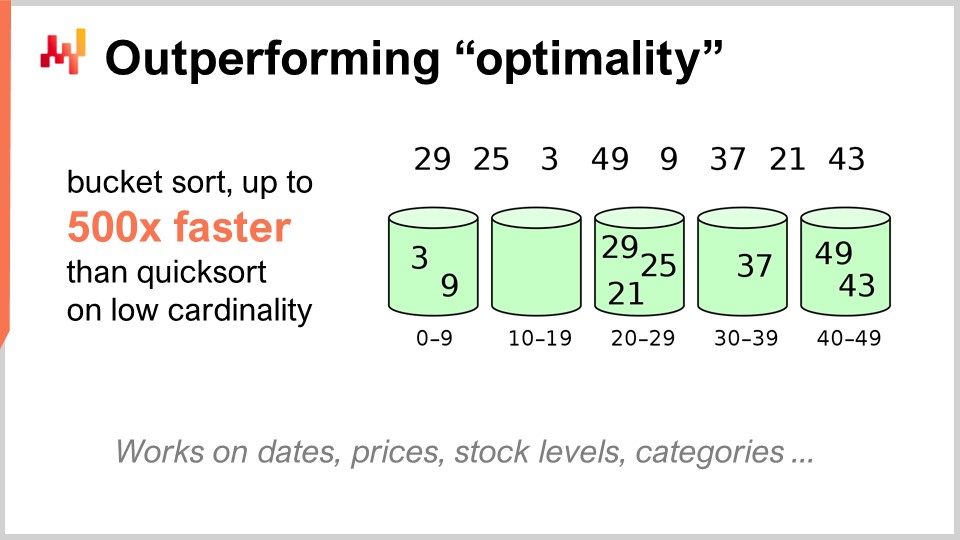
Por ejemplo, el algoritmo quicksort, según la teoría general de algoritmos, es óptimo en el sentido de que no se puede introducir un algoritmo que sea arbitrariamente mejor que quicksort. Así que, en este sentido, quicksort es tan bueno como podría ser. Sin embargo, si nos enfocamos específicamente en supply chain, es posible lograr aceleraciones sorprendentes. En particular, si observas problemas de ordenamiento donde la cardinalidad de los conjuntos de datos de interés es baja, como fechas, precios, stock levels, o categorías, todos esos son conjuntos de datos de baja cardinalidad. Por lo tanto, si tienes supuestos adicionales, como encontrarte en una situación de baja cardinalidad, entonces puedes usar el bucket sort. En producción, hay muchas situaciones en las que puedes lograr aceleraciones absolutamente monumentales, hasta 500 veces más rápido que quicksort. Así, puedes ser órdenes de magnitud más rápido que lo que supuestamente era óptimo, simplemente porque no estás en el caso general, sino en el caso de supply chain. Eso es algo muy importante, y creo que aquí reside la clave de los resultados sorprendentes que podemos lograr aprovechando los algoritmos para supply chain.
Creo que esta perspectiva es equivocada por al menos dos razones. Primero, como hemos visto, no es necesariamente el algoritmo estándar lo que interesa. Hemos observado que existe un algoritmo supuestamente óptimo como quicksort, pero si abordas el mismo problema desde el ángulo de supply chain, en realidad puedes lograr aceleraciones masivas. Por lo tanto, es de suma importancia estar familiarizado con los algoritmos, aunque sea solo para poder revisar los clásicos y conseguir aceleraciones masivas, simplemente porque no estás en el caso general, sino en el caso de supply chain.
La segunda razón por la que considero que esta perspectiva es equivocada es que los algoritmos están muy ligados a las estructuras de datos. Las estructuras de datos son maneras de organizar la información para poder operar de manera más eficiente sobre ella. Lo interesante es que todas estas estructuras forman una especie de vocabulario, y tener acceso a este vocabulario es esencial para poder describir situaciones de supply chain de una forma que facilite su traducción al software. Si comienzas con una descripción en términos simples, usualmente terminas con cosas que son extremadamente difíciles de traducir al software. Si esperas que un ingeniero de software, que no sabe nada acerca de supply chain, implemente esta traducción por ti, eso podría ser una receta para el desastre. Es mucho más sencillo si conoces este vocabulario, de modo que puedas hablar directamente en los términos que facilitan la traducción de las ideas que tienes al software.
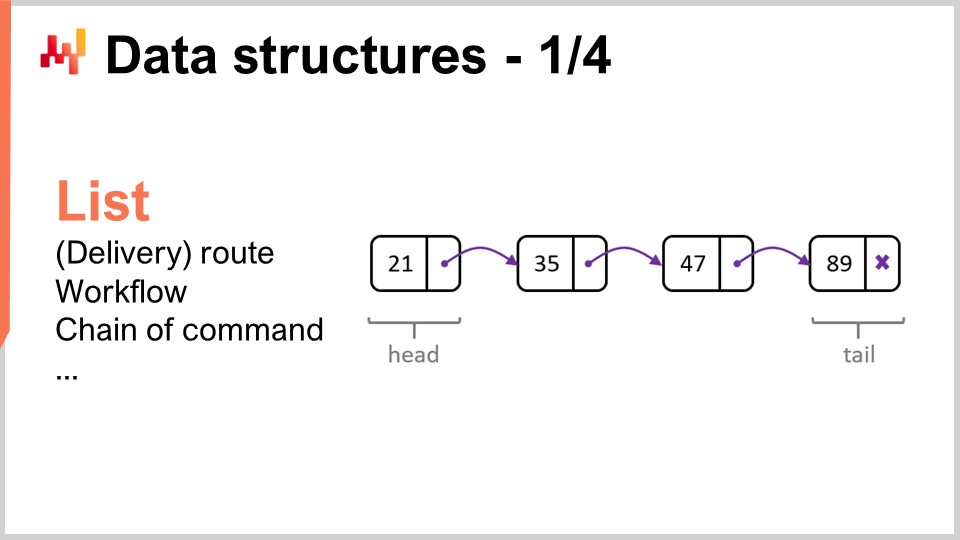
Revisemos las estructuras de datos más populares y sencillas. La primera sería la lista. La lista puede usarse, por ejemplo, para representar una ruta de entrega, que sería la secuencia de entregas a realizar, con una entrada por entrega. Puedes enumerar la ruta de entrega a medida que avanzas en ella. Una lista también puede representar un workflow, que es una secuencia de operaciones necesarias para fabricar cierto equipo, o una cadena de mando, que determina quién se supone que debe tomar ciertas decisiones.
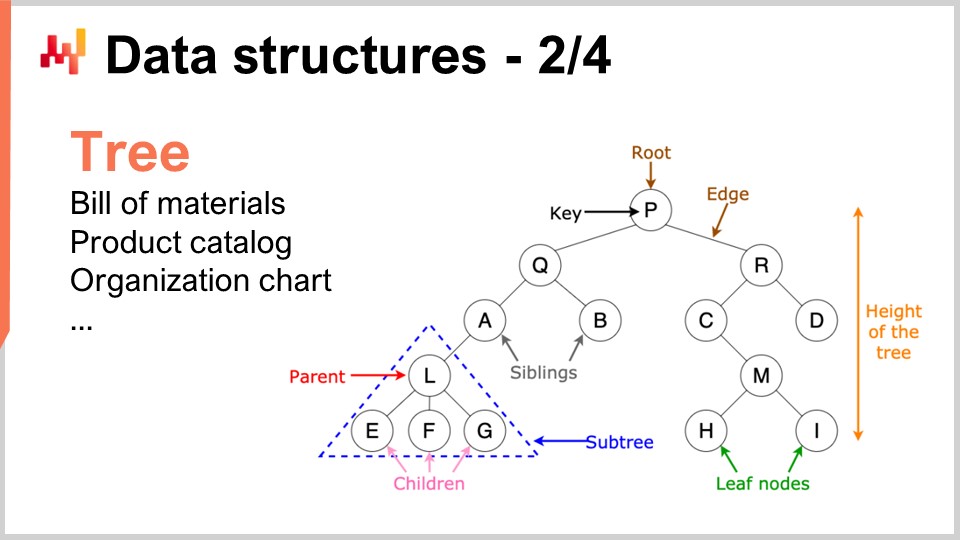
De manera similar, los árboles son otra estructura de datos ubicua. Por cierto, los árboles algorítmicos están invertidos, con la raíz en la parte superior y las ramas en la parte inferior. Los árboles te permiten describir todo tipo de jerarquías, y los supply chains tienen jerarquías por todas partes. Por ejemplo, una bill of material es un árbol; tienes un equipo que deseas fabricar, y este equipo está compuesto por ensamblajes. Cada ensamblaje se compone de sub-ensamblajes, y cada sub-ensamblaje se compone de piezas. Si expandes completamente la bill of material, obtienes un árbol. De manera similar, un catálogo de productos, en el que tienes familias de productos, categorías de productos, productos, subcategorías, etc., con frecuencia tiene una arquitectura tipo árbol adjunta. Un organigrama, con el CEO en la parte superior, los ejecutivos de nivel C debajo, y así sucesivamente, también se representa mediante un árbol. La teoría algorítmica te ofrece una multitud de herramientas y métodos para procesar árboles y realizar operaciones de forma eficiente sobre ellos. Por eso, esto es de gran interés.
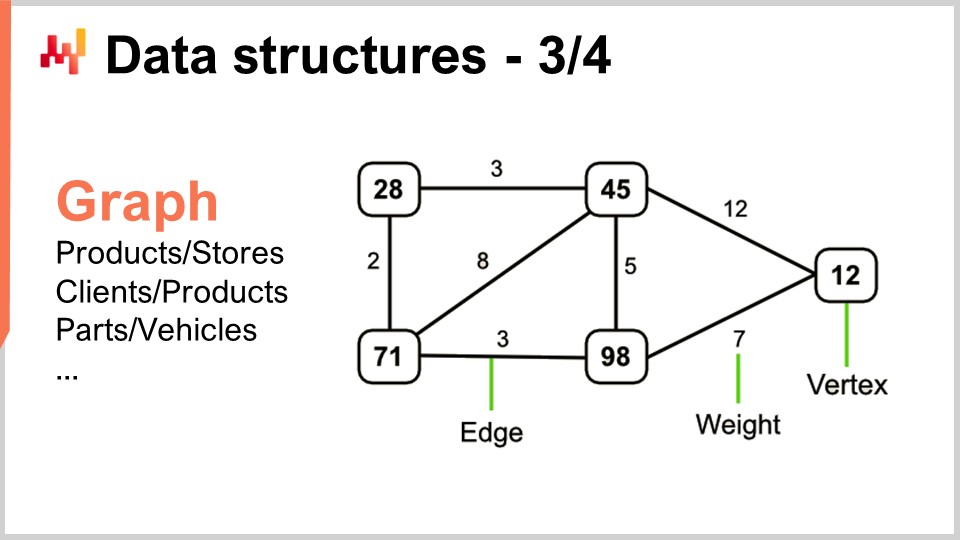
Ahora, los grafos te permiten describir todo tipo de redes. Por cierto, un grafo, en el sentido matemático, es un conjunto de vértices y un conjunto de aristas, donde las aristas conectan dos vértices. El término “grafo” puede resultar un poco engañoso porque no tiene nada que ver con gráficos. Un grafo es simplemente un objeto matemático, no un dibujo o algo gráfico. Cuando aprendas a identificar grafos, verás que los supply chains tienen grafos por todas partes.
Algunos ejemplos: Un surtido en una red minorista, que es fundamentalmente un grafo bipartito, conecta productos y tiendas. Si tienes un programa de loyalty en el que registras qué cliente ha comprado qué producto a lo largo del tiempo, tienes otro grafo bipartito que conecta clientes y productos. En el mercado de repuestos automotrices, donde tienes reparaciones que ejecutar, típicamente necesitas usar una matriz de compatibilidad que te indique la lista de partes que son mecánicamente compatibles con el vehículo de interés. Esta matriz de compatibilidad es esencialmente un grafo. Existe una enorme cantidad de literatura sobre todo tipo de algoritmos que te permiten trabajar con grafos, por lo que resulta muy interesante cuando puedes caracterizar un problema como soportado por una estructura de grafo, ya que todos los métodos conocidos en la literatura se ponen a disposición.
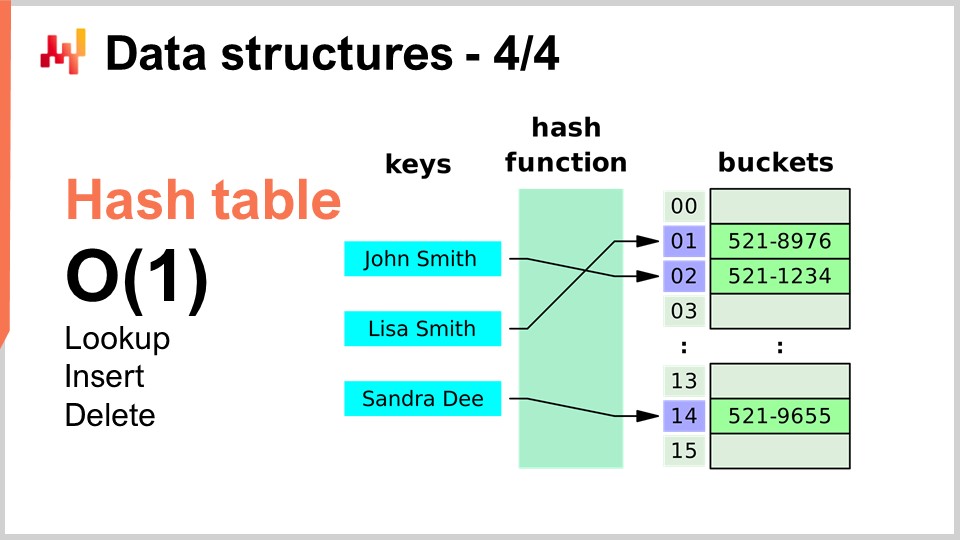
Finalmente, la última estructura de datos que cubriré hoy es la tabla hash. La tabla hash es, esencialmente, la navaja suiza de los algoritmos. No es nueva; ninguna de las estructuras de datos que he introducido es reciente según ningún estándar. La tabla hash es probablemente la más reciente del conjunto, datando de los años 50, así que no es reciente. No obstante, la tabla hash es una estructura de datos increíblemente útil. Es un contenedor que almacena pares de llaves y valores. La idea es que, con este contenedor, puedes guardar mucha información, y te brinda un rendimiento de Big O(1) para búsqueda, inserción y eliminación. Tienes un contenedor en el que, en tiempo constante, puedes añadir datos, comprobar si ciertos datos están presentes (al mirar la llave) y, potencialmente, eliminar datos. Esto es muy interesante y útil. Las tablas hash están literalmente en todas partes y se utilizan extensamente dentro de otros algoritmos.
Una cosa que señalaré, y a la que volveremos más adelante, es que el rendimiento de una tabla hash depende en gran medida del rendimiento de la función hash que utilices.

Ahora, echemos un vistazo a las recetas mágicas, y cambiaremos completamente a una perspectiva diferente. Los números mágicos son fundamentalmente un anti-patrón. En la clase anterior, la de conocimiento negativo para supply chain, discutimos cómo los anti-patrones generalmente comienzan con una buena intención pero terminan con consecuencias no deseadas que deshacen los beneficios supuestamente aportados por la solución. Los números mágicos son un anti-patrón de programación bien conocido. Este anti-patrón consiste en escribir código repleto de constantes que parecen surgir de la nada, haciendo que tu software sea muy difícil de mantener. Cuando tienes toneladas de constantes, no queda claro por qué existen esas restricciones y cómo fueron elegidas.
Generalmente, cuando ves números mágicos en un programa, es mejor aislar todas esas constantes en un lugar donde sean más manejables. Sin embargo, hay situaciones en las que una elección cuidadosa de constantes hace algo completamente inesperado, y obtienes beneficios casi mágicos, completamente no intencionados, al usar números que parecen haber caído del cielo. Esto es exactamente de lo que trata el brevísimo algoritmo que presento aquí.
En supply chain, muy frecuentemente, queremos poder lograr una especie de simulación. Las simulaciones o procesos Monte Carlo son uno de los trucos básicos que puedes usar en una miríada de situaciones de supply chain. Sin embargo, el rendimiento de tu simulación depende en gran medida de tu capacidad para generar números aleatorios. Para realizar simulaciones, generalmente se involucra cierto grado de aleatoriedad generada, y por lo tanto necesitas un algoritmo para generar dicha aleatoriedad. En lo que respecta a las computadoras, se trata típicamente de pseudorandomness – no es verdadera aleatoriedad; es simplemente algo que se asemeja a números aleatorios y tiene los atributos estadísticos de los números aleatorios, pero en realidad no es aleatorio.
La pregunta es, ¿con qué eficiencia puedes generar números aleatorios? Resulta que existe un algoritmo llamado “Shift”, publicado en 2003 por George Marsaglia, que es bastante impresionante. Este algoritmo genera números aleatorios de altísima calidad, creando una permutación completa de 2 a la potencia de 64 menos 1 bits. Va a circular por todas las combinaciones de 64 bits, menos una, con el cero como punto fijo. Hace esto con esencialmente seis operaciones: tres desplazamientos binarios y tres operaciones XOR (o exclusivo), que son operaciones a nivel de bits. Los desplazamientos también son operaciones a nivel de bits.
Lo que vemos es que hay tres números mágicos en medio de eso: 13, 7 y 17. Por cierto, todos esos números son números primos; esto no es un accidente. Resulta que si eliges esas constantes tan específicas, obtienes un generador de números aleatorios excelente que resulta ser súper rápido. Cuando digo súper rápido, me refiero a que literalmente puedes generar 10 megabytes por segundo de números aleatorios. Esto es absolutamente enorme. Si volvemos a la clase anterior, podemos ver por qué este algoritmo es tan eficiente. No solo contamos con únicamente seis instrucciones que se mapean directamente a las instrucciones soportadas de forma nativa por el hardware subyacente, como el procesador, sino que además no tenemos ninguna bifurcación. No hay ninguna prueba, y eso significa que este algoritmo, una vez ejecutado, aprovechará al máximo la capacidad de pipelining del procesador porque no hay ramificaciones. Literalmente podemos exprimir al máximo la profunda capacidad de pipelining que tenemos en un procesador moderno. Esto es muy interesante.
La pregunta es, ¿podríamos elegir otros números para hacer que este algoritmo funcione? La respuesta es no. Solo existen unas pocas docenas o tal vez alrededor de cien combinaciones diferentes de números que realmente funcionarían, y todas las demás te darán un generador de números de muy baja calidad. Ahí es donde resulta mágico. Verás, esta es una tendencia reciente en el desarrollo algorítmico: encontrar algo completamente inesperado, donde se descubre alguna constante semi-mágica que proporciona beneficios completamente no intencionados al mezclar operaciones binarias muy inesperadas. La generación de números aleatorios es de importancia crítica para supply chain.

Pero, como decía, las tablas hash están en todas partes, y también es de gran interés disponer de una función hash genérica de altísimo rendimiento. ¿Existe? Sí. Han existido clases enteras de funciones hash disponibles durante décadas, pero en 2019 se publicó otro algoritmo que ofrece un rendimiento récord. Este es el que puedes ver en la pantalla, “WyHash” de Wang Yi. Esencialmente, puedes ver que la estructura es muy similar al algoritmo XORShift. Es un algoritmo que no tiene bifurcaciones, como XORShift, y también utiliza la operación XOR. El algoritmo emplea seis instrucciones: cuatro operaciones XOR y dos operaciones Multiply-No-Flags.
Multiply-No-Flags es simplemente la multiplicación básica entre dos enteros de 64 bits, y como resultado, obtienes los 64 bits altos y los 64 bits bajos. Esta es una instrucción real disponible en los procesadores modernos, implementada a nivel de hardware, por lo que cuenta como una sola instrucción de computadora. Contamos con dos de ellas. Nuevamente, tenemos tres números mágicos, escritos en forma hexadecimal. Por cierto, esos son números primos, nuevamente, completamente semi-mágicos. Si aplicas este algoritmo, tendrás una función hash no criptográfica absolutamente excelente que opera casi a la velocidad de memcpy. Es muy rápida y de gran interés.

Ahora, cambiemos a algo completamente diferente de nuevo. El éxito de deep learning y de muchos otros métodos modernos de machine learning radica en algunos conocimientos algorítmicos clave sobre problemas que pueden ser acelerados masivamente por hardware de computación dedicado. Eso es de lo que hablé en mi conferencia anterior cuando hablaba de procesadores con instrucciones superescalares y, si quieres más, GPUs e incluso TPUs. Revisemos este conocimiento para ver cómo surgió todo de manera algo caótica. Sin embargo, creo que los conocimientos relevantes se han cristalizado en los últimos años. Para entender dónde nos encontramos hoy en día, tenemos que volver a la notación de Einstein, que fue introducida hace poco más de un siglo por Albert Einstein en uno de sus artículos. La intuición es simple: tienes una expresión y que es una suma desde i igual a 1 hasta i igual a 3 de c_y por x_y. Tenemos expresiones escritas así, y la intuición de la notación de Einstein es decir, en este tipo de situación, debemos escribirla omitiendo completamente la suma. En términos de software, la suma sería un bucle for. La idea es omitir la suma por completo y decir que, por convención, realizamos la suma sobre todos los índices para la variable i que tengan sentido.
Esta intuición simple produce dos resultados muy sorprendentes pero positivos. El primero es la corrección de diseño. Cuando escribimos la suma explícitamente, corremos el riesgo de no incluir los índices adecuados, lo que puede conducir a errores de índices fuera de rango en el software. Al eliminar la suma explícita y afirmar que tomaremos todas las posiciones de índice válidas por definición, tenemos un enfoque correcto por diseño. Esto por sí solo es de interés primordial y está relacionado con la programación con arreglos, un paradigma de programación que toqué brevemente en una de mis conferencias anteriores.
La segunda intuición, que es más reciente y de gran interés en la actualidad, es que si puedes escribir tu problema en la forma en que se aplica la notación de Einstein, tu problema puede beneficiarse de una aceleración masiva de hardware en la práctica. Este es un elemento revolucionario.

Para entender por qué, existe un artículo muy interesante llamado “Tensor Comprehensions” publicado en 2018 por el equipo de investigación de Facebook. Ellos introdujeron la noción de tensor comprehensions. Primero, permíteme definir las dos palabras. En el campo de la informática, un tensor es esencialmente una matriz multidimensional (en física, los tensores son completamente diferentes). Un valor escalar es un tensor de dimensión cero, un vector es un tensor de dimensión uno, una matriz es un tensor de dimensión dos, y puedes tener tensores con dimensiones aún mayores. Los tensores son objetos a los que se les adjuntan propiedades similares a las de un arreglo.
Comprehension es algo así como un álgebra con las cuatro operaciones básicas – suma, resta, multiplicación y división – así como otras operaciones. Es más extenso que el álgebra aritmética regular; por eso tienen un tensor comprehension en lugar de un tensor algebra. Es más abarcador pero no tan expresivo como un lenguaje de programación completo. Cuando tienes un comprehension, es más restrictivo que un lenguaje de programación completo donde puedes hacer lo que quieras.
La idea es que si miras la función MV (def MV), es fundamentalmente una función, y MV significa matrix-vector. En este caso, se trata de una multiplicación matrix-vector, y esta función está esencialmente realizando una multiplicación entre la matriz A y el vector X. Vemos en esta definición que la notación de Einstein está en juego: escribimos C_i = A_ik * X_k. ¿Qué valores debemos escoger para i y k? La respuesta es todas las combinaciones válidas para esas variables que son índices. Tomamos todos los valores de índices válidos, realizamos la suma, y en la práctica, esto nos da una multiplicación matrix-vector.
En la parte inferior de la pantalla, puedes ver el mismo método MV reescrito con bucles for, especificando explícitamente los rangos de valores. El logro clave del equipo de investigación de Facebook es que cada vez que puedes escribir un programa con esta sintaxis de tensor comprehension, han desarrollado un compilador que te permite beneficiarte extensamente de la aceleración de hardware utilizando GPUs. Básicamente, te permiten acelerar cualquier programa que puedas escribir con esta sintaxis de tensor comprehension. Siempre que puedas escribir un programa de esta forma, te beneficiarás de una aceleración masiva de hardware, y estamos hablando de algo que será dos órdenes de magnitud más rápido que un procesador regular. Este es un resultado asombroso en sí mismo.

Ahora veamos lo que podemos hacer desde una perspectiva de supply chain con este enfoque. Un interés clave para la práctica moderna de supply chain es probabilistic forecasting. Probabilistic forecasting, que abordé en una conferencia anterior, es la idea de que no vas a tener un forecast puntual, sino que vas a forecastear todas las diversas probabilidades para una variable de interés. Consideremos, por ejemplo, un forecast de lead time. Quieres forecastear tu lead time y tener un forecast probabilístico de lead time.
Ahora digamos que tu lead time puede descomponerse en el lead time de manufactura y el lead time de transporte. En realidad, lo más probable es que tengas un forecast probabilístico para el lead time de manufactura, que será una variable aleatoria discreta que te dará la probabilidad de observar un tiempo de un día, dos días, tres días, cuatro días, etc. Puedes pensar en ello como un gran histograma que te proporciona las probabilidades de observar esta duración para el lead time de manufactura. Luego tendrás un proceso similar para el lead time de transporte, con otra variable aleatoria discreta proporcionando un forecast probabilístico.
Ahora, quieres calcular el lead time total. Si los lead times forecastados fueran números, simplemente harías una suma simple. Sin embargo, los dos lead times forecastados no son números; son distribuciones de probabilidad. Por lo tanto, tenemos que combinar estas dos distribuciones de probabilidad para obtener una tercera distribución de probabilidad, que es la distribución de probabilidad para el lead time total. Resulta que si asumimos que los dos lead times, el lead time de manufactura y el lead time de transporte, son independientes, la operación que podemos hacer para realizar esta suma de variables aleatorias es simplemente una convolución unidimensional. Puede sonar complejo, pero en realidad no lo es. Lo que he implementado, y lo que puedes ver en la pantalla, es la implementación de una convolución unidimensional entre un vector que representa el histograma de las probabilidades del lead time de manufactura (A) y el histograma asociado con las probabilidades del lead time de transporte (B). El resultado es el tiempo total, que es la suma de esos lead times forecastados.
Ahora, si volvemos a la notación Big O que introduje anteriormente en esta conferencia, vemos que tenemos fundamentalmente un algoritmo cuadrático. Es Big O de N^2, siendo N el tamaño característico de los arreglos para A y B. Como mencioné, el rendimiento cuadrático es el punto óptimo de los problemas de predicción. Entonces, ¿qué podemos hacer para abordar este problema? Primero, tenemos que considerar que esto es un problema de supply chain, y tenemos la ley de los números pequeños que podemos usar a nuestro favor. Como discutimos en la conferencia anterior, las supply chains se tratan predominantemente de números pequeños. Si estamos considerando los lead times, podemos asumir razonablemente que esos lead times serán menores a, digamos, 400 días. Eso ya es bastante tiempo para este histograma de probabilidad.
Entonces, lo que nos queda es un Big O de N^2, pero con N menor que 400. 400 puede ser bastante grande, ya que 400 por 400 es 160,000. Ese es un número significativo, y recuerda que sumar a esta distribución de probabilidad es una operación muy básica. En cuanto comencemos a hacer probabilistic forecasting, querrás combinar tus forecasts de varias maneras, y lo más probable es que termines haciendo millones de estas convoluciones, simplemente porque, fundamentalmente, estas convoluciones no son más que una suma glorificada proyectada en el ámbito de las variables aleatorias. Así, incluso si hemos limitado N a ser menor que 400, es de gran interés llevar la aceleración de hardware a la mesa, y eso es precisamente lo que podemos lograr con tensor comprehension.
Lo principal a recordar es que en cuanto puedas escribir ese algoritmo, debes aprovechar lo que sabes sobre los conceptos de supply chain para aclarar los supuestos aplicables y luego aprovechar las herramientas que tienes para obtener aceleración de hardware.

Ahora, discutamos las meta técnicas. Las meta técnicas son de gran interés porque pueden estar sobrepuestas a los algoritmos existentes, y así, si tienes un algoritmo, hay una posibilidad de que puedas usar una de estas meta técnicas para mejorar su rendimiento. La primera intuición clave es la compresión, simplemente porque los datos más pequeños significan un procesamiento más rápido. Como hemos visto en la conferencia anterior, no tenemos acceso a memoria uniforme. Si deseas acceder a más datos, necesitas acceder a diferentes tipos de memoria física, y a medida que la memoria crece, llegas a diferentes tipos de memoria que son mucho menos eficientes. La caché L1 dentro del procesador es muy pequeña, alrededor de 64 kilobytes, pero es muy rápida. La RAM, o memoria principal, es cientos de veces más lenta que esta pequeña caché, pero literalmente puedes tener un terabyte de RAM. Por lo tanto, es de gran interés asegurarse de que tus datos sean lo más pequeños posible, ya que esto casi invariablemente hará que tus algoritmos se ejecuten más rápido. Hay una serie de trucos que puedes utilizar en este sentido.
Primero, puedes limpiar y organizar tus datos. Este es el ámbito del software empresarial. Cuando tienes un algoritmo que se ejecuta contra datos, a menudo hay muchos datos sin usar que no contribuyen a la solución de interés. Es esencial asegurarse de que no termines con que los datos de interés se entrelacen con datos que se ignoran.
La segunda idea es el bit packing. Hay muchas situaciones donde puedes empaquetar algunas banderas dentro de otros elementos, como punteros. Podrías tener un puntero de 64 bits, pero es muy raro que realmente necesites un rango de direcciones de 64 bits en su totalidad. Puedes sacrificar unos pocos bits de tu puntero para inyectar algunas banderas, lo que te permite minimizar tus datos con casi ninguna pérdida de rendimiento.
Además, puedes ajustar tu precisión. ¿Necesitas 64 bits de precisión de punto flotante en supply chain? Es muy raro que realmente necesites esa precisión. Normalmente, 32 bits de precisión son suficientes, e incluso hay muchas situaciones donde 16 bits de precisión son suficientes. Podrías pensar que reducir la precisión no es significativo, pero frecuentemente, cuando puedes dividir el tamaño de los datos por un factor de dos, no solo aceleras tu algoritmo por un factor de 2; literalmente lo aceleras por un factor de 10. Empaquetar los datos produce beneficios completamente no lineales en términos de velocidad de ejecución.
Finalmente, tienes la codificación por entropía, que es esencialmente compresión. Sin embargo, no necesariamente quieres usar algoritmos tan eficientes en compresión como, digamos, el algoritmo utilizado para un archivo ZIP. Quieres algo que pueda ser un poco menos eficiente en términos de compresión pero mucho más rápido en ejecución.
La compresión gira fundamentalmente en torno a la idea de que puedes intercambiar un poco de uso extra de CPU para disminuir la presión sobre la memoria, y en casi todas las situaciones, este es el truco de interés.
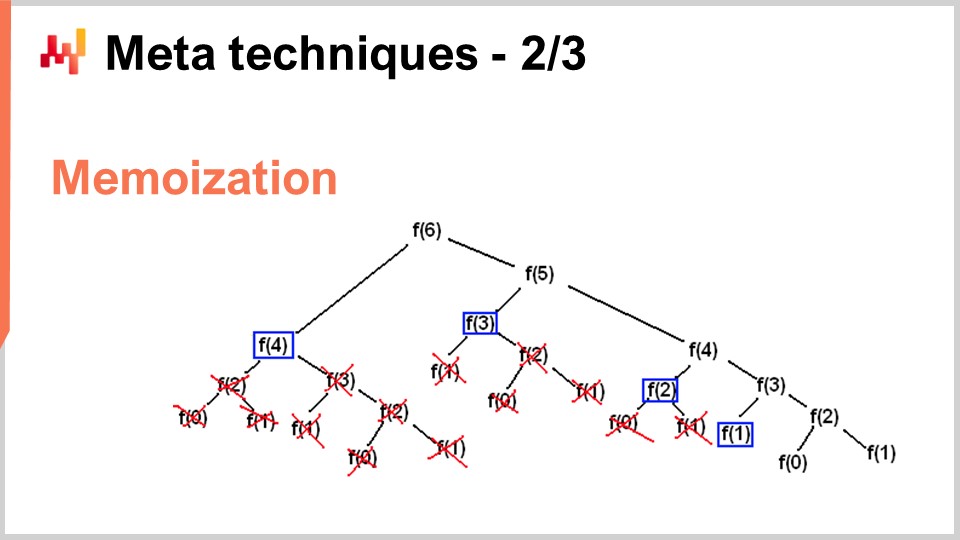
Sin embargo, hay situaciones en las que quieres hacer exactamente lo opuesto – intercambiar memoria para reducir drásticamente tu consumo de CPU. Eso es precisamente lo que haces con el truco de la memoización. La memoización es fundamentalmente la idea de que si una función es llamada muchas veces durante la ejecución de tu solución, y la misma función es llamada con los mismos inputs, no necesitas recomputarla. Puedes registrar el resultado, ponerlo a un lado (por ejemplo, en una tabla hash), y cuando vuelvas a llamar a la misma función, podrás comprobar si la tabla hash ya contiene una clave asociada con el input o si la tabla hash ya contiene el resultado porque ha sido precomputado. Si la función que estás memoizando es muy costosa, puedes lograr una aceleración masiva. Lo interesante es cuando empiezas a usar memoización no en la memoria principal, ya que, como vimos en la conferencia anterior, la DRAM es muy costosa. Se vuelve muy interesante cuando comienzas a almacenar tus resultados en disco o SSDs, que son baratos y abundantes. La idea es que puedes intercambiar SSDs a cambio de una reducción de la presión de CPU, lo cual es, de alguna manera, exactamente lo opuesto a la compresión que acabo de describir.
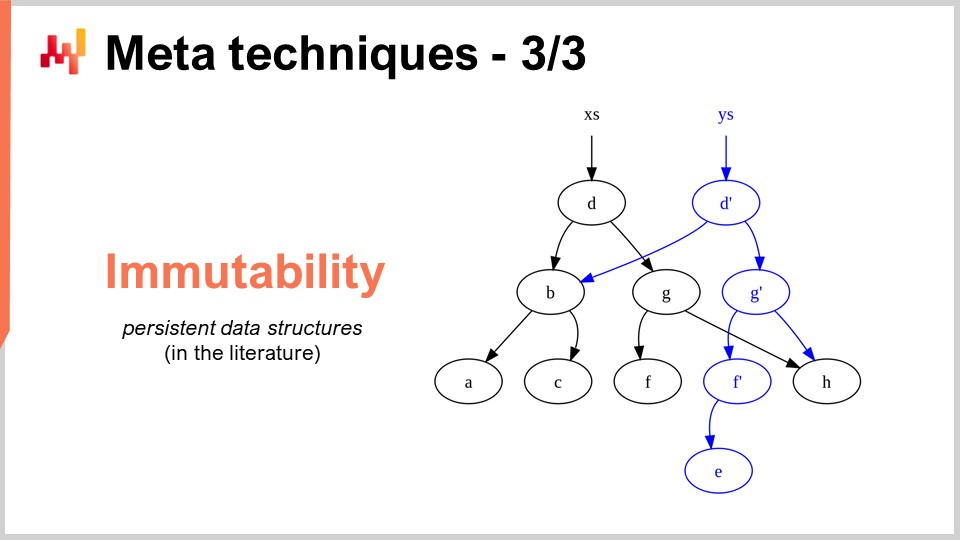
La última meta técnica es la inmutabilidad. Las estructuras de datos inmutables son fundamentalmente estructuras de datos que nunca se modifican. La idea es que los cambios se van superponiendo. Por ejemplo, con una tabla hash inmutable, cuando agregas un elemento, lo que vas a devolver es una nueva tabla hash que contiene todo lo de la tabla hash antigua más el nuevo elemento. La manera muy ingenua de hacer eso es realizar una copia completa de la estructura de datos y devolver toda la copia; sin embargo, es muy ineficiente. La intuición clave con las estructuras de datos inmutables es que cuando modificas la estructura de datos, devuelves una nueva estructura de datos que solo implementa el cambio, pero esta nueva estructura de datos recicla todas las partes de la estructura antigua que no han sido tocadas.
Casi todas las estructuras de datos clásicas, tales como listas, árboles, grafos y tablas hash, tienen sus contrapartes inmutables. En muchas situaciones, es de gran interés usarlas. Por cierto, existen lenguajes de programación modernos que han apostado completamente por la inmutabilidad, como Clojure, por ejemplo, para aquellos que puedan estar familiarizados con este lenguaje de programación.
¿Por qué es de tan alto interés? Primero, porque simplifica masivamente la paralelización de algoritmos. Como hemos visto en la conferencia anterior, no es posible encontrar un procesador que funcione a 100 GHz para procesadores de computadoras de escritorio generales. Lo que sí se puede encontrar, sin embargo, es una máquina con 50 núcleos, cada uno funcionando a 2 GHz. Si quieres aprovechar esos muchos núcleos, tienes que paralelizar tu ejecución, y entonces tu paralelización está en riesgo de errores muy desagradables llamados race conditions. Se vuelve muy difícil entender si el algoritmo que has escrito es correcto o no porque puede que tengas varios procesadores que, al mismo tiempo, intenten escribir en la misma parte de la memoria de la computadora.
Sin embargo, si tienes estructuras de datos inmutables, esto nunca sucede por diseño, simplemente porque una vez presentada una estructura de datos, nunca cambiará—solo surgirá una nueva estructura de datos. Así, puedes lograr una aceleración masiva en el rendimiento con el camino inmutable, simplemente porque puedes implementar versiones paralelas de tus algoritmos con mayor facilidad. Ten en cuenta que, generalmente, el cuello de botella para implementar aceleraciones algorítmicas es el tiempo que se tarda en implementar los algoritmos. Si tienes algo que, por diseño, te permite aplicar algún tipo de principio de concurrencia sin miedo, en realidad puedes desplegar aceleraciones algorítmicas mucho más rápido, con menos recursos en términos del número de programadores involucrados. Otro beneficio importante de las estructuras de datos inmutables es que facilitan enormemente la depuración. Cuando modificas destructivamente una estructura de datos y encuentras un error, puede ser muy difícil averiguar cómo llegaste allí. Con un depurador, puede ser una experiencia bastante desagradable identificar el problema. Lo interesante de las estructuras de datos inmutables es que los cambios no son destructivos, por lo que puedes ver la versión anterior de tu estructura de datos y comprender más fácilmente cómo llegaste al punto en que enfrentas algún tipo de comportamiento incorrecto.

Para concluir, los mejores algoritmos pueden sentirse como superpoderes. Con mejores algoritmos, obtienes más del mismo hardware de computación, y esos beneficios son indefinidos. Es un esfuerzo único, y luego tienes un potencial indefinido porque has ganado acceso a capacidades de cómputo superiores, considerando la misma cantidad de recursos informáticos dedicados a un determinado problema de supply chain de interés. Creo que esta perspectiva ofrece oportunidades para mejoras masivas en la gestión de supply chain.
Si observamos un campo completamente diferente, como los videojuegos, han establecido sus propias tradiciones algorítmicas y hallazgos dedicados a la experiencia de juego. Los gráficos impresionantes que experimentas con los videojuegos modernos son el producto de una comunidad que pasó décadas replanteando toda la pila de algoritmos para maximizar la calidad de la experiencia de juego. La perspectiva en el ámbito de los videojuegos no es tener un modelo 3D que sea correcto desde una perspectiva física o científica, sino maximizar la calidad percibida en términos de la experiencia gráfica para el jugador, y han afinado los algoritmos para lograr resultados impresionantes.
Creo que este tipo de trabajo apenas ha comenzado para las supply chains. El software empresarial de supply chain está estancado, y en mi propia percepción, ni siquiera estamos utilizando el 1% de lo que el hardware de computación moderno puede hacer por nosotros. La mayoría de las oportunidades están por delante y pueden capturarse a través de algoritmos, no solo algoritmos de supply chain como los algoritmos de ruteo de vehículos, sino revisitando algoritmos clásicos desde una perspectiva de supply chain para lograr aceleraciones masivas en el camino.

Ahora, echaré un vistazo a las preguntas.
Pregunta: Has estado hablando sobre los aspectos específicos de supply chain, como los números pequeños. Cuando sabemos de antemano que tenemos números pequeños en nuestras posibles decisiones, ¿qué tipo de simplificación trae esto? Por ejemplo, cuando sabemos que podemos ordenar como máximo uno o dos contenedores, ¿puedes pensar en algún ejemplo concreto de cómo esto influiría en el nivel de granularidad de los forecast holísticos que se utilizarán para calcular la función de recompensa de stock?
Primero, todo lo que he presentado hoy está en producción en Lokad. Todos estos insights, de una manera u otra, son muy aplicables a supply chain porque están en producción en Lokad. Tienes que darte cuenta de que lo que obtienes del software moderno es algo que no ha sido afinado para aprovechar al máximo el hardware de computación. Solo piensa que, como presenté en mi última conferencia, hoy en día tenemos computadoras que son mil veces más capaces que las computadoras de hace unas décadas. ¿Funcionan mil veces más rápido? No lo hacen. ¿Pueden abordar problemas que son fantástica y muchísimo más complicados que lo que teníamos hace unas décadas? No lo hacen. Así que no subestimes el hecho de que existen potenciales muy grandes de mejora.
El bucket sort que he presentado en esta conferencia es un ejemplo simple. Tienes operaciones de ordenamiento por doquier en supply chain, y hasta donde yo sé, es muy raro que alguna pieza de software empresarial aproveche algoritmos especializados que encajan bien con las situaciones de supply chain. Ahora, cuando sabemos que tenemos uno o dos contenedores, ¿aprovechamos esos elementos en Lokad? Sí, lo hacemos todo el tiempo, y hay montones de trucos que se pueden implementar a ese nivel.
Los trucos suelen estar a un nivel inferior, y los beneficios simplemente se reflejarán en la solución global. Tienes que pensar en descomponer los problemas de llenado de contenedores en todas sus partes. Puedes obtener beneficios aplicando las ideas y trucos que he presentado hoy a un nivel inferior.
Por ejemplo, ¿qué tipo de precisión numérica necesitas si estamos hablando de contenedores? Quizás números de 16 bits con solo 16 bits de precisión sean suficientes. Eso hace que los datos sean más pequeños. ¿Cuántos productos distintos estamos ordenando? Quizás solo estemos ordenando unos pocos miles de productos distintos, por lo que podemos usar el bucket sort. La distribución de probabilidad es un número inferior, más pequeño, así que en teoría, tenemos histogramas que pueden ir desde cero unidades, una unidad, tres unidades, hasta infinito, pero ¿vamos hasta el infinito? No, no lo hacemos. Tal vez podamos hacer algunas suposiciones inteligentes sobre el hecho de que es muy raro que nos enfrentemos a un histograma en el que superemos las 1,000 unidades. Cuando tengamos eso, podemos aproximar. No necesariamente necesitamos tener una precisión de 2 unidades si estamos tratando con un contenedor que contiene 1,000 unidades. Podemos aproximar y tener un histograma con cubos más grandes y ese tipo de cosas. No se trata tanto, diría yo, de introducir principios algorítmicos como el tensor comprehension, que son increíbles porque simplifican todo de una manera muy genial. Sin embargo, la mayoría de las aceleraciones algorítmicas al final resultan en un algoritmo más rápido pero ligeramente más complicado. No es necesariamente más sencillo porque, por lo general, el algoritmo más simple también es algo ineficiente. Un algoritmo más apropiado para un caso podría ser un poco más largo de escribir y más complejo, pero al final, funcionará más rápido. Esto no es siempre el caso, como hemos visto con las recetas mágicas, pero lo que quería mostrar era que necesitamos revisar los bloques fundamentales de lo que estamos haciendo para realmente construir software empresarial.
Pregunta: ¿Qué tan ampliamente se implementan estos insights en proveedores de ERP, APS y en lo mejor de su clase como GTA?
Lo interesante es que estos insights son, fundamentalmente, en su mayoría, completamente incompatibles con el software transaccional. La mayoría del software empresarial se construye alrededor de un núcleo que es una base de datos transaccional, y todo se canaliza a través de la base de datos. Esta base de datos no es una base de datos específica de supply chain; es una base de datos genérica que se supone que debe ser capaz de manejar todas las posibles situaciones que se te ocurran, desde finanzas hasta computación científica, pasando por historiales médicos y más.
El problema es que, si la pieza de software que estás observando tiene una base de datos transaccional en su núcleo, entonces los insights que he propuesto no pueden implementarse por diseño. Es como que se acabó el juego. Si miras los videojuegos, ¿cuántos videojuegos están construidos sobre una base de datos transaccional? La respuesta es cero. ¿Por qué? Porque no puedes tener un buen rendimiento gráfico implementado sobre una base de datos transaccional. No se pueden hacer gráficos por computadora en una base de datos transaccional.
Una base de datos transaccional es muy buena; te ofrece transaccionalidad, pero te encierra en un mundo donde casi todas las aceleraciones algorítmicas que se te ocurran simplemente no se pueden aplicar. Creo que cuando empezamos a pensar en APS, no hay nada avanzado en estos sistemas. Han estado estancados en el pasado durante décadas, y están estancados porque, en el núcleo de su diseño, están completamente concebidos en torno a una base de datos transaccional que les impide aplicar cualquiera de los insights que han surgido en el campo de los algoritmos durante las últimas, probablemente, cuatro décadas.
Ese es el meollo del problema en el campo del software empresarial. Las decisiones de diseño que tomas en el primer mes del diseño de tu producto te perseguirán durante décadas, esencialmente hasta el fin de los tiempos. No puedes actualizar una vez que has decidido un diseño específico para tu producto; estás atrapado con él. Así como no puedes simplemente reingeniar un automóvil para que sea eléctrico, si quieres tener un automóvil eléctrico muy bueno, reingeniarás el automóvil completamente en torno a la idea de que el motor de propulsión será eléctrico. No se trata simplemente de cambiar el motor y decir: “Aquí hay un automóvil eléctrico.” No funciona así. Este es uno de esos principios fundamentales de diseño en los que, una vez que te has comprometido a producir un automóvil eléctrico, necesitas replantear todo alrededor del motor para que encaje bien. Lamentablemente, los ERP y APS que son muy centrados en la base de datos simplemente no pueden usar ninguno de estos insights, me temo. Siempre es posible tener una burbuja aislada donde te beneficies de estos trucos, pero será un complemento añadido; nunca formará parte del núcleo.
En cuanto a las impresionantes capacidades de Blue Yonder, por favor ten paciencia conmigo, ya que Lokad es un competidor directo de Blue Yonder, y es un desafío para mí ser completamente imparcial. En el mercado del software empresarial, tienes que hacer afirmaciones ridículamente audaces para mantenerte competitivo. No estoy convencido de que haya alguna sustancia en ninguna de esas afirmaciones. Desafío la premisa de que alguien en este mercado tenga algo que se pueda calificar como impresionante.
Si quieres ver algo asombroso y ultra impresionante, mira la última demo del Unreal Engine o algoritmos especializados de videojuegos. Considera los gráficos por computadora en el hardware de la PlayStation 5 de próxima generación; es absolutamente impresionante. ¿Tenemos algo en la misma liga de logros tecnológicos en el campo del software empresarial? En lo que a Lokad respecta, tengo una opinión super sesgada, pero al observar el mercado de manera más general, veo un océano de personas que han estado intentando exprimir al máximo las bases de datos relacionales durante décadas. A veces introducen otros tipos de bases de datos, como las bases de datos de grafos, pero eso pierde por completo el punto de los insights que he presentado. No proporciona nada de sustancia para entregar valor al mundo de supply chain.
El mensaje clave aquí para la audiencia es que se trata de una cuestión de diseño. Tenemos que asegurarnos de que las decisiones iniciales que formaron parte del diseño de tu software empresarial no sean del tipo de cosas que, por diseño, impidan que estas clases de técnicas se utilicen siquiera en primer lugar.
La próxima conferencia tendrá lugar dentro de tres semanas, el miércoles a las 3 p.m. hora de París. Será el 13 de junio, y revisaremos el tercer capítulo, que trata sobre el personal de supply chain, rasgos de personalidad sorprendentes y empresas ficticias. ¡La próxima vez, hablaremos de queso. Nos vemos entonces!


