Odd Pricing

Odd pricing is a pricing method aimed at maximizing profit by making micro-adjustments in pricing structure. It relies on the assumption that consumers are calculation-averse and will therefore only read the first digits of a price when making their purchasing decision. According to this method, the relevant information of any given price does not usually relate to the last digits, but rather to the first digits, or in other words, to the order of magnitude of the numbers. For example, the price of $17.99 looks more like $17 and not like $18.

This pricing method is widely spread. According to Judith Holdershaw et al, more than 90% of prices in New Zealand end with a digit greater than 5, and 60% of them end with a “9”.

Why use odd pricing?

The odd pricing strategy relies on the fact that consumers highly value their time when evaluating prices. There is an increasing time cost associated with examining each additional digit within any given number, which means that when examining a price, the first digits carry more weight than the last ones. We can define a relevance rate for each digit and hence define the two concepts of “perceived price” and “true price”.

A consumer needs to evaluate the price of $1743.99. The first digit carries more than 50% of the information because $1000 represents more than 50% of the price, meaning that the consumer will read and understand this figure clearly. Since the second digit ($700) carries about 40% of the meaning of the price, the consumer will read this number too. Then, the third digit ($40) carries only 2% of the overall price information, and is therefore less relevant. In this case, the relevant price for the consumer is either $1740.00 or $1700.00, depending on the desired relevance threshold.

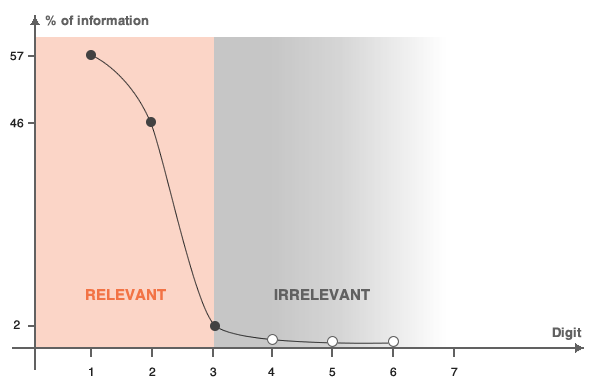
Once we have defined the relevant part or, in other words, the perceived part of a price, we can maximize profit on this figure by changing all the irrelevant digits to “nines”. Adding “irrelevant” numbers to the perceived price will still retain the same perceived price, and will therefore not have any impact on the demand or the sales of that particular item. The additional – unperceived - digits in the price will be entirely converted into profit. This is the case of the 99c in the $1743.99 example above. Given the overall price of the product, the 99c does not impact the consumer’s decision to purchase a given product and is therefore entirely converted into profit.

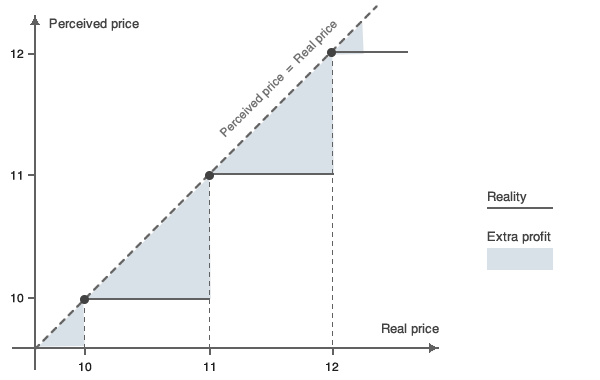
One issue that needs to be considered when using this method is related to price ranges. Today, most e-commerce websites give the option to filter goods by price ranges such as $50-$99. Setting a price at $99.99 instead of $100 implies falling into the $50-99 price range, which can, potentially, have a positive impact on demand.

This method also has two effects on the accounting field. First, if all prices end with “.99”, it is easy to calculate the daily amount of sales. For example, if the cash flow at the end of the day ends with “.38”, this means that 62 sales (or 162, 262, etc.) took place on that day. Second, this pricing method makes it more difficult to steal cash in businesses where cash is easily accessible to staff (for instance, in supermarkets). One would have to take an amount composed of a “.99” figure from the cash register in order to make it look like a sale, which is more difficult to do with “.00” prices.

Does it work?

Do we see a shift in demand when comparing “.99” and “.00” prices? If we do, that means that the signal carried by the “.99” price is stronger than the one cent which separates them.

According to Guéden et al, this effect can indeed be quite significant. Their study is centered on a little pizzeria-grill restaurant in France. A list of nine main dishes was proposed in the restaurant and included five different pizzas. The effect of the price-ending of one pizza was tested. During 2 weeks, all the pizzas were proposed with a round 00‑ending price (i.e. 9.00 Euro) whereas for the other 2 weeks a target-pizza was proposed with a nine-ending price (i.e. 8.99 Euro) whereas the four others were proposed with a round 00‑ending price. A last, a third 2 weeks period was tested where all the pizzas were proposed with a nine-ending price. Results showed that an increase in the choice of the target-pizza by the customers was observed when the price of this item was a nine-ending price and the prices of the other items ended with zero. No difference in the choice of the target-pizza was observed when all the items were presented with the same type of ending (9 or 0). This shows that comparatively the effect of nine-ending prices on market share can indeed be highly significant.

Schindler and Kibarian also carried out a study on the effects of odd pricing, but this time on a larger scale. More precisely, they examined price endings for a women’s fashion e-commerce, where they compared the effect on sales of “.88”, “.99” and “.00” prices. The sales of “.99”-priced items turned out to be 8% higher compared to “.00” prices. This however was not the case for “.88” prices. According to the odd pricing theory, the perception associated with “.99” and “.88” prices should not be any different, and should therefore lead to the same customer demand. Empirical evidence demonstrates however that a better purchasing signal is achieved with “.99” prices. When it comes to odd pricing, it seems that what matters is the consumer feeling regarding “well-priced” products. And this is what consequently leads to an increase in their willingness to buy.

What are the main issues of odd pricing?

Odd pricing strongly relies on the hypothesis that consumers tend to take odd prices at their face value and do not invest a lot of time or effort in actually understanding what lies behind the last digits of a given price. However, this assumption does not always hold true. To take an example, let’s look at the real estate industry. If we rely on the odd pricing hypothesis outlined above, a consumer should technically not make much difference between the same property priced at $1,860,000.99 or at $1,810,000.99. Nevertheless, the $50,000 difference in two prices is highly significant and is very unlikely to be neglected by the property buyer. As a result, this example demonstrates that odd pricing does indeed not work under all circumstances.

Another issue is linked to the psychological effects associated with odd pricing. Products whose prices end in “.99” are often perceived as promotional or cheap items. Therefore, it is probable that modifying the last digit in a price changes the perception of product quality. If we assume that estimated product quality has an impact on the demand, then a perceived decrease in quality associated with “.99” prices results in lower demand and therefore lower profits.

To illustrate, consumers may consider that a coffee maker priced under $20 is not expensive enough and see the price a sign of a low quality. Therefore, setting the price of the coffee maker at $19.99 will lower the demand considerably, demonstrating the inefficiency of odd pricing in this specific case.

References

• Anderson E. T. & Simester D. I., “Price cues and customer price knowledge”, 2008
• Guéguen N., Jacob C., Legoherel P. & Ngobo P., “Nine-ending priceing and consumer’s behavior : A field study in a restaurant”, International Journal of Hospitality Management, 2009
• Holdershaw J., Gendall P. & Garland R., “The widespread of use of odd pricing in the retail sector”, Marketing Bulletin, 1997
• Nyström H., Retail Pricing. An Integrated Economic and Psychological Approach, 1970
• Schindler R. M. & Kirbarian T. M., “Increased consumer sales response though use of 99-Ending prices”, Journal of Retailing, 1996