00:01 Introduction
02:18 The modern forecast
06:37 Going postal probabilistic
11:58 The story so far
15:10 Probable plan for today
17:18 Bestiary of predictions
28:10 Metrics - CRPS - 1/2
33:21 Metrics - CRPS - 2/2
37:20 Metrics - Monge-Kantorovich
42:07 Metrics - likelihood - 1/3
47:23 Metrics - likelihood - 2/3
51:45 Metrics - likelihood - 3/3
55:03 1D distributions - 1/4
01:01:13 1D distributions - 2/4
01:06:43 1D distributions - 3/4
01:15:39 1D distributions - 4/4
01:18:24 Generators - 1/3
01:24:00 Generators - 2/3
01:29:23 Generators - 3/3
01:37:56 Please wait while we ignore you
01:40:39 Conclusion
01:43:50 Upcoming lecture and audience questions
Описание
Прогноз называется вероятностным, а не детерминированным, если он содержит набор вероятностей, связанных со всеми возможными будущими исходами, вместо того чтобы указывать один конкретный исход в качестве прогноза. Вероятностные прогнозы важны, когда неопределенность не может быть устранена, что практически всегда имеет место при работе со сложными системами. Для цепочек поставок вероятностные прогнозы необходимы для принятия надежных решений в условиях неопределенности будущего.
Полная стенограмма

Добро пожаловать в эту серию лекций о цепочках поставок. Меня зовут Юаннес Верморель, и сегодня я представлю «Вероятностное прогнозирование для цепочки поставок». Вероятностное прогнозирование является одним из самых важных, если не самым важным, сдвигов парадигмы за более чем век в науке статистического прогнозирования. Однако на техническом уровне это в основном то же самое. Если мы рассматриваем модели вероятностного прогнозирования или их альтернативы, используется та же статистика, те же вероятности. Вероятностное прогнозирование отражает изменение в том, как мы должны воспринимать сам процесс прогнозирования. Самое значимое изменение для цепочек поставок заключается не в науке прогнозирования, а в том, как цепочки поставок управляются и оптимизируются с учетом предиктивных моделей.
Цель сегодняшней лекции — дать простое техническое введение в вероятностное прогнозирование. К концу этой лекции вы сможете понять, в чем заключается суть вероятностного прогнозирования, как отличить вероятностные прогнозы от невероятностных, как оценивать качество вероятностного прогноза и даже создать свою собственную модель начального уровня для вероятностного прогнозирования. Сегодня я не буду рассматривать использование вероятностных прогнозов для принятия решений в контексте цепочек поставок. Основное внимание уделяется исключительно закладке основ вероятностного прогнозирования. Улучшение процессов принятия решений в цепочке поставок с помощью вероятностных прогнозов будет рассмотрено в следующей лекции.

Чтобы понять значение вероятностных прогнозов, необходимо немного исторического контекста. Современная форма прогнозирования, статистический прогноз, в отличие от гадания, возникла в начале 20 века. Прогнозирование появилось в более широком научном контексте, когда точные науки, такие как кинетика, электромагнетизм и химия, смогли добиться, казалось бы, произвольно точных результатов. Эти результаты были получены благодаря многовековым усилиям, которые можно проследить, например, до Галилео Галилея, разрабатывавшего передовые технологии для более совершенных измерений. Более точные измерения, в свою очередь, способствовали дальнейшему научному прогрессу, позволяя ученым тестировать и оспаривать свои теории и прогнозы с еще большей точностью.
В этом более широком контексте, где некоторые науки были чрезвычайно успешными, зарождающаяся область прогнозирования в начале 20 века взяла на себя задачу воспроизвести успехи этих точных наук в экономике. Например, если мы взглянем на пионеров, таких как Роджер Бабсон, один из основателей современного экономического прогнозирования, он основал успешную компанию по экономическому прогнозированию в Соединенных Штатах в начале 20 века. Девиз компании был буквально: “На каждое действие есть равное и противоположное противодействие”. Видение Бабсона заключалось в том, чтобы перенести успех ньютоновской физики в область экономики и, в конечном итоге, добиться столь же точных результатов.
Однако после более чем века статистических академических прогнозов, на основе которых функционируют цепочки поставок, идея достижения произвольно точных результатов, что в терминах прогнозирования означает получение произвольно точных прогнозов, остается такой же недосягаемой, как и более века назад. На протяжении нескольких десятилетий в широком мире цепочек поставок звучали голоса, опасавшиеся, что эти прогнозы никогда не станут достаточно точными. Существовало движение, такое как бережливое производство, которое, среди прочего, настойчиво выступало за значительное сокращение зависимости цепочек поставок от этих ненадежных прогнозов. Суть just-in-time состоит в том, что если вы можете производить и поставлять всё, что требуется рынку, в нужный момент, то внезапно вам больше не нужен надежный, точный прогноз.
В этом контексте вероятностное прогнозирование представляет собой переосмысление прогнозирования, но с гораздо более скромными амбициями. Оно исходит из идеи, что неопределенность будущего не может быть устранена. Все варианты будущего возможны, но не все они равновероятны, и задача вероятностного прогнозирования — сравнительно оценить вероятность каждого из этих альтернативных вариантов, а не сводить все возможные варианты будущего к единственному.

Ньютоновский подход к статистическим экономическим прогнозам в сущности потерпел неудачу. Мнение в нашем сообществе о том, что когда-либо можно будет добиться произвольно точных прогнозов, утратило силу. И всё же, странным образом, почти всё программное обеспечение для цепочек поставок и значительная часть общепринятых практик управления цепями поставок на самом деле основаны на предположении, что такие прогнозы в конечном итоге будут доступны.
Например, Планирование продаж и операций (S&OP) базируется на идее, что можно достичь единого, количественно определенного видения компании, если все заинтересованные стороны объединятся и совместно разработают прогноз. Аналогичным образом, метод open-to-buy также по существу базируется на идее составления бюджета сверху вниз, исходя из предположения о возможности создания произвольно точных прогнозов. Более того, даже если рассмотреть многие инструменты, широко применяемые для прогнозирования и планирования в цепочках поставок, такие как бизнес-аналитика и таблицы, они в значительной степени ориентированы на точечный анализ временных рядов. По сути, идея заключается в том, что вы можете продолжить использовать исторические данные для прогнозирования будущего, имея по одной точке на интересующий период. Эти инструменты по своей природе испытывают огромные трудности даже с пониманием тех расчетов, которые связаны с вероятностным прогнозом, где существует не один единственный вариант будущего, а все возможные.
Действительно, вероятностное прогнозирование не сводится к украшению классического прогноза элементами неопределенности. Оно также не предполагает составление короткого списка сценариев, где каждый сценарий является обычным прогнозом сам по себе. Общепринятые методы в цепочках поставок, как правило, не работают с вероятностными прогнозами, поскольку в их основе подразумевается наличие эталонного прогноза, вокруг которого всё будет строиться. В отличие от этого, вероятностное прогнозирование представляет собой прямую числовую оценку всех возможных вариантов будущего.
Конечно, нас ограничивает количество вычислительных ресурсов, поэтому, когда я говорю «все возможные варианты будущего», на практике мы рассматриваем только конечное число вариантов. Однако, учитывая современную вычислительную мощность, количество вариантов, которые мы можем фактически учесть, исчисляется миллионами. Именно здесь бизнес-аналитика и таблицы сталкиваются с трудностями. Они не предназначены для выполнения тех расчетов, которые связаны с вероятностными прогнозами. Это проблема проектирования программного обеспечения. Видите ли, таблица имеет доступ к тем же компьютерам и вычислительной мощности, но если программное обеспечение не обладает надлежащей архитектурой, некоторые задачи могут оказаться невероятно сложными, даже если у вас есть огромные вычислительные ресурсы.
Таким образом, с точки зрения цепочек поставок главная проблема внедрения вероятностного прогнозирования заключается в отказе от десятилетий использования инструментов и практик, основанных на весьма амбициозной, но, как я считаю, ошибочной цели – а именно, в возможности достижения произвольно точных прогнозов. Хочу сразу отметить, что было бы крайне ошибочно воспринимать вероятностное прогнозирование как способ получения более точных прогнозов. Это не так. Вероятностные прогнозы не являются более точными и не могут служить заменой классическим, общепринятым прогнозам. Их преимущество заключается в том, как они могут быть использованы для целей цепочек поставок, особенно для принятия решений в их контексте. Тем не менее, наша задача сегодня — просто понять, в чем заключается суть этих вероятностных прогнозов; их практическое применение будет рассмотрено в следующей лекции.

Эта лекция является частью серии лекций о цепочках поставок. Я стараюсь сделать эти лекции достаточно независимыми друг от друга. Однако наступает момент, когда зрителям действительно помогает просмотр лекций в последовательном порядке, поскольку я часто буду ссылаться на материалы, представленные в предыдущих лекциях.
Таким образом, эта лекция является третьей в пятой главе, посвященной прогнозированию. В самой первой главе этой серии я представил свои взгляды на цепочки поставок как на область исследований и практики. Во второй главе я рассказал о методологиях. Действительно, большинство ситуаций в цепочках поставок носит характер противостояния, и такие ситуации склонны опровергать наивные методологии. Нам необходимы адекватные методы, если мы хотим добиться какого-либо успеха в этой области.
Третья глава была посвящена экономии в цепочках поставок с исключительным вниманием к проблеме и самой природе вызова, с которым мы сталкиваемся в различных ситуациях. Идея экономии в цепочках поставок заключается в том, чтобы полностью игнорировать аспекты, связанные с решением, поскольку мы хотим сосредоточиться исключительно на проблеме, прежде чем подобрать способ её решения.
В четвертой главе я рассмотрел широкий спектр вспомогательных наук. Эти науки не являются непосредственно цепочками поставок; это смежные или поддерживающие области исследований. Однако я считаю, что базовое знание этих вспомогательных дисциплин необходимо для современной практики в области цепочек поставок.
Наконец, в пятой главе мы углубляемся в методы, позволяющие количественно оценивать будущее, особенно для формирования заключений о нём. Действительно, всё, что мы делаем в цепочках поставок, в той или иной мере связано с предвидением будущего. Если мы сможем лучше предвидеть будущее, то сможем принимать более обоснованные решения. Именно об этом и пойдёт речь в пятой главе: о том, как получить количественно более точное представление о будущем. В этой главе вероятностные прогнозы играют ключевую роль в нашем подходе к будущем.
Остальная часть этой лекции разделена на четыре раздела неравной длины. Во-первых, мы рассмотрим наиболее распространенные типы прогнозов, помимо классического. Я поясню, что имею в виду под классическим прогнозом, чуть позже. Действительно, слишком немногие в кругах цепочек поставок осознают, что существует множество вариантов. Вероятностное прогнозирование следует воспринимать как обобщающий термин, охватывающий достаточно разнообразный набор инструментов и методов.
Во-вторых, мы введем метрики для оценки качества вероятностных прогнозов. Вне зависимости от обстоятельств, хорошо разработанный вероятностный прогноз всегда сообщает: “Возможно, это могло произойти.” Вопрос заключается в том, как отличить действительно хороший вероятностный прогноз от плохого. Здесь на помощь приходят специальные метрики, созданные именно для оценки вероятностных прогнозов.
В-третьих, мы подробно рассмотрим одномерные распределения. Это самый простой тип распределений, и, хотя у них есть определённые ограничения, они являются самым простым входом в область вероятностного прогнозирования.
В-четвертых, мы кратко коснемся генераторов, которые часто называют методами Монте-Карло. Действительно, существует двойственность между генераторами и оценщиками плотности вероятности, и методы Монте-Карло дадут нам возможность решать задачи более высокой размерности и применять другие формы вероятностного прогнозирования.

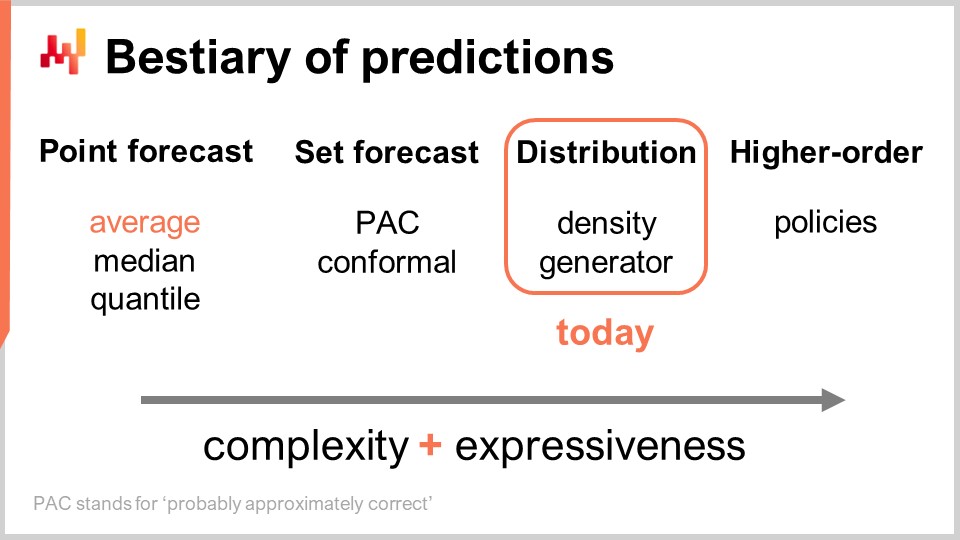
Существует несколько типов прогнозов, и этот аспект не следует путать с тем, что существует несколько типов моделей прогнозирования. Когда модели не принадлежат к одному и тому же типу или классу прогнозов, они даже не решают одни и те же задачи. Наиболее распространённым типом прогноза является точечный прогноз. Например, если я говорю, что завтра суммарные продажи в магазине в евро составят 10 000 евро за общий объём продаж за день, я делаю точечный прогноз того, что произойдёт в этом магазине завтра. Если я повторю это упражнение и начну строить прогноз временного ряда, делая прогноз для завтрашнего дня, затем для послезавтра, у меня будет несколько точек данных. Однако всё это по сути остаётся точечным прогнозом, потому что, по сути, мы выбираем нашу задачу, определяя определённый уровень агрегации, и на этом уровне наши прогнозы дают нам одно число, которое должно быть ответом.
Теперь, в рамках точечного прогноза, существует несколько подтипов прогнозов в зависимости от того, какая метрика оптимизируется. Наиболее часто используемая метрика, вероятно, квадратичная ошибка, поэтому у нас есть среднеквадратичная ошибка, которая даёт вам средний прогноз. Кстати, этот прогноз, как правило, используется чаще всего, потому что он единственный, который, по крайней мере, отчасти аддитивен. Ни один прогноз никогда не является полностью аддитивным; он всегда сопровождается множеством оговорок. Тем не менее, некоторые прогнозы более аддитивны, чем другие, и, безусловно, средние прогнозы, как правило, являются наиболее аддитивными. Если вы хотите получить средний прогноз, то по сути у вас есть точечный прогноз, оптимизированный по среднеквадратичной ошибке. Если вы используете другую метрику, например, абсолютную ошибку, и оптимизируете по ней, то получите медианный прогноз. Если вы используете функцию потерь pinball loss function, которую мы представили ещё в первой лекции этой пятой главы в серии лекций по цепочке поставок, то вы получите квантильный прогноз. Кстати, как мы видим сегодня, я классифицирую квантильные прогнозы как ещё один тип точечного прогноза. Действительно, с квантильным прогнозом вы, по сути, получаете единственную оценку. Эта оценка может иметь смещение, что и является задумкой. Вот суть квантилей, но, тем не менее, на мой взгляд, это полностью соответствует определению точечного прогноза, поскольку форма прогноза – всего одна точка.
Теперь существует наборный прогноз, который возвращает набор точек вместо одной точки. Существует вариация в зависимости от того, как вы формируете этот набор. Если мы рассмотрим прогноз PAC, где PAC означает Probably Approximately Correct (вероятно, приблизительно правильный). Это, по сути, концепция, представленная Валянтом примерно два десятилетия назад, которая утверждает, что набор, являющийся вашим прогнозом, обладает определённой вероятностью того, что наблюдаемый исход попадёт в этот набор с заданной вероятностью. Набор, который вы создаёте, на самом деле состоит из всех точек, попадающих в область, характеризующуюся максимальным расстоянием до опорной точки. Таким образом, подход PAC к прогнозированию уже является наборным прогнозом, потому что результат уже не является отдельной точкой. Однако у нас всё ещё есть опорная точка, центральный результат, и существует максимальное расстояние до этой точки. Мы просто говорим, что с определённой заданной вероятностью наблюдаемый исход в конечном итоге окажется в пределах нашего предсказанного набора.
Подход PAC можно обобщить с помощью конформного подхода. Конформное прогнозирование утверждает: “Вот набор, и я говорю вам, что существует заданная вероятность того, что результат окажется в этом наборе.” Отличие конформного прогнозирования от подхода PAC заключается в том, что конформные прогнозы уже не привязаны к наличию опорной точки и расстоянию до неё. Вы можете задать форму этого набора любым способом, и он по-прежнему будет частью парадигмы наборного прогноза.
Будущее можно представить ещё более детально и сложно: прогноз распределения. Прогноз распределения даёт вам функцию, которая отображает все возможные исходы в их соответствующие локальные плотности вероятности. Таким образом, мы начинаем с точечного прогноза, где прогноз представлен одной точкой. Затем мы переходим к наборному прогнозу, где прогноз – это набор точек. Наконец, прогноз распределения технически является функцией или чем-то, что обобщает функцию. Кстати, когда я употребляю термин “распределение” в этой лекции, он всегда подразумевает распределение вероятностей. Прогнозы распределения представляют собой нечто ещё более богатое и сложное, чем набор, и это станет нашим основным фокусом сегодня.
Существует два общих подхода к работе с распределениями: подход плотности и подход генератора. Когда я говорю “плотность”, это, по сути, относится к локальной оценке плотностей вероятности. Подход генератора включает в себя Монте-Карло генеративный процесс, который генерирует исходы, называемые отклонениями, которые должны отражать ту же локальную плотность вероятности. Это два основных способа решения задачи прогнозирования распределения.
Помимо распределения, существуют конструкции высшего порядка. Это может показаться несколько сложным для понимания, но моя суть в том, что, хотя сегодня мы не будем углубляться в конструкции высшего порядка, важно отметить, что вероятностное прогнозирование, когда сосредоточено на генерации распределений, не является конечной целью; это лишь один из этапов, и существует нечто большее. Конструкции высшего порядка важны, если мы хотим когда-либо получать удовлетворительные ответы даже в простых случаях.
Чтобы понять суть конструкций высшего порядка, давайте рассмотрим простой розничный магазин с действующей скидочной политикой для товаров, приближающихся к истечению срока годности. Очевидно, магазин не хочет иметь залежавшиеся запасы, поэтому автоматически применяется скидка, когда товары находятся очень близко к истечению срока годности. Спрос, который генерирует этот магазин, сильно зависит от данной политики. Таким образом, прогноз, который нам хотелось бы получить, и который может представлять собой распределение, отражающее вероятности всех возможных исходов, должен зависеть от этой политики. Однако эта политика является математическим объектом; это функция. Мы хотели бы иметь не просто вероятностный прогноз, а нечто более мета – конструкцию высшего порядка, которая, заданная политика, может генерировать соответствующее распределение.
С точки зрения цепочки поставок, когда мы переходим от одного типа прогноза к следующему, мы получаем намного больше информации. Это не следует путать с повышением точности прогноза; речь идёт о получении совершенно другого вида информации, как если бы вы видели мир в чёрно-белых тонах и внезапно обрели способность видеть цвета, а не просто получили дополнительное разрешение. С точки зрения инструментов, электронные таблицы и инструменты бизнес-аналитики несколько адекватны для работы с точечными прогнозами. В зависимости от типа наборного прогноза, который вы рассматриваете, они могут быть адекватными, но вы уже нагрузите их возможности проектирования. Они не предназначены для работы с каким-либо сложным наборным прогнозом помимо очевидного, когда вы просто определяете диапазон с минимальными и максимальными значениями ожидаемых результатов. Мы увидим, что, по сути, если мы хотим хоть как-то работать с прогнозами распределения или даже конструкциями высшего порядка, нам нужны совершенно другие инструменты, хотя это станет понятнее чуть позже.
Чтобы начать работу с вероятностными прогнозами, давайте попробуем охарактеризовать, что делает их хорошими. Действительно, независимо от того, какой исход вы наблюдаете, вероятностный прогноз сообщит вам, что для этого события была предусмотрена определённая вероятность. Итак, при таких условиях, чем хороший вероятностный прогноз отличается от плохого? Конечно, тем, что именно потому, что прогноз вероятностный, это не означает, что внезапно все модели прогнозирования становятся хорошими.
Именно этим и занимаются метрики, предназначенные для вероятностного прогнозирования, и Непрерывный ранжированный вероятностный счет (CRPS) является обобщением абсолютной ошибки для одномерных вероятностных прогнозов. Мне действительно жаль это ужасное название – CRPS. Я не придумывал эту терминологию; она была мне передана. Формула CRPS показана на экране. По сути, функция F является функцией накопленного распределения; это и есть вероятностный прогноз, который делается. Точка x – это фактическое наблюдение, а значение CRPS – это то, что вы вычисляете между вашим вероятностным прогнозом и тем наблюдением, которое вы только что сделали.
Мы видим, что, по сути, наблюдаемая точка превращается в квазивероятностный прогноз посредством функции Хевисайда. Применение функции Хевисайда эквивалентно тому, что наблюдаемая точка превращается в дираковское распределение вероятностей, то есть распределение, концентрирующее всю массу вероятности в одном исходе. Затем идёт интеграл, и, по сути, CRPS выполняет своего рода сопоставление форм. Мы сопоставляем форму ФНР (функции накопленного распределения) с формой другой ФНР, соответствующей дираковскому распределению, которое соответствует наблюдаемой точке.
С точки зрения точечного прогноза, CRPS вызывает вопросы не только из-за сложной формулы, но и потому, что эта метрика принимает два аргумента, которые не имеют одинакового типа. Один из этих аргументов – распределение, а другой – всего лишь одна точка данных. Таким образом, здесь присутствует асимметрия, которой нет у большинства других метрик точечных прогнозов, таких как абсолютная ошибка и среднеквадратичная ошибка. В CRPS мы, по сути, сравниваем точку с распределением.
Если мы хотим лучше понять, что мы вычисляем с помощью CRPS, интересно отметить, что CRPS имеет ту же единицу измерения, что и наблюдение. Например, если x выражено в евро, и значение CRPS между F и x также выражено в евро, то именно поэтому я говорю, что CRPS является обобщением абсолютной ошибки. Кстати, если свести ваш вероятностный прогноз к дираковскому распределению, CRPS даст вам значение, которое точно совпадает с абсолютной ошибкой.

Хотя CRPS может показаться довольно устрашающим и сложным, его реализация на самом деле достаточно проста. На экране представлен небольшой скрипт на Envision, который иллюстрирует, как CRPS может использоваться с точки зрения программирования. Envision — это предметно-ориентированный язык программирования, предназначенный для предиктивной оптимизации цепочек поставок, разработанный компанией Lokad. В этих лекциях я использую Envision ради ясности и краткости. Однако обратите внимание, что нет ничего уникального в Envision; те же результаты можно было бы получить на любом другом языке программирования, будь то Python, Java, JavaScript, C#, F# или любой другой. Моя мысль в том, что это просто потребовало бы больше строк кода, поэтому я остаюсь с Envision. Все приведённые фрагменты кода в этой лекции и, кстати, в предыдущих, являются автономными и полными. Вы могли бы технически скопировать и вставить этот код, и он бы работал. Нет никаких модулей, скрытого кода или необходимости настраивать окружение.
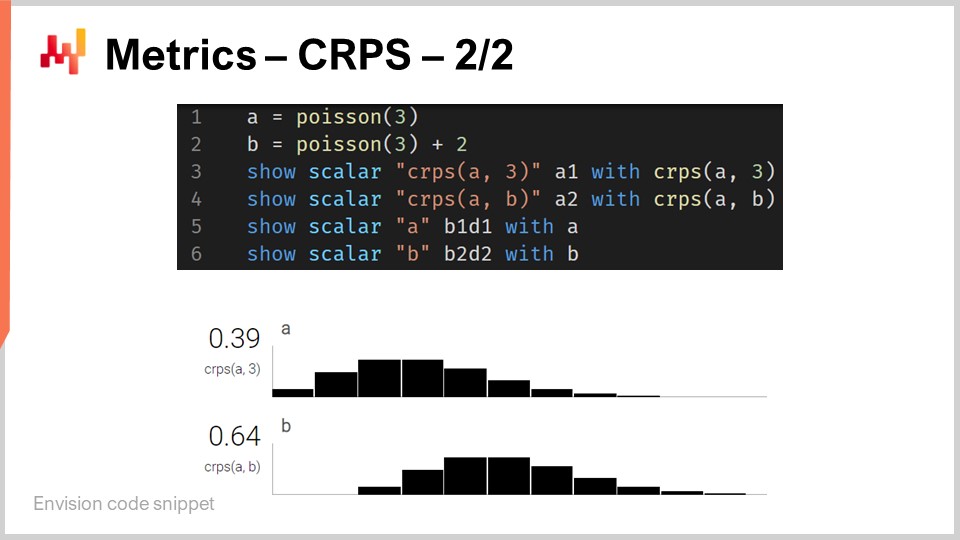
Итак, возвращаясь к фрагменту кода. В строках один и два мы определяем одномерные распределения. Я вернусь к тому, как именно эти одномерные распределения работают в Envision, но здесь у нас два распределения: одно — пуассоновское распределение, которое является одномерным дискретным распределением, а второе на строке два — то же самое пуассоновское распределение, но смещённое на 2 единицы вправо. Именно это означает “+2”. На строке три мы вычисляем расстояние CRPS между распределением и значением 3, которое является числом. Таким образом, здесь мы наблюдаем асимметрию с точки зрения типов данных, о которой я упоминал. Далее результаты отображаются внизу, как вы можете видеть в нижней части экрана.
На строке четыре мы вычисляем CRPS между распределением A и распределением B. Хотя классическое определение CRPS подразумевает вычисление между распределением и отдельной точкой, вполне очевидно обобщить это определение для пары распределений. Всё, что вам нужно сделать, — это взять ту же самую формулу для CRPS и заменить функцию Хевисайда на функцию накопленного распределения второго распределения. Операторы “show” со строк с трёх по шесть приводят к отображению, которое вы видите в нижней части экрана, что буквально является снимком экрана.
Таким образом, мы видим, что использование CRPS не сложнее и не труднее, чем использование какой-либо специальной функции, например, функции косинуса. Конечно, если вам пришлось бы самому реализовывать косинус, это было бы немного затруднительно, но, учитывая всё, нет ничего особенно сложного в CRPS. А теперь, давайте продолжим.

Задача Монжа-Канторовича даёт нам представление о том, как можно подходить к процессу сопоставления форм, как в CRPS, только уже в более высоких измерениях. Помните, что CRPS на самом деле ограничен одним измерением. Сопоставление форм концептуально может быть обобщено на любое число измерений, и задача Монжа-Канторовича очень интересна, тем более что, в своей основе, она на самом деле является задачей в цепочке поставок.
Задача Монжа-Канторовича, изначально не связанная с вероятностным прогнозированием, была представлена французским учёным Гаспаром Монжем в труде 1781 года под названием “Mémoire sur la théorie des déblais et des remblais”, что можно приблизительно перевести как “Мемуары о теории перемещения грунта”. Один из способов понять задачу Монжа-Канторовича — представить ситуацию, в которой у нас есть список шахт, обозначенных как M на экране, и список заводов, обозначенных как F. Шахты добывают руду, а заводы её потребляют. Наша цель — составить транспортный план T, который сопоставляет всю руду, добываемую шахтами, с потребностями заводов.
Монж определил капитал C как стоимость перемещения всей руды от шахт к заводам. Стоимость представляет собой сумму затрат на транспортировку всей руды от каждой шахты к каждому заводу, но, очевидно, существуют крайне неэффективные способы транспортировки руды. Таким образом, когда мы говорим, что существует определённая стоимость, мы подразумеваем, что эта стоимость отражает оптимальный транспортный план. Этот капитал C представляет собой наилучшую стоимость, достижимую с учётом оптимального транспортного плана.
Это, по сути, проблема цепочки поставок, которая была всесторонне изучена на протяжении веков. В полной формулировке задачи существуют ограничения на T. Ради краткости, я не показывал все ограничения на экране. Например, существует ограничение, что транспортный план не должен превышать производственные мощности каждой шахты, а каждое предприятие должно быть полностью удовлетворено, получив распределение, соответствующее его требованиям. Ограничений много, но они довольно многословны, поэтому я не включил их в показ.
Теперь, хотя задача транспортировки сама по себе интересна, если мы начнем интерпретировать список шахт и список заводов как два распределения вероятностей, мы получим способ преобразовать метрику, измеряемую по точкам, в метрику, измеряемую по распределению. Это ключевое наблюдение в сопоставлении форм в более высоких измерениях через призму Моне-Канторовского подхода. Другой термин для этого подхода — метрика Васерштейна, хотя он в основном касается недискретного случая, который для нас менее важен.
Моне-Канторовский подход позволяет преобразовать метрику, измеряемую по точкам, которая может вычислять разницу между двумя числами или двумя векторами чисел, в метрику, применимую к распределениям вероятностей, работающим в одном и том же пространстве. Это очень мощный механизм. Однако задача Моне-Кантора оказывается сложной для решения и требует значительных вычислительных ресурсов. В оставшейся части лекции я буду использовать техники, которые проще реализовать и выполнить.

Баезиановский подход заключается в рассмотрении серии наблюдений с точки зрения априорных убеждений. Баезиановский взгляд обычно противопоставляется фрейкуентистскому подходу, который оценивает частоту событий на основе фактических наблюдений. Идея заключается в том, что фрейкуентистский метод не предполагает наличие априорных убеждений. Таким образом, баезиановский подход предоставляет нам инструмент, известный как правдоподобие, для оценки степени неожиданности при анализе наблюдений и данной модели. Модель, которая по сути является моделью вероятностного прогнозирования, представляет собой формализацию наших априорных убеждений. Баезиановский подход позволяет оценить набор данных с точки зрения модели вероятностного прогнозирования. Чтобы понять, как это делается, следует начать с правдоподобия для одной точки данных. Правдоподобие, когда у нас есть наблюдение x, — это вероятность наблюдения x согласно модели. Здесь предполагается, что модель полностью характеризуется параметрами theta. Баезиановский подход обычно предполагает, что модель имеет некоторую параметрическую форму, а theta является полным вектором всех параметров модели.
Когда мы говорим о theta, мы подразумеваем, что у нас есть полное описание вероятностной модели, которое дает нам локальную функцию плотности для всех точек. Таким образом, правдоподобие — это вероятность наблюдения этой единственной точки данных. Когда у нас есть правдоподобие для модели theta, оно представляет собой совместную вероятность наблюдения всех точек данных в наборе. Мы предполагаем, что эти точки независимы, поэтому правдоподобие является произведением вероятностей.
Если у нас есть тысячи наблюдений, правдоподобие, будучи произведением тысяч значений, меньших единицы, скорее всего, станет численно ничтожно малым. Такое ничтожно малое значение обычно трудно представить в форме, в которой хранятся числа с плавающей запятой в компьютерах. Вместо того чтобы работать напрямую с правдоподобием, которое является ничтожно малым числом, мы предпочитаем работать с логарифмом правдоподобия. Логарифм правдоподобия — это просто логарифм правдоподобия, обладающий удивительным свойством превращать умножение в сложение.
Логарифм правдоподобия для модели theta представляет собой сумму логарифмов всех отдельных правдоподобий для всех точек данных, как показано в последней строке уравнения на экране. Правдоподобие — это метрика, отражающая качество подгонки для данного вероятностного прогноза. Оно показывает, с какой вероятностью модель сгенерировала наблюдаемый нами набор данных. Если у нас есть два конкурирующих вероятностных прогноза, и если на время отложить все остальные вопросы подгона модели, следует выбрать ту модель, которая дает наибольшее правдоподобие или наибольший логарифм правдоподобия, поскольку чем выше, тем лучше.
Правдоподобие очень интересно тем, что оно может работать в высоких измерениях без сложностей, в отличие от метода Моне-Кантора. Пока у нас есть модель, предоставляющая локальную плотность вероятности, мы можем использовать правдоподобие, или, что более реалистично, логарифм правдоподобия, в качестве метрики.

Более того, как только у нас появляется метрика, способная представлять качество подгонки, это означает, что мы можем оптимизировать модель относительно этой же метрики. Все, что необходимо — это модель с хотя бы одной степенью свободы, что, по сути, означает, что в ней есть хотя бы один параметр. Если мы оптимизируем эту модель по критерию правдоподобия, нашей метрике качества подгонки, то, надеюсь, получим обученную модель, которая способна выдавать хотя бы приемлемый вероятностный прогноз. Именно это и демонстрируется на экране.
На строках один и два мы генерируем модельный набор данных. Мы создаем таблицу с 2000 строк, а затем на строке два генерируем 2000 случайных отклонений, наших наблюдений из распределения Пуассона со средним значением два. Таким образом, у нас есть 2000 наблюдений. На строке три мы запускаем блок autodiff, который является частью парадигмы дифференцируемого программирования. Этот блок будет выполнять стохастический градиентный спуск и многократно перебирать все наблюдения из таблицы наблюдений. Здесь таблица наблюдений называется T.
На строке четыре мы объявляем единственный параметр модели, называемый lambda. Мы указываем, что этот параметр должен быть исключительно положительным. Именно этот параметр мы попытаемся восстановить с помощью стохастического градиентного спуска. На строке пять мы определяем функцию потерь, которая представляет собой минус логарифм правдоподобия. Мы хотим максимизировать правдоподобие, но блок autodiff стремится минимизировать функцию потерь. Таким образом, если мы хотим максимизировать логарифм правдоподобия, нам необходимо добавить этот минус перед логарифмом правдоподобия, что и было сделано.
Выученный параметр lambda выводится на экран на строке шесть. Неудивительно, что найденное значение очень близко к двум, поскольку мы исходили из распределения Пуассона со средним значением два. Мы создали модель вероятностного прогнозирования, которая также параметрическая и имеет ту же форму, то есть распределение Пуассона. Мы хотели восстановить единственный параметр распределения Пуассона, и именно это и произошло. Мы получаем модель, значение которой отличается примерно на один процент от первоначальной оценки.
Мы только что изучили нашу первую модель вероятностного прогнозирования, и все, что для этого потребовалось, — это, по сути, три строки кода. Очевидно, что эта модель очень простая; тем не менее, она показывает, что в вероятностном прогнозировании нет ничего по своей сути сложного. Это не обычный прогноз по среднеквадратичной ошибке, но, помимо этого, с правильными инструментами, такими как дифференцируемое программирование, он не сложнее классического точечного прогноза.
Функция log_likelihood.poisson, которую мы использовали ранее, является частью стандартной библиотеки Envision. Однако здесь нет ничего волшебного. Давайте посмотрим, как эта функция реализована изнутри. Первые две строки вверху представляют собой реализацию логарифма правдоподобия для распределения Пуассона. Распределение Пуассона полностью характеризуется своим единственным параметром, lambda, и функция логарифма правдоподобия принимает только два аргумента: этот единственный параметр, полностью характеризующий распределение Пуассона, и фактическое наблюдение. Фактическая формула, которую я написал, — это буквально учебный материал. Это то, что вы получаете, когда реализуете учебную формулу, описывающую распределение Пуассона. Здесь нет ничего изысканного.
Обратите внимание на то, что эта функция помечена ключевым словом autodiff. Как мы видели в предыдущей лекции, ключевое слово autodiff обеспечивает корректное прохождение автоматического дифференцирования через эту функцию. Логарифм правдоподобия распределения Пуассона также использует другую специальную функцию, log_gamma. Функция log_gamma — это логарифм гамма-функции, которая является обобщением функции факториала для комплексных чисел. Здесь нам нужно лишь обобщение функции факториала для положительных вещественных чисел.
Реализация функции log_gamma немного многословна, но опять же это учебный материал. Она использует приближение в виде цепной дроби для функции log_gamma. Прелесть в том, что автоматическое дифференцирование работает для нас на всех уровнях. Мы начинаем с блока autodiff, вызываем функцию log_likelihood.poisson, которая реализована как функция с поддержкой autodiff. Эта функция, в свою очередь, вызывает функцию log_gamma, также реализованную с маркером autodiff. По сути, мы можем создать наши вероятностные методы прогнозирования в три строки кода, потому что у нас есть хорошо спроектированная стандартная библиотека, реализованная с учетом автоматического дифференцирования.
Теперь перейдем к особому случаю одномерных дискретных распределений. Эти распределения повсюду в цепочке поставок и представляют собой нашу точку входа в вероятностное прогнозирование. Например, если мы хотим прогнозировать сроки поставки с дневной детализацией, мы можем сказать, что существует определенная вероятность того, что срок поставки составит один день, другая вероятность — что он составит два дня, три дня и так далее. Всё это формирует гистограмму вероятностей для сроков поставки. Аналогично, если мы рассматриваем спрос для данной SKU в определенный день, мы можем сказать, что существует вероятность наблюдения нулевого спроса, одного, двух единиц спроса и так далее.
Если мы соберем все эти вероятности вместе, мы получим гистограмму, их представляющую. Аналогично, если мы рассматриваем уровень запасов для SKU, нас может заинтересовать, сколько запасов останется для данного SKU в конце сезона. Мы можем использовать вероятностный прогноз, чтобы определить вероятность того, что в конце сезона у нас останется ноль единиц запасов, одна единица, две единицы и так далее. Все эти ситуации соответствуют схеме, в которой каждое отдельное дискретное событие представлено в виде корзины гистограммы.
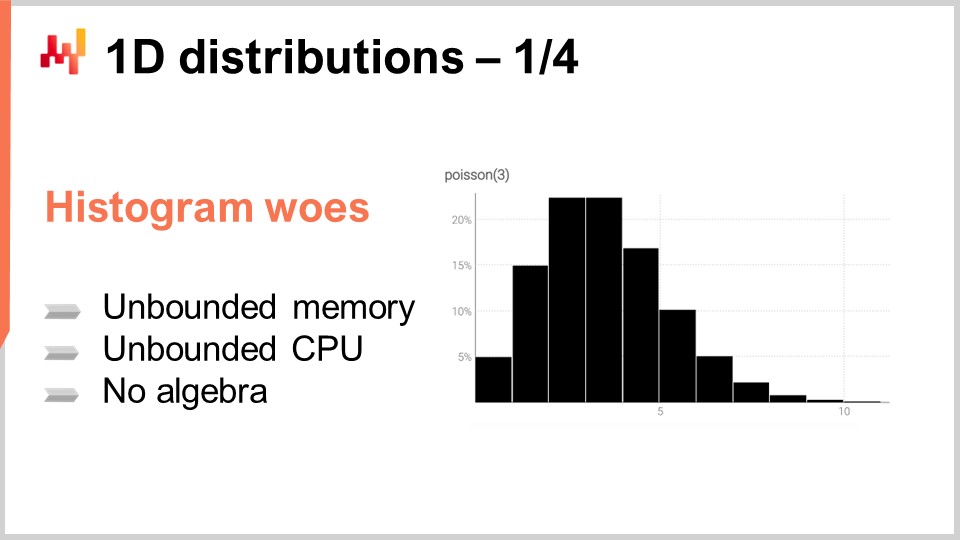
Гистограмма является каноническим способом представления одномерного дискретного распределения. Каждая корзина соответствует вероятностной массе дискретного события. Однако, отклав в сторону использование гистограмм для визуализации данных, гистограммы кажутся несколько скудными. Действительно, работа с гистограммами оказывается затруднительной, если мы хотим делать нечто большее, чем просто визуализировать эти распределения вероятностей. По существу, у гистограмм есть два класса проблем: первая связана с вычислительными ресурсами, а вторая — с выразительностью программирования гистограмм.
С точки зрения вычислительных ресурсов, следует учитывать, что объем памяти, необходимый для гистограммы, в принципе неограничен. Можно воспринимать гистограмму как массив, который растет до необходимого размера. При работе с одной гистограммой, даже если она исключительно большая с точки зрения цепочки поставок, объем памяти не представляет проблемы для современного компьютера. Проблема возникает, когда у вас есть не одна гистограмма, а миллионы гистограмм для миллионов SKU в контексте цепочки поставок. Если каждая гистограмма может быть довольно большой, управление этими гистограммами может стать вызовом, особенно учитывая, что современные компьютеры, как правило, предлагают неравномерный доступ к памяти.
Наоборот, объем процессорного времени, необходимый для обработки этих гистограмм, также неограничен. Несмотря на то, что операции с гистограммами в основном являются линейными, время обработки увеличивается по мере роста объема памяти из-за неравномерного доступа к ней. В результате возникает значительный интерес к установлению строгих ограничений на объем необходимой памяти и CPU.
Вторая проблема гистограмм заключается в отсутствии присущей им алгебры. Хотя вы можете выполнять покорзинное сложение или умножение значений при сравнении двух гистограмм, такая операция не приведет к осмысленному результату, если трактовать гистограмму как представление случайной величины. Например, если вы возьмете две гистограммы и выполните покомпонентное умножение, в итоге получите гистограмму, суммарная вероятность которой даже не равна одному. Это недопустимая операция с точки зрения алгебры случайных величин. Фактически, сложение или умножение гистограмм невозможно, поэтому возможности их использования ограничены.
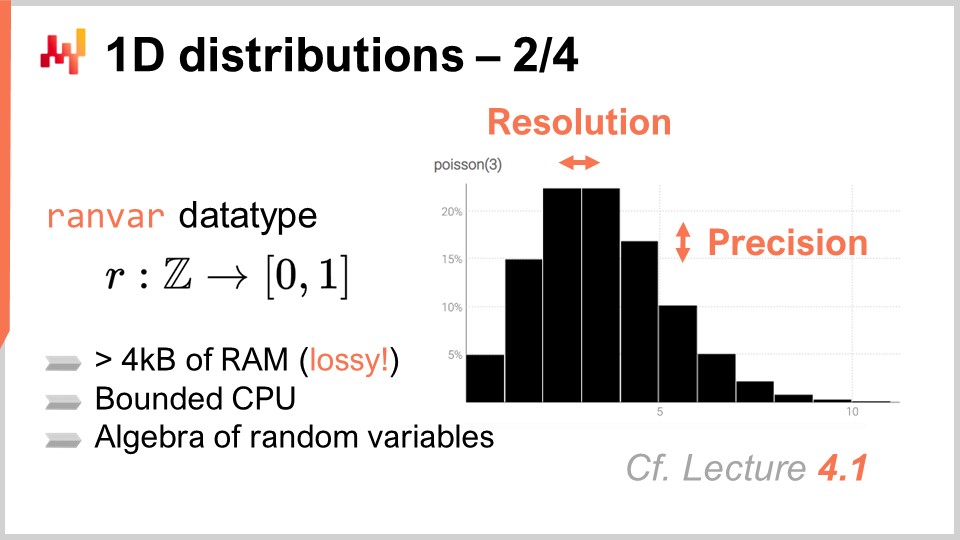
В компании Lokad самый практичный подход к работе с этими вездесущими одномерными дискретными распределениями — это введение специализированного типа данных. Вероятно, аудитория знакома с обычными типами данных, присутствующими в большинстве языков программирования, такими как целые числа, числа с плавающей запятой и строки. Это типичные примитивные типы данных, встречающиеся повсеместно. Однако ничто не мешает вам вводить более специализированные типы данных, которые особенно подходят для наших требований с точки зрения цепочки поставок. Именно это и сделала компания Lokad, представив тип данных ranvar.
Тип данных ranvar предназначен для одномерных дискретных распределений, и его название является сокращением от «random variable» (случайная величина). С технической точки зрения, в формальном плане, ranvar — это функция от Z (множества всех целых чисел, как положительных, так и отрицательных) к вероятностям, которые являются числами от нуля до единицы. Общая масса Z всегда равна одному, так как она представляет собой распределение вероятностей.
С чисто математической точки зрения, некоторые могут утверждать, что объем информации, который можно вложить в такую функцию, может быть произвольно большим. Это правда; однако, с точки зрения цепочки поставок, существует очень четкий предел тому, сколько релевантной информации может содержаться в одном ranvar. Хотя теоретически возможно создать вероятностьное распределение, которое потребовало бы мегабайт для представления, таких распределений, имеющих практическую значимость для цепочки поставок, не существует.
Возможно разработать верхнюю границу в 4 килобайта для типа данных ranvar. Установив ограничение на объем памяти, которую может занимать этот ranvar, мы также получаем предельную нагрузку на процессор для всех операций, что очень важно. Вместо наивного ограничения, ограничивающего количество корзин до 1,000, Lokad вводит схему сжатия для типа данных ranvar. Это сжатие представляет собой с потерями репрезентацию исходных данных, теряя разрешение и точность. Однако идея состоит в том, чтобы разработать схему сжатия, которая обеспечивает достаточно точное представление гистограмм, так что степень введенной аппроксимации ничтожно мала с точки зрения цепочки поставок.
Мелкие нюансы алгоритма сжатия, связанного с типом данных ranvar, выходят за рамки этой лекции. Однако это очень простой алгоритм сжатия, который на порядки проще алгоритмов, используемых для сжатия изображений на вашем компьютере. В качестве дополнительного преимущества ограничения объема памяти, который может занимать этот ranvar, мы также получаем верхнюю границу нагрузки на процессор для всех операций, что крайне важно. Наконец, с типом данных ranvar самое важное заключается в том, что мы получаем алгебру переменных, позволяющую нам фактически работать с этими типами данных и выполнять все те операции, которые мы хотим делать с примитивными типами данных, то есть иметь всевозможные примитивы для их комбинации в соответствии с нашими требованиями.
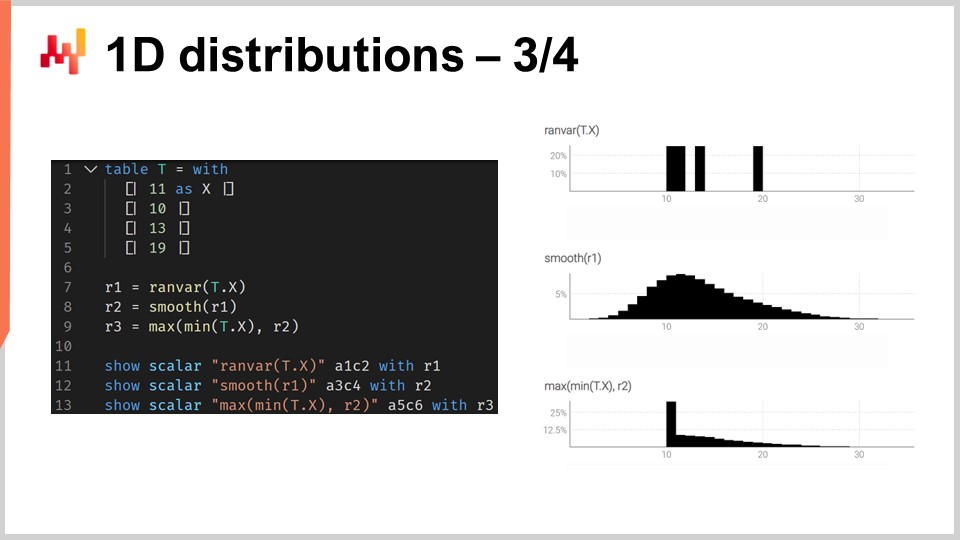
Чтобы проиллюстрировать, что означает работа с ranvar, рассмотрим ситуацию прогнозирования времени выполнения заказа, а точнее, вероятностного прогнозирования времени выполнения заказа. На экране представлен короткий скрипт Envision, демонстрирующий, как построить такой вероятностный прогноз. На строках 1-5 мы представляем таблицу T, которая содержит четыре варианта времени выполнения заказа со значениями 11 дней, 10 дней, 13 дней и 90 дней. Хотя четыре наблюдения — это очень мало, к сожалению, весьма часто так бывает, что данных по времени выполнения заказа очень ограничено. Действительно, если рассматривать зарубежного поставщика, который получает два заказа в год, для сбора этих четырех точек потребуется два года. Поэтому важно иметь методики, способные работать даже с невероятно ограниченным набором наблюдений.
На строке 7 мы создаем ranvar, напрямую агрегируя четыре наблюдения. Здесь термин “ranvar”, появляющийся на строке 7, фактически является агрегатором, который принимает серию чисел в качестве входных данных и возвращает одно значение типа данных ranvar. Результат отображается в верхнем правом углу экрана — это эмпирический ranvar.
Однако этот эмпирический ranvar не является реалистичным отображением фактического распределения. Например, хотя мы можем наблюдать время выполнения заказа в 11 дней и в 13 дней, кажется нереалистичным, если невозможно наблюдать время выполнения заказа в 12 дней. Если интерпретировать этот ranvar как вероятностный прогноз, он покажет, что вероятность наблюдения времени выполнения заказа в 12 дней равна нулю, что выглядит неверно. Очевидно, что это проблема переобучения.
Чтобы исправить эту ситуацию, на строке 8 мы сглаживаем исходный ranvar, вызывая функцию “smooth”. Функция smooth по сути заменяет исходный ranvar смесью распределений. Для каждой корзины исходного распределения мы заменяем ее распределением Пуассона со средним, центрированным на этой корзине, с весом, соответствующим вероятности этой корзины. Благодаря сглаженному распределению мы получаем гистограмму, отображаемую в центре справа на экране. Теперь все выглядит гораздо лучше; пропусков, как раньше, нет, и посередине отсутствует нулевая вероятность. Более того, при рассмотрении вероятности наблюдения времени выполнения заказа в 12 дней эта модель дает ненулевую вероятность, что выглядит гораздо разумнее. Она также дает ненулевую вероятность превышения 20 дней, и, учитывая, что у нас было четыре точки данных и мы уже наблюдали время выполнения заказа в 19 дней, идея о том, что время выполнения может достигать 20 дней, кажется весьма разумной. Таким образом, с этим вероятностным прогнозом мы получаем приличное распределение, которое демонстрирует ненулевую вероятность для этих событий, что очень хорошо.
Однако, слева у нас наблюдается нечто странное. Пока нормально, что это распределение вероятностей распространяется вправо, то же нельзя сказать о левой стороне. Если учесть, что наблюдавшиеся времена выполнения заказа являются результатом транспортировки, поскольку грузовику требуется девять дней для прибытия (truck остается неизменным), маловероятно, что мы когда-либо наблюдали время выполнения заказа в три дня. В этом отношении модель выглядит довольно нереалистичной.
Таким образом, на строке 9 мы вводим условно скорректированный ranvar, устанавливая требование, чтобы его значение было больше, чем самое маленькое время выполнения заказа, когда-либо наблюдавшееся. Мы используем “min_of(T, x)”, которое выбирает минимальное значение из чисел таблицы T, а затем используем “max”, чтобы вычислить максимум между распределением и числом. Результат должен быть больше этого значения. Скорректированный ranvar отображается справа в самом нижнем углу, и здесь мы видим наш окончательный прогноз времени выполнения заказа. Последний выглядит как вполне разумный вероятностный прогноз времени выполнения, учитывая, что у нас крайне ограниченный набор данных всего из четырех точек. Мы не можем утверждать, что это превосходный вероятностный прогноз; однако я бы сказал, что это прогноз промышленного уровня, и такого рода методики отлично работают в производственной среде, в отличие от обычного точечного прогноза, который существенно недооценивает риск вариативности времени выполнения заказа.
Преимущество вероятностных прогнозов заключается в том, что, хотя они могут быть весьма примитивными, они уже предоставляют определенный потенциал для смягчения последствий необоснованных решений, которые могли бы возникнуть при наивном применении среднего прогноза, основанного на наблюдаемых данных.
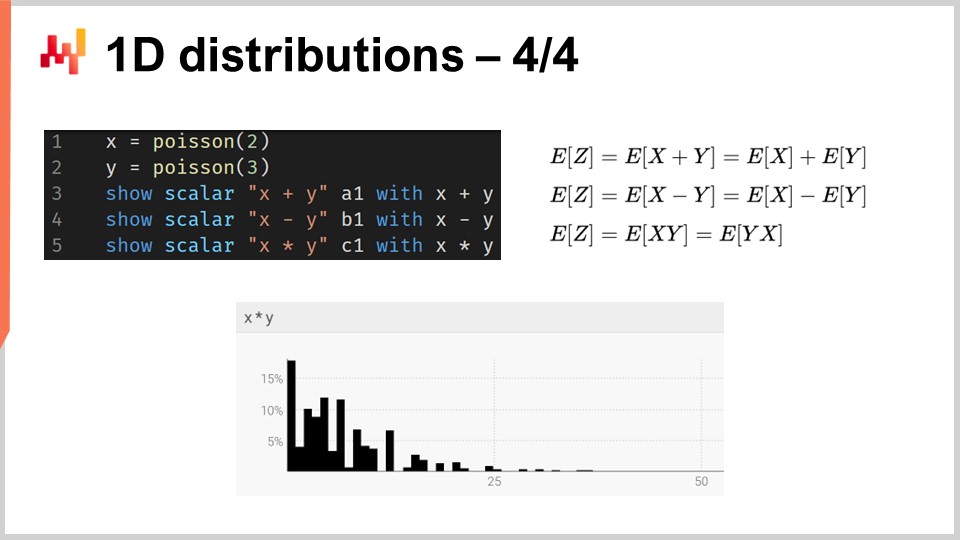
В более общем смысле, ranvar поддерживает целый ряд операций: можно складывать, вычитать и умножать ranvar, как можно складывать, вычитать и умножать целые числа. Под капотом, поскольку мы имеем дело с дискретными случайными величинами с точки зрения семантики, все эти операции реализованы через свертки. На экране гистограмма внизу получается в результате умножения двух распределений Пуассона, со средними значениями два и три соответственно. В цепочке поставок умножение случайных величин называется прямой сверткой. В контексте цепочки поставок умножение двух случайных величин имеет смысл для представления, например, результатов, которые можно получить, когда клиенты выбирают одни и те же продукты, но с различными множителями. Допустим, у нас есть книжный магазин, обслуживающий две группы клиентов. С одной стороны, первая группа состоит из студентов, которые покупают один экземпляр, заходя в магазин. В этом иллюстративном магазине вторая группа состоит из профессоров, которые приобретают 20 книг при входе в магазин.
С точки зрения моделирования, мы могли бы иметь один вероятностный прогноз, представляющий уровень поступления клиентов в книжный магазин — как студентов, так и профессоров. Это дало бы вероятность того, что за день не придет ни один клиент, один клиент, два клиента и так далее, раскрывая распределение вероятности наблюдения определенного числа клиентов в любой сутки. Вторая переменная предоставила бы соответствующие вероятности покупки одного экземпляра (студентами) по сравнению с покупкой 20 экземпляров (профессорами). Чтобы получить представление о спросе, мы просто перемножаем эти две случайные величины, что приводит к, на первый взгляд, хаотичной гистограмме, отражающей множители, присутствующие в потребительских моделях ваших групп.

Генераторы Монте-Карло, или просто генераторы, представляют собой альтернативный подход к вероятностному прогнозированию. Вместо того чтобы демонстрировать распределение, которое дает локальную плотность вероятности, мы можем использовать генератор, который, как следует из названия, генерирует результаты, ожидаемо следующие тем же локальным распределениям вероятности. Существует двойственность между генераторами и плотностями вероятности, что означает, что они по сути являются двумя сторонами одного и того же подхода.
Если у вас есть генератор, всегда можно усреднить полученные им результаты, чтобы восстановить оценки локальных плотностей вероятности. И наоборот, если у вас есть локальные плотности вероятности, всегда можно сгенерировать отклонения в соответствии с этим распределением. По сути, эти два подхода — это просто разные способы взглянуть на ту же вероятностную или стохастическую природу явления, которое мы пытаемся моделировать.
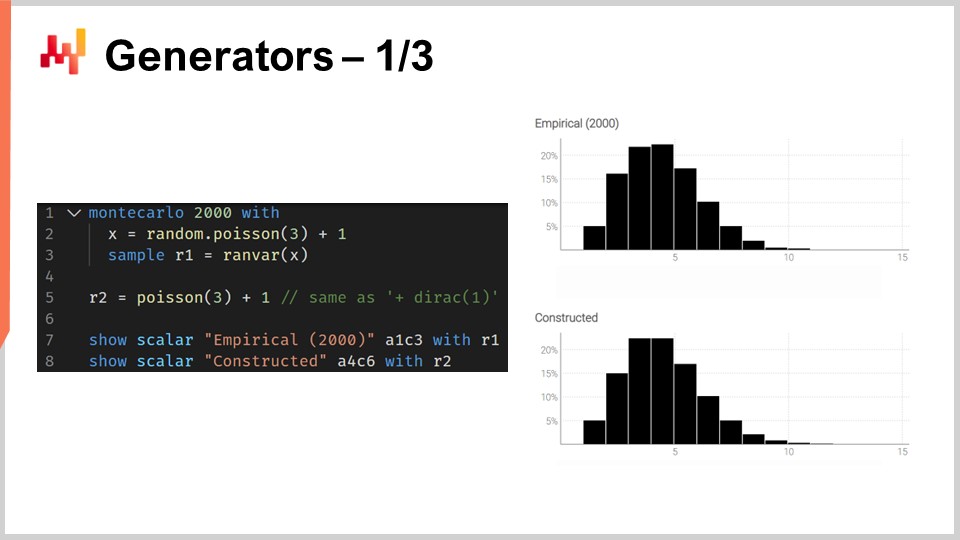
Скрипт на экране иллюстрирует эту двойственность. На строке один мы вводим блок Монте-Карло, который будет выполняться системой, как и блоки автодифференцирования, проходящие через множество шагов стохастического градиентного спуска. Блок Монте-Карло будет выполнен 2,000 раз, и из этого блока мы соберем 2,000 отклонений.
На строке два мы генерируем отклонение из распределения Пуассона со средним значением три, а затем прибавляем к нему единицу. По сути, мы получаем случайное число из этого распределения и прибавляем один. На строке три мы собираем это отклонение в L1, который выступает в роли аккумулятора для агрегатора ranvar. Это тот же самый агрегатор, который мы вводили ранее в примере с временем выполнения заказа. Здесь мы собираем все наблюдения в L1, что дает нам одномерное распределение, полученное посредством процесса Монте-Карло. На строке пять мы строим точно такое же одномерное дискретное распределение, но на этот раз с использованием алгебры случайных величин. Таким образом, мы просто используем выражение Poisson минус три и прибавляем единицу. На строке пять не происходит процесса Монте-Карло; это чисто дело дискретных вероятностей и сверток.
Когда мы визуально сравниваем два распределения на строках семь и восемь, мы видим, что они почти идентичны. Я говорю “почти”, потому что, хотя мы используем 2,000 итераций, что довольно много, это не бесконечно. Отклонения между точными вероятностями, полученными с помощью ranvar, и приближенными вероятностями, полученными посредством Монте-Карло, все еще заметны, хоть и не велики.
Генераторы иногда называют симуляторами, но без заблуждений — это одно и то же. Когда у вас есть симулятор, у вас есть генеративный процесс, который неявно лежит в основе процесса вероятностного прогнозирования. Если используется симулятор или генератор, вопрос, который должен возникать, таков: какова точность этой симуляции? Она не является точной по замыслу, так же как можно получить совершенно неточные прогнозы, вероятностные или нет. Вы очень легко можете получить совершенно неточную симуляцию.
С помощью генераторов мы видим, что симуляции — это лишь один из способов взглянуть на перспективу вероятностного прогнозирования, но это больше техническая деталь. Это не меняет того факта, что в конечном итоге вы хотите получить нечто, что точно отражает систему, которую пытаетесь охарактеризовать своим прогнозом, вероятностным или нет.
Генеративный подход не только очень полезен, как мы увидим на конкретном примере через минуту, но и концептуально несколько легче для восприятия по сравнению с подходом через плотности вероятности. Однако подход Монте-Карло не лишен технических особенностей. Есть несколько важных моментов, если вы хотите сделать этот подход жизнеспособным в производственной среде для реальной цепочки поставок.
Во-первых, генераторы должны быть быстрыми. Монте-Карло всегда представляет собой компромисс между числом итераций, которые вы хотели бы иметь, и числом итераций, которые вы можете себе позволить, учитывая доступные вычислительные ресурсы. Да, современные компьютеры обладают огромной вычислительной мощностью, но процессы Монте-Карло могут потреблять невероятное количество ресурсов. Вам нужно, чтобы они по умолчанию были сверхбыстрыми. Если вернуться к ингредиентам, представленным во второй лекции четвертой главы, у нас есть очень быстрые функции, такие как ExhaustShift или WhiteHash, которые являются ключевыми для построения примитивов, позволяющих генерировать элементарные случайные генераторы с высокой скоростью. Это необходимо, иначе у вас будут проблемы. Во-вторых, нужно распределять выполнение. Наивная реализация программы Монте-Карло сводится к циклу, выполняющемуся последовательно. Однако, если вы используете только один процессор для удовлетворения требований Монте-Карло, вы фактически возвращаетесь к вычислительной мощности, которая была у компьютеров двадцать лет назад. Этот момент был затронут уже на первой лекции четвертой главы. За последние два десятилетия компьютеры стали мощнее, но в основном за счет добавления процессоров и повышения степени параллелизма. Таким образом, необходим распределенный подход для ваших генераторов.
Наконец, выполнение должно быть детерминированным. Что это означает? Это означает, что если один и тот же код запускается дважды, он должен давать абсолютно одинаковые результаты. Это может показаться противоинтуитивным, поскольку мы имеем дело с рандомизированными методами. Однако необходимость детерминизма проявилась очень быстро. Это было болезненно обнаружено в 90-х годах, когда финансы начали использовать генераторы Монте-Карло для ценообразования. Финансовая сфера уже давно пошла путем вероятностного прогнозирования и широко использовала генераторы Монте-Карло. Одно из того, чему они научились, заключалось в том, что если нет детерминизма, становится почти невозможно воспроизвести условия, вызвавшие ошибку или сбой. С точки зрения цепочки поставок ошибки в расчетах заказов могут оказаться невероятно дорогостоящими.
Если вы хотите достичь определенного уровня готовности программного обеспечения, управляющего вашей цепочкой поставок, вам необходимо обеспечить детерминированность всякий раз, когда вы работаете с Монте-Карло. Учтите, что многие решения с открытым исходным кодом поступают из академической среды и совершенно не заботятся о готовности к производству. Убедитесь, что при работе с Монте-Карло ваш процесс по замыслу является сверхбыстрым, распределенным и детерминированным, чтобы у вас была возможность диагностировать ошибки, которые неизбежно возникнут со временем в вашей производственной среде.
Мы видели ситуацию, когда генератор был введён для воспроизведения того, что обычно выполнялось с помощью ranvar. Как правило, когда можно обойтись только плотностями вероятности и случайными величинами без участия Монте-Карло, это лучше. Вы получаете более точные результаты и не беспокоитесь о численной стабильности, которая всегда несколько проблематична при использовании Монте-Карло. Однако выразительность алгебры случайных величин ограничена, и именно здесь Монте-Карло действительно сияет. Эти генераторы более выразительны, потому что позволяют охватывать ситуации, с которыми невозможно справиться только алгеброй случайных величин.
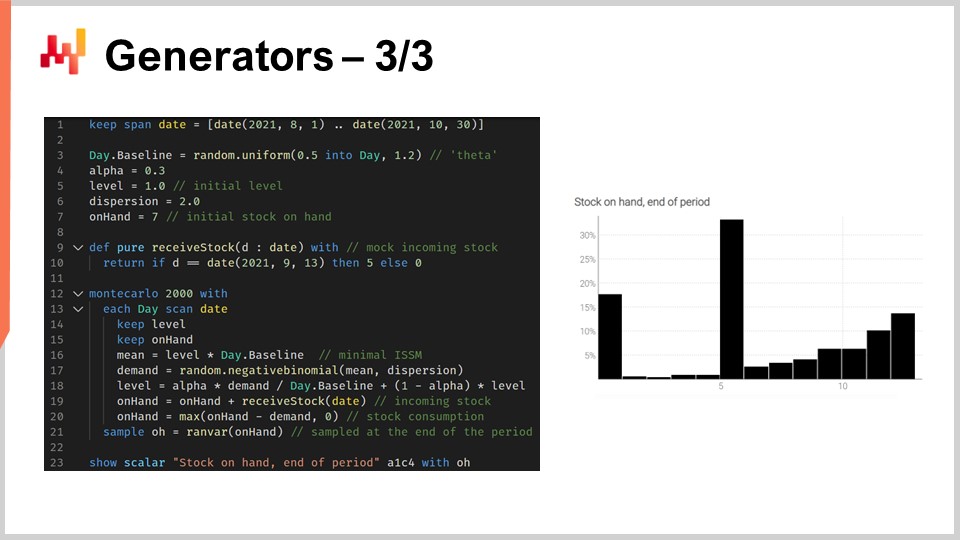
Давайте проиллюстрируем это на примере логистической цепочки. Рассмотрим один SKU с начальным уровнем запасов, вероятностным прогнозом спроса и периодом, охватывающим три месяца, с поступлением товара в середине периода. Мы предполагаем, что спрос либо сразу удовлетворяется за счёт имеющихся запасов, либо теряется навсегда. Нам необходимо знать ожидаемый уровень запасов в конце периода для этого SKU, поскольку это поможет определить, насколько велик риск замороженных запасов.
Ситуация опасна, потому что она разработана таким образом, что существует третий шанс возникновения дефицита товара прямо в середине периода. Наивный подход заключался бы в том, чтобы взять начальный уровень запасов, распределение спроса за весь период и вычесть спрос из запасов, получив оставшиеся запасы. Однако это не учитывает того факта, что мы можем потерять значительную часть спроса, если произойдёт дефицит в то время, когда поступление пополнения запасов ещё не произошло. Такой наивный подход приведёт к недооценке количества запасов в конце периода и переоценке объёма обслуженного спроса.
Представленный скрипт моделирует возникновение дефицита, чтобы мы могли получить корректную оценку уровня запасов этого SKU в конце периода. Со строк 1 по 10 мы задаём тестовые данные, характеризующие нашу модель. Строки 3–6 содержат параметры модели ISSM. Мы уже видели модель ICSM в самой первой лекции этой пятой главы. По сути, эта модель генерирует траекторию спроса с одной точкой данных в день. Период, представляющий интерес, определяется в таблице дней, а параметры для этой траектории задаются в самом начале.
В предыдущих лекциях мы представили модель AICSM и методы, необходимые с помощью дифференцируемого программирования для обучения этим параметрам. Сегодня мы используем модель, предполагая, что всё необходимое уже изучено. На строке 7 мы определяем начальный уровень запасов, который обычно получают из ERP или WMS. В строках 9 и 10 задаём количество и дату пополнения. Эти данные обычно получаются в виде предполагаемого времени прибытия, указанного поставщиком и сохранённого в ERP. Мы предполагаем, что дата доставки известна с абсолютной точностью; однако заменить эту единственную дату на вероятностный прогноз срока поставки было бы довольно просто.
Со строк 12 по 21 находится модель ISSM, которая генерирует траекторию спроса. Мы находимся внутри цикла Монте-Карло, и для каждой итерации этого цикла перебираем каждый день интересующего периода. Итерация по дням начинается на строке 13. Механика ESSM работает, но на строках 19 и 20 мы обновляем переменную запасов на руках. Эта переменная не является частью модели ISSM; она добавлена дополнительно. На строке 19 мы указываем, что запасы на руках равны запасам от вчера плюс поступление, которое будет равно нулю в большинство дней и составит пять единиц 13 сентября. Затем, на строке 20, мы обновляем запасы, вычитая количество единиц, потреблённых в течение дня, при этом с помощью функции max 0 гарантируем, что уровень запасов не станет отрицательным.
Наконец, на строке 21 мы фиксируем итоговые запасы, а на строке 23 эти итоговые запасы выводятся на экран. Это гистограмма, которую вы видите справа. Здесь мы наблюдаем распределение с очень нерегулярной формой. Эту форму нельзя получить с помощью алгебры случайных величин. Генераторы невероятно выразительны; однако не стоит путать их выразительность с точностью. Хотя генераторы чрезвычайно выразительны, оценить их точность не так просто. Без заблуждений: каждый раз, когда используется генератор или симулятор, применяется вероятностный прогноз, и симуляции могут оказаться драматически неточными, как и любой прогноз, независимо от его вероятностного характера.

Лекция уже получилась длинной, и всё же я не коснулся многих тем сегодня. Например, принятие решений: если все варианты будущего возможны, как мы можем что-либо определить? Я не дал ответа на этот вопрос, но он будет рассмотрен в следующей лекции.
Также важно учитывать более высокие измерения. Одномерное распределение — это отправная точка, но логистическая цепочка требует большего. Например, если для данного SKU наступает дефицит, может возникнуть эффект каннибализации, когда покупатели естественным образом переключаются на заменитель. Мы хотели бы смоделировать это, даже если в примитивной форме.
Конструкции высшего порядка также играют свою роль. Как я уже говорил, прогнозирование спроса не похоже на предсказание движения планет. У нас встречаются самоисполняющиеся пророчества повсюду. В какой-то момент мы захотим учитывать наши ценовые стратегии и правила пополнения запасов. Для этого нам потребуются конструкции высшего порядка, то есть, имея определённую политику, вы получаете вероятностный прогноз результата, но при этом нужно встроить эту политику в конструкции высшего порядка.
Кроме того, овладение вероятностными прогнозами требует множества числовых приёмов и глубокого знания предметной области, чтобы понять, какие распределения с наибольшей вероятностью подходят для конкретных ситуаций. В этой серии лекций мы позже представим больше примеров.
Наконец, существует вызов перемен. Вероятностное прогнозирование — это радикальный отход от общепринятых практик в логистических цепочках. Часто технические детали, связанные с вероятностными прогнозами, составляют лишь малую часть проблемы. Самое сложное — это перестроить саму организацию, чтобы она начала использовать эти вероятностные прогнозы вместо опоры на точечные прогнозы, которые по сути являются мечтательством. Все эти аспекты будут рассмотрены в последующих лекциях, но на это потребуется время, так как предстоит пройти большой путь.

В заключение, вероятностные прогнозы представляют собой радикальный отход от подхода точечных прогнозов, при котором мы ожидаем достижения некоторого консенсуса относительно единственного будущего, которое должно наступить. Вероятностное прогнозирование основывается на наблюдении, что неопределённость будущего неизбежна. Столетие науки прогнозирования показало, что все попытки создать даже приблизительно точные прогнозы оказались неудачными. Таким образом, мы остаёмся с множеством неопределённых вариантов будущего. Однако вероятностные прогнозы предоставляют нам методы и инструменты для количественной оценки и анализа этих будущих вариантов. Вероятностное прогнозирование — значительное достижение. Потребовалось почти столетие, чтобы осознать, что экономическое прогнозирование не похоже на астрономическое. Хотя мы можем с большой точностью предсказать точное положение планеты через сто лет, в сфере логистики нам не грозит достижение чего-либо подобного. Идея о наличии одного универсального прогноза навсегда ушла. Тем не менее, многие компании продолжают надеяться, что когда-нибудь будет достигнут поистине точный прогноз. После столетия попыток это, по сути, мечтательность.
С современными компьютерами перспектива единственного будущего уже не является единственной. У нас есть альтернативы. Вероятностное прогнозирование существует с 90-х годов, то есть уже три десятилетия. В компании Lokad мы уже более десяти лет используем вероятностное прогнозирование для управления логистическими цепочками в производстве. Возможно, оно ещё не стало мейнстримом, но оно далёко от научной фантастики. Это стало реальностью для многих компаний в финансовой сфере на протяжении трёх десятилетий и в мире логистики уже десятилетие.
Хотя вероятностные прогнозы могут показаться пугающими и высокотехнологичными, с правильными инструментами они сводятся к нескольким строкам кода. В вероятностном прогнозировании нет ничего особенно сложного или проблематичного, по крайней мере по сравнению с другими типами прогнозов. Самая большая сложность заключается в том, чтобы отказаться от уверенности, связанной с иллюзией полного контроля над будущим. Будущее никогда не будет абсолютно под контролем и никогда таковым не станет, и, с учетом всех обстоятельств, это, вероятно, к лучшему.

На сегодня лекция окончена. В следующий раз, 6 апреля, я представлю тему принятия решений при распределении розничных запасов, и мы увидим, как вероятностные прогнозы, представленные сегодня, могут быть использованы для реализации базового логистического решения, а именно пополнения запасов в розничной сети. Лекция состоится в тот же день недели — среду, в то же время, в 15:00, и это будет первая среда апреля.
Вопрос: Можем ли мы оптимизировать соотношение разрешения к точности и объёма оперативной памяти в Envision?
Да, абсолютно, хотя не в самом Envision. Это выбор, который мы сделали при разработке Envision. Мой подход, когда речь идёт о специалистах по цепям поставок, заключается в том, чтобы освободить их от низкоуровневых технических деталей. 4 килобайта в Envision — это много места, позволяющее точно отобразить ситуацию в вашей логистической цепочке. Таким образом, потеря точности и разрешения при аппроксимации не играет существенной роли.
Конечно, когда дело доходит до разработки вашего алгоритма сжатия, необходимо учитывать множество компромиссов. Например, корзины, очень близкие к нулю, должны иметь идеальное разрешение. Если вы хотите определить вероятность наблюдения нуля спроса, вы не захотите, чтобы ваша аппроксимация объединяла корзины для нулевого спроса, одной единицы и двух единиц. Однако, если речь идёт о корзинах для вероятности наблюдения 1000 единиц спроса, объединение корзин для 1000 и 1001 единиц, вероятно, допустимо. Таким образом, существует множество приёмов для разработки алгоритма сжатия, который действительно удовлетворяет требованиям цепей поставок. Это в несколько порядков проще, чем задачи, связанные с сжатием изображений. По моему мнению, правильно разработанные инструменты фактически абстрагируют проблему для специалистов по цепям поставок. Это слишком низкоуровневая задача, и в большинстве случаев нет необходимости в микрооптимизации. Если вы Walmart и у вас не просто 1 миллион SKU, а несколько сотен миллионов, микрооптимизация может иметь смысл. Однако, если речь не идёт о чрезвычайно больших цепях поставок, я считаю, что можно достичь такого уровня, при котором снижение производительности из-за отсутствия полной оптимизации будет практически незначительным.
Вопрос: Какие практические соображения следует учитывать с точки зрения цепей поставок при оптимизации этих параметров?
Когда речь идёт о вероятностном прогнозировании в цепях поставок, точность, превышающая одну часть из 100 000, обычно не имеет значения, поскольку у вас никогда не будет достаточно данных для оценки вероятностей с детализацией выше одной части из 100 000.
Вопрос: Какая отрасль получает наибольшую выгоду от подхода вероятностного прогнозирования?
Краткий ответ таков: чем более непредсказуемы и нерегулярны ваши паттерны, тем больше выгода. Если у вас прерывистый спрос, выгода будет значительной; если спрос хаотичный — выгода велика; если сроки поставки сильно варьируются и в цепях поставок происходят резкие скачки, выгода максимальна. На противоположном конце спектра, например, если рассматривать цепь поставок системы водоснабжения, потребление воды чрезвычайно ровное и почти никогда не имеет резких скачков — максимум, микроскачки. Такой тип задачи не выигрывает от вероятностного подхода. Суть в том, что существуют ситуации, когда классические точечные прогнозы дают очень точные предсказания. Если у вас прогнозы всех ваших продуктов имеют ошибку менее пяти процентов при взгляде в будущее, вероятностные прогнозы вам не нужны; вы находитесь в ситуации, когда действительно точный прогноз работает. Однако, если, как и во многих компаниях, точность ваших прогнозов очень низкая, с расхождением в 30% и более, тогда вы значительно выигрываете от вероятностного прогнозирования.
Вопрос: Так как сроки поставки могут иметь сезонный характер, разделите ли вы прогнозы сроков поставки на несколько отдельных, по одному на каждый сезон, чтобы избежать получения мультимодального распределения?
Это хороший вопрос. Идея заключается в том, что обычно вы строите параметрическую модель для ваших сроков выполнения, включающую сезонный профиль. Работа с сезонностью сроков выполнения не принципиально отличается от работы с любой другой цикличностью, как мы делали в предыдущей лекции для спроса. Обычно не строят несколько моделей, потому что, как вы правильно заметили, если у вас будет несколько моделей, вы столкнетесь с самыми разными странными скачками при переходе от одной модели к другой. Как правило, лучше иметь одну модель с встроенным сезонным профилем. Это будет похоже на параметрическое разложение, где у вас есть вектор, задающий недельный эффект, который влияет на срок выполнения в определённую неделю года. Возможно, в следующей лекции у нас найдется время, чтобы привести более подробный пример.
Вопрос: Является ли вероятностное прогнозирование хорошим подходом при прогнозировании прерывистого спроса?
Абсолютно. На самом деле, я считаю, что при прерывистом спросе вероятностное прогнозирование является не только хорошим методом, но и классический точечный прогноз оказывается совершенно бессмысленным. При классическом прогнозировании вы обычно сталкиваетесь с проблемой многочисленных нулевых значений. Что делать с этими нулями? В итоге вы получаете значение, которое очень низкое и дробное, что действительно не имеет смысла. При прерывистом спросе главный вопрос, на который вы хотите ответить, заключается в следующем: достаточно ли у меня запасов, чтобы обслужить те всплески спроса, которые время от времени возникают? Если использовать средний прогноз, вы никогда этого не узнаете.
Чтобы вернуться к примеру с книжным магазином, если в течение данной недели в среднем наблюдается одна единица спроса в день, сколько книг вам нужно держать в магазине, чтобы обеспечить высокий уровень обслуживания? Предположим, что магазин пополняется каждый день. Если обслуживаемыми клиентами являются только студенты, то при среднем значении в одну единицу спроса в день наличие трёх книг на складе обеспечит очень высокий уровень сервиса. Однако, если время от времени заходит профессор, и он заказывает одновременно 20 книг, то качество обслуживания при наличии всего трех книг будет ужасным, поскольку вы не сможете обслужить ни одного профессора. Это типичный случай прерывистого спроса — дело не только в том, что спрос прерывен, но и в том, что некоторые всплески могут существенно различаться по величине. Вот где действительно блестяще проявляет себя вероятностное прогнозирование, поскольку оно способно уловить тонкую структуру спроса, а не просто свести всё к средним значениям, где эта структура теряется.
Вопрос: Если мы заменим срок выполнения на распределение, будет ли всплеск, представленный плавной кривой колокола на первом слайде генератора?
В некоторой степени, если вы добавляете больше случайности, результаты будут распределяться более равномерно. На первом слайде, посвященном генератору, нам пришлось бы провести эксперимент с различными настройками, чтобы увидеть, к каким результатам мы придем. Идея заключается в том, что когда мы хотим заменить срок выполнения на распределение, мы делаем это, потому что понимаем проблему и знаем, что срок выполнения изменчив. Если мы абсолютно доверяем нашему поставщику и он оказывается невероятно надежным, то вполне допустимо считать, что ETA (расчетное время прибытия) есть то, что есть, и является почти идеальной оценкой реального времени. Однако, если мы замечали в прошлом, что поставщики иногда ведут себя непредсказуемо или не успевают выполнить заказ, то лучше заменить срок выполнения на распределение.
Введение распределения вместо фиксированного срока выполнения не обязательно сгладит итоговые показатели; это зависит от того, на что вы смотрите. Например, если рассматривать самый экстремальный случай избыточных запасов, изменчивость срока выполнения может даже усилить риск возникновения «мертвого» запаса. Почему так происходит? Если у вас очень сезонный продукт, и срок выполнения изменчив, и товар поступает после окончания сезона, вы остаетесь с продуктом, который уже не актуален, что увеличивает риск возникновения «мертвого» запаса к концу сезона. Таким образом, ситуация сложная. Превращение переменной в её вероятностное представление не обязательно приводит к сглаживанию наблюдаемых результатов; иногда оно может сделать распределение еще более резким. Итак, ответ: всё зависит.
Отлично, думаю, на сегодня всё. До встречи в следующий раз.