Escasez: cuando la medida de accuracy falla

Joannes Vermorel

Hace tres años, publicábamos [Overfitting: when accuracy measure goes wrong](/blog/2009/4/22/overfitting-when-accuracy-measure-goes-wrong/), sin embargo overfitting está lejos de ser la única situación en la que medidas simples de accuracy pueden ser muy engañosas. Hoy, nos centramos en una situación muy propensa a errores: demanda intermitente que se encuentra típicamente al observar ventas a nivel de tienda (o Ecommerce).

Creemos que este único problema por sí solo ha impedido a la mayoría de los minoristas avanzar hacia sistemas avanzados de forecast a nivel de tienda. Al igual que con la mayoría de los problemas de forecast, es sutil, es contraintuitivo, y algunas compañías cobran mucho para ofrecer respuestas pobres a la cuestión.

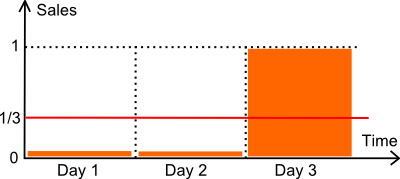
Las métricas de error más populares en el sales forecasting son el Error Absoluto Medio (MAE) y el Error Porcentual Absoluto Medio (MAPE). Como pauta general, sugerimos ceñirse al MAE ya que el MAPE se comporta muy mal cada vez que las series de tiempo no son suaves, es decir, siempre, en lo que concierne a los minoristas. Sin embargo, hay situaciones en las que el MAE también se comporta mal. Los bajos volúmenes de ventas entran en esas situaciones.

Revisemos la ilustración anterior. Tenemos un artículo vendido durante 3 días. El número de unidades vendidas durante los dos primeros días es cero. El tercer día, se vende una unidad. Supongamos que la demanda es, de hecho, de exactamente 1 unidad cada 3 días. Técnicamente hablando, es una distribución de Poisson con λ=1/3.

A continuación, comparamos dos modelos de forecast:

• un modelo plano M a 1/3 cada día (la media).
• un modelo plano Z a cero cada día.

En lo que respecta a la optimización de inventario, el modelo cero (Z) es sumamente perjudicial. Suponiendo que se utilice el análisis de stock de seguridad para calcular un punto de reorden, es muy probable que un forecast de cero produzca también un punto de reorden en cero, causando faltantes de stock frecuentes. Una métrica de accuracy que favoreciera al modelo cero sobre forecasts más razonables se comportaría bastante mal.

Revisemos nuestros dos modelos en comparación con el MAPE (*) y el MAE.

• M tiene un MAPE de 44%.
• Z tiene un MAPE de 33%.
• M tiene un MAE de 0.44.
• Z tiene un MAE de 0.33.

(*) La definición clásica de MAPE implica una división por cero cuando el valor real es cero. Asumimos aquí que el valor real se reemplaza por 1 cuando es cero. Alternativamente, también podríamos haber dividido por el forecast (en lugar del valor real), o usar el sMAPE. Esos cambios no hacen diferencia: la conclusión de la discusión permanece igual.

En conclusión, aquí, según tanto el MAPE como el MAE, prevalece el modelo cero.

Sin embargo, se podría argumentar que esta es una situación simplista, y que no refleja la complejidad de una tienda real. Esto no es del todo cierto. Hemos realizado benchmarks en docenas de tiendas minoristas, y generalmente el modelo ganador (según el MAE o el MAPE) es el modelo cero - el modelo que siempre devuelve cero. Además, este modelo típicamente gana por un margen cómodo sobre todos los demás modelos.

En la práctica, a nivel de tienda, depender ya sea del MAE o del MAPE para evaluar la calidad de los modelos de forecast es invitar a problemas: la métrica favorece a los modelos que devuelven ceros; cuantos más ceros, mejor. Esta conclusión se mantiene en casi todas las tiendas que hemos analizado hasta ahora (excepto en los pocos artículos de alto volumen que no sufren este problema).

Los lectores que están familiarizados con las métricas de accuracy podrían proponer optar, en cambio, por el Error Cuadrático Medio (MSE), que no favorecerá al modelo cero. Esto es cierto, sin embargo, el MSE cuando se aplica a datos erráticos - y las ventas a nivel de tienda son erráticas - no es numéricamente estable. En la práctica, cualquier valor atípico en el historial de ventas sesgará enormemente los resultados finales. Este tipo de problema es LA razón por la que los estadísticos han estado trabajando tan arduamente en estadísticas robustas desde el principio. No hay almuerzo gratis aquí.

¿Cómo evaluar los forecasts a nivel de tienda entonces?

Nos llevó un tiempo muy, muy largo, encontrar una solución satisfactoria al problema de cuantificar la accuracy de los forecasts a nivel de tienda. En 2011 y antes, básicamente estábamos haciendo trampa. En lugar de observar puntos de datos diarios, cuando los datos de ventas eran demasiado escasos, típicamente cambiábamos a agregados semanales (o incluso a agregados mensuales para datos extremadamente escasos). Al cambiar a períodos de agregación más largos, estábamos aumentando artificialmente los volúmenes de ventas por período, haciendo así que el MAE fuera utilizable de nuevo.

El avance se produjo tan solo hace unos pocos meses a través de cuantiles. En esencia, la iluminación fue: olvida los forecasts, solo los puntos de reorden importan. Al intentar optimizar nuestros forecasts clásicos contra las métricas X, Y o Z, estábamos tratando de resolver el problema equivocado.

¡Espera! Dado que los puntos de reorden se calculan en base a los forecasts, ¿cómo puedes decir que los forecasts son irrelevantes?

No estamos diciendo que los forecasts y la accuracy de los forecasts sean irrelevantes. Sin embargo, afirmamos que solo importa la accuracy de los propios puntos de reorden. El forecast, o cualquier otra variable que se utilice para calcular puntos de reorden, no puede ser evaluado por sí solo. Solo la accuracy de los puntos de reorden debe evaluarse.

Resulta que existe una métrica para evaluar los puntos de reorden: es la función de pérdida pinball, una función que ha sido conocida por los estadísticos durante décadas. La pinball loss es ampliamente superior no por sus propiedades matemáticas, sino simplemente porque se ajusta a la compensación de inventario: demasiado stock vs demasiados faltante de stock.