連続順位確率スコア (CRPS)

learn menu
元々はJoannes Vermorelによって2016年6月に執筆されました. Alexey Tikhonovにより2024年5月に更新されました.

確率的予測は、あらゆる可能な未来に対して確率を割り当てます。しかし、すべての確率的予測が同じ精度を持つわけではなく、それぞれの予測の精度を評価するための指標が必要です。単純な accuracy metrics（例えばMAE（平均絶対誤差）やMAPE（平均絶対パーセント誤差））は確率的予測には直接適用できません。Continuous Ranked Probability Score (CRPS) は、確率的予測の場合にMAEを一般化したものであり、cross entropy と共に、CRPSは確率的予測が関与する際に最も広く用いられる精度指標のひとつです.

概要

CRPSは、2つの probabilistic forecasting models の精度を評価するために頻繁に使用されます。特に、この指標は、同じデータセット上で複数の測定値を活用して精度評価を安定化するために、backtesting プロセスと組み合わせることができます.

この指標は、MAEなどの単純な指標とは異なり、その非対称的な表現により、予測が確率的である一方、観測値は決定論的である点が特徴です。pinball loss function とは異なり、CRPSは確率分布の特定の一点に焦点を当てるのではなく、予測全体の分布を考慮します.

定義

ランダム変数 $${X}$$ とする.

$${F}$$ を $${X}$$ の累積分布関数 (CDF) とし、$${F(y)=\mathbf{P}\left[X \leq y\right]}$$ とする.

観測値を $${x}$$ とし、$${F}$$ を経験的確率予測に関連付けられたCDFとする.

$${x}$$ と $${F}$$ の間のCRPSは次のように定義される:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^{\infty}\Big(F(y)- 𝟙(y - x)\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \qquad \tag{1}$$

ここで $${𝟙}$$ は Heaviside step function であり、実数軸に沿って以下の値をとる階段関数を示す:

  • 実数の引数が正または0の場合、値は1,
  • それ以外の場合は0.

CRPSは観測された変数と同じ単位で表される（例えば、製品の需要が単位で予測されている場合、CRPSも同じ単位で表される）.

CRPSは平均絶対誤差 (MAE) を一般化したもので、予測が決定論的である場合にはMAEに帰着する。この点は以下のチャートDで示されている.

既知の特性

GneitingとRaftery (2004) は、連続順位確率スコアが次のように同値表現できることを示している:

$$\qquad \qquad \qquad \qquad {CRPS(F,x) = \mathbf{E}\Big[|X-x|\Big]-\frac{1}{2}\mathbf{E}\Big[|X-X^*|\Big]} \qquad \qquad \qquad \qquad \qquad \qquad \tag{2}$$

ここで

  • $${X}$$ と $${X^*}$$ は線形ランダム変数の独立したコピーであり,
  • $${X}$$ は累積分布関数 $${F}$$ に関連付けられたランダム変数であり,
  • $${\mathbf{E} }$$ は $${X}$$ の期待値である.

数値評価

数値的な観点から、CRPSを計算する簡単な方法は、Heaviside階段関数を簡略化するために元の積分を適切な境界における2つの積分に分解することであり、次の式が得られる:

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \int_{-\infty}^x F(y)^2dy + \int_x^{\infty}\Big(F(y)- 1\Big)^2dy} \qquad \qquad \qquad \qquad \qquad \tag{3}$$

実際には、$$F$$ が予測モデルにより得られる経験的分布であるため、対応するランダム変数 $${X}$$ はコンパクトな定義域を持ち、$${\mathbf{P}[X = x] \gt 0}$$ となる点が有限個に限られる。また、すべての$$x$$は離散値である。したがって、以下の式および次節のチャートBに示すように、積分は離散的な有限和に変換することができる.

$$\qquad \qquad \qquad \qquad{CRPS(F, x) = \sum_{k=0}^x F(y_k)^2 + \sum_{x+1}^{n} (F(y_k) - 1)^2} \qquad \qquad \qquad \qquad \qquad \qquad \tag{4}$$

式(4)において、指数 $$n$$ は、確率分布の右裾の最後の要素（例えば、非ゼロの確率を持つ最大の需要値）を表す.

最後に、CRPSの計算は1つの時点について行われるため、一定の評価期間（例：サプライヤの lead time と reorder 期間の合計である責任ウィンドウ）にわたるCRPSを計算するには、その期間における各CRPS値の平均を取る必要がある.

$$\qquad \qquad \qquad \qquad \qquad \qquad {CRPS = \frac{1}{T} \sum_{t=1}^{T} CRPS_t} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \tag{5}$$

視覚的直感

CRPSの計算を説明するために、次の例を考えてみよう（以下のチャートを参照）:

A: 最初に、負の二項分布を用い、確率が0.1%未満の極めて起こりにくい事象（例えば3年に一度程度の事象）を切り捨てることで、確率的需要予測を構築した。非ゼロの確率を持つ予測需要値は1から26単位の範囲に及んだ。後に、実際の需要が15単位であったことが判明した（垂直の赤い破線で示されている）.

B: 上記の4番目の式（「数値評価」を参照）に従ってCRPSを計算した。得られたCRPS値は、淡い赤色で塗られた2つの領域の合計を表す.

C: チャートAと同様だが、比較のために点予測が追加されている.

D: 点予測に適用されたCRPSの計算は、点予測にCRPSを適用すると結果がMAEの精度指標になることを示している。実際、点予測は1つの値に対して暗黙的に100%の確率を割り当てる単純な確率的予測の形式である。その結果、CRPSの累積確率チャートは、点予測用と実際の需要用の2つの階段関数で表される。これは、点予測と実測値の相対的位置に応じて、CRPSの式(4)の2つの和のうちどちらかがゼロになること、すなわち、過大予測の場合は最初の和が、過小予測の場合は2番目の和がゼロになることを意味する.

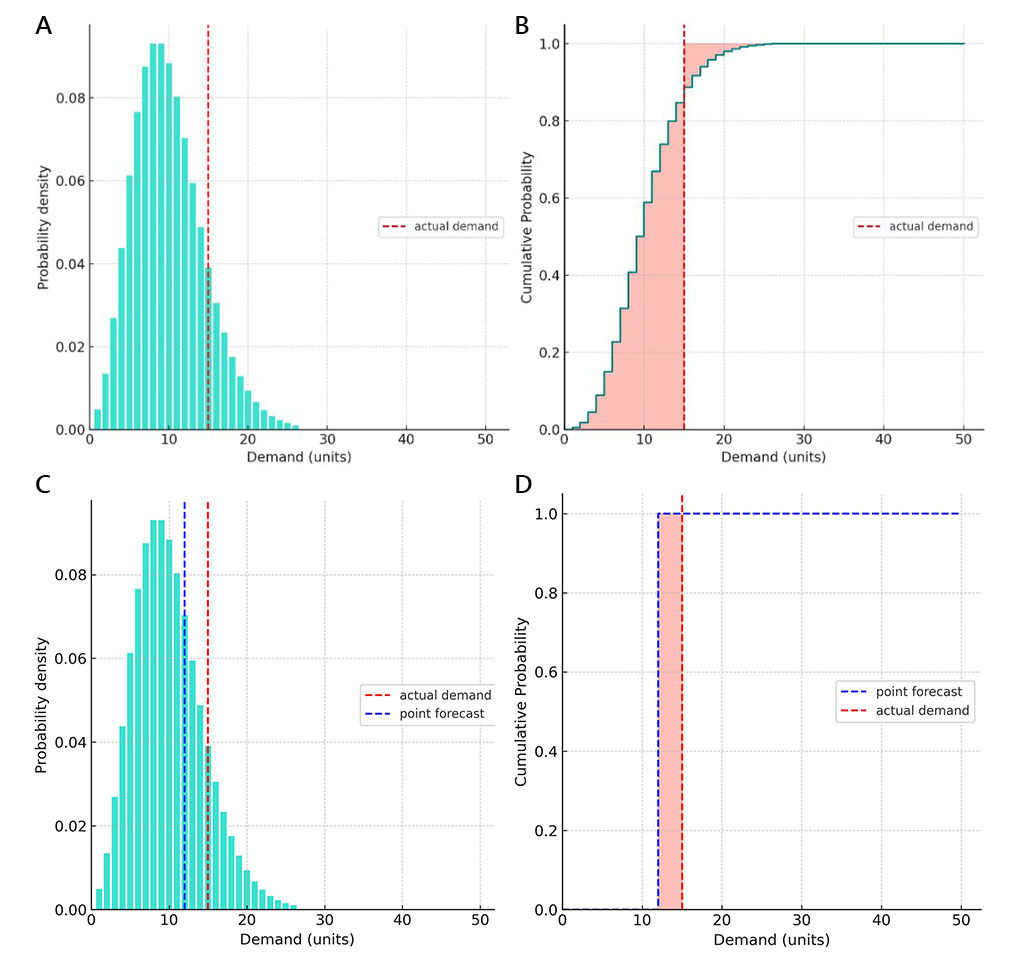
A chart illustrating probabilistic forecast and CRPS metric for evaluating its accuracy.
A: 確率的予測。 B: CRPS。 C: 確率的予測と点予測の比較。 D: 点予測に対するCRPSはMAEである。

これら4つのチャートで示された例では、確率的予測と点予測のCRPS値がそれぞれ3.32と3であった。数値を見ると、点予測の精度指標がより小さい（優れている）ため、点予測の方が more accurate と結論付けられるかもしれない。しかし、この結論は誤りである.

上記の例では実際の需要の1つの値のみを考慮したが、確率的予測が過去のデータを用いて学習されると、需要値の出現頻度に応じて確率は調整される。適切に選択されれば、テストデータセットにおける平均CRPS値は、テストデータにおける異なる需要値の出現頻度を十分に反映するため、トレーニング/検証データセットのそれと比較可能となる.

以下のチャートは、点予測に対する確率的予測の優位性を示している.

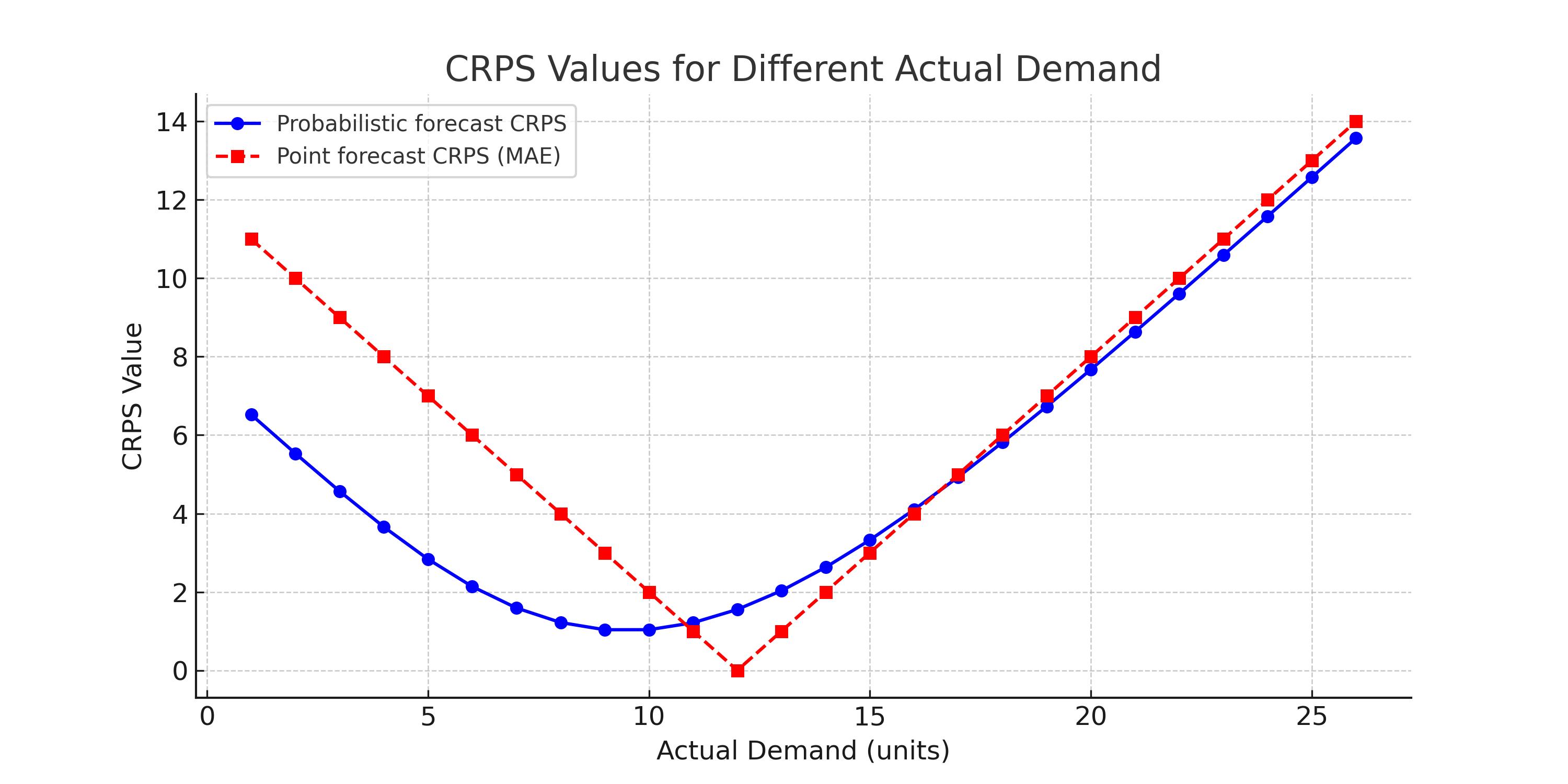
A chart illustrating how CRPS changes depending on the actual values for both probabilistic and point forecasts.

実際の値が異なるにつれてCRPSがどれほど滑らかに変化するかに注目せよ。さらに、点予測が実測値に非常に近いごく小さな領域を除き、他のすべての領域では確率的予測のCRPSが点予測のそれよりも小さいことに留意されたい.

複数の異なる点予測があったとしても、この観察結果は変わらない。点予測に応じて赤い曲線を左右に動かす必要があるかもしれないが、確率的予測の優位性は依然として有効である.

参考文献

Gneiting, T. and Raftery, A. E. (2004). Strictly proper scoring rules, prediction, and estimation. Technical Report no. 463, Department of Statistics, University of Washington, Seattle, Washington, USA.