00:01 Introducción
02:18 El forecast moderno
06:37 Volviéndose postal probabilístico
11:58 La historia hasta ahora
15:10 Plan probable para hoy
17:18 Bestiario de predicciones
28:10 Métricas - CRPS - 1/2
33:21 Métricas - CRPS - 2/2
37:20 Métricas - Monge-Kantorovich
42:07 Métricas - likelihood - 1/3
47:23 Métricas - likelihood - 2/3
51:45 Métricas - likelihood - 3/3
55:03 Distribuciones 1D - 1/4
01:01:13 Distribuciones 1D - 2/4
01:06:43 Distribuciones 1D - 3/4
01:15:39 Distribuciones 1D - 4/4
01:18:24 Generadores - 1/3
01:24:00 Generadores - 2/3
01:29:23 Generadores - 3/3
01:37:56 Por favor, espera mientras te ignoramos
01:40:39 Conclusión
01:43:50 Próxima lección y preguntas de la audiencia
Descripción
Se dice que un forecast es probabilístico, en lugar de determinista, si contiene un conjunto de probabilidades asociadas a todos los posibles resultados futuros, en lugar de señalar un resultado particular como el forecast. Forecast probabilísticos son importantes siempre que la incertidumbre es irreducible, lo cual ocurre casi siempre cuando se trata de sistemas complejos. Para los supply chain, los forecast probabilísticos son esenciales para producir decisiones robustas contra condiciones futuras inciertas.
Transcripción completa

Bienvenidos a esta serie de conferencias de supply chain. Soy Joannes Vermorel, y hoy presentaré “Probabilistic Forecasting for Supply Chain.” El forecast probabilístico es uno de los cambios de paradigma más importantes, si no el más importante, en más de un siglo de ciencia de statistical forecasting. Sin embargo, a nivel técnico, es en su mayoría lo mismo. Si observamos modelos de forecast probabilístico o sus alternativas no probabilísticas, es la misma estadística, las mismas probabilidades. El forecast probabilístico refleja un cambio en la forma en la que debemos pensar sobre el forecast en sí. El mayor cambio que el forecast probabilístico ha traído al supply chain no se encuentra en la ciencia del forecast. El mayor cambio se encuentra en la forma en que los supply chain son operados y optimizados en presencia de modelos predictivos.
El objetivo de la lección de hoy es ofrecer una introducción técnica suave al forecast probabilístico. Al final de esta lección, deberías ser capaz de comprender de qué trata el forecast probabilístico, cómo diferenciar los forecast probabilísticos de los forecast no probabilísticos, cómo evaluar la calidad de un forecast probabilístico, e incluso ser capaz de diseñar tu propio modelo de forecast probabilístico de nivel básico. Hoy, no abordaré la explotación de los forecast probabilísticos para propósitos de decision-making en el contexto de supply chain. El enfoque actual es exclusivamente establecer las bases del forecast probabilístico. La mejora de los procesos de toma de decisiones en supply chain mediante forecast probabilísticos se abordará en la próxima lección.

Para entender la importancia de los forecast probabilísticos, es necesario un poco de contexto histórico. La forma moderna del forecasting, el forecast estadístico, en contraposición a la adivinación, surgió a comienzos del siglo XX. El forecasting surgió en un contexto científico más amplio, donde las ciencias duras, unas pocas disciplinas muy exitosas como la cinética, el electromagnetismo y la química, lograron obtener resultados aparentemente arbitariamente precisos. Estos resultados se obtuvieron mediante lo que esencialmente equivalió a un esfuerzo de varios siglos, que se puede rastrear, por ejemplo, hasta Galileo Galilei, en el desarrollo de tecnologías superiores que permitieran formas superiores de medición. Mediciones más precisas, a su vez, impulsarían un mayor desarrollo científico al permitir a los científicos probar y desafiar sus teorías y predicciones de maneras aún más precisas.
En este contexto más amplio, en el que algunas ciencias tuvieron un éxito increíble, el campo emergente del forecasting a comienzos del siglo XX se propuso replicar esencialmente lo que esas ciencias duras habían logrado en el ámbito de la economía. Por ejemplo, si observamos a pioneros como Roger Babson, uno de los padres del forecasting económico moderno, él fundó una exitosa compañía de forecasting económico en los Estados Unidos a comienzos del siglo XX. El lema de la compañía era, literalmente, “For every action, there is an equal and opposite reaction.” La visión de Babson era transponer el éxito de la física newtoniana al ámbito de la economía y, en última instancia, lograr resultados igualmente precisos.
Sin embargo, después de más de un siglo de forecast estadísticos académicos, en los que operan los supply chain, la idea de lograr resultados arbitrariamente precisos, lo que en términos de forecasting se traduce en alcanzar forecast arbitrariamente accurate forecasts, sigue siendo tan inalcanzable como lo fue hace más de un siglo. Durante un par de décadas, han surgido voces en el mundo del supply chain que han expresado su preocupación de que estos forecast nunca serán lo suficientemente precisos. Ha existido un movimiento, como el lean manufacturing, que entre otros, ha sido un fuerte defensor de disminuir en gran medida la dependencia de los supply chain en estos forecast poco fiables. De eso se trata el just-in-time: si puedes fabricar y servir justo a tiempo todo lo que el mercado necesita, de repente ya no necesitas un forecast confiable y preciso.
En este contexto, el forecast probabilístico es una rehabilitación del forecasting, pero con ambiciones mucho más modestas. El forecast probabilístico parte de la idea de que existe una incertidumbre irreducible sobre el futuro. Todos los futuros son posibles, pero no todos tienen la misma probabilidad, y el objetivo del forecast probabilístico es evaluar comparativamente la probabilidad respectiva de todos esos futuros alternativos, y no colapsar todos los posibles futuros en un solo futuro.

La perspectiva newtoniana sobre los forecast económicos estadísticos ha fracasado esencialmente. La creencia en nuestra comunidad de que se podrán alcanzar forecast arbitrariamente precisos ha desaparecido en gran medida. Sin embargo, curiosamente, casi todo el supply chain software y una gran cantidad de las supply chain practices convencionales están, en su esencia, basados en la suposición de que dichos forecast estarán disponibles finalmente.
Por ejemplo, Sales and Operations Planning (S&OP) se basa en la idea de que se puede lograr una visión unificada y cuantificada de la empresa si todos los interesados se reúnen y colaboran en la construcción de un forecast en conjunto. De manera similar, open-to-buy es, esencialmente, un método basado en la idea de que es posible construir forecast top-down arbitrariamente precisos. Además, incluso cuando observamos muchas herramientas que son muy comunes en el ámbito del forecasting y la planificación en supply chain, tales como business intelligence y spreadsheets, estas herramientas están ampliamente orientadas hacia un forecast de time-series. Esencialmente, la idea es que puedes tener tus datos históricos extendidos hacia el futuro, teniendo un punto por cada período de tiempo de interés. Estas herramientas, por diseño, tienen una enorme cantidad de fricción cuando se trata incluso de comprender el tipo de cálculos que implica un forecast probabilístico, donde no hay un solo futuro, sino todos los posibles futuros.
En efecto, el forecast probabilístico no se trata de decorar un forecast clásico con algún tipo de incertidumbre. Tampoco se trata de establecer una lista corta de escenarios, donde cada escenario es, por sí mismo, un forecast clásico. Los métodos convencionales de supply chain, generalmente, no trabajan con forecast probabilísticos porque, en esencia, se basan, de manera implícita o explícita, en la idea de que existe algún tipo de forecast de referencia, y que todo girará en torno a este forecast de referencia. En contraste, el forecast probabilístico es la evaluación numérica frontal de todos los posibles futuros.
Naturalmente, estamos limitados por la cantidad de recursos de computación que tenemos, así que cuando digo “todos los posibles futuros”, en la práctica, solo consideraremos una cantidad finita de futuros. Sin embargo, considerando la capacidad de procesamiento moderna que poseemos, el número de futuros que realmente podemos considerar alcanza cifras de millones. Ahí es donde el business intelligence y los spreadsheets tienen dificultades. No están orientados hacia el tipo de cálculos que se requieren cuando se trabaja con forecast probabilísticos. Este es un problema de diseño de software. Verás, un spreadsheet tiene acceso a las mismas computadoras y la misma potencia de procesamiento, pero si el software no viene con el diseño adecuado, algunas tareas pueden ser increíblemente difíciles de lograr, incluso si dispones de una vasta cantidad de potencia de procesamiento.
Así, desde una perspectiva de supply chain, el mayor desafío para adoptar el forecast probabilístico es dejar de lado décadas de herramientas y prácticas que se basan en una meta muy ambiciosa, pero que considero equivocada, a saber, que es posible lograr forecast arbitrariamente precisos. Me gustaría señalar de inmediato que sería sumamente equivocado pensar en el forecast probabilístico como una forma de lograr forecasts más precisos. No es así. Los forecast probabilísticos no son más precisos y no pueden usarse como un reemplazo directo de los forecasts clásicos y convencionales. La superioridad de los forecast probabilísticos radica en las formas en que dichos forecasts pueden explotarse para fines de supply chain, especialmente para la toma de decisiones en el contexto de supply chain. Sin embargo, nuestro objetivo hoy es simplemente entender de qué tratan esos forecast probabilísticos, y la explotación de dichos forecast vendrá en la próxima lección.

Esta lección forma parte de una serie de conferencias de supply chain. Estoy intentando mantener esas lecciones bastante independientes entre sí. Sin embargo, estamos llegando a un punto en el que realmente ayudará a la audiencia que esas lecciones se vean en secuencia, ya que referenciaré frecuentemente lo que se presentó en lecciones anteriores.
Así que, esta lección es la tercera del quinto capítulo, que está dedicado a predictive modeling. En el primer capítulo de esta serie, presenté mis puntos de vista sobre los supply chain tanto como campo de estudio como de práctica. En el segundo capítulo, presenté metodologías. De hecho, la mayoría de las situaciones en supply chain son de naturaleza adversaria, y esas situaciones tienden a derrotar las metodologías ingenuas. Necesitamos contar con metodologías adecuadas si queremos lograr algún grado de éxito en el ámbito de los supply chain.
El tercer capítulo estuvo dedicado a la parsimonia en supply chain, con un enfoque exclusivo en el problema y en la propia naturaleza del desafío que enfrentamos en las diversas situaciones que cubren los supply chain. La idea detrás de la parsimonia en supply chain es ignorar por completo todos los aspectos que pertenecen a la solución, ya que solo queremos poder centrarnos en el problema antes de elegir la solución que deseamos utilizar para abordarlo.
En el cuarto capítulo, revisé una amplia variedad de ciencias auxiliares. Estas ciencias no son supply chain per se; son otros campos de investigación que son adyacentes o de apoyo. Sin embargo, creo que un dominio básico de esas ciencias auxiliares es un requisito para la práctica moderna de los supply chain.
Finalmente, en el quinto capítulo, profundizamos en las técnicas que nos permiten cuantificar y evaluar el futuro, especialmente para producir afirmaciones sobre el futuro. De hecho, todo lo que hacemos en supply chain refleja, en cierta medida, una anticipación del futuro. Si podemos anticipar el futuro de una mejor manera, podremos tomar mejores decisiones. De eso trata este quinto capítulo: obtener de manera cuantificable mejores perspectivas sobre el futuro. En este capítulo, los forecast probabilísticos representan una vía fundamental en nuestro enfoque para abordar el futuro.
El resto de esta lección se divide en cuatro secciones de longitud desigual. Primero, vamos a repasar los tipos de forecast más comunes, más allá del forecast clásico. Aclararé a qué me refiero con forecast clásico en un momento. De hecho, muy pocas personas en los círculos de supply chain se dan cuenta de que hay muchas opciones sobre la mesa. El forecast probabilístico en sí mismo debe entenderse como un paraguas que abarca un conjunto bastante diverso de herramientas y técnicas.
Segundo, introduciremos métricas para evaluar la calidad de los forecast probabilísticos. Pase lo que pase, un forecast probabilístico bien diseñado siempre te dirá: “Bueno, había una probabilidad de que esto sucediera.” Entonces, la pregunta es: ¿cómo discernir qué forecast probabilístico es realmente bueno y cuál es malo? Ahí es donde entran en juego esas métricas. Existen métricas especializadas que están completamente dedicadas a la situación del forecast probabilístico.
Tercero, realizaremos un análisis profundo de las distribuciones unidimensionales. Son el tipo más simple de distribución, y aunque tienen limitaciones evidentes, también son el punto de entrada más sencillo al ámbito del forecast probabilístico.
Cuarto, tocaremos brevemente el tema de los generadores, que son frecuentemente conocidos como métodos Monte Carlo. De hecho, existe una dualidad entre los generadores y los estimadores de densidad de probabilidad, y esos métodos Monte Carlo nos proporcionarán un camino para abordar problemas de mayor dimensión y formas de forecast probabilístico.

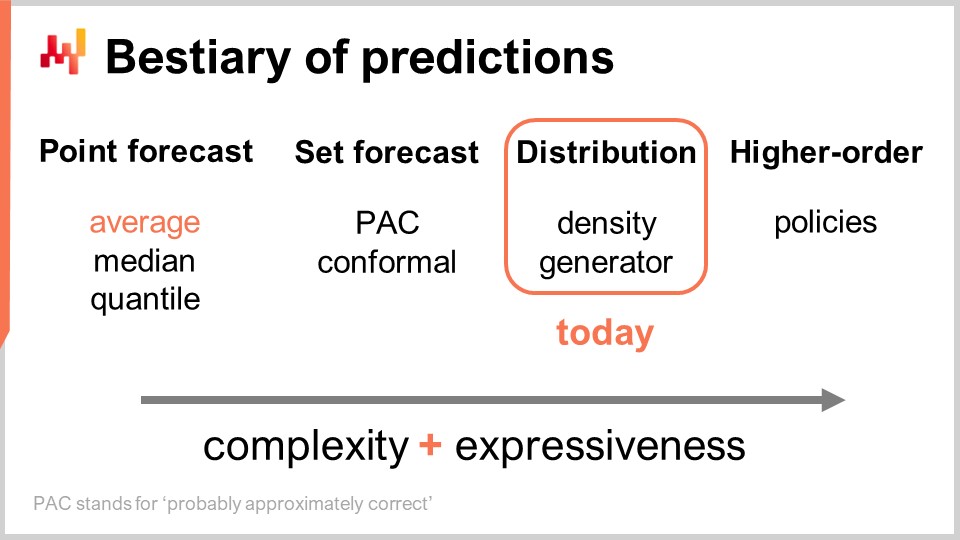
Existen múltiples tipos de forecast, y este aspecto no debe confundirse con el hecho de que existen múltiples tipos de modelos de forecast. Cuando los modelos no pertenecen al mismo tipo o clase de forecast, ni siquiera están resolviendo los mismos problemas. El tipo de forecast más común es el point forecast. Por ejemplo, si digo que mañana las ventas totales en euros en una tienda serán 10.000 euros para el agregado total de ventas del día, estoy haciendo un point forecast sobre lo que sucederá en esta tienda mañana. Si repito este ejercicio y comienzo a construir un forecast de series temporales haciendo una afirmación para el día de mañana, y luego otra afirmación para el día de pasado mañana, tendré múltiples datos. Sin embargo, todo eso sigue siendo un point forecast porque, esencialmente, estamos eligiendo nuestra batalla al escoger un cierto nivel de agregación y, en ese nivel de agregación, nuestros forecast nos dan un solo número, que se supone es la respuesta.
Ahora, dentro del tipo de point forecast, existen múltiples subtipos de forecast dependiendo de qué métrica se esté optimizando. La métrica más comúnmente utilizada es probablemente el error cuadrático, por lo que tenemos un error cuadrático medio, que te da el forecast promedio. Por cierto, este tiende a ser el forecast más comúnmente utilizado porque es el único forecast que es al menos algo aditivo. Ningún forecast es completamente aditivo; siempre viene con montones de advertencias. Sin embargo, algunos forecast son más aditivos que otros, y claramente, los forecast promedio tienden a ser los más aditivos de todos. Si deseas obtener un forecast promedio, lo que tienes es esencialmente un point forecast que se optimiza contra el error cuadrático medio. Si utilizas otra métrica, como el error absoluto, y la optimizas, lo que obtendrás es un median forecast. Si utilizas la pinball loss function que introdujimos en la primera clase de este quinto capítulo en esta serie de lectures de supply chain, lo que obtendrás es un quantile forecast. Por cierto, como podemos ver hoy, estoy clasificando los quantile forecast como simplemente otro tipo de point forecast. De hecho, con el quantile forecast, esencialmente obtienes una única estimación. Esta estimación puede venir con un sesgo, que es intencionado. De eso tratan los cuantiles, pero no obstante, en mi opinión, califica completamente como un point forecast porque la forma del forecast es simplemente un solo punto.
Ahora, está el set forecast, que devuelve un conjunto de puntos en lugar de un solo punto. Existe una variación dependiendo de cómo construyas el conjunto. Si observamos un PAC forecast, PAC significa Probably Approximately Correct. Este es esencialmente un marco teórico introducido por Valiant hace aproximadamente dos décadas, y establece que el conjunto, que es tu predicción, tiene una cierta probabilidad de que se observe un resultado dentro del conjunto que estás prediciendo con una cierta probabilidad. El conjunto que produces es en realidad todos los puntos que caen dentro de una región caracterizada por una distancia máxima a un punto de referencia. De una manera, la perspectiva PAC sobre el forecast ya es un set forecast porque la salida ya no es un punto. Sin embargo, lo que tenemos sigue siendo un punto de referencia, un resultado central, y lo que tenemos es una distancia máxima a este punto central. Solo estamos diciendo que hay una cierta probabilidad especificada de que el resultado finalmente se observe dentro de nuestro conjunto de predicción.
El enfoque PAC puede generalizarse a través del enfoque conformal. La predicción conformal establece: “Aquí hay un conjunto, y te digo que existe esta probabilidad dada de que el resultado esté dentro de este conjunto.” Donde la predicción conformal generaliza el enfoque PAC es que las predicciones conformales ya no están vinculadas a tener un punto de referencia y la distancia al punto de referencia. Puedes formar este conjunto de la manera que desees, y seguirás siendo parte del paradigma de set forecast.
El futuro puede representarse de una forma aún más granular y compleja: el distribution forecast. El distribution forecast te da una función que asigna todos los posibles resultados a sus respectivas densidades de probabilidad locales. De una manera, comenzamos con el point forecast, donde el forecast es solo un punto. Luego pasamos al set forecast, donde el forecast es un conjunto de puntos. Finalmente, el distribution forecast es técnicamente una función o algo que generaliza una función. Por cierto, cuando uso el término “distribution” en esta clase, siempre se referirá implícitamente a una distribución de probabilidades. Los distribution forecast representan algo aún más rico y complejo que un conjunto, y este será nuestro enfoque hoy.
Existen dos formas comunes de abordar las distributions: el enfoque de densidad y el enfoque de generador. Cuando digo “density,” básicamente se refiere a la estimación local de densidades de probabilidad. El enfoque de generador involucra un proceso generativo Monte Carlo que genera resultados, llamados deviates, que se supone reflejan la misma densidad de probabilidad local. Estas son las dos formas principales de abordar los distribution forecast.
Más allá de la distribution, tenemos constructs de orden superior. Esto puede ser un poco complicado de entender, pero mi punto aquí, aunque no vamos a cubrir constructs de orden superior hoy, es simplemente delinear que el probabilistic forecasting, cuando se centra en generar distributions, no es el final; es solo un paso, y hay más. Los constructs de orden superior son importantes si queremos alguna vez poder lograr respuestas satisfactorias a situaciones simples.
Para entender de qué tratan los constructs de orden superior, consideremos una tienda minorista simple con una política de descuento para productos que se acercan a sus fechas de caducidad. Obviamente, la tienda no quiere tener inventory muerto en sus manos, por lo que se activa un descuento automático cuando los productos están muy cerca de sus fechas de caducidad. La demanda que generaría esta tienda depende en gran medida de esta política. Así, el forecast que nos gustaría tener, que puede ser una distribution representando las probabilidades para todos los posibles resultados, debería depender de esta política. Sin embargo, esta política es un objeto matemático; es una función. Lo que nos gustaría tener no es un probabilistic forecast sino algo más meta: un construct de orden superior que, dado una política, pueda generar la distribution resultante.
Desde una perspectiva de supply chain, cuando pasamos de un tipo de forecast a otro, ganamos mucha más información. Esto no debe confundirse con hacer el forecast más preciso; se trata de acceder a un tipo de información completamente diferente, como ver el mundo en blanco y negro y de repente adquirir la capacidad de ver colores en lugar de solo ganar resolución extra. En términos de herramientas, las hojas de cálculo y las herramientas de business intelligence son algo adecuadas para tratar con point forecast. Dependiendo del tipo de set forecast que estés considerando, pueden ser adecuadas, pero ya estás poniendo a prueba sus capacidades de diseño. No están realmente diseñadas para lidiar con ningún tipo de set forecast sofisticado más allá del obvio, donde simplemente defines un rango con valores mínimos y máximos en el rango de valores esperados. Veremos que, esencialmente, si queremos tener alguna posibilidad de trabajar con distribution forecast o incluso constructs de orden superior, necesitamos un tipo de herramienta completamente diferente, aunque esto debería quedar más claro en un momento.
Para comenzar con los probabilistic forecast, intentemos caracterizar qué hace que un probabilistic forecast sea bueno. De hecho, pase lo que pase, un probabilistic forecast te dirá que, sin importar qué tipo de resultado llegues a observar, existía una probabilidad de que esto ocurriera. Entonces, bajo esas condiciones, ¿cómo diferencias un buen probabilistic forecast de uno malo? Ciertamente, no es porque sea probabilístico que de repente todos los modelos de forecast sean buenos.
Esto es exactamente de lo que tratan las métricas dedicadas al probabilistic forecasting, y el Continuous Ranked Probability Score (CRPS) es la generalization del error absoluto para probabilistic forecast unidimensionales. Estoy absolutamente apenado por este nombre horrendo – el CRPS. No fui yo quien ideó esta terminología; me fue entregada. La fórmula del CRPS se muestra en la pantalla. Esencialmente, la función F es la función de distribución acumulada; es el probabilistic forecast que se está realizando. El punto x es la observación real, y el valor CRPS es algo que se calcula entre tu probabilistic forecast y la única observación que acabas de hacer.
Podemos ver que, esencialmente, el punto se convierte en un forecast casi-probabilístico propio mediante la función escalón de Heaviside. Introducir la función escalón de Heaviside es simplemente el equivalente a convertir el punto que acabamos de observar en una distribution de probabilidad de Dirac, que es una distribution que concentra toda la masa de probabilidad en un solo resultado. Luego tenemos una integral, y esencialmente, el CRPS está haciendo una especie de coincidencia de formas. Estamos haciendo coincidir la forma de la CDF (función de distribución acumulada) con la forma de otra CDF, la asociada con el Dirac que coincide con el punto que observamos.
Desde una perspectiva de point forecast, el CRPS es desconcertante no solo por la fórmula complicada, sino también porque esta métrica toma dos argumentos que no tienen el mismo tipo. Uno de esos argumentos es una distribution, y el otro es simplemente un único dato. Así, tenemos una asimetría que no existe con la mayoría de las otras métricas de point forecast, como el error absoluto y el error cuadrático medio. En el CRPS, esencialmente estamos comparando un punto con una distribution.
Si queremos entender más sobre lo que calculamos con el CRPS, una observación interesante es que el CRPS tiene la misma unidad que la observación. Por ejemplo, si x se expresa en euros, y el valor CRPS entre F y x también es homogéneo en términos de unidades a euros, por eso digo que el CRPS es una generalization del error absoluto. Por cierto, si colapsas tu probabilistic forecast en una distribution de Dirac, el CRPS te da un valor que es exactamente el error absoluto.

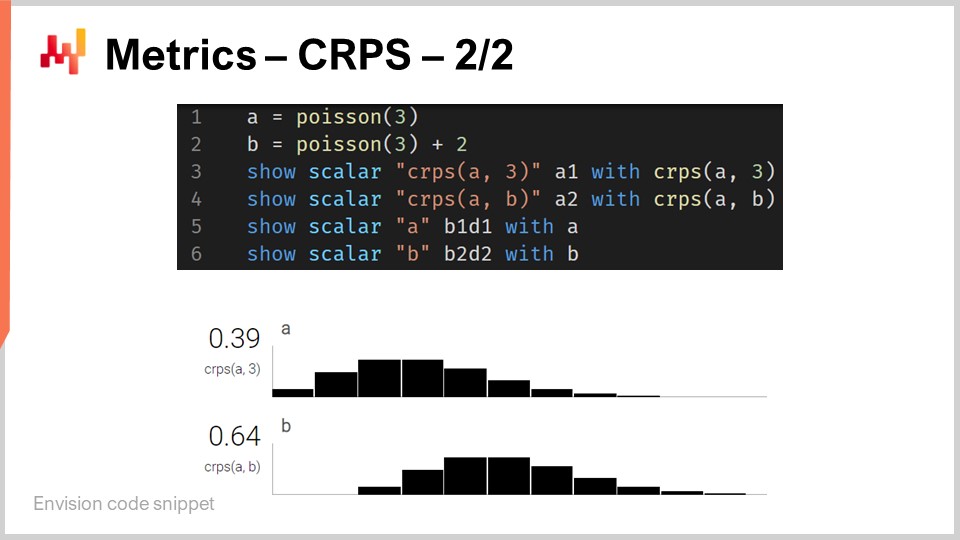
Aunque el CRPS pueda parecer bastante intimidante y complicado, la implementación es en realidad razonablemente sencilla. En la pantalla hay un pequeño script de Envision que ilustra cómo se puede utilizar el CRPS desde una perspectiva de lenguaje de programación. Envision es un lenguaje de programación específico de dominio dedicado a la optimización predictiva de supply chains, desarrollado por Lokad. En estas lectures, estoy usando Envision por claridad y concisión. Sin embargo, ten en cuenta que no hay nada único en Envision; los mismos resultados podrían obtenerse en cualquier lenguaje de programación, ya sea Python, Java, JavaScript, C#, F# u otro. Mi punto es que simplemente requeriría más líneas de código, así que me quedo con Envision. Todos los fragmentos de código dados aquí en esta lecture y, por cierto, en las anteriores también, son independientes y completos. Técnicamente, podrías copiar y pegar este código, y funcionaría. No hay módulos involucrados, ni código oculto, ni un entorno que configurar.
Entonces, volviendo al fragmento de código. En las líneas uno y dos, definimos distributions unidimensionales. Volveré a explicar cómo funcionan realmente esas distributions unidimensionales en Envision, pero tenemos dos distributions aquí: una es una distribution Poisson, que es una distribution discreta unidimensional, y la segunda en la línea dos es la misma distribution Poisson pero desplazada dos unidades hacia la derecha. Eso es por lo que significa el “+2”. En la línea tres, calculamos la distancia CRPS entre una distribution y el valor 3, que es un número. Así, aquí, encontramos esta asimetría en términos de tipos de datos de la que estaba hablando. Luego, los resultados se muestran en la parte inferior, como puedes ver en la parte inferior de la pantalla.
En la línea cuatro, calculamos el CRPS entre la distribution A y la distribution B. Aunque la definición clásica de CRPS es entre una distribution y un solo punto, es completamente sencillo generalizar esta definición a un par de distributions. Todo lo que tienes que hacer es tomar la misma fórmula para el CRPS y reemplazar la función escalón de Heaviside por la función de distribución acumulada de la segunda distribution. Las instrucciones “show” de las líneas tres a seis resultan en la visualización que puedes ver en la parte inferior de la pantalla, que es literalmente una captura de pantalla.
Así, vemos que usar el CRPS no es más difícil o complicado que usar cualquier función especial, como la función coseno. Obviamente, es un poco fastidioso si tienes que reimplementar el coseno tú mismo, pero considerando todo, no hay nada especialmente complicado en el CRPS. Ahora, pasemos al siguiente tema.

El problema de Monge-Kantorovich nos da una idea de cómo abordar el proceso de coincidencia de formas que se utiliza en el CRPS pero con mayores dimensiones. Recuerda, el CRPS está realmente atado a la dimensión uno. La coincidencia de formas es conceptualmente algo que podría generalizarse a cualquier número de dimensiones, y el problema de Monge-Kantorovich es muy interesante, doblemente interesante porque, en esencia, es en realidad un problema de supply chain.
El problema de Monge-Kantorovich, originalmente no relacionado con el probabilistic forecasting, fue introducido por el científico francés Gaspard Monge en un memorando de 1781 titulado “Mémoire sur la théorie des déblais et des remblais,” que podría traducirse aproximadamente como “Memorando sobre la Teoría de Mover Tierra.” Una forma de entender el problema de Monge-Kantorovich es pensar en una situación donde tenemos una lista de minas, denotadas como M en la pantalla, y una lista de fábricas denotadas como F. Las minas producen mineral, y las fábricas consumen mineral. Lo que queremos es construir un plan de transporte, T, que asigne todo el mineral producido por las minas al consumo requerido por las fábricas.
Monge definió el capital C como el costo de mover todo el mineral de las minas a las fábricas. El costo es la suma del transporte de todo el mineral de cada mina a cada fábrica, pero obviamente existen formas muy ineficientes de transportar el mineral. Entonces, cuando decimos que tenemos un costo específico, queremos decir que el costo refleja el plan de transporte óptimo. Este capital C representa el mejor costo alcanzable al considerar el plan de transporte óptimo.
Esto es esencialmente un problema de supply chain que ha sido estudiado extensamente a lo largo de los siglos. En la formulación completa del problema, hay restricciones sobre T. Por brevedad, no puse todas las restricciones en la pantalla. Hay una restricción, por ejemplo, de que el plan de transporte no debe exceder la capacidad de producción de cada mina, y cada fábrica debe estar completamente satisfecha, teniendo una asignación que se ajuste a sus requerimientos. Hay muchas restricciones, pero son bastante extensas, por lo que no las incluí en la pantalla.
Ahora bien, aunque el problema del transporte es interesante por sí solo, si empezamos a interpretar la lista de minas y la lista de fábricas como dos distribuciones de probabilidad, tenemos una forma de transformar una métrica puntual en una métrica distribucional. Esta es una idea clave sobre la correspondencia de formas en dimensiones superiores a través de la perspectiva de Monge-Kantorovich. Otro término para esta perspectiva es la métrica de Wasserstein, aunque mayormente se refiere al caso no discreto, que es de menor interés para nosotros.
La perspectiva de Monge-Kantorovich nos permite transformar una métrica puntual, que puede calcular la diferencia entre dos números o dos vectores de números, en una métrica que se aplica a distribuciones de probabilidad que operan sobre el mismo espacio. Este es un mecanismo muy poderoso. Sin embargo, el problema de Monge-Kantorovich es difícil de resolver y requiere de un poder de procesamiento sustancial. Para el resto de la conferencia, me ceñiré a técnicas que son más sencillas de implementar y ejecutar.

La perspectiva bayesiana consiste en observar una serie de observaciones desde el punto de vista de una creencia a priori. La perspectiva bayesiana se entiende usualmente en oposición a la perspectiva frecuentista, que estima la frecuencia de resultados basándose en observaciones reales. La idea es que la perspectiva frecuentista no viene con creencias a priori. Por lo tanto, la perspectiva bayesiana nos proporciona una herramienta conocida como la verosimilitud para evaluar el grado de sorpresa al considerar las observaciones y un modelo dado. El modelo, que es esencialmente un modelo de forecast probabilístico, es la formalización de nuestras creencias a priori. La perspectiva bayesiana nos ofrece una forma de evaluar un conjunto de datos con respecto a un modelo de forecast probabilístico. Para entender cómo se hace esto, debemos empezar con la verosimilitud para un solo dato. La verosimilitud, cuando tenemos una observación x, es la probabilidad de observar x según el modelo. Aquí, se asume que el modelo está completamente caracterizado por theta, los parámetros del modelo. La perspectiva bayesiana asume típicamente que el modelo tiene algún tipo de forma paramétrica, y theta es el vector completo de todos los parámetros del modelo.
Cuando decimos theta, implícitamente asumimos que tenemos una caracterización completa del modelo probabilístico, lo que nos da una densidad de probabilidad local para todos los puntos. Por lo tanto, la verosimilitud es la probabilidad de observar ese único dato. Cuando tenemos la verosimilitud para el modelo theta, es la probabilidad conjunta de observar todos los datos en el conjunto. Asumimos que estos datos son independientes, así que la verosimilitud es un producto de probabilidades.
Si tenemos miles de observaciones, la verosimilitud, como producto de miles de valores menores que uno, es probablemente numéricamente ínfima. Un valor ínfimo es típicamente difícil de representar con la forma en que los números de punto flotante son representados en las computadoras. En lugar de trabajar directamente con la verosimilitud, que es un número ínfimo, tendemos a trabajar con el log verosimilitud. El log verosimilitud es simplemente el logaritmo de la verosimilitud, que tiene la increíble propiedad de transformar la multiplicación en adición.
El log verosimilitud del modelo theta es la suma del log de todas las verosimilitudes individuales para todos los datos, como se muestra en la línea final de la ecuación en la pantalla. La verosimilitud es una métrica que nos indica la bondad de ajuste para un forecast probabilístico dado. Nos dice cuán probable es que el modelo haya generado el conjunto de datos que terminamos observando. Si tenemos dos forecasts probabilísticos en competencia, y si dejamos de lado todas las demás cuestiones de ajuste por un momento, deberíamos elegir el modelo que nos dé la verosimilitud más alta o el log verosimilitud más alto, porque cuanto más alto, mejor.
La verosimilitud es muy interesante porque puede operar en altas dimensiones sin complicaciones, a diferencia del método de Monge-Kantorovich. Siempre que tengamos un modelo que nos proporcione una densidad de probabilidad local, podemos usar la verosimilitud, o más realísticamente, el log verosimilitud como métrica.

Además, tan pronto como tenemos una métrica que puede representar la bondad de ajuste, significa que podemos optimizar contra esta misma métrica. Todo lo que se necesita es un modelo con al menos un grado de libertad, lo que básicamente significa al menos un parámetro. Si optimizamos este modelo contra la verosimilitud, nuestra métrica de bondad de ajuste, esperamos obtener un modelo entrenado en el que hayamos aprendido a producir al menos un forecast probabilístico decente. Esto es exactamente lo que se está haciendo aquí en la pantalla.
En las líneas uno y dos, generamos un conjunto de datos ficticio. Creamos una tabla con 2,000 líneas, y luego en la línea dos, generamos 2,000 desviaciones, nuestras observaciones de una distribución de Poisson con una media de dos. Así, tenemos nuestras 2,000 observaciones. En la línea tres, iniciamos un bloque de autodiff, que es parte del paradigma de programación diferenciable. Este bloque ejecutará un descenso por gradiente estocástico e iterará muchas veces sobre todas las observaciones en la tabla de observaciones. Aquí, la tabla de observaciones es la tabla T.
En la línea cuatro, declaramos el único parámetro del modelo, llamado lambda. Especificamos que este parámetro debe ser exclusivamente positivo. Este parámetro es lo que intentaremos redescubrir mediante el descenso por gradiente estocástico. En la línea cinco, definimos la función de pérdida, que es simplemente menos el log verosimilitud. Queremos maximizar la verosimilitud, pero el bloque de autodiff está intentando minimizar la pérdida. Así, si queremos maximizar el log verosimilitud, tenemos que añadir este signo menos delante del log verosimilitud, que es exactamente lo que hemos hecho.
El parámetro lambda aprendido se muestra en la línea seis. No es sorprendente que el valor encontrado esté muy cerca del valor dos, porque empezamos con una distribución de Poisson con una media de dos. Creamos un modelo de forecast probabilístico que también es paramétrico y de la misma forma, una distribución de Poisson. Queríamos redescubrir el único parámetro de la distribución de Poisson, y eso es exactamente lo que obtenemos. Obtenemos un modelo que está a aproximadamente un uno por ciento de la estimación original.
Acabamos de aprender nuestro primer modelo de forecast probabilístico, y todo lo que se necesitó fueron esencialmente tres líneas de código. Este es obviamente un modelo muy simple; sin embargo, muestra que no hay nada intrínsecamente complicado en el forecast probabilístico. No es tu forecast de media cuadrática habitual, pero aparte de eso, con las herramientas adecuadas como la programación diferenciable, no es más complicado que un forecast puntual clásico.
La función log_likelihood.poisson que usamos anteriormente es parte de la biblioteca estándar de Envision. Sin embargo, no hay magia involucrada. Echemos un vistazo a cómo se implementa realmente esta función internamente. Las dos primeras líneas en la parte superior nos dan la implementación del log verosimilitud de la distribución de Poisson. Una distribución de Poisson está completamente caracterizada por su único parámetro, lambda, y la función de log verosimilitud solo toma dos argumentos: el único parámetro que caracteriza completamente la distribución de Poisson y la observación real. La fórmula actual que he escrito es literalmente material de libro de texto. Es lo que se obtiene cuando se implementa la fórmula de libro de texto que caracteriza la distribución de Poisson. No hay nada sofisticado aquí.
Presta atención al hecho de que esta función está marcada con la palabra clave autodiff. Como vimos en la conferencia anterior, la palabra clave autodiff garantiza que la diferenciación automática pueda fluir correctamente a través de esta función. El log verosimilitud de la distribución de Poisson también utiliza otra función especial, log_gamma. La función log_gamma es el logaritmo de la función gamma, que es la generalización de la función factorial a números complejos. Aquí, solo necesitamos la generalización de la función factorial a números reales positivos.
La implementación de la función log_gamma es ligeramente extensa, pero nuevamente es material de libro de texto. Utiliza una aproximación por fracción continua para la función log_gamma. La belleza aquí es que tenemos la diferenciación automática funcionando para nosotros hasta el final. Empezamos con el bloque autodiff, llamando a la función log_likelihood.poisson, que está implementada como una función autodiff. Esta función, a su vez, llama a la función log_gamma, también implementada con el marcador autodiff. Esencialmente, somos capaces de producir nuestros forecasting methods probabilísticos en tres líneas de código porque tenemos una biblioteca estándar bien diseñada que se ha implementado, prestando atención a la diferenciación automática.
Ahora, pasemos al caso especial de las distribuciones discretas unidimensionales. Estas distribuciones están por todas partes en un supply chain y representan nuestro punto de entrada al forecast probabilístico. Por ejemplo, si queremos forecast lead times con granularidad diaria, podemos decir que hay una cierta probabilidad de tener un tiempo de entrega de un día, otra probabilidad de tener un tiempo de entrega de dos días, tres días y así sucesivamente. Todo eso se acumula en un histograma de probabilidades para los lead times. De manera similar, si analizamos la demanda para un determinado SKU en un día dado, podemos decir que hay una probabilidad de observar cero unidades de demanda, una unidad de demanda, dos unidades de demanda, y así sucesivamente.
Si agrupamos todas estas probabilidades, obtenemos un histograma que las representa. De manera similar, si pensamos en el nivel de stock de un SKU, podríamos estar interesados en evaluar cuántas unidades quedarán para ese SKU al final de la temporada. Podemos usar un forecast probabilístico para determinar la probabilidad de que nos queden cero unidades en stock al final de la temporada, una unidad en stock, dos unidades, y así sucesivamente. Todas estas situaciones se ajustan al patrón de ser representadas mediante un histograma con compartimientos asociados a cada resultado discreto del fenómeno de interés.
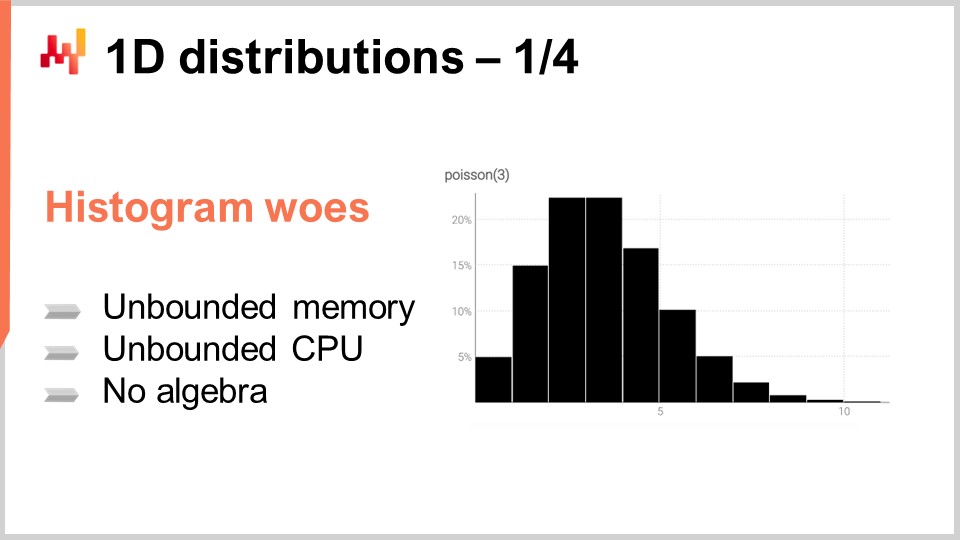
El histograma es la forma canónica de representar una distribución discreta unidimensional. Cada compartimiento está asociado con la masa de probabilidad para el resultado discreto. Sin embargo, dejando a un lado el caso de uso de visualización de datos, los histogramas resultan algo poco impresionantes. De hecho, operar sobre histogramas es un poco complicado si queremos hacer algo más que visualizar esas distribuciones de probabilidad. Esencialmente, tenemos dos clases de problemas con los histogramas: la primera dificultad está relacionada con los recursos computacionales, y la segunda clase de dificultad está relacionada con la expresividad de programación de los histogramas.
En términos de recursos computacionales, debemos considerar que la cantidad de memoria necesaria para un histograma es fundamentalmente ilimitada. Puedes pensar en un histograma como un arreglo que crece lo que sea necesario. Al tratar un solo histograma, incluso uno excepcionalmente grande desde una perspectiva de supply chain, la cantidad de memoria necesaria no es un problema para una computadora moderna. El problema surge cuando no se tiene un solo histograma, sino millones de histogramas para millones de SKUs en un contexto de supply chain. Si cada histograma puede crecer considerablemente, gestionarlos puede convertirse en un desafío, especialmente considerando que las computadoras modernas tienden a ofrecer acceso a memoria no uniforme.
Por el contrario, la cantidad de CPU necesaria para procesar estos histogramas también es ilimitada. Aunque las operaciones en histogramas son mayoritariamente lineales, el tiempo de procesamiento aumenta a medida que la memoria crece debido al acceso a memoria no uniforme. Como resultado, hay un interés significativo en imponer límites estrictos a la cantidad de memoria y CPU requeridos.
La segunda dificultad con los histogramas es la falta de un álgebra asociada. Si bien se puede realizar una suma o multiplicación compartimento a compartimento de valores al considerar dos histogramas, hacerlo no dará como resultado algo que tenga sentido al interpretar el histograma como la representación de una variable aleatoria. Por ejemplo, si tomas dos histogramas y realizas una multiplicación punto a punto, terminas con un histograma que ni siquiera tiene una masa de uno. Esta no es una operación válida desde la perspectiva de un álgebra de variables aleatorias. Realmente no se pueden sumar o multiplicar histogramas, por lo que estás limitado en lo que puedes hacer con ellos.
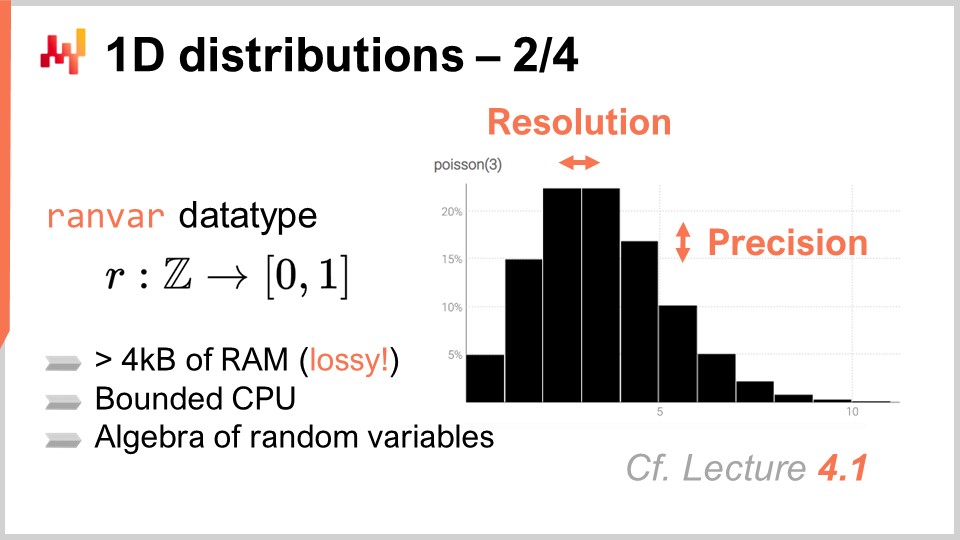
En Lokad, el enfoque que hemos encontrado más práctico para tratar estas ubicuas distribuciones discretas unidimensionales es introducir un tipo de dato dedicado. Probablemente el público esté familiarizado con los tipos de datos comunes que existen en la mayoría de los lenguajes de programación, tales como enteros, números de punto flotante y cadenas. Estos son los tipos de datos primitivos que se encuentran en todas partes. Sin embargo, nada impide introducir tipos de datos más especializados que sean especialmente adecuados para nuestros requerimientos desde una perspectiva de supply chain. Esto es exactamente lo que hizo Lokad con el tipo de dato ranvar.
El tipo de dato ranvar está dedicado a distribuciones discretas unidimensionales, y el nombre es una abreviatura de variable aleatoria. Técnicamente, desde una perspectiva formal, el ranvar es una función de Z (el conjunto de todos los enteros, positivos y negativos) a probabilidades, que son números entre cero y uno. La masa total de Z es siempre igual a uno, ya que representa distribuciones de probabilidad.
Desde una perspectiva puramente matemática, algunos podrían argumentar que la cantidad de información que puede comprimirse en tal función puede ser arbitrariamente grande. Esto es cierto; sin embargo, la realidad es que, desde una perspectiva de supply chain, existe un límite muy claro de cuánta información relevante puede contenerse en un solo ranvar. Aunque es teóricamente posible idear una distribución de probabilidad que requiera megabytes para representarse, no existe tal distribución que sea relevante para propósitos de supply chain.
Es posible diseñar un límite superior de 4 kilobytes para el tipo de datos ranvar. Al tener un límite en la memoria que este ranvar puede ocupar, también terminamos con un límite superior en CPU para todas las operaciones, lo cual es muy importante. En lugar de tener un límite ingenuo que restrinja los contenedores a 1,000, Lokad introduce un esquema de compresión con el tipo de datos ranvar. Esta compresión es esencialmente una representación con pérdida de los datos originales, perdiendo resolución y precisión. Sin embargo, la idea es diseñar un esquema de compresión que proporcione una representación lo suficientemente precisa de los histogramas, de modo que el grado de aproximación introducido sea insignificante desde una perspectiva de supply chain.
La letra pequeña del algoritmo de compresión asociado con el tipo de datos ranvar está fuera del alcance de esta lección. Sin embargo, se trata de un algoritmo de compresión muy simple que es varias órdenes de magnitud más simple que los tipos de algoritmos de compresión utilizados para las imágenes en tu computadora. Como beneficio adicional de tener un límite en la memoria que este ranvar puede ocupar, también terminamos con un límite superior en CPU para todas las operaciones, lo cual es muy importante. Finalmente, con el tipo de datos ranvar, el punto más importante es que obtenemos un álgebra de variables que nos da una manera de operar realmente sobre estos tipos de datos y hacer todo tipo de cosas que queremos hacer con los tipos de datos primitivos, es decir, tener todo tipo de primitivas para combinarlos de maneras que se ajusten a nuestros requerimientos.
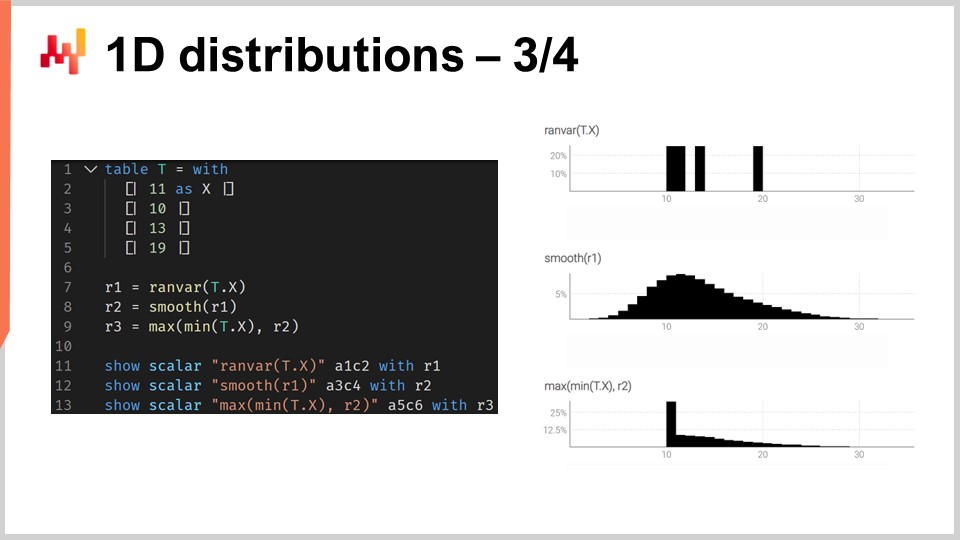
Para ilustrar lo que significa trabajar con ranvars, consideremos una situación de forecast de lead time, más específicamente, un forecast probabilístico de un lead time. En la pantalla se muestra un breve script de Envision que enseña cómo construir dicho forecast probabilístico. En las líneas 1-5, introducimos la tabla T que contiene los cuatro lead times de variación, con valores de 11 días, 10 días, 13 días y 90 días. Aunque cuatro observaciones son muy pocas, desafortunadamente es muy común tener muy pocos puntos de datos en lo que respecta a las observaciones de lead time. De hecho, si consideramos un proveedor extranjero que recibe dos órdenes de compra por año, entonces se necesitan dos años para recolectar esos cuatro puntos de datos. Por lo tanto, es importante tener técnicas que puedan operar incluso con un conjunto de observaciones increíblemente limitado.
En la línea 7, creamos un ranvar agregando directamente las cuatro observaciones. Aquí, el término “ranvar” que aparece en la línea 7 es en realidad un agregador que toma una serie de números como entradas y retorna un único valor del tipo de datos ranvar. El resultado se muestra en la parte superior derecha de la pantalla, que es un ranvar empírico.
Sin embargo, este ranvar empírico no es una representación realista de la distribución real. Por ejemplo, aunque podemos observar un lead time de 11 días y un lead time de 13 días, resulta poco realista no poder observar un lead time de 12 días. Si interpretamos este ranvar como un forecast probabilístico, diría que la probabilidad de observar alguna vez un lead time de 12 días es cero, lo cual parece incorrecto. Esto es, obviamente, un problema de sobreajuste.
Para remediar esta situación, en la línea 8, suavizamos el ranvar original llamando a la función “smooth”. La función smooth esencialmente reemplaza el ranvar original con una mezcla de distribuciones. Por cada contenedor de la distribución original, reemplazamos el contenedor con una distribución de Poisson con una media centrada en dicho contenedor, ponderada de acuerdo con la probabilidad respectiva de los contenedores. A través de la distribución suavizada, obtenemos el histograma que se muestra en el centro a la derecha de la pantalla. Esto ya se ve mucho mejor; ya no tenemos huecos extraños, y ya no tenemos una probabilidad cero en el medio. Además, al observar la probabilidad de observar un lead time de 12 días, este modelo nos da una probabilidad no nula, lo que resulta mucho más razonable. También nos da una probabilidad no nula de ir más allá de los 20 días, y considerando que teníamos cuatro puntos de datos y ya se observó un lead time de 19 días, la idea de que un lead time tan alto como 20 días es posible resulta muy razonable. Así, con este forecast probabilístico, tenemos una buena dispersión que representa una probabilidad no nula para esos eventos, lo cual es muy bueno.
Sin embargo, a la izquierda, tenemos algo un poco extraño. Aunque está bien que esta distribución de probabilidad se extienda hacia la derecha, lo mismo no se puede decir de la izquierda. Si consideramos que los lead times que observamos fueron el resultado de los tiempos de transporte, debido a que se necesitan nueve días para que el truck llegue, resulta poco probable que alguna vez observemos un lead time de tres días. En este sentido, el modelo es bastante poco realista.
Así, en la línea 9, introducimos un ranvar ajustado condicionalmente al indicar que debe ser mayor que el lead time más pequeño jamás observado. Tenemos “min_of(T, x)” que toma el valor más pequeño entre los números de la tabla T, y luego usamos “max” para hacer el máximo entre una distribución y un número. El resultado tiene que ser mayor que este valor. El ranvar ajustado se muestra a la derecha, en la parte inferior, y aquí vemos nuestro forecast final de lead time. Este último se siente como un forecast probabilístico muy razonable del lead time, considerando que tenemos un conjunto de datos increíblemente limitado con solo cuatro puntos de datos. No podemos decir que sea un gran forecast probabilístico; sin embargo, argumentaría que este es un forecast de nivel de producción, y este tipo de técnicas funcionaría bien en producción, a diferencia de un forecast puntual promedio que subestimaría enormemente el riesgo de lead times variables.
La belleza de los forecast probabilísticos es que, aunque pueden ser muy crudos, ya te ofrecen cierto potencial de mitigación para decisiones mal informadas que resultarían de la aplicación ingenua de un forecast promedio basado en los datos observados.
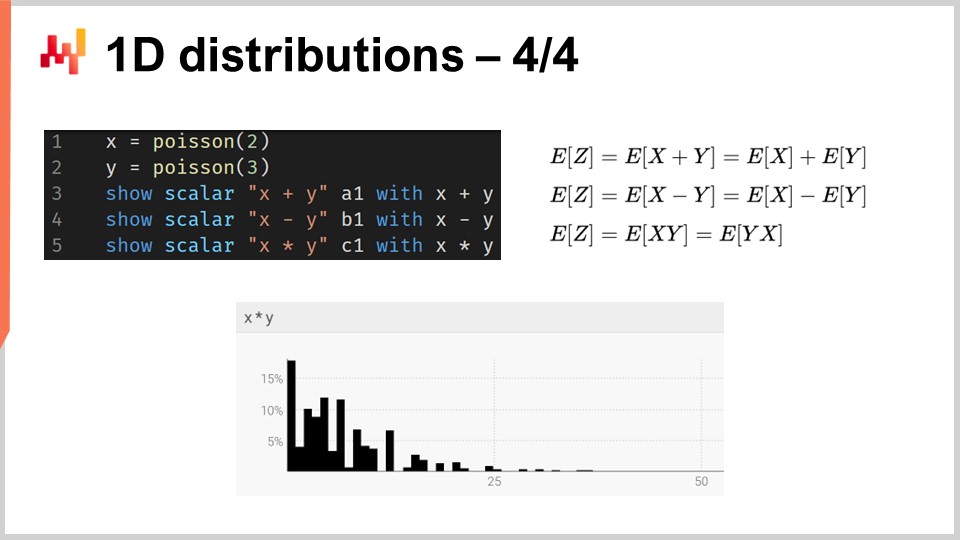
De manera más general, los ranvars soportan una amplia gama de operaciones: es posible sumar, restar y multiplicar ranvars, tal como es posible sumar, restar y multiplicar enteros. Bajo el capó, debido a que estamos tratando con variables aleatorias discretas en términos de semántica, todas estas operaciones se implementan como convoluciones. En la pantalla, el histograma mostrado en la parte inferior se obtiene mediante la multiplicación de dos distribuciones de Poisson, de medias dos y tres, respectivamente. En supply chain, la multiplicación de variables aleatorias se denomina convolución directa. En el contexto de supply chain, la multiplicación de dos variables aleatorias tiene sentido para representar, por ejemplo, los resultados que se pueden obtener cuando los clientes buscan los mismos productos pero con multiplicadores variables. Supongamos que tenemos una librería que atiende a dos cohortes de clientes. Por un lado, tenemos la primera cohorte compuesta por estudiantes, que compran una unidad cuando entran a la tienda. En esta librería ilustrativa, tenemos una segunda cohorte compuesta por profesores, quienes compran 20 libros cuando ingresan a la tienda.
Desde una perspectiva de modelado, podríamos tener un forecast probabilístico que represente las tasas de llegada en la librería de estudiantes o profesores. Esto nos daría la probabilidad de observar cero clientes en el día, un cliente, dos clientes, etc., revelando la distribución de probabilidad de observar un cierto número de clientes en un día dado. La segunda variable te daría las probabilidades respectivas de comprar una (estudiantes) versus comprar 20 (profesores). Para tener una representación de la demanda, simplemente multiplicaríamos esas dos variables aleatorias, resultando en un histograma aparentemente errático que refleja los multiplicadores presentes en los patrones de consumo de tus cohortes.

Los generadores de Monte Carlo, o simplemente generadores, representan un enfoque alternativo al forecast probabilístico. En lugar de mostrar una distribución que nos da la densidad de probabilidad local, podemos mostrar un generador que, como su nombre lo indica, genera resultados que se espera sigan implícitamente las mismas distribuciones de probabilidad locales. Existe una dualidad entre generadores y densidades de probabilidad, lo que significa que ambos son esencialmente dos facetas de la misma perspectiva.
Si tienes un generador, siempre es posible promediar los resultados obtenidos de este generador para reconstruir estimaciones de las densidades de probabilidad locales. A la inversa, si tienes densidades de probabilidad locales, siempre es posible extraer desviaciones según esta distribución. Fundamentalmente, estos dos enfoques son simplemente diferentes maneras de observar la misma naturaleza probabilística o estocástica del fenómeno que estamos tratando de modelar.
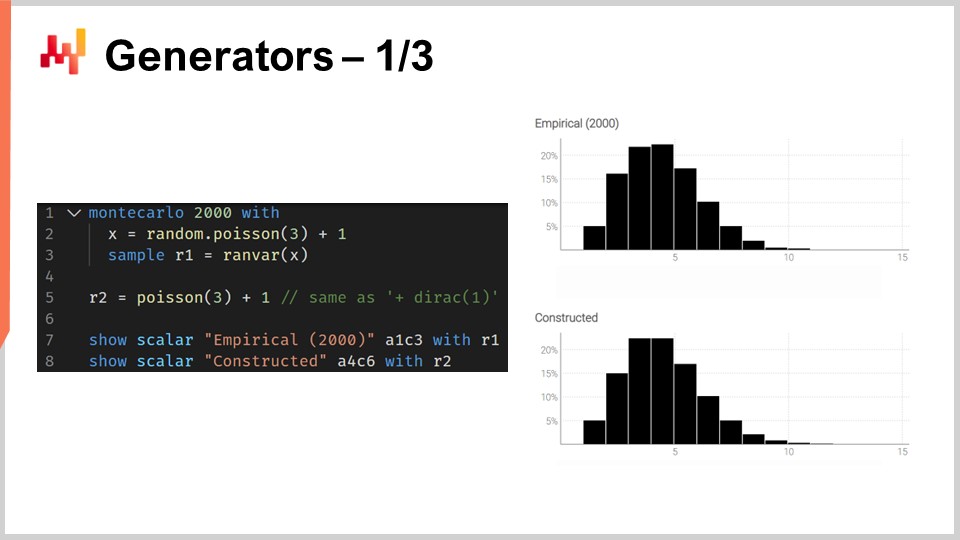
El script en la pantalla ilustra esta dualidad. En la línea uno, introducimos un bloque de Monte Carlo, que será iterado por el sistema, tal como los bloques de auto-diferenciación son iterados a través de muchos pasos de descenso de gradiente estocástico. El bloque de Monte Carlo se ejecutará 2,000 veces, y de este bloque, recogeremos 2,000 desviaciones.
En la línea dos, extraemos una desviación de una distribución de Poisson de media tres y luego se le suma uno a la desviación. Esencialmente, obtenemos un número aleatorio de esta distribución de Poisson y luego le sumamos uno. En la línea tres, recogemos esta desviación en L1, que actúa como un acumulador para el ranvar agregador. Este es el mismo agregador exacto que introdujimos previamente para nuestro ejemplo de lead time. Aquí, estamos recopilando todas esas observaciones en L1, lo que nos da una distribución unidimensional obtenida a través de un proceso de Monte Carlo. En la línea cinco, construimos la misma distribución discreta unidimensional, pero esta vez, lo hacemos con el álgebra de variables aleatorias. Así, simplemente usamos Poisson menos tres y sumamos uno. En la línea cinco, no hay un proceso de Monte Carlo en curso; es cuestión pura de probabilidades discretas y convoluciones.
Cuando comparamos visualmente las dos distribuciones en las líneas siete y ocho, vemos que son casi idénticas. Digo “casi” porque, aunque estamos usando 2,000 iteraciones, lo cual es mucho, no es infinito. Las desviaciones entre las probabilidades exactas que obtienes con ranvar y las probabilidades aproximadas que obtienes con el proceso de Monte Carlo aún son notables, aunque no grandes.
A veces se les llama simuladores a los generadores, pero no te equivoques, son lo mismo. Siempre que tienes un simulador, tienes un proceso generativo que subyace implícitamente a un proceso de forecast probabilístico. Siempre que haya un simulador o generador involucrado, la pregunta que debería estar en tu mente es: ¿cuál es la precisión de esta simulación? No es precisa por diseño, tal como es muy posible tener forecasts completamente inexactos, probabilísticos o no. Es muy fácil obtener una simulación completamente inexacta.
Con los generadores, vemos que las simulaciones son solo una forma de ver la perspectiva del forecast probabilístico, pero esto es más bien un detalle técnico. No cambia nada del hecho de que, al final, quieres tener algo que sea una representación precisa del sistema que estás tratando de caracterizar con tu forecast, probabilístico o no.
El enfoque generativo no solo es muy útil, como veremos con un ejemplo específico en breve, sino que además es conceptualmente más fácil de entender, al menos en cierta medida, en comparación con el enfoque de densidades de probabilidad. Sin embargo, el enfoque de Monte Carlo tampoco está exento de tecnicismos. Hay algunas cosas que son necesarias si quieres hacer viable este enfoque en un contexto de producción para una supply chain real.
Primero, los generadores deben ser rápidos. Monte Carlo es siempre un trade-off entre el número de iteraciones que te gustaría tener y el número de iteraciones que puedes permitirte, considerando los recursos de cómputo disponibles. Sí, las computadoras modernas tienen mucha potencia de procesamiento, pero los procesos de Monte Carlo pueden consumir recursos de manera increíble. Quieres algo que, por defecto, sea súper rápido. Si volvemos a los ingredientes introducidos en la segunda lección del cuarto capítulo, tenemos funciones muy rápidas como ExhaustShift o WhiteHash, que son esenciales para la construcción de las primitivas que te permiten generar generadores aleatorios elementales que son súper rápidos. Necesitas eso, de lo contrario, vas a tener dificultades. Segundo, necesitas distribuir tu ejecución. La implementación ingenua de un programa de Monte Carlo es simplemente tener un bucle que itera secuencialmente. Sin embargo, si estás usando solo una CPU para abordar tus requerimientos de Monte Carlo, esencialmente, estás volviendo a la potencia de cómputo que caracterizaba a las computadoras hace dos décadas. Este punto se tocó en la primera lección del cuarto capítulo. En las últimas dos décadas, las computadoras se han vuelto más potentes, pero fue principalmente añadiendo CPUs y grados de paralelización. Por lo tanto, necesitas tener una perspectiva distribuida para tus generadores.
Por último, la ejecución debe ser determinista. ¿Qué significa eso? Significa que si se ejecuta el mismo código dos veces, debería darte exactamente los mismos resultados. Esto puede parecer contraintuitivo porque estamos tratando con métodos aleatorizados. No obstante, la necesidad de determinismo surgió muy rápidamente. Se descubrió de manera dolorosa durante los años ‘90 cuando las finanzas comenzaron a usar generadores de Monte Carlo para sus valoraciones. Las finanzas tomaron el camino del forecast probabilístico hace bastante tiempo y hicieron un uso extensivo de los generadores de Monte Carlo. Una de las cosas que aprendieron fue que si no tienes determinismo, se vuelve casi imposible replicar las condiciones que generaron un error o un fallo. Desde una perspectiva de supply chain, errores en los cálculos de órdenes de compra pueden ser increíblemente costosos.
Si deseas lograr cierto grado de preparación para producción en el software que gobierna tu supply chain, necesitas tener esta propiedad determinista cada vez que estés tratando con Monte Carlo. Ten en cuenta que muchas soluciones de código abierto provienen de la academia y no se preocupan en absoluto por la preparación para producción. Asegúrate de que cuando estés tratando con Monte Carlo, tu proceso sea, por diseño, súper rápido, distribuido por diseño y determinista, de modo que tengas la posibilidad de diagnosticar los errores que inevitablemente surgirán con el tiempo en tu configuración de producción.
Hemos visto una situación donde se introdujo un generador para replicar lo que de otra manera se hacía con un ranvar. Como regla general, siempre que puedas arreglártelas únicamente con densidades de probabilidad de variables aleatorias sin involucrar Monte Carlo, es mejor. Obtienes resultados más precisos, y no tienes que preocuparte por la estabilidad numérica, que siempre es un poco complicada con Monte Carlo. Sin embargo, la expresividad del álgebra de variables aleatorias es limitada, y ahí es donde Monte Carlo realmente destaca. Estos generadores son más expresivos porque te permiten abordar situaciones que no se pueden enfrentar solo con un álgebra de variables aleatorias.
Ilustremos esto con una situación de supply chain. Considera un único SKU con un nivel inicial de stock, un forecast probabilístico para la demanda, y un periodo de interés que abarca tres meses, con un envío entrante en la mitad del periodo. Asumimos que la demanda se atiende inmediatamente desde el stock disponible o se pierde para siempre. Queremos conocer el nivel de stock esperado al final del periodo para el SKU, ya que saberlo nos ayudará a decidir cuánto riesgo tenemos en términos de inventario muerto.
La situación es traicionera porque ha sido diseñada de tal forma que existe una tercera posibilidad de que ocurra un faltante de stock justo en medio del periodo. El enfoque ingenuo sería tomar el nivel de stock inicial, la distribución de la demanda para todo el periodo, y restar la demanda del nivel de stock, resultando en el stock restante. Sin embargo, esto no toma en cuenta que podríamos perder una parte considerable de la demanda si ocurre un faltante de stock mientras el reabastecimiento entrante aún está pendiente. Hacerlo de forma ingenua subestimaría la cantidad de stock que tendremos al final del periodo y sobreestimaría la cantidad de demanda que será atendida.
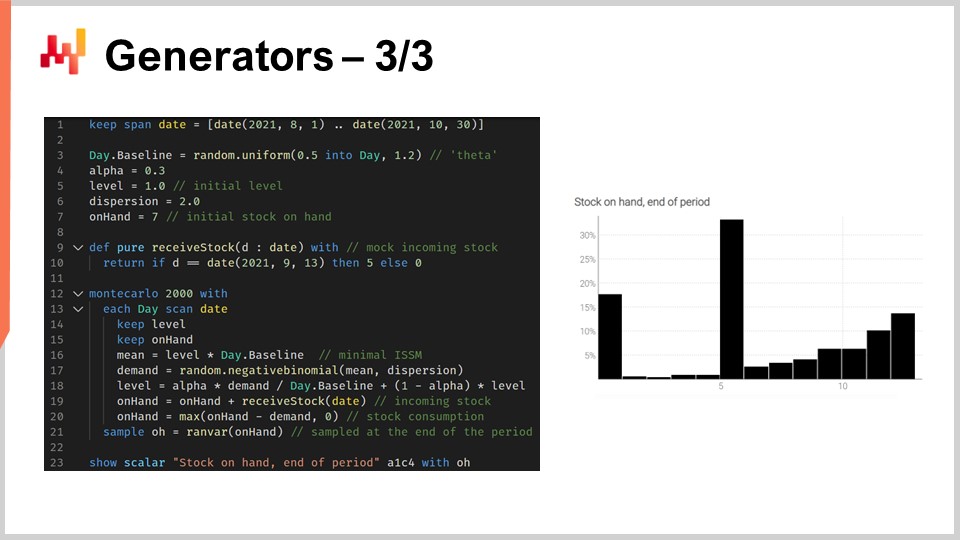
El script que se muestra modela la ocurrencia de faltantes de stock para que podamos tener un estimador correcto del nivel de stock para este SKU al final del periodo. Desde las líneas 1 a 10, definimos los datos simulados que caracterizan nuestro modelo. Las líneas 3 a 6 contienen los parámetros para el modelo ISSM. Ya hemos visto el modelo ICSM en la primera conferencia de este quinto capítulo. Esencialmente, este modelo genera una trayectoria de demanda con un dato por cada día. El periodo de interés se define en la tabla de días, y tenemos los parámetros para esta trayectoria al comienzo.
En las conferencias anteriores, introdujimos el modelo AICSM y los métodos necesarios a través de la programación diferenciable para aprender estos parámetros. Hoy, estamos utilizando el modelo, asumiendo que hemos aprendido todo lo que necesitamos aprender. En la línea 7, definimos el stock inicial disponible, que típicamente se obtendría del ERP o WMS. En las líneas 9 y 10, definimos la cantidad y la fecha para el reabastecimiento. Estos puntos de datos típicamente se obtendrían como un tiempo estimado de llegada proporcionado por el proveedor y almacenado en el ERP. Asumimos que la fecha de entrega es perfectamente conocida; sin embargo, sería sencillo reemplazar esta única fecha con un forecast probabilístico del tiempo de entrega.
Desde las líneas 12 a 21, tenemos el modelo ISSM que genera la trayectoria de demanda. Estamos dentro de un bucle de Monte Carlo, y para cada iteración de Monte Carlo, iteramos sobre cada día del periodo de interés. La iteración de días comienza en la línea 13. Tenemos la mecánica ESSM en marcha, pero en las líneas 19 y 20, actualizamos la variable de stock disponible. La variable de stock disponible no forma parte del modelo ISSM; esto es algo extra. En la línea 19, decimos que el stock disponible es el stock de ayer más el envío entrante, que será cero en la mayoría de los días y cinco unidades para el 13 de septiembre. Luego, en la línea 20, actualizamos el stock disponible diciendo que un cierto número de unidades son consumidas por la demanda del día, y usamos este max 0 para indicar que el nivel de stock no puede volverse negativo.
Finalmente, recopilamos el stock final disponible en la línea 21, y en la línea 23, este stock final se muestra en pantalla. Este es el histograma que ves a la derecha de la pantalla. Aquí, observamos una distribución con una forma muy irregular. Esta forma no se puede obtener mediante el álgebra de variables aleatorias. Los generadores son increíblemente expresivos; sin embargo, no debes confundir la expresividad de estos generadores con la precisión. Aunque los generadores son increíblemente expresivos, no es trivial evaluar la precisión de tales generadores. No te equivoques, cada vez que tienes un generador o simulador en juego, tienes un forecast de probabilidad en juego, y las simulaciones pueden ser dramáticamente inexactas, al igual que cualquier forecast, probabilistic o de otro tipo.

La conferencia ya ha sido larga, y sin embargo hay muchos temas que ni siquiera he tocado hoy. La toma de decisiones, por ejemplo, si todos los futuros son posibles, ¿cómo decidimos algo? No he respondido a esta pregunta, pero se abordará en la próxima conferencia.
También es importante considerar dimensiones superiores. La distribución unidimensional es un punto de partida, pero una supply chain necesita más. Por ejemplo, si tenemos un faltante de stock para un SKU dado, podemos experimentar canibalización, donde los clientes naturalmente recurren a un sustituto. Nos gustaría modelar esto, aunque sea de forma rudimentaria.
Los constructos de orden superior también juegan un papel. Como dije, predecir la demanda no es como predecir los movimientos de los planetas. Tenemos efectos autoproféticos por todas partes. En algún momento, queremos considerar e incorporar nuestras políticas de precios y de reabastecimiento de stock. Para hacer eso, necesitamos constructos de orden superior, lo que significa que, dada una política, obtienes un forecast probabilístico del resultado, pero tienes que inyectar la política dentro de los constructos de orden superior.
Además, dominar los forecasts probabilísticos implica numerosas recetas numéricas y experiencia en el dominio para saber qué distribuciones encajan mejor en ciertas situaciones. En esta serie de conferencias, presentaremos más ejemplos más adelante.
Finalmente, está el desafío del cambio. El forecasting probabilístico es una ruptura radical con las prácticas convencionales de supply chain. Con frecuencia, las tecnicalidades involucradas en los forecasts probabilísticos son solo una pequeña parte del desafío. La parte difícil es reinventar la organización en sí, para que pueda comenzar a utilizar estos forecasts probabilísticos en lugar de depender de forecasts puntuales, que son esencialmente un deseo ilusorio. Todos estos elementos se tratarán en conferencias posteriores, pero tomará tiempo ya que tenemos mucho terreno por cubrir.

En conclusión, los forecasts probabilísticos representan una ruptura radical con la perspectiva de forecast puntual, en la que se espera algún tipo de consenso sobre el único futuro que se supone que ha de ocurrir. El forecasting probabilístico se basa en la observación de que la incertidumbre del futuro es irreducible. Un siglo de ciencia de forecast ha demostrado que todos los intentos de lograr forecasts siquiera cercanos a ser precisos han fallado. Así, estamos atrapados con muchos futuros indefinidos. Sin embargo, los forecasts probabilísticos nos brindan técnicas y herramientas para cuantificar y evaluar estos futuros. El forecasting probabilístico es un logro significativo. Se tardó casi un siglo en aceptar la idea de que el forecasting económico no era como la astronomía. Si bien podemos predecir la posición exacta de un planeta dentro de un siglo con gran precisión, no tenemos ninguna esperanza de lograr algo remotamente equivalente en el ámbito de las supply chains. La idea de tener un único forecast que lo gobierne todo simplemente no volverá. Sin embargo, muchas empresas aún se aferran a la esperanza de que en algún momento se logrará el único forecast verdaderamente preciso. Después de un siglo de intentos, esto es esencialmente un deseo ilusorio.
Con las computadoras modernas, esta perspectiva de un único futuro no es la única en juego. Tenemos alternativas. El forecasting probabilístico existe desde los años 90, es decir, hace tres décadas. En Lokad, hemos estado utilizando el forecasting probabilístico para impulsar supply chains en producción durante más de una década. Puede que aún no sea convencional, pero está muy lejos de ser ciencia ficción. Ha sido una realidad para muchas empresas en finanzas durante tres décadas y en el mundo de supply chain durante una década.
Si bien los forecasts probabilísticos pueden parecer intimidantes y altamente técnicos, con las herramientas adecuadas, son solo unas pocas líneas de código. No hay nada particularmente difícil o desafiante en el forecasting probabilístico, al menos no en comparación con otros tipos de forecasts. El mayor desafío en el forecasting probabilístico es renunciar a la comodidad asociada con la ilusión de que el futuro está perfectamente bajo control. El futuro no está perfectamente bajo control y nunca lo estará, y considerando todo, probablemente sea lo mejor.

Esto concluye la conferencia de hoy. La próxima vez, el 6 de abril, presentaré la toma de decisiones en el despacho de inventario en retail, y veremos cómo los forecasts probabilísticos presentados hoy pueden ponerse a buen uso para impulsar una decisión básica de supply chain, a saber, el reabastecimiento de inventario en una red de retail. La conferencia se llevará a cabo el mismo día de la semana, miércoles, a la misma hora, las 3 PM, y será el primer miércoles de abril.
Pregunta: ¿Podemos optimizar la resolución en precisión versus el volumen de RAM para Envision?
Sí, absolutamente, aunque no en Envision mismo. Esta es una elección que hicimos en el diseño de Envision. Mi enfoque cuando se trata de supply chain scientists es liberarlos de las tecnicidades de bajo nivel. Los 4 kilobytes de Envision son mucho espacio, permitiendo una representación precisa de tu situación de supply chain. Así que, la aproximación que pierdes en términos de resolución y precisión es intrascendente.
Ciertamente, cuando se trata del diseño de tu algoritmo de compresión, hay muchos compromisos que deben considerarse. Por ejemplo, los buckets que están muy cerca de cero necesitan tener una resolución perfecta. Si quieres tener la probabilidad de observar cero unidades de demanda, no quieres que tu aproximación agrupe los buckets para demanda cero, una unidad y dos unidades. Sin embargo, si estás analizando buckets para la probabilidad de observar 1,000 unidades de demanda, agrupar 1,000 y 1,001 unidades de demanda probablemente esté bien. Así, existen muchos trucos para desarrollar un algoritmo de compresión que realmente se ajuste a los requisitos de supply chain. Esto es órdenes de magnitud más simple comparado con lo que sucede en la compresión de imágenes. Mi opinión es que una herramienta correctamente diseñada básicamente abstraería el problema para los supply chain scientists. Esto es demasiado a bajo nivel, y no necesitas micro-optimizarlos en la mayoría de los casos. Si eres Walmart y no solo tienes 1 millón de SKUs sino varios cientos de millones de SKUs, entonces la micro-optimizacion podría tener sentido. Sin embargo, a menos que estemos hablando de supply chains excesivamente grandes, creo que puedes tener algo lo suficientemente bueno de modo que el impacto en el rendimiento por no tener una optimización completa sea mayormente intrascendente.
Pregunta: ¿Cuáles son las consideraciones prácticas que se deben tener en cuenta desde una perspectiva de supply chain al optimizar esos parámetros?
Cuando se trata de forecasting probabilístico en supply chain, tener una precisión de más de una de cada 100,000 es típicamente intrascendente, simplemente porque nunca tienes suficientes datos para lograr una exactitud en la estimación de tus probabilidades que sea más granular que una parte de cada 100,000.
Pregunta: ¿Qué industria se beneficia más del enfoque de forecasting probabilístico?
La respuesta corta es que, cuanto más erráticos e irregulares sean tus patrones, mayores serán los beneficios. Si tienes una demanda intermitente, obtienes grandes beneficios; si tienes una demanda errática, obtienes grandes beneficios; si tienes tiempos de entrega ampliamente variables y choques erráticos en tus supply chains, te beneficias aún más. En el otro extremo del espectro, por ejemplo, si analizáramos la supply chain de distribución de agua, el consumo de agua es extremadamente suave y casi nunca tiene grandes choques, – sólo micro choques como máximo. Este es el tipo de problema que no se beneficia del enfoque probabilístico. La idea es que hay algunas situaciones en las que los forecasts puntuales clásicos te ofrecen forecasts muy precisos. Si estás en una situación en la que tus forecasts para todos tus productos tienen menos de un cinco por ciento de error al mirar hacia adelante, entonces no necesitas forecasts probabilísticos; estás en una situación en la que tener un forecast realmente preciso funciona. Sin embargo, si eres como muchas empresas en situaciones donde la precisión de tu forecast es muy baja, con una divergencia del 30% o más, entonces te beneficiarás enormemente del forecasting probabilístico. Por cierto, cuando digo un error del 30% en el forecast, siempre me refiero al forecast muy desagregado. Muchas empresas te dirán que sus forecasts son precisos al 5%, pero si lo agregas todo, esto puede dar una percepción muy engañosa de la precisión de tus forecasts. La precisión de tus forecasts solo importa a nivel más desagregado, típicamente al nivel del SKU y del día, porque tus decisiones se toman a nivel de SKU y diario. Si a nivel de SKU y diario puedes obtener tus forecasts más desagregados con una precisión del 5%, entonces no necesitas forecasts probabilísticos. Sin embargo, si observas inexactitudes de dos dígitos en términos porcentuales, entonces te beneficiarás enormemente del forecasting probabilístico.
Pregunta: Dado que los tiempos de entrega pueden ser estacionales, ¿descompondrías los forecasts de tiempo de entrega en varios, uno para cada temporada distinta, para evitar observar una distribución multimodal?
Esta es una buena pregunta. La idea aquí es que típicamente construirías un modelo paramétrico para tus lead times que incluya un perfil de estacionalidad. Tratar la estacionalidad en los lead times no es fundamentalmente muy diferente de tratar cualquier otra ciclicidad, como lo hicimos en la conferencia anterior para la demanda. La manera típica no es construir múltiples modelos, porque como señalaste correctamente, si tienes múltiples modelos, observarás todo tipo de saltos extraños al pasar de una modalidad a otra. Generalmente es mejor tener un solo modelo con un perfil de estacionalidad en el centro del mismo. Sería como una descomposición paramétrica donde tienes un vector que te da el efecto semanal que impacta el lead time en cierta semana del año. Quizás tengamos tiempo en una conferencia posterior para dar un ejemplo más extenso de ello.
Pregunta: ¿Es el forecast probabilístico un buen enfoque cuando se quiere forecast la demanda intermitente?
Absolutamente. De hecho, creo que cuando tienes demanda intermitente, el forecast probabilístico no solo es un buen método, sino que el forecast puntual clásico es completamente absurdo. Con el forecast clásico, típicamente lucharías para lidiar con todos esos ceros. ¿Qué hacer con esos ceros? Terminas con un valor muy bajo y fraccional, que realmente no tiene sentido. Con la demanda intermitente, la pregunta a la que realmente quieres responder es: ¿Es mi stock lo suficientemente grande para atender esos picos de demanda que tienden a surgir de vez en cuando? Si usas un forecast promedio, nunca lo sabrás.
Para volver al ejemplo de la librería, si dices que en una semana determinada observas en promedio una unidad de demanda por día, ¿cuántos libros necesitas tener en tu librería para ofrecer un servicio de alta calidad? Supongamos que la librería se repone cada día. Si las únicas personas a las que sirves son estudiantes, entonces, si tienes en promedio una unidad de demanda cada día, tener tres libros en stock resultará en un servicio de muy alta calidad. Sin embargo, si de vez en cuando entra un profesor que busca 20 libros de una vez, entonces tu nivel de servicio, si solo tienes tres libros en la tienda, será abismal porque nunca podrás atender a ninguno de los profesores. Este es típicamente el caso con la demanda intermitente: no se trata solo de que la demanda sea intermitente, sino también de que algunos picos de demanda pueden variar significativamente en magnitud. Ahí es donde el forecast probabilístico realmente brilla, ya que puede capturar la estructura fina de la demanda en lugar de simplemente agrupar todo en promedios donde se pierde toda esa estructura fina.
Pregunta: Si reemplazamos el lead time por una distribución, ¿aparecerá el pico representado por una curva de campana suave en la primera diapositiva para el generador?
En cierta medida, si aleatorizas más, tiendes a dispersar las cosas. En la primera diapositiva sobre el generador, tendríamos que ejecutar el experimento con varias configuraciones para ver qué obtenemos. La idea es que cuando queremos reemplazar el lead time por una distribución, lo hacemos porque tenemos un entendimiento del problema que nos indica que el lead time está variando. Si confiamos en nuestro proveedor absolutamente y ha sido increíblemente confiable, entonces es perfectamente aceptable decir que el ETA (tiempo estimado de llegada) es lo que es y es una estimación casi perfecta de la realidad. Sin embargo, si hemos visto que en el pasado los proveedores a veces han sido erráticos o no han alcanzado la meta, entonces es mejor reemplazar el lead time por una distribución.
Incorporar una distribución para reemplazar el lead time no necesariamente suaviza los resultados que obtienes al final; depende de lo que estés observando. Por ejemplo, si observas el caso más extremo de sobrestock, un lead time variable incluso puede exacerbar el riesgo de tener inventario muerto. ¿Por qué es eso? Si tienes un producto muy estacional y un lead time variable, y el producto llega después del fin de la temporada, te quedas con un producto fuera de temporada, lo que magnifica el riesgo de tener inventario muerto al final de la temporada. Así que, es complicado. El hecho de convertir una variable en su reemplazo probabilístico no suavizará de forma natural lo que observes; a veces, puede hacer que la distribución sea incluso más pronunciada. Así que, la respuesta es: depende.
Excelente, creo que eso es todo por hoy. Nos vemos la próxima vez.