00:00 Introducción
02:55 El caso de los tiempos de entrega
09:25 Tiempos de entrega en el mundo real (1/3)
12:13 Tiempos de entrega en el mundo real (2/3)
13:44 Tiempos de entrega en el mundo real (3/3)
16:12 La historia hasta ahora
19:31 ETA: 1 hora a partir de ahora
22:16 CPRS (repaso) (1/2)
23:44 CPRS (repaso) (2/2)
24:52 Validación cruzada (1/2)
27:00 Validación cruzada (2/2)
27:40 Suavizado de tiempos de entrega (1/2)
31:29 Suavizado de tiempos de entrega (2/2)
40:51 Composición del tiempo de entrega (1/2)
44:19 Composición del tiempo de entrega (2/2)
47:52 Tiempo de entrega cuasi-estacional
54:45 Modelo log-logístico de tiempo de entrega (1/4)
57:03 Modelo log-logístico de tiempo de entrega (2/4)
01:00:08 Modelo log-logístico de tiempo de entrega (3/4)
01:03:22 Modelo log-logístico de tiempo de entrega (4/4)
01:05:12 Modelo de tiempo de entrega incompleto (1/4)
01:08:04 Modelo de tiempo de entrega incompleto (2/4)
01:09:30 Modelo de tiempo de entrega incompleto (3/4)
01:11:38 Modelo de tiempo de entrega incompleto (4/4)
01:14:33 Demanda durante el tiempo de entrega (1/3)
01:17:35 Demanda durante el tiempo de entrega (2/3)
01:24:49 Demanda durante el tiempo de entrega (3/3)
01:28:27 Modularidad de las técnicas predictivas
01:31:22 Conclusión
01:32:52 Próxima lección y preguntas de la audiencia
Descripción
Los tiempos de entrega son una faceta fundamental de la mayoría de las situaciones de supply chain. Los tiempos de entrega pueden y deben ser forecast al igual que la demanda. Se pueden utilizar modelos de forecasting probabilístico dedicados a los tiempos de entrega. Se presenta una serie de técnicas para elaborar forecasts probabilísticos de tiempos de entrega para fines de supply chain. La composición de esos forecasts, el tiempo de entrega y la demanda, es una piedra angular del modelado predictivo en supply chain.
Transcripción completa

Bienvenidos a esta serie de conferencias de supply chain. Soy Joannes Vermorel, y hoy presentaré “Forecasting Lead Times.” Los tiempos de entrega, y más generalmente todos los retrasos aplicables, son un aspecto fundamental de supply chain al intentar equilibrar la oferta y la demanda. Se deben considerar los retrasos involucrados. Por ejemplo, consideremos la demanda de un juguete. La correcta anticipación del pico estacional de demanda antes de Navidad no tiene sentido si los productos se reciben en enero. Los tiempos de entrega rigen los detalles del planeamiento tanto como la demanda.
Los tiempos de entrega varían; varían mucho. Esto es un hecho, y en un minuto presentaré algunas evidencias. Sin embargo, a primera vista, esta proposición resulta desconcertante. No está claro por qué debería variar tanto el tiempo de entrega en primer lugar. Contamos con procesos de manufactura que pueden operar con menos de un micrómetro de tolerancia. Además, como parte del proceso de manufactura, podemos controlar un efecto, por ejemplo la aplicación de una fuente de luz, hasta el orden de un microsegundo. Si podemos controlar la transformación de la materia hasta el micrómetro y hasta el microsegundo, con la dedicación suficiente, deberíamos ser capaces de controlar el flujo de demandas con un grado de precisión comparable. O tal vez no.
Esta línea de pensamiento podría explicar por qué los tiempos de entrega parecen estar tan subestimados en la literatura de supply chain. Los libros de supply chain y, en consecuencia, el supply chain software apenas reconocen la existencia de los tiempos de entrega más allá de introducirlos como un parámetro de entrada para su modelo de inventario. Para esta conferencia, habrá tres objetivos:
Queremos entender la importancia y la naturaleza de los tiempos de entrega. Queremos entender cómo se pueden forecast los tiempos de entrega, con un interés específico en modelos probabilísticos que nos permiten abrazar la incertidumbre. Queremos combinar los forecasts de tiempos de entrega con los forecasts de demanda de maneras que sean de interés para supply chain.

Según la literatura principal de supply chain, los tiempos de entrega apenas merecen un par de notas al pie. Esta afirmación podría parecer una exageración extravagante, pero me temo que no lo es. Según Google Scholar, un buscador especializado en literatura científica, la consulta “demand forecasting” para el año 2021 arroja 10,500 artículos. Una inspección superficial de los resultados indica que, de hecho, la gran mayoría de esas entradas discuten el forecasting de la demanda en todo tipo de situaciones y mercados. La misma consulta, también para el año 2021, en Google Scholar para “lead time forecasting” arroja 71 resultados. Los resultados para la consulta de lead time forecasting son tan limitados que apenas se necesitan unos minutos para revisar toda la investigación de un año.
Resulta que solo hay alrededor de una docena de entradas que realmente discuten el forecast de los tiempos de entrega. De hecho, la mayoría de las coincidencias se encuentran en expresiones como “long lead time forecast” o “short lead time forecast” que se refieren a un forecast de la demanda, y no a un forecast del tiempo de entrega. Es posible repetir este ejercicio con “demand prediction” y “lead time prediction” y otras expresiones similares en otros años. Dejaré eso como un ejercicio para la audiencia.
Así, como una estimación aproximada, tenemos aproximadamente mil veces más artículos sobre forecasting de la demanda que sobre forecasting del tiempo de entrega. Los libros de supply chain y el supply chain software siguen la misma línea, dejando los tiempos de entrega como ciudadanos de segunda clase y como una trivialidad inconsecuente. Sin embargo, el personal de supply chain que ha sido introducido en esta serie de conferencias cuenta una historia diferente. Este personal podría representar empresas ficticias, pero refleja arquetipos de supply chain. Nos muestran el tipo de situación que debería considerarse típica. Veamos lo que este personal nos dice en lo que respecta a los tiempos de entrega.
Paris es una marca de moda ficticia que opera su propia red de tiendas. Paris realiza pedidos a proveedores del extranjero, con tiempos de entrega largos y, a veces, superiores a seis meses. Estos tiempos de entrega se conocen de manera imperfecta, y sin embargo, la nueva colección debe llegar a la tienda en el momento adecuado, tal como lo define la operación de marketing asociada con la nueva colección. Los tiempos de entrega de los proveedores requieren una debida anticipación; en otras palabras, requieren un forecast.
Amsterdam es una empresa de FMCG ficticia que se especializa en la producción de quesos, cremas y mantequilla. El proceso de maduración del queso es conocido y controlado, pero varía, con desviaciones de unos pocos días. Sin embargo, unos pocos días es precisamente la duración de las intensas promociones desencadenadas por las retail chains que resultan ser el canal de ventas principal de Amsterdam. Estos tiempos de entrega de manufactura requieren un forecast.
Miami es un aviation MRO ficticio. MRO significa mantenimiento, reparación y revisión. Cada avión necesita miles de piezas anualmente para seguir volando. La falta de una sola pieza puede hacer que la aeronave quede en tierra. La duración de la reparación para una pieza reparable, también conocida como TAT (turnaround time), define cuándo la pieza rotativa vuelve a estar en servicio. Sin embargo, el TAT varía de días a meses, dependiendo del alcance de las reparaciones, que no se conocen en el momento en que la pieza se retira del avión. Estos TAT requieren un forecast.
San Jose es una empresa de ecommerce ficticia que distribuye una variedad de artículos para el hogar y accesorios. Como parte de su servicio, San Jose ofrece un compromiso para una fecha de entrega para cada transacción. Sin embargo, la entrega en sí depende de empresas de terceros que están lejos de ser perfectamente confiables. Por lo tanto, San Jose requiere una estimación fundamentada sobre la fecha de entrega que se pueda prometer para cada transacción. Esta estimación fundamentada es, de manera implícita, un forecast de tiempo de entrega.
Finalmente, Stuttgart es una empresa ficticia del aftermarket automotriz. Opera sucursales que ofrecen reparaciones de automóviles. El precio de compra más bajo de las piezas de automóvil se puede obtener de mayoristas que ofrecen tiempos de entrega largos y algo irregulares. Existen proveedores más confiables que son más caros y están más cerca. Elegir al proveedor adecuado para cada pieza requiere un análisis comparativo adecuado de los respectivos tiempos de entrega asociados con varios proveedores.
Como podemos ver, cada miembro del personal de supply chain presentado hasta ahora requiere la anticipación de al menos un, y frecuentemente varios, tiempos de entrega. Si bien se podría argumentar que forecast de la demanda requiere más atención y esfuerzo que forecast de los tiempos de entrega, al final, ambos son necesarios para casi todas las situaciones de supply chain.
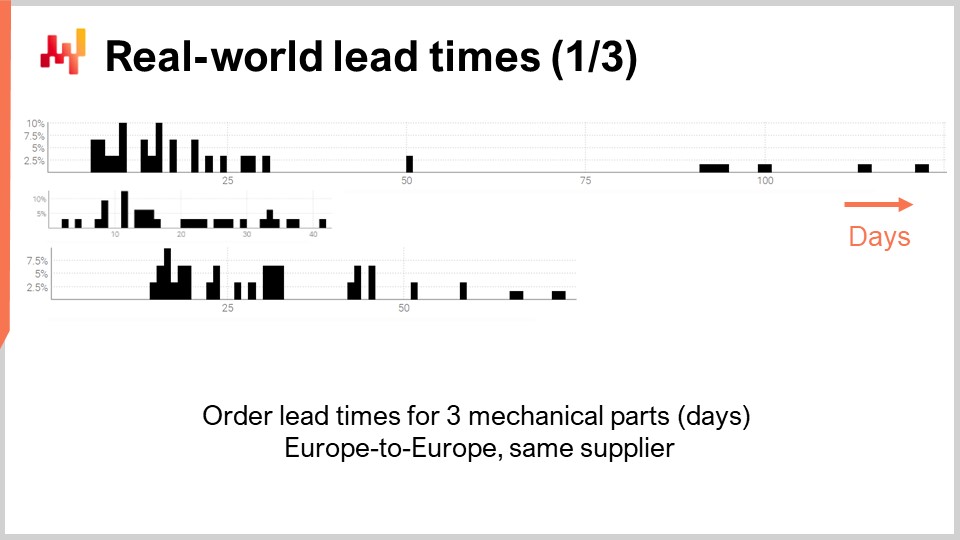
Así, echemos un vistazo a algunos tiempos de entrega reales. En la pantalla se muestran tres histogramas que se han trazado compilando los tiempos de entrega observados asociados con tres piezas mecánicas. Estas piezas se piden al mismo proveedor ubicado en Europa Occidental. Los pedidos provienen de una empresa igualmente situada en Europa Occidental. El eje x indica la duración de los tiempos de entrega observados expresada en días, y el eje y indica el número de observaciones expresado en porcentaje. A continuación, todos los histogramas adoptarán las mismas convenciones, con el eje x asociado a duraciones expresadas en días y el eje y reflejando la frecuencia. A partir de estas tres distribuciones, ya podemos hacer algunas observaciones.
Primero, los datos son escasos. Solo tenemos unas pocas docenas de puntos de datos, y estas observaciones se han recopilado a lo largo de varios años. Esta situación es típica; si la empresa realiza un pedido solo una vez al mes, se necesita casi una década para recopilar más de 100 observaciones de tiempos de entrega. Así, sea lo que sea que hagamos en términos de estadísticas, debe orientarse a números pequeños en lugar de números grandes. De hecho, rara vez tendremos el lujo de trabajar con grandes cantidades.
Segundo, los tiempos de entrega son erráticos. Tenemos observaciones que van desde unos pocos días hasta un trimestre. Aunque siempre es posible calcular un tiempo de entrega promedio, depender de cualquier tipo de valor promedio para cualquiera de esas piezas sería imprudente. También es evidente que ninguna de esas distribuciones es siquiera remotamente normal.
Tercero, tenemos tres piezas que son algo comparables en tamaño y precio, y sin embargo los tiempos de entrega varían mucho. Aunque podría ser tentador agrupar esas observaciones para hacer que los datos sean menos escasos, obviamente no es prudente hacerlo, ya que se estarían mezclando distribuciones que son muy disímiles. Esas distribuciones no tienen la misma media, mediana, ni siquiera el mismo mínimo o máximo.
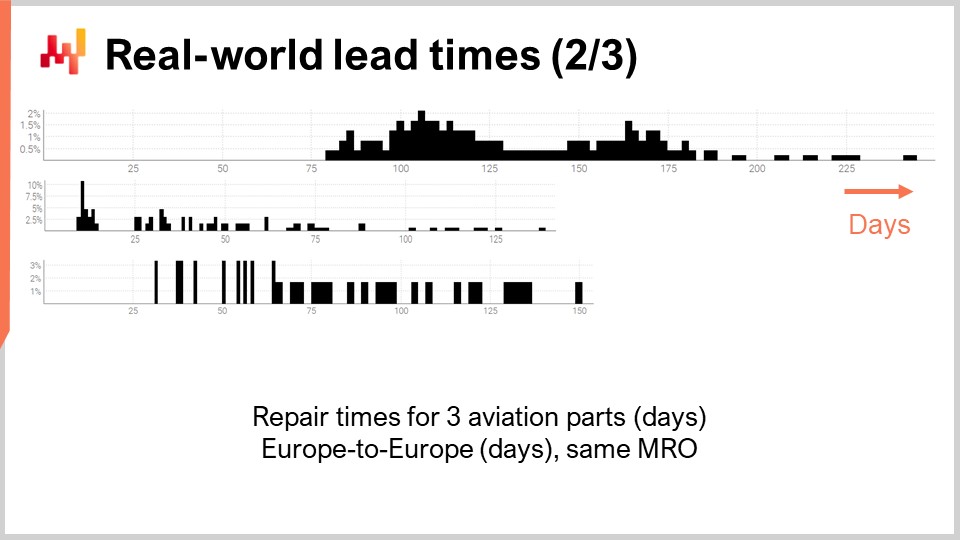
Echemos un vistazo a un segundo conjunto de tiempos de entrega. Estas duraciones reflejan el tiempo que se tarda en reparar tres piezas de aeronaves distintas. La primera distribución parece tener dos modas más una cola. Cuando una distribución presenta dos modas, generalmente da a entender la existencia de una variable oculta que explica esas dos modas. Por ejemplo, podrían existir dos tipos distintos de operaciones de reparación, cada tipo asociado con un tiempo de entrega propio. La segunda distribución parece tener una moda más una cola. Esta moda coincide con una duración relativamente corta, de aproximadamente dos semanas. Podría reflejar un proceso en el que la pieza es inspeccionada primero y, a veces, se considera que la pieza es apta para el servicio sin necesidad de intervención adicional, por lo tanto, un tiempo de entrega mucho más corto. La tercera distribución parece estar completamente dispersa, sin una moda o cola evidente. Podría haber múltiples procesos de reparación en juego que se agrupan juntos. La escasez de datos, con solo tres docenas de observaciones, hace difícil decir algo más. Volveremos a analizar esta tercera distribución más adelante en esta conferencia.
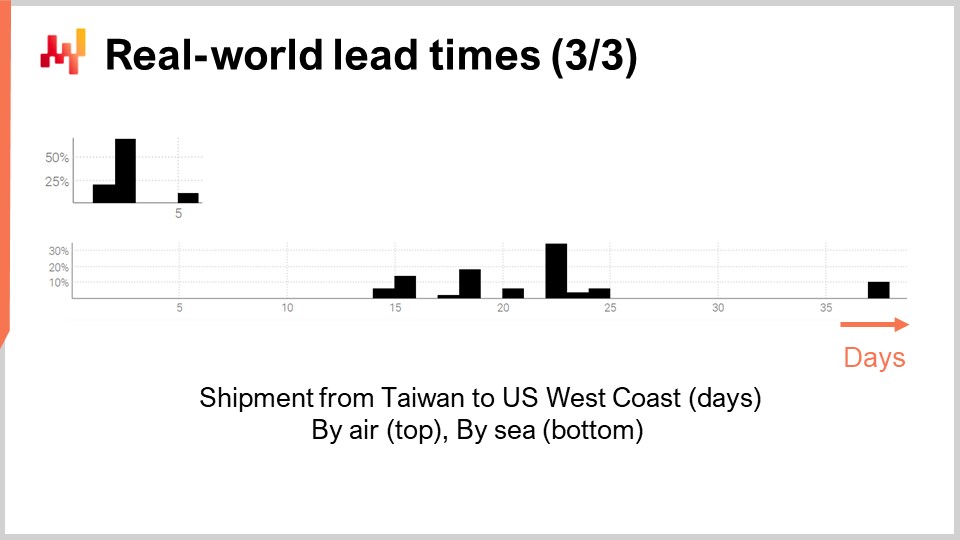
Finalmente, echemos un vistazo a dos tiempos de entrega que reflejan los retrasos en el envío desde Taiwán a la costa oeste de Estados Unidos, ya sea por vía aérea o marítima. No es sorprendente que los aviones de carga sean más rápidos que los buques de carga. La segunda distribución parece indicar que, a veces, un envío por mar podría perder su buque original y luego enviarse con el siguiente buque, casi duplicando el retraso. El mismo fenómeno podría ocurrir con el envío aéreo, aunque los datos son tan limitados que es solo una conjetura. Cabe señalar que tener acceso a solo un par de observaciones no es raro en lo que respecta a los tiempos de entrega. Estas situaciones son frecuentes. Es importante tener en cuenta que en esta conferencia buscamos herramientas e instrumentos que nos permitan trabajar con los datos de tiempos de entrega que tenemos, incluso si son solo un puñado de observaciones, y no con los datos de tiempos de entrega que desearíamos tener, como miles de observaciones. Los cortos intervalos en ambas distribuciones también sugieren un patrón cíclico basado en el día de la semana, aunque la visualización actual del histograma no es adecuada para validar esta hipótesis.
A partir de esta breve revisión de los tiempos de entrega en el mundo real, ya podemos captar algunos de los fenómenos subyacentes que están en juego. De hecho, los tiempos de entrega están altamente estructurados; los retrasos no ocurren sin causa, y esas causas pueden ser identificadas, descompuestas y cuantificadas. Sin embargo, los detalles de la descomposición del tiempo de entrega frecuentemente no se registran en los sistemas informáticos, al menos no todavía. Incluso cuando se dispone de una descomposición extensa del tiempo de entrega observado, como podría ser el caso en ciertas industrias como la aviación, ello no implica que los tiempos de entrega puedan anticiparse perfectamente. Es probable que los subsegmentos o fases dentro del tiempo de entrega exhiban su propia incertidumbre irreducible.
Esta serie de conferencias de supply chain presenta mis puntos de vista y percepciones tanto sobre el estudio como sobre la práctica de supply chain. Estoy intentando mantener estas conferencias algo independientes, pero tienen más sentido cuando se ven en secuencia. El resto de esta conferencia depende de elementos que se han introducido previamente en esta serie, aunque haré un repaso en un minuto.
El primer capítulo es una introducción general al campo y estudio de supply chain. Aclara la perspectiva que se adopta en esta serie de conferencias. Como ya habrás deducido, esta perspectiva difiere sustancialmente de lo que se consideraría la perspectiva dominante en supply chain.
El segundo capítulo presenta una serie de metodologías. De hecho, supply chain vence a las metodologías ingenuas. Las supply chain están compuestas por personas que tienen sus propias agendas; no existe tal cosa como una parte neutral en supply chain. Este capítulo aborda esas complicaciones, incluyendo mi propio conflicto de interés como CEO de Lokad, una empresa de software empresarial que se especializa en la optimización predictiva de supply chain optimization.
El tercer capítulo examina una serie de “personas” de supply chain. Estos personas son empresas ficticias que hemos revisado brevemente hoy, y están destinados a representar arquetipos de situaciones de supply chain. El propósito de estas personas es centrarse exclusivamente en los problemas, posponiendo la presentación de soluciones.
El cuarto capítulo revisa las ciencias auxiliares de supply chain. Estas ciencias no tratan sobre supply chain per se, pero deben considerarse esenciales para una práctica moderna de supply chain. Este capítulo incluye una progresión a través de los niveles de abstracción, comenzando desde el hardware de computación hasta las preocupaciones de ciberseguridad.
El quinto y presente capítulo está dedicado al modelado predictivo. El modelado predictivo es una perspectiva más general que el forecast; no se trata solo de forecast de demanda. Se trata del diseño de modelos que pueden utilizarse para estimar y cuantificar factores futuros de la supply chain de interés. Hoy, profundizamos en los lead times, pero más generalmente en supply chain, cualquier cosa que no se sepa con un grado razonable de certeza merece un forecast.
El sexto capítulo explica cómo se pueden calcular decisiones optimizadas aprovechando modelos predictivos y, más específicamente, modelos probabilísticos que fueron introducidos en el quinto capítulo. El séptimo capítulo vuelve a una perspectiva mayormente no técnica para discutir la ejecución corporativa real de una iniciativa de Supply Chain Quantitativa.

Hoy, nos centramos en los lead times. Acabamos de ver por qué los lead times importan, y acabamos de repasar una breve serie de lead times del mundo real. Por lo tanto, procederemos con elementos del modelado de lead times. Dado que adoptaré una perspectiva probabilística, reintroduciré brevemente el Continuous Rank Probability Score (CRPS), una métrica para evaluar la bondad de un probabilistic forecast. También introduciré cross-validation y una variante de cross-validation que es adecuada para nuestra perspectiva probabilística. Con esas herramientas en mano, introduciremos y evaluaremos nuestro primer modelo probabilístico no ingenuo para los lead times. Los datos de lead times son escasos, y el primer punto en nuestra agenda es suavizar esas distribuciones. Los lead times pueden descomponerse en una serie de fases intermedias. Por lo tanto, asumiendo que se dispone de algunos datos de lead times descompuestos, necesitamos algo para recomponer esos lead times preservando el ángulo probabilístico.
Luego, reintroduciremos differentiable programming. Differentiable programming ya se ha utilizado en esta serie de conferencias para forecast de demanda, pero también se puede utilizar para forecast de lead times. Lo haremos comenzando con un ejemplo simple destinado a captar el impacto del Año Nuevo Chino en los lead times, un patrón típico observado al importar productos desde Asia.
Luego procederemos con un modelo probabilístico paramétrico para los lead times, aprovechando la distribución log-logística. Nuevamente, differentiable programming será instrumental para aprender los parámetros del modelo. Luego extenderemos este modelo considerando observaciones incompletas de lead times. De hecho, incluso las órdenes de compra que aún no se han completado nos brindan algo de información sobre el lead time.
Finalmente, juntamos un probabilistic lead time forecast y un probabilistic demand forecast dentro de una única situación de replenishment. Esta será la oportunidad para demostrar por qué la modularidad es una preocupación esencial cuando se trata de modelado predictivo, aún más importante que los detalles minuciosos de los modelos en sí.

En la Conferencia 5.2 sobre probabilistic forecasting, ya hemos introducido algunas herramientas para evaluar la calidad de un probabilistic forecast. De hecho, las habituales accuracy metrics como el error cuadrático medio o el error absoluto medio sólo se aplican a point forecasts, no a probabilistic forecasts. Sin embargo, no es porque nuestros forecasts se vuelvan probabilísticos que la exactitud en el sentido general se vuelva irrelevante. Sólo necesitamos un instrumento estadístico que sea compatible con la perspectiva probabilística.
Entre esos instrumentos, se encuentra el Continuous Rank Probability Score (CRPS). La fórmula se muestra en la pantalla. El CRPS es una generalización de la métrica L1, es decir, el error absoluto, pero para distribuciones de probabilidad. La versión habitual del CRPS compara una distribución, llamada F aquí, con una observación, llamada X aquí. El valor obtenido de la función CRPS es homogéneo con la observación. Por ejemplo, si X es un lead time expresado en días, entonces el valor del CRPS también se expresa en días.

El CRPS puede generalizarse para la comparación de dos distribuciones. Esto es lo que se está haciendo en la pantalla. Es solo una variación menor de la fórmula anterior. La esencia de esta métrica sigue sin cambios. Si F es la distribución verdadera de lead times y F_hat es una estimación de la distribución de lead times, entonces el CRPS se expresa en días. El CRPS refleja la cantidad de diferencia entre ambas distribuciones. El CRPS también puede interpretarse como la cantidad mínima de energía necesaria para transportar toda la masa de la primera distribución de modo que adopte la forma exacta de la segunda distribución.
Ahora tenemos un instrumento para comparar dos distribuciones de probabilidad unidimensionales. Esto se volverá de interés en un momento, cuando introduzcamos nuestro primer modelo probabilístico para los lead times.
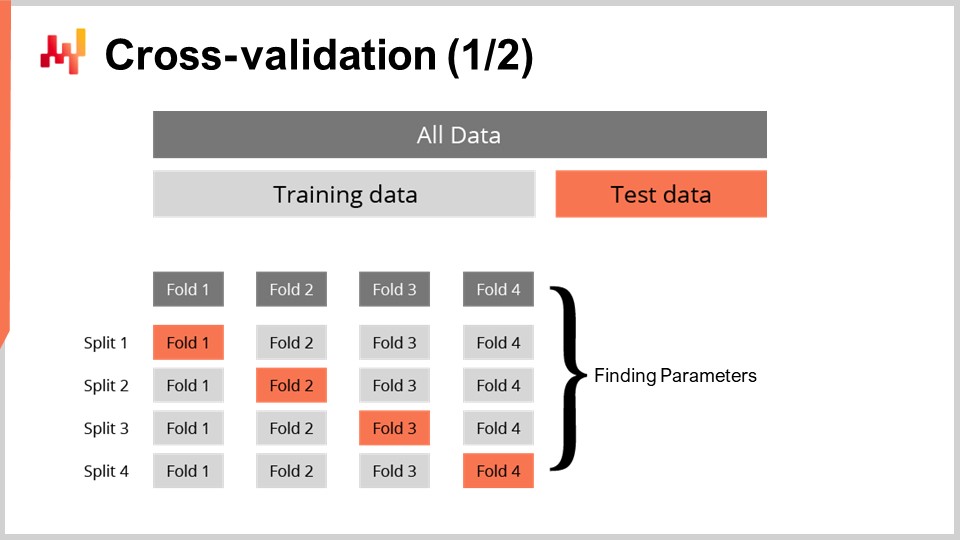
Tener una métrica para medir la calidad de un probabilistic forecast no es del todo suficiente. La métrica mide la calidad sobre los datos que tenemos; sin embargo, lo que realmente queremos es ser capaces de evaluar la calidad de nuestro forecast con datos que no tenemos. De hecho, los lead times futuros son los que nos interesan, no los lead times que ya se han observado en el pasado. Nuestra capacidad para que un modelo funcione bien en datos que no tenemos se llama generalización. Cross-validation es una técnica general de validación de modelos diseñada precisamente para evaluar la capacidad de un modelo para generalizar bien.
En su forma más simple, cross-validation consiste en particionar las observaciones en un pequeño número de subconjuntos. En cada iteración, se deja de lado un subconjunto al que se denomina conjunto de prueba. Luego, el modelo se genera o entrena basado en los otros subconjuntos de datos, denominados conjuntos de entrenamiento. Tras el entrenamiento, el modelo se valida contra el conjunto de prueba. Este proceso se repite un cierto número de veces, y la bondad promedio obtenida en todas las iteraciones representa el resultado final validado por cross-validation.
Cross-validation se utiliza raramente en el contexto de forecasting de time series debido a la dependencia temporal entre observaciones. De hecho, cross-validation, tal como se presentó, asume que las observaciones son independientes. Cuando se trata de series temporales, se utiliza backtesting en su lugar. El backtesting puede considerarse como una forma de cross-validation que tiene en cuenta la dependencia temporal.
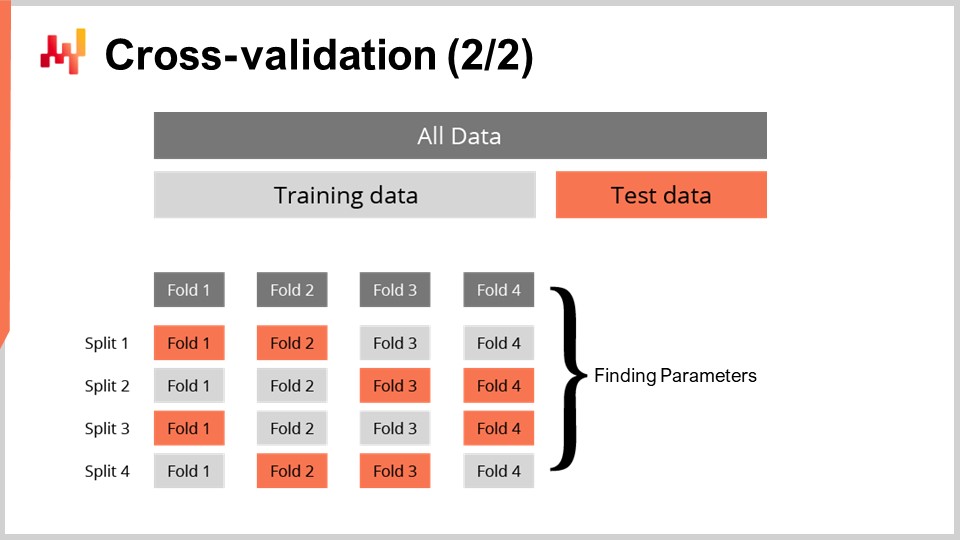
La técnica de cross-validation viene con numerosas variantes que reflejan una amplia gama de posibles ángulos que podrían necesitar ser abordados. No revisaremos esas variantes para el propósito de esta conferencia. Utilizaré una variante específica en la que, en cada partición, el conjunto de entrenamiento y el conjunto de prueba tienen un tamaño aproximadamente igual. Esta variante se introduce para abordar la validación de un modelo probabilístico, como veremos con algo de código en un momento.
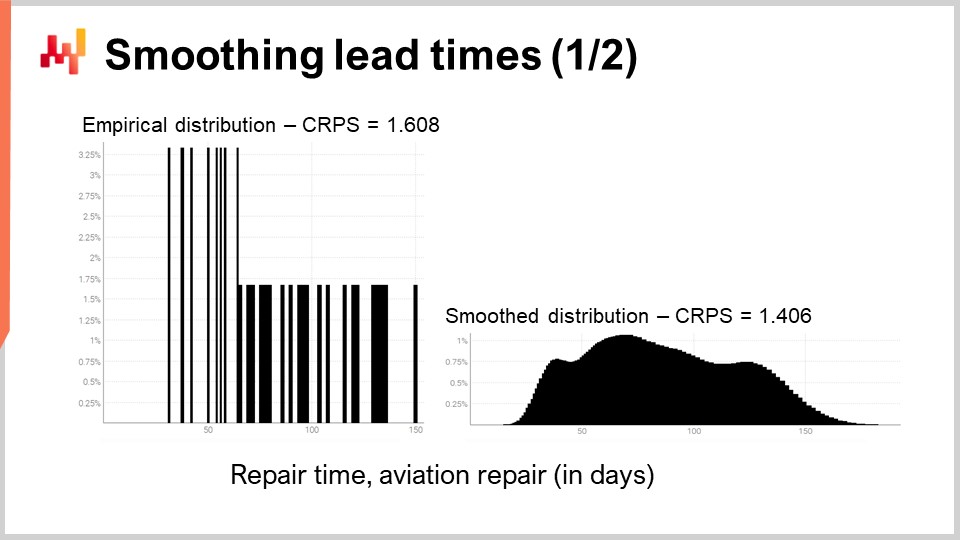
Revisemos uno de los lead times del mundo real que hemos visto previamente en la pantalla. A la izquierda, el histograma está asociado a la tercera distribución de tiempos de reparación de aviación. Esas son las mismas observaciones vistas anteriormente, y el histograma simplemente se ha estirado verticalmente. Al hacerlo, los dos histogramas, el de la izquierda y el de la derecha, comparten la misma escala. Para el histograma de la izquierda, tenemos alrededor de 30 observaciones. No es mucho, pero ya es más de lo que frecuentemente obtendremos.
El histograma de la izquierda se conoce como una distribución empírica. Es literalmente el histograma bruto obtenido de las observaciones. El histograma tiene un contenedor por cada duración expresada en un número entero de días. Para cada contenedor, contamos el número de lead times observados. Debido a la escasez, la distribución empírica se asemeja a un código de barras.
Hay un problema aquí. Si tenemos dos lead times observados exactamente a 50 días, ¿tiene sentido decir que la probabilidad de observar 49 días o 51 días es exactamente cero? No es así. Claramente, existe un espectro de duraciones; simplemente no contamos con suficientes puntos de datos para observar la verdadera distribución subyacente, que es, muy probablemente, mucho más suave que esta distribución similar a un código de barras.
Por lo tanto, cuando se trata de suavizar esta distribución, existe un número indefinido de maneras de realizar esta operación de suavizado. Algunos métodos de suavizado pueden parecer buenos, pero no son estadísticamente sólidos. Como punto de partida, nos gustaría asegurar que un modelo suave sea más preciso que el empírico. Resulta que ya hemos introducido dos instrumentos, el CRPS y cross-validation, que nos permitirán hacer eso.
En un momento, los resultados se muestran. El error CRPS asociado con la distribución tipo código de barras es de 1.6 días, mientras que el error CRPS asociado con la distribución suavizada es de 1.4 días. Estas dos cifras se han obtenido mediante cross-validation. El error menor indica que, en el sentido del CRPS, la distribución de la derecha es la más precisa de las dos. La diferencia de 0.2 entre 1.4 y 1.6 no es mucha; sin embargo, la propiedad clave aquí es que tenemos una distribución suave que no deja de manera errática ciertas duraciones intermedias con una probabilidad cero. Esto es razonable, ya que nuestra comprensión de las reparaciones nos dice que esas duraciones probablemente terminarían ocurriendo si se repitieran las reparaciones. El CRPS no refleja la verdadera magnitud de la mejora que acabamos de lograr al suavizar la distribución. Sin embargo, al menos, bajar el CRPS confirma que esta transformación es razonable desde una perspectiva estadística.
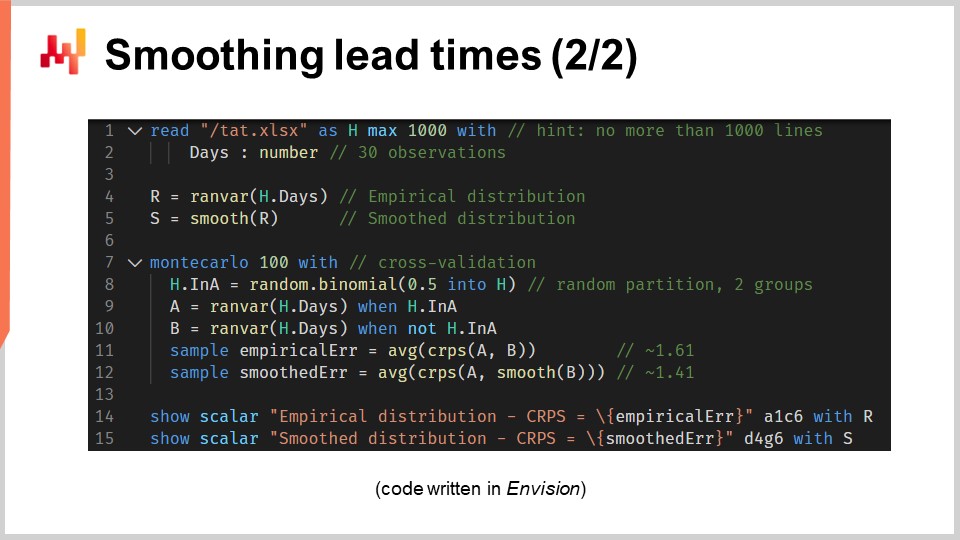
Echemos ahora un vistazo al código fuente que ha producido esos dos modelos y ha mostrado esos dos histogramas. En total, esto se logra en 12 líneas de código si se excluyen las líneas en blanco. Como de costumbre en esta serie de conferencias, el código está escrito en Envision, el lenguaje de programación específico de dominio de Lokad dedicado a la optimización predictiva de supply chain. Sin embargo, no hay magia; esta lógica podría haberse escrito en Python. Pero para el tipo de problemas que estamos considerando en esta conferencia, Envision es más conciso y autosuficiente.
Revisemos esas 12 líneas de código. En las líneas 1 y 2, estamos leyendo una spreadsheet de Excel que tiene una única columna de datos. La spreadsheet contiene 30 observaciones. Estos datos se recogen en una tabla llamada “H” que tiene una única columna llamada “days.” En la línea 4, estamos construyendo una distribución empírica. La variable “R” tiene el tipo de dato “ranvar,” y en el lado derecho de la asignación, la función “ranvar” es un agregador que toma observaciones como entrada y devuelve el histograma representado con un tipo de dato “ranvar.” Como resultado, el tipo de dato “ranvar” está dedicado a distribuciones enteras unidimensionales. Introdujimos el tipo de dato “ranvar” en una conferencia anterior de este capítulo. Este tipo de dato garantiza un uso constante de memoria y un tiempo de cómputo constante para cada operación. La desventaja del “ranvar” como tipo de dato es que se involucra una compresión con pérdida, aunque la pérdida de datos causada por la compresión ha sido diseñada para ser intrascendente para los propósitos de supply chain.
En la línea 5, estamos suavizando la distribución con la función incorporada llamada “smooth.” Bajo el capó, esta función reemplaza la distribución original con una mezcla de distribuciones de Poisson. Cada contenedor del histograma se transforma en una distribución de Poisson con una media igual a la posición entera del contenedor, y finalmente, la mezcla asigna un peso a cada distribución de Poisson proporcional al peso del contenedor mismo. Otra manera de entender lo que hace la función “smooth” es considerar que es equivalente a reemplazar cada observación individual por una distribución de Poisson con una media igual a la propia observación. Todas esas distribuciones de Poisson, una por observación, se mezclan luego. Mezclar significa promediar los valores respectivos de los contenedores del histograma. Las variables “ranvar” “R” y “S” no se utilizarán de nuevo hasta las líneas 14 y 15, donde se mostrarán.
En la línea 7, iniciamos un bloque Monte Carlo. Este bloque es una especie de bucle, y se ejecutará 100 veces, según lo especificado por los 100 valores que aparecen justo después de la palabra clave Monte Carlo. El bloque Monte Carlo está diseñado para recopilar observaciones independientes que se generan de acuerdo con un proceso que implica un cierto grado de aleatoriedad. Quizás te preguntes por qué existe una construcción específica de Monte Carlo en Envision en lugar de tener simplemente un bucle, como suele ser el caso en los lenguajes de programación convencionales. Resulta que tener una construcción dedicada aporta beneficios sustanciales. Primero, garantiza que las iteraciones sean verdaderamente independientes, hasta las semillas utilizadas para derivar la pseudorandomness. Segundo, ofrece un objetivo explícito para la distribución automatizada de la carga de trabajo a través de varios núcleos de CPU o incluso entre varias máquinas.
En la línea 8, creamos un vector aleatorio de valores booleanos dentro de la tabla “H.” Con esta línea, estamos generando valores aleatorios independientes, llamados deviates (true o false), para cada línea de la tabla “H.” Como de costumbre en Envision, los bucles se abstraen mediante la programación en arreglos. Con esos valores booleanos, estamos particionando la tabla “H” en dos grupos. Esta división aleatoria se utiliza para el proceso de validación cruzada.
En las líneas 9 y 10, estamos creando dos “ranvars” llamados “A” y “B,” respectivamente. Estamos utilizando nuevamente el agregador “ranvar,” pero esta vez aplicamos un filtro con la palabra clave “when” justo después de la llamada al agregador. “A” se genera utilizando solo las líneas en que el valor en “a” es true; para “B,” sucede lo contrario. “B” se genera utilizando únicamente las líneas en que el valor en “a” es false.
En las líneas 11 y 12, recopilamos las cifras de interés del bloque Monte Carlo. En Envision, la palabra clave “sample” solo puede ubicarse dentro de un bloque Monte Carlo. Se utiliza para recolectar las observaciones realizadas al iterar muchas veces a través del proceso Monte Carlo. En la línea 11, estamos calculando el error promedio, expresado en términos de CRPS, entre dos distribuciones empíricas: una submuestra del conjunto original de plazos de entrega. La palabra clave “sample” especifica que los valores se recogen durante las iteraciones Monte Carlo. El agregador “AVG”, que significa “average” en el lado derecho de la asignación, se utiliza para producir una única estimación al final del bloque.
En la línea 12, hacemos algo casi idéntico a lo ocurrido en la línea 11. Esta vez, sin embargo, aplicamos la función “smooth” al “ranvar” “B.” Queremos evaluar qué tan cercana está la variante smooth de la distribución empírica ingenua. Resulta que está más cerca, al menos en términos de CRPS, que sus contrapartes empíricas originales.
En las líneas 14 y 15, exhibimos los histogramas y los valores de CRPS. Esas líneas generan las figuras que hemos visto en la diapositiva anterior. Este script nos proporciona nuestra línea base para la calidad de la distribución empírica de nuestro modelo. De hecho, si bien este modelo, el de “barcode”, puede considerarse ingenuo, sigue siendo un modelo, y además probabilístico. Así, este script también nos ofrece un mejor modelo, al menos en el sentido del CRPS, mediante una variante smooth de la distribución empírica original.
En este momento, dependiendo de tu familiaridad con los lenguajes de programación, puede parecer mucho para asimilar. Sin embargo, me gustaría señalar lo sencillo que es producir una distribución de probabilidad razonable, incluso cuando no contamos con más de unas pocas observaciones. Aunque tenemos 12 líneas de código, solo las líneas 4 y 5 representan la verdadera parte de modelado del ejercicio. Si solo nos interesara la variante smooth, entonces el “ranvar” “S” podría escribirse en una sola línea de código. Literalmente, es una línea única en términos de código: primero, se aplica una agregación con ranvar, y segundo, se aplica un operador smooth, y ya está. El resto es solo instrumentación y exhibición. Con las herramientas adecuadas, el modelado probabilístico, ya sea de plazos de entrega u otra cosa, puede hacerse extremadamente sencillo. No hay matemáticas grandiosas involucradas, ni algoritmos grandiosos, ni piezas de software grandiosas. Es simple y notablemente así.

¿Cómo se consigue que un envío llegue con seis meses de retraso? La respuesta es obvia: un día a la vez. Más seriamente, los plazos de entrega generalmente pueden descomponerse en una serie de retrasos. Por ejemplo, un plazo de entrega de un supplier puede descomponerse en un retraso de espera mientras la orden se coloca en una cola de pendientes, seguido de un retraso de fabricación mientras se producen los bienes, y finalmente seguido de un retraso en el tránsito mientras los bienes son enviados. Así, si los plazos de entrega pueden descomponerse, también resulta interesante poder recomponerlos.
Si viviéramos en un mundo altamente determinista donde el futuro pudiera anticiparse con precisión, entonces recomponer los plazos de entrega sería simplemente cuestión de sumar. Volviendo al ejemplo que acabo de mencionar, componer el plazo de entrega del pedido sería la suma del retraso en la cola en días, el retraso de fabricación en días y el retraso en el tránsito en días. Sin embargo, no vivimos en un mundo en el que el futuro se pueda anticipar con precisión. Las distribuciones de plazos de entrega en el mundo real que presentamos al comienzo de esta conferencia respaldan esta afirmación. Los plazos de entrega son erráticos, y hay pocas razones para creer que esto cambiará fundamentalmente en las próximas décadas.
Por lo tanto, los plazos de entrega futuros deben abordarse como variables aleatorias. Estas variables aleatorias abarcan y cuantifican la incertidumbre en lugar de descartarla. Más específicamente, esto significa que cada componente del plazo de entrega también debe modelarse individualmente como una variable aleatoria. Volviendo a nuestro ejemplo, el plazo de entrega del pedido es una variable aleatoria, y se obtiene como la suma de tres variables aleatorias asociadas, respectivamente, con el retraso en la cola, el retraso de fabricación y el retraso en el tránsito.
La fórmula para la suma de dos variables aleatorias independientes, unidimensionales y con valores enteros se presenta en la pantalla. Esta fórmula simplemente estipula que si obtenemos una duración total de Z días, y si tenemos K días para la primera variable aleatoria X, entonces debemos tener Z menos K días para la segunda variable aleatoria Y. Este tipo de suma es conocido, en términos generales, en matemáticas como convoluciones.
Aunque parece que hay un número infinito de términos en esta convolución, en la práctica, solo nos interesamos por un número finito de términos. Primero, todas las duraciones negativas tienen una probabilidad cero; de hecho, retrasos negativos significarían viajar en el tiempo. Segundo, para retrasos grandes, las probabilidades se vuelven tan pequeñas que, para fines prácticos de supply chain, se pueden aproximar de forma confiable a cero.
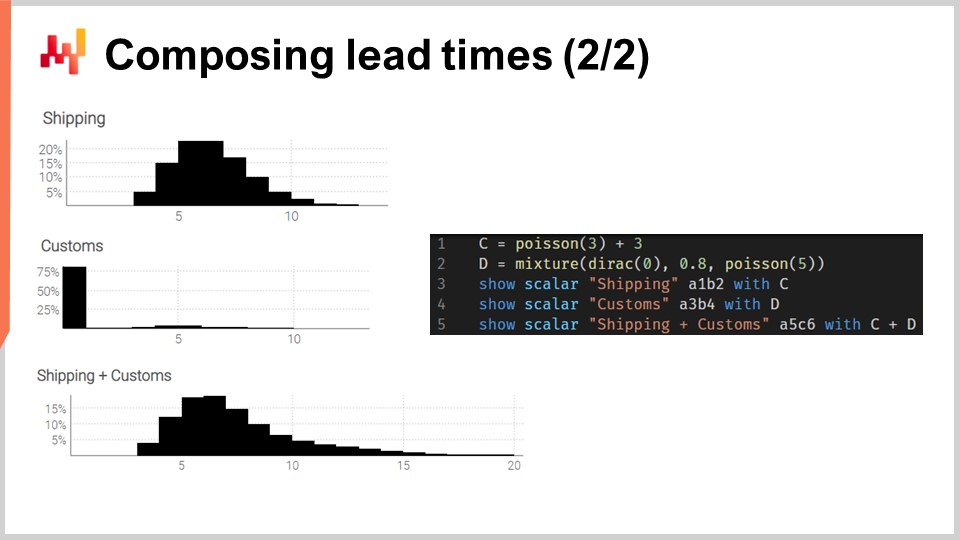
Pongamos en práctica estas convoluciones. Consideremos un tiempo de tránsito que puede descomponerse en dos fases: un retraso en el envío seguido de un retraso en la liberación en aduanas. Queremos modelar estas dos fases con dos variables aleatorias independientes y luego recomponer el tiempo de tránsito sumando esas dos variables aleatorias.
En la pantalla, los histogramas a la izquierda son producidos por el script a la derecha. En la línea 1, el retraso en el envío se modela como una convolución de una distribución de Poisson más una constante. La función Poisson devuelve un tipo de dato “ranvar”; sumar tres tiene el efecto de desplazar la distribución hacia la derecha. El “ranvar” resultante se asigna a la variable “C.” Este “ranvar” se muestra en la línea 3. Se puede ver a la izquierda como el histograma superior. Reconocemos la forma de una distribución de Poisson que ha sido desplazada hacia la derecha por algunas unidades, tres unidades en este caso. En la línea dos, la liberación en aduanas se modela como una mezcla de un Dirac en cero y un Poisson en cinco. El Dirac en cero ocurre el ochenta por ciento del tiempo; eso es lo que significa esta constante 0.8. Refleja situaciones en las que, la mayoría del tiempo, los bienes ni siquiera son inspeccionados por aduanas y pasan sin ningún retraso notable. Alternativamente, el veinte por ciento del tiempo, los bienes son inspeccionados en aduanas, y el retraso se modela como una distribución de Poisson con una media de cinco. El “ranvar” resultante se asigna a una variable llamada D. Este “ranvar” se muestra en la línea cuatro y se puede ver a la izquierda como el histograma del medio. Este aspecto asimétrico refleja que la mayoría del tiempo, la aduana no añade ningún retraso.
Finalmente, en la línea cinco, calculamos C más D. Esta suma es una convolución, ya que tanto C como D son ranvars, no números. Esta es la segunda convolución en este script, ya que una convolución ya tuvo lugar en la línea uno. El ranvar resultante se muestra y es visible a la izquierda como el tercer y último histograma. Este tercer histograma es similar al primero, excepto que la cola se extiende mucho más hacia la derecha. Una vez más, vemos que con unas pocas líneas de código podemos abordar efectos del mundo real no triviales, tales como los retrasos en la liberación en aduanas.
Sin embargo, se podrían hacer dos críticas a este ejemplo. Primero, no se indica de dónde provienen las constantes; en la práctica, queremos aprender esas constantes a partir de datos históricos. Segundo, aunque la distribución de Poisson tiene la ventaja de la simplicidad, puede que no sea una forma muy realista para el modelado de plazos de entrega, especialmente considerando situaciones de fat-tail. Por lo tanto, abordaremos esos dos puntos en orden.
Para aprender parámetros a partir de datos, vamos a retomar un paradigma de programación que ya hemos introducido en esta serie de conferencias, a saber, la programación diferenciable. Si no has visto las conferencias anteriores en este capítulo, te invito a que las revises después del final de la presente conferencia. La programación diferenciable se presenta con mayor detalle en esas conferencias.
La programación diferenciable es una combinación de dos técnicas: descenso del gradiente estocástico y diferenciación automática. El descenso del gradiente estocástico es una técnica de optimización que ajusta los parámetros una observación a la vez en la dirección opuesta de los gradientes. La diferenciación automática es una técnica de compilación, como en el compilador de un lenguaje de programación; calcula los gradientes para todos los parámetros que aparecen dentro de un programa general.
Ilustremos la programación diferenciable con un problema de plazos de entrega. Esto servirá ya sea como un repaso o como una introducción, dependiendo de tu familiaridad con este paradigma. Queremos modelar el impacto del Año Nuevo Chino en los plazos de entrega asociados con las importaciones de China. De hecho, a medida que las fábricas cierran durante dos o tres semanas debido al Año Nuevo Chino, los plazos de entrega se alargan. El Año Nuevo Chino es cíclico; ocurre cada año. Sin embargo, no es estrictamente estacional, al menos no en el sentido del calendario gregoriano.
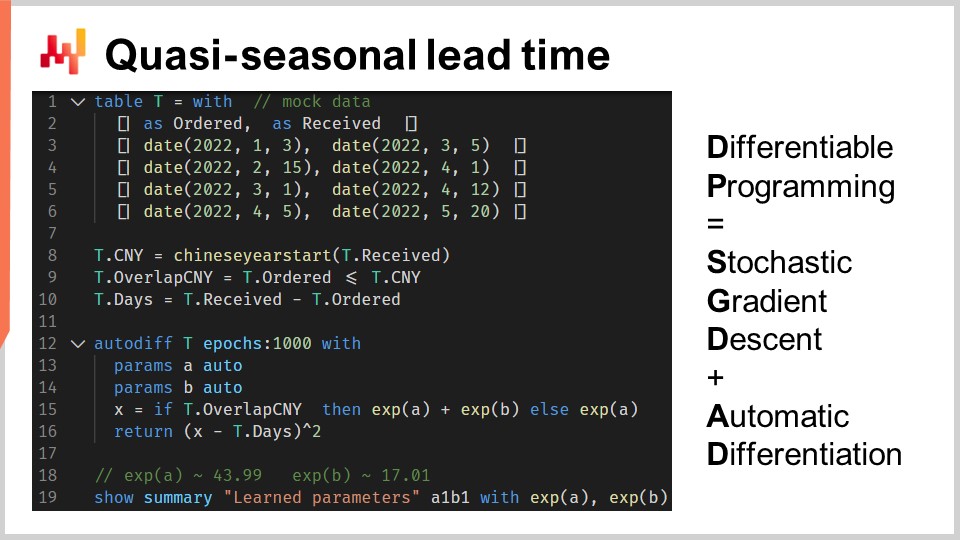
En las líneas uno a seis, presentamos algunos pedidos de compra simulados con cuatro observaciones, con una fecha de pedido y una fecha de recepción. En la práctica, estos datos no estarían codificados a mano, sino que cargaríamos estos datos históricos desde los sistemas de la empresa. En las líneas ocho y nueve, calculamos si el plazo de entrega se solapa con el Año Nuevo Chino. La variable “T.overlap_CNY” es un vector booleano; indica si la observación se ve afectada por el Año Nuevo Chino o no.
En la línea 12, introducimos un bloque “autodiff”. La tabla T se utiliza como tabla de observaciones, y hay 1000 epochs. Esto significa que cada observación, o sea cada línea de la tabla T, se visitará mil veces. Un paso del descenso del gradiente estocástico corresponde a una ejecución de la lógica dentro del bloque “autodiff”.
En las líneas 13 y 14, se declaran dos parámetros escalares. El bloque “autodiff” aprenderá estos parámetros. El parámetro A refleja el plazo de entrega base sin el efecto del Año Nuevo Chino, y el parámetro B refleja el retraso extra asociado con el Año Nuevo Chino. En la línea 15, calculamos X, la predicción del plazo de entrega de nuestro modelo. Se trata de un modelo determinista, no probabilístico; X es un forecast puntual de plazo de entrega. El lado derecho de la asignación es sencillo: si la observación se solapa con el Año Nuevo Chino, entonces devolvemos la base más el componente del Año Nuevo; de lo contrario, devolvemos solo la base. Dado que el bloque “autodiff” toma solo una observación a la vez, en la línea 15, la variable T.overlap_CNY se refiere a un valor escalar y no a un vector. Este valor coincide con la línea elegida como observación dentro de la tabla T.
Los parámetros A y B se envuelven en la función exponencial “exp,” lo cual es un pequeño truco de programación diferenciable. De hecho, el algoritmo que dirige el descenso del gradiente estocástico tiende a ser relativamente conservador en lo que respecta a las variaciones incrementales de los parámetros. Así, si queremos aprender un parámetro positivo que pueda crecer más allá de, digamos, 10, envolver este parámetro en un proceso exponencial acelera la convergencia.
En la línea 16, devolvemos un error cuadrático medio entre nuestra predicción X y la duración observada, expresada en días (T.days). Nuevamente, dentro de este bloque “autodiff”, T.days es un valor escalar y no un vector. Dado que la tabla T se utiliza como tabla de observaciones, el valor devuelto se considera la pérdida que se minimiza mediante el descenso del gradiente estocástico. La diferenciación automática propaga los gradientes desde la pérdida de vuelta a los parámetros A y B. Finalmente, en la línea 19, mostramos los dos valores que hemos aprendido, respectivamente, para A y B, que son la base y el componente del Año Nuevo de nuestro plazo de entrega.
Esto concluye nuestra reintroducción de la programación diferenciable como una herramienta versátil que aprende patrones estadísticos. A partir de aquí, retomaremos los bloques “autodiff” con situaciones más elaboradas. Sin embargo, vale la pena señalar una vez más que, aunque pueda parecer un poco abrumador, no hay nada realmente complicado ocurriendo aquí. Posiblemente, la parte de código más compleja en este script es la implementación subyacente de la función “ChineseYearStart,” llamada en la línea ocho, que resulta ser parte de la biblioteca estándar de Envision. Con unas pocas líneas de código, introducimos un modelo con dos parámetros y aprendemos esos parámetros. Una vez más, esta simplicidad es notable.
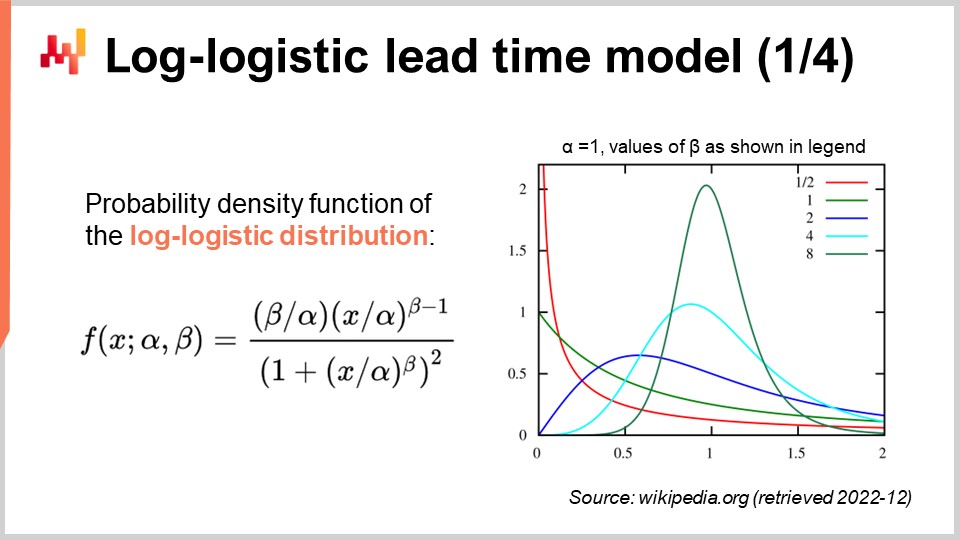
Los tiempos de entrega suelen tener colas pesadas; es decir, cuando un tiempo de entrega se desvía, se desvía mucho. Por lo tanto, para modelar el tiempo de entrega, resulta interesante adoptar distribuciones que puedan reproducir ese comportamiento de colas pesadas. La literatura matemática presenta una extensa lista de tales distribuciones, y bastantes se adecuarían a nuestro propósito. Sin embargo, simplemente recorrer el panorama matemático nos tomaría horas. Basta señalar que la distribución de Poisson no tiene una cola pesada. Así, hoy, escogeré la distribución log-logística, que resulta ser una distribución de cola pesada. La justificación principal para esta elección es que los equipos de Lokad están modelando los tiempos de entrega mediante distribuciones log-logísticas para varios clientes. Funciona bien con un mínimo número de complicaciones. Tengamos en cuenta, sin embargo, que la distribución log-logística de ninguna manera es una solución mágica, y existen numerosas situaciones en las que Lokad modela los tiempos de entrega de forma diferente.
En la pantalla, tenemos la función de densidad de probabilidad de la distribución log-logística. Se trata de una distribución paramétrica que depende de dos parámetros, alpha y beta. El parámetro alpha es la mediana de la distribución, y el parámetro beta gobierna la forma de la distribución. A la derecha, se puede obtener una breve serie de formas mediante varios valores de beta. Aunque esta fórmula de densidad pueda parecer intimidante, es literalmente material de libro de texto, al igual que la fórmula para calcular el volumen de una esfera. Puedes intentar descifrar y memorizar esta fórmula, pero ni siquiera es necesario; solo necesitas saber que existe una fórmula analítica. Una vez que sabes que la fórmula existe, encontrarla en línea toma menos de un minuto.

Nuestro objetivo es aprovechar la distribución log-logística para aprender un modelo probabilístico de tiempo de entrega. Para ello, vamos a minimizar el log-likelihood. De hecho, en la conferencia anterior de este quinto capítulo, hemos visto que existen varias métricas apropiadas para la perspectiva probabilística. Hace un rato, repasamos el CRPS (Continuous Ranked Probability Score). Aquí, repasamos el log-likelihood, que adopta una perspectiva bayesiana.
En resumen, dada dos parámetros, la distribución log-logística nos indica la probabilidad de observar cada dato tal como aparece en el conjunto de datos empírico. Queremos aprender los parámetros que maximizan este log-likelihood. El logaritmo, es decir, el log-likelihood en lugar del likelihood simple, se introduce para evitar underflows numéricos. Los underflows numéricos ocurren cuando procesamos números muy pequeños, muy cercanos a cero; esos números no se comportan bien con la representación en punto flotante, tal como se encuentra comúnmente en el hardware de cómputo moderno.
Así, para calcular el log-likelihood de la distribución log-logística, aplicamos el logaritmo a su función de densidad de probabilidad. La expresión analítica se muestra en la pantalla. Esta expresión puede ser implementada, y esto es exactamente lo que se hace en las tres líneas de código a continuación.
En la línea uno, se introduce la función “L4”. L4 significa “log-likelihood of log-logistic” – sí, son muchas L’s y muchos logs. Esta función toma tres argumentos: los dos parámetros alpha y beta, además de la observación x. Esta función devuelve el logaritmo de la likelihood. La función L4 está decorada con la palabra clave “autodiff”; dicha palabra clave indica que esta función está destinada a diferenciarse mediante diferenciación automática. En otras palabras, los gradientes pueden fluir hacia atrás desde el valor devuelto por esta función hasta sus argumentos, los parámetros alpha y beta. Técnicamente, el gradiente también fluye hacia atrás a través de la observación x; sin embargo, dado que mantendremos las observaciones inmutables durante el proceso de aprendizaje, los gradientes no tendrán efecto sobre ellas. En la línea tres, obtenemos la transcripción literal de la fórmula matemática justo encima del script.
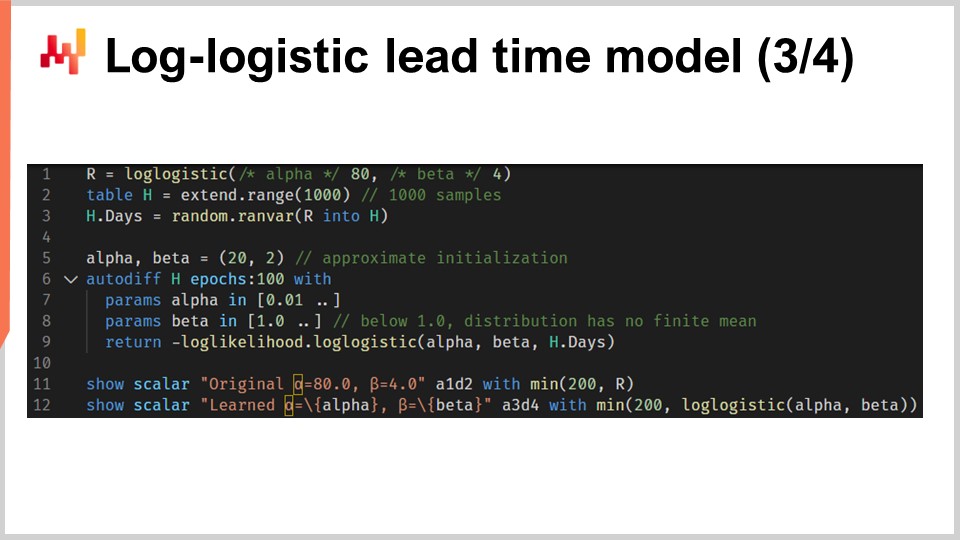
Ahora, unamos todo con un script que aprende los parámetros de un modelo probabilístico de tiempo de entrega basado en la distribución log-logística. En las líneas uno y tres, generamos nuestro conjunto de datos de entrenamiento simulado. En escenarios del mundo real, utilizaríamos datos históricos en lugar de generar datos simulados. En la línea uno, creamos una “ranvar” que representa la distribución original. Para el ejercicio, queremos recuperar esos parámetros, alpha y beta. La función log-logística es parte de la biblioteca estándar de Envision y devuelve una “ranvar”. En la línea dos, creamos la tabla “H”, que contiene 1,000 entradas. En la línea tres, extraemos 1,000 desviaciones que se muestrean aleatoriamente de la distribución original “R”. Este vector “H.days” representa el conjunto de datos de entrenamiento.
En la línea seis, tenemos un bloque “autodiff”; aquí es donde ocurre el aprendizaje. En las líneas siete y ocho, declaramos dos parámetros, alpha y beta, y para evitar problemas numéricos como la división por cero, se aplican límites a esos parámetros. Alpha debe mantenerse mayor que 0.01 y beta debe mantenerse mayor que 1.0. En la línea nueve, devolvemos la pérdida, que es lo opuesto al log-likelihood. De hecho, por convención, los bloques “autodiff” minimizan la función de pérdida, y por ello queremos maximizar la likelihood, de ahí el signo negativo. La función “log_likelihood.logistic” es parte de la biblioteca estándar de Envision, pero internamente, es simplemente la función “L4” que hemos implementado en la diapositiva anterior. Por lo tanto, no hay magia en juego; es toda la diferenciación automática la que permite que el gradiente fluya hacia atrás desde la pérdida hasta los parámetros alpha y beta.
En las líneas 11 y 12 se grafican la distribución original y la distribución aprendida. Los histogramas se limitan a 200; este límite hace que el histograma sea un poco más legible. Volveremos a eso en un momento. En caso de que te preguntes sobre el rendimiento de la parte “autodiff” de este script, se ejecuta en menos de 80 milisegundos en un solo núcleo de CPU. La programación diferenciable no solo es versátil, sino que también hace un buen uso de los recursos de cómputo moderno.
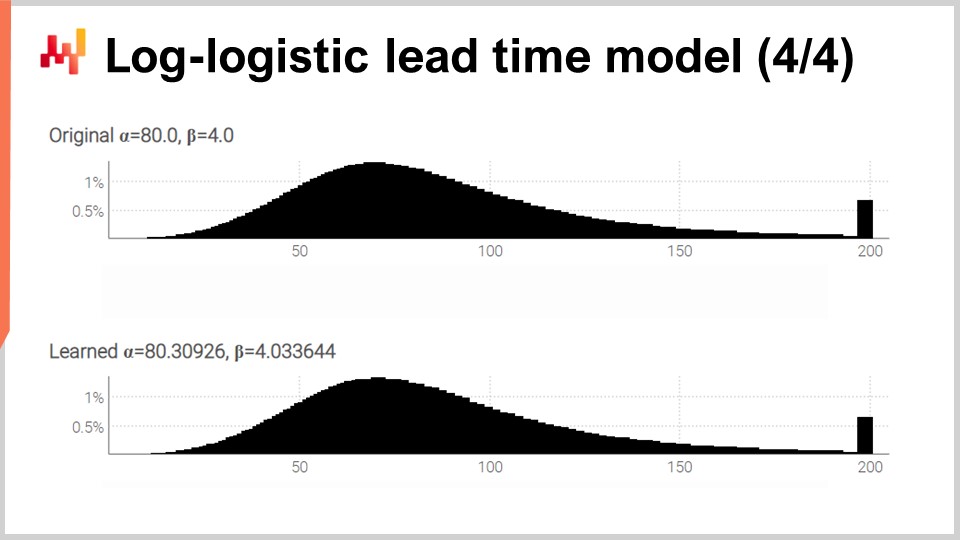
En la pantalla, tenemos los dos histogramas producidos por nuestro script que acabamos de revisar. En la parte superior, la distribución original con sus dos parámetros originales, alpha y beta, en 80 y 4, respectivamente. En la parte inferior, la distribución aprendida con dos parámetros aprendidos mediante la programación diferenciable. Esos dos picos en el extremo derecho están asociados con las colas que hemos truncado, ya que se extienden bastante. Por cierto, aunque es raro, sucede que ciertos bienes se reciben más de un año después de haber sido ordenados. Este no es el caso en todos los sectores, ciertamente no en el de lácteos, pero para piezas mecánicas o electrónica, ocurre ocasionalmente.
Aunque el proceso de aprendizaje no es exacto, obtenemos resultados dentro de un uno por ciento de los valores originales de los parámetros. Esto demuestra, al menos, que esta maximización del log-likelihood mediante la programación diferenciable funciona en la práctica. La distribución log-logística puede o no ser adecuada; depende de la forma de la distribución de tiempos de entrega a la que te enfrentes. Sin embargo, prácticamente podemos elegir cualquier distribución paramétrica alternativa. Todo lo que se necesita es una expresión analítica de la función de densidad de probabilidad. Existe una amplia variedad de tales distribuciones. Una vez que tienes una fórmula de libro de texto, una implementación sencilla mediante programación diferenciable suele hacer el resto.
Los tiempos de entrega no se observan solo una vez que la transacción está finalizada. Mientras la transacción aún está en marcha, ya sabes algo; ya cuentas con una observación de tiempo de entrega incompleta. Considera que hace 100 días realizaste un pedido. Los bienes aún no han sido recibidos; sin embargo, ya sabes que el tiempo de entrega es de al menos 100 días. Esa duración de 100 días representa el límite inferior para un tiempo de entrega que aún no se ha observado completamente. Esos tiempos de entrega incompletos son frecuentemente bastante importantes. Como mencioné al comienzo de esta conferencia, los conjuntos de datos de tiempos de entrega suelen ser escasos. No es inusual tener un conjunto de datos que solo incluya media docena de observaciones. En esas situaciones, es importante aprovechar al máximo cada observación, incluidas aquellas que aún están en progreso.
Consideremos el siguiente ejemplo: tenemos cinco pedidos en total. Tres pedidos ya han sido entregados con valores de tiempo de entrega muy cercanos a 30 días. Sin embargo, los dos últimos pedidos han estado pendientes durante 40 y 50 días, respectivamente. Según las primeras tres observaciones, el tiempo de entrega promedio debería estar en torno a los 30 días. No obstante, los dos pedidos que aún están incompletos desmienten esta hipótesis. Los dos pedidos pendientes a 40 y 50 días indican un tiempo de entrega sustancialmente mayor. Por lo tanto, no debemos descartar los últimos pedidos solo porque están incompletos. Debemos aprovechar esta información y actualizar nuestra creencia hacia tiempos de entrega más largos, tal vez 60 días.
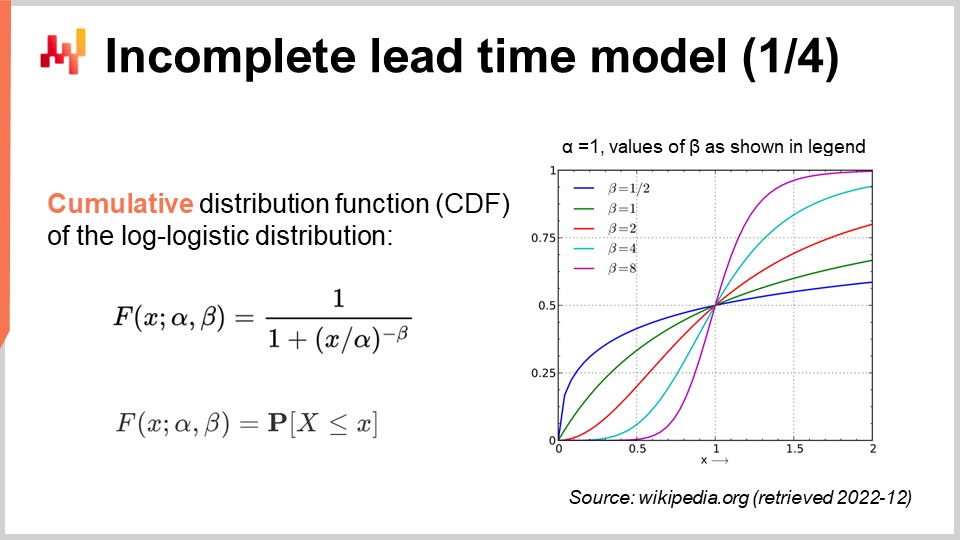
Revisitemos nuestro modelo probabilístico de tiempo de entrega, pero esta vez, teniendo en cuenta las observaciones incompletas. En otras palabras, queremos abordar aquellas observaciones que a veces son solo un límite inferior para el tiempo de entrega final. Para ello, podemos utilizar la función de distribución acumulada (CDF) de la distribución log-logística. Esta fórmula está escrita en la pantalla; nuevamente, es material de libro de texto. La CDF de la distribución log-logística se beneficia de una expresión analítica sencilla. A continuación, me referiré a esta técnica como la “técnica de probabilidad condicional” para abordar datos censurados.

Basándonos en esta expresión analítica de la CDF, podemos revisar el log-likelihood de la distribución log-logística. El script en la pantalla ofrece una implementación revisada de nuestra implementación L4 anterior. En la línea uno, tenemos prácticamente la misma declaración de función. Esta función toma un cuarto argumento adicional, un valor booleano llamado “is_incomplete” que indica, como sugiere el nombre, si la observación es incompleta o no. En las líneas dos y tres, si la observación es completa, entonces recurrimos a la situación anterior con la distribución log-logística regular. De esta forma, llamamos a la función log-likelihood que forma parte de la biblioteca estándar. Podría haber repetido el código de la implementación L4 anterior, pero esta versión es más concisa. En las líneas cuatro y cinco, expresamos el log-likelihood de observar finalmente un tiempo de entrega mayor que la observación incompleta actual, “X”. Esto se logra a través de la CDF y, más precisamente, mediante el logaritmo de la CDF.
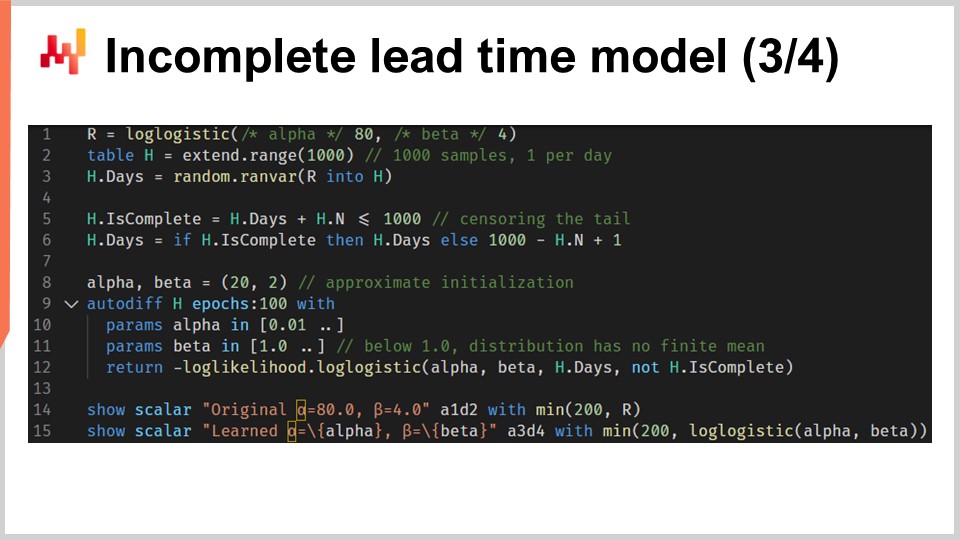
Ahora podemos repetir nuestra configuración con un script que aprende los parámetros de la distribución log-logística, pero esta vez en presencia de tiempos de entrega incompletos. El script en la pantalla es casi idéntico al anterior. En las líneas uno a tres, generamos los datos; estas líneas no han cambiado. Cabe señalar que H.N es un vector autogenerado que se crea implícitamente en la línea dos. Este vector numera las líneas generadas, comenzando en uno. La versión anterior de este script no utilizaba este vector autogenerado, pero actualmente, el vector H.N aparece al final de la línea seis.
Las líneas cinco y seis son, de hecho, las importantes. Aquí, censuramos los tiempos de entrega. Es como si hiciéramos una observación de tiempo de entrega por día y truncáramos las observaciones que son demasiado recientes para tener información. Esto significa, por ejemplo, que un tiempo de entrega de 20 días iniciado hace siete días aparece como un tiempo de entrega incompleto de siete días. Al final de la línea seis, hemos generado una lista de tiempos de entrega en la que algunas de las observaciones recientes (las que terminarían más allá de la fecha actual) están incompletas. El resto del script permanece sin cambios, excepto en la línea 12, donde se pasa el vector H.is_complete como cuarto argumento de la función log-likelihood. Así, en la línea 12 estamos llamando a la función de programación diferenciable que acabamos de introducir hace un minuto.
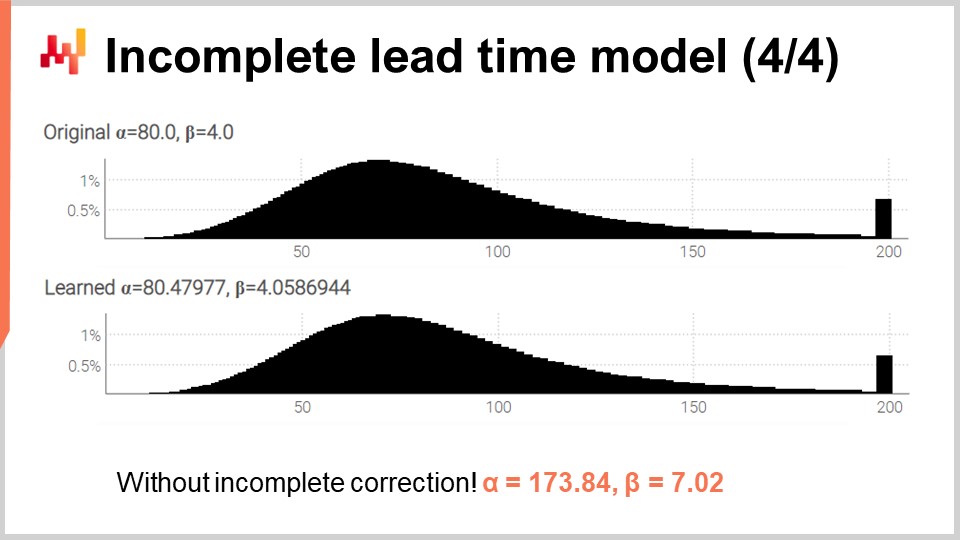
Finalmente, en la pantalla, se producen los dos histogramas generados por este script revisado. Los parámetros aún se aprenden con alta precisión, mientras que ahora estamos en presencia de numerosos tiempos de entrega incompletos. Para validar que tratar con tiempos incompletos no era una complicación innecesaria, he reejecutado el script, pero esta vez con una variación modificada con la sobrecarga de tres argumentos de la función log-likelihood (la que usamos inicialmente y asumíamos que todas las observaciones estaban completas). Para alpha y beta, obtenemos los valores mostrados en la parte inferior de la pantalla. Como se esperaba, esos valores no coinciden en absoluto con los valores originales de alpha y beta.
En esta serie de conferencias, no es la primera vez que se introduce una técnica para tratar con datos censurados. En la segunda conferencia de este capítulo, se presentó la técnica de enmascaramiento de pérdida para abordar los faltantes de stock. De hecho, en general queremos predecir la demanda futura, no las ventas futuras. Los faltantes de stock introducen un sesgo a la baja, ya que no llegamos a observar todas las ventas que habrían ocurrido si no se hubiera producido el faltante de stock. La técnica de probabilidad condicional puede usarse para abordar la demanda censurada, tal como sucede con los faltantes de stock. La técnica de probabilidad condicional es un poco más compleja que el enmascaramiento de pérdida, por lo que probablemente no deba usarse si el enmascaramiento de pérdida es suficiente.
En el caso de los tiempos de entrega, la escasez de datos es la motivación principal. Podemos tener tan pocos datos que resulte fundamental aprovechar al máximo cada observación, incluso las incompletas. De hecho, la técnica de probabilidad condicional es más poderosa que el enmascaramiento de pérdida en el sentido de que aprovecha las observaciones incompletas en lugar de simplemente descartarlas. Por ejemplo, si hay una unidad en stock y si esa única unidad en stock se vende, entonces, sugiriendo un faltante de stock, la técnica de probabilidad condicional aún utiliza la información de que la demanda fue mayor o igual a una.
Aquí, obtenemos un beneficio sorprendente del modelado probabilístico: nos ofrece una forma elegante de tratar con la censura, un efecto que se presenta en numerosas situaciones de supply chain. A través de la probabilidad condicional, podemos eliminar clases enteras de sesgos sistemáticos.
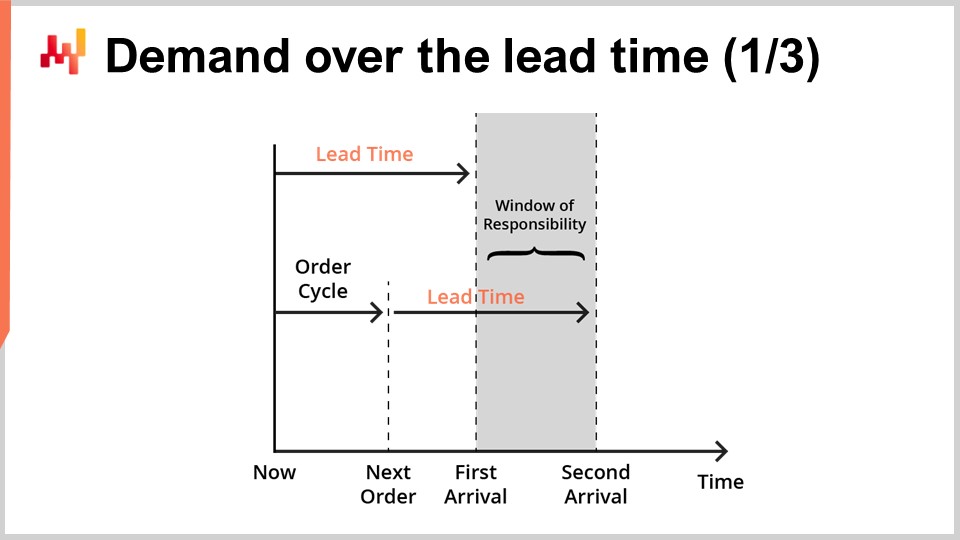
Los forecast de lead time están típicamente destinados a combinarse con los forecast de demanda. De hecho, consideremos ahora una situación simple de reposición de inventario, como se ilustra en la pantalla.
Servimos un solo producto, y el inventario puede ser repuesto mediante un reorden de un único proveedor. Buscamos un forecast que apoye nuestra decisión de reordenar o no al proveedor. Podemos reordenar ahora, y si lo hacemos, los bienes llegarán en el momento señalado como “first arrival.” Más tarde, tendremos otra oportunidad para reordenar. Esta oportunidad posterior ocurre en un momento señalado como “next order,” y en este caso, los bienes llegarán en el momento señalado como “second arrival.” El período indicado como la “window of responsibility” es el período que importa en lo que concierne a nuestra decisión de reordenar.
De hecho, lo que decidamos reordenar no llegará antes del primer lead time. Por lo tanto, ya hemos perdido el control sobre el servicio de la demanda para todo lo que ocurra antes de la first arrival. Luego, ya que tendremos una oportunidad posterior de reordenar, el servicio de la demanda después de la second arrival ya no es nuestra responsabilidad; es responsabilidad del próximo reorden. Por lo tanto, reordenar con la intención de atender la demanda más allá de la second arrival debería posponerse hasta la siguiente oportunidad de reorden.
Para apoyar la decisión de reordenar, hay dos factores que deben ser forecast. Primero, debemos forecast el inventario esperado en el momento de la first arrival. De hecho, si para el momento de la first arrival aún queda mucho inventario, entonces no hay razón para reordenar ahora. Segundo, debemos forecast la demanda esperada para la duración de la window of responsibility. En un escenario real, también tendríamos que forecast la demanda más allá de la window of responsibility para evaluar el carrying cost de los bienes que estamos reordenando ahora, ya que podrían quedar excedentes que se extienden a períodos posteriores. Sin embargo, por cuestiones de concisión y timing, hoy nos centraremos en el inventario esperado y en la demanda esperada en lo que respecta a la window of responsibility.
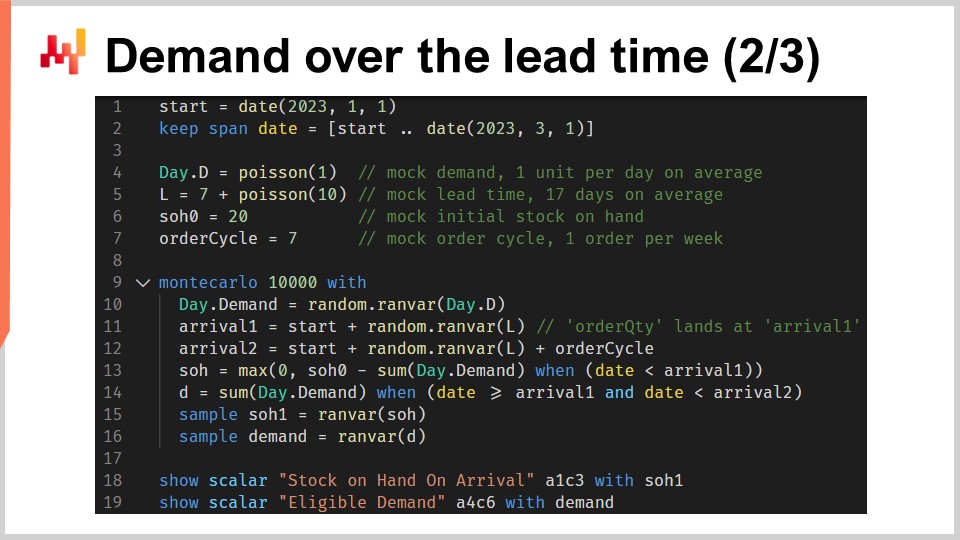
Este script implementa los factores de la window of responsibility o los forecast que acabamos de discutir. Toma como entrada un forecast probabilístico de lead time y un forecast probabilístico de demanda. Devuelve dos distribuciones de probabilidades, a saber, el inventario en mano al momento de la llegada y la demanda elegible según lo definido por la window of responsibility.
En las líneas uno y dos, configuramos las líneas de tiempo, que comienzan el 1 de enero y terminan el 1 de marzo. En un escenario de predicción, esta línea de tiempo no estaría codificada de forma rígida. En la línea cuatro, se introduce un modelo probabilístico simplista de demanda: una distribución de Poisson repetida día a día durante toda la duración de esta línea de tiempo. La demanda será de una unidad por día en promedio. Estoy utilizando aquí un modelo simplista para la demanda por motivos de claridad. En un escenario real, por ejemplo, usaríamos un ESSM (Ensemble State Space Model). Los modelos de espacio de estados son modelos probabilísticos, y fueron introducidos en la primera conferencia de este capítulo.
En la línea cinco, se introduce otro modelo probabilístico simplista. Este segundo modelo está destinado a los lead times. Es una distribución de Poisson desplazada siete días a la derecha. El desplazamiento se realiza mediante una convolución. En la línea seis, definimos el inventario inicial en mano. En la línea siete, definimos el ciclo de reorden. Este valor se expresa en días y caracteriza cuándo tendrá lugar el próximo reorden.
De la línea 9 a la 16, tenemos un bloque de Monte Carlo que representa la lógica central del script. Anteriormente, en esta conferencia, ya habíamos introducido otro bloque de Monte Carlo para apoyar nuestra lógica de validación cruzada. Aquí, estamos usando este constructo nuevamente, pero para un propósito diferente. Queremos calcular dos variables aleatorias que reflejen, respectivamente, el inventario en mano a la llegada y la demanda elegible. Sin embargo, el álgebra de variables aleatorias no es lo suficientemente expresiva para realizar este cálculo. Por lo tanto, estamos utilizando un bloque de Monte Carlo en su lugar.
En la tercera conferencia de este capítulo, señalé que existe una dualidad entre el forecasting probabilístico y las simulaciones. El bloque de Monte Carlo ilustra esta dualidad. Comenzamos con un forecast probabilístico, lo convertimos en una simulación y, finalmente, convertimos los resultados de la simulación nuevamente en otro forecast probabilístico.
Echemos un vistazo a los detalles. En la línea 10, generamos una trayectoria para la demanda. En la línea 11, generamos la fecha de llegada para el primer pedido, asumiendo que estamos ordenando hoy. En la línea 12, generamos la fecha de llegada para el segundo pedido, asumiendo que estamos ordenando un ciclo de reorden a partir de ahora. En la línea 13, calculamos lo que queda como inventario en mano en la fecha de la first arrival. Es el inventario inicial en mano menos la demanda observada durante la duración del primer lead time. El máximo de cero indica que el inventario no puede ser negativo. En otras palabras, asumimos que no aceptamos backlogs. Este supuesto de no backlog podría modificarse. El caso de backlog se deja como ejercicio para la audiencia. Como pista, la programación diferenciable puede usarse para evaluar el porcentaje de la demanda no servida que se convierte exitosamente en backlogs, dependiendo de cuántos días falten antes de la disponibilidad renovada del inventario.
Volviendo al script, en la línea 14, calculamos la demanda elegible, que es la demanda que ocurre durante la window of responsibility. En las líneas 15 y 16, recogemos dos variables aleatorias de interés mediante la palabra clave “sample”. A diferencia del primer script Envision de esta conferencia, que trataba sobre la validación cruzada, aquí buscamos obtener distribuciones de probabilidades de este bloque de Monte Carlo, y no solo promedios. En ambas líneas 15 y 16, la variable aleatoria que aparece en el lado derecho de la asignación es un agregador. En la línea 15, obtenemos una variable aleatoria para el inventario en mano a la llegada. En la línea 16, obtenemos otra variable aleatoria para la demanda que ocurre dentro de la window of responsibility.
En las líneas 18 y 19, esas dos variables aleatorias se muestran en pantalla. Ahora, hagamos una pausa por un segundo y reconsideremos todo este script. Las líneas del uno al siete están dedicadas únicamente a la configuración de los datos simulados. Las líneas 18 y 19 solo muestran los resultados. La única lógica real ocurre en las ocho líneas entre la 9 y la 16. De hecho, toda la lógica real se ubica, en cierto sentido, en las líneas 13 y 14.
Con tan solo unas pocas líneas de código, menos de 10 sin importar cómo las contemos, combinamos un forecast probabilístico de lead time con un forecast probabilístico de demanda para componer una especie de forecast probabilístico híbrido de significado real en la supply chain. Notemos que no hay nada aquí que dependa realmente de las especificaciones de ya sea el forecast de lead time o el forecast de demanda. Se han utilizado modelos simples, pero se podrían haber utilizado modelos sofisticados en su lugar. No habría cambiado nada. El único requisito es tener dos modelos probabilísticos para que sea posible generar esas trayectorias.
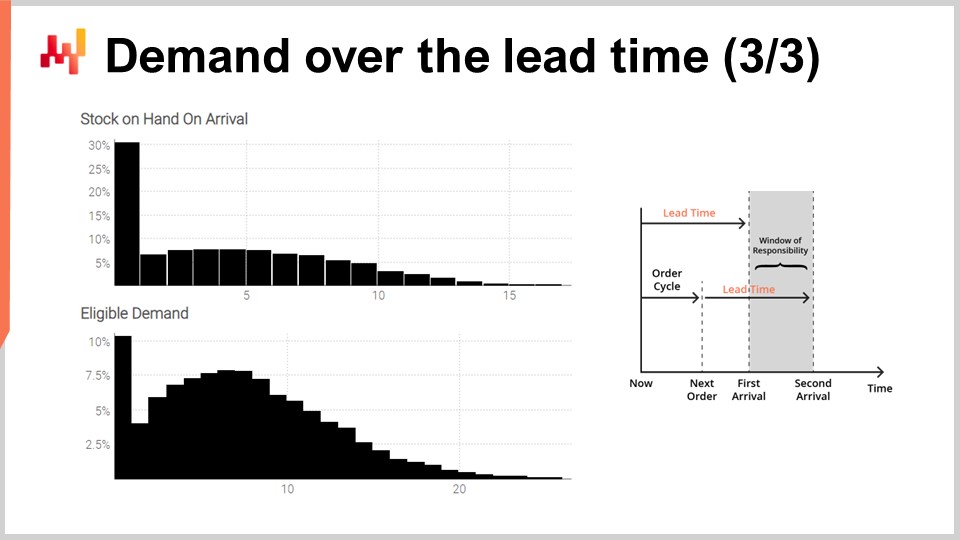
Finalmente, en la pantalla, los histogramas producidos por el script. El histograma superior representa el inventario en mano a la llegada. Hay aproximadamente un 30% de probabilidad de enfrentar un inventario inicial en cero. En otras palabras, hay un 30% de probabilidad de que ocurra un faltante de stock en el último día justo antes de la first arrival. El valor promedio del inventario podría ser algo así como cinco unidades. Sin embargo, si juzgáramos esta situación solo por su promedio, estaríamos interpretándola seriamente de forma errónea. Un forecast probabilístico es esencial para reflejar adecuadamente la situación inicial del inventario.
El histograma inferior representa la demanda asociada con la window of responsibility. Tenemos aproximadamente un 10% de probabilidad de enfrentar cero demanda. Este resultado también podría percibirse como sorprendente. De hecho, comenzamos este ejercicio con una demanda estacionaria de Poisson de una unidad por día en promedio. Tenemos siete días entre pedidos. Si no fuera por el lead time variable, la probabilidad de obtener cero demanda en siete días sería inferior al 0.1%. Sin embargo, el script demuestra que esta ocurrencia es mucho más frecuente. La razón es que puede ocurrir una window of responsibility pequeña si el primer lead time es más largo de lo habitual y si el segundo lead time es más corto de lo habitual.
Enfrentar cero demanda durante la window of responsibility significa que el inventario en mano probablemente se vuelva bastante alto en determinado momento. Dependiendo de la situación, esto podría o no ser crítico, pero podría serlo, por ejemplo, si existe un límite de capacidad de almacenamiento o si el inventario es perecedero. Una vez más, la demanda promedio, probablemente alrededor de ocho, no proporciona una visión confiable de cómo fue la demanda. Recuerda que hemos obtenido esta distribución altamente asimétrica a partir de una demanda estacionaria inicial de una unidad por día en promedio. Este es el efecto del lead time variable en acción.
Esta configuración simple demuestra la importancia de los lead times en lo que respecta a situaciones de reposición de inventario. Desde una perspectiva de supply chain, aislar los forecast de lead time de los forecast de demanda es, en el mejor de los casos, una abstracción práctica. La demanda diaria no es lo que realmente nos interesa. Lo que verdaderamente importa es la composición de la demanda con el lead time. Si otros factores estocásticos estuvieran presentes, como backlogs o devoluciones, esos factores también habrían formado parte del modelo.

El presente capítulo en esta serie de conferencias se titula “Predictive Modeling” en lugar de “Demand Forecasting”, como típicamente sería en los libros de texto convencionales de supply chain. La razón de este título de capítulo debería haberse vuelto progresivamente obvia a medida que avanzamos en la presente conferencia. De hecho, desde una perspectiva de supply chain, queremos forecast la evolución del sistema de supply chain. La demanda es ciertamente un factor importante, pero no es el único factor. Otros factores variables, como el lead time, deben ser forecast. Aún más importante, todos esos factores deben ser, al final, forecast juntos.
De hecho, necesitamos reunir esos componentes predictivos para apoyar un proceso de decision-making. Por lo tanto, lo que importa no es buscar algún tipo de modelo definitivo de demand forecasting. Esta tarea es en gran parte inútil, en última instancia, porque la precisión extra se ganará de maneras que van en contra del mejor interés de la empresa. Más sofisticación significa más opacidad, más errores, más recursos informáticos. Como regla general, cuanto más sofisticado es el modelo, más difícil se vuelve componer operacionalmente este modelo con otro. Lo que importa es ensamblar una colección de técnicas predictivas que puedan componerse a voluntad. De esto se trata la modularidad desde una perspectiva de predictive modeling. En esta conferencia se han presentado media docena de técnicas. Estas técnicas son útiles ya que abordan ángulos críticos del mundo real, como las observaciones incompletas. También son simples; ninguno de los ejemplos de código presentados hoy excedió las 10 líneas de lógica real. Lo más importante es que estas técnicas son modulares, como bloques de Lego. Funcionan bien juntas y pueden recombinarse casi indefinidamente.
El objetivo final del predictive modeling para supply chain, tal como debe entenderse, es la identificación de dichas técnicas. Cada técnica debe ser, por sí misma, una oportunidad para revisar cualquier modelo predictivo preexistente con el fin de simplificar o mejorar dicho modelo.

En conclusión, a pesar de que el lead time es en gran medida ignorado por la comunidad académica, el lead time puede y debe ser forecast. Al revisar una breve serie de distribuciones de lead time en el mundo real, hemos identificado dos desafíos: primero, los lead times varían; segundo, los lead times son escasos. Por lo tanto, hemos introducido técnicas de modelado que son apropiadas para tratar con observaciones de lead time que resultan ser tanto escasas como erráticas.
Estos modelos de lead time son probabilísticos y son, en gran medida, la continuación de los modelos que se han ido introduciendo gradualmente a lo largo de este capítulo. También hemos visto que la perspectiva de la probabilidad sí proporciona una solución elegante al problema de la observación incompleta, un aspecto casi ubicuo en la supply chain. Este problema ocurre siempre que hay faltantes de stock y siempre que hay pedidos pendientes. Finalmente, hemos visto cómo componer un forecast probabilístico de lead time con un forecast probabilístico de demanda para elaborar el modelo predictivo que necesitamos para apoyar un posterior proceso de toma de decisiones.

La próxima conferencia será el 8 de marzo. Será un miércoles a la misma hora del día, 3 PM hora de París. La conferencia de hoy fue técnica, pero la próxima será en gran medida no técnica, y discutiré el caso del supply chain scientist. De hecho, los libros de texto convencionales de supply chain abordan la supply chain como si los modelos de forecast y los modelos de optimización surgieran y operaran de la nada, ignorando por completo su componente “wetware”, es decir, las personas a cargo. Por lo tanto, examinaremos más de cerca los roles y responsabilidades del supply chain scientist, una persona que se espera lidere la iniciativa de Supply Chain Quantitativa.
Ahora, procederé con las preguntas.
Question: ¿Qué pasa si alguien quiere conservar su inventario para una mayor innovación o por razones distintas a just in time u otros conceptos?
Esta es, sin duda, una pregunta muy importante. El concepto se aborda típicamente mediante el modelado económico de la supply chain, que técnicamente llamamos los “economic drivers” en esta serie de conferencias. Lo que preguntas es si es mejor no atender a un cliente hoy porque, en un momento posterior, habrá una oportunidad de atender la misma unidad a otra persona que importe más por cualquier razón. En esencia, lo que dices es que hay más valor en captar sirviendo a otro cliente más tarde, quizás un cliente VIP, que atendiendo a un cliente hoy.
Esto podría ser el caso, y sucede. Por ejemplo, en la industria de la aviación, supongamos que eres un proveedor MRO (Maintenance, Repair, and Overhaul). Tienes a tus habituales clientes VIP — las aerolíneas a las que sirves rutinariamente con contratos a largo plazo, y son muy importantes. Cuando esto sucede, quieres asegurarte de que siempre podrás servir a esos clientes. Pero, ¿qué pasa si otra aerolínea te llama y solicita una unidad? En este caso, lo que sucederá es que podrías servir a esa persona, pero no tienes un contrato a largo plazo con ella. Entonces, lo que harás es ajustar tu precio para que sea muy alto, asegurándote de obtener suficiente valor para compensar el potencial faltante de stock que podrías enfrentar en un momento posterior. En resumen, para esta primera pregunta, creo que no se trata realmente de un forecast, sino más bien de un modelado adecuado de los impulsores económicos. Si quieres preservar stock, lo que deseas es generar un modelo —un modelo de optimización— donde la respuesta racional no sea servir al cliente que pide una unidad mientras aún tienes stock en reserva.
Por cierto, otra situación típica para eso es cuando estás vendiendo kits. Un kit es un conjunto de muchas partes que se venden juntas, y te queda solo una parte que vale únicamente una pequeña fracción del valor total del kit. El problema es que si vendes esta última unidad, ya no podrás armar tu kit y venderlo a su precio completo. Por lo tanto, podrías encontrarte en una situación en la que prefieres mantener la unidad en stock simplemente para poder vender el kit en otro momento, potencialmente con algo de incertidumbre. Pero, de nuevo, se reduce a los impulsores económicos, y esa sería la manera en la que abordaría esta situación.
Question: Durante los últimos años, la mayoría de los retrasos en la supply chain ocurrieron debido a la guerra o a la pandemia, lo cual es muy difícil de forecast porque no habíamos tenido tales situaciones antes. ¿Cuál es tu opinión al respecto?
Mi opinión es que los tiempos de entrega han estado variando desde siempre. He estado en el mundo de la supply chain desde 2008, y mis padres trabajaban en supply chain incluso 30 años antes que yo. Hasta donde podemos recordar, los tiempos de entrega han sido erráticos y variables. Siempre sucede algo, ya sea una protesta, una guerra o un cambio en las tarifas. Sí, los últimos años han sido sumamente erráticos, pero los tiempos de entrega ya variaban bastante.
Estoy de acuerdo en que nadie puede pretender ser capaz de forecast la próxima guerra o pandemia. Si fuera posible predecir estos eventos matemáticamente, la gente no se involucraría en guerras ni invertiría en supply chain; simplemente jugarían en el mercado de valores y se enriquecerían anticipando los movimientos del mercado.
La conclusión es que lo que puedes hacer es planificar para lo inesperado. Si no tienes confianza en el futuro, en realidad puedes inflar las variaciones en tus forecasts. Es lo opuesto a tratar de hacer tu forecast más preciso: preservas tus expectativas promedio, pero simplemente inflas la cola para que las decisiones que tomes basadas en esos forecasts probabilísticos sean más resilientes a la variación. Has diseñado que tus variaciones esperadas sean mayores de lo que actualmente observas. La conclusión es que la idea de que algo sea fácil o difícil de forecast proviene de una perspectiva de forecast puntual, donde te gustaría jugar el juego como si fuera posible tener una anticipación precisa del futuro. Este no es el caso — no existe tal cosa como una anticipación precisa del futuro. Lo único que puedes hacer es trabajar con distribuciones de probabilidad con una gran dispersión que manifiesten y cuantifiquen tu ignorancia del futuro.
En lugar de afinar decisiones que dependen críticamente de la ejecución minuciosa del plan exacto, estás teniendo en cuenta y planificando para un grado interesante de variación, haciendo que tus decisiones sean más robustas contra esas variaciones. Sin embargo, esto solo se aplica al tipo de variación que no impacta tu supply chain de manera demasiado brutal. Por ejemplo, puedes lidiar con tiempos de entrega de proveedores más largos, pero si tu warehouse ha sido bombardeado, ningún forecast te salvará en esa situación.
Question: ¿Podemos crear estos histogramas y calcular el CRPS en Microsoft Excel, por ejemplo, utilizando complementos de Excel como itsastat o que albergan muchas distribuciones?
Sí, se puede. Uno de nosotros en Lokad ha producido en realidad una hoja de cálculo de Excel que representa un modelo probabilístico para una situación de reposición de inventario. El meollo del problema es que Excel no tiene un tipo de datos nativo para histogramas, por lo que lo único que tienes en Excel son números — una celda, un número. Sería elegante y simple tener un valor que sea un histograma, donde tuvieras un histograma completo empaquetado en una celda. Sin embargo, hasta donde yo sé, esto no es posible en Excel. No obstante, si estás dispuesto a dedicar unas 100 líneas más o menos para representar el histograma, aunque no será tan compacto y práctico, puedes implementar una distribución en Excel y hacer algo de modelado probabilístico. Publicaremos el enlace al ejemplo en la sección de comentarios.
Ten en cuenta que es una tarea relativamente dolorosa porque Excel no está idealmente preparado para esta tarea. Excel es un lenguaje de programación, y puedes hacer cualquier cosa con él, por lo que ni siquiera necesitas un complemento para lograrlo. Sin embargo, será un poco verboso, así que no esperes algo súper ordenado.
Question: El tiempo de entrega se puede desglosar en componentes como el tiempo de pedido, el tiempo de producción, el tiempo de transporte, etc. Si uno quiere un control más granular sobre los tiempos de entrega, ¿cómo cambiaría este enfoque?
Primero, necesitamos considerar qué significa tener más control sobre el tiempo de entrega. ¿Quieres reducir el tiempo de entrega promedio o reducir la variabilidad del tiempo de entrega? Curiosamente, he visto a muchas empresas lograr reducir el tiempo de entrega promedio, pero a costa de intercambiar algo de variación extra en el tiempo de entrega. En promedio, el tiempo de entrega es más corto, pero de vez en cuando, es mucho más largo.
En esta conferencia, nos estamos involucrando en un ejercicio de modelado. Por sí solo, no hay ninguna acción; se trata simplemente de observar, analizar y predecir. Sin embargo, si podemos descomponer el tiempo de entrega y analizar la distribución subyacente, podemos utilizar modelado probabilístico para evaluar qué componentes están variando más y cuáles tienen el impacto negativo más significativo en nuestra supply chain. Podemos realizar escenarios de “what-if” con esta información. Por ejemplo, toma una parte de tu tiempo de entrega y pregunta: “¿Y si la cola de este tiempo de entrega fuera un poco más corta, o si el promedio fuera un poco más corto?” Luego puedes recomponer todo, volver a ejecutar tu modelo predictivo para toda tu supply chain, y comenzar a evaluar el impacto.
Este enfoque te permite razonar de forma fraccionada sobre ciertos fenómenos, incluidos los erráticos. No sería tanto un cambio de enfoque, sino una continuación de lo que hemos hecho, llevando al Capítulo 6, que trata sobre la optimización de decisiones reales basadas en estos modelos probabilísticos.
Question: Creo que esto ofrece la oportunidad de recalcular nuestros tiempos de entrega en SAP para proporcionar un marco de tiempo más realista y ayudar a minimizar el pull-in y pull-out de nuestro sistema. ¿Es posible?
Descargo de responsabilidad: SAP es un competidor de Lokad en el ámbito de la optimización de supply chain. Mi respuesta inicial es no, SAP no puede hacer eso. La realidad es que SAP tiene cuatro soluciones distintas que se ocupan de la optimización de supply chain, y depende de a qué stack te refieras. Sin embargo, todos esos stacks tienen en común una visión centrada en forecasts puntuales. Todo en SAP ha sido diseñado bajo la premisa de que los forecasts serán precisos.
Sí, SAP tiene algunos parámetros para afinar, como la distribución normal que mencioné al inicio de esta conferencia. Sin embargo, las distribuciones de tiempo de entrega que observamos no estaban distribuidas de manera normal. Hasta donde sé, las configuraciones convencionales de SAP para la optimización de supply chain adoptan una distribución normal para los tiempos de entrega. El problema es que, en el fondo, el software está haciendo una suposición matemática ampliamente incorrecta. No puedes recuperarte de una suposición tan errónea que se adentra en el núcleo de la arquitectura de tu software simplemente afinando un parámetro. Tal vez puedas hacer alguna ingeniería inversa loca y descubrir un parámetro que termine generando la decisión correcta. Teóricamente, esto es posible, pero en la práctica presenta tantos problemas que la pregunta es, ¿por qué querrías realmente hacer eso?
Para adoptar una perspectiva probabilística, tienes que comprometerte por completo, lo que significa que tus forecasts son probabilísticos, y tus modelos de optimización también aprovechan modelos probabilísticos. El problema aquí es que, incluso si pudiéramos afinar el modelado probabilístico para obtener tiempos de entrega ligeramente mejores, el resto del stack de SAP volverá a caer en forecasts puntuales. No importa lo que suceda, colapsaremos esas distribuciones en puntos. La idea de que podrías aproximar esto por un promedio es preocupante y simplemente incorrecta. Así que, técnicamente, podrías afinar los tiempos de entrega, pero te encontrarás con tantos problemas después de eso que podría no valer la pena el esfuerzo.
Question: Hay situaciones en las que ordenas las mismas partes de diferentes proveedores. Esta es información importante para procesar en el forecast de tiempo de entrega. ¿Realizas el forecast de tiempo de entrega por artículo o hay situaciones en las que aprovechas agrupar artículos en familias?
Esta es una pregunta notablemente interesante. Tenemos dos proveedores para el mismo artículo. La pregunta será cuánta similitud hay entre los artículos y los proveedores. Primero, necesitamos observar la situación. Si un proveedor resulta estar a la vuelta de la esquina y el otro está al otro lado del mundo, realmente debes considerar esas cosas por separado. Pero supongamos la situación interesante en la que los dos proveedores son bastante similares y es el mismo artículo. ¿Deberías agrupar esas observaciones o no?
Lo interesante es que, a través de la programación diferenciable, puedes componer un modelo que asigne cierto peso al proveedor y cierto peso al artículo y dejar que la magia del aprendizaje haga su magia. Se ajustará si debemos dar más peso al componente del artículo en el tiempo de entrega o al componente del proveedor. Podría ser que dos proveedores que sirven productos prácticamente del mismo tipo tengan algún sesgo en el que un proveedor es, en promedio, un poco más rápido que el otro. Pero hay artículos que definitivamente toman más tiempo, y así, si seleccionas artículos, no queda muy claro que un proveedor sea más rápido que el otro, porque realmente depende de los artículos que estés considerando. Lo más probable es que tengas muy pocos datos si desagregas todo hasta cada proveedor y cada artículo. Por lo tanto, lo interesante, y lo que recomendaría aquí, sería diseñar a través de la programación diferenciable. De hecho, podríamos intentar revisar esta situación en una conferencia posterior, una situación en la que pongas algunos parámetros a nivel de artículo y algunos parámetros a nivel de proveedor. Entonces, tendrías un número total de parámetros que no es el número de artículos por el número de proveedores; sería el número de artículos más el número de proveedores, o quizás más el número de proveedores por categorías, o algo similar. No haces explotar tu número de parámetros; simplemente añades un parámetro, un elemento que tenga afinidad con el proveedor, y que te permita hacer algún tipo de mezcla dinámica impulsada por tus datos históricos.
Question: Creo que la cantidad que se ordena y qué productos se ordenan juntos también podrían impactar el tiempo de entrega al final. ¿Podrías repasar la complejidad de incluir todas las variables en este tipo de problema?
En el último ejemplo, tuvimos dos tipos de duración: el ciclo de pedido y el tiempo de entrega en sí. El ciclo de pedido es interesante porque solo es incierto en la medida en que aún no se ha tomado la decisión. Es, fundamentalmente, algo que puedes decidir prácticamente en cualquier momento, por lo que el ciclo de pedido es completamente interno y de tu propia autoría. Esto no es lo único en la supply chain de esta manera; los precios son lo mismo. Tienes demanda, observas la demanda, pero en realidad puedes elegir el precio que deseas. Algunos precios son obviamente poco sensatos, pero es lo mismo: es de tu propia autoría.
El ciclo de pedido es de tu propia autoría. Ahora, lo que estás diciendo es que hay incertidumbre sobre el momento exacto para el próximo tiempo de entrega del pedido porque no sabes exactamente cuándo vas a hacer el pedido. De hecho, estás completamente en lo correcto. Lo que sucede es que cuando tienes la capacidad de implementar este modelado probabilístico, de repente, como se discute en el sexto capítulo de esta serie de conferencias, no quieres decir que el ciclo de pedido es de siete días. En cambio, quieres adoptar una política de reordenamiento que maximice el retorno de la inversión para tu empresa. Así, lo que puedes hacer es planificar el futuro de manera que, si haces un nuevo pedido ahora, puedas tomar una decisión ahora y luego aplicar tu política día a día. En algún punto en el futuro, realizas un reordenamiento, y ahora lo que tienes es una especie de situación de “serpiente comiéndose su cola” porque la mejor decisión de pedido para hoy depende de la decisión del próximo pedido, la que aún no has tomado. Este tipo de problema se conoce como un problema de política, y es un problema de decisión secuencial. Bajo el capó, lo que realmente deseas es elaborar alguna especie de política, un objeto matemático que rija tu proceso de toma de decisiones.
El problema de la optimización de políticas es bastante complicado, y tengo la intención de cubrirlo en el sexto capítulo. Pero la conclusión es que tenemos, si volvemos a tu pregunta, dos componentes distintos. Tenemos el componente que varía independientemente de lo que hagas, el tiempo de entrega que es el tiempo de entrega de tu proveedor, y luego tienes el tiempo de pedido, que es algo que está realmente impulsado internamente por tu proceso y debe tratarse como una cuestión de optimización.
Concluyendo este pensamiento, vemos una convergencia entre la optimización y el modelado predictivo. Al final, ambos terminan siendo prácticamente lo mismo porque existen interacciones entre las decisiones que tomas y lo que sucede en el futuro.
Eso es todo por hoy. No olvides, el 8 de marzo, a la misma hora del día, será miércoles, a las 3 PM. Gracias, y nos vemos la próxima vez.


