Funzione di perdita del pinball

Di Joannès Vermorel, febbraio 2012

La funzione di perdita del pinball, anche nota come perdita di quantili, è una metrica utilizzata per valutare l’accuratezza di una previsione di quantili.

Valutare l’accuratezza di una previsione di quantili è un problema sottile. Infatti, a differenza delle previsioni classiche in cui l’obiettivo è avere la previsione il più vicino possibile ai valori osservati, la situazione è sbilanciata (volutamente) quando si tratta di previsioni di quantili. Pertanto, il confronto ingenuo osservato vs previsioni non è soddisfacente. La funzione di perdita del pinball restituisce un valore che può essere interpretato come l’accuratezza di un modello di previsione di quantili.

Formula

Sia $${\tau}$$ il quantile target, $${y}$$ il valore reale e $${z}$$ la previsione di quantile, allora $${L_\tau}$$, la funzione di perdita del pinball, può essere scritta come:

$${ \begin{eqnarray} L_{\tau}(y,z) & = & (y - z) \tau & \textrm{ se } y \geq z \\\ & = & (z - y) (1 - \tau) & \textrm{ se } z > y \end{eqnarray} }$$

Download: pinball-loss-function.xlsx

Il foglio di calcolo illustra come calcolare la funzione di perdita del pinball in Microsoft Excel. La formula effettiva non è più complicata rispetto alla maggior parte degli indicatori di accuratezza come ad esempio il MAPE.

Illustrazione

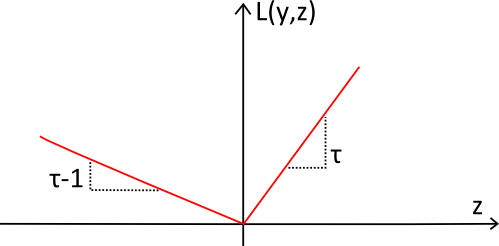
La funzione di perdita del pinball (in rosso) è stata chiamata così a causa della sua forma che assomiglia alla traiettoria di una palla su un flipper. La funzione è sempre positiva e più ci si allontana dal valore target $${y}$$, maggiore è il valore di $${L_\tau(y,z)}$$. La pendenza viene utilizzata per riflettere lo squilibrio desiderato nella previsione di quantili.

Il modello di quantili migliore ha la perdita del pinball più bassa

Il risultato più importante associato alla funzione di perdita del pinball è che più bassa è la perdita del pinball, più accurata è la previsione di quantili.

È possibile dimostrare che la funzione che minimizza la perdita del pinball fornisce anche il quantile ottimale. Tuttavia, il formalismo richiesto per la dimostrazione va oltre lo scopo di questo articolo.

Pertanto, al fine di confrontare l’accuratezza rispettiva di due modelli di quantili (ad esempio Lokad vs altri), è sufficiente calcolare la perdita media del pinball di ciascun modello su un numero di serie temporali sufficientemente grande per garantire che la differenza osservata sia statisticamente significativa. In pratica, alcune centinaia di serie temporali sono sufficienti per valutare quale modello di quantili sia il più accurato.

Il trucco di Lokad

La presunta semplicità della nozione di accuratezza per una previsione classica (cioè la previsione media) è sopravvalutata secondo la nostra opinione. Le previsioni, sia medie che di quantili, sono soggette a sovradattamento che complica notevolmente il confronto tra modelli di previsione. Tuttavia, la funzione di perdita del pinball costituisce un modo molto semplice per valutare l’accuratezza relativa di due modelli di previsione di quantili.

Ulteriori letture

Sequential Quantile Prediction of Time Series, marzo 2011, di Gerard Biau e Benoit Patra, Information Theory, IEEE Transactions
Continuous Ranked Probability Score (CRPS), una generalizzazione della funzione di perdita del pinball per previsioni probabilistiche