Структурированное предиктивное моделирование для цепочки поставок - Лекция 5.1

00:01 Введение
02:44 Обзор предиктивных потребностей
05:57 Модели против моделирования
12:26 История до сих пор
15:50 Немного теории и немного практики
17:41 Дифференцируемое программирование, SGD 1/6
24:56 Дифференцируемое программирование, autodiff 2/6
31:07 Дифференцируемое программирование, функции 3/6
35:35 Дифференцируемое программирование, мета-параметры 4/6
37:59 Дифференцируемое программирование, параметры 5/6
40:55 Дифференцируемое программирование, особенности 6/6
43:41 Прохождение, прогнозирование розничного спроса
45:49 Прохождение, подбор параметров 1/6
53:14 Прохождение, совместное использование параметров 2/6
01:04:16 Прохождение, маскирование потерь 3/6
01:09:34 Прохождение, интеграция ковариат 4/6
01:14:09 Прохождение, разреженное разложение 5/6
01:21:17 Прохождение, свободное масштабирование 6/6
01:25:14 Белый ящик
01:33:22 Возврат к экспериментальной оптимизации
01:39:53 Заключение
01:44:40 Предстоящая лекция и вопросы аудитории

Описание

Дифференцируемое программирование (DP) является генеративной парадигмой, используемой для создания широкого класса статистических моделей, которые оказываются исключительно подходящими для предиктивных задач в управлении цепями поставок. DP превосходит почти всю «классическую» литературу по прогнозированию на основе параметрических моделей. DP также превосходит «классические» машинного обучения алгоритмы — по состоянию на конец 2010-х — практически по всем параметрам, важным для практического применения в цепочках поставок, включая простоту внедрения специалистами.

Полная расшифровка

Добро пожаловать в эту серию лекций о цепочках поставок. Я Йоаннес Верморель, и сегодня я представлю «Структурированное предиктивное моделирование с дифференцируемым программированием в цепочках поставок». Выбор правильного курса действий требует детального количественного представления о будущем. Действительно, каждое решение — будь то закупка или наращивание производства — отражает определённое предвидение будущего. При этом основная теория цепочек поставок неизменно подчёркивает понятие прогнозирования для решения этой задачи. Однако подход к прогнозированию, по крайней мере в его классической форме, имеет два недостатка.

Во-первых, он делает акцент на узком подходе к прогнозированию с использованием временных рядов, который, к сожалению, не учитывает многообразие проблем, возникающих в реальных цепочках поставок. Во-вторых, он делает акцент на узкой оценке точности прогнозирования, что также не решает основную проблему. Прирост точности на несколько процентных пунктов не означает автоматического увеличения доходности вашей цепочки поставок.

Цель данной лекции — найти альтернативный подход к прогнозированию, который отчасти является технологией и отчасти методологией. Технологией будет дифференцируемое программирование, а методологией — структурированные предиктивные модели. К концу этой лекции вы должны будете уметь применять этот подход к конкретным ситуациям в цепочке поставок. Этот подход не является теоретическим; он уже несколько лет является основным направлением работы компании Lokad. Также, если вы не смотрели предыдущие лекции, данная лекция не должна быть совершенно непонятной. Однако в этой серии лекций мы доходим до такой точки, когда будет очень полезно, если вы будете смотреть лекции по порядку. В этой лекции мы вновь коснемся ряда элементов, представленных в предыдущих лекциях.

Прогнозирование будущего спроса является очевидным кандидатом в обзоре предиктивных потребностей для нашей цепочки поставок. Действительно, лучшее предвидение спроса — это критически важный компонент для таких базовых решений, как увеличение закупок и производства. Однако, исходя из принципов управления цепями поставок, которые мы представили в третьей главе этой серии лекций, мы увидели, что существует достаточно широкий спектр ожиданий в отношении предиктивных требований, необходимых для эффективного управления цепочкой поставок.

В частности, например, сроки поставки варьируются и проявляют сезонные закономерности. Практически каждое решение, связанное с управлением запасами, требует предвидения не только будущего спроса, но и будущих сроков поставок. Следовательно, сроки поставки необходимо прогнозировать. Возвраты иногда составляют до половины потока. Это имеет место, например, в модной электронной коммерции в Германии. В таких случаях предвидение возвратов становится критически важным, и эти возвраты значительно различаются от продукта к продукту. Таким образом, в таких ситуациях возвраты необходимо прогнозировать.

С точки зрения предложения, производство само по себе может меняться, и не только из-за дополнительных задержек или варьирующихся сроков поставок. Например, производство может быть сопряжено с определённой степенью неопределённости. Это происходит в отраслях с низкими технологиями, таких как сельское хозяйство, но может случаться и в высокотехнологичных секторах, например, в фармацевтической промышленности. Следовательно, урожайность производства также необходимо прогнозировать. Наконец, поведение клиентов тоже имеет большое значение. Например, стимулирование спроса через продукты, обеспечивающие привлечение клиентов, является очень важным, и, наоборот, наличие дефицита товара на продуктах, которые приводят к высокой текучести клиентов, когда эти продукты отсутствуют именно из-за дефицита, также имеет большое значение. Таким образом, эти параметры требуют анализа, прогнозирования – другими словами, их необходимо прогнозировать. Главное, что следует отметить, это то, что прогнозирование на основе временных рядов — лишь часть пазла. Мы нуждаемся в предиктивном подходе, который сможет охватить все эти ситуации и не только, поскольку это необходимо, если мы хотим иметь подход, способный справиться со всеми сложностями, с которыми может столкнуться реальная цепочка поставок.

Основной подход в решении предиктивных задач — это представление модели. Этот подход используется в литературе по прогнозированию временных рядов на протяжении десятилетий и, я бы сказал, до сих пор остаётся основным направлением в кругах машинного обучения. Этот подход, ориентированный на модель, как я собираюсь его назвать, настолько распространён, что порой сложно сделать шаг назад и объективно оценить, что же на самом деле происходит в рамках данного модельно-центрированного взгляда.

Моё предложение для этой лекции заключается в том, что цепочка поставок требует техники моделирования, подхода, ориентированного на моделирование, и что серия моделей, каким бы обширным она ни была, никогда не сможет удовлетворить все требования, встречающиеся в реальных цепочках поставок. Давайте проясним разницу между модельно-центрированным подходом и подходом, ориентированным на моделирование.

Модельно-центрированный подход прежде всего акцентирует внимание на самой модели. Модель представлена как пакет, набор числовых рецептов который, как правило, воплощается в виде программного обеспечения, которое вы можете запустить. Даже если такого программного обеспечения нет, ожидается, что если у вас есть модель, но нет ПО, то модель должна быть описана с математической точностью, что позволяет её полную переработку. Этот пакет, модель в виде ПО, считается конечной целью.

С идеальной точки зрения, эта модель должна вести себя точно как математическая функция: на входе получая данные, а на выходе выдавая результаты. Если у модели остаётся возможность настройки, то эти настраиваемые элементы рассматриваются как свободные параметры, как проблемы, которые ещё предстоит полностью решить. Действительно, каждая опция настройки ослабляет обоснованность модели. Когда в модельно-центрированном подходе присутствует возможность настройки и слишком много опций, модель склонна распадаться на множество моделей, и внезапно мы больше не можем производить корректное сравнение, потому что понятие единственной модели утрачивает смысл.

Подход, ориентированный на моделирование, кардинально инвертирует вопрос настройки. Максимизация выразительности модели становится конечной целью. Это не ошибка; это особенность. Ситуация может показаться весьма запутанной, когда мы рассматриваем модельно-ориентированный подход, поскольку при его представлении мы видим демонстрацию моделей. Однако эти модели имеют совсем иное предназначение.

Если рассматривать подход, ориентированный на моделирование, то представленная модель является всего лишь иллюстрацией. Она не претендует на полноту или на то, чтобы быть окончательным решением проблемы. Это лишь шаг на пути демонстрации самой техники моделирования. Основная проблема техники моделирования заключается в том, что сразу становится очень сложно оценить подход. Действительно, мы утрачиваем возможность простого сравнения, потому что, применяя модельно-ориентированный подход, мы получаем потенциал множества моделей. Мы не фокусируемся на сравнении одной модели с другой; это даже не соответствует правильному мышлению. Что у нас имеется, так это обоснованное мнение.

Однако, я хотел бы сразу отметить, что наличие бенчмарка и числовых показателей не делает подход автоматически научным. Числа могут быть просто бессмысленными, и, наоборот, не то чтобы обоснованное мнение делало его менее научным. Таким образом, это просто другой подход, и реальность такова, что в различных сообществах оба подхода сосуществуют.

Например, если мы обратимся к статье “Forecasting at Scale”, опубликованной командой Facebook в 2017 году, мы увидим, по сути, архетип модельно-центрированного подхода. В этой статье представлена модель Facebook Prophet. А в другой статье “Tensor Comprehension”, опубликованной в 2018 году другой командой из Facebook, по сути рассматривается техника моделирования. Эту статью можно считать архетипом подхода, ориентированного на моделирование. Таким образом, можно заметить, что даже исследовательские команды, работающие в одной компании и практически одновременно, могут решать проблему под разными углами, в зависимости от ситуации.

Эта лекция является частью серии лекций о цепочках поставок. В первой главе я изложил свои взгляды на цепочки поставок как на область изучения, так и на практическую деятельность. Уже с самой первой лекции я утверждал, что доминирующая теория цепочек поставок не оправдывает ожиданий. Оказывается, что основная теория цепочек поставок сильно опирается на модельно-центрированный подход, и я считаю, что этот единственный аспект является одной из главных причин трения между доминирующей теорией цепочек поставок и потребностями реальных цепочек поставок.

Во второй главе этой серии лекций я представил ряд методологий. Действительно, наивные методологии обычно оказываются бессильными перед эпизодическим и часто оппозиционным характером ситуаций в цепочках поставок. В частности, лекция под названием “Эмпирическая экспериментальная оптимизация”, которая была частью второй главы, представляет тот взгляд, который я применяю сегодня.

В третьей главе я представил ряд персонажей цепочек поставок. Эти персонажи характеризуют сосредоточенность исключительно на проблемах, которые мы пытаемся решить, полностью игнорируя любые предполагаемые решения. Они играют ключевую роль в понимании многообразия предиктивных вызовов, с которыми сталкиваются реальные цепочки поставок. Я считаю, что эти персонажи необходимы, чтобы не застрять в узкой перспективе временных рядов, которая является отличительной чертой теории цепочек поставок, уделяющей мало внимания мелким, но важным деталям реальных цепочек поставок.

В четвёртой главе я представил ряд вспомогательных наук. Эти науки отличаются от цепочек поставок, но базовое знание этих дисциплин необходимо для современной практики в цепочках поставок. Мы уже кратко коснулись темы дифференцируемого программирования в этой главе, но я собираюсь вновь подробно рассказать об этой парадигме программирования через несколько минут.

Наконец, в первой лекции пятой главы мы рассмотрели простую, некоторые даже назвали бы её упрощённой, модель, которая достигла передового уровня точности прогнозирования на мировом соревновании по прогнозированию, состоявшемся в 2020 году. Сегодня я представляю серию техник, которые можно использовать для обучения параметров, задействованных в модели, представленной в предыдущей лекции.

Остальная часть этой лекции будет условно разделена на два блока, за которыми последуют несколько заключительных замечаний. Первый блок посвящён дифференцируемому программированию. Мы уже касались этой темы в четвёртой главе, однако сегодня мы рассмотрим её гораздо подробнее. К концу лекции вы почти сможете создать собственную реализацию дифференцируемого программирования. Говорю «почти», потому что результаты могут варьироваться в зависимости от используемой технической базы. Кроме того, дифференцируемое программирование — это своего рода ремесло, требующее определённого опыта для его плавной работы на практике.

Второй блок этой лекции представляет собой пошаговый разбор ситуации прогнозирования розничного спроса. Этот разбор является продолжением предыдущей лекции, где мы представили модель, занявшую первое место на соревновании M5 по прогнозированию в 2020 году. Однако в той лекции мы не детализировали, как именно рассчитывались параметры модели. Данный разбор как раз это и покажет, а также мы осветим важные элементы, такие как дефицит товаров и акции, которые остались без внимания в предыдущей лекции. Наконец, на основе всех этих элементов я выскажу свои взгляды на пригодность дифференцируемого программирования для нужд цепочек поставок.

Стохастический градиентный спуск (SGD) является одним из двух столпов дифференцируемого программирования. SGD выглядит обманчиво простым, и тем не менее до конца неясно, почему он работает так хорошо. Абсолютно понятно, почему он работает; что не очень понятно — почему он работает так хорошо.

Историю стохастического градиентного спуска можно проследить до 1950-х годов, поэтому у него довольно длинная история. Однако эта техника получила широкое признание только в последнее десятилетие с появлением глубокого обучения. Стохастический градиентный спуск глубоко укоренился в математической оптимизации. У нас есть функция потерь Q, которую мы хотим минимизировать, и набор реальных параметров, обозначаемых W, которые представляют все возможные решения. То, что мы хотим найти, — это комбинация параметров W, минимизирующая функцию потерь Q.

Функция потерь Q должна обладать одним фундаментальным свойством: её можно аддитивно разложить на ряд слагаемых. Наличие этого аддитивного разложения делает возможным применение стохастического градиентного спуска. Если вашу функцию потерь нельзя разложить аддитивно таким образом, то метод стохастического градиентного спуска неприменим. В этом контексте X представляет собой набор всех слагаемых, вносящих вклад в функцию потерь, а Qx представляет собой частичную потерю, отражающую вклад одного из этих слагаемых.

Хотя стохастический градиентный спуск не является специфичным для задач обучения, он отлично подходит для всех сценариев обучения, и когда я говорю об обучении, я имею в виду задачи машинного обучения. Действительно, если у нас есть обучающий набор данных, этот набор принимает форму списка наблюдений, где каждое наблюдение представляет собой пару: признаки, являющиеся входом модели, и метки, отражающие выход. По сути, с точки зрения обучения, мы стремимся создать модель, которая будет показывать наилучшие результаты по эмпирической ошибке и другим метрикам, наблюдаемым на этом обучающем наборе. Таким образом, с точки зрения обучения X фактически представляет список наблюдений, а параметры — это те параметры модели машинного обучения, которые мы пытаемся оптимизировать, чтобы наилучшим образом соответствовать этому набору данных.

Стохастический градиентный спуск по существу является итеративным процессом, который случайным образом проходит по наблюдениям, выбирая по одному за раз. Мы выбираем одно наблюдение, обозначаемое как небольшой X, и для этого наблюдения вычисляем локальный градиент, представленный как ∇Qx. Это всего лишь локальный градиент, который применяется только к одному слагаемому функции потерь. Это не градиент полной функции потерь, а локальный градиент, применимый лишь к одному слагаемому – его можно рассматривать как частичный градиент.

Шаг стохастического градиентного спуска заключается в том, чтобы использовать этот локальный градиент для небольшого изменения параметров W на основе данного частичного наблюдения градиента. Именно это и происходит здесь: W обновляется по правилу W = W - eta * ∇QxW. Иными словами, параметр W сдвигается в направлении локального градиента, вычисленного для X, где X — это одно из наблюдений вашего набора данных, если мы решаем задачу с точки зрения обучения. Затем процесс повторяется случайным образом с применением этого локального градиента.

Интуитивно понятна эффективность стохастического градиентного спуска: он демонстрирует компромисс между более быстрой итерацией и более шумными градиентами, что позволяет добиться более детальной и, соответственно, более быстрой итерации. Суть стохастического градиентного спуска в том, что нас не волнует несовершенство измерений градиентов, если мы можем получить их очень быстро. Если можно сместить баланс в пользу более быстрой итерации, даже ценой более шумных градиентов, мы это делаем. Вот почему стохастический градиентный спуск так эффективен для минимизации вычислительных ресурсов, необходимых для достижения определённого качества решения параметра W.

Наконец, у нас есть переменная eta, которую называют скоростью обучения. На практике скорость обучения не является постоянной; эта переменная изменяется в процессе работы стохастического градиентного спуска. В компании Lokad мы используем алгоритм Adam для контроля эволюции этой переменной eta, отвечающей за скорость обучения. Adam — это метод, опубликованный в 2014 году, и он очень популярен в кругах машинного обучения, когда применяется стохастический градиентный спуск.

Второй столп дифференцируемого программирования — автоматическое дифференцирование. Мы уже сталкивались с этой концепцией в предыдущей лекции. Давайте вернёмся к ней, рассмотрев пример кода. Этот код написан на Envision — предметно-ориентированном языке программирования, разработанном компанией Lokad для предиктивной оптимизации цепей поставок. Я выбираю Envision, потому что, как вы увидите, примеры получаются гораздо более лаконичными и, надеюсь, более понятными по сравнению с альтернативными презентациями, если бы я использовал Python, Java или C#. Однако хочу отметить, что, несмотря на использование Envision, здесь нет никакой секретной магии. Вы могли бы полностью переписать все эти примеры на других языках программирования. Скорее всего, это увеличило бы количество строк кода в 10 раз, но в общем масштабе это несущественно. Для лекции Envision позволяет нам получить очень ясную и сжатую презентацию.

Давайте посмотрим, как дифференцируемое программирование может быть использовано для решения задачи линейной регрессии. Это учебная задача; для линейной регрессии нам не обязательно применять дифференцируемое программирование. Цель заключается лишь в том, чтобы познакомиться с синтаксисом дифференцируемого программирования. С строк 1 по 6 мы объявляем таблицу T, которая представляет таблицу наблюдений. Когда я говорю «таблица наблюдений», просто вспомните множество, использованное при стохастическом градиентном спуске, которое называлось X. Это одно и то же. Таблица имеет два столбца: один с признаком, обозначенным как X, и один с меткой, обозначенной как Y. Мы хотим, чтобы на вход подавался X, и чтобы можно было предсказать Y с помощью линейной, точнее, аффинной модели. Очевидно, что в таблице T всего четыре точки данных. Это абсурдно маленький набор данных, выбранный исключительно для наглядности изложения.

На строке 8 мы вводим блок autodiff. Блок autodiff можно рассматривать как цикл в Envision. Это цикл, который проходит по таблице, в данном случае по таблице T. Эти итерации отражают шаги стохастического градиентного спуска. Таким образом, при входе в блок autodiff происходит серия повторяющихся операций: мы выбираем строки из таблицы наблюдений, а затем применяем шаги стохастического градиентного спуска. Для этого нам требуются градиенты.

Откуда берутся градиенты? Здесь мы написали программу — небольшое выражение нашей модели: Ax + B. Мы вводим функцию потерь, которая представляет собой среднеквадратичную ошибку, и хотим получить градиент. Для такой простой задачи мы могли бы записать градиент вручную. Однако автоматическое дифференцирование — это техника, позволяющая скомпилировать программу в двух формах: первая — это прямое выполнение программы, а вторая — обратное выполнение, которое вычисляет градиенты, связанные со всеми параметрами программы.

На строках 9 и 10 происходит объявление двух параметров, A и B, с использованием ключевого слова “auto”, которое говорит Envision автоматически инициализировать значения этих параметров. A и B — скалярные величины. Автоматическое дифференцирование применяется ко всем программам, содержащимся в этом блоке autodiff. По сути, это техника на уровне компилятора, которая компилирует программу дважды: один раз для прямого прохода и второй раз для получения значений градиентов. Прелесть автоматического дифференцирования заключается в том, что оно гарантирует соответствие объёма ЦПУ, необходимого для вычисления обычной программы, объёму ЦПУ для вычисления градиента при обратном проходе. Это очень важное свойство. Наконец, на строке 14 мы выводим параметры, которые только что были получены в блоке autodiff.

Дифференцируемое программирование действительно проявляет себя как мощная парадигма программирования. Можно составить произвольно сложную программу и автоматически получить её дифференцирование. Такая программа может включать ветвления и вызовы функций, например. В данном примере кода вновь рассматривается функция потерь pinball, введённая в предыдущей лекции. Функция потерь pinball может быть использована для получения оценок квантилей при наблюдении отклонений от эмпирического распределения вероятностей. Если минимизировать среднеквадратичную ошибку, вы получите оценку среднего эмпирического распределения. Если минимизировать функцию потерь pinball, вы получите оценку целевого квантиля. Если вы нацеливаетесь на 90-й квантиль, это означает, что это значение в вашем распределении, ниже которого окажется 90% будущих наблюдаемых значений (при 90% цели) или, наоборот, только 10% окажутся выше. Это напоминает анализ уровня сервиса, применяемый в цепях поставок.

На строках 1 и 2 мы создаём таблицу наблюдений, заполненную отклонениями, случайным образом взятыми из распределения Пуассона. Значения распределения выбираются со средним равным 3, и мы получаем 10 000 отклонений. На строках 4 и 5 мы представляем нашу специализированную реализацию функции потерь pinball. Эта реализация практически идентична коду, приведённому в предыдущей лекции. Однако к объявлению функции теперь добавлено ключевое слово “autodiff”. Это ключевое слово, присоединённое к объявлению функции, гарантирует, что компилятор Envision сможет автоматически дифференцировать эту функцию. Хотя в теории автоматическое дифференцирование может применяться к любой программе, на практике существует множество программ и функций, для которых это не имеет смысла. Например, рассмотрите функцию, которая принимает два текстовых значения и их конкатенирует. С точки зрения автоматического дифференцирования применение этой техники в данном случае бессмысленно, так как она требует наличия числовых значений на входе и выходе функции.

Со строк 7 по 9 у нас находится блок autodiff, который вычисляет оценку целевого квантиля для эмпирического распределения, полученного из таблицы наблюдений. Внутри, по сути, используется распределение Пуассона. Оценка квантиля объявлена как параметр с именем “quantile” на строке 8, а на строке 9 происходит вызов нашей реализации функции потерь pinball. Целевой квантиль установлен равным 0.5, то есть мы фактически ищем медиану распределения. Наконец, на строке 11 выводятся результаты для значения, полученного в результате работы блока autodiff. Этот пример кода демонстрирует, как программа, которую мы собираемся дифференцировать автоматически, может включать как вызов функции, так и ветвление, и всё это происходит полностью автоматически.

Я уже упоминал, что блоки autodiff можно интерпретировать как цикл, выполняющий серию шагов стохастического градиентного спуска по таблице наблюдений, выбирая по одной строке за раз. Однако я не рассказал подробно об условии остановки этого процесса. Когда же останавливается стохастический градиентный спуск в Envision? По умолчанию стохастический градиентный спуск завершается после 10 эпох. Эпоха, в терминологии машинного обучения, означает полный проход по таблице наблюдений. На строке 7 к блоку autodiff может быть добавлен атрибут с именем “epochs”. Этот атрибут является необязательным; по умолчанию его значение равно 10, но если указать атрибут, можно выбрать иное количество. Здесь мы задаём 100 эпох. Имейте в виду, что общее время вычислений почти строго линейно зависит от количества эпох. Таким образом, если эпох вдвое больше, время вычислений увеличится вдвое.

Также, на строке 7 мы вводим второй атрибут с именем “learning_rate”. Этот атрибут также является необязательным, и по умолчанию его значение составляет 0.01, привязанное к блоку autodiff. Эта скорость обучения используется для инициализации алгоритма Adam, который контролирует эволюцию скорости обучения. Это та самая переменная eta, которую мы видели в шаге стохастического градиентного спуска. Она управляет алгоритмом Adam. По сути, это параметр, который обычно не требует вмешательства, но иногда его корректировка может существенно сэкономить вычислительные ресурсы. Не удивительно, что, точно настроив этот параметр, можно сэкономить примерно 20% общего времени вычислений стохастического градиентного спуска.

Инициализация параметров, которые обучаются в блоке autodiff, также требует более внимательного рассмотрения. До сих пор мы использовали ключевое слово “auto”, и в Envision это означает, что параметр инициализируется случайным образом путем выбора значения из гауссовского распределения со средним 1 и стандартным отклонением 0.1. Такая инициализация отличается от обычной практики в глубоких нейронных сетях, где параметры случайным образом инициализируются распределением с центром в нуле. Причина, по которой Lokad выбрал иной подход, станет яснее позже в этой лекции, когда мы перейдём к реальной задаче прогнозирования розничного спроса.

В Envision можно переопределять и контролировать инициализацию параметров. Параметр “quantile”, например, объявляется на строке 9, но инициализировать его не обязательно. Действительно, на строке 7, сразу перед блоком autodiff, мы имеем переменную “quantile”, которой присвоено значение 4.2, и, таким образом, переменная уже инициализирована конкретным значением. Автоматическая инициализация больше не требуется. Также возможно задать диапазон допустимых значений для параметров, и это делается с помощью ключевого слова “in” на строке 9. Фактически, мы определяем, что “quantile” должен находиться в пределах от 1 до 10 включительно. При наличии таких ограничений, если обновление, полученное от алгоритма Adam, подтолкнет значение параметра за допустимые границы, мы ограничиваем изменение от Adam так, чтобы оно оставалось в этом диапазоне. Кроме того, мы обнуляем значения момента, которые обычно прикреплены к алгоритму Adam “под капотом”. Ограничение параметров расходится с классической практикой глубокого обучения; однако преимущества этой функции станут очевидны, как только мы начнем обсуждать реальный пример прогнозирования розничного спроса.

Дифференцируемое программирование сильно опирается на стохастический градиентный спуск. Именно стохастичность делает спуск чрезвычайно быстрым. Это палка о двух концах; шум, возникающий из-за частичных потерь, является не просто недостатком, но и особенностью. Небольшое количество шума позволяет спуску избегать застревания в зонах с очень плоскими градиентами. Таким образом, наличие этого шумного градиента не только ускоряет итерации, но и помогает вывести процесс из областей с практически нулевым градиентом, где спуск замедляется. Однако следует помнить, что при использовании стохастического градиентного спуска сумма градиентов не равна градиенту суммы. В результате стохастический градиентный спуск имеет небольшие статистические смещения, особенно когда дело касается хвостовых распределений. Но когда возникают эти проблемы, относительно просто “заклеить” численные рецепты, даже если теория остается несколько неясной.

Дифференцируемое программирование (DP) не следует путать с произвольным математическим оптимизатором. Для работы дифференцируемого программирования градиент должен протекать через программу. Дифференцируемое программирование может работать с произвольно сложными программами, но эти программы должны быть разработаны с учетом принципов дифференцируемого программирования. Кроме того, дифференцируемое программирование — это культура; это набор советов и хитростей, хорошо сочетающихся со стохастическим градиентным спуском. С учетом всего вышесказанного, дифференцируемое программирование находится на легкой стороне спектра методов машинного обучения. Эта техника весьма доступна для понимания. Тем не менее, требуется определенное мастерство, чтобы овладеть этой парадигмой и успешно внедрить ее в производство.

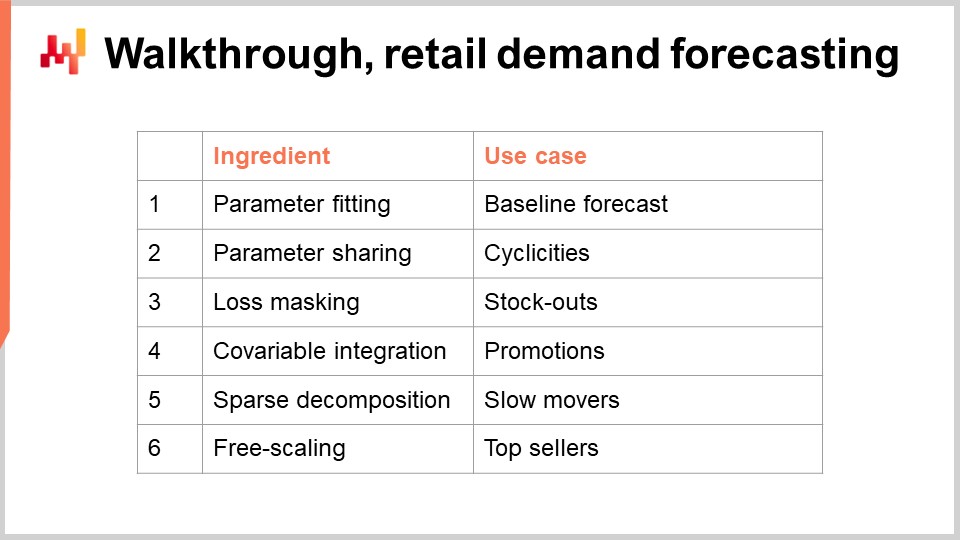
Теперь мы готовы приступить ко второму блоку этой лекции: практическому разбору. Мы проведем walkthrough для нашей задачи прогнозирования розничного спроса. Это моделирование соответствует задаче прогнозирования, которую мы представили в предыдущей лекции. Короче говоря, мы хотим прогнозировать ежедневный спрос на уровне SKU в розничной сети. SKU, или единица складского учета, технически представляет собой декартово произведение продуктов и магазинов, отфильтрованное по ассортименту. Например, если у нас 100 магазинов и 10 000 продуктов, и если каждый продукт присутствует во всех магазинах, то в итоге получается 1 миллион SKU.

Существуют инструменты для преобразования детерминированной оценки в вероятностную. Один из таких инструментов мы уже видели в предыдущей лекции с помощью техники ESSM. Мы вернемся к этому вопросу — преобразованию оценок в вероятностные — с большей детализацией на следующей лекции. Однако сегодня нас интересует только оценка средних значений, а все остальные типы оценок (квантили, вероятностные) появятся позже как естественные расширения основного примера, который я представлю сегодня. В этом walkthrough мы будем обучать параметры простой модели прогнозирования спроса. Простой вид этой модели обманчив, поскольку данный класс моделей действительно демонстрирует передовые результаты прогнозирования, как это было показано на конкурсе прогнозирования M5 в 2020 году.

Для нашей параметрической модели спроса давайте введем один параметр для каждого SKU. Это абсолютно примитивная форма модели; спрос моделируется как константа для каждого SKU. Однако это не одна и та же константа для всех SKU. Как только у нас появляется эта константная среднесуточная величина, она остается неизменной на протяжении всего жизненного цикла SKU.

Посмотрим, как это делается с помощью дифференцируемого программирования. С строк 1 по 4 мы вводим блок имитационных данных. На практике эта модель и все ее варианты зависели бы от данных, полученных из бизнес-систем: ERP, WMS, TMS и т.д. Проведение лекции, в которой я интегрирую математическую модель в реалистичное представление данных, как они получаются из ERP, привело бы к множеству случайных осложнений, не имеющих отношения к теме лекции. Поэтому здесь я ввожу блок имитационных данных, который даже не претендует на реализм, или на тип данных, которые можно наблюдать в реальной розничной ситуации. Единственная цель этих имитационных данных — представить таблицы и взаимосвязи между ними, а также убедиться, что приведенный пример кода является полным, компилируемым и исполняемым. Все примеры кода, которые вы видели до сих пор, являются полностью автономными; никаких скрытых частей до или после. Единственная цель блока имитационных данных — обеспечить наличие автономного куска кода.

В каждом примере этого walkthrough мы начинаем с этого блока имитационных данных. На строке 1 мы вводим таблицу дат с “dates” в качестве первичного ключа. Здесь у нас диапазон дат, представляющий по сути два года и один месяц. Затем, на строке 2, мы вводим таблицу SKUs, которая представляет список SKU. В этом минималистичном примере у нас всего три SKU. В реальной розничной ситуации для крупной сети у нас было бы миллионы, если не десятки миллионов, SKU. Но здесь, ради примера, я беру очень маленькое число. На строке 3 у нас таблица “T”, которая представляет декартово произведение между SKU и датой. По сути, что вы получаете через эту таблицу “T”, так это матрицу, в которой присутствует каждый SKU и каждый день. Она имеет два измерения.

На строке 6 мы вводим наш реальный блок autodiff. Таблица наблюдений — это таблица SKUs, и стохастический градиентный спуск здесь будет выбирать по одному SKU за раз. На строке 7 мы вводим “level”, который станет нашим единственным параметром. Это векторный параметр, и до сих пор в наших блоках autodiff мы вводили только скалярные параметры. Ранее параметры были просто числом; здесь же “SKU.level” на самом деле является вектором. Это вектор, в котором имеется одно значение для каждого SKU, и это буквально наша константная величина спроса, смоделированная на уровне SKU. Мы задаем диапазон, и увидим, почему это важно, через мгновение. Он должен быть не менее 0.01, а верхняя граница для среднего суточного спроса установлена в 1000 для этого параметра. Этот параметр автоматически инициализируется значением, близким к единице, что является разумной отправной точкой. В этой модели у нас всего одна степень свободы на каждый SKU. Наконец, на строках 8 и 9 мы фактически реализуем саму модель. На строке 8 мы вычисляем “dot.delta”, что представляет собой разность между прогнозируемым спросом модели и наблюдаемым значением, которое есть “T.sold”.

Чтобы понять, что здесь происходит, у нас действуют механизмы трансляции (broadcasting). Таблица “T” является перекрестной таблицей между SKU и датой. Блок autodiff представляет собой итерацию по строкам таблицы наблюдений. На строке 9 мы находимся внутри блока autodiff, поэтому выбрана строка из таблицы SKUs. Значение “SKUs.level” здесь уже не вектор, а просто скаляр, одно значение, поскольку выбрана только одна строка таблицы наблюдений. Затем “T.sold” уже не матрица, так как мы выбрали один SKU. Остается, что “T.sold” на самом деле является вектором, размерность которого соответствует таблице дат. Когда мы выполняем вычитание “SKUs.level - T.sold”, мы получаем вектор, выровненный с таблицей дат, и присваиваем его переменной “D.delta”, которая также является вектором с одной строкой для каждого дня — в сумме два года и один месяц. Наконец, на строке 9 мы вычисляем функцию потерь, которая представляет собой среднеквадратичную ошибку. Эта модель крайне примитивна. Посмотрим, что можно сделать с календарными закономерностями.

Совместное использование параметров, вероятно, является одной из самых простых и полезных техник дифференцируемого программирования. Параметр считается совместно используемым, если он влияет на несколько строк наблюдений. Совмещая параметры через наблюдения, мы можем стабилизировать градиентный спуск и смягчить проблемы переобучения. Рассмотрим закономерность по дням недели. Мы могли бы ввести семь параметров, представляющих различные веса для каждого SKU. На данный момент у одного SKU имеется только один параметр, который представляет собой константный спрос. Если мы захотим обогатить эту модель спроса, можно сказать, что каждый день недели имеет свой собственный вес, и поскольку в неделе семь дней, мы можем иметь семь весов, которые применяются мультипликативно.

Однако маловероятно, что у каждого SKU будет уникальная закономерность по дням недели. На практике гораздо разумнее предположить, что существует категория или иерархия, такая как семейство продуктов, категория товаров, подкатегория или даже отдел в магазине, которые корректно отображают эту закономерность дней недели. Идея состоит в том, что мы не хотим вводить семь параметров для каждого SKU; мы хотим ввести семь параметров на каждую категорию — на том уровне группировки, где предполагается однородное поведение в отношении закономерностей по дням недели.

Если мы решим ввести эти семь параметров с мультипликативным эффектом на уровень спроса, то это именно тот подход, который был использован в предыдущей лекции для этой модели, что позволило ей занять первое место на уровне SKU в конкурсе M5. У нас есть уровень спроса и мультипликативный эффект, обусловленный закономерностью по дням недели.

В коде, на строках 1–5, у нас имеется блок имитационных данных, как и ранее, и мы вводим дополнительную таблицу с названием “category”. Эта таблица представляет группировку SKU, и концептуально для каждой строки в таблице SKU существует ровно одна строка в таблице category. В языке Envision мы говорим, что категория находится “выше” таблицы SKUs. На строке 7 вводится таблица для дней недели. Эта таблица имеет служебное значение, и мы создаем ее с определенной структурой, отражающей циклическую закономерность, которую мы хотим зафиксировать. На строке 7 мы создаем таблицу дней недели, агрегируя даты по остатку от деления на семь. Мы создаем таблицу, которая будет состоять ровно из семи строк, и эти семь строк будут представлять каждый из семи дней недели. Для каждой строки в таблице дат существует ровно одна соответствующая строка в таблице дней недели. Таким образом, согласно языку Envision, таблица дней недели располагается “выше” таблицы “date”.

Теперь у нас есть таблица “CD”, которая представляет декартово произведение между категорией и днями недели. По количеству строк эта таблица будет иметь столько строк, сколько категорий, умноженное на семь, так как дней недели ровно семь. На строке 12 мы вводим новый параметр с названием “CD.DOW” (DOW означает день недели), который является еще одним векторным параметром, принадлежащим таблице CD. С точки зрения степеней свободы, у нас будет ровно семь значений параметров, умноженные на число категорий, что и требуется. Мы хотим модель, способную уловить закономерность дней недели, но с одной закономерностью на категорию, а не индивидуально для каждого SKU.

Мы объявляем этот параметр и используем ключевое слово “in”, чтобы указать, что значение для “CD.DOW” должно находиться в диапазоне от 0.1 до 100. На строке 13 мы записываем спрос, как он выражается моделью. Спрос вычисляется как “SKUs.level * CD.DOW”, что представляет собой спрос. Вычитаем из него наблюдаемое значение “T.sold”, и получаем дельту. Затем вычисляется среднеквадратичная ошибка.

На строке 13 происходит настоящая магия трансляции. “CD.DOW” — это перекрестная таблица между категорией и днем недели. Поскольку мы находимся внутри блока autodiff, таблица CD является перекрестной таблицей между категорией и днем недели. Так как мы итеративно обрабатываем таблицу SKUs, при выборе одного SKU мы фактически выбираем одну категорию, так как таблица категорий находится “выше”. Это означает, что CD.DOW уже не матрица, а вектор размерности семь. Однако, он находится “выше” таблицы “date”, поэтому эти семь строк могут быть трансляционными на таблицу дат. Существует только один способ выполнить эту трансляцию, поскольку каждая строка таблицы дней недели ассоциирована с определенными строками таблицы дат. Происходит двойная трансляция, и в итоге мы получаем спрос, представляющий собой ряд значений с циклическим характером по дням недели для данного SKU. Это и есть наша модель на данном этапе, а остальная часть функции потерь остается неизменной.

Мы наблюдаем очень элегантный способ работы с цикличностью, когда комбинируются механизмы трансляции, вытекающие из реляционной природы Envision, и возможности дифференцируемого программирования. Мы можем описать календарные цикличности всего в трех строках кода. Этот подход хорошо работает, даже если имеются очень разреженные данные. Он будет корректно работать даже для товаров, которые в среднем продают лишь одну единицу в месяц. В таких случаях разумно иметь категорию, которая объединяет десятки, если не сотни товаров. Эта техника может быть также использована для отражения других циклических закономерностей, таких как месяц года или день месяца.

Модель, представленная в предыдущей лекции, которая достигла передовых результатов на конкурсе M5, представляла собой мультипликативное сочетание трех цикличностей: дня недели, месяца года и дня месяца. Все эти закономерности были объединены посредством умножения. Реализация двух других вариантов оставлена внимательной аудитории, но это всего лишь пара строк кода для каждой цикличности, что делает реализацию очень лаконичной.

В предыдущей лекции мы представили модель прогнозирования продаж. Однако нас интересует не сами продажи, а спрос. Не стоит путать нулевые продажи с нулевым спросом. Если в магазине в конкретный день не осталось товара для покупки, в Lokad применяется техника маскирования потерь для компенсации отсутствия запасов. Это самая простая техника для борьбы с отсутствием товара, но она не единственная. Насколько мне известно, у нас есть как минимум еще две техники, которые используются в производстве, каждая со своими плюсами и минусами. Эти другие техники сегодня рассматривать не будем, но они будут затронуты в последующих лекциях.

Возвращаясь к примеру кода, строки 1-3 остаются без изменений. Давайте рассмотрим, что следует далее. На строке 6 мы дополняем тестовые данные булевым флагом наличия товара на складе. Для каждого отдельного SKU и каждого дня у нас имеется булевое значение, которое указывает, произошел ли дефицит товара в конце дня для магазина. На строке 15 мы модифицируем функцию потерь, исключая путем обнуления те дни, когда в конце дня наблюдался дефицит товара. Обнуляя эти дни, мы гарантируем, что градиент не будет распространяться обратно в ситуациях, когда присутствует смещение, вызванное дефицитом.

Самый запутывающий аспект техники маскирования потерь заключается в том, что она даже не изменяет модель. Действительно, если мы взглянем на модель, приведенную на строке 14, она остается абсолютно той же; она не была изменена. Изменяется только сама функция потерь. Эта техника может быть простой, но она кардинально отличается от модельно-центрированного подхода. По сути, это техника, ориентированная на моделирование. Мы улучшаем ситуацию, признавая смещение, вызванное дефицитом, и отражая это в наших моделирующих усилиях. Однако мы делаем это, изменяя метрику точности, а не саму модель. Другими словами, мы изменяем оптимизируемую функцию потерь, что делает эту модель несравнимой с другими моделями с точки зрения чистой числовой ошибки.

Для ситуации, подобной Walmart, как обсуждалось в предыдущей лекции, техника маскирования потерь подходит для большинства товаров. Как правило, эта техника хорошо работает, если спрос не настолько разрежен, что в большинстве случаев на складе остается только одна единица товара. Кроме того, следует избегать товаров, для которых дефициты происходят очень часто, поскольку это является осознанной стратегией ритейлера — закончить день с отсутствием товара. Это обычно происходит с некоторыми ультрасвежими товарами, когда ритейлер стремится к ситуации отсутствия товара к концу дня. Альтернативные техники исправляют эти ограничения, но у нас нет времени сегодня их рассматривать.

Акции являются важным аспектом розничной торговли. Более того, существует множество способов, с помощью которых ритейлер может влиять на спрос и формировать его, таких как ценообразование или перемещение товаров на полке. Переменные, предоставляющие дополнительную информацию для прогнозирования, обычно называют ковариатами в кругах цепочек поставок. Существует много оптимистичных представлений о сложных ковариатах, таких как данные о погоде или данные социальных сетей. Однако, прежде чем углубляться в продвинутые темы, мы должны обратить внимание на главную проблему, например, на информацию о ценах, которая, очевидно, оказывает значительное влияние на наблюдаемый спрос. Таким образом, на строке 7 в этом примере кода мы вводим для каждого отдельного дня на строке 14 переменную “category.ed”, где “ed” означает эластичность спроса. Это общий векторный параметр с одной степенью свободы для каждой категории, предназначенный для представления эластичности спроса. На строке 16 мы вводим экспоненциальную форму ценовой эластичности как экспоненту от (-category.ed * t.price). Интуитивно, с такой формой, когда цена увеличивается, спрос быстро стремится к нулю из-за экспоненциальной функции. И наоборот, когда цена стремится к нулю, спрос экспоненциально возрастает.

Эта экспоненциальная форма реакции на изменение цены является упрощенной, а использование общих параметров обеспечивает высокую степень числовой стабильности даже при наличии этой экспоненциальной функции в модели. В реальных условиях, особенно для ситуаций, подобных Walmart, у нас будет несколько видов ценовой информации, таких как скидки, разница с обычной ценой, ковариаты, представляющие маркетинговые воздействия от поставщика, или категориальные переменные, которые вводят такие элементы, как полки. Благодаря дифференцируемому программированию очень просто создавать произвольно сложные реакции на цену, которые точно соответствуют ситуации. Интегрировать ковариаты практически любого типа с дифференцируемым программированием очень просто.

Товары с медленным оборотом — это реальность в розничной торговле и во многих других отраслях. Модель, представленная до сих пор, имеет один параметр, одну степень свободы для каждого SKU, а если учитывать общие параметры, то их еще больше. Однако это может оказаться слишком много, особенно для SKU, которые обновляются только раз в год или всего несколько раз в год. В таких случаях мы не можем позволить себе даже одну степень свободы для каждого SKU, поэтому решение состоит в том, чтобы опираться исключительно на общие параметры и убрать все параметры со степенью свободы на уровне SKU.

На строках 2 и 4 мы вводим две таблицы с названиями “products” и “stores”, а таблица “SKUs” формируется как отфильтрованная подтаблица декартова произведения между продуктами и магазинами, что является самой сутью ассортимента. На строках 15 и 16 мы ввели два общих векторных параметра: один уровень, связанный с таблицей продуктов, и другой уровень, связанный с таблицами магазинов. Эти параметры также определены в конкретном диапазоне — от 0.01 до 100, что является максимальным значением.

Теперь, на строке 18, уровень для каждого SKU рассчитывается как произведение уровня продукта и уровня магазина. Остальная часть скрипта остается без изменений. Итак, как это работает? На строке 19 SKU.level является скаляром. У нас есть блок autodesk, который итерируется по таблице SKUs — таблице наблюдений. Таким образом, SKUs.level на строке 18 представляет собой просто скалярное значение. Затем у нас есть products.level. Поскольку таблица продуктов расположена выше таблицы SKUs, для каждого отдельного SKU существует ровно один продукт. Следовательно, products.level — это просто скалярное число. То же самое относится к таблице магазинов, которая также расположена выше таблицы SKUs. На строке 18 к данному SKU привязан только один магазин. Таким образом, мы имеем произведение двух скалярных величин, что дает нам SKU.level. Остальная часть модели остается без изменений.

Эти техники придают совершенно новый смысл утверждению, что иногда данных недостаточно или они слишком разрежены. Действительно, с точки зрения дифференцируемого подхода такие утверждения даже не имеют смысла. Нет такого понятия, как «слишком мало данных» или «данные слишком разрежены», по крайней мере, не в абсолютном выражении. Существуют просто модели, которые можно модифицировать в сторону разреженности и, возможно, даже экстремальной разреженности. Наложенная структура похожа на направляющие, которые делают процесс обучения не только возможным, но и численно стабильным.

По сравнению с другими методами машинного обучения, которые пытаются позволить модели самостоятельно обнаруживать все закономерности ex nihilo, этот структурированный подход задает именно ту структуру, которую нам необходимо изучить. Таким образом, статистический механизм, действующий здесь, имеет ограниченную свободу в том, чему он может научиться. Следовательно, с точки зрения эффективности использования данных он может быть невероятно эффективным. Естественно, все это зависит от того, что мы выбрали правильную структуру.

Как видите, проводить эксперименты очень просто. Мы уже делаем нечто очень сложное, и менее чем за 50 строк кода мы можем справиться с довольно сложной ситуацией, подобной Walmart. Это действительно достижение. Процесс носит эмпирический характер, но на самом деле он не так велик. Речь идет всего о нескольких десятках строк. Имейте в виду, что ERP-система, управляющая компанией или крупной розничной сетью, как правило, содержит тысячу таблиц и 100 полей в каждой таблице. Таким образом, сложность бизнес-систем совершенно колоссальна по сравнению со сложностью этой структурированной предиктивной модели. Если нам придется потратить немного времени на итерации, это ничтожная трата ресурсов.

Более того, как показано на конкурсе прогнозирования M5, реальность такова, что специалисты по цепочкам поставок уже знают закономерности. Когда команда M5 использовала три календарных шаблона — день недели, месяц года и день месяца, все эти закономерности были самоочевидны для любого опытного специалиста по цепочкам поставок. Реальность в цепочках поставок такова, что мы не пытаемся открыть какую-то скрытую закономерность. Тот факт, что, например, при резком снижении цены спрос резко возрастает, никого не удивит. Единственный вопрос, который остается, — это точная величина эффекта и точная форма реакции. Это довольно технические детали, и если вы дадите себе возможность провести несколько экспериментов, вы сможете решить эти проблемы относительно легко.

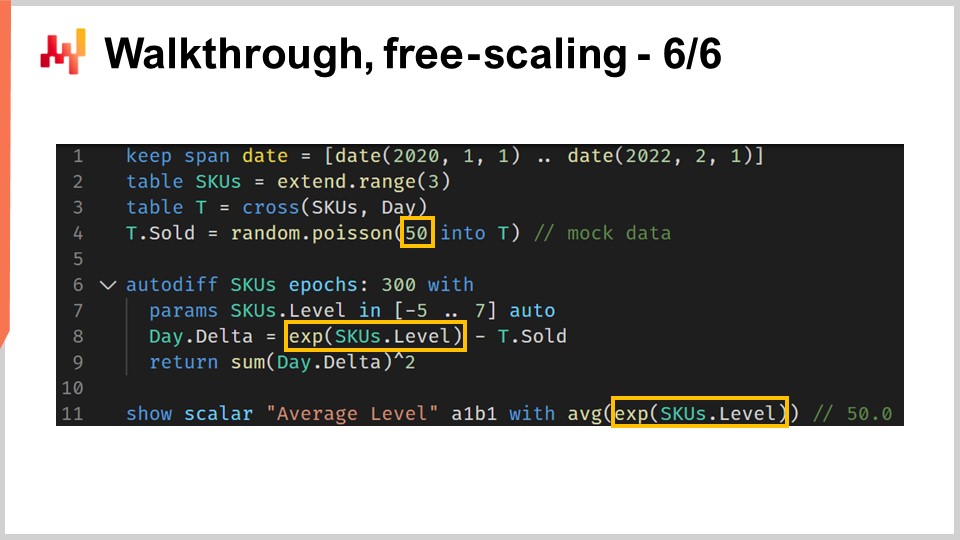
В заключительном этапе этого обзора я хотел бы отметить одну небольшую особенность дифференцируемого программирования. Не следует путать дифференцируемое программирование с обычным решателем математической оптимизации. Нужно помнить, что здесь применяется градиентный спуск. Более конкретно, алгоритм, используемый для оптимизации и обновления параметров, имеет максимальную скорость спуска, равную скорости обучения, предусмотренной в алгоритме ADAM. В Envision скорость обучения по умолчанию составляет 0.01.

Если мы взглянем на код, то на строке 4 мы ввели инициализацию, при которой количество продаваемого товара выбирается из пуассоновского распределения со средним значением 50. Если мы хотим определить уровень, то технически нам необходим уровень порядка 50. Однако, при автоматической инициализации параметра, мы начинаем со значения, близкого к единице, и можем изменять его только шагами по 0.01. Потребовалось бы около 5 000 эпох, чтобы действительно достичь значения 50. Поскольку у нас есть необщий параметр SKU.level, этот параметр за эпоху обновляется только один раз. Таким образом, нам потребовалось бы 5 000 эпох, что ненужно замедлило бы вычисления.

Мы могли бы увеличить скорость обучения, чтобы ускорить спуск, что было бы одним из решений. Однако я не советую завышать скорость обучения, так как это, как правило, не является правильным способом решения проблемы. В реальной ситуации у нас будут общие параметры помимо этого необщего параметра. Эти общие параметры будут подвергаться многочисленным обновлениям стохастическим градиентным спуском в течение каждой эпохи. Если вы значительно увеличите скорость обучения, то рискуете создать числовую нестабильность для общих параметров. Можно увеличить скорость изменения уровня SKU, но при этом возникнут проблемы числовой стабильности для остальных параметров.

Лучшей техникой было бы использовать трюк с перенормировкой и обернуть параметр в экспоненциальную функцию, что именно и делается на строке 8. С этим оберткой теперь мы можем достигать значений параметра уровня, которые могут быть либо очень низкими, либо очень высокими, за гораздо меньшее количество эпох. Эта особенность, по сути, единственная, которую мне нужно было ввести для получения реалистичного примера ситуации прогнозирования розничного спроса в этом обзоре. В общем, это незначительная особенность. Тем не менее, она напоминает о том, что дифференцируемое программирование требует внимания к потоку градиентов. Дифференцируемое программирование обеспечивает плавный процесс разработки, но это не магия.

Несколько заключительных мыслей: структурированные модели действительно достигают передовой точности прогнозирования. Этот момент был подробно рассмотрен в предыдущей лекции. Однако, исходя из представленных сегодня элементов, я бы сказал, что точность даже не является решающим фактором в пользу дифференцируемого программирования с использованием структурированной параметрической модели. Что мы получаем, так это понимание; мы получаем не просто программное обеспечение, способное делать прогнозы, но и прямое понимание тех закономерностей, которые мы пытаемся зафиксировать. Например, представленная сегодня модель непосредственно даст нам прогноз спроса с явными весами для дней недели и с явной эластичностью спроса. Если бы мы решили расширить этот прогноз, чтобы учесть, например, всплеск, связанный с Черной пятницей, квази-сезонным событием, которое не происходит каждый год в одно и то же время, мы могли бы это сделать. Мы просто добавили бы коэффициент, и тогда получили бы оценку повышения спроса на Черную пятницу отдельно от всех остальных паттернов, таких как шаблон по дням недели. Это имеет первостепенное значение.

То, что мы получаем благодаря структурированному подходу, — это понимание, и оно гораздо больше, чем просто сырая модель. Например, если мы получим отрицательную эластичность, то есть ситуацию, когда модель говорит, что при повышении цены спрос возрастает, что в ситуации, подобной Walmart, является крайне сомнительным результатом. Скорее всего, это указывает на то, что реализация вашей модели имеет недочеты или что возникают серьезные проблемы. Независимо от того, что говорит метрика точности, если вы попадаете в ситуацию, когда повышение цены приводит к увеличению продаж, вам следует всерьез пересмотреть всю систему обработки данных, потому что, скорее всего, что-то не так. Именно в этом и заключается суть понимания.

Также модель открыта для изменений. Дифференцируемое программирование невероятно выразительно. Модель, которую мы имеем, — это всего лишь одна итерация в длинном пути. Если рынок трансформируется или если сама компания претерпевает изменения, мы можем быть уверены, что наша модель сможет естественным образом отразить эту эволюцию. Не существует автоматической эволюции; для её отражения потребуется усилие от учёного по цепям поставок. Однако можно ожидать, что это усилие будет относительно минимальным. Всё сводится к тому, что если у вас есть очень маленькая, аккуратная модель, то когда придётся вернуться к ней позже для корректировки структуры, это будет относительно небольшая задача по сравнению со случаем, когда модель превращается в инженерного монстра.

При тщательной инженерной проработке модели, созданные с помощью дифференцируемого программирования, оказываются очень стабильными. Стабильность зависит от выбора структуры. Стабильность не гарантирована для любой программы, оптимизируемой посредством дифференцируемого программирования; это то, что достигается, когда структура очень ясна и параметры обладают конкретным семантическим значением. Например, если у вас модель, в которой при каждом переобучении получаются совершенно разные веса для дней недели, значит, реальность в вашем бизнесе не меняется так быстро. Если запустить модель дважды, вы должны получить довольно стабильные значения для дней недели. Если это не так, значит, в вашем моделировании спроса что-то серьёзно не так. Таким образом, при мудром выборе структуры модели можно добиться невероятно стабильных числовых результатов. Делая это, мы избегаем ловушек, которые часто подстерегают сложные модели машинного обучения при попытке их использования в контексте цепей поставок. Действительно, с точки зрения цепей поставок числовые нестабильности смертоносны, поскольку эффекты нарастания встречаются повсюду. Если оценка спроса колеблется, это означает, что случайным образом вы можете инициировать заказ на покупку или производство просто напрасно. Как только заказ на производство запущен, вы не сможете на следующей неделе решить, что это была ошибка и что её не следовало делать. Вы застреете с принятым решением. Если оценщик будущего спроса постоянно колеблется, в итоге вы получите завышенное пополнение запасов и завышенные производственные заказы. Проблему можно решить, обеспечив стабильность, что является вопросом дизайна.

Одной из самых больших проблем при внедрении машинного обучения в производство является доверие. Когда вы работаете с миллионами евро или долларов, крайне важно понимать, что происходит в вашей числовой рецептуре. Ошибки в цепях поставок могут обернуться колоссальными затратами, и существует множество примеров бедствий, вызванных неправильным применением плохо понятных алгоритмов. Несмотря на огромный потенциал дифференцируемого программирования, создаваемые им модели оказываются невероятно простыми. Эти модели на самом деле могли бы работать в Excel таблице, поскольку они, как правило, представляют собой простые мультипликативные модели с ветвлениями и функциями. Единственный аспект, который не мог работать в таблице Excel, — это автоматическое дифференцирование, и, очевидно, если у вас миллионы SKU, не пытайтесь реализовать это в Excel. Однако по части простоты они вполне совместимы с тем, что можно разместить в таблице. Эта простота играет огромную роль в установлении доверия и внедрении машинного обучения в производство, вместо того чтобы оставлять их всего лишь в виде эффектных прототипов, которым люди никогда не могут полностью доверять.

Наконец, объединяя все эти свойства, мы получаем высокоточное технологическое решение. Этот аспект был обсуждён ещё в первой главе этой серии лекций. Мы хотим превратить все усилия, вложенные в цепи поставок, в капиталистические инвестиции, а не рассматривать специалистов и практиков цепей поставок как расходный материал, которому приходится выполнять одни и те же задачи снова и снова. Такой подход позволяет рассматривать все эти усилия как инвестиции, которые будут генерировать и продолжать генерировать возврат инвестиций со временем. Дифференцируемое программирование отлично сочетается с таким капиталистическим взглядом на цепи поставок.

Во второй главе мы представили важную лекцию под названием “Экспериментальная оптимизация”, которая предложила один из возможных ответов на простой, но фундаментальный вопрос: что значит действительно улучшать или добиваться большего в цепи поставок? Перспектива дифференцируемого программирования даёт очень конкретное понимание многих проблем, с которыми сталкиваются специалисты по цепям поставок. Корпоративные поставщики программного обеспечения часто обвиняют плохие данные в провалах своих цепей поставок. Однако я считаю, что это неверный взгляд на проблему. Данные есть такие, какие они есть. Ваш ERP никогда не был создан для науки о данных, но он работает без сбоев годами, если не десятилетиями, и люди в компании тем не менее управляют цепочкой поставок. Даже если ваш ERP, собирающий данные о цепочке поставок, не идеален, это нормально. Если вы ожидаете, что у вас будут идеальные данные, это всего лишь мечты. Мы говорим о цепях поставок; мир очень сложен, поэтому системы несовершенны. На самом деле у вас нет одной бизнес-системы; их около полдюжины, и они не всегда полностью согласованы друг с другом. Это просто факт жизни. Однако когда корпоративные поставщики винят плохие данные, на самом деле используется очень конкретная модель прогнозирования, разработанная с набором предположений о компании. Проблема в том, что если ваша компания случайно нарушает любое из этих предположений, технология полностью рушится. В такой ситуации у вас есть модель прогнозирования с неразумными предположениями, вы подаёте данные, они неидеальны, и, следовательно, технология даёт сбой. Абсолютно неразумно утверждать, что вина лежит на компании. Виноватая технология — та, которую навязывает поставщик, делающий совершенно нереалистичные предположения о том, какими вообще могут быть данные в контексте цепей поставок.

Я сегодня не представлял никаких эталонных показателей для какой-либо метрики точности. Однако моя позиция заключается в том, что эти метрики точности в основном не имеют большого значения. Прогностическая модель — это инструмент для принятия решений. Важно то, хороши или плохи эти решения — что покупать, что производить, повышать или понижать цены. Плохие решения, безусловно, могут быть связаны с прогностической моделью. Однако чаще всего проблема не в точности. Например, у нас была модель прогнозирования продаж, и мы исправили проблему отсутствия запасов, которая не управлялась должным образом. Но, исправив проблему с отсутствием запасов, мы по сути исправили саму метрику точности. Таким образом, исправление прогностической модели не означает улучшение точности; зачастую это буквально пересмотр самой проблемы и точки зрения, в которой вы работаете, а затем модификация метрики точности или даже что-то более глубинное. Проблема классической точки зрения в том, что она подразумевает, что метрика точности — достойная цель. Это не совсем так.

Цепи поставок функционируют в реальном мире, и здесь происходит множество неожиданных, а порой даже аномальных событий. Например, может случиться так, что из-за корабля Суэцкий канал окажется заблокирован; это абсолютно аномальное событие. В такой ситуации все модели прогнозирования сроков поставки, ориентированные на этот регион, сразу перестанут работать. Очевидно, что такое ранее не происходило, поэтому мы не можем провести ретроспективное тестирование. Однако даже если у нас будет такая исключительная ситуация с блокировкой Суэцкого канала, мы все равно сможем исправить модель, по крайней мере, если мы используем такой подход в виде “white-box”, который я предлагаю сегодня. Это исправление будет включать некую степень догадок, что приемлемо. Лучше быть примерно правым, чем абсолютно ошибочным. Например, если мы рассматриваем блокировку Суэцкого канала, можно просто сказать: “давайте добавим один месяц к сроку поставки для всех запасов, которые должны были пройти по этому маршруту”. Это очень приближенно, но лучше предположить, что задержки не будет вовсе, даже если у вас уже есть информация. Кроме того, изменения часто происходят изнутри. Например, рассмотрим розничную сеть с одним старым распределительным центром и новым распределительным центром, обслуживающим несколько десятков магазинов. Предположим, что происходит миграция, при которой запасы для магазинов постепенно переносятся из старого центра в новый. Такая ситуация случается почти единожды в истории данного ритейлера, и её нельзя полноценно подвергнуть ретроспективному тестированию. Однако с подходом дифференцируемого программирования совершенно просто реализовать модель, которая подойдет для такой постепенной миграции.

В заключение, дифференцируемое программирование — это технология, которая предоставляет нам способ структурировать наши представления о будущем. Дифференцируемое программирование позволяет буквально формировать то, как мы смотрим на будущее. Оно относится к стороне восприятия в этой картине. Исходя из этого восприятия, мы можем принимать лучшие решения для цепей поставок, а эти решения определяют действия на другой стороне. Одно из самых больших заблуждений мейнстримного подхода к цепям поставок состоит в том, что восприятие и действие можно рассматривать как строго изолированные компоненты. Это проявляется, например, в наличии одной команды, отвечающей за планирование (то есть за восприятие), и одной независимой команды, отвечающей за пополнение запасов (то есть за действие).

Однако цикл обратной связи между восприятием и действием чрезвычайно важен; он имеет первостепенное значение. Это буквально тот механизм, который ведёт вас к корректному восприятию. Если у вас нет этого цикла обратной связи, то неясно, смотрите ли вы на то, что действительно важно, или же на то, что не соответствует вашим ожиданиям. Вам необходим этот механизм, и именно через него вы можете направить свои модели к правильной количественной оценке будущего, релевантной для дальнейших действий в цепи поставок. Мейнстримные подходы к цепям поставок практически полностью игнорируют этот аспект, поскольку, по сути, я считаю, что они застряли на очень жесткой форме прогнозирования. Эта модель-центричная форма прогнозирования может быть как старой, например, модель Хольта-Винтерса, так и современной, например, Facebook Prophet. Суть остаётся той же: если вы застряли на одной модели прогнозирования, то вся обратная связь, которую вы можете получить со стороны действия, оказывается ни к чему, поскольку вы не можете ничего с ней сделать, кроме как полностью игнорировать.

Если вы застряли на конкретной модели прогнозирования, вы не сможете переработать или перестроить свою модель по мере поступления информации со стороны действий. С другой стороны, дифференцируемое программирование с его структурированным подходом к моделированию предлагает совершенно другую парадигму. Прогностическая модель становится полностью расходным ресурсом — всей. Если обратная связь, полученная от действий, требует радикальных изменений в вашей прогностической перспективе, просто внедрите эти радикальные изменения. Нет никакой привязанности к конкретной итерации модели. Сохранение простоты модели существенно помогает сохранить возможность её изменения после выхода в производство. Ведь, если то, что вы создали, превратится в зверя, инженерного монстра, то после внедрения изменить его будет невероятно сложно. Один из ключевых аспектов заключается в том, что если вы хотите постоянно вносить изменения, вам нужна модель, которая будет максимально проста в плане количества строк кода и внутренней сложности. Именно здесь дифференцируемое программирование проявляет себя наилучшим образом. Дело не в достижении большей точности, а в достижении большей релевантности. Без релевантности все метрики точности теряют смысл. Дифференцируемое программирование и структурированное моделирование дают вам путь к достижению релевантности и ее поддержанию со временем.

На этом сегодняшняя лекция завершится. В следующий раз, второго марта, в то же время, в 15:00 по парижскому времени, я представлю вероятностное моделирование для цепей поставок. Мы подробнее рассмотрим технические аспекты анализа всех возможных будущих сценариев вместо того, чтобы выбирать один единственный сценарий и объявлять его правильным. Действительно, учет всех возможных будущих вариантов очень важен, если вы хотите, чтобы ваша цепь поставок была эффективно устойчива к рискам. Если вы выбираете лишь один вариант будущего, это рецепт для получения чего-то невероятно хрупкого, если ваш прогноз окажется не совершенно точным. И знаете, прогноз никогда не бывает полностью корректным. Именно поэтому так важно принять идею о необходимости рассматривать все возможные будущие сценарии, и мы рассмотрим, как сделать это с помощью современных числовых методов.

Вопрос: Стохастический шум добавляется для избежания локальных минимумов, но как он используется или масштабируется, чтобы избежать больших отклонений и чтобы градиентный спуск не ушёл далеко от своей цели?

Это очень интересный вопрос, и ответ на него состоит из двух частей.

Во-первых, именно поэтому алгоритм Adam является очень консервативным в отношении величины изменений. Градиент по своей природе неограничен; он может достигать значений в тысячи или миллионы. Однако в Adam максимальный шаг фактически ограничен величиной шага обучения. Таким образом, Adam использует числовой рецепт, который буквально обеспечивает максимально допустимый шаг, и, надеюсь, это предотвращает значительную числовую нестабильность.

Теперь, если случайным образом, несмотря на то, что у нас есть эта скорость обучения, можно сказать, что лишь из-за чистой случайности мы будем двигаться итеративно, шаг за шагом, но часто в неверном направлении — это возможно. Вот почему я говорю, что стохастический градиентный спуск до конца не понят. Он работает невероятно хорошо на практике, но почему он работает так хорошо, почему он сходится так быстро и почему мы не сталкиваемся с большим числом потенциальных проблем — до конца не ясно, особенно если учесть, что стохастический градиентный спуск происходит в высоких измерениях. Обычно задействовано буквально десятки, если не сотни параметров на каждом шаге. Интуиция, которую можно построить в двух или трёх измерениях, сильно вводит в заблуждение; поведение вещей существенно меняется в более высоких измерениях.

Таким образом, суть вопроса: он весьма актуален. С одной стороны, существует магия Адама, проявляющаяся в крайне осторожном подходе к масштабам ваших градиентных шагов, а с другой — аспект, который плохо понимается, но на практике работает очень хорошо. Кстати, я считаю, что тот факт, что стохастический градиентный спуск не является полностью интуитивным, также объясняет, почему на протяжении почти 70 лет эта техника была известна, но не признавалась эффективной. На протяжении почти 70 лет люди знали о её существовании, но были чрезвычайно скептичны. Лишь благодаря огромному успеху глубокого обучения сообщество признало и подтвердило, что она действительно работает очень хорошо, даже если мы не до конца понимаем почему.

Вопрос: Как понять, когда определённый шаблон является слабым и его следует удалить из модели?

Опять же, очень хороший вопрос. Нет строгих критериев; это буквально зависит от суждения специалиста по цепочкам поставок. Дело в том, что если внедряемый вами шаблон приносит минимальную пользу, и в плане моделирования это занимает всего две строки кода, а влияние на время вычислений незначительно, и если вы когда-либо решите удалить этот шаблон позже, что будет относительно просто, можно сказать: “Ну, я могу просто оставить его. Кажется, он не причиняет вреда и не приносит особой пользы. Я могу представить ситуации, когда этот сейчас слабый шаблон может стать сильным.” С точки зрения поддержки это приемлемо.

Однако можно рассмотреть и другую сторону медали, когда шаблон почти ничего не охватывает, но значительно увеличивает вычислительную нагрузку модели. Ничего не даётся бесплатно; каждый раз, когда вы добавляете параметр или логику, вы увеличиваете объём вычислительных ресурсов, необходимых для работы модели, делая её медленнее и менее управляемой. Если вы считаете, что этот слабый шаблон может стать сильным, но в негативном смысле, приводя к нестабильности и создавая хаос в прогнозном моделировании, обычно возникает мысль: “Нет, вероятно, его стоит удалить.”

Видите ли, всё зависит от вашего суждения. Дифференцируемое программирование — это культура; вы не одиноки. У вас есть коллеги и единомышленники, которые, возможно, пробовали разные подходы в Lokad. Именно такую культуру мы стремимся развивать. Я понимаю, что это может несколько разочаровать по сравнению с всесильной перспективой искусственного интеллекта, идеей о том, что у нас может быть искусственный интеллект, способный решить все эти проблемы за нас. Но реальность такова, что цепочки поставок настолько сложны, а наши методы ИИ настолько примитивны, что нам не найти реальной замены человеческому интеллекту. Когда я говорю “суждение”, я имею в виду, что к делу требуется здоровая доза прикладного, по-настоящему человеческого интеллекта, поскольку все алгоритмические трюки даже близко не подходят для получения удовлетворительного результата.

Тем не менее, это не означает, что вы не можете разработать какой-либо инструмент. Это уже другая тема; посмотрим, охватываю ли я на самом деле инструмент, который мы предоставляем в Lokad для облегчения проектирования. Если приходится принимать решение по суждению, давайте постараемся обеспечить всю необходимую инструментальную поддержку, чтобы это решение можно было принять быстро, сводя к минимуму проблемы, связанные с нерешительностью, когда специалист по цепочкам поставок должен определить дальнейшую судьбу текущей модели.

Вопрос: Каков порог сложности цепочки поставок, после которого машинное обучение и дифференцируемое программирование дают существенно лучшие результаты?

В Lokad нам, как правило, удаётся добиться значительных результатов для компаний с годовым оборотом от 10 миллионов долларов и выше. Я бы сказал, что настоящий эффект начинается, если у вас компания с годовым оборотом от 50 миллионов долларов и более.

Причина в том, что в первую очередь необходимо создать очень надёжный поток данных. Нужно уметь извлекать все релевантные данные из ERP-системы ежедневно. Я не имею в виду, что данные будут хорошими или плохими; просто данные, которые есть, могут иметь множество дефектов. Тем не менее, это означает, что требуется достаточно много инфраструктурной работы только для того, чтобы ежедневно извлекать базовые транзакции. Если компания слишком мала, то обычно у неё даже нет специализированного IT-отдела, и она не может обеспечить надёжное ежедневное извлечение, что серьезно сказывается на результатах.

Что касается отраслей или сложности, то, по моему мнению, в большинстве компаний и цепочек поставок оптимизация даже не началась. Как я уже говорил, общепринятая теория цепочек поставок подчеркивает, что необходимо добиваться более точных прогнозов. Сокращение процента ошибок прогнозирования является целью, и многие компании, например, пытаются этого добиться, создавая команду по планированию или прогнозированию. Однако, по моему мнению, всё это не добавляет ценности бизнесу, поскольку по сути предоставляют очень изощрённые ответы на неправильно поставленные вопросы.

Может показаться удивительным, но дифференцируемое программирование выделяется не тем, что по сути является супер мощным — оно таковым и является — а тем, что обычно это первый случай, когда в компании внедряется что-то по-настоящему значимое для бизнеса. Если привести пример, то большинство решений, реализованных в цепочках поставок, — это, как правило, модели типа резервного запаса, которые абсолютно не имеют отношения к реальным цепочкам поставок. Например, в модели резервного запаса предполагается, что возможна отрицательная продолжительность выполнения заказа, то есть вы заказываете сейчас, а получаете товар вчера. Это не имеет смысла, и вследствие этого операционные результаты по резервным запасам обычно неудовлетворительны.

Дифференцируемое программирование выделяется за счёт достижения релевантности, а не благодаря какой-то грандиозной числовой превосходности или лучшему качеству по сравнению с другими методами машинного обучения. Суть заключается в достижении релевантности в мире, который чрезвычайно сложен, хаотичен, враждебен, постоянно меняется и где приходится иметь дело с полукошмарным ландшафтом приложений, отражающих данные, которые нужно обработать.

Кажется, вопросов больше нет. В этом случае, думаю, увидимся в следующем месяце на лекции по вероятностному моделированию для цепочек поставок.