00:00 Введение
02:55 Проблема сроков поставки
09:25 Сроки поставки в реальности (1/3)
12:13 Сроки поставки в реальности (2/3)
13:44 Сроки поставки в реальности (3/3)
16:12 Что уже было
19:31 Ожидаемое время: через 1 час
22:16 CPRS (резюме) (1/2)
23:44 CPRS (резюме) (2/2)
24:52 Кросс-валидация (1/2)
27:00 Кросс-валидация (2/2)
27:40 Сглаживание сроков поставки (1/2)
31:29 Сглаживание сроков поставки (2/2)
40:51 Составление сроков поставки (1/2)
44:19 Составление сроков поставки (2/2)
47:52 Квази-сезонный срок поставки
54:45 Лог-логистическая модель сроков поставки (1/4)
57:03 Лог-логистическая модель сроков поставки (2/4)
01:00:08 Лог-логистическая модель сроков поставки (3/4)
01:03:22 Лог-логистическая модель сроков поставки (4/4)
01:05:12 Неполная модель сроков поставки (1/4)
01:08:04 Неполная модель сроков поставки (2/4)
01:09:30 Неполная модель сроков поставки (3/4)
01:11:38 Неполная модель сроков поставки (4/4)
01:14:33 Спрос в течение срока поставки (1/3)
01:17:35 Спрос в течение срока поставки (2/3)
01:24:49 Спрос в течение срока поставки (3/3)
01:28:27 Модульность прогностических методов
01:31:22 Заключение
01:32:52 Предстоящая лекция и вопросы аудитории
Описание
Сроки поставки являются фундаментальным аспектом большинства ситуаций в цепочке поставок. Сроки поставки могут и должны прогнозироваться так же, как спрос. Вероятностное прогнозирование моделей, предназначенных для сроков поставки, может быть использовано. Представлена серия методик для создания вероятностных прогнозов сроков поставки для нужд цепочки поставок. Составление этих прогнозов — сроков поставки и спроса — является краеугольным камнем прогнозного моделирования в цепочке поставок.
Полная расшифровка

Добро пожаловать в эту серию лекций по цепочке поставок. Я — Жоанн Верморель, и сегодня я представлю «Прогнозирование сроков поставки». Сроки поставки, а в более широком смысле – все сопутствующие задержки – являются фундаментальным аспектом цепочки поставок при попытке сбалансировать спрос и предложение. Необходимо учитывать все участвующие задержки. Например, рассмотрим спрос на игрушку. Правильное предвидение сезонного пикового спроса перед Рождеством не имеет значения, если товары поступают в январе. Сроки поставки определяют тонкости планирования не меньше, чем спрос.
Сроки поставки различаются; они сильно варьируются. Это факт, и я приведу некоторые доказательства через минуту. Однако на первый взгляд это утверждение кажется загадочным. Неясно, почему сроки поставки должны так сильно различаться. У нас есть производственные процессы, которые могут работать с точностью менее одного микрометра. Более того, в рамках производственного процесса мы можем контролировать такой эффект, как применение источника света, с точностью до одной микросекунды. Если мы можем контролировать преобразование материи с точностью до микрометра и микросекунды, при достаточной отдаче, мы должны быть в состоянии контролировать поток спроса с сопоставимой степенью точности. Или, может быть, нет.
Такой образ мышления может объяснить, почему сроки поставки кажутся такими недооценёнными в литературе по цепочке поставок. Книги по цепочке поставок и, следовательно, программное обеспечение для цепочки поставок едва упоминают существование сроков поставки, ограничиваясь введением их в качестве входного параметра для своей модели инвентаризации. Для этой лекции поставлены три цели:
Мы хотим понять значение и природу сроков поставки. Мы хотим разобраться, как можно прогнозировать сроки поставки, с особым акцентом на вероятностные модели, позволяющие учитывать неопределённость. Мы хотим объединить прогнозы сроков поставки и прогнозы спроса таким образом, чтобы это было полезно для нужд цепочки поставок.

Согласно основной литературе по цепочке поставок, сроки поставки едва заслуживают пары сносок. Это утверждение может показаться чрезмерным преувеличением, но, боюсь, это не так. Согласно Google Scholar — специализированному поисковику научной литературы — запрос “demand forecasting” за 2021 год возвращает 10 500 работ. При беглом просмотре результатов видно, что действительно подавляющее большинство этих записей обсуждают прогнозирование спроса во всевозможных ситуациях и на различных рынках. Тот же запрос, также за 2021 год, в Google Scholar по запросу “lead time forecasting” возвращает 71 результат. Результаты по запросу прогнозирования сроков поставки так ограничены, что для обзора исследований за целый год требуется всего несколько минут.
Оказывается, существует всего около дюжины публикаций, которые действительно посвящены прогнозированию сроков поставки. Действительно, большинство совпадений находится в выражениях типа “прогноз длинных сроков поставки” или “прогноз коротких сроков поставки”, которые относятся к прогнозированию спроса, а не сроков поставки. Этот эксперимент можно повторить с запросами “demand prediction” и “lead time prediction” и другими аналогичными выражениями за другие годы. Такие вариации дают похожие результаты. Оставлю это в качестве упражнения для аудитории.
Таким образом, если прикинуть, мы имеем примерно в тысячу раз больше публикаций о прогнозировании спроса, чем о прогнозировании сроков поставки. Книги по цепочке поставок и программное обеспечение для цепочки поставок следуют этой тенденции, оставляя сроки поставки в статусе второго плана и как незначительную техническую деталь. Однако специалисты по цепочке поставок, о которых говорилось в этой серии лекций, рассказывают другую историю. Эти специалисты могут представлять вымышленные компании, но они отражают архетипы в цепочке поставок. Они рассказывают нам о типичных ситуациях, которые следует считать стандартными. Посмотрим, что они говорят о сроках поставки.
Paris — вымышленный модный бренд, управляющий собственной сетью розничной торговли. Paris заказывает у зарубежных поставщиков, причем сроки поставки длительные и иногда превышают шесть месяцев. Эти сроки поставки известны лишь частично, и тем не менее новая коллекция должна поступить в магазин в нужное время, определённое маркетинговой кампанией, связанной с новой коллекцией. Сроки поставки поставщиков требуют надлежащего прогнозирования; другими словами, они требуют прогноза.
Amsterdam — вымышленная компания FMCG, специализирующаяся на производстве сыров, сливок и масла. Процесс созревания сыра известен и контролируется, но варьируется с отклонениями на несколько дней. Однако несколько дней — именно та продолжительность интенсивных акций, запускаемых розничными сетями, которые являются основным каналом продаж Amsterdam. Эти производственные сроки поставки требуют прогноза.
Miami — вымышленный авиационный центр MRO. MRO расшифровывается как техническое обслуживание, ремонт и капитальный ремонт. Каждый авиалайнер нуждается в тысячах запчастей ежегодно, чтобы оставаться в воздухе. Одна отсутствующая деталь может привести к приземлению самолёта. Время ремонта ремонтоспособной детали, также известное как TAT (turnaround time — время оборота), определяет, когда подвижная деталь снова становится готовой к эксплуатации. Однако TAT варьируется от нескольких дней до месяцев, в зависимости от объёма ремонта, который неизвестен на момент снятия детали с самолёта. Эти TAT требуют прогноза.
San Jose — вымышленная компания электронной коммерции, распространяющая разнообразные товары для дома и аксессуары. В рамках своего сервиса San Jose предоставляет обязательство по дате доставки для каждой сделки. Однако сама доставка зависит от сторонних компаний, которые совершенно ненадёжны. Таким образом, San Jose требуется обоснованная оценка даты доставки, которую можно обещать для каждой сделки. Эта обоснованная оценка по сути является прогнозом сроков поставки.
Наконец, Stuttgart — вымышленная компания автомобильного послепродажного обслуживания. Она управляет филиалами, предоставляющими услуги по ремонту автомобилей. Самая низкая закупочная цена на автозапчасти может быть получена от оптовых продавцов, которые предлагают длительные и несколько нерегулярные сроки поставки. Существует также более надёжные поставщики, которые дороже и расположены ближе. Выбор подходящего поставщика для каждой детали требует надлежащего сравнительного анализа соответствующих сроков поставки, предлагаемых различными поставщиками.
Как видим, каждый специалист по цепочке поставок, представленный до сих пор, требует прогнозирования как минимум одного, а зачастую и нескольких сроков поставки. Хотя можно утверждать, что прогнозирование спроса требует больше внимания и усилий, чем прогнозирование сроков поставки, в конечном итоге для почти всех ситуаций в цепочке поставок необходимы оба.
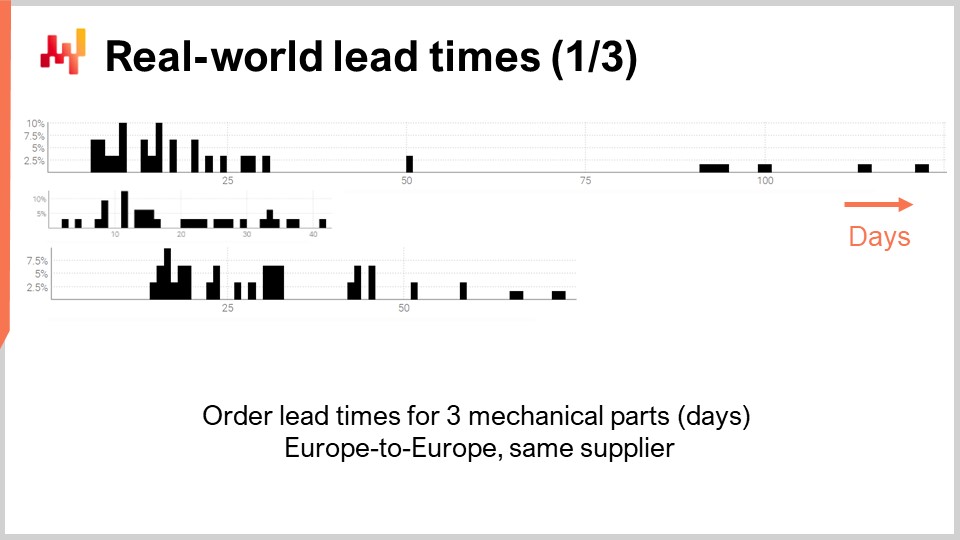
Итак, давайте взглянем на несколько реальных сроков поставки. На экране представлены три гистограммы, построенные на основе наблюдаемых сроков поставки для трёх механических деталей. Эти детали заказываются у одного и того же поставщика, расположенного в Западной Европе. Заказы поступают от компании, также находящейся в Западной Европе. По оси x указана продолжительность наблюдаемых сроков поставки, выраженная в днях, а по оси y — количество наблюдений, выраженное в процентах. В дальнейшем все гистограммы будут придерживаться тех же обозначений: ось x будет соответствовать продолжительностям, выраженным в днях, а ось y — частоте. Из этих трёх распределений мы уже можем сделать несколько наблюдений.
Во-первых, данные скудны. У нас всего несколько десятков наблюдений, собранных за несколько лет. Такая ситуация типична: если компания заказывает всего раз в месяц, для накопления более 100 наблюдений по срокам поставки требуется почти десятилетие. Таким образом, что бы мы ни делали в статистике, это должно быть рассчитано на малые выборки, а не на большие. Действительно, нам редко предоставляется роскошь работать с большим количеством данных.
Во-вторых, сроки поставки нестабильны. У нас есть наблюдения, варьирующиеся от нескольких дней до квартала. Хотя всегда можно вычислить средний срок поставки, опираться на какое-либо среднее значение для любой из этих деталей было бы неразумно. Также очевидно, что ни одно из этих распределений даже отдалённо не является нормальным.
В-третьих, у нас есть три детали, которые по размеру и цене примерно сопоставимы, и, тем не менее, сроки поставки сильно различаются. Хотя может возникнуть соблазн объединить эти наблюдения, чтобы сделать данные менее скудными, это, очевидно, неразумно, так как это было бы смешением распределений, которые сильно различаются. У этих распределений нет одного и того же среднего, медианы или даже одинаковых минимальных и максимальных значений.
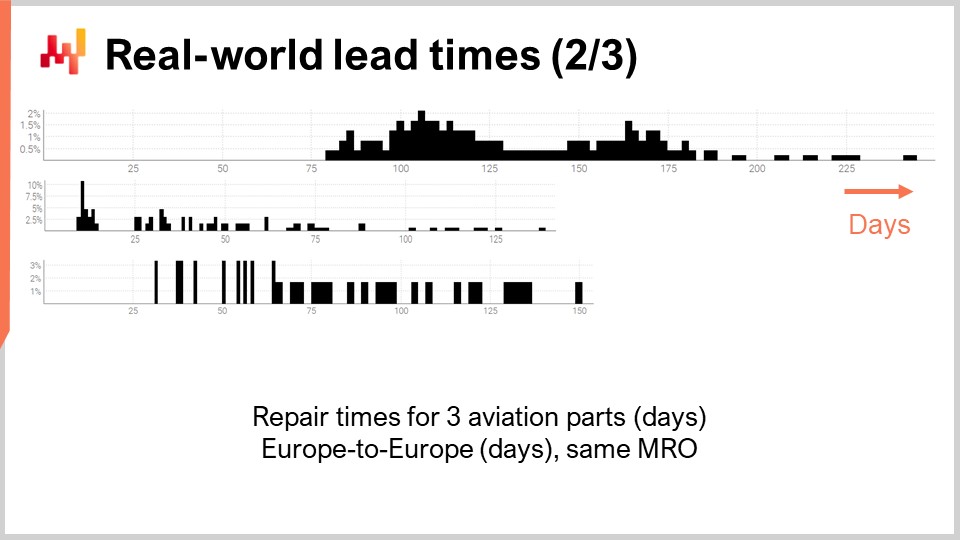
Давайте рассмотрим вторую группу сроков поставки. Эти продолжительности отражают время, необходимое для ремонта трёх различных авиационных деталей. Первое распределение, похоже, имеет два модальных значения и хвост. Когда распределение имеет два мод, это обычно намекает на существование скрытой переменной, которая объясняет эти два модальных значения. Например, может существовать два различных типа ремонтных операций, каждое из которых связано со своим сроком поставки. Второе распределение, по-видимому, имеет один мод и хвост. Этот мод соответствует относительно короткой продолжительности — примерно двум неделям. Возможно, это отражает процесс, при котором деталь сначала проверяется, и иногда деталь оказывается годной к эксплуатации без дополнительного вмешательства, следовательно, со значительно более коротким сроком поставки. Третье распределение кажется полностью растянутым, без явного модального значения или хвоста. Возможно, здесь задействовано несколько ремонтных процессов, которые сгруппированы вместе. Скудность данных — всего три десятка наблюдений — затрудняет более подробный анализ. Мы вернёмся к этому третьему распределению позже в лекции.
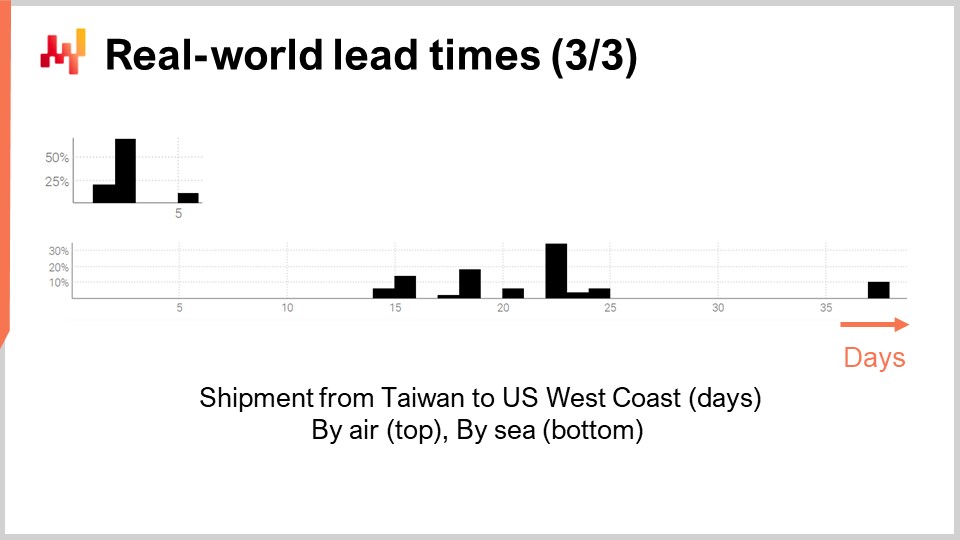
Наконец, давайте рассмотрим два срока поставки, отражающих задержки при доставке из Тайваня на западное побережье США, осуществляемые либо воздушным, либо морским транспортом. Неудивительно, что грузовые самолёты быстрее грузовых судов. Второе распределение, похоже, намекает на то, что иногда морская перевозка может пропустить свой первоначальный корабль и затем быть отправлена следующим судном, что почти удваивает задержку. Тот же феномен может наблюдаться и при воздушных перевозках, хотя данных настолько мало, что это всего лишь дикая гипотеза. Стоит отметить, что получение всего лишь пары наблюдений — не редкость в случае сроков поставки. Такие ситуации часты. Важно помнить, что в этой лекции мы ищем инструменты и методы, позволяющие работать с имеющимися данными по срокам поставки, даже если это всего лишь несколько наблюдений, а не те данные по срокам поставки, которые мы хотели бы иметь, как тысячи наблюдений. Короткие промежутки в обоих распределениях также указывают на существование циклического паттерна по дням недели, хотя используемая сейчас визуализация гистограммы не подходит для проверки этой гипотезы.
Из этого краткого обзора реальных сроков поставки мы уже можем уловить некоторые из лежащих в основе явлений. Действительно, сроки поставки имеют высокую структурированность; задержки не происходят без причины, и эти причины могут быть идентифицированы, разложены и количественно оценены. Однако детали декомпозиции сроков поставки часто не фиксируются в ИТ-системах, по крайней мере пока что. Даже когда имеется обширная декомпозиция наблюдаемого срока поставки, как это может быть в таких отраслях, как авиация, это не означает, что сроки поставки можно предсказать идеально. Под-сегменты или фазы внутри срока поставки, вероятно, будут обладать своей собственной неизбежной неопределённостью.
Эта серия лекций по цепочке поставок представляет мои взгляды и соображения как по исследованию, так и по практике в области цепочки поставок. Я стараюсь, чтобы эти лекции были несколько независимыми, но они имеют больше смысла, когда их смотрят последовательно. Остальная часть этой лекции зависит от элементов, ранее представленных в этой серии, хотя я вскоре проведу краткое повторение.
Первая глава является общим введением в область и изучение цепочек поставок. Она разъясняет перспективу, на основе которой построена эта серия лекций. Как вы, возможно, уже поняли, эта перспектива существенно отличается от того, что принято считать мейнстримовой в цепочке поставок.
Вторая глава представляет серию методологий. Действительно, цепочки поставок опровергают наивные методологии. Цепочки поставок состоят из людей, у которых есть собственные интересы; нейтральной стороны в цепочке поставок не существует. Эта глава рассматривает эти сложности, включая мой собственный конфликт интересов в качестве генерального директора Lokad — компании, специализирующейся на программном обеспечении для прогностической оптимизации цепочек поставок.
Третья глава обзорно рассматривает ряд «персонажей» цепочки поставок. Эти персонажи — вымышленные компании, которые мы кратко рассмотрели сегодня, и они предназначены для представления архетипов ситуаций в цепочках поставок. Цель этих персонажей — сосредоточиться исключительно на проблемах, откладывая представление решений.
Четвертая глава рассматривает вспомогательные науки, связанные с цепочками поставок. Эти науки не касаются самой цепочки поставок, но их следует считать необходимыми для современной практики работы с цепочками поставок. Эта глава включает последовательное рассмотрение уровней абстракции — от вычислительного оборудования до вопросов кибербезопасности.
Пятая, текущая глава посвящена прогнозированию с помощью моделирования. Прогностическое моделирование — более широкий подход, чем просто предсказание; речь идёт не только о прогнозировании спроса. Речь идёт о создании моделей, которые могут использоваться для оценки и количественной оценки будущих факторов интересующей цепочки поставок. Сегодня мы углубимся в изучение сроков выполнения, но, в более общем случае, в цепочках поставок всё, что не известно с достаточной степенью определённости, заслуживает прогноза.
Шестая глава объясняет, как можно вычислять оптимизированные решения с использованием прогностических моделей, а точнее, вероятностных моделей, представленных в пятой главе. Седьмая глава возвращается к в основном нетехническому подходу, чтобы обсудить реальное корпоративное воплощение инициативы по количественному управлению цепочками поставок.

Сегодня мы сосредотачиваемся на сроках выполнения. Мы только что увидели, почему сроки выполнения важны, и рассмотрели короткий ряд реальных примеров сроков выполнения. Таким образом, мы перейдём к элементам моделирования сроков выполнения. Поскольку я буду использовать вероятностную перспективу, я кратко повторю концепцию Непрерывного рейтингового вероятностного скоринга (CRPS) — метрики для оценки качества вероятностного прогноза. Я также представлю кросс-валидацию и её вариант, подходящий для нашей вероятностной перспективы. С этими инструментами мы представим и оценим нашу первую не наивную вероятностную модель для сроков выполнения. Данные о сроках выполнения разрежены, и первая задача в нашем плане — сгладить эти распределения. Сроки выполнения можно разбить на серию промежуточных фаз. Таким образом, при наличии некоторых разложенных данных о сроках выполнения нам необходимо нечто, что позволит воссоздать полное время выполнения, сохраняя вероятностный подход.
Затем мы повторно введём концепцию дифференцируемого программирования. Дифференцируемое программирование уже использовалось в этой серии лекций для прогнозирования спроса, но его можно применять и для предсказания сроков выполнения. Мы проделаем это, начиная с простого примера, предназначенного для демонстрации влияния Китайского Нового года на сроки выполнения — типичного явления при импорте товаров из Азии.
Затем мы перейдём к параметрической вероятностной модели для сроков выполнения, используя лог-логистическое распределение. Опять же, дифференцируемое программирование станет ключевым инструментом для определения параметров модели. После этого мы расширим модель, учитывая неполные наблюдения сроков выполнения. Действительно, даже заказы, которые ещё не завершены, предоставляют некоторую информацию о сроках выполнения.
Наконец, мы объединяем вероятностный прогноз сроков выполнения и вероятностный прогноз спроса в единой ситуации пополнения запасов. Это будет возможностью продемонстрировать, почему модульность является важнейшим аспектом в прогностическом моделировании, еще более важным, чем мельчайшие детали самих моделей.

В лекции 5.2 по вероятностному прогнозированию мы уже представили некоторые инструменты для оценки качества вероятностного прогноза. Действительно, обычные метрики точности, такие как среднеквадратичная ошибка или средняя абсолютная ошибка, применимы только к точечным прогнозам, а не к вероятностным. Однако тот факт, что наши прогнозы стали вероятностными, не делает измерение точности в целом неактуальным. Нам просто нужен статистический инструмент, который оказался бы совместим с вероятностной перспективой.
Среди этих инструментов есть Непрерывный рейтинговый вероятностный скор (CRPS). Формула приведена на экране. CRPS представляет собой обобщение L1-метрики, то есть абсолютной ошибки, но для распределений вероятностей. Обычный вариант CRPS сравнивает распределение, обозначенное здесь как F, с наблюдением, обозначенным как X. Значение, полученное с помощью функции CRPS, имеет ту же размерность, что и наблюдение. Например, если X представляет собой время выполнения, выраженное в днях, то значение CRPS также выражается в днях.

CRPS можно обобщить для сравнения двух распределений. Именно это демонстрируется на экране. Это лишь незначительное изменение предыдущей формулы. Суть этой метрики остаётся неизменной. Если F — истинное распределение сроков выполнения, а F_hat — оценка распределения сроков выполнения, то CRPS выражается в днях. CRPS отражает степень различия между двумя распределениями. Его также можно интерпретировать как минимальное количество энергии, необходимое для транспортировки всей массы из первого распределения так, чтобы оно приняло точную форму второго распределения.
Теперь у нас есть инструмент для сравнения двух одномерных распределений вероятностей. Это станет актуальным через минуту, когда мы представим нашу первую вероятностную модель для сроков выполнения.
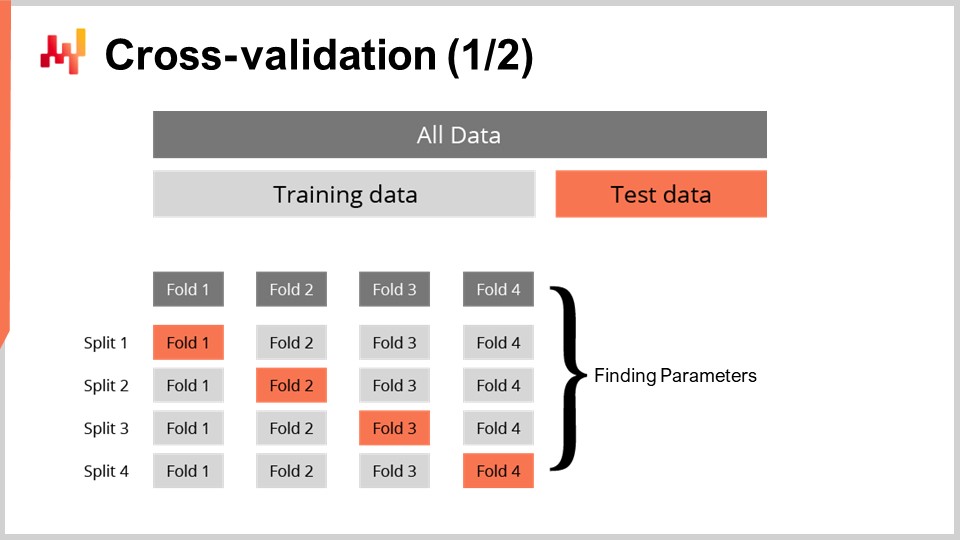
Наличие метрики для измерения качества вероятностного прогноза недостаточно. Метрика измеряет качество на имеющихся у нас данных; однако нас действительно интересует способность прогноза правильно работать на данных, которых у нас нет. Ведь нас интересуют будущие сроки выполнения, а не те, что уже наблюдались в прошлом. Наша способность создать модель, которая хорошо работает на неизвестных данных, называется обобщением. Кросс-валидация — это методика валидации модели, предназначенная именно для оценки способности модели к обобщению.
В своей самой простой форме кросс-валидация заключается в разбиении наблюдений на небольшое число подмножеств. На каждой итерации одно подмножество откладывается и называется тестовым. Модель затем создаётся или обучается на остальных подмножествах, называемых обучающими. После обучения модель проверяется на тестовом подмножестве. Этот процесс повторяется определённое количество раз, и среднее значение качества, полученное по всем итерациям, представляет финальный результат кросс-валидации.
Кросс-валидация редко используется в контексте прогнозирования временных рядов из-за зависимости наблюдений от времени. Действительно, предложенная кросс-валидация предполагает, что наблюдения независимы. Когда речь идёт о временных рядах, вместо этого используется ретроспективное тестирование. Ретроспективное тестирование можно рассматривать как форму кросс-валидации, учитывающую временную зависимость.
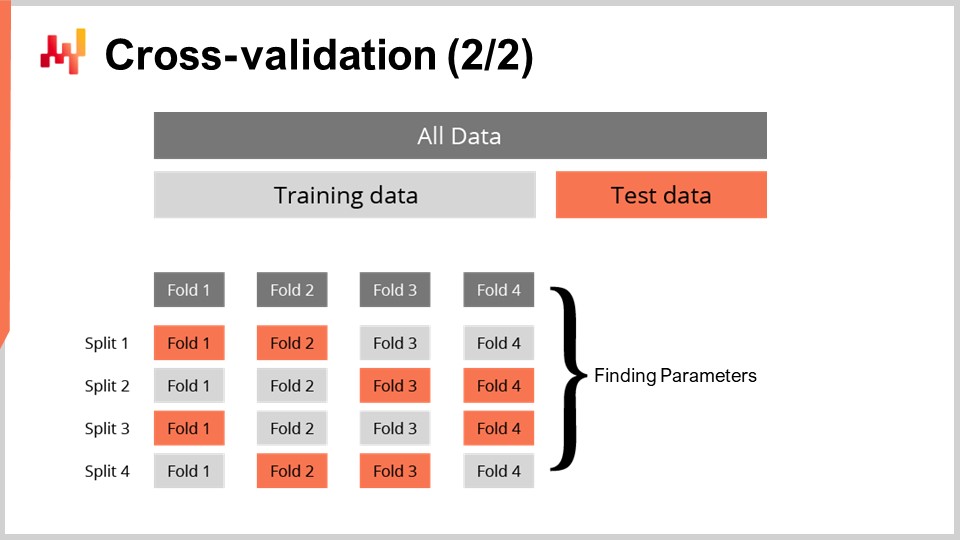
Методика кросс-валидации имеет множество вариантов, отражающих широкий спектр возможных аспектов, которые могут потребовать внимания. В рамках этой лекции мы не будем рассматривать все эти варианты. Я буду использовать конкретный вариант, при котором на каждом разбиении обучающее и тестовое подмножества имеют приблизительно равный размер. Этот вариант введён для валидации вероятностной модели, как мы увидим на примере кода через минуту.
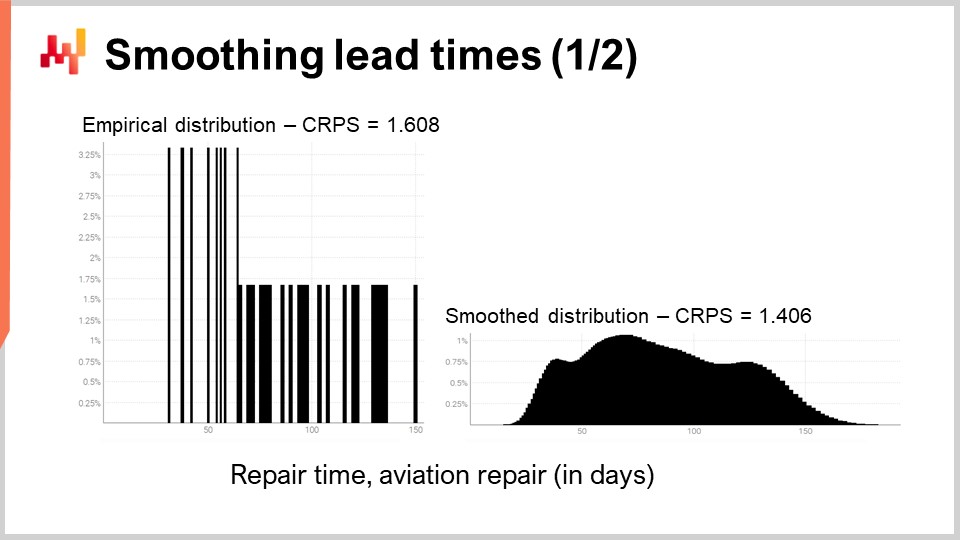
Давайте ещё раз рассмотрим один из реальных сроков выполнения, который мы уже видели на экране. Слева гистограмма относится к третьему распределению времени ремонта в авиации. Это те же наблюдения, что и ранее, просто гистограмма была растянута по вертикали. Таким образом, обе гистограммы, слева и справа, имеют одинаковую шкалу. Для левой гистограммы у нас примерно 30 наблюдений. Это немного, но уже больше, чем мы обычно получаем.
Гистограмма слева называется эмпирическим распределением. Это буквально необработанная гистограмма, полученная из наблюдений. Гистограмма имеет одно ведро для каждого значения длительности, выраженного целым числом дней. Для каждого ведра мы подсчитываем количество наблюдаемых сроков выполнения. Из-за разреженности эмпирическое распределение выглядит как штрих-код.
Здесь возникает проблема. Если у нас есть два наблюдаемых срока выполнения ровно в 50 дней, имеет ли смысл утверждать, что вероятность наблюдения 49 или 51 дня равна нулю? Нет. Очевидно, что существует спектр длительностей; нам просто может не хватать данных, чтобы увидеть истинное скрытое распределение, которое, скорее всего, намного сглаженнее этого штрих-кодоподобного распределения.
Таким образом, при сглаживании этого распределения существует бесконечное число способов выполнения операции сглаживания. Некоторые методы сглаживания могут выглядеть хорошо, но не быть статистически обоснованными. В качестве хорошей отправной точки мы хотели бы убедиться, что сглаженная модель является более точной чем эмпирическая. Оказывается, что мы уже представили два инструмента — CRPS и кросс-валидацию, — которые позволят нам добиться этого.
Через минуту результаты будут продемонстрированы. Ошибка CRPS для штрих-кодного распределения составляет 1.6 дня, в то время как ошибка CRPS для сглаженного распределения — 1.4 дня. Эти два значения были получены с помощью кросс-валидации. Более низкая ошибка указывает на то, что с точки зрения CRPS распределение справа является наиболее точным из двух. Разница в 0.2 между 1.4 и 1.6 не так велика, однако ключевой момент здесь в том, что у нас есть сглаженное распределение, которое не оставляет без внимания определённые промежуточные длительности с нулевой вероятностью. Это разумно, поскольку наше понимание ремонтных работ подсказывает, что эти длительности, скорее всего, наступят при повторении ремонтов. CRPS не отражает всей глубины улучшения, достигнутого благодаря сглаживанию распределения. Однако, по крайней мере, снижение CRPS подтверждает, что данное преобразование является статистически обоснованным.
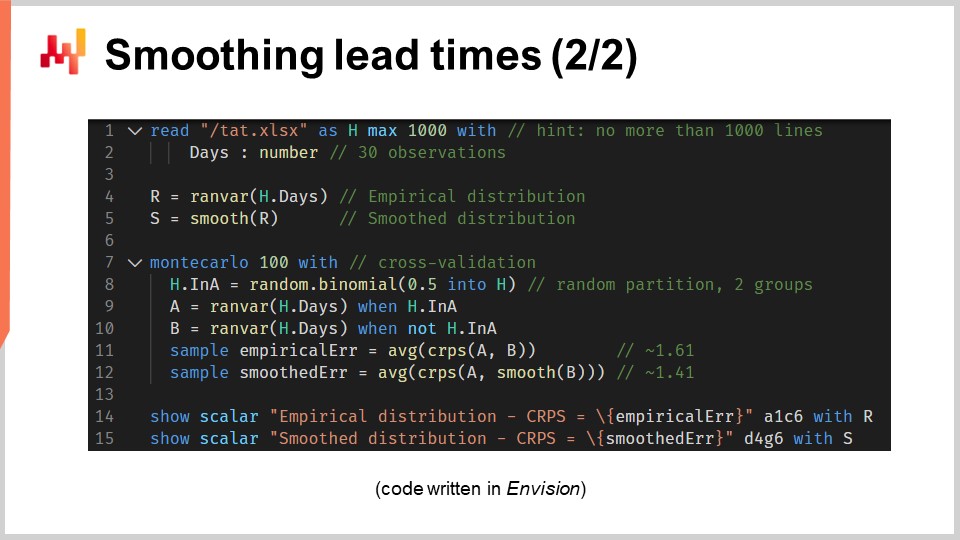
Теперь давайте рассмотрим исходный код, который создал эти две модели и вывел на экран обе гистограммы. В целом, это реализовано в 12 строках кода, если не считать пустые строки. Как обычно в этой серии лекций, код написан на Envision — доменно-специфическом языке программирования Lokad, предназначенном для прогностической оптимизации цепочек поставок. Однако здесь нет никакой магии; эту логику можно было бы реализовать на Python. Но для задач, рассматриваемых в этой лекции, Envision оказывается более лаконичным и самодостаточным.
Давайте рассмотрим эти 12 строк кода. В строках 1 и 2 мы считываем Excel таблицу, содержащую один столбец данных. Таблица содержит 30 наблюдений. Эти данные собраны в таблице с именем “H”, которая имеет единственный столбец под названием “days”. В строке 4 мы создаём эмпирическое распределение. Переменная “R” имеет тип данных “ranvar”, и с правой стороны присваивания функция “ranvar” является агрегатором, который принимает наблюдения на входе и возвращает гистограмму, представленную типом данных “ranvar”. Таким образом, тип данных “ranvar” предназначен для одномерных целочисленных распределений. Мы вводили тип данных “ranvar” в предыдущей лекции этой главы. Этот тип данных гарантирует постоянное использование памяти и постоянное время вычислений для каждой операции. Недостатком типа “ranvar” является то, что используется сжатие с потерями, хотя потеря данных, вызванная этим сжатием, была разработана так, чтобы быть незначительной для целей цепочек поставок.
В строке 5 мы сглаживаем распределение с помощью встроенной функции под названием “smooth”. Внутренне эта функция заменяет исходное распределение смесью распределений Пуассона. Каждое ведро гистограммы преобразуется в распределение Пуассона со средним, равным целочисленной позиции ведра, и, наконец, смесь назначает вес каждому распределению Пуассона, пропорциональный весу самого ведра. Другой способ понять, что делает функция “smooth”, заключается в том, что она эквивалентна замене каждого отдельного наблюдения на распределение Пуассона со средним, равным самому наблюдению. Все эти распределения Пуассона, по одному на наблюдение, затем смешиваются. Смешивание означает усреднение значений соответствующих ведер гистограммы. Переменные “R” и “S” типа “ranvar” не будут использоваться снова до строк 14 и 15, где они выводятся.
На строке 7 мы начинаем блок Монтекарло. Этот блок представляет собой своего рода цикл, который будет выполнен 100 раз, как указано 100 значений, следующих сразу после ключевого слова Монтекарло. Блок Монтекарло предназначен для сбора независимых наблюдений, генерируемых в соответствии с процессом, содержащим элемент случайности. Возможно, вам интересно, почему в Envision существует специальная конструкция Монтекарло, а не просто обычный цикл, как в большинстве распространенных языков программирования. Оказывается, наличие специализированной конструкции дает существенные преимущества. Во-первых, это гарантирует, что итерации действительно независимы, вплоть до семян, используемых для получения псевдослучайности. Во-вторых, это предоставляет явную цель для автоматизированного распределения нагрузки между несколькими ядрами ЦП или даже несколькими машинами.
На строке 8 мы создаем случайный вектор булевых значений в таблице “H”. С этой строкой мы создаем независимые случайные значения, называемые отклонениями (true или false), для каждой строки таблицы “H”. Как обычно в Envision, циклы абстрагированы через массивное программирование. С помощью этих булевых значений мы делим таблицу “H” на две группы. Это случайное разделение используется для процесса кросс-валидации.
На строках 9 и 10 мы создаем два “ranvar” с именами “A” и “B” соответственно. Мы снова используем агрегатор “ranvar”, но на этот раз применяем фильтр с ключевым словом “when” сразу после вызова агрегатора. “A” генерируется с использованием только тех строк, где значение в “a” истинно; для “B” все наоборот. “B” генерируется только для строк, где значение в “a” ложно.
На строках 11 и 12 мы собираем интересующие нас показатели из блока Монтекарло. В Envision ключевое слово “sample” может использоваться только внутри блока Монтекарло. Оно применяется для сбора наблюдений, полученных при многократном выполнении Монтекарло. На строке 11 мы вычисляем среднюю ошибку, выраженную в терминах CRPS, между двумя эмпирическими распределениями: подвыборкой из первоначального набора временных задержек. Ключевое слово “sample” указывает, что значения, собранные в ходе итераций Монтекарло, агрегируются с помощью агрегатора “AVG”, что означает “среднее”, и используется для получения единственной оценки в конце блока.
На строке 12 мы выполняем почти идентичное действие, что и на строке 11. Однако в этот раз мы применяем функцию “smooth” к “ranvar” “B”. Мы хотим оценить, насколько сглаженная версия отличается от наивного эмпирического распределения. Оказывается, что в терминах CRPS она ближе, чем оригинальное эмпирическое распределение.
На строках 14 и 15 мы выводим на экран гистограммы и значения CRPS. Эти строки генерируют графики, которые мы видели на предыдущем слайде. Этот скрипт дает нам эталонное значение качества эмпирического распределения нашей модели. Хотя эта модель, модель “barcode”, возможно, является наивной, она все же является моделью, причем вероятностной. Таким образом, этот скрипт также предоставляет нам более совершенную модель, по крайней мере, в смысле CRPS, через сглаженную версию исходного эмпирического распределения.
Сейчас, в зависимости от вашего знакомства с языками программирования, это может показаться сложным для усвоения. Однако я хотел бы отметить, насколько просто получить разумное распределение вероятностей, даже если у нас не так много наблюдений. Пока что у нас 12 строк кода, и только строки 4 и 5 представляют собой истинную модельную часть упражнения. Если бы нас интересовала только сглаженная версия, то “ranvar” “S” можно было бы написать одной строкой кода. Таким образом, это буквально однострочник: сначала применить агрегирование ranvar, а затем применить оператор сглаживания, и всё готово. Остальное — это просто инструментирование и отображение. С правильными инструментами вероятностное моделирование, будь то временные задержки или что-либо еще, может быть чрезвычайно прямолинейным. Здесь нет грандиозной математики, ни грандиозного алгоритма, ни сложного программного обеспечения. Всё просто и удивительно просто.

Как добиться того, чтобы поставка опоздала на шесть месяцев? Ответ очевиден: шаг за шагом, день за днем. Более серьезно, временные задержки обычно можно разложить на ряд задержек. Например, задержку поставки у поставщика можно разложить на задержку ожидания, когда заказ помещается в очередь, затем на производственную задержку при изготовлении товаров, и, наконец, на задержку при транспортировке товаров. Таким образом, если задержки можно разложить, интересно также уметь их собрать обратно.
Если бы мы жили в совершенно детерминированном мире, где будущее можно предсказать с точностью, то восстановление временных задержек свелось бы к простой сумме. Вернувшись к приведенному примеру, составление времени заказа было бы суммой задержки в очереди в днях, производственной задержки в днях и транспортной задержки в днях. Однако мы не живем в мире, где будущее предсказуемо. Эмпирические распределения временных задержек, представленные в начале этой лекции, подтверждают эту мысль. Задержки нестабильны, и маловероятно, что это кардинально изменится в ближайшие десятилетия.
Таким образом, будущие временные задержки следует рассматривать как случайные величины. Эти случайные величины охватывают и количественно определяют неопределенность, а не игнорируют её. Более конкретно, это означает, что каждый компонент временной задержки также должен быть моделирован как случайная величина. Вернувшись к нашему примеру, время заказа является случайной величиной и определяется как сумма трех случайных величин, соответствующих задержке в очереди, производственной задержке и транспортной задержке соответственно.
На экране представлена формула суммы двух независимых одномерных случайных величин, принимающих целочисленные значения. Эта формула просто указывает, что если общее время равно Z дням, и если для первой случайной величины X выделено K дней, то для второй случайной величины Y должно быть Z минус K дней. Этот тип суммирования в математике обычно называют сверткой.
Хотя кажется, что в этой свертке присутствует бесконечное число слагаемых, на практике нас интересует только конечное число слагаемых. Во-первых, все отрицательные продолжительности имеют вероятность ноль; ведь отрицательные задержки означали бы перемещение назад во времени. Во-вторых, для больших задержек вероятности становятся настолько малы, что для практических целей цепочки поставок их можно с уверенностью приближать нулями.
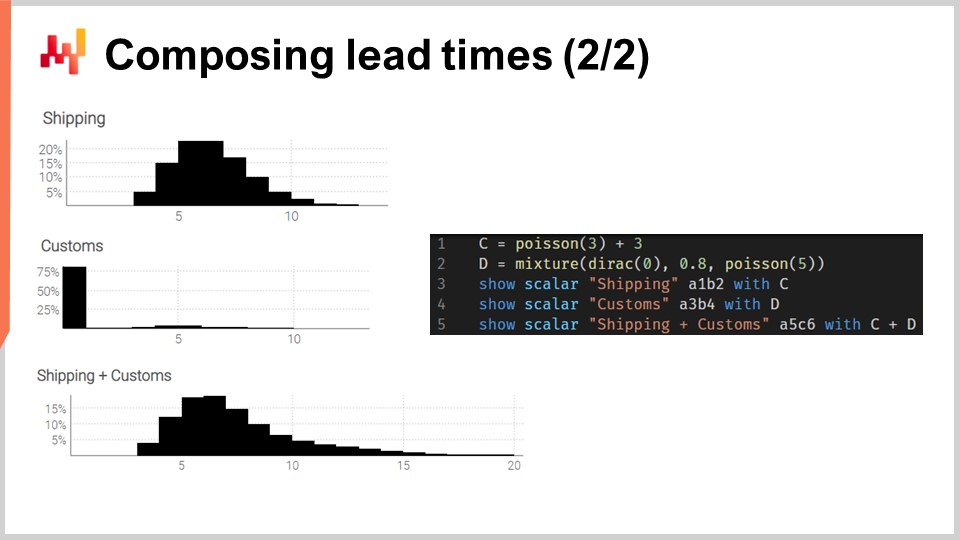
Давайте применим эти свертки на практике. Рассмотрим время транзита, которое можно разложить на две фазы: задержку при отправке и задержку на таможенной очистке. Мы хотим смоделировать эти две фазы с помощью двух независимых случайных величин, а затем восстановить время транзита, сложив эти две случайные величины.
На экране гистограммы слева созданы с помощью скрипта справа. На строке 1 задержка при отправке моделируется как свертка распределения Пуассона с константой. Функция Пуассона возвращает тип данных “ranvar”; прибавление трех приводит к сдвигу распределения вправо. Полученная “ranvar” присваивается переменной “C”. Эта “ranvar” отображается на строке 3 и видна слева как верхняя гистограмма. Мы распознаем форму распределения Пуассона, сдвинутую вправо на несколько единиц, в данном случае на три единицы. На строке 2 таможенная очистка моделируется как смесь дирака в нуле и распределения Пуассона с параметром пять. Дирак в нуле встречается в 80% случаев; именно это означает константа 0.8. Это отражает ситуации, когда товары большую часть времени даже не проходят проверку на таможне и проходят без значительной задержки. Альтернативно, в 20% случаев товары проверяются на таможне, и задержка моделируется как распределение Пуассона со средним значением пять. Полученная ranvar присваивается переменной с именем D. Эта ranvar отображается на строке 4 и видна слева как средняя гистограмма. Этот асимметричный аспект отражает то, что большинство раз таможня не добавляет задержки.
Наконец, на строке 5 мы вычисляем сумму C плюс D. Это сложение представляет собой свертку, поскольку и C, и D являются ranvar, а не числами. Это вторая свертка в данном скрипте, так как свертка уже происходила на строке 1. Полученная ranvar отображается и видна слева как третья и самая нижняя гистограмма. Эта третья гистограмма похожа на первую, за исключением того, что хвост распределения значительно дальше вытянут вправо. Снова мы видим, что с помощью нескольких строк кода можно смоделировать нетривиальные реальные эффекты, такие как задержки при таможенной очистке.
Однако в этом примере можно сделать две критики. Во-первых, не указано, откуда берутся константы; на практике мы хотим обучать эти константы на основе исторических данных. Во-вторых, хотя распределение Пуассона обладает преимуществом простоты, его форма может быть не самой реалистичной для моделирования временных задержек, особенно с учетом ситуации с «толстыми хвостами». Таким образом, мы последовательно рассмотрим эти два вопроса.
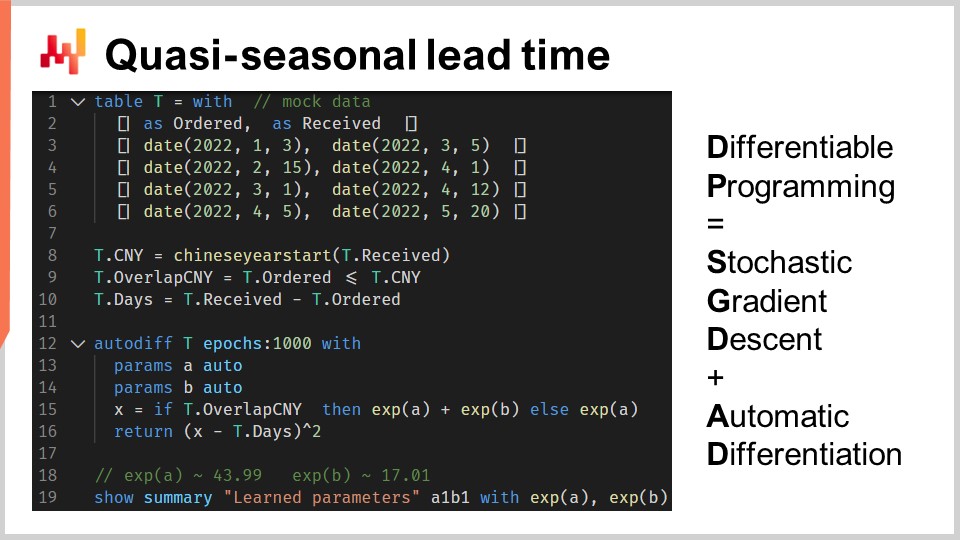
Чтобы выучить параметры на основе данных, мы вернемся к парадигме программирования, которую уже вводили в этой серии лекций, а именно дифференцируемому программированию. Если вы еще не смотрели предыдущие лекции этой главы, я приглашаю вас ознакомиться с ними после окончания текущей лекции. Дифференцируемое программирование рассматривается более подробно в тех лекциях.
Дифференцируемое программирование представляет собой комбинацию двух техник: стохастического градиентного спуска и автоматического дифференцирования. Стохастический градиентный спуск — это метод оптимизации, который пошагово корректирует параметры, основываясь на одной наблюдении за раз в направлении, противоположном градиентам. Автоматическое дифференцирование — это техника компиляции, аналогичная компилятору языка программирования, которая вычисляет градиенты для всех параметров, присутствующих в общей программе.
Давайте проиллюстрируем дифференцируемое программирование на примере проблемы временных задержек. Это послужит либо кратким повторением, либо введением, в зависимости от вашего знакомства с этой парадигмой. Мы хотим смоделировать влияние Китайского Нового Года на временные задержки, связанные с импортом из Китая. Действительно, поскольку фабрики закрываются на две или три недели из-за Китайского Нового Года, временные задержки увеличиваются. Китайский Новый Год имеет циклический характер; он происходит каждый год. Однако он не является строго сезонным, по крайней мере, не в соответствии с григорианским календарем.
На строках с одной по шесть мы вводим несколько фиктивных заказов с четырьмя наблюдениями, содержащими как дату заказа, так и дату получения. На практике эти данные не будут захардкожены, а будут загружаться из систем компании. На строках восемь и девять мы вычисляем, перекрывается ли время задержки с Китайским Новым Годом. Переменная “T.overlap_CNY” является булевым вектором; она указывает, затронуто ли наблюдение Китайским Новым Годом или нет.
На строке 12 мы вводим блок “autodiff”. Таблица T используется в качестве таблицы наблюдений, и установлено 1000 эпох. Это означает, что каждое наблюдение, то есть каждая строка в таблице T, будет обрабатываться тысячу раз. Один шаг стохастического градиентного спуска соответствует одному выполнению логики внутри блока “autodiff”.
На строках 13 и 14 объявляются два скалярных параметра. Блок “autodiff” будет обучать эти параметры. Параметр A отражает базовое время задержки без эффекта Китайского Нового Года, а параметр B отражает дополнительную задержку, связанную с Китайским Новым Годом. На строке 15 мы вычисляем X, прогноз времени задержки нашей модели. Это детерминированная модель, а не вероятностная; X — это точечный прогноз времени задержки. Правая часть присваивания проста: если наблюдение перекрывается с Китайским Новым Годом, то мы возвращаем сумму базового значения и компонента Нового Года; иначе возвращается только базовое значение. Поскольку блок “autodiff” обрабатывает по одному наблюдению за раз, на строке 15 переменная T.overlap_CNY представляет собой скалярное значение, а не вектор. Это значение соответствует одной строке, выбранной в качестве наблюдения в таблице T.
Параметры A и B оборачиваются в экспоненциальную функцию “exp”, что является небольшим трюком дифференцируемого программирования. Действительно, алгоритм стохастического градиентного спуска, управляющий процессом, как правило, ведет себя достаточно консервативно в отношении приращения параметров. Таким образом, если мы хотим обучить положительный параметр, который может вырасти больше, чем, скажем, 10, оборачивание этого параметра в экспоненциальную функцию ускоряет сходимость.
На строке 16 мы возвращаем среднеквадратичную ошибку между нашим прогнозом X и наблюдаемой продолжительностью, выраженной в днях (T.days). Снова, внутри блока “autodiff” T.days является скалярным значением, а не вектором. Поскольку таблица T используется в качестве таблицы наблюдений, возвращаемое значение трактуется как функция потерь, минимизируемая с помощью стохастического градиентного спуска. Автоматическое дифференцирование распространяет градиенты от функции потерь на параметры A и B. Наконец, на строке 19 мы выводим два значения, которые мы получили на обучении для A и B, представляющих собой базовую задержку и компоненту Нового Года нашей модели задержки.
На этом мы завершаем наше повторное введение дифференцируемого программирования в качестве универсального инструмента для изучения статистических закономерностей. Отсюда мы вернемся к блокам “autodiff” в более сложных ситуациях. Однако еще раз отметим, что, хотя это может показаться немного ошеломляющим, здесь на самом деле ничего сложного не происходит. Возможно, самым сложным фрагментом кода в этом скрипте является внутренняя реализация функции “ChineseYearStart”, вызываемой на строке 8, которая является частью стандартной библиотеки Envision. Всего за несколько строк кода мы задаем модель с двумя параметрами и обучаем эти параметры. И снова, эта простота поразительна.
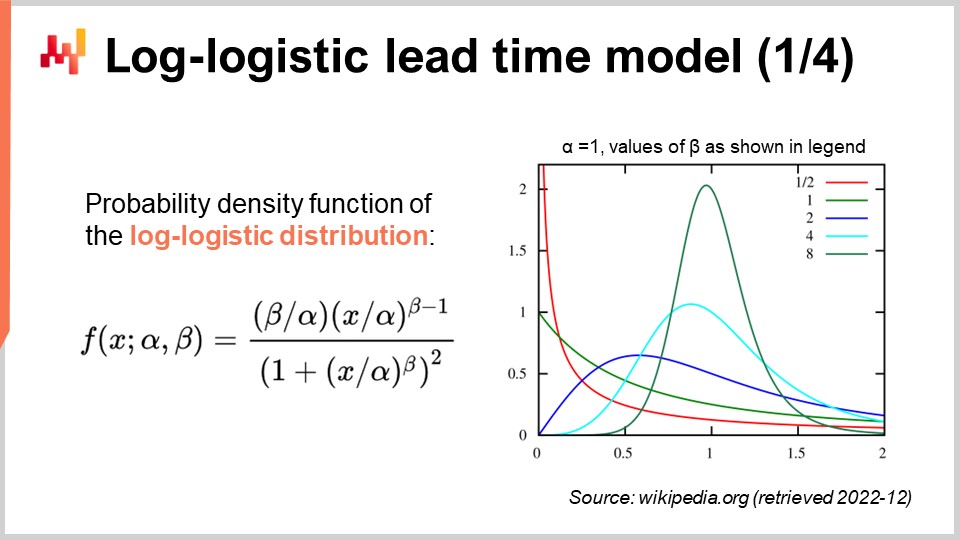
Время выполнения часто имеет распределение с толстыми хвостами; то есть, когда время выполнения отклоняется, оно отклоняется существенно. Таким образом, чтобы смоделировать время выполнения, имеет смысл использовать распределения, способные воспроизводить такое поведение с толстыми хвостами. Математическая литература представляет обширный список таких распределений, и достаточно многие из них подошли бы для наших целей. Однако простое изучение математического ландшафта заняло бы у нас часы. Давайте просто отметим, что распределение Пуассона не имеет толстого хвоста. Таким образом, сегодня я выберу лог-логистическое распределение, которое является распределением с толстым хвостом. Основное обоснование этого выбора в том, что команды Lokad для нескольких клиентов моделируют время выполнения с помощью лог-логистических распределений. Это оказывается эффективным решением с минимальным количеством осложнений. Стоит помнить, однако, что лог-логистическое распределение ни в коем случае не является панацеей, и существует множество ситуаций, когда Lokad моделирует время выполнения по-другому.
На экране мы видим функцию плотности вероятности лог-логистического распределения. Это параметрическое распределение зависит от двух параметров — альфа и бета. Параметр альфа является медианой распределения, а параметр бета определяет форму распределения. Справа представлена короткая серия графиков, полученных при различных значениях бета. Хотя эта формула плотности может выглядеть устрашающе, она фактически является учебным материалом, подобно формуле для вычисления объема сферы. Вы можете попытаться расшифровать и запомнить эту формулу, но это даже не обязательно; достаточно знать, что существует аналитическая формула. Как только вы узнаете, что формула существует, найти её в интернете займет менее минуты.

Наша цель — использовать лог-логистическое распределение для обучения вероятностной модели времени выполнения. Для этого мы собираемся минимизировать логарифм правдоподобия. Действительно, в предыдущей лекции пятой главы мы увидели несколько метрик, которые подходят для вероятностного подхода. Недавно мы вновь рассмотрели CRPS (Непрерывную отсортированную оценку вероятности). Здесь мы возвращаемся к логарифму правдоподобия, который представляет байесовский подход.
Вкратце, зная два параметра, лог-логистическое распределение сообщает нам вероятность наблюдения каждого значения, как оно встречается в эмпирическом наборе данных. Мы хотим подобрать такие параметры, которые максимизируют это правдоподобие. Логарифм, а значит логарифм правдоподобия вместо простого правдоподобия, используется для предотвращения числовых недополнений. Числовые недополнения возникают, когда мы обрабатываем очень маленькие числа, почти равные нулю; такие числа плохо работают с представлением чисел с плавающей запятой, как это принято в современных вычислительных устройствах.
Таким образом, чтобы вычислить логарифм правдоподобия лог-логистического распределения, мы применяем логарифм к его функции плотности вероятности. Аналитическое выражение приведено на экране. Это выражение можно реализовать, и именно это делается в трех строках кода ниже.
На первой строке представлена функция “L4”. L4 означает “логарифм правдоподобия лог-логистического распределения” — да, здесь много L и log. Эта функция принимает три аргумента: два параметра alpha и beta, а также наблюдение x. Функция возвращает логарифм правдоподобия. Функция L4 аннотирована ключевым словом “autodiff”; это ключевое слово указывает, что функция предназначена для автоматического дифференцирования. Иными словами, градиенты могут передаваться назад от значения, возвращаемого функцией, к её аргументам, параметрам alpha и beta. Технически, градиент также проходит через наблюдение x; однако, поскольку мы оставляем наблюдения неизменными во время процесса обучения, градиенты не оказывают на них влияния. На третьей строке мы получаем буквальную транскрипцию математической формулы, приведенной непосредственно над скриптом.
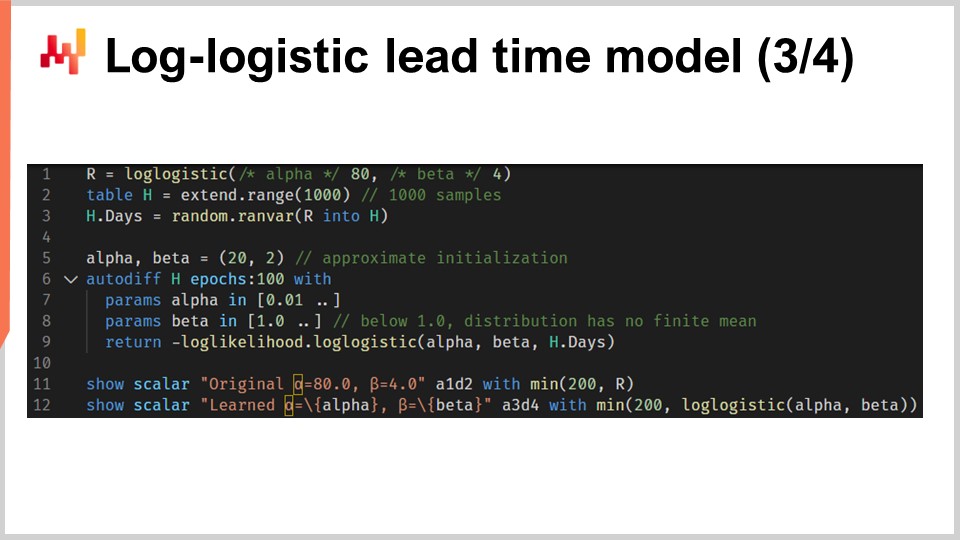
Давайте теперь соберем всё вместе в скрипт, который обучает параметры вероятностной модели времени выполнения на основе лог-логистического распределения. На строках один и три мы генерируем наш имитационный тренировочный набор данных. В реальных условиях вместо генерации имитационных данных мы использовали бы исторические данные. На строке один мы создаем “ranvar”, который представляет исходное распределение. Ради упражнения мы хотим восстановить те параметры — alpha и beta. Функция лог-логистического распределения является частью стандартной библиотеки Envision и возвращает “ranvar”. На строке два мы создаем таблицу “H”, содержащую 1000 записей. На строке три мы выбираем 1000 значений, случайным образом взятых из исходного распределения “R”. Этот вектор “H.days” представляет тренировочный набор данных.
На строке шесть у нас блок “autodiff”; здесь происходит обучение. На строках семь и восемь мы объявляем два параметра, alpha и beta, и чтобы избежать числовых проблем, таких как деление на ноль, к этим параметрам применяются ограничения. Значение alpha должно быть больше 0.01, а значение beta — больше 1.0. На строке девять мы возвращаем функцию потерь, которая является отрицанием логарифма правдоподобия. Действительно, согласно соглашению, блоки “autodiff” минимизируют функцию потерь, и, таким образом, мы хотим максимизировать правдоподобие, отсюда знак минус. Функция “log_likelihood.logistic” является частью стандартной библиотеки Envision, но под капотом она просто вызывает функцию “L4”, которую мы реализовали на предыдущем слайде. Таким образом, никакой магии не происходит; всё осуществляется за счёт автоматического дифференцирования, позволяющего градиенту перемещаться назад от функции потерь к параметрам alpha и beta.
На строках 11 и 12 отображаются графики исходного распределения и распределения, полученного в результате обучения. Гистограммы ограничены 200; это ограничение делает гистограмму немного более читаемой. Мы вернемся к этому через минуту. Если вам интересно, насколько эффективна часть со “автодиффом” в этом скрипте, выполнение занимает менее 80 миллисекунд на одном процессорном ядре. Дифференцируемое программирование не только универсально, но и эффективно использует вычислительные ресурсы современных вычислительных устройств.
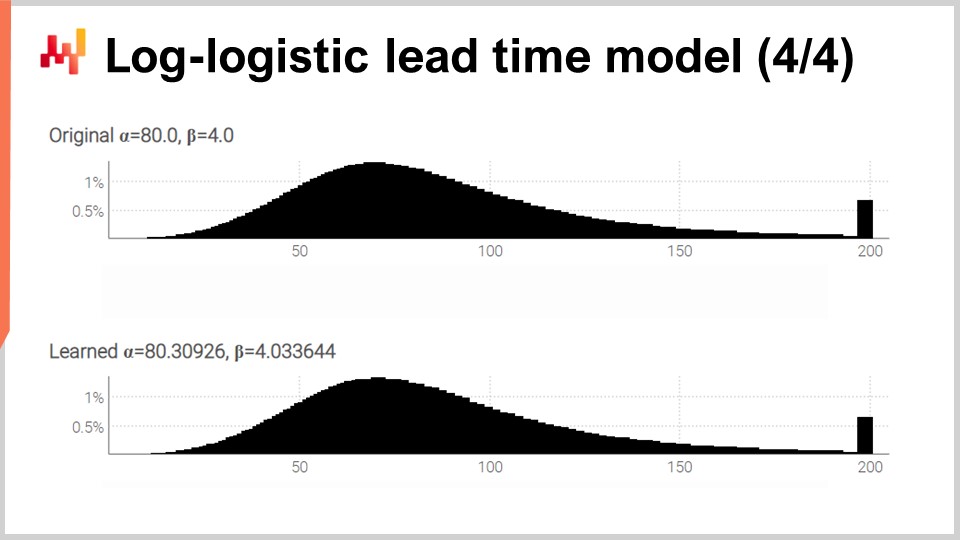
На экране представлены две гистограммы, созданные нашим скриптом, который мы только что рассмотрели. Вверху — исходное распределение с его двумя исходными параметрами, alpha и beta, равными 80 и 4 соответственно. Внизу — распределение, полученное в результате обучения с помощью дифференцируемого программирования. Эти два пика на самом правом конце связаны с усечёнными хвостами, так как эти хвосты достигают довольно больших значений. Кстати, хотя это происходит редко, для некоторых товаров бывает, что они поступают более чем через год после заказа. Это не характерно для всех отраслей, определенно не для молочной продукции, но для механических частей или электроники такое иногда случается.
Хотя процесс обучения не является идеальным, мы получаем результаты с отклонением не более одного процента от исходных значений параметров. Это демонстрирует, по крайней мере, что максимизация логарифма правдоподобия посредством дифференцируемого программирования действительно работает на практике. Лог-логистическое распределение может оказаться подходящим или нет — это зависит от формы распределения времени выполнения, с которой вы сталкиваетесь. Однако практически любое альтернативное параметрическое распределение может быть использовано, если имеется его аналитическое выражение функции плотности вероятности. Существует огромный выбор таких распределений. Как только у вас есть формула из учебника, прямая реализация через дифференцируемое программирование обычно делает всё остальное.
Время выполнения наблюдается не только после завершения транзакции. Пока транзакция ещё продолжается, вы уже что-то знаете; у вас уже есть неполное наблюдение времени выполнения. Представьте, что 100 дней назад вы разместили заказ. Товары ещё не получены, однако вы уже знаете, что время выполнения составляет как минимум 100 дней. Этот 100-дневный период представляет собой нижнюю границу для времени выполнения, которое ещё не было полностью зафиксировано. Такие неполные наблюдения времени выполнения часто оказываются весьма значимыми. Как я уже упоминал в начале этой лекции, наборы данных по времени выполнения зачастую бывают скудными. Не редкость, когда набор данных содержит всего несколько наблюдений. В таких ситуациях важно максимально использовать каждое наблюдение, включая те, которые ещё находятся в процессе.
Рассмотрим следующий пример: у нас всего пять заказов. Три заказа уже доставлены, и время выполнения для них было очень близко к 30 дням. Однако два последних заказа находятся в ожидании уже 40 и 50 дней соответственно. Согласно первым трём наблюдениям среднее время выполнения должно составлять около 30 дней. Но два незавершённых заказа опровергают эту гипотезу. Два подтверждённых заказа с 40 и 50 днями намекают на существенно более длительное время выполнения. Таким образом, мы не должны отбрасывать последние заказы только потому, что они ещё не завершены. Мы должны использовать эту информацию и скорректировать наше представление в пользу более длительного времени выполнения, возможно, до 60 дней.
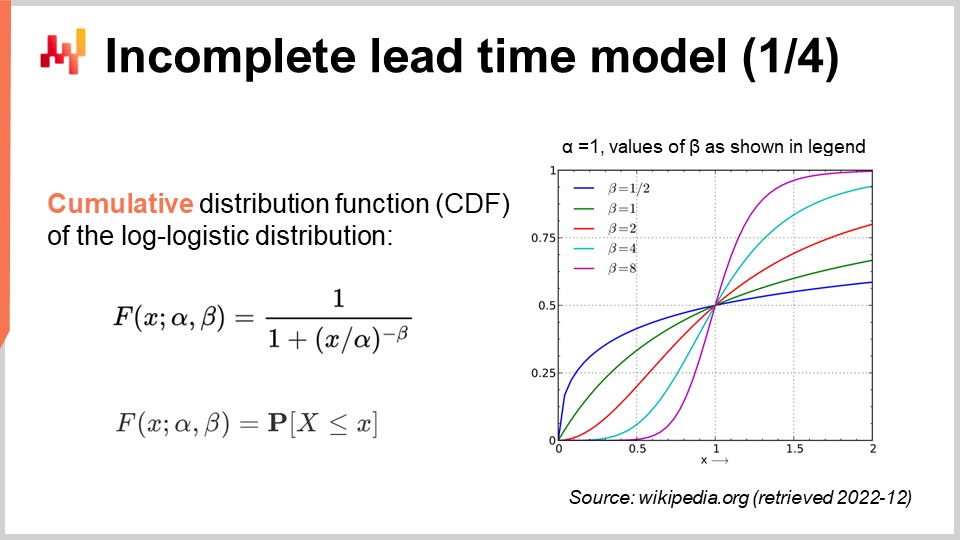
Давайте вновь рассмотрим нашу вероятностную модель времени выполнения, но на этот раз примем во внимание неполные наблюдения. Другими словами, мы хотим работать с наблюдениями, которые иногда представляют собой лишь нижнюю границу для окончательного времени выполнения. Для этого мы можем воспользоваться функцией накопленного распределения (CDF) лог-логистического распределения. Эта формула приведена на экране; снова, это материал из учебников. Функция накопленного распределения лог-логистического распределения обладает простой аналитической формой. В дальнейшем я буду называть этот метод “техникой условной вероятности” для работы с цензурированными данными.

Основываясь на этом аналитическом выражении функции накопленного распределения, мы можем пересмотреть логарифм правдоподобия лог-логистического распределения. Скрипт на экране предоставляет пересмотренную реализацию нашей предыдущей реализации L4. На строке один почти не изменилось объявление функции. Эта функция принимает дополнительный четвертый аргумент — логическое значение “is_incomplete”, которое указывает, является ли наблюдение неполным или нет. На строках два и три, если наблюдение полное, то мы возвращаемся к предыдущему случаю с обычным лог-логистическим распределением, то есть вызываем функцию логарифма правдоподобия, являющуюся частью стандартной библиотеки. Я мог бы повторить код предыдущей реализации L4, но эта версия более лаконична. На строках четыре и пять мы выражаем логарифм правдоподобия фактического наблюдения того, что время выполнения в итоге превысит текущее неполное наблюдение “X”. Это достигается с помощью CDF и, точнее, логарифма CDF.
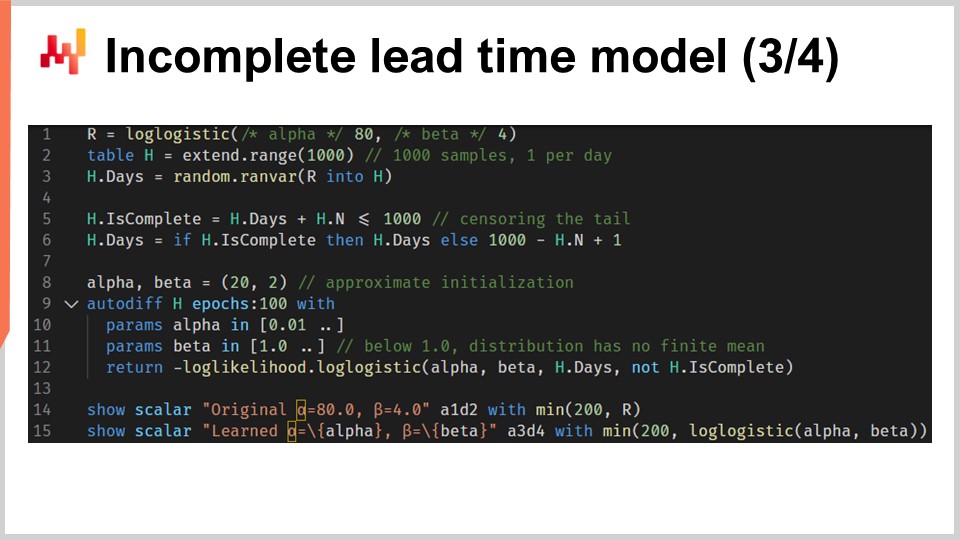
Теперь мы можем повторить нашу настройку со скриптом, который обучает параметры лог-логистического распределения, но уже с учётом неполных времён выполнения. Скрипт на экране почти идентичен предыдущему. На строках один до трёх мы генерируем данные; эти строки не изменились. Замечу, что H.N — это автоматически сгенерированный вектор, который неявно создается на строке два. Этот вектор нумерует сгенерированные строки, начиная с единицы. Предыдущая версия этого скрипта не использовала этот автоматически сгенерированный вектор, но сейчас вектор H.N появляется в конце строки шесть.
Строки пять и шесть действительно являются ключевыми. Здесь мы подвергаем цензуре времена выполнения. Это всё равно, что если бы мы делали по одному наблюдению времени выполнения в день и отсеивали те наблюдения, которые слишком свежи, чтобы предоставить полную информацию. Это означает, например, что 20-дневное время выполнения, начатое семь дней назад, отображается как неполное 7-дневное время выполнения. К концу строки шесть мы получаем список времен выполнения, где некоторые недавние наблюдения (те, которые должны были бы завершиться после текущей даты) являются неполными. Остальная часть скрипта осталась без изменений, за исключением строки 12, где вектор H.is_complete передается в качестве четвертого аргумента функции логарифма правдоподобия. Таким образом, на строке 12 мы вызываем функцию дифференцируемого программирования, которую мы представили всего минуту назад.
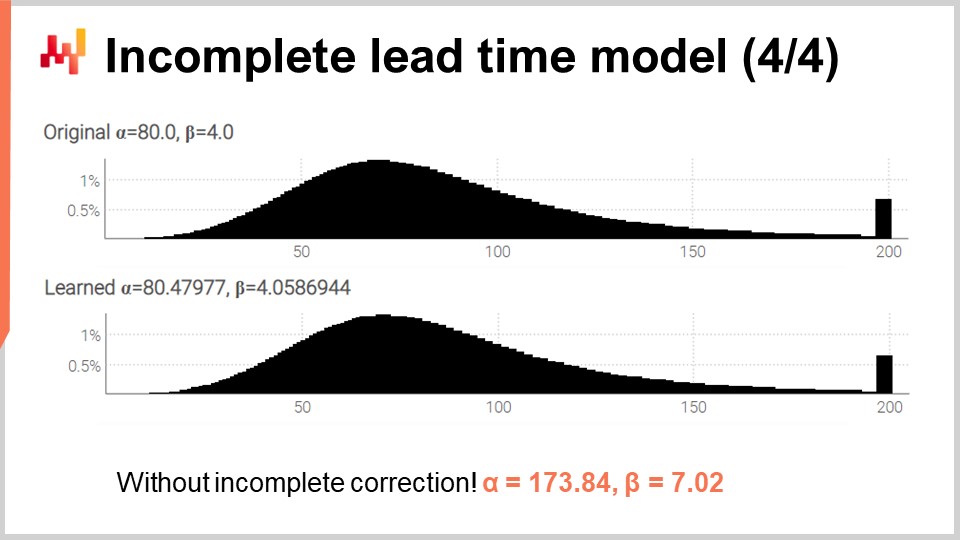
Наконец, на экране отображаются две гистограммы, созданные этим пересмотренным скриптом. Параметры по-прежнему обучаются с высокой точностью, несмотря на наличие множества неполных времен выполнения. Чтобы убедиться, что обработка неполных времен не является лишней сложностью, я повторно запустил скрипт, но на этот раз с модифицированной версией, использующей перегрузку функции логарифма правдоподобия с тремя аргументами (той, которую мы использовали изначально, предполагая, что все наблюдения полные). Для alpha и beta мы получаем значения, отображенные в нижней части экрана. Как и ожидалось, эти значения совершенно не совпадают с исходными значениями alpha и beta.
В этой серии лекций это не первый раз, когда представлена техника для работы с цензурированными данными. Во второй лекции этой главы была представлена техника маскирования потерь для работы с дефицитом товара. Действительно, мы обычно стараемся прогнозировать будущий спрос, а не будущие продажи. Дефицит товара приводит к занижению, так как мы не можем наблюдать все продажи, которые произошли бы, если бы дефицита не было. Техника условной вероятности может быть использована для работы с цензурированным спросом, как это происходит при дефиците товара. Техника условной вероятности несколько сложнее маскирования потерь, поэтому её, вероятно, не следует применять, если маскирование потерь оказывается достаточным.
В случае времени выполнения основная мотивация — скудность данных. Мы можем иметь настолько мало данных, что критически важно максимально использовать каждое наблюдение, даже неполное. Действительно, техника условной вероятности мощнее маскирования потерь в том смысле, что она позволяет использовать неполные наблюдения вместо того, чтобы просто их отбрасывать. Например, если имеется одна единица на складе и эта единица оказывается проданной, то, намекая на недостаток товара, техника условной вероятности всё же использует информацию о том, что спрос был равен или превышал одну.
Здесь мы наблюдаем удивительное преимущество вероятностного моделирования: оно предоставляет элегантный способ обработки цензуры — явления, которое встречается во многих ситуациях в цепочке поставок. С помощью условной вероятности мы можем устранить целые классы систематических смещений.
Прогнозы времени выполнения заказа обычно предназначены для комбинирования с прогнозами спроса. Действительно, давайте теперь рассмотрим простую ситуацию пополнения запасов, как показано на экране.
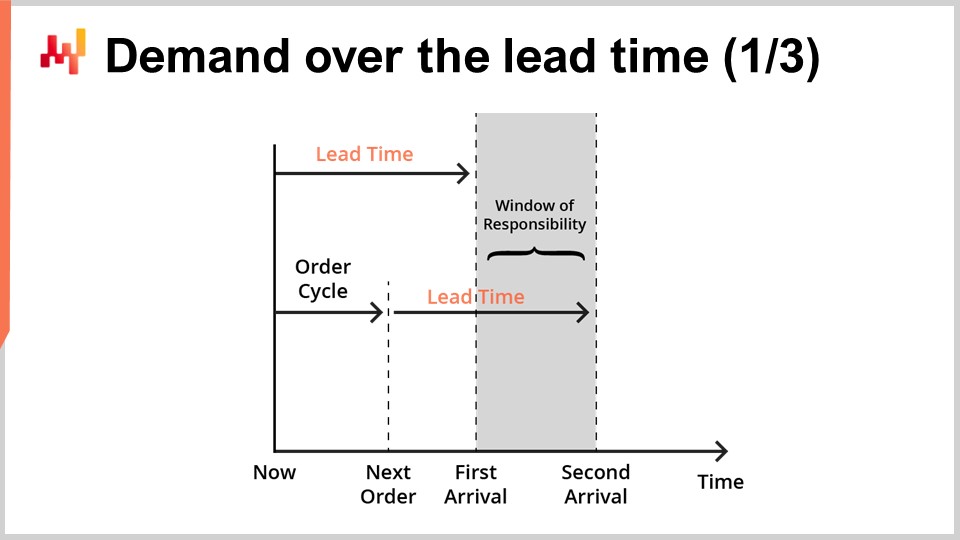
Мы обслуживаем один продукт, и запасы можно пополнить, делая повторный заказ у единственного поставщика. Мы ищем прогноз, который поддержал бы наше решение о том, заказывать ли повторно у поставщика или нет. Мы можем заказать сейчас, и если мы это сделаем, товары прибудут в момент, обозначенный как “первое поступление”. Позже у нас будет еще одна возможность заказать. Эта более поздняя возможность происходит в момент, обозначенный как “следующий заказ”, и в этом случае товары прибудут в момент, обозначенный как “второе поступление”. Период, обозначенный как “период ответственности”, — это тот отрезок времени, который имеет значение для нашего решения о повторном заказе.
Действительно, что бы мы ни решили заказать, оно не прибудет до первого времени выполнения заказа. Таким образом, мы уже теряем контроль над удовлетворением спроса на все, что происходит до первого поступления. Затем, поскольку у нас будет более поздняя возможность заказать снова, удовлетворение спроса после второго поступления уже не является нашей ответственностью; это ответственность следующего заказа. Таким образом, повторный заказ с намерением удовлетворить спрос сверх второго поступления следует отложить до следующей возможности заказа.
Чтобы поддержать решение о повторном заказе, необходимо спрогнозировать два фактора. Во-первых, мы должны спрогнозировать ожидаемые запасы на момент первого поступления. Действительно, если к моменту первого поступления запасов все еще достаточно, то нет никакой причины заказывать сейчас. Во-вторых, мы должны спрогнозировать ожидаемый спрос на период ответственности. В реальной ситуации нам также пришлось бы прогнозировать спрос за пределами периода ответственности, чтобы оценить стоимость запасов товаров, которые мы заказываем сейчас, поскольку могут остаться излишки, переходящие в последующие периоды. Однако, в целях краткости и своевременности, сегодня мы сосредоточимся только на ожидаемых запасах и ожидаемом спросе в пределах периода ответственности.
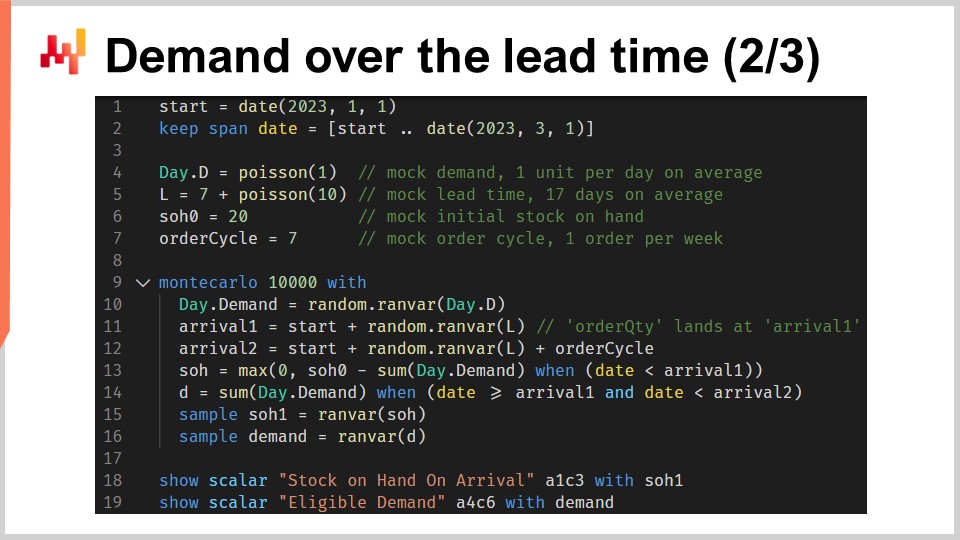
Этот скрипт реализует факторы или прогнозы периода ответственности, о которых мы только что говорили. Он принимает на вход вероятностный прогноз времени выполнения заказа и вероятностный прогноз спроса. Он возвращает два распределения вероятностей, а именно запасы на момент поступления и допустимый спрос, определяемый рамками периода ответственности.
В строках один и два мы настраиваем временные линии, которые начинаются 1 января и заканчиваются 1 марта. В предсказательной установке эта временная линия не была бы захардкожена. В строке четыре представлен упрощенный вероятностный модель спроса: распределение Пуассона, повторяемое день за днем на протяжении всего этого периода. Спрос составит в среднем одну единицу в день. Здесь я использую упрощенную модель спроса для наглядности. В реальной ситуации мы, например, применили бы ESSM (Ensemble State Space Model). Модели состояния являются вероятностными и были представлены в самой первой лекции этой главы.
В строке пять представлен еще один упрощенный вероятностный модель. Эта вторая модель предназначена для времени выполнения заказа. Это распределение Пуассона, смещенное на семь дней вправо. Смещение выполняется посредством свертки. В строке шесть мы задаем начальные запасы. В строке семь мы определяем цикл заказа. Это значение выражается в днях и характеризует, когда произойдет следующий повторный заказ.
С 9 по 16 строку у нас есть блок Монте-Карло, представляющий основную логику скрипта. Ранее в этой лекции мы уже вводили другой блок Монте-Карло для поддержки нашей логики кросс-валидации. Здесь мы используем этот конструкт снова, но для другой цели. Мы хотим вычислить две случайные величины, отражающие, соответственно, запасы на момент поступления и допустимый спрос. Однако алгебра случайных величин недостаточно выразительна для выполнения этого вычисления. Поэтому мы используем блок Монте-Карло.
В третьей лекции этой главы я отметил, что существует двойственность между вероятностным прогнозированием и симуляциями. Блок Монте-Карло иллюстрирует эту двойственность. Мы начинаем с вероятностного прогноза, превращаем его в симуляцию и, наконец, преобразуем результаты симуляции обратно в другой вероятностный прогноз.
Давайте взглянем на детали. В строке 10 мы генерируем одну траекторию спроса. В строке 11 мы генерируем дату прибытия для первого заказа, предполагая, что мы заказываем сегодня. В строке 12 мы генерируем дату прибытия для второго заказа, предполагая, что мы заказываем через один цикл заказа. В строке 13 мы вычисляем, какой остаток остается в запасах на момент первого поступления. Это начальные запасы минус спрос, наблюдаемый за период первого времени выполнения заказа. Функция max zero указывает, что запасы не могут уходить в отрицательную область. Другими словами, мы предполагаем, что не накапливаются невыполненные заказы. Это предположение об отсутствии отставания может быть изменено. Случай с отставанием оставлен в качестве упражнения для аудитории. В качестве подсказки: дифференцируемое программирование может быть использовано для оценки процента неудовлетворенного спроса, который успешно превращается в отставание, в зависимости от того, сколько дней остается до возобновления доступности запасов.
Возвращаясь к скрипту, в строке 14 мы вычисляем допустимый спрос, то есть спрос, который возникает в течение периода ответственности. В строках 15 и 16 мы собираем две случайные величины, представляющие интерес, с помощью ключевого слова “sample”. В отличие от первого скрипта Envision этой лекции, который касался кросс-валидации, здесь мы стремимся собрать распределения вероятностей из этого блока Монте-Карло, а не просто средние значения. В обеих строках 15 и 16 случайная величина, которая появляется справа от оператора присваивания, является агрегатором. В строке 15 мы получаем случайную величину для запасов на момент поступления. В строке 16 мы получаем другую случайную величину для спроса, возникающего в рамках периода ответственности.
В строках 18 и 19 эти две случайные величины выводятся на экран. Теперь давайте сделаем паузу на мгновение и пересмотрим весь этот скрипт. Строки с один по семь предназначены лишь для настройки тестовых данных. Строки 18 и 19 просто выводят результаты. Вся фактическая логика происходит в восьми строках между строками 9 и 16. Фактически, вся реальная логика расположена, так сказать, в строках 13 и 14.
Всего несколькими строками кода, менее 10, как бы мы ни считали, мы комбинируем вероятностный прогноз времени выполнения заказа с вероятностным прогнозом спроса, чтобы составить некий гибридный вероятностный прогноз, имеющий практическое значение для цепочки поставок. Заметим, что здесь нет ничего, что действительно зависело бы от специфики как прогноза времени выполнения заказа, так и прогноза спроса. Были использованы простые модели, но могли бы быть применены и более сложные. Это ничего бы не изменило. Единственное требование — наличие двух вероятностных моделей, чтобы можно было генерировать эти траектории.
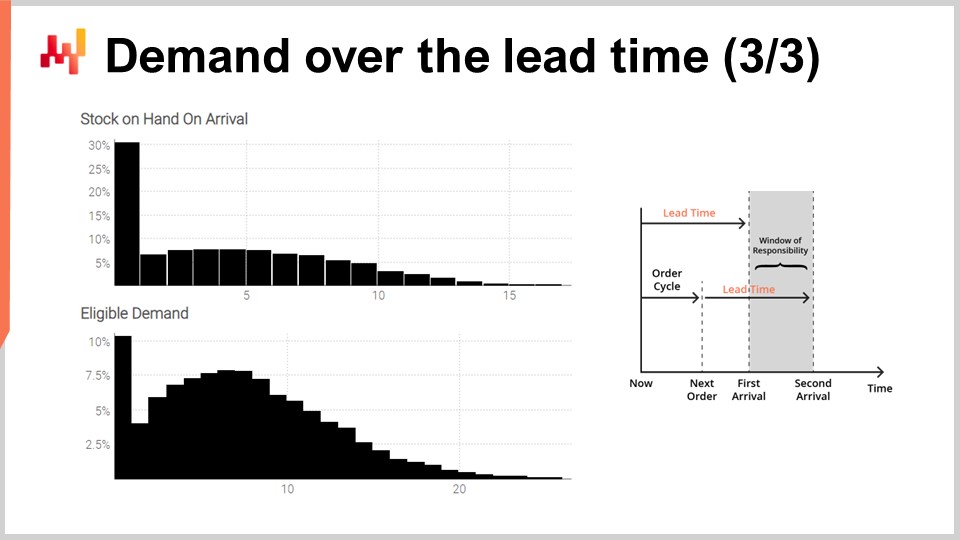
Наконец, на экране появляются гистограммы, созданные скриптом. Верхняя гистограмма представляет запасы на момент поступления. Существует примерно 30%-я вероятность, что начальный запас окажется равным нулю. Другими словами, есть около 30%-я вероятность, что к последнему дню непосредственно перед первым поступлением произошел дефицит запасов. Среднее значение запасов может составлять около пяти единиц. Однако, если судить о ситуации по среднему значению, мы серьезно неправильно поймем ситуацию. Вероятностный прогноз необходим для того, чтобы правильно отразить начальную ситуацию с запасами.
Нижняя гистограмма представляет спрос, связанный с периодом ответственности. У нас есть примерно 10%-я вероятность столкнуться с нулевым спросом. Этот результат также может показаться удивительным. Действительно, мы начали это упражнение с стационарным спросом, распределенным по Пуассону, в среднем одна единица в день. Между заказами семь дней. Если бы не изменчивость времени выполнения заказа, вероятность нулевого спроса за семь дней была бы менее 0,1%. Однако скрипт демонстрирует, что такое событие происходит значительно чаще. Причина в том, что узкий период ответственности может возникнуть, если первое время выполнения заказа дольше обычного, а второе — короче обычного.
Столкновение с нулевым спросом в течение периода ответственности означает, что запасы на момент поступления, скорее всего, окажутся довольно высокими в определенный момент времени. В зависимости от ситуации это может быть критично, например, если существует ограничение по вместимости склада или если товар является скоропортящимся. Еще раз: средний спрос, вероятно, около восьми, не дает надежного представления о том, каким был спрос. Помните, что мы получили это крайне асимметричное распределение из исходного стационарного спроса, равного в среднем одной единице в день. Это и есть эффект изменчивости времени выполнения заказа.
Эта простая модель демонстрирует важность времени выполнения заказа в ситуациях пополнения запасов. С точки зрения цепочки поставок отделение прогноза времени выполнения заказа от прогноза спроса — в лучшем случае практическая абстракция. Ежедневный спрос — это не то, что нас действительно интересует. Нас на самом деле интересует состав спроса с учетом времени выполнения заказа. Если бы присутствовали и другие стохастические факторы, такие как отставания или возвраты, они также были бы частью модели.

Настоящая глава этой серии лекций называется “Прогнозирующее моделирование” вместо “Прогнозирования спроса”, как это обычно бывает в основных учебниках по цепочкам поставок. Причина такого названия должна становиться все более очевидной по мере прохождения этой лекции. Действительно, с точки зрения цепочки поставок, мы хотим прогнозировать эволюцию системы. Спрос, безусловно, важен, но он не единственный фактор. Другие изменчивые факторы, такие как время выполнения заказа, также должны прогнозироваться. Более того, в конечном итоге все эти факторы должны прогнозироваться вместе.
Действительно, нам необходимо объединить эти прогностические компоненты для поддержки процесса принятия решений. Таким образом, важно не искать какую-то финальную модель прогнозирования спроса. Эта задача в конечном итоге оказывается бессмысленной, поскольку дополнительная точность достигается методами, противоречащими интересам компании. Чем сложнее модель, тем больше непрозрачность, ошибок и требуемых вычислительных ресурсов. Как правило, чем сложнее модель, тем труднее успешно интегрировать её с другой моделью в оперативную систему. Главное — собрать набор прогностических методов, которые можно комбинировать по мере необходимости. Именно об этом и речь в модульности с точки зрения прогностического моделирования. В этой лекции было представлено полдюжины техник. Эти техники полезны, так как они учитывают критически важные реальные аспекты, такие как неполные наблюдения. Они также просты; ни один из приведенных сегодня примеров кода не превышал 10 строк реальной логики. И что самое главное, эти техники являются модульными, как конструктор Лего. Они хорошо работают вместе и могут быть практически бесконечно рекомбинированы.
Конечная цель прогностического моделирования для цепочки поставок, как следует понимать, заключается в выявлении таких техник. Каждая техника сама по себе должна представлять возможность пересмотра любой ранее существующей прогностической модели с целью её упрощения или улучшения.

В заключение, несмотря на то, что время выполнения заказа в значительной степени игнорируется академическим сообществом, его можно и нужно прогнозировать. Анализируя короткую серию реальных распределений времени выполнения заказа, мы выявили две проблемы: во-первых, время выполнения заказа варьируется; во-вторых, данные по времени выполнения заказа разрежены. Таким образом, мы представили методы моделирования, подходящие для работы с наблюдениями времени выполнения заказа, которые оказываются как разреженными, так и непредсказуемыми.
Эти модели времени выполнения заказа являются вероятностными и во многом представляют собой продолжение моделей, постепенно вводимых в этой главе. Мы также увидели, что вероятностный подход действительно предоставляет элегантное решение проблемы неполных наблюдений, практически повсеместной проблемы в цепочке поставок. Эта проблема возникает всякий раз, когда наблюдаются дефициты запасов и когда есть незавершенные заказы. Наконец, мы увидели, как объединить вероятностный прогноз времени выполнения заказа с вероятностным прогнозом спроса для создания прогностической модели, необходимой для поддержки последующего процесса принятия решений.

Следующая лекция состоится 8 марта. Она пройдет в среду в то же время, в 15:00 по парижскому времени. Сегодняшняя лекция была технической, но следующая будет в основном нетехнической, и я расскажу о специалисте по цепям поставок. Действительно, фундаментальные учебники по цепям поставок рассматривают цепочку поставок так, как будто модели прогнозирования и оптимизации возникают из ниоткуда и работают самостоятельно, полностью игнорируя их “человеческий” компонент — то есть людей, ответственных за процесс. Таким образом, мы подробнее рассмотрим роли и обязанности специалиста по цепям поставок, человека, от которого ожидается ведение количественной инициативы в этой области.
Теперь я перейду к вопросам.
Вопрос: Что, если кто-то хочет сохранить свои запасы для дальнейших инноваций или по другим причинам, помимо принципа just in time или других концепций?
Это действительно очень важный вопрос. Концепция обычно рассматривается через экономическое моделирование цепочки поставок, которое мы технически называем “экономическими драйверами” в этой серии лекций. Вы спрашиваете, не лучше ли не обслуживать клиента сегодня, потому что в более поздний момент времени появится возможность обслужить ту же единицу другому человеку, которому это будет гораздо важнее по каким-либо причинам. По сути, вы говорите, что большую ценность можно извлечь, обслужив другого клиента позже, возможно, VIP-клиента, чем обслужив клиента сегодня.
Это может быть так, и такое действительно происходит. Например, в авиационной отрасли, допустим, вы являетесь поставщиком услуг по техническому обслуживанию, ремонту и капитальному ремонту (MRO). У вас есть обычные VIP-клиенты — авиакомпании, с которыми вы регулярно работаете по долгосрочным контрактам, и они очень важны. Когда это происходит, вы хотите убедиться, что всегда сможете обслуживать этих клиентов. Но что, если другая авиакомпания позвонит и попросит одну единицу? В этом случае вы сможете обслужить этого клиента, но у вас нет с ним долгосрочного контракта. Поэтому вы собираетесь скорректировать свою цену так, чтобы она была очень высокой, гарантируя, что вы получите достаточную прибыль, чтобы компенсировать потенциальное отсутствие запасов, с которым вы можете столкнуться позже. Итог по первому вопросу: я считаю, что речь идёт не столько о прогнозировании, сколько о правильном моделировании экономических драйверов. Если вы хотите сохранить запасы, вам нужно создать модель — оптимизационную модель, где рациональным решением будет не обслуживать клиента, просящего одну единицу, пока у вас ещё есть резерв.
Кстати, ещё одна типичная ситуация возникает, когда вы продаёте комплекты. Комплект — это сборка из множества деталей, продаваемых вместе, и у вас осталась только одна деталь, стоимость которой составляет лишь малую долю общей стоимости комплекта. Проблема в том, что если вы продадите эту последнюю единицу, то не сможете собрать комплект и продать его по полной цене. Таким образом, вы можете оказаться в ситуации, когда предпочитаете оставить эту единицу на складе, чтобы иметь возможность продать комплект позже, возможно, с некоторой неопределённостью. Но, опять же, всё сводится к экономическим драйверам, и это, по-моему, правильный подход в данной ситуации.
Вопрос: За последние несколько лет большинство задержек в цепочке поставок происходило из-за войны или пандемии, что крайне сложно предсказать, так как подобных ситуаций у нас не было раньше. Как вы к этому относитесь?
Мое мнение таково: сроки поставки всегда были изменчивыми. Я работаю в сфере цепей поставок с 2008 года, а мои родители занимались цепями поставок ещё за 30 лет до меня. Насколько мы помним, сроки поставки всегда были непредсказуемыми и варьировались. Всегда что-то происходило — будь то протест, война или изменение тарифов. Да, последние несколько лет были чрезвычайно непредсказуемыми, но сроки поставки уже всегда отличались высокой вариативностью.
Я согласен с тем, что никто не может притворяться способным предсказать следующую войну или пандемию. Если бы было возможно математически предсказать эти события, люди не ввязывались бы в войны или инвестировали в цепи поставок; они просто играли бы на фондовом рынке и становились богатыми, предугадывая движения рынка.
Суть в том, что вы можете планировать на случай непредвиденных обстоятельств. Если вы не уверены в будущем, вы можете фактически увеличить вариации в своих прогнозах. Это противоположно попытке сделать прогнозы более точными — вы сохраняете свои средние ожидания, но увеличиваете «хвост», чтобы принимаемые на основе этих вероятностных прогнозов решения были более устойчивыми к колебаниям. Вы искусственно увеличили ожидаемые вариации так, чтобы они были больше, чем те, которые вы наблюдаете в данный момент. Суть в том, что идея о том, что прогнозировать легко или трудно, исходит из точечной оценки, когда хочется играть так, будто можно точно предвидеть будущее. Это не так — точного предвидения будущего не существует. Единственное, что вы можете сделать, — работать с вероятностными распределениями с большой дисперсией, которое отражает и количественно выражает ваше незнание будущего.
Вместо того чтобы тонко настраивать решения, которые критически зависят от точного выполнения плана, вы учитываете и планируете определённую степень вариации, делая свои решения более устойчивыми к этим изменениям. Однако это относится только к тем видам вариаций, которые не влияют на вашу цепь поставок слишком резкими способами. Например, вы можете справиться с увеличенными сроками поставки от поставщиков, но если ваш склад был подвергнут бомбардировке, никакой прогноз не спасёт вас в такой ситуации.
Вопрос: Можем ли мы создать эти гистограммы и вычислить CRPS в Microsoft Excel, например, с помощью дополнений Excel, таких как itsastat или других, поддерживающих множество распределений?
Да, можно. Один из наших сотрудников в Lokad на самом деле создал Excel-таблицу, которая представляет вероятностную модель для ситуации пополнения запасов. Суть проблемы в том, что в Excel нет встроенного типа данных для гистограмм, поэтому в Excel у вас есть только числа — одна ячейка, одно число. Было бы элегантно и просто, если бы было одно значение, представляющее собой гистограмму, где вся гистограмма упакована в одну ячейку. Однако, насколько мне известно, это невозможно в Excel. Тем не менее, если вы готовы потратить около 100 строк для представления гистограммы, даже если это не будет так компактно и удобно, вы можете реализовать распределение в Excel и провести вероятностное моделирование. Мы разместим ссылку на этот пример в разделе комментариев.
Имейте в виду, что это довольно болезненная задача, так как Excel не идеально подходит для этой работы. Excel — это язык программирования, и с его помощью можно сделать практически всё, так что вам даже не понадобится дополнение для реализации этого. Однако это будет довольно многословно, так что не рассчитывайте на что-то супер аккуратное.
Вопрос: Срок поставки можно разделить на компоненты, такие как время заказа, время производства, время транспортировки и т.д. Если требуется более детальный контроль над сроками поставки, как изменится этот подход?
Во-первых, нам нужно понять, что значит иметь больший контроль над сроком поставки. Вы хотите сократить средний срок поставки или уменьшить его вариативность? Что интересно, я видел, как многим компаниям удавалось сократить средний срок поставки, но за счет увеличения вариативности. В среднем срок поставки оказывается короче, но иногда он значительно длиннее.
В этой лекции мы занимаемся упражнением по моделированию. Само по себе это не подразумевает никаких действий — это просто наблюдение, анализ и прогнозирование. Однако, если мы сможем разложить срок поставки на составляющие и проанализировать его базовое распределение, мы сможем использовать вероятностное моделирование для оценки того, какие компоненты варьируются сильнее всего и какие оказывают наибольшее негативное воздействие на нашу цепь поставок. Мы можем проводить сценарные анализы «что если» с этой информацией. Например, возьмите одну часть вашего срока поставки и спросите: «А что если хвост этого срока поставки был бы немного короче или среднее значение немного снизилось?» Затем вы можете пересобрать всё, запустить вашу модель прогнозирования для всей цепи поставок заново и начать оценивать влияние.
Этот подход позволяет рассуждать по частям о различных явлениях, включая непредсказуемые. Это не столько изменение подхода, сколько продолжение того, что мы уже сделали, что приведёт нас к Главе 6, посвящённой оптимизации реальных решений на основе этих вероятностных моделей.
Вопрос: Я считаю, что это предоставляет возможность пересчитать наши сроки поставки в SAP, чтобы обеспечить более реалистичные временные рамки и помочь минимизировать рывковые изменения в системе. Возможно ли это?
Отказ от ответственности: SAP является конкурентом Lokad в области оптимизации цепей поставок. Мой первоначальный ответ — нет, SAP не может этого сделать. Дело в том, что у SAP есть четыре различных решения для оптимизации цепей поставок, и это зависит от того, о каком наборе решений идёт речь. Однако все эти наборы объединяет видение, основанное на точечных прогнозах. Всё в SAP сконструировано с предположением, что прогнозы будут точными.
Да, в SAP существуют некоторые параметры для настройки, например, нормальное распределение, которое я упомянул в начале этой лекции. Однако распределения сроков поставки, которые мы наблюдали, не были нормальными. Насколько мне известно, основные настройки SAP для оптимизации цепей поставок предполагают нормальное распределение сроков поставки. Проблема в том, что в основе программного обеспечения лежит широко неверное математическое предположение. Вы не можете исправить это фундаментально неверное предположение, заложенное в ядро архитектуры вашего программного обеспечения, простым изменением параметра. Возможно, вы сможете провести какую-то сумасшедшую обратную разработку и найти параметр, который приведёт к правильному решению. Теоретически это возможно, но на практике это вызывает столько проблем, что возникает вопрос: зачем вам вообще это делать?
Чтобы принять вероятностную перспективу, нужно идти ва-банк, то есть ваши прогнозы должны быть вероятностными, а ваши оптимизационные модели также использовать вероятностные модели. Проблема в том, что даже если мы сможем настроить вероятностное моделирование для немного лучших сроков поставки, остальная часть набора решений SAP снова вернётся к точечным прогнозам. Вне зависимости от обстоятельств, мы сведём эти распределения к точечным значениям. Идея о том, что можно приблизить их средним значением, тревожна и просто неверна. Так что, технически, вы можете настраивать сроки поставки, но после этого столкнётесь с таким количеством проблем, что, возможно, это не стоит усилий.
Вопрос: Бывают ситуации, когда вы заказываете одни и те же детали у разных поставщиков. Это важная информация для прогнозирования сроков поставки. Вы проводите прогнозирование сроков поставки по каждой позиции или иногда используете группировку позиций по семействам?
Это чрезвычайно интересный вопрос. У нас есть два поставщика для одной и той же позиции. Вопрос в том, насколько схожи сами позиции и поставщики. Сначала нужно рассмотреть ситуацию. Если один поставщик находится по соседству, а другой — на другом конце света, то их действительно следует рассматривать отдельно. Но давайте предположим интересный случай, когда два поставщика достаточно схожи и речь идет об одной и той же позиции. Объединять ли такие наблюдения или нет?
Интересно то, что с помощью дифференцируемого программирования вы можете составить модель, которая приписывает некоторый вес поставщику и некоторый вес позиции, и позволить обучающему алгоритму сделать своё дело. Он определит, стоит ли больше полагаться на компонент позиции в сроке поставки или на компонент поставщика. Возможно, что два поставщика, обслуживающие практически одинаковые товары, могут иметь некоторую систематическую разницу, при которой один из них в среднем работает немного быстрее другого. Но существуют позиции, выполнение которых требует больше времени, и если вы будете выбирать позиции выборочно, не всегда будет ясно, что один поставщик быстрее другого, поскольку всё зависит от того, какие позиции рассматриваются. Скорее всего, у вас будет очень мало данных, если вы детализируете всё до каждого отдельного поставщика и каждой позиции. Таким образом, интересным, и то, что я бы рекомендовал, является использование дифференцируемого программирования. Возможно, мы вернёмся к этой ситуации в одной из последующих лекций, когда вы установите некоторые параметры на уровне детали и некоторые параметры на уровне поставщика. Тогда общее число параметров будет не равно числу деталей, умноженному на число поставщиков; оно будет равно числу деталей плюс числу поставщиков, или, возможно, плюс числу поставщиков, умноженному на категории, или что-то в этом роде. Вы не взорвете число параметров; вы просто добавите параметр, элемент, имеющий аффинитет к поставщику, который позволит вам осуществлять некий динамический микс, основанный на ваших исторических данных.
Вопрос: Я считаю, что количество заказываемых товаров и то, какие товары заказываются вместе, также может в конечном итоге влиять на срок поставки. Можете рассказать о сложности включения всех переменных в такого рода задачу?
В последнем примере у нас было два вида продолжительности: цикл заказа и сам срок поставки. Цикл заказа интересен тем, что он неопределён только в той мере, в какой мы ещё не приняли решение. По сути, это нечто, что вы можете решить практически в любой момент времени, так что цикл заказа полностью определяется вами. Это не единственное подобное явление в цепочке поставок; цены работают по тому же принципу. Есть спрос, вы наблюдаете спрос, но при этом вы можете выбрать желаемую цену. Некоторые цены, очевидно, неразумны, но принцип остаётся тем же — они зависят от вас.
Цикл заказа определяется вами. Теперь, что вы говорите, так это то, что существует неопределённость относительно точного момента для следующего заказа, потому что вы не знаете, когда именно будете заказывать. Действительно, вы абсолютно правы. Суть в том, что когда у вас появляется возможность реализовать вероятностное моделирование, внезапно, как обсуждалось в шестой главе этой серии лекций, вы не захотите утверждать, что цикл заказа составляет семь дней. Вместо этого вы хотите принять политику повторного заказа, которая максимизирует возврат инвестиций для вашей компании. Таким образом, вы можете планировать будущее таким образом, что если вы делаете повторный заказ сейчас, то можете принять решение сейчас и затем применять свою политику день за днём. В какой-то момент в будущем вы делаете повторный заказ, и тогда возникает ситуация, своего рода «змея, которая ест свой хвост», поскольку лучшее решение по заказу на сегодня зависит от решения по следующему заказу, которое вы ещё не приняли. Такая проблема известна как проблема политики, и это последовательная задача принятия решений.
Проблема оптимизации политики довольно сложна, и я намерен рассмотреть её в шестой главе. Но суть в том, что, если вернуться к вашему вопросу, у нас есть два различных компонента. Один компонент изменяется независимо от того, что вы делаете, — это срок поставки от вашего поставщика, а другой — время заказа, которое определяется внутренне вашим процессом и должно рассматриваться как объект оптимизации.
Подводя итог, мы видим слияние оптимизации и предиктивного моделирования. В конечном итоге они оказываются практически одинаковыми, поскольку существует взаимосвязь между принятыми решениями и тем, что происходит в будущем.
На сегодня это всё. Не забудьте, что 8 марта, в то же время, будет среда, 15:00. Спасибо, и до встречи в следующий раз.


