Stock de Seguridad
El stock de seguridad es un método de optimización de inventario que indica cuánto inventario se debe mantener más allá de la demanda esperada para alcanzar un determinado nivel de servicio. El stock adicional actúa como un “colchón de seguridad” —de ahí el nombre— para proteger a la empresa frente a las fluctuaciones futuras esperadas. La fórmula del stock de seguridad depende tanto de la demanda futura esperada como del lead time futuro esperado. Se asume que la incertidumbre se distribuye normalmente para ambos factores. La fórmula del stock de seguridad es ubicua en la mayoría de los sistemas de gestión de inventario, incluyendo los más notables ERPs y MRPs.
Actualización julio 2020: El enfoque detallado a continuación es el típico supply chain de manual, desafortunadamente, también resulta ser muy disfuncional. En particular, ni la demanda futura ni el lead time futuro se distribuyen normalmente (es decir, no son gaussianos). Además, toda la perspectiva pierde por completo de vista que todos los SKUs que pueden ser ordenados o producidos por la empresa compiten por los mismos recursos. Recomendamos encarecidamente no utilizar ningún modelo de stock de seguridad en lo que respecta a supply chains reales.
Público objetivo: Este documento está destinado principalmente a profesionales de supply chain en el comercio minorista o la fabricación. Sin embargo, este documento también es útil para editores de software de contabilidad / ERP / eCommerce que deseen ampliar sus aplicaciones con funciones de gestión de inventario.
Hemos tratado de mantener los requisitos matemáticos lo más simples posible, sin embargo, no podemos evitar por completo las fórmulas ya que el propósito preciso de este documento es ser una guía práctica que explique cómo calcular el stock de seguridad.
Descargar: calculate-safety-stocks.xls (Hoja de cálculo de Microsoft Excel)
Introducción
La gestión de inventario es un trade-off financiero entre los costes de inventario y los costes de faltante de stock. Cuanto más stock haya, mayor será el capital de trabajo necesario y mayor la depreciación del stock. Por otro lado, si no se dispone de suficiente stock, se producen faltantes de inventario, se pierden ventas potenciales y se puede interrumpir todo el proceso de producción.
El inventario depende esencialmente de dos factores
- demanda anticipada: la cantidad de artículos que serán consumidos o comprados.
- lead time: el retraso entre la decisión de reabastecimiento y la disponibilidad renovada.
Sin embargo, esos dos factores están sujetos a incertidumbres
- variaciones en la demanda: los comportamientos de los clientes pueden evolucionar de manera bastante impredecible.
- variaciones en el lead time: los proveedores o transportistas pueden enfrentarse a dificultades no planificadas.
Decidir el nivel de stock de seguridad equivale implícitamente a hacer un trade-off entre esos costes considerando las incertidumbres.
El equilibrio entre los costes de inventario y los costes de faltante de stock depende mucho del negocio. Por lo tanto, en lugar de considerar directamente esos costes, introduciremos ahora la noción clásica de nivel de servicio.
El nivel de servicio expresa la probabilidad de que un cierto nivel de stock de seguridad no conduzca a un faltante de stock. Naturalmente, cuando se incrementa el stock de seguridad, el nivel de servicio también aumenta. Cuando el stock de seguridad se vuelve muy elevado, el nivel de servicio tiende al 100% (es decir, a una probabilidad cero de encontrarse con un faltante de stock).
Escoger el nivel de servicio, es decir, la probabilidad aceptable de faltante de stock, está fuera del alcance de esta guía, pero disponemos de una guía separada sobre cálculo de niveles de servicio óptimos.
Modelo de reposición de inventario
El punto de reorden es la cantidad de inventario que debería desencadenar una orden. Si no existiera incertidumbre (es decir, si la demanda futura fuera perfectamente conocida y el suministro perfectamente confiable), el punto de reorden sería simplemente igual a la demanda forecast durante el lead time, también llamada demanda del lead time.
En la práctica, debido a las incertidumbres, tenemos
punto de reorden = demanda del lead time + stock de seguridad
Si asumimos que los forecasts no tienen bias (estadísticamente hablando), tener cero stock de seguridad llevaría a un nivel de servicio del 50%. De hecho, forecasts sin bias significan que hay la misma probabilidad de que la demanda futura sea mayor o menor que la demanda del lead time (recordemos que la demanda del lead time es solo un valor forecast).
Precaución: los forecasts pueden ser sin bias sin ser exactos. El bias indica un error sistemático del modelo de forecast (p.ej.: siempre sobreestimar la demanda en un 20%).
Distribución normal del error
En este punto, necesitamos una forma de representar la incertidumbre en la demanda del lead time. A continuación, asumiremos que el error se distribuye normalmente, véase la imagen a continuación.
Notas estadísticas: esta asunción de distribución normal no es del todo arbitraria. Bajo ciertas situaciones, los estimadores estadísticos convergen a una distribución normal como lo establece el teorema del límite central. Pero esas consideraciones están fuera del alcance de esta guía.
Una distribución normal se define únicamente por dos parámetros: su media y su varianza. Dado que asumimos que los forecasts son sin bias, asumimos que la media de la distribución del error es cero, lo que no significa que estemos asumiendo un error nulo.
Determinar la varianza del error forecast es una tarea más delicada. Lokad, al igual que la mayoría de los toolkits de forecast, proporciona estimaciones de MAPE (Error Porcentual Absoluto Medio) asociadas a sus forecasts. Para mayor completitud, explicaremos cómo heurísticas simples pueden ser utilizadas para superar este problema.
En particular, la varianza dentro de los datos históricos puede utilizarse como una buena heurística para estimar la varianza del error forecast. David Piasecki también sugiere utilizar la demanda forecast en lugar de la demanda media en la expresión de la varianza, es decir
donde $$E$$ es el operador media, $$y_t$$ es la demanda histórica para el período $$t$$ (típicamente la cantidad de ventas) y $$y’$$ la demanda forecast.
La idea clave detrás de esta asunción es que el error forecast a menudo está correlacionado con la cantidad de variación esperada: cuanto mayores sean las variaciones venideras, mayor será el error en los forecasts.
En realidad, el cálculo de esta varianza del error implica algunas sutilezas que se tratarán con mayor detalle a continuación.
Expresión del stock de seguridad
En este punto, hemos determinado tanto la media como la varianza, por lo que se conoce la distribución del error. Ahora debemos calcular el nivel de error aceptable dentro de esta distribución. Anteriormente, hemos introducido la noción de nivel de servicio (un porcentaje) para ello.
Notas: Estamos asumiendo un lead time estático. Sin embargo, se puede usar un enfoque muy similar para un lead time variable. Véase
Para convertir el nivel de servicio en un nivel de error también llamado factor de servicio, debemos usar la distribución normal acumulativa inversa (a veces también llamada distribución normal inversa) (véase NORMSINV para la función correspondiente de Excel). Aunque pueda sonar complicado, no lo es; sugerimos echar un vistazo al applet de distribución normal para obtener una visión más visual. Como se puede ver, la función acumulativa transforma el porcentaje en un área bajo la curva, con el umbral del eje X correspondiente al valor del factor de servicio.
Intuitivamente, calculamos
stock de seguridad = desviación estándar del error * factor de servicio
De manera más formal, sea $$S$$ el stock de seguridad, tenemos
donde $$\sigma$$ es la desviación estándar (es decir, la raíz cuadrada de $$\sigma^2$$, la varianza definida anteriormente), $$cdf$$ es la distribución normal acumulativa normalizada (media cero y varianza igual a uno) y $$P$$ el nivel de servicio.
Recordando que
punto de reorden = demanda del lead time + stock de seguridad
Sea $$R$$ el punto de reorden, tenemos
Ajustando el lead time y el período de forecast
Hasta ahora, hemos asumido simplemente que para un lead time dado, éramos capaces de producir directamente el forecast de la demanda futura correspondiente. En la práctica, no funciona exactamente así. El análisis de los datos históricos usualmente comienza agregando los datos en períodos de tiempo (semanas o meses, típicamente).
Sin embargo, el período elegido puede no coincidir exactamente con el lead time; por lo tanto, se requieren cálculos adicionales para expresar la demanda del lead time y su varianza asociada (teniendo en cuenta que aún estamos asumiendo una distribución normal para el error forecast, como se detalla en la sección anterior).
Intuitivamente, se puede calcular la demanda del lead time como la suma de los valores forecast para los períodos futuros que intersectan el segmento del lead time. Se debe tener cuidado de ajustar adecuadamente el último período forecast.
Formalmente, sea $$T$$ el período y $$L$$ el lead time. Escribimos
donde $$k$$ es un entero y $$0 ≤ α < 1$$. Sea $$D$$ la demanda del lead time. Entonces, tenemos la expresión final para la demanda del lead time
donde $$y’_n$$ es la demanda forecast para el $$n^{ésimo}$$ período en el futuro.
Considerando las mismas asunciones de distribución normal, podemos calcular la varianza del error forecast como
donde $$y’$$ es el forecast promedio por período
Sin embargo, $$\sigma^2$$ se calcula aquí como una varianza por período mientras que se necesitaría una varianza que se ajuste al lead time. Sea $$\sigma_{L}^2$$ la varianza ajustada por lead time, tenemos
Finalmente, podemos reexpresar el punto de reorden como
Usando Excel para calcular el punto de reorden
Esta sección detalla cómo calcular el punto de reorden con Microsoft Excel. Sugerimos echar un vistazo a la hoja de cálculo de muestra de Excel proporcionada.
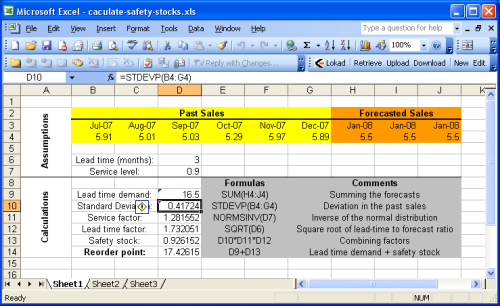
La hoja de muestra se divide básicamente en dos secciones: las asunciones en la parte superior y los cálculos en la parte inferior. Se asume que los forecasts forman parte de las asunciones porque el forecast de ventas (o demanda) está fuera del alcance de esta guía. Puedes consultar nuestro tutorial para el forecast de ventas con Microsoft Excel para más detalles.
La mayoría de las fórmulas introducidas en la sección anterior son operaciones muy simples (sumas, multiplicaciones) que son muy fáciles de realizar con Microsoft Excel. Sin embargo, dos funciones destacan
- NORMSINV (Microsoft KB): estima la distribución normal acumulativa, denominada cdf anteriormente.
- STDEV (Microsoft KB): estima la desviación estándar, denominada $$σ$$ anteriormente. Recordamos que la desviación estándar $$σ$$ es la raíz cuadrada de la varianza $${σ^2}$$.
Para simplificar, la primera hoja no implementa la heurística $${σ^2 = E[ (y_t - y’)^2 ]}$$ al calcular el factor de servicio. Este enfoque se implementa en Sheet2 (la segunda hoja del documento de Excel). Dado que hemos asumido forecasts estacionarios en el ejemplo, el punto de reorden permanece idéntico con o sin esta heurística.
Recursos
Inventory Management and Production Planning and Scheduling, Edward A. Silver, David F. Pyke, Rein Peterson, Wiley; 3ª edición, 1998