Forecast probabilístico (Supply Chain)

Se dice que un forecast es probabilístico, en lugar de determinista, si contiene un conjunto de probabilidades asociadas a todos los posibles resultados futuros, en lugar de señalar un resultado en particular como “el” forecast. Los forecast probabilísticos son importantes cuando la incertidumbre es irreducible, lo cual ocurre casi siempre en sistemas complejos. Para las supply chain, los forecast probabilísticos son esenciales para producir decisiones robustas frente a condiciones futuras inciertas. En particular, la demanda y lead time, dos aspectos clave del análisis de la supply chain, se abordan de la mejor manera mediante forecast probabilístico. La perspectiva probabilística se presta naturalmente a la priorización económica de las decisiones basadas en sus retornos esperados pero inciertos. Una gran variedad de modelos estadísticos ofrece forecast probabilísticos. Algunos son estructuralmente cercanos a sus contrapartes deterministas, mientras que otros son muy diferentes. Evaluar la precisión de un forecast probabilístico requiere métricas específicas, que difieren de las utilizadas para los forecast deterministas. El uso de forecast probabilísticos requiere herramientas especializadas que divergen de sus contrapartes deterministas.

Forecast deterministas vs. forecast probabilísticos

La optimización de las supply chain depende de la correcta anticipación de los eventos futuros. Numéricamente, estos eventos se anticipan mediante forecasts, que abarcan una gran variedad de métodos numéricos utilizados para cuantificar dichos eventos. Desde la década de 1970, la forma más utilizada de forecast ha sido el forecast determinista de series de tiempo: una cantidad medida a lo largo del tiempo —por ejemplo, la demanda en unidades de un producto— se proyecta hacia el futuro. La sección pasada de la serie de tiempo corresponde a los datos históricos, mientras que la sección futura es el forecast.

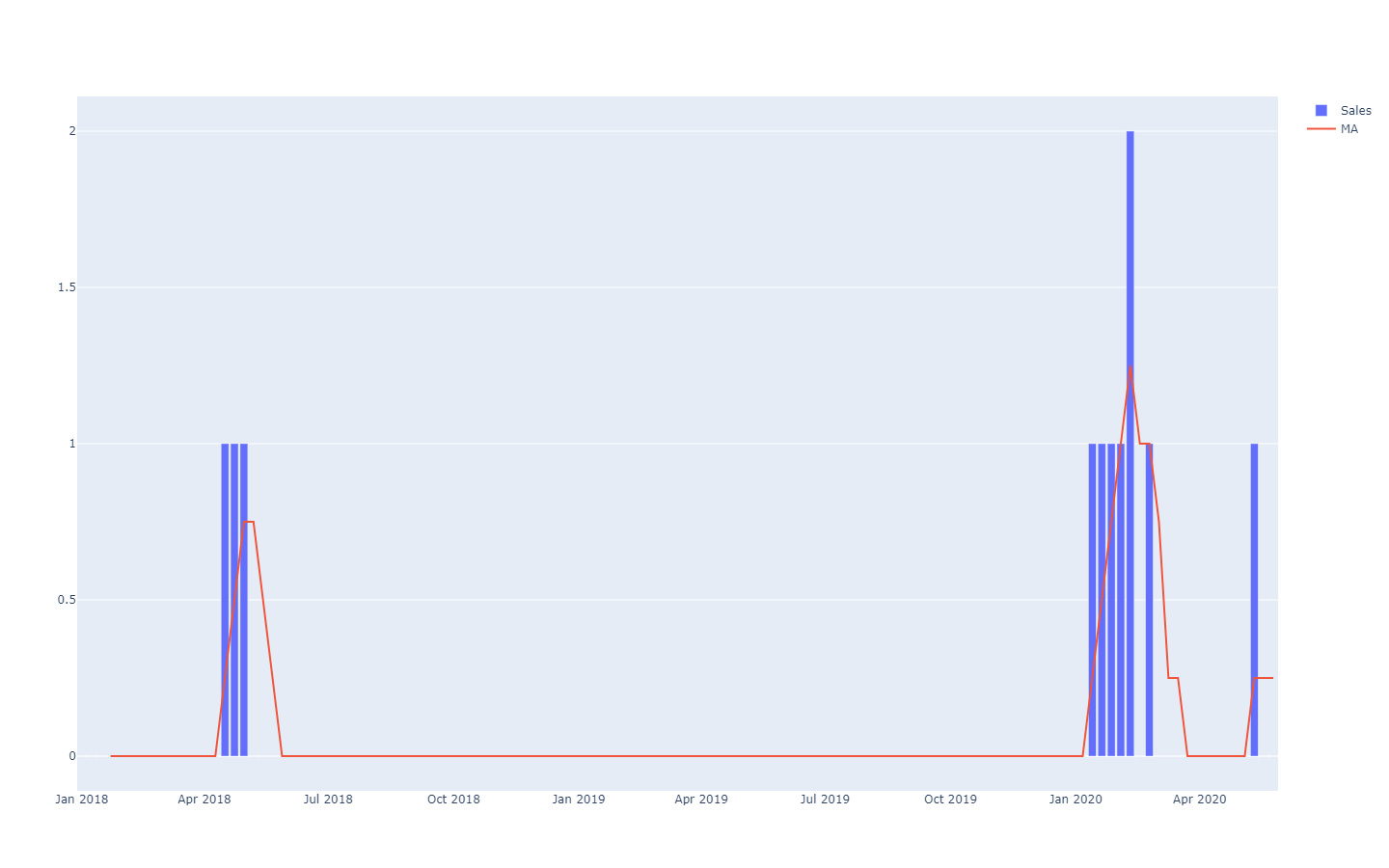
Se dice que estos forecasts de series de tiempo son deterministas porque, para cada punto en el futuro, el forecast proporciona un único valor que se espera se ajuste lo más posible al resultado futuro. De hecho, aunque el forecast es de un único valor, se entiende ampliamente que tiene poca posibilidad de ser perfectamente correcto. Los resultados futuros divergerán del forecast. La adherencia del forecast determinista a sus resultados futuros se evalúa cuantitativamente mediante métricas de precisión, como el error cuadrático medio (MSE), por ejemplo.

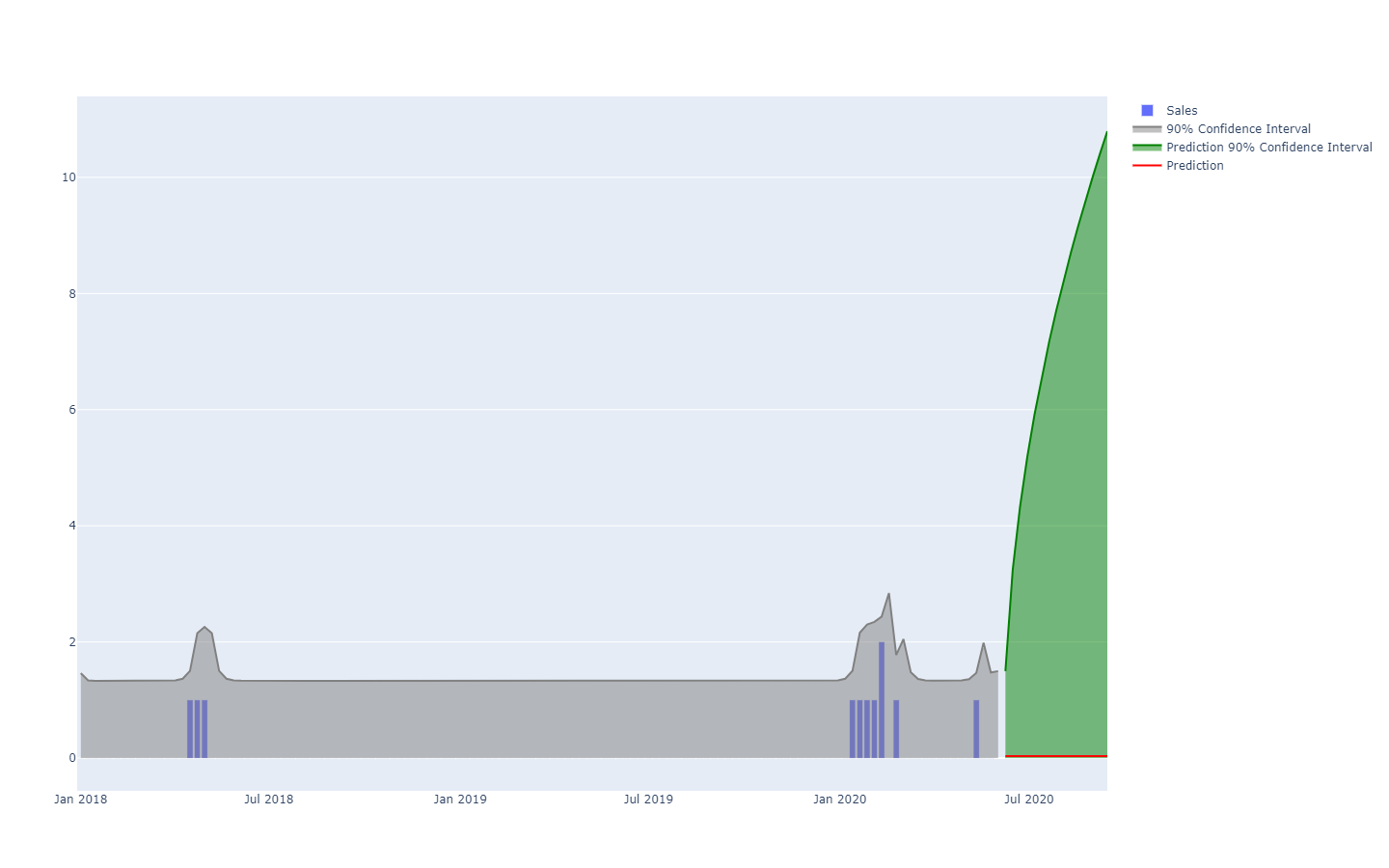
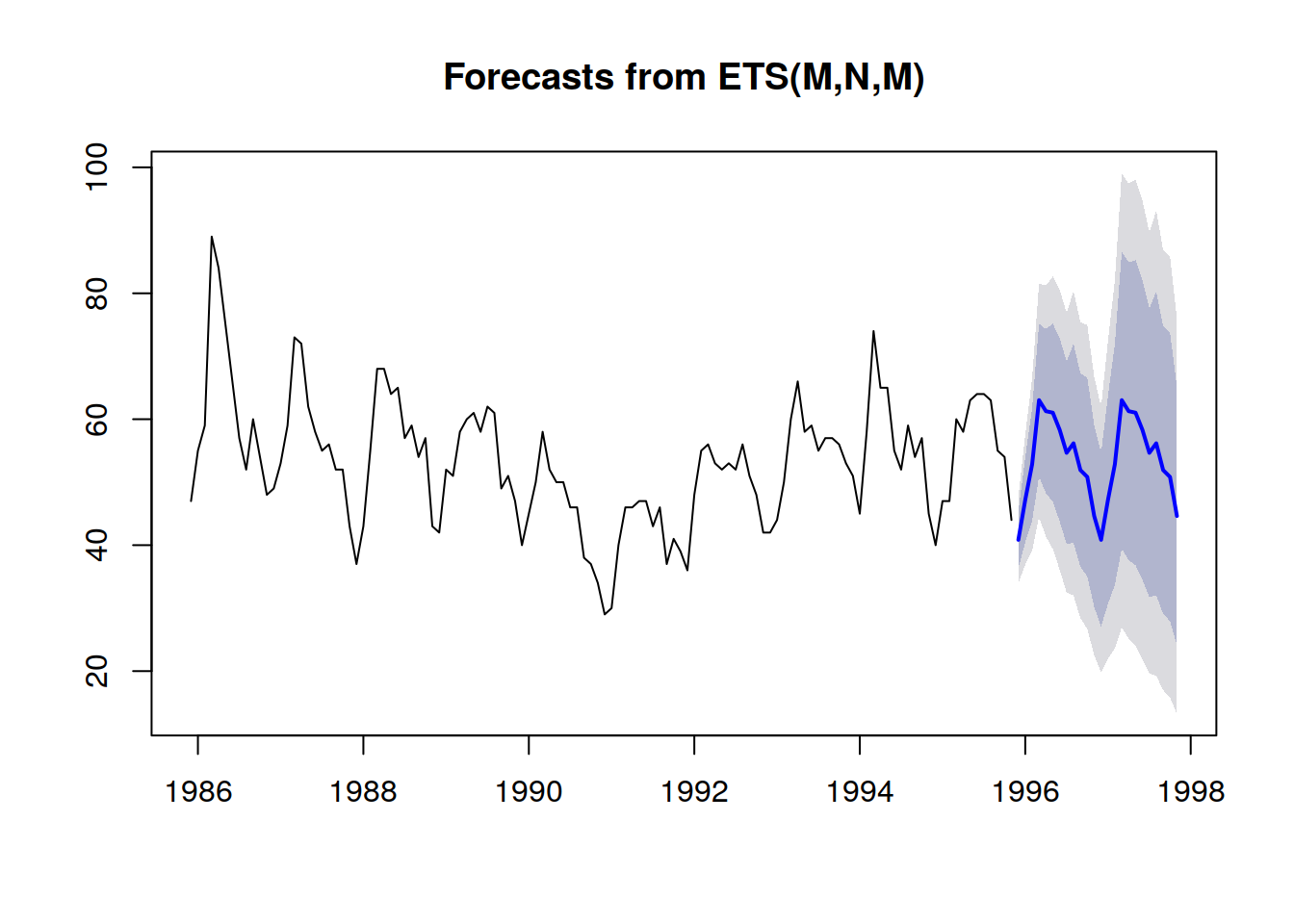
Los forecasts probabilísticos adoptan una perspectiva diferente sobre la anticipación de los resultados futuros. En lugar de producir un único valor como el “mejor” resultado, el forecast probabilístico consiste en asignar una probabilidad a cada resultado posible. En otras palabras, todos los eventos futuros siguen siendo posibles, solo que no son igualmente probables. A continuación se muestra la visualización de un forecast probabilístico de series de tiempo que exhibe el “efecto escopeta”, típicamente observado en la mayoría de las situaciones del mundo real. Revisaremos esta visualización en mayor detalle a continuación.

Las series de tiempo, una cantidad medida a lo largo del tiempo, son probablemente el modelo de datos más conocido y utilizado. Este modelo de datos puede ser forecast tanto mediante métodos deterministas como probabilísticos. Sin embargo, existen muchos modelos de datos alternativos, normalmente más ricos, que también se prestan a ambos tipos de forecast. Por ejemplo, una empresa que repara motores de aviones puede desear anticipar la lista exacta de repuestos que se necesitarán para una operación de mantenimiento próxima. Esta anticipación puede tomar la forma de un forecast, pero no será un forecast de series de tiempo. El forecast determinista asociado con esta operación es la lista exacta de piezas y sus cantidades. En cambio, el forecast probabilístico es la probabilidad de que cada combinación de piezas (incluidas las cantidades) sea la necesaria para realizar las reparaciones.

Además, aunque el término “forecast” enfatiza una anticipación de algún tipo, la idea puede generalizarse a cualquier tipo de afirmación estadísticamente inferida sobre un sistema, incluyendo sus propiedades pasadas (pero desconocidas). La práctica de forecast estadístico surgió durante el siglo XX, antes del advenimiento de la perspectiva más moderna del statistical learning, que abarca todas las extrapolaciones impulsadas por datos que pueden realizarse, independientemente de cualquier dimensión temporal. Para mayor claridad, seguiremos utilizando el término “forecast” a lo largo del texto, incluso si el aspecto temporal siempre asocia lo pasado con lo conocido y lo futuro con lo desconocido. Por ejemplo, una empresa puede desear estimar las ventas que se habrían realizado de un producto en una tienda si el producto no hubiera estado faltante de stock ese día. La estimación es útil para cuantificar la magnitud del problema en términos de calidad del servicio. Sin embargo, dado que el evento es pasado, la cifra de ventas “real” nunca se observará. No obstante, asumiendo que aún no se ha observado trivialmente, la estimación estadística de la demanda pasada es un problema muy cercano a la estimación de la demanda futura.

Los forecasts probabilísticos son más ricos —en términos de información— que sus homólogos deterministas. Mientras que el forecast determinista proporciona una “mejor estimación” del resultado futuro, no dice nada sobre las alternativas. De hecho, siempre es posible convertir un forecast probabilístico en su contraparte determinista tomando la media, la mediana, la moda, … de la distribución de probabilidad. Sin embargo, lo contrario no es cierto: no es posible recuperar un forecast probabilístico a partir de uno determinista.

Sin embargo, aunque los forecasts probabilísticos son estadísticamente superiores a los forecasts deterministas, siguen siendo utilizados de forma poco frecuente en la supply chain. No obstante, su popularidad ha ido en aumento constante durante la última década. Históricamente, los forecasts probabilísticos surgieron más tarde, ya que requieren significativamente más recursos computacionales. Aprovechar los forecasts probabilísticos para fines de supply chain también requiere herramientas de software especializadas, que a menudo están indisponibles.

Casos de uso en supply chain

Optimizar una supply chain consiste en tomar la decisión “correcta” —en el momento presente— que abordará de manera más rentable una situación futura que solo se puede estimar de forma imperfecta. Sin embargo, la incertidumbre asociada con los eventos futuros es en gran medida irreducible. Por lo tanto, la empresa necesita que la decisión sea robusta si la anticipación del evento futuro —es decir, el forecast— es imperfecta. Esto se ha hecho mínimamente desde mediados del siglo XX mediante el análisis de safety stock. Sin embargo, como veremos a continuación, además del interés histórico, ya no hay ninguna razón para favorecer los safety stocks sobre los numerical recipes.

La perspectiva de forecast probabilístico adopta una postura radical frente a la incertidumbre: este enfoque intenta cuantificar la incertidumbre al máximo posible. En la supply chain, los costos tienden a concentrarse en los extremos estadísticos: es la demanda inesperadamente alta la que crea el faltante de stock, y es la demanda inesperadamente baja la que genera la cancelación del inventario. Entre tanto, el inventario rota de manera adecuada. Los forecasts probabilísticos son —en términos sencillos— un intento de gestionar estas situaciones de baja frecuencia y alto costo que son ubicuas en las modern supply chains. Los forecasts probabilísticos pueden y deben considerarse como un ingrediente fundamental de cualquier práctica de gestión de riesgos dentro de la supply chain.

Muchos aspectos de las supply chain son particularmente adecuados para el forecast probabilístico, tales como:

• demanda: prendas, accesorios, repuestos; así como muchos otros tipos de productos, tienden a asociarse con una demanda errática y/o intermitente. Los lanzamientos de productos pueden ser un éxito o un fracaso. Las Promociones de los competidores pueden canibalizar de forma temporal y errática grandes porciones de las cuotas de mercado.
• lead time: las importaciones del extranjero pueden experimentar una serie de retrasos en cualquier punto de la cadena (producción, transporte, aduanas, recepción, etc.). Incluso los proveedores locales pueden tener, en ocasiones, lead times largos si enfrentan un problema de faltante de stock. Los lead times tienden a seguir distribuciones de “cola gruesa.”
• yield (fresh food): la cantidad y la calidad de la producción de muchos productos frescos dependen de condiciones, como el clima, que están fuera del control de la empresa. El forecast probabilístico cuantifica estos factores para toda la temporada y ofrece la posibilidad de ir más allá del horizonte de relevancia de los forecast del tiempo clásicos.
• returns (ecommerce): cuando un cliente pide el mismo producto en tres tallas diferentes, las probabilidades son altas de que dos de esas tallas sean devueltas. Más generalmente, aunque existen marcadas diferencias regionales, los clientes tienden a aprovechar políticas de return favorables cuando estas existen. Se debe evaluar la probabilidad de returns para cada pedido.
• scraps (aviation): las piezas reparables de aeronaves —frecuentemente denominadas rotables— a veces no pueden ser reparadas. En este caso, la pieza se desecha, ya que no es apta para volver a montarse en una aeronave. Aunque generalmente no es posible saber de antemano si una pieza sobrevivirá a su reparación o no, se deben estimar las probabilidades de que la pieza sea descartada.
• stocks (B2C retail): los clientes pueden desplazar, dañar o incluso robar productos de una tienda minorista. Por lo tanto, el stock level electrónico es solo una aproximación de la disponibilidad real en estantería según la percepción de los clientes. El stock level, tal como lo perciben los clientes, debe ser estimado mediante un forecast probabilístico.
• …

Esta breve lista ilustra que los enfoques aptos para un forecast probabilístico exceden con creces al único enfoque tradicional de “demand forecasting”. La optimización bien diseñada de una supply chain requiere tener en cuenta todas las fuentes relevantes de incertidumbre. Aunque a veces es posible reducir la incertidumbre —como lo enfatiza el lean manufacturing—, generalmente están involucrados trade-offs, y como resultado, queda una cierta cantidad de incertidumbre que es irreducible.

Los forecasts, sin embargo, son meramente opiniones fundamentadas sobre el futuro. Si bien los forecasts probabilísticos pueden considerarse como opiniones sorprendentemente detalladas, no son fundamentalmente diferentes de sus contrapartes deterministas en este sentido. El valor, en términos de supply chain, de los forecasts probabilísticos se encuentra en la forma en que se explota esta estructura detallada para ofrecer decisiones más rentables. En particular, no se espera que los forecasts probabilísticos sean más precisos que los forecasts deterministas si se utilizan métricas de precisión deterministas para evaluar la calidad de los forecasts.

En defensa de la variabilidad

A pesar de lo que muchos enfoques de supply chain abogan, la variabilidad ha venido para quedarse, de ahí la necesidad de los forecasts probabilísticos. El primer concepto erróneo es que la variabilidad es necesariamente algo negativo para una supply chain; no lo es. El segundo concepto erróneo es que la variabilidad puede eliminarse mediante la ingeniería; no es posible.

La variabilidad tiene implicaciones positivas para las supply chain en múltiples situaciones. Por ejemplo, en el lado de la demanda, la mayoría de los sectores se impulsan por la novedad, como la moda, los productos culturales, el soft y hard luxury —al igual que los negocios de “éxito o fracaso”. La mayoría de los new products no son éxitos (fracasos), pero aquellos que tienen éxito (hits) generan retornos masivos. La variabilidad extra es beneficiosa porque aumenta la probabilidad de retornos desproporcionados, mientras que las desventajas se mantienen limitadas (en el peor de los casos, todo el inventario es cancelado). El flujo interminable de new products lanzados al mercado asegura la renovación constante de los “hits”, mientras que los antiguos se van desvaneciendo.

En el lado de la oferta, un proceso de sourcing que garantice ofertas de precios altamente variables es superior —todo lo demás siendo igual— a un proceso alternativo que genere precios mucho más consistentes (es decir, menos variables). De hecho, se selecciona la opción con el precio más bajo mientras que las demás son descartadas. No importa si el precio “promedio” obtenido es bajo, lo que importa es descubrir fuentes con precios aún más bajos. Por lo tanto, el buen proceso de sourcing debe estar diseñado para aumentar la variabilidad, por ejemplo, enfatizando la exploración rutinaria de nuevos proveedores en lugar de limitar el proceso de sourcing a los ya bien establecidos.

A veces, la variabilidad puede ser beneficiosa por razones más sutiles. Por ejemplo, si una marca es demasiado predecible en lo que respecta a sus operaciones promocionales, los clientes identifican el patrón y comienzan a retrasar su compra al saber que se aproxima una promoción. La variabilidad —incluso la erraticidad— de las actividades promocionales mitiga este comportamiento en cierta medida.

Otro ejemplo es la presencia de factores de confusión dentro de la propia supply chain. Si los new products se lanzan siempre con una campaña de TV y una de radio, se vuelve estadísticamente difícil distinguir los impactos respectivos de la TV y de la radio. Agregar variabilidad a la intensidad de cada campaña dependiendo del canal asegura que se pueda extraer más información estadística de esas operaciones posteriormente, la cual puede transformarse en insights para una mejor asignación de los recursos de marketing.

Naturalmente, no toda la variabilidad es buena. Lean manufacturing es correcto al enfatizar que, en el lado de producción de la supply chain, la variabilidad suele ser perjudicial, especialmente cuando se trata de retrasos que varían. De hecho, procesos LIFO (last-in first-out) pueden introducirse accidentalmente, lo que, a su vez, exacerba la variabilidad del tiempo de entrega. En esas situaciones, la variabilidad accidental debe eliminarse, normalmente mediante un proceso mejor, y en ocasiones mediante mejores equipos o instalaciones.

La variabilidad –incluso cuando es perjudicial– es frecuentemente irreducible. Como veremos en la siguiente sección, las supply chain se rigen por la ley de los números pequeños. Es ilusorio pensar que el nivel de una tienda alguna vez se pueda predecir de forma fiable – desde una perspectiva determinista – mientras los clientes no siempre saben ellos mismos lo que están a punto de comprar. En general, reducir la variabilidad siempre tiene un costo (y reducirla aún más cuesta aún más), mientras que la reducción marginal de la variabilidad sólo trae rendimientos decrecientes. Por lo tanto, incluso cuando se puede reducir la variabilidad, en la práctica rara vez se puede eliminar por completo debido a las implicaciones económicas.

La Ley de los Números Pequeños

La ley de los números pequeños en la supply chain puede establecerse como: los números pequeños prevalecen en toda la cadena. Esta ley observacional resulta de las economías de escala y de algunas otras fuerzas que impulsan la mayoría de los aspectos estructurales de las supply chain:

• un proveedor que suministra decenas de miles de unidades de materiales por día probablemente tenga cantidades mínimas de pedido (MOQ) o descuentos que impidan que se realicen órdenes de compra con demasiada frecuencia. El número de órdenes de compra transmitidas en un día a un proveedor rara vez supera un dígito.
• una fábrica que produce decenas de miles de unidades por día probablemente opere en grandes lotes de miles de unidades. La producción suele estar empaquetada en pallets enteros. El número de lotes durante cualquier día es, como máximo, un pequeño número de dos dígitos.
• un almacén que recibe decenas de miles de unidades por día probablemente reciba entregas mediante trucks, cada camión descargando toda su carga en el almacén. El número de entregas de camiones en cualquier día rara vez supera un número de dos dígitos, incluso para almacenes muy grandes.
• una tienda minorista que puede almacenar decenas de miles de unidades en stock probablemente distribuya su surtido en miles de referencias de producto distintas. La cantidad de unidades en stock para cada producto rara vez supera un dígito.
• …

Naturalmente, cambiando la unidad de medida, siempre es posible inflar los números. Por ejemplo, si en lugar de contar el número de pallets contamos el número de gramos de pallets, o sus valores monetarios en centavos USD, aparecen números grandes. Sin embargo, la ley de los números pequeños debe entenderse con la noción de contar las cosas desde una perspectiva sensata de supply chain. Aunque, en teoría, este principio puede parecer bastante subjetivo, no es así en la práctica, debido a las evidentes implicaciones discretas de las supply chain modernas: bundles, cajas, pallets, contenedores, trucks …

Esta ley es de gran relevancia para la perspectiva de forecast probabilístico. Primero, establece que los forecast discretos dominan en situaciones de supply chain, es decir, el resultado a anticipar (o decidir) es un entero, en contraposición a un número fraccional. Los forecast probabilísticos son particularmente adecuados para situaciones discretas, porque se puede estimar una probabilidad para cada resultado discreto. En contraste, los forecast determinísticos tienen dificultades con los resultados discretos. Por ejemplo, ¿qué se supone que significa que las ventas diarias esperadas de un producto sean de 1.3 unidades? Las unidades no se venden de forma fraccionada. Aunque se puedan inferir interpretaciones “discretas” más sensatas a partir de esta afirmación, su contraparte probabilística (por ejemplo, 27% de probabilidad de 0 unidad de demanda, 35% de probabilidad de 1 unidad de demanda, 23% de probabilidad de 2 unidades de demanda, etc.) es mucho más directa, ya que abraza la naturaleza discreta del fenómeno de interés.

Segundo, aunque los forecast probabilísticos puedan parecer radicalmente más desafiantes en términos de recursos computacionales en bruto, en realidad no es así en la práctica, precisamente debido a la ley de los números pequeños. De hecho, volviendo a las ventas diarias de productos discutidas anteriormente, no tiene sentido evaluar numéricamente las probabilidades de que la demanda supere las 100 en cualquier día dado. Esas probabilidades pueden redondearse a cero – o a algún valor arbitrariamente pequeño. El impacto en la precisión numérica del modelo de supply chain permanece siendo insignificante. Como regla general, es razonable considerar que los forecast probabilísticos requieren aproximadamente tres órdenes de magnitud más de recursos computacionales que sus contrapartes determinísticas. Sin embargo, a pesar de esta sobrecarga, los beneficios en términos de supply chain performance superan con creces el costo de los recursos computacionales.

Métricas de precisión para forecast probabilísticos

Pase lo que pase, un forecast probabilístico razonablemente bien diseñado indica que, efectivamente, existía una probabilidad no nula de que ocurriera este resultado. Esto es intrigante porque, a primera vista, podría parecer que los forecast probabilísticos fueran de alguna manera inmunes a la realidad, como un adivino que hace declaraciones proféticas vagamente ambiguas que nunca pueden demostrarse erróneas, ya que el adivino siempre puede inventar una explicación posterior sobre la forma adecuada de interpretar las profecías después de los hechos. En realidad, existen múltiples maneras de evaluar cuantitativamente la calidad de un forecast probabilístico. Algunas de estas maneras son métricas similares en espíritu a las utilizadas para evaluar la precisión de los forecast determinísticos. Otras divergen hacia enfoques más radicales y profundos en comparación con la perspectiva determinística.

Revisemos brevemente cuatro enfoques distintos para evaluar la precisión de un forecast probabilístico:

• la función de pérdida pinball
• el continuous ranked probability score (CRPS)
• la likelihood bayesiana
• la perspectiva generativa adversarial

La función de pérdida pinball proporciona una métrica de precisión para que se derive una estimación de cuantiles a partir de un forecast probabilístico. Por ejemplo, si deseamos evaluar la cantidad de stock que tiene un 98% de probabilidad de ser mayor o igual que la demanda del cliente en una tienda para un producto dado, dicha cantidad se puede obtener directamente de los forecast probabilísticos simplemente sumando las probabilidades empezando desde 0 unidades de demanda, 1 unidad de demanda, … hasta que la probabilidad supere el 98%. La función de pérdida pinball proporciona una medida directa de la calidad de esta estimación sesgada de la demanda futura. Se puede ver como una herramienta para evaluar la calidad de cualquier punto de la función de densidad acumulada del forecast probabilístico.

El continuously ranked probability score (CRPS) proporciona una métrica, que puede interpretarse como la “cantidad de desplazamiento” de la masa de probabilidades necesaria para mover toda la masa de probabilidad al resultado observado. Es la generalización más directa del error absoluto medio (MAE) hacia una perspectiva probabilística. El valor del CRPS es homogéneo con la unidad de medida del propio resultado. Esta perspectiva puede generalizarse a espacios métricos arbitrarios, en lugar de solo situaciones unidimensionales, a través de lo que se conoce como “teoría del transporte” y la distancia de Monge-Kantorovich (lo cual excede el alcance del presente documento).

La likelihood y su primo de entropía cruzada adoptan la perspectiva bayesiana del menor grado de sorpresa: cuanto mayor sea la probabilidad de los resultados observados, mejor. Por ejemplo, tenemos dos modelos probabilísticos, A y B: el modelo A establece que la probabilidad de observar 0 unidad de demanda es del 50% para cualquier día; el modelo B establece que la probabilidad de observar 0 unidad de demanda es del 1% para cualquier día. Observamos la demanda durante 3 días y obtenemos las siguientes observaciones: 0, 0, 1. El modelo A tenía aproximadamente un 10% de probabilidad de generar estas observaciones, mientras que para el modelo B, era solo alrededor de un 0,01%. Así, el modelo B es mucho menos probable de ser el modelo correcto en comparación con el modelo A. La likelihood se desvía de la perspectiva determinística de tener un criterio absoluto significativo para evaluar modelos. En su lugar, proporciona un mecanismo para comparar modelos, pero numéricamente, este mecanismo no puede usarse para nada más que para comparar modelos.

La perspectiva generativa adversarial es la más moderna sobre el tema (Ian Goodfellow et al., 2014). Esencialmente, esta perspectiva establece que el modelo probabilístico “óptimo” es aquel que puede utilizarse para generar resultados – monte-carlo style – que sean indistinguibles de resultados reales. Por ejemplo, si consideráramos la lista histórica de transacciones en un hipermercado local, podríamos truncar este historial en un punto arbitrario en el pasado y usar el modelo probabilístico para generar transacciones ficticias pero realistas a partir de entonces. El modelo se consideraría “perfecto” si fuera imposible, mediante análisis estadístico, recuperar el momento en que el conjunto de datos pasa de ser “real” a “falso”. El objetivo del enfoque generativo adversarial es “aprender” las métricas que exacerban la falla de cualquier modelo probabilístico. En lugar de centrarse en una métrica particular, esta perspectiva aprovecha de forma recursiva técnicas de machine learning para “aprender” las propias métricas.

Buscar mejores formas de evaluar la calidad de los forecast probabilísticos sigue siendo un área activa de investigación. No existe una delimitación clara entre las dos preguntas “¿Cómo producir un forecast mejor?” y “¿Cómo saber si un forecast es mejor?”. Trabajos recientes han difuminado considerablemente la línea entre ambas, y es probable que los próximos avances involucren cambios adicionales en la forma misma en que se abordan los forecast probabilísticos.

Probabilidades ínfimas y log likelihood

Probabilidades muy pequeñas surgen naturalmente al observar una situación de muchas dimensiones a través del prisma de los forecast probabilísticos. Esas probabilidades diminutas son problemáticas porque las computadoras no procesan números con precisión indefinida. Los valores de probabilidad en bruto son frecuentemente tan pequeños que se redondean a cero debido a los límites de precisión numérica. La solución a este problema no es actualizar el software hacia cálculos de precisión arbitraria – lo cual es muy ineficiente en términos de recursos computacionales – sino utilizar el “log-trick”, que transforma las multiplicaciones en sumas. Este truco es utilizado – de una forma u otra – por prácticamente cada aplicación de software que maneja forecast probabilísticos.

Supongamos que tenemos $$X_1, X_2, \ldots, X_n$$ variables aleatorias que representan la demanda del día para todos los $$n$$ productos distintos atendidos en una determinada tienda. Sea $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ la demanda empírica observada al final del día para cada producto. Para el primer producto – gobernado por $$X_1$$ – la probabilidad de observar $$\hat{x}_1$$ se escribe $$P(X_1=\hat{x}_1)$$ . Ahora, supongamos, de manera algo abusiva pero por el bien de la claridad, que todos los productos son estrictamente independientes en cuanto a la demanda. La probabilidad del evento conjunto de observar $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ es:

Si $$P(X_k=\hat{x}_k) \approx \tfrac{1}{2}$$ (aproximación burda) y $$n=10000$$, entonces la probabilidad conjunta anterior es del orden de $$\tfrac{1}{{2^{10000}}} \approx 5 \times 10^{-3011}$$, lo cual es un valor muy pequeño. Este valor sufre underflow, es decir, cae por debajo del número pequeño representable, incluso considerando los números de punto flotante de 64 bits que se utilizan típicamente para la computación científica.

El “log-trick” consiste en trabajar con el logaritmo de la expresión, es decir:

El logaritmo convierte la serie de multiplicaciones en una serie de sumas, lo que resulta ser mucho más estable numéricamente que una serie de multiplicaciones.

El uso del “log-trick” es frecuente siempre que se involucran forecast probabilísticos. El log likelyhood es, literalmente, el logaritmo de la likelihood (introducida previamente) precisamente porque la likelihood en bruto usualmente no podría representarse numéricamente considerando los tipos comunes de números de punto flotante.

Enfoques algorítmicos de forecast probabilísticos

La cuestión de la generación computarizada de forecast probabilísticos es casi tan vasta como el campo del machine learning en sí. Las delimitaciones entre ambos campos, si es que existen, son en su mayoría una cuestión de elecciones subjetivas. No obstante, esta sección presenta una lista bastante selectiva de enfoques algorítmicos notables que pueden emplearse para obtener forecast probabilísticos.

A principios del siglo XX, posiblemente a finales del siglo XIX, surgió la idea del safety stock, donde la incertidumbre de la demanda se modela según una distribución normal. Dado que ya se habían establecido tablas precalculadas de la distribución normal para otras ciencias, especialmente la física, la aplicación del safety stock solo requería multiplicar un nivel de demanda por un coeficiente de “safety stock” extraído de una tabla preexistente. Anecdóticamente, muchos libros de texto de supply chain escritos hasta los años 90 todavía contenían tablas de la distribución normal en sus apéndices. Desafortunadamente, la principal desventaja de este enfoque es que las distribuciones normales no son una propuesta razonable para las supply chain. Primero, en lo que respecta a las supply chain, es seguro asumir que nada se distribuye normalmente. Segundo, la distribución normal es una distribución continua, lo cual está en desacuerdo con la naturaleza discreta de los eventos en la supply chain (véase “La Ley de los Números Pequeños” arriba). Así, aunque técnicamente los “safety stocks” tienen un componente probabilístico, la metodología subyacente y las recetas numéricas están decididamente orientadas hacia la perspectiva determinística. No obstante, este enfoque se incluye aquí por el bien de la claridad.

Avancemos rápidamente a principios de los años 2000, los métodos de ensemble learning – cuyos representantes más conocidos son probablemente los random forests y los gradient boosted trees – son relativamente sencillos de extender desde sus orígenes deterministas hacia la perspectiva probabilística. La idea clave detrás de ensemble learning es combinar numerosos predictores deterministas débiles, tales como los árboles de decisión, en un predictor determinista superior. Sin embargo, es posible ajustar el proceso de mezcla para obtener probabilidades en lugar de un solo agregado, convirtiendo así el método de ensemble learning en un forecast probabilístico. Estos métodos son no paramétricos y capaces de ajustar distribuciones de cola gruesa y/o multimodales, como se encuentran comúnmente en la supply chain. Estos métodos tienden a tener dos inconvenientes notables. Primero, por construcción, la función de densidad de probabilidad producida por esta clase de modelos tiende a incluir muchos ceros, lo cual impide cualquier intento de aprovechar la métrica de log-likelihood. Más generalmente, estos modelos no encajan realmente con la perspectiva bayesiana, ya que las nuevas observaciones son frecuentemente declaradas “imposibles” (es decir, de probabilidad cero) por el modelo. Este problema, sin embargo, puede resolverse mediante métodos de regularización¹. Segundo, los modelos tienden a ser tan grandes como una fracción considerable del conjunto de datos de entrada, y la operación de “predict” tiende a ser casi tan costosa computacionalmente como la operación de “learn”.

Los métodos hiperparamétricos conocidos colectivamente bajo el nombre de “deep learning”, que surgieron de forma explosiva en la década de 2010, fueron, casi accidentalmente, probabilísticos. De hecho, aunque la gran mayoría de las tareas en las que deep learning realmente brilla (por ejemplo, clasificación de imágenes) se centra únicamente en forecast deterministas, resulta que la métrica de cross-entropy – una variante del log likelihood discutida anteriormente – exhibe gradientes muy pronunciados que son frecuentemente adecuados para el descenso por gradiente estocástico (SGD), que es el núcleo de los métodos de deep learning. Así, los modelos de deep learning resultan estar diseñados como probabilísticos, no porque las probabilidades fueran de interés, sino porque el descenso por gradiente converge más rápido cuando la función de pérdida refleja un forecast probabilístico. De este modo, en lo que respecta a deep learning, la supply chain se distingue por su interés en la salida probabilística real del modelo de deep learning, mientras que la mayoría de otros usos colapsan la distribución de probabilidad a su media, mediana o moda. Las Mixture Density Networks son un tipo de red de deep learning orientada a aprender distribuciones de probabilidad complejas. El resultado en sí es una distribución paramétrica, posiblemente compuesta de gaussianas. Sin embargo, a diferencia de los “safety stocks”, una mezcla de muchas gaussianas puede, en la práctica, reflejar los comportamientos de cola gruesa que se observan en la supply chain. Aunque los métodos de deep learning son frecuentemente considerados el estado del arte, es importante señalar que lograr la estabilidad numérica, especialmente cuando se involucran mezclas de densidad, sigue siendo algo de un “arte oscuro”.

La programación diferenciable es un descendiente del deep learning, que ganó popularidad a finales de la década de 2010. Comparte muchos atributos técnicos con el deep learning, pero difiere significativamente en su enfoque. Mientras que el deep learning se centra en aprender funciones arbitrariamente complejas (es decir, jugar al Go) apilando un gran número de funciones sencillas (por ejemplo, capas convolucionales), la programación diferenciable se enfoca en la estructura fina del proceso de aprendizaje. La estructura más minuciosa y expresiva, literalmente, puede formatearse como un programa, que involucra ramas, bucles, llamadas a funciones, etc. La programación diferenciable es de gran interés para la supply chain, porque los problemas tienden a presentarse de formas altamente estructuradas, y esas estructuras son conocidas por los expertos². Por ejemplo, las ventas de una determinada camiseta pueden ser canibalizadas por otra camiseta de un color diferente, pero no por las ventas de una camiseta que difiera en tres tallas. Dichos priors estructurales son clave para lograr una alta eficiencia de datos. De hecho, desde la perspectiva de la supply chain la cantidad de datos tiende a ser muy limitada (cf. la ley de los números pequeños). Así, enmarcar estructuralmente el problema ayuda a asegurar que se aprendan los patrones estadísticos deseados, incluso cuando se cuenta con datos limitados. Además, los priors estructurales ayudan a abordar los problemas de estabilidad numérica. En comparación con los métodos de ensemble, los priors estructurales suelen requerir menos tiempo que la ingeniería de características; el mantenimiento del modelo también se simplifica. Por otro lado, la programación diferenciable sigue siendo una perspectiva bastante incipiente hasta la fecha.

La perspectiva de Monte Carlo (1930 / 1940) puede utilizarse para abordar los forecast probabilísticos desde un ángulo diferente. Los modelos discutidos hasta ahora proporcionan funciones de densidad de probabilidad (PDFs) explícitas. Sin embargo, desde una perspectiva de Monte Carlo, un modelo puede sustituirse por un generador – o muestreador – que genera aleatoriamente posibles resultados (a veces llamados “deviates”). Las PDFs pueden recuperarse promediando los resultados del generador, aunque frecuentemente se omiten las PDFs para reducir los requerimientos en términos de recursos computacionales. De hecho, el generador suele estar diseñado para ser mucho más compacto – en datos – que las PDFs que representa. La mayoría de los métodos de machine learning – incluidos aquellos mencionados anteriormente para abordar directamente los forecast probabilísticos – pueden contribuir a aprender un generador. Los generadores pueden tomar la forma de modelos paramétricos de baja dimensión (por ejemplo, modelos de espacio de estados) o de modelos hiperparamétricos (por ejemplo, los modelos LSTM y GRU en deep learning). Los métodos de ensemble rara vez se utilizan para apoyar procesos generativos debido a sus elevados costes computacionales en las operaciones de “predict”, de las que se depende extensamente para respaldar el enfoque Monte Carlo.

Trabajando con forecast probabilísticos

Obtener insights útiles y tomar decisiones a partir de forecast probabilísticos requiere herramientas numéricas especializadas. A diferencia de los forecast deterministas, donde se manejan números concretos, los forecast en sí son ya sean funciones de densidad de probabilidad explícitas o generadores Monte Carlo. La calidad de las herramientas probabilísticas es, en la práctica, tan importante como la calidad de los forecast probabilísticos. Sin estas herramientas, la explotación de los forecast probabilísticos se reduce a un proceso determinista (más sobre esto en la sección “Antipatterns” a continuación).

Por ejemplo, las herramientas deberían poder realizar tareas tales como:

• Combinar el tiempo de entrega de producción incierto con el tiempo de entrega de transporte incierto, para obtener el tiempo de entrega “total” incierto.
• Combinar la demanda incierta con el tiempo de entrega incierto, para obtener la demanda “total” incierta que debe cubrirse con el stock que está a punto de ordenarse.
• Combinar las devoluciones inciertas de pedidos (ecommerce) con la fecha de llegada incierta del pedido al proveedor en tránsito, para obtener el tiempo de entrega al cliente incierto.
• Aumentar el forecast de demanda, producido por un método estadístico, con un riesgo de cola derivado manualmente a partir de una comprensión a alto nivel de un contexto no reflejado en los datos históricos, como una pandemia.
• Combinar la demanda incierta con un estado incierto del stock respecto a la fecha de caducidad (retail de alimentos), para obtener el stock sobrante incierto al final del día.
• …

Una vez que todos los forecast probabilísticos – no solo los de demanda – estén debidamente combinados, debería llevarse a cabo la optimización de las decisiones de la supply chain. Esto implica una perspectiva probabilística de las restricciones, así como de la función de puntuación. Sin embargo, este aspecto de herramientas va más allá del alcance del presente documento.

Existen dos grandes “sabores” de herramientas para trabajar con forecast probabilísticos: primero, álgebras sobre variables aleatorias, y segundo, programación probabilística. Estos dos enfoques se complementan ya que no tienen la misma mezcla de ventajas y desventajas.

Un álgebra de variables aleatorias trabaja típicamente con funciones de densidad de probabilidad explícitas. El álgebra soporta las operaciones aritméticas habituales (suma, resta, multiplicación, etc.) pero trasladadas a sus contrapartes probabilísticas, tratando frecuentemente a las variables aleatorias como estadísticamente independientes. El álgebra proporciona una estabilidad numérica que está casi a la par con su contraparte determinista (es decir, números concretos). Todos los resultados intermedios pueden persistirse para un uso posterior, lo que resulta muy útil para organizar y solucionar problemas en la tuberia de extracción de datos. Por otro lado, la expresividad de estas álgebras tiende a ser limitada, ya que típicamente no es posible expresar todas las sutiles dependencias condicionales que existen entre las variables aleatorias.

La programación probabilística adopta una perspectiva Monte Carlo para el problema. La lógica se escribe una única vez, normalmente manteniéndose en una perspectiva completamente determinista, pero se ejecuta muchas veces a través de la herramienta (es decir, el proceso Monte Carlo) para recopilar las estadísticas deseadas. Se alcanza la máxima expresividad mediante construcciones “programáticas”: es posible modelar dependencias arbitrarias y complejas entre las variables aleatorias. Escribir la lógica misma a través de la programación probabilística también resulta algo más sencillo en comparación con un álgebra de variables aleatorias, ya que la lógica solo involucra números concretos. Por otro lado, existe un compromiso constante entre la estabilidad numérica (más iteraciones brindan mejor precisión) y los recursos computacionales (más iteraciones cuestan más). Además, los resultados intermedios típicamente no están disponibles, ya que su existencia es solo transitoria – precisamente para aliviar la presión sobre los recursos computacionales..

Trabajos recientes en deep learning también indican que existen otros enfoques más allá de los dos presentados anteriormente. Por ejemplo, los autoencoders variacionales ofrecen perspectivas para realizar operaciones sobre latent spaces obteniendo resultados impresionantes mientras buscan transformaciones muy complejas en los datos (ej: eliminar automáticamente las gafas de un retrato fotográfico). Aunque estos enfoques son conceptualmente muy intrigantes, hasta la fecha no han demostrado tener mucha relevancia práctica al abordar problemas de la supply chain.

Visualización de forecast probabilísticos

La forma más sencilla de visualizar una distribución de probabilidad discreta es mediante un histograma, donde el eje vertical indica la probabilidad y el eje horizontal el valor de la variable aleatoria de interés. Por ejemplo, un forecast probabilístico de un tiempo de entrega puede mostrarse como:

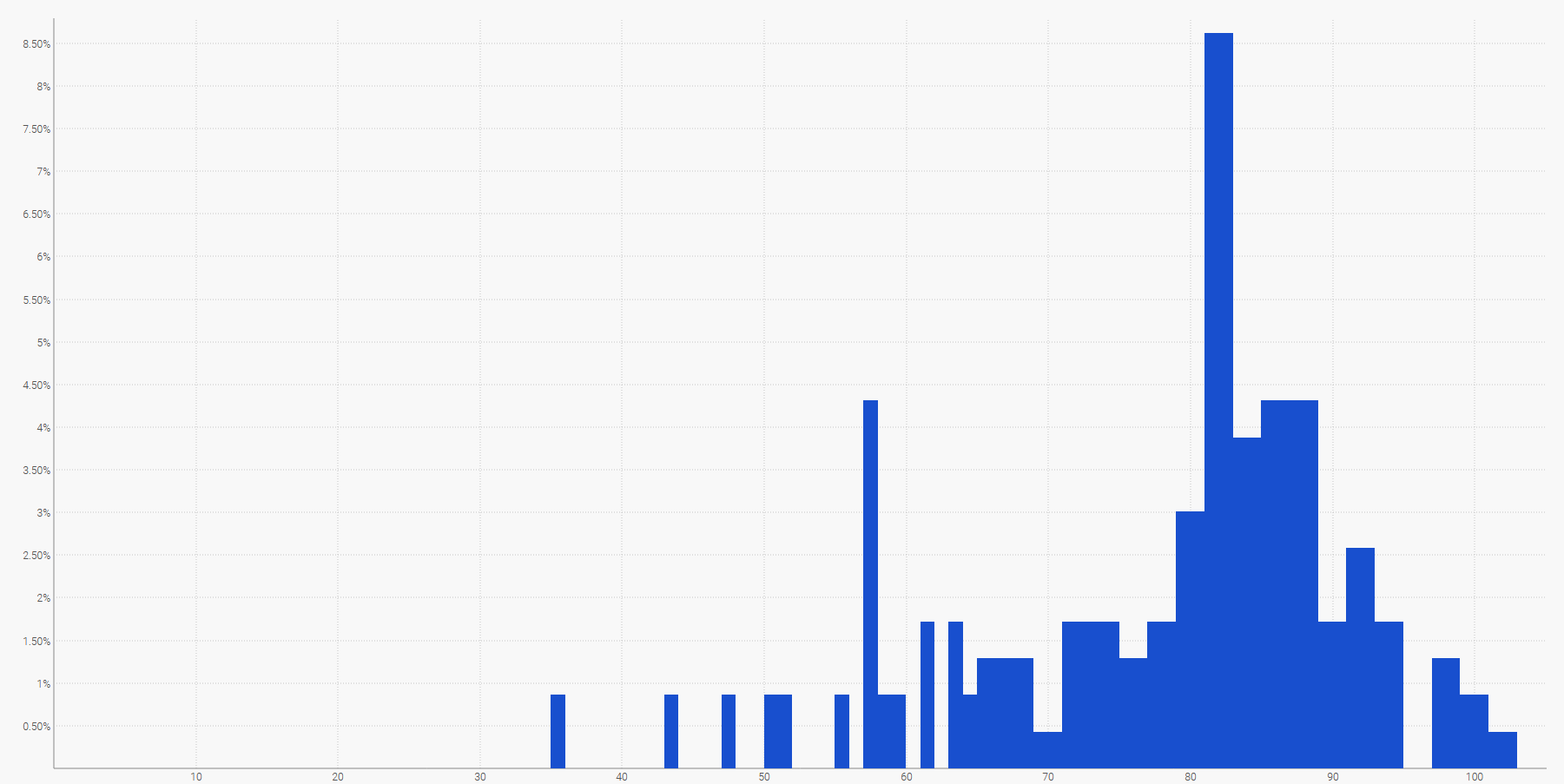
La demanda futura, sumada durante un período de tiempo especificado, también puede representarse mediante un histograma. Más en general, el histograma es muy adecuado para todas las variables aleatorias unidimensionales sobre $${ℤ}$$, el conjunto de enteros relativos.

La visualización del equivalente probabilístico de una serie temporal equiespaciada – es decir, una cantidad que varía en periodos de tiempo discretos de igual duración – resulta ya mucho más desafiante. De hecho, a diferencia de la variable aleatoria unidimensional, no existe una visualización canónica para tal distribución. Tenga cuidado, ya que no se puede asumir que los periodos sean independientes. Así, aunque es posible representar una serie temporal “probabilística” alineando una serie de histogramas – uno por periodo – esta representación distorsionaría la forma en que se desarrollan los eventos en una supply chain.

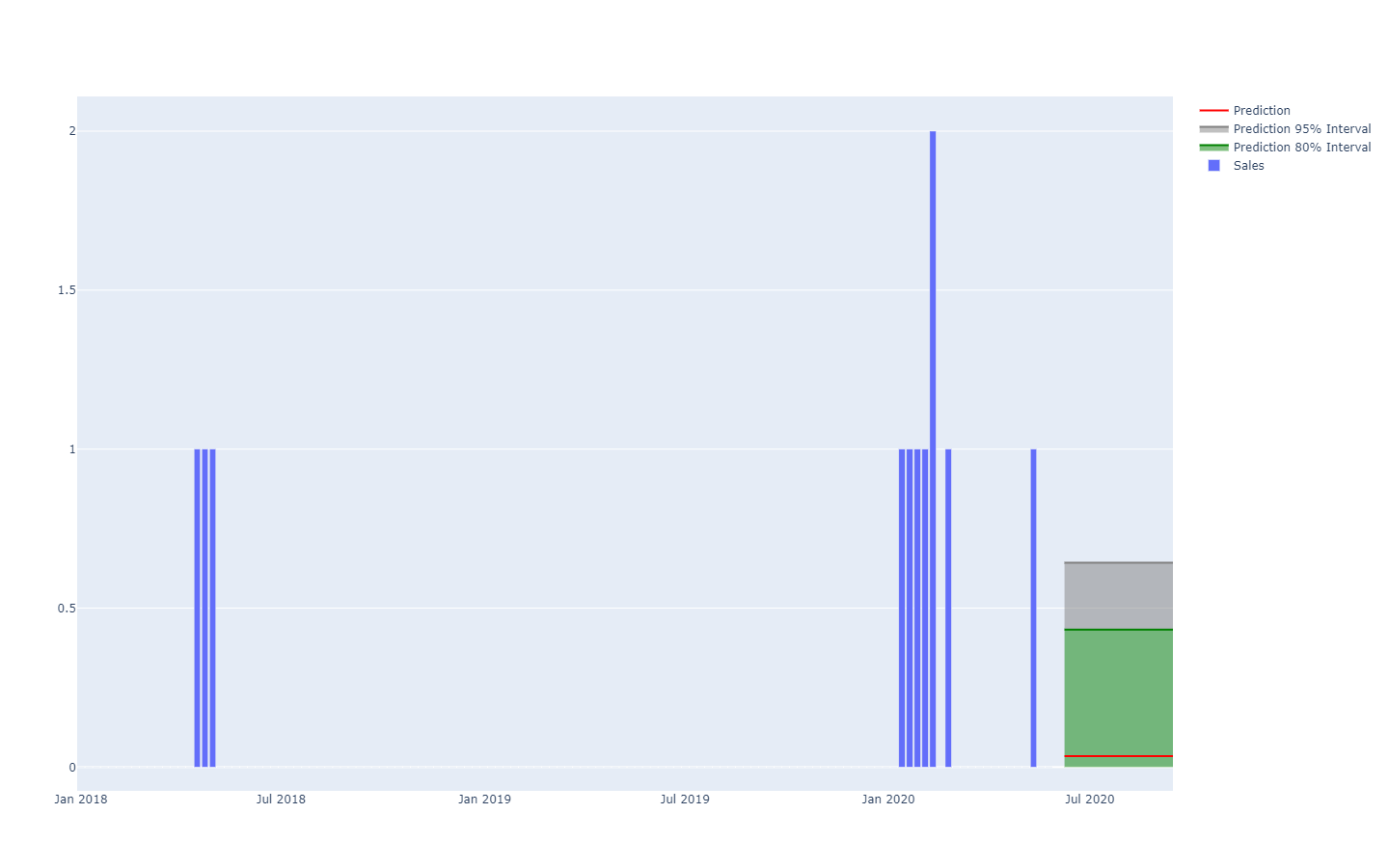
Por ejemplo, no es demasiado improbable que un producto recién lanzado tenga un buen desempeño y alcance altos volúmenes de ventas (un éxito). Tampoco es demasiado improbable que el mismo producto recién lanzado fracase y genere bajos volúmenes de ventas (un fracaso). Sin embargo, oscilaciones vastas de un día para otro entre niveles de ventas exitosos o fallidos son sumamente improbables.

Los intervalos de predicción, comúnmente encontrados en la literatura de la supply chain, son algo engañosos. Tienden a enfatizar situaciones de baja incertidumbre que no representan las situaciones reales de la supply chain;

Observe cómo estos intervalos de predicción son exactamente las distribuciones de probabilidad, dispuestas una al lado de la otra con un esquema de colores que resalta umbrales de cuantiles específicos.

Una mejor representación – es decir, que no omita las fuertes dependencias interperiodo – es observar los valores acumulativos a lo largo del tiempo, tomando sus cuantiles y luego diferenciándolos para recuperar los incrementos por periodo (véase la primera ilustración de un forecast probabilístico presentada al inicio del presente artículo). La visualización es la misma, pero el significado subyacente difiere. Ahora estamos observando cuantiles sobre escenarios, delineando los escenarios extremadamente favorables (resp. desfavorables).

Antipatterns de forecast probabilísticos

Los forecast probabilísticos desafían la manera en que muchas personas piensan “instintivamente” sobre el futuro. En esta sección cubrimos algunos de los aspectos más frecuentemente malinterpretados de los forecast probabilísticos.

No existe tal cosa como eventos ‘impredecibles’

Desde la perspectiva determinista, predecir el resultado de la lotería es imposible, ya que las probabilidades de acertar son “una en un millón”. Sin embargo, desde una perspectiva probabilística, el problema es trivial: cada boleto tiene una probabilidad de “una en un millón” de ganar. La altísima varianza del resultado no debe confundirse con alguna “incognoscibilidad” del fenómeno en sí, el cual puede entenderse perfectamente, como es el caso de la lotería. El forecast probabilístico trata de cuantificar y estructurar la varianza, no de eliminarla.

No existe tal cosa como distribuciones ‘normales’

Las distribuciones normales, también conocidas como gaussianas, son ubicuas tanto en los libros de texto de supply chain como en los de física. Sin embargo, en lo que respecta a los asuntos humanos, casi nada se distribuye de manera “normal”. Las distribuciones normales, por diseño, hacen que las grandes desviaciones (en comparación con las desviaciones promedio) sean extremadamente raras, hasta el punto de ser descartadas por el modelo como simplemente imposibles, es decir, probabilidades inferiores a una en mil millones. La demanda, el tiempo de espera, las devoluciones son muchos patrones que categóricamente no se distribuyen de manera normal. La única ventaja de las distribuciones normales es que son perfectas para idear ejercicios de libros de texto para estudiantes, ya que se prestan a soluciones analíticas explícitas.

Selección selectiva de probabilidades

Cuando se enfrenta a una distribución de probabilidades, resulta tentador seleccionar un único punto de la distribución, posiblemente la media o la mediana, y proceder basándose en ese número. Este proceso va en contra de la esencia misma del aspecto probabilístico del forecast. Las probabilidades no deben reducirse a una única estimación puntual, ya que, sin importar qué punto se elija, este proceso conlleva una pérdida masiva de información. Así, aunque algo perturbador, se pretende preservar las probabilidades tal como son durante el mayor tiempo posible. El punto de colapso es típicamente la decisión final de supply chain, que maximiza los retornos al enfrentar futuros inciertos.

Eliminando los valores atípicos estadísticos

La mayoría de los métodos numéricos clásicos -firmemente basados en la perspectiva determinista de los forecasts (por ejemplo, promedios móviles)- se comportan muy mal al encontrarse con valores atípicos estadísticos. Por lo tanto, muchas empresas establecen procesos para “limpiar” manualmente los datos históricos de esos outliers. Sin embargo, esta necesidad de un proceso de limpieza solo resalta las deficiencias de esos métodos numéricos. Por el contrario, los outliers estadísticos son un ingrediente esencial del forecast probabilístico, ya que contribuyen a obtener una mejor visión de lo que sucede en la cola de la distribución. En otras palabras, esos outliers son la clave para cuantificar la probabilidad de encontrar más outliers.

Llevar una espada a un tiroteo

Se requiere herramientas especializadas para manipular distribuciones de probabilidad. Producir el forecast probabilístico es solo un paso entre muchos para generar cualquier valor real para la empresa. Muchos profesionales de supply chain terminan desestimando los forecasts probabilísticos por la falta de herramientas adecuadas para hacer algo con ellos. Muchos software vendors empresariales se han sumado a la tendencia y ahora afirman soportar “probabilistic forecasting” (junto con “AI” y “blockchain”), pero nunca llegaron a implementar más que unos pocos modelos probabilísticos de manera cosmética (véase la sección anterior). Exhibir un modelo de probabilistic forecasting no vale casi nada sin las extensas herramientas para aprovechar sus resultados numéricos.

Notas