Previsione probabilistica (Supply Chain)

Si dice che una previsione sia probabilistica, anziché deterministica, se contiene un insieme di probabilità associate a tutti i possibili esiti futuri, anziché individuare un esito particolare come “la” previsione. Le previsioni probabilistiche sono importanti ogni qualvolta l’incertezza sia irreducibile, il che si verifica quasi sempre quando si tratta di sistemi complessi. Per le supply chain, le previsioni probabilistiche sono essenziali per produrre decisioni robuste contro condizioni future incerte. In particolare, la domanda e lead time, due aspetti chiave dell’analisi della supply chain, sono entrambi meglio affrontati tramite la previsione probabilistica. La prospettiva probabilistica si presta naturalmente alla prioritizzazione economica delle decisioni in base ai loro ritorni attesi ma incerti. Una vasta gamma di modelli statistici fornisce previsioni probabilistiche. Alcuni sono strutturalmente vicini ai loro omologhi deterministici, mentre altri sono molto diversi. Valutare l’accuratezza di una previsione probabilistica richiede metriche specifiche, che differiscono da quelle dei corrispettivi deterministici. L’utilizzo delle previsioni probabilistiche richiede strumenti specializzati che si discostano da quelli deterministici.

Previsioni deterministiche vs. probabilistiche

L’ottimizzazione delle supply chain si basa sulla corretta anticipazione degli eventi futuri. Numericamente, tali eventi sono anticipati tramite previsioni, che comprendono una vasta gamma di metodi numerici utilizzati per quantificare questi eventi futuri. Dagli anni ‘70 in poi, la forma di previsione più utilizzata è stata la previsione deterministica serie temporali: una quantità misurata nel tempo - per esempio la domanda in unità di un prodotto - viene proiettata nel futuro. La parte passata della serie temporali rappresenta i dati storici, mentre la parte futura rappresenta la previsione.

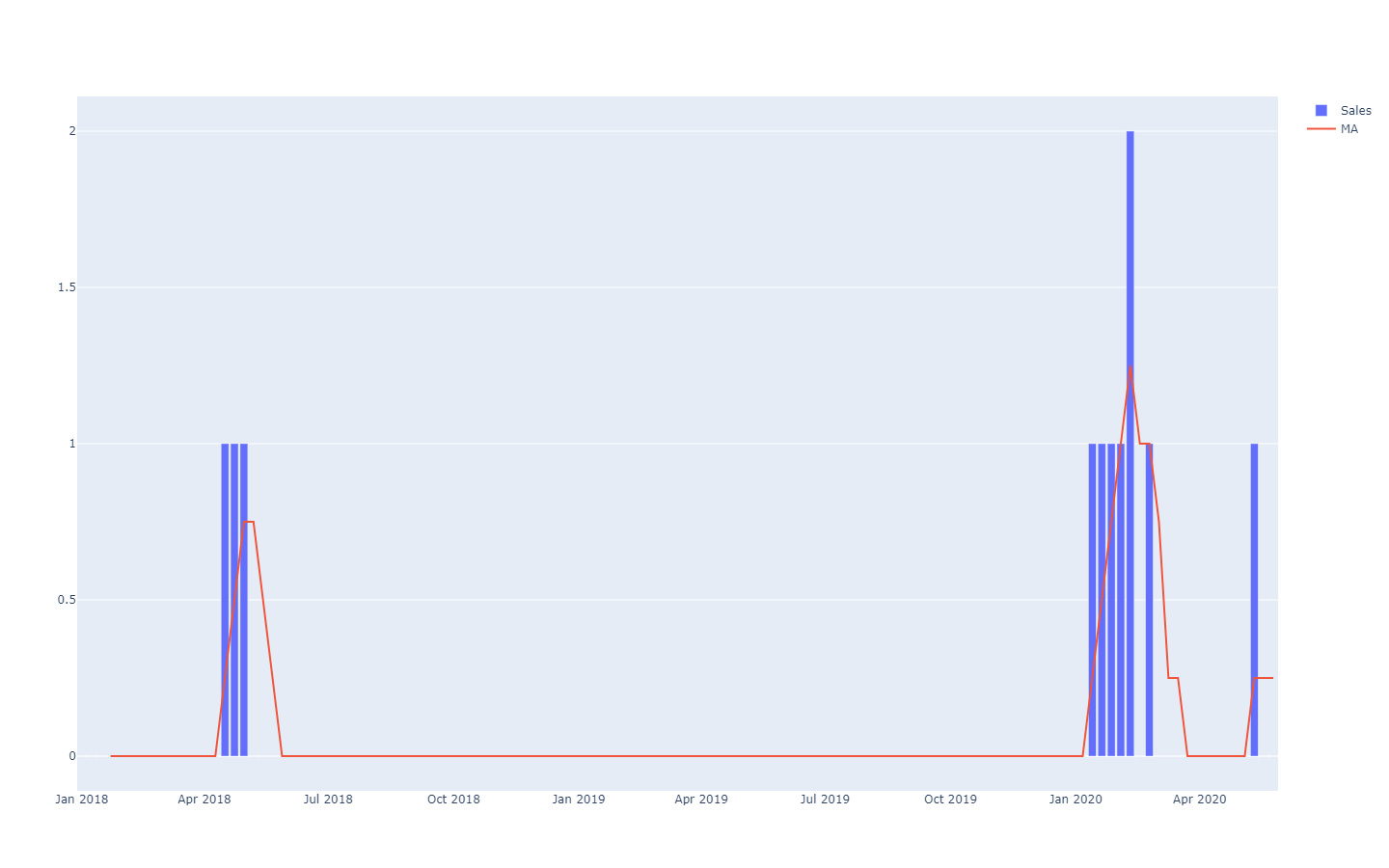
Si dice che queste previsioni delle serie temporali siano deterministiche perché per ogni punto nel futuro, la previsione fornisce un singolo valore che si prevede corrisponda il più possibile all’esito futuro. Infatti, pur essendo la previsione un valore singolo, è ampiamente compreso che essa ha poche possibilità di essere perfettamente corretta. Gli esiti futuri si discosteranno dalla previsione. L’aderenza della previsione deterministica ai suoi esiti futuri viene valutata quantitativamente attraverso metriche di accuratezza, come ad esempio l’errore quadratico medio (MSE).

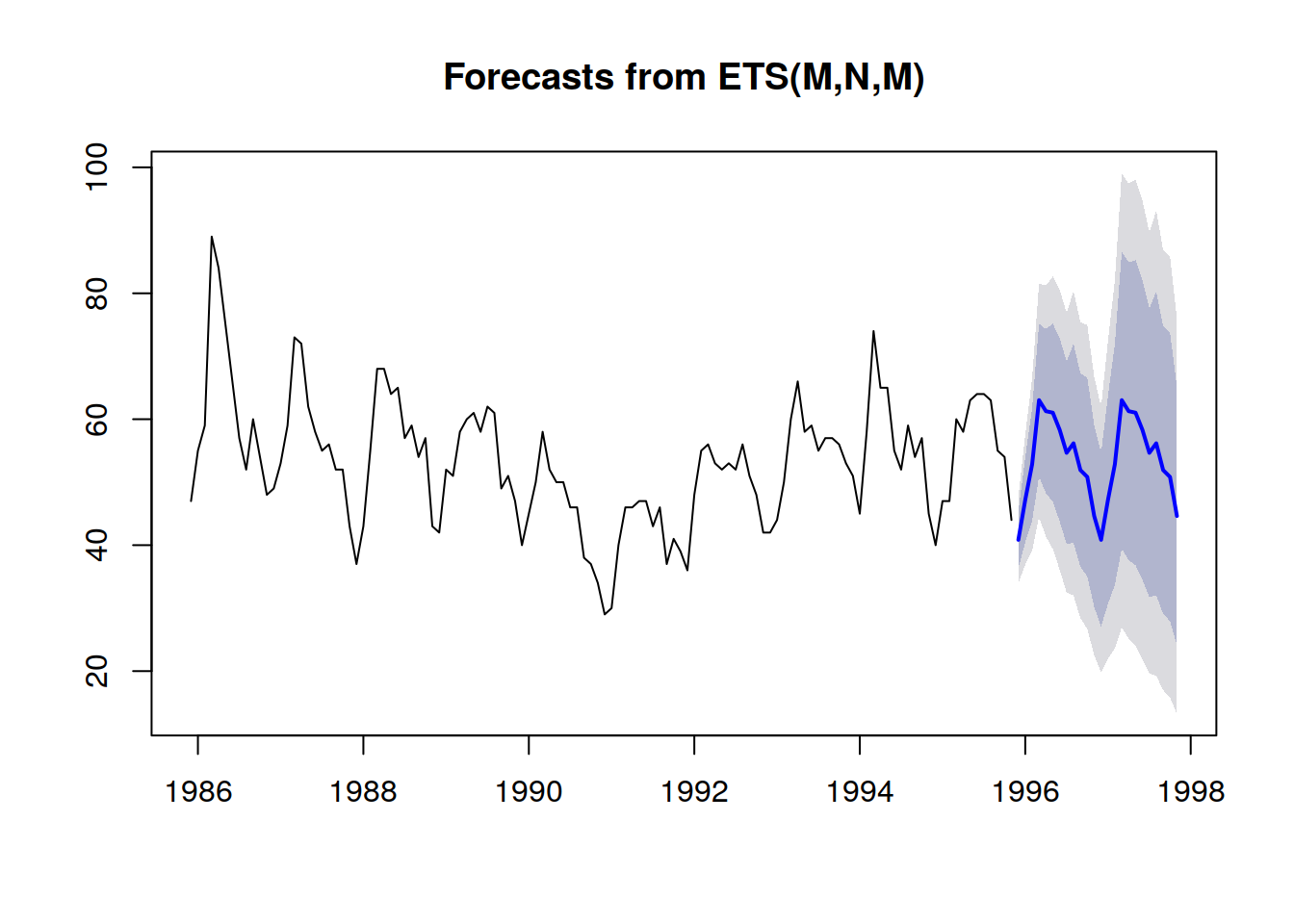
Le previsioni probabilistiche adottano una prospettiva diversa nell’anticipazione degli esiti futuri. Invece di produrre un unico valore come esito “ottimale”, la previsione probabilistica consiste nell’assegnare una probabilità a ogni possibile risultato. In altre parole, tutti gli eventi futuri rimangono possibili, sebbene non siano ugualmente probabili. Di seguito è riportata la visualizzazione di una previsione delle serie temporali probabilistica che mostra il “shotgun effect”, tipicamente osservato nella maggior parte delle situazioni reali. Riprenderemo questa visualizzazione in maggior dettaglio a seguire.

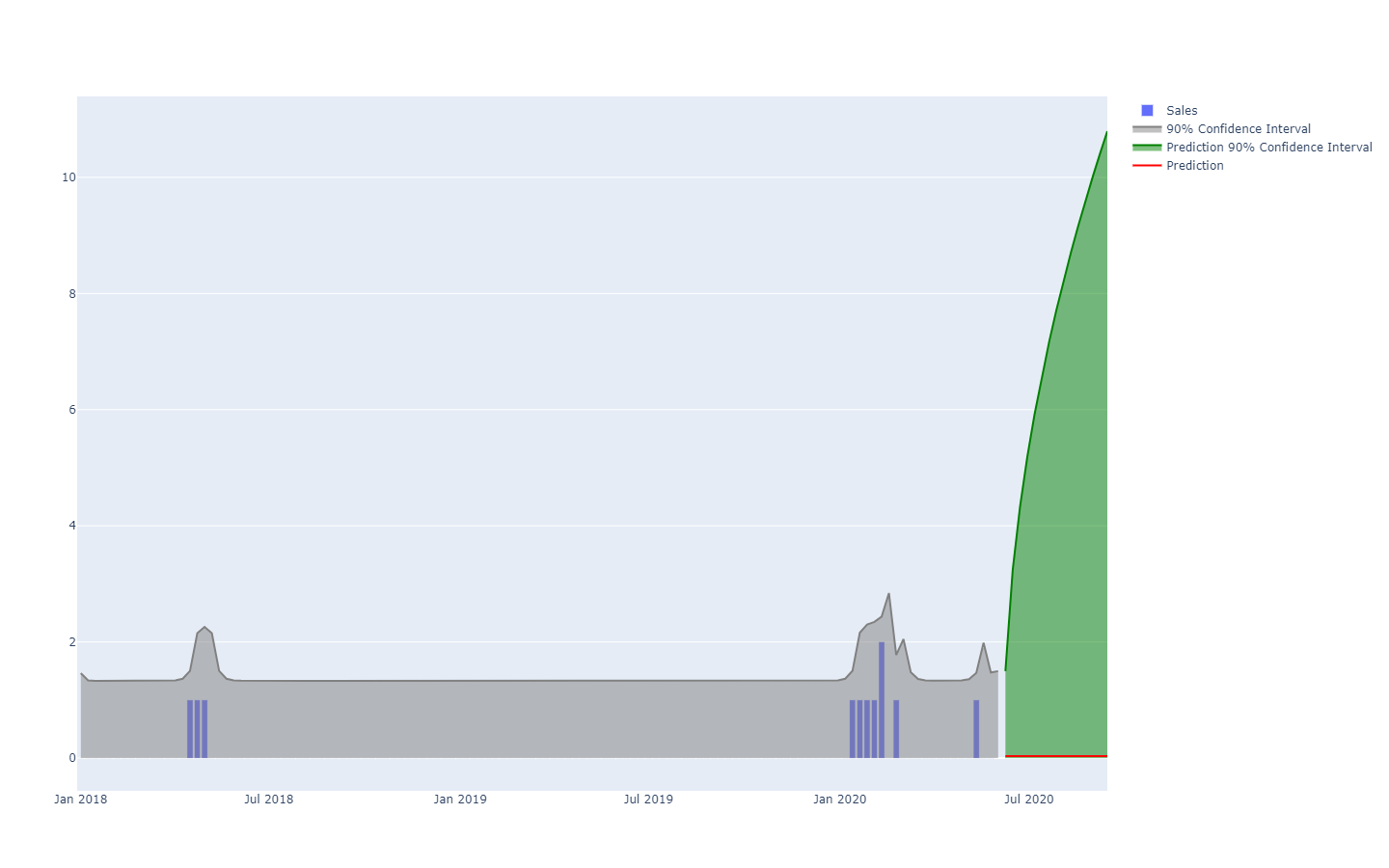
Le serie temporali, una quantità misurata nel tempo, sono probabilmente il modello di dati più noto e più utilizzato. Questo modello di dati può essere previsto sia con modalità deterministiche che probabilistiche. Tuttavia, esistono molti modelli di dati alternativi, tipicamente più ricchi, che si prestano anch’essi a previsioni di entrambe le tipologie. Ad esempio, un’azienda che ripara motori a reazione potrebbe voler anticipare l’elenco esatto dei pezzi di ricambio che saranno necessari per una prossima operazione di manutenzione. Tale anticipazione può assumere la forma di una previsione, ma non sarà una previsione basata su serie temporali. La previsione deterministica associata a questa operazione è l’elenco esatto dei pezzi e delle loro quantità. Al contrario, la previsione probabilistica rappresenta la probabilità che ciascuna combinazione di pezzi (incluse le quantità) sia quella necessaria per effettuare le riparazioni.

Inoltre, sebbene il termine “previsione” enfatizzi un’anticipazione di qualche tipo, l’idea può essere generalizzata a qualsiasi tipo di affermazione inferita statisticamente su un sistema, comprese le sue proprietà passate (ma sconosciute). La pratica della previsione statistica emerse nel corso del XX secolo, prima dell’avvento della più moderna prospettiva del statistical learning, che comprende tutte le estrapolazioni basate sui dati che possono essere effettuate, indipendentemente da qualsiasi dimensione temporale. Per chiarezza, continueremo a utilizzare il termine “previsione” quanto segue, anche se l’aspetto temporale equivarrebbe sempre a passati come noto e futuri come sconosciuto. Ad esempio, un’azienda potrebbe voler stimare le vendite che si sarebbero realizzate per un prodotto in un negozio se il prodotto non fosse stato esaurito quel giorno. La stima è utile per quantificare la magnitudine del problema in termini di qualità del servizio. Tuttavia, poiché l’evento è passato, il dato “reale” delle vendite non sarà mai osservato. Ciononostante, supponendo che non sia stato ancora trivialmente osservato, la stima statistica della domanda passata è un problema molto vicino a quello della stima della domanda futura.

Le previsioni probabilistiche sono più ricche - in termini di informazioni - rispetto ai loro omologhi deterministici. Mentre la previsione deterministica fornisce una “migliore stima” dell’esito futuro, essa non dice nulla sulle alternative. In effetti, è sempre possibile convertire una previsione probabilistica nel suo corrispettivo deterministico prendendo la media, la mediana, la moda, … della distribuzione di probabilità. Tuttavia, il contrario non è vero: non è possibile recuperare una previsione probabilistica da una deterministica.

Eppure, sebbene le previsioni probabilistiche siano statisticamente superiori a quelle deterministiche, esse rimangono usate raramente nella supply chain. Tuttavia, la loro popolarità è aumentata costantemente nell’ultimo decennio. Storicamente, le previsioni probabilistiche emersero più tardi, poiché richiedono risorse di calcolo significativamente maggiori. Sfruttare le previsioni probabilistiche per scopi della supply chain richiede anche strumenti software specializzati, che spesso non sono disponibili.

Casi d’uso della supply chain

Ottimizzare una supply chain consiste nell’adottare la decisione “giusta” - al momento presente - che affronterà nel modo più redditizio una situazione futura stimata solo in modo imperfetto. Tuttavia, l’incertezza associata agli eventi futuri è in gran parte irreducibile. Di conseguenza, l’azienda ha bisogno che la decisione sia robusta se l’anticipazione dell’evento futuro - ovvero la previsione - è imperfetta. Ciò è stato fatto minimamente a partire dalla metà del XX secolo tramite l’analisi delle scorte di sicurezza. Tuttavia, come vedremo di seguito, oltre a un interesse storico, non c’è più alcun motivo per favorire le scorte di sicurezza rispetto alle “native” ricette numeriche.

La prospettiva della previsione probabilistica adotta un approccio radicale verso l’incertezza: questo approccio tenta di quantificare l’incertezza nella massima misura possibile. Nella supply chain, i costi tendono a concentrarsi sugli estremi statistici: è la domanda inaspettatamente alta a creare una rottura di stock, è la domanda inaspettatamente bassa a creare la svalutazione dell’inventario. Nel mezzo, l’inventario si muove senza problemi. Le previsioni probabilistiche sono - in termini semplici - un tentativo di gestire queste situazioni a bassa frequenza e alto costo che sono ubiquitarie nelle supply chain moderne. Le previsioni probabilistiche possono e dovrebbero essere considerate un ingrediente fondamentale di qualsiasi pratica di gestione del rischio all’interno della supply chain.

Molti aspetti delle supply chain sono particolarmente adatti alla previsione probabilistica, come ad esempio:

• domanda: abbigliamento, accessori, ricambi; così come molti altri tipi di prodotti, tendono ad essere associati a una domanda erratica e/o intermittente. Il lancio di un prodotto può avere successo oppure no. Le promozioni dei concorrenti possono temporaneamente ed in modo erratico cannibalizzare grandi porzioni delle quote di mercato.
• lead time: le importazioni dall’estero possono subire una serie di ritardi in qualsiasi fase della catena (produzione, trasporto, dogana, ricezione, ecc.). Anche i fornitori locali possono occasionalmente avere tempi di consegna lunghi se affrontano un problema di stock-out. I lead time tendono ad avere distribuzioni a “code pesanti”.
• resa (prodotti freschi): la quantità e la qualità della produzione di molti prodotti freschi dipendono da condizioni, come il meteo, che sono al di fuori del controllo dell’azienda. La previsione probabilistica quantifica questi fattori per l’intera stagione e offre la possibilità di andare oltre l’orizzonte di rilevanza delle previsioni meteorologiche classiche.
• resi (ecommerce): quando un cliente ordina lo stesso prodotto in tre diverse taglie, le probabilità sono alte che due di queste taglie vengano restituite. Più in generale, sebbene esistano forti differenze regionali, i clienti tendono a sfruttare politiche di reso vantaggiose quando sono disponibili. La probabilità dei resi per ogni ordine dovrebbe essere valutata.
• rottami (aviazione): le parti di aerei riparabili - frequentemente chiamate rotabili - a volte non riescono a essere riparate. In questo caso, il pezzo viene rottamato, poiché non è più adatto ad essere montato nuovamente su un aereo. Sebbene di solito non sia possibile sapere in anticipo se una parte sopravviverà alla riparazione o meno, le probabilità che il pezzo venga rottamato dovrebbero essere stimate.
• scorte (retail B2C): i clienti possono spostare, danneggiare o addirittura rubare merci da un negozio. Pertanto, il livello elettronico delle scorte è solo un’approssimazione della reale disponibilità sugli scaffali, come percepita dai clienti. Il livello delle scorte, così percepito, dovrebbe essere stimato tramite una previsione probabilistica.
• …

Questa breve lista dimostra che gli ambiti ammissibili per una previsione probabilistica superano di gran lunga i soli ambiti tradizionali della “previsione della domanda”. L’ottimizzazione ben ingegnerizzata di una supply chain richiede di considerare tutte le fonti di incertezza rilevanti. Sebbene a volte sia possibile ridurre l’incertezza - come evidenziato dal lean manufacturing - di solito sono coinvolti trade-off economici e, di conseguenza, una certa quantità di incertezza rimane irreducibile.

Le previsioni, tuttavia, sono semplicemente opinioni fondate sul futuro. Sebbene le previsioni probabilistiche possano essere considerate opinioni sorprendentemente dettagliate, non sono fondamentalmente diverse dai loro omologhi deterministici in questo senso. Il valore, in termini di supply chain, delle previsioni probabilistiche risiede nel modo in cui questa struttura fine viene sfruttata per fornire decisioni più redditizie. In particolare, non ci si aspetta che le previsioni probabilistiche siano tipicamente più accurate dei loro corrispettivi deterministici se si utilizzano metriche di accuratezza deterministica per valutarne la qualità.

In difesa della variabilità

Contrariamente a quanto sostengono molti approcci alla supply chain, la variabilità è destinata a rimanere - da qui la necessità delle previsioni probabilistiche. Il primo equivoco è che la variabilità sia necessariamente un male per una supply chain; non lo è. Il secondo equivoco è che la variabilità possa essere eliminata attraverso l’ingegneria; non può.

La variabilità ha implicazioni positive per le supply chain in molteplici situazioni. Ad esempio, sul lato della domanda, la maggior parte dei settori verticali è guidata dalla novità, come la moda, i prodotti culturali, il lusso soft e hard - così come le attività “hit or miss”. La maggior parte dei nuovi prodotti non riscuote successo (fallimenti), ma quelli che riescono (successi) producono ritorni massicci. Un’ulteriore variabilità è positiva perché aumenta la probabilità di ritorni sopra la media, mentre gli svantaggi rimangono contenuti (nel peggiore dei casi, l’intero inventario viene svalutato). Il flusso incessante di nuovi prodotti immessi sul mercato garantisce il rinnovamento costante dei “successi”, mentre i vecchi sono in discesa.

Sul lato dell’offerta, un processo di approvvigionamento che garantisce offerte con prezzi altamente variabili è superiore - a parità di condizioni - rispetto a un processo alternativo che genera prezzi molto più coerenti (cioè, meno variabili). Infatti, viene selezionata l’opzione dal prezzo più basso mentre le altre vengono scartate. Non importa se il prezzo “medio” ottenuto sia basso, ciò che conta è scoprire fonti a prezzi inferiori. Pertanto, un buon processo di approvvigionamento dovrebbe essere progettato per aumentare la variabilità, ad esempio enfatizzando l’esplorazione routinaria di nuovi fornitori invece di limitare il processo ai soli fornitori consolidati.

Talvolta, la variabilità può essere vantaggiosa per ragioni più sottili. Ad esempio, se un marchio è troppo prevedibile per quanto riguarda le sue operazioni promozionali, i clienti identificano il modello e iniziano a ritardare il loro acquisto, sapendo che in arrivo una promozione e quando. La variabilità - o addirittura l’erraticità - delle attività promozionali mitiga in una certa misura questo comportamento.

Un altro esempio è la presenza di fattori di confusione all’interno della stessa supply chain. Se i nuovi prodotti vengono sempre lanciati con una campagna TV e una campagna radio, diventa statisticamente difficile distinguere gli impatti rispettivi della TV e della radio. L’aggiunta di variabilità all’intensità delle rispettive campagne a seconda del canale garantisce che venga estratta più informazione statistica da queste operazioni, che in seguito può essere trasformata in spunti per una migliore allocazione delle risorse di marketing.

Naturalmente, tutta la variabilità non è buona. Il lean manufacturing è corretto nell’enfatizzare che, sul lato di produzione della supply chain, la variabilità è solitamente dannosa, soprattutto quando si tratta di ritardi variabili. Infatti, i processi LIFO (last-in first-out) possono infiltrarsi accidentalmente, il che, a sua volta, aggrava la variabilità dei tempi di consegna. In tali situazioni, la variabilità accidentale dovrebbe essere eliminata mediante ingegneria, tipicamente attraverso un processo migliore, a volte attraverso attrezzature o strutture migliori.

La variabilità - anche quando è dannosa - è frequentemente irriducibile. Come vedremo nella sezione seguente, le supply chain obbediscono alla legge dei piccoli numeri. È illusorio pensare che il livello di negozio possa mai essere previsto in modo affidabile - da una prospettiva deterministica - mentre i clienti non sanno sempre cosa stanno per acquistare. Più in generale, ridurre la variabilità comporta sempre un costo (e ridurla ulteriormente costa ancora di più), mentre la riduzione marginale della variabilità porta solo a rendimenti decrescenti. Così, anche quando la variabilità può essere ridotta, a tutti gli effetti, essa può raramente essere eliminata completamente a causa delle implicazioni economiche.

La legge dei piccoli numeri

La legge dei piccoli numeri della supply chain può essere enunciata così: piccoli numeri prevalgono ovunque lungo la catena. Questa legge osservazionale deriva dalle economie di scala e da alcune altre forze che determinano la maggior parte degli aspetti strutturali delle supply chain:

• un fornitore che fornisce decine di migliaia di unità di materiali al giorno probabilmente ha quantità minime d’ordine (MOQ) o sconti che impediscono che gli ordini di acquisto vengano effettuati troppo frequentemente. Il numero di ordini di acquisto inoltrati a un fornitore in un dato giorno raramente supera una cifra.
• una fabbrica che produce decine di migliaia di unità al giorno probabilmente opera in grandi lotti da migliaia di unità. La produzione viene solitamente confezionata in interi pallet. Il numero di lotti in un dato giorno è al massimo un piccolo numero a due cifre.
• un magazzino che riceve decine di migliaia di unità al giorno probabilmente viene rifornito da trucks, con ogni camion che scarica l’intero carico nel magazzino. Il numero di consegne di camion in un dato giorno raramente supera un numero a due cifre, anche per magazzini molto grandi.
• un negozio al dettaglio che può contenere decine di migliaia di unità in magazzino probabilmente distribuisce il suo assortimento su migliaia di referenze di prodotto distinte. Il numero di unità detenute per ciascun prodotto raramente supera una cifra.
• …

Naturalmente, cambiando l’unità di misura, è sempre possibile gonfiare i numeri. Ad esempio, se invece di contare il numero di pallet contassimo il numero di grammi di pallet, o il loro valore monetario in centesimi di USD, appaiono numeri elevati. Tuttavia, la legge dei piccoli numeri dovrebbe essere intesa con la nozione di contare le cose da una sensata supply chain perspective. Pur potendo, in teoria, questo principio apparire abbastanza soggettivo, in pratica non lo è, a causa delle ovvie praticità discrete delle moderne supply chain: bundles, scatole, pallet, container, camion …

Questa legge è di grande rilevanza per la prospettiva della previsione probabilistica. In primo luogo, evidenzia che le previsioni discrete dominano nelle situazioni della supply chain, ovvero il risultato da prevedere (o decidere) è un intero, anziché un numero frazionario. Le previsioni probabilistiche sono particolarmente adatte per situazioni discrete, perché per ogni risultato discreto è possibile stimare una probabilità. Al contrario, le previsioni deterministiche fanno fatica a gestire risultati discreti. Ad esempio, cosa significa che le vendite giornaliere attese di un prodotto siano pari a 1,3 unità? Le unità non vengono vendute in frazioni. Pur potendo essere dedotte interpretazioni “discrete” più sensate da questa affermazione, il suo corrispettivo probabilistico (ad es. 27% di probabilità di 0 unità di domanda, 35% di probabilità di 1 unità di domanda, 23% di probabilità di 2 unità di domanda, ecc.) risulta molto più immediato, perché abbraccia la natura discreta del fenomeno in esame.

In secondo luogo, mentre le previsioni probabilistiche possono apparire radicalmente più impegnative in termini di risorse computazionali, in realtà non lo sono nella pratica, proprio a causa della legge dei piccoli numeri. Infatti, riprendendo le vendite giornaliere dei prodotti discusse sopra, non ha senso valutare numericamente le probabilità che la domanda superi 100 in un dato giorno. Tali probabilità possono essere arrotondate a zero - o a un valore arbitrariamente piccolo. L’impatto sulla precisione numerica del modello della supply chain rimane trascurabile. Come regola empirica, è ragionevole considerare che le previsioni probabilistiche richiedano circa tre ordini di grandezza in più di risorse computazionali rispetto alle loro controparti deterministiche. Tuttavia, nonostante questo sovraccarico, i benefici in termini di supply chain performance superano di gran lunga il costo delle risorse computazionali.

Metriche di accuratezza per le previsioni probabilistiche

A prescindere da quanto accada, una previsione probabilistica ragionevolmente ben progettata indica che vi era certamente una probabilità diversa da zero che questo risultato si verificasse. Ciò è intrigante perché, a prima vista, potrebbe sembrare che le previsioni probabilistiche fossero in qualche modo immuni alla realtà, proprio come un indovino che enuncia profezie vaghe che non possono mai essere confutate, dato che l’indovino può sempre inventare una spiegazione successiva sul modo corretto di interpretare le profezie. In realtà, esistono diversi modi per valutare quantitativamente la qualità di una previsione probabilistica. Alcuni di questi metodi sono metriche in linea di principio con quelle usate per valutare l’accuratezza delle previsioni deterministiche. Altri approcci divergono in modi più radicali e profondi rispetto alla prospettiva deterministica.

Esaminiamo brevemente quattro approcci distinti per valutare l’accuratezza di una previsione probabilistica:

• la funzione di perdita pinball
• il continuous ranked probability score (CRPS)
• la verosimiglianza bayesiana
• la prospettiva generativa avversaria

La funzione di perdita pinball fornisce una metrica di accuratezza per ottenere una stima di quantile derivata da una previsione probabilistica. Ad esempio, se desideriamo valutare la quantità in magazzino che ha il 98% di probabilità di essere maggiore o uguale alla domanda del cliente in un negozio per un determinato prodotto, questa quantità può essere ottenuta direttamente dalle previsioni probabilistiche semplicemente sommando le probabilità a partire da 0 unità di domanda, 1 unità di domanda, … fino a quando la probabilità non supera il 98%. La funzione di perdita pinball fornisce una misura diretta della qualità di questa stima distorta della domanda futura. Può essere considerata uno strumento per valutare la qualità di qualsiasi punto della funzione di densità cumulativa della previsione probabilistica.

Il continuously ranked probability score (CRPS) fornisce una metrica, che può essere interpretata come la “quantità di spostamento” della massa di probabilità necessaria a concentrare tutta la massa verso il risultato osservato. È la generalizzazione più diretta dell’errore medio assoluto (MAE) in una prospettiva probabilistica. Il valore del CRPS è omogeneo con l’unità di misura del risultato stesso. Questa prospettiva può essere generalizzata a spazi metrici arbitrari, anziché limitarsi a situazioni unidimensionali, attraverso quella che è nota come “teoria del trasporto” e la distanza di Monge-Kantorovich (che va oltre l’ambito del presente documento).

La verosimiglianza e il suo cugino dell’entropia incrociata adottano la prospettiva bayesiana del minimo grado di sorpresa: maggiore è la probabilità dei risultati osservati, migliore è. Ad esempio, abbiamo due modelli probabilistici A e B: il modello A afferma che la probabilità di osservare 0 unità di domanda è del 50% per ogni giorno; il modello B afferma che la probabilità di osservare 0 unità di domanda è dell'1% per ogni giorno. Osserviamo la domanda per 3 giorni e otteniamo le seguenti osservazioni: 0, 0, 1. Il modello A aveva circa il 10% di probabilità di generare queste osservazioni, mentre per il modello B era solo di circa lo 0,01%. Pertanto, il modello B è di gran lunga meno probabile da considerarsi quello corretto rispetto al modello A. La verosimiglianza si discosta dalla prospettiva deterministica che prevede un criterio assoluto significativo per valutare i modelli. Invece, essa offre un meccanismo per comparare i modelli, che, numericamente, può essere utilizzato soltanto per compararli.

La prospettiva generativa avversaria è la più moderna in materia (Ian Goodfellow et al., 2014). In sostanza, questa prospettiva afferma che il modello probabilistico “migliore” è quello che può essere utilizzato per generare risultati – in stile Monte Carlo – che siano indistinguibili dai risultati reali. Ad esempio, se prendessimo in considerazione l’elenco storico delle transazioni in un ipermercato locale, potremmo troncare questa storia a un punto arbitrario del passato e utilizzare il modello probabilistico per generare transazioni false ma realistiche a partire da quel momento. Il modello verrebbe considerato “perfetto” se risultasse impossibile, attraverso un’analisi statistica, individuare il punto nel tempo in cui il dataset passa dai dati “reali” a quelli “falsi”. Lo scopo dell’approccio generativo avversario è “apprendere” le metriche che esacerbano i limiti di qualsiasi modello probabilistico. Invece di concentrarsi su una metrica particolare, questa prospettiva sfrutta ricorsivamente le tecniche di machine learning per “apprendere” le metriche stesse.

La ricerca di modi migliori per valutare la qualità delle previsioni probabilistiche è ancora un campo di studio attivo. Non esiste una delimitazione chiara tra le due domande “Come produrre una previsione migliore?” e “Come capire se una previsione è migliore?”. Studi recenti hanno notevolmente sfumato i confini tra le due, ed è probabile che le prossime scoperte comporteranno ulteriori cambiamenti nel modo stesso in cui le previsioni probabilistiche vengono concepite.

Probabilità estremamente piccole e log likelihood

Probabilità molto piccole sorgono naturalmente quando si esamina una situazione multidimensionale attraverso il prisma delle previsioni probabilistiche. Tali probabilità ridotte sono problematiche perché i computer non elaborano numeri con precisione infinita. I valori di probabilità grezzi sono frequentemente “estremamente” piccoli nel senso che vengono arrotondati a zero a causa dei limiti di precisione numerica. La soluzione a questo problema non è aggiornare il software per calcoli a precisione arbitraria – cosa molto inefficiente in termini di risorse computazionali – ma utilizzare il “log-trick”, che trasforma le moltiplicazioni in addizioni. Questo trucco è sfruttato – in un modo o nell’altro – da praticamente ogni pezzo di software che si occupa di previsioni probabilistiche.

Supponiamo di avere $$X_1, X_2, \ldots, X_n$$ variabili casuali che rappresentano la domanda del giorno per tutti i $$n$$ prodotti distinti serviti in un determinato negozio. Indichiamo con $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ la domanda empirica osservata alla fine della giornata per ciascun prodotto. Per il primo prodotto – governato da $$X_1$$ – la probabilità di osservare $$\hat{x}_1$$ è scritta come $$P(X_1=\hat{x}_1)$$ . Ora, supponiamo, in maniera un po’ abusiva ma per chiarezza, che tutti i prodotti siano strettamente indipendenti per quanto riguarda la domanda. La probabilità dell’evento congiunto di osservare $$\hat{x}_1, \hat{x}_2, \ldots, \hat{x}_n$$ è:

Se $$P(X_k=\hat{x}_k) \approx \tfrac{1}{2}$$ (approssimazione grossolana) e $$n=10000$$, allora la probabilità congiunta sopra espressa è dell’ordine di $$\tfrac{1}{{2^{10000}}} \approx 5 \times 10^{-3011}$$, un valore molto piccolo. Tale valore va in underflow, cioè scende al di sotto del numero piccolo rappresentabile, anche considerando i numeri in virgola mobile a 64 bit, tipicamente usati nel calcolo scientifico.

Il “log-trick” consiste nel lavorare con il logaritmo dell’espressione, ossia:

Il logaritmo trasforma la serie di moltiplicazioni in una serie di addizioni, risultando molto più stabile numericamente rispetto a una serie di moltiplicazioni.

L’uso del “log-trick” è frequente ogni volta che sono coinvolte previsioni probabilistiche. Il log likelihood è letteralmente il logaritmo della likelihood (introdotta precedentemente) proprio perché la likelihood grezza solitamente non sarebbe rappresentabile numericamente considerando i tipi comuni di numeri in virgola mobile.

Varianti algoritmiche delle previsioni probabilistiche

La questione della generazione, tramite computer, di previsioni probabilistiche è quasi vasta quanto il campo del machine learning stesso. Le delimitazioni tra i due campi, se esistono, sono per lo più una questione di scelte soggettive. Tuttavia, questa sezione presenta un elenco piuttosto elettivo di notevoli approcci algoritmici che possono essere utilizzati per ottenere previsioni probabilistiche.

All’inizio del XX secolo, possibilmente alla fine del XIX secolo, emerse l’idea dello safety stock, in cui l’incertezza della domanda viene modellata secondo una distribuzione normale. Poiché tabelle pre-calcolate della distribuzione normale erano già state stabilite per altre scienze, in particolare la fisica, l’applicazione dello safety stock richiedeva solo una moltiplicazione di un livello di domanda per un coefficiente di “safety stock” prelevato da una tabella preesistente. Aneddoticamente, molti manuali di supply chain scritti fino agli anni ‘90 contenevano ancora tabelle della distribuzione normale nei loro allegati. Purtroppo, il principale svantaggio di questo approccio è che le distribuzioni normali non rappresentano una proposta ragionevole per le supply chain. Innanzitutto, per quanto riguarda le supply chain, è lecito assumere che niente sia mai normalmente distribuito. In secondo luogo, la distribuzione normale è una distribuzione continua, in contrasto con la natura discreta degli eventi della supply chain (vedi “La legge dei piccoli numeri” sopra). Così, sebbene tecnicamente gli “safety stocks” abbiano una componente probabilistica, la metodologia sottostante e le ricette numeriche sono decise in favore della prospettiva deterministica. Questo approccio è elencato qui, tuttavia, per motivi di chiarezza.

Avanziamo rapidamente ai primi anni 2000, i metodi di ensemble learning - i cui rappresentanti più noti sono probabilmente le random forests e gli gradient boosted trees - sono relativamente semplici da estendere dalle loro origini deterministic alle prospettive probabilistiche. L’idea chiave alla base dell’ensemble learning è combinare numerosi deboli predittori deterministic, come gli alberi decisionali, in un predittore deterministic superiore. Tuttavia, è possibile regolare il processo di miscelazione per ottenere probabilità anziché un singolo aggregato, trasformando così il metodo ensemble learning in un metodo di previsione probabilistico. Questi metodi sono non parametrici e capaci di adattarsi a distribuzioni a code pesanti e/o multimodali, come comunemente si riscontra nella supply chain. Questi metodi tendono ad avere due svantaggi notevoli. Primo, per costruzione, la funzione di densità di probabilità prodotta da questa classe di modelli tende a includere molti zeri, il che impedisce qualsiasi tentativo di sfruttare la metrica della log-verosimiglianza. Più in generale, questi modelli non si adattano realmente alla prospettiva bayesiana, poiché le nuove osservazioni vengono frequentemente dichiarate “impossibili” (cioè probabilità zero) dal modello. Questo problema, tuttavia, può essere risolto attraverso metodi di regolarizzazione¹. Secondo, i modelli tendono ad essere grandi quanto una porzione consistente del dataset di input, e l’operazione di “predict” risulta quasi altrettanto costosa computazionalmente dell’operazione di “learn”.

I metodi iperparametrici, collettivamente noti come “deep learning”, che sono esplosi negli anni 2010, sono stati, quasi accidentalmente, probabilistici. Infatti, mentre la stragrande maggioranza dei compiti in cui il deep learning brilla davvero (ad es. la classificazione di immagini) si concentra solo sulle previsioni deterministic, si scopre che la metrica di cross-entropia - una variante della log likelihood di cui sopra - mostra gradienti molto ripidi che sono frequentemente ben adatti per lo stochastic gradient descent (SGD), che sta al cuore dei metodi di deep learning. Così, i modelli di deep learning risultano essere progettati come probabilistici, non perché le probabilità fossero di interesse, ma perché il gradient descent converge più rapidamente quando la funzione di loss riflette una previsione probabilistica. Pertanto, per quanto riguarda il deep learning, la supply chain si distingue per il suo interesse per il reale output probabilistico del modello di deep learning, mentre la maggior parte degli altri casi d’uso collassa la distribuzione di probabilità nella sua media, mediana o moda. Le Mixture Density Networks sono un tipo di rete di deep learning orientata all’apprendimento di complesse distribuzioni di probabilità. Il risultato stesso è una distribuzione parametrica, possibilmente costituita da Gaussiane. Tuttavia, a differenza degli ‘safety stocks, una miscela di molte Gaussiane può, in pratica, riflettere i comportamenti a coda pesante che si osservano nelle supply chains. Mentre i metodi di deep learning sono frequentemente considerati all’avanguardia, va notato che raggiungere la stabilità numerica, specialmente quando sono coinvolte miscele di densità, rimane un po’ una “dark art”.

La programmazione differenziabile è un discendente del deep learning, che ha guadagnato popolarità alla fine degli anni 2010. Condivide molte caratteristiche tecniche con il deep learning, ma differisce significativamente per il focus. Mentre il deep learning si concentra sull’apprendimento di funzioni arbitrariamente complesse (cioè, giocare a Go) impilando un gran numero di funzioni semplici (cioè, strati convoluzionali), la programmazione differenziabile si concentra sulla struttura fine del processo di apprendimento. La struttura più dettagliata, la più espressiva, può letteralmente essere formattata come un programma, che coinvolge rami, cicli, chiamate a funzioni, ecc. La programmazione differenziabile è di grande interesse per la supply chain, perché i problemi tendono a presentarsi in modi altamente strutturati, e tali strutture sono note agli esperti². Ad esempio, le vendite di una determinata camicia possono essere cannibalizzate da un’altra camicia di colore diverso, ma non saranno cannibalizzate dalle vendite di una camicia con tre taglie di differenza. Tali priorità strutturali sono fondamentali per raggiungere un’alta efficienza dei dati. Infatti, dal punto di vista della supply chain, la quantità di dati tende ad essere molto limitata (cfr. la legge dei piccoli numeri). Quindi, inquadrare strutturalmente il problema aiuta a garantire che i pattern statistici desiderati vengano appresi, anche in presenza di dati limitati. I priors strutturali aiutano anche ad affrontare i problemi di stabilità numerica. Rispetto ai metodi ensemble, i priors strutturali tendono ad essere meno dispendiosi in termini di tempo rispetto all’ingegneria delle feature; la manutenzione del modello è anche semplificata. D’altro canto, la programmazione differenziabile rimane una prospettiva piuttosto nascente ad oggi.

La prospettiva Monte Carlo (1930 / 1940) può essere utilizzata per affrontare le previsioni probabilistiche da un’angolazione diversa. I modelli discussi finora forniscono funzioni di densità di probabilità (PDF) esplicite. Tuttavia, da una prospettiva Monte Carlo, un modello può essere sostituito da un generatore - o campionatore - che genera casualmente possibili esiti (a volte chiamati “deviates”). Le PDF possono essere recuperate mediando i risultati del generatore, sebbene le PDF vengano spesso completamente bypassate per ridurre i requisiti in termini di risorse computazionali. Infatti, il generatore è frequentemente progettato per essere molto più compatto - in termini di dati - rispetto alle PDF che rappresenta. La maggior parte dei metodi di machine learning - inclusi quelli elencati sopra per affrontare direttamente le previsioni probabilistiche - può contribuire all’apprendimento di un generatore. I generatori possono assumere la forma di modelli parametrici a bassa dimensione (ad es. modelli a spazio di stato) o di modelli iperparametrici (ad es. i modelli LSTM e GRU nel deep learning). I metodi ensemble sono raramente utilizzati per supportare processi generativi a causa dei loro elevati costi computazionali per le operazioni di “predict”, ampiamente utilizzate per supportare l’approccio Monte Carlo.

Lavorare con le previsioni probabilistiche

Derivare intuizioni utili e decisioni dalle previsioni probabilistiche richiede strumenti numerici specializzati. A differenza delle previsioni deterministic, in cui ci sono numeri semplici, le previsioni stesse sono funzioni di densità di probabilità esplicite o generatori Monte Carlo. La qualità degli strumenti probabilistici è, in pratica, importante quanto la qualità delle previsioni probabilistiche. Senza questi strumenti, lo sfruttamento delle previsioni probabilistiche degenera in un processo deterministic (ulteriori dettagli nella sezione “Antipatterns” qui sotto).

Ad esempio, gli strumenti dovrebbero essere in grado di eseguire compiti quali:

• Combinare il tempo di consegna di produzione incerto con il tempo di consegna del trasporto incerto, per ottenere il tempo di consegna totale incerto.
• Combinare la domanda incerta con il tempo di consegna incerto, per ottenere la domanda totale incerta da coprire con lo stock che sta per essere ordinato.
• Combinare i resi incerti degli ordini (ecommerce) con la data di arrivo incerta dell’ordine del fornitore in transito, per ottenere il tempo di consegna incerto al cliente.
• Integrare la previsione della domanda, prodotta da un metodo statistico, con un rischio di coda derivato manualmente da una comprensione di alto livello di un contesto non riflesso dai dati storici, come una pandemia.
• Combinare la domanda incerta con uno stato incerto dello stock in relazione alla data di scadenza (retail alimentare), per ottenere lo stock residuo incerto a fine giornata.
• …

Una volta che tutte le previsioni probabilistiche - non solo quelle sulla domanda - sono state correttamente combinate, dovrebbe aver luogo l’ottimizzazione delle decisioni della supply chain. Ciò comporta una prospettiva probabilistica sia sui vincoli sia sulla funzione di punteggio. Tuttavia, questo aspetto degli strumenti va oltre l’ambito del presente documento.

Esistono due ampi “approcci” per lavorare con le previsioni probabilistiche: primo, le algebre sulle variabili casuali, e secondo, la programmazione probabilistica. Questi due approcci si integrano a vicenda poiché non presentano lo stesso mix di vantaggi e svantaggi.

Un’algebra di variabili casuali lavora tipicamente su funzioni di densità di probabilità esplicite. L’algebra supporta le consuete operazioni aritmetiche (addizione, sottrazione, moltiplicazione, ecc.) trasposte nelle loro controparti probabilistiche, trattando frequentemente le variabili casuali come statisticamente indipendenti. L’algebra offre una stabilità numerica quasi pari a quella del suo equivalente deterministic (cioè, numeri semplici). Tutti i risultati intermedi possono essere conservati per usi successivi, cosa che si rivela molto utile per organizzare e risolvere i problemi della data pipeline. D’altro canto, l’espressività di queste algebre tende ad essere limitata, poiché solitamente non è possibile esprimere tutte le sottili dipendenze condizionali esistenti tra le variabili casuali.

La programmazione probabilistica adotta una prospettiva Monte Carlo sul problema. La logica viene scritta una volta, generalmente aderendo a una prospettiva completamente deterministic, ma eseguita molte volte tramite gli strumenti (cioè, il processo Monte Carlo) per raccogliere le statistiche desiderate. L’espressività massima si ottiene attraverso costrutti “programmativi”: è possibile modellare dipendenze arbitrariamente complesse tra le variabili casuali. Scrivere la logica stessa tramite la programmazione probabilistica tende anche a essere leggermente più semplice rispetto a un’algebra di variabili casuali, poiché la logica comprende solo numeri regolari. D’altro canto, è presente un costante compromesso tra la stabilità numerica (più iterazioni garantiscono una precisione migliore) e le risorse computazionali (più iterazioni costano di più). Inoltre, i risultati intermedi solitamente non sono immediatamente accessibili, poiché la loro esistenza è solo transitoria - proprio per alleviare la pressione sulle risorse di calcolo.

Studi recenti nel deep learning indicano anche che esistono ulteriori approcci oltre a quelli presentati sopra. Ad esempio, gli autoencoder variazionali offrono prospettive per eseguire operazioni su spazi latenti ottenendo risultati impressionanti mentre cercano trasformazioni molto complesse sui dati (es.: rimuovere automaticamente gli occhiali da un ritratto fotografico). Sebbene questi approcci siano concettualmente molto intriganti, non hanno finora dimostrato una notevole rilevanza pratica nell’affrontare problemi della supply chain.

Visualizzazione delle previsioni probabilistiche

Il modo più semplice per visualizzare una distribuzione di probabilità discreta è un istogramma, in cui l’asse verticale indica la probabilità e l’asse orizzontale il valore della variabile casuale di interesse. Ad esempio, una previsione probabilistica di un tempo di consegna può essere rappresentata come:

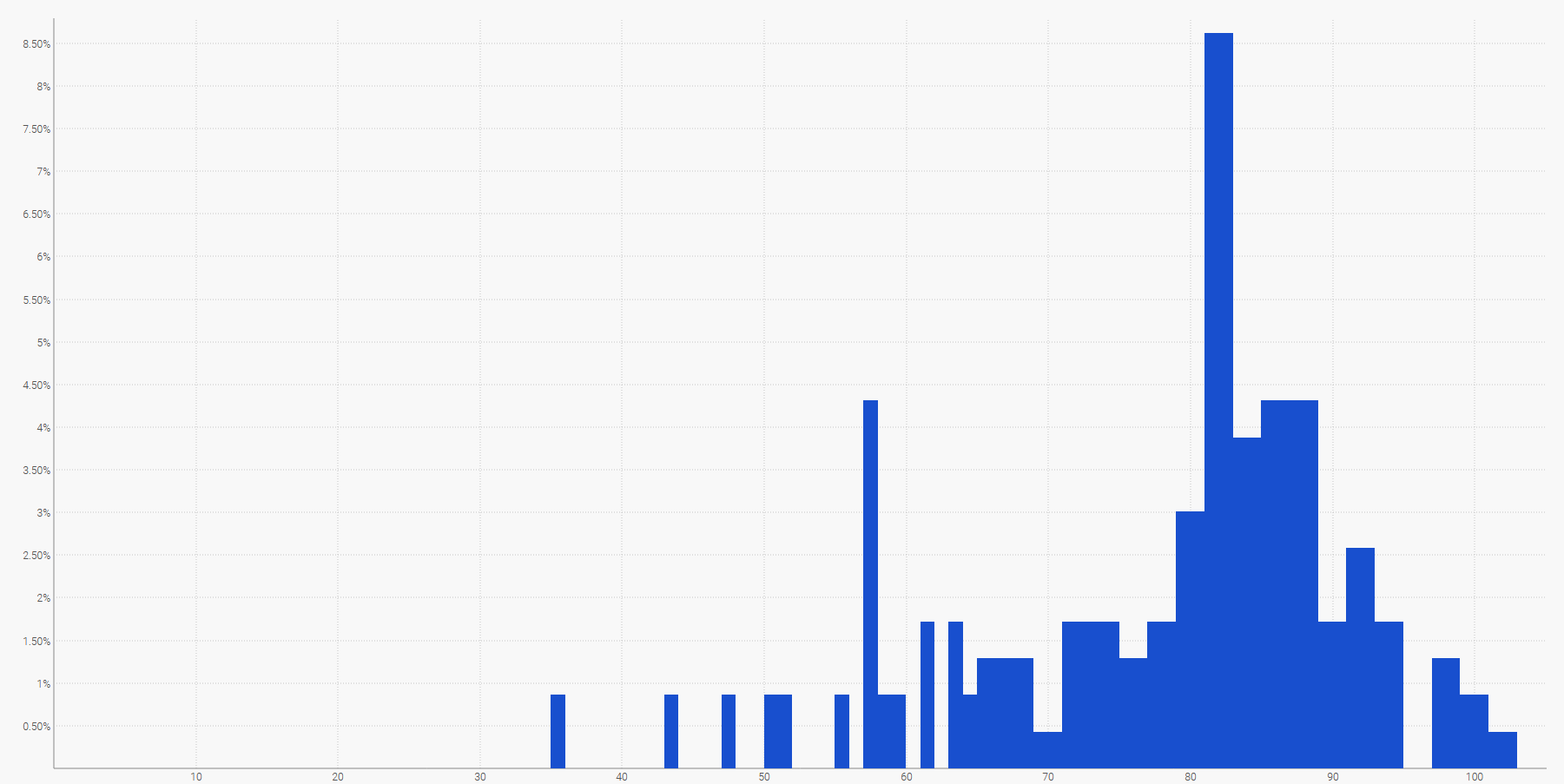
La domanda futura, sommata su un periodo di tempo specificato, può anche essere rappresentata mediante un istogramma. Più in generale, l’istogramma è adatto per tutte le variabili casuali unidimensionali su $${ℤ}$$, l’insieme degli interi relativi.

La visualizzazione dell’equivalente probabilistico di una serie temporale a intervalli equidistanti - cioè una quantità che varia su periodi di tempo discreti di uguale lunghezza - è già molto più impegnativa. Infatti, a differenza della variabile casuale unidimensionale, non esiste una visualizzazione canonica di tale distribuzione. Attenzione, i periodi non possono essere considerati indipendenti. Quindi, sebbene sia possibile rappresentare una serie temporale “probabilistica” allineando una serie di istogrammi - uno per periodo -, questa rappresentazione rappresenterebbe in modo molto impreciso il modo in cui gli eventi si sviluppano nella supply chain.

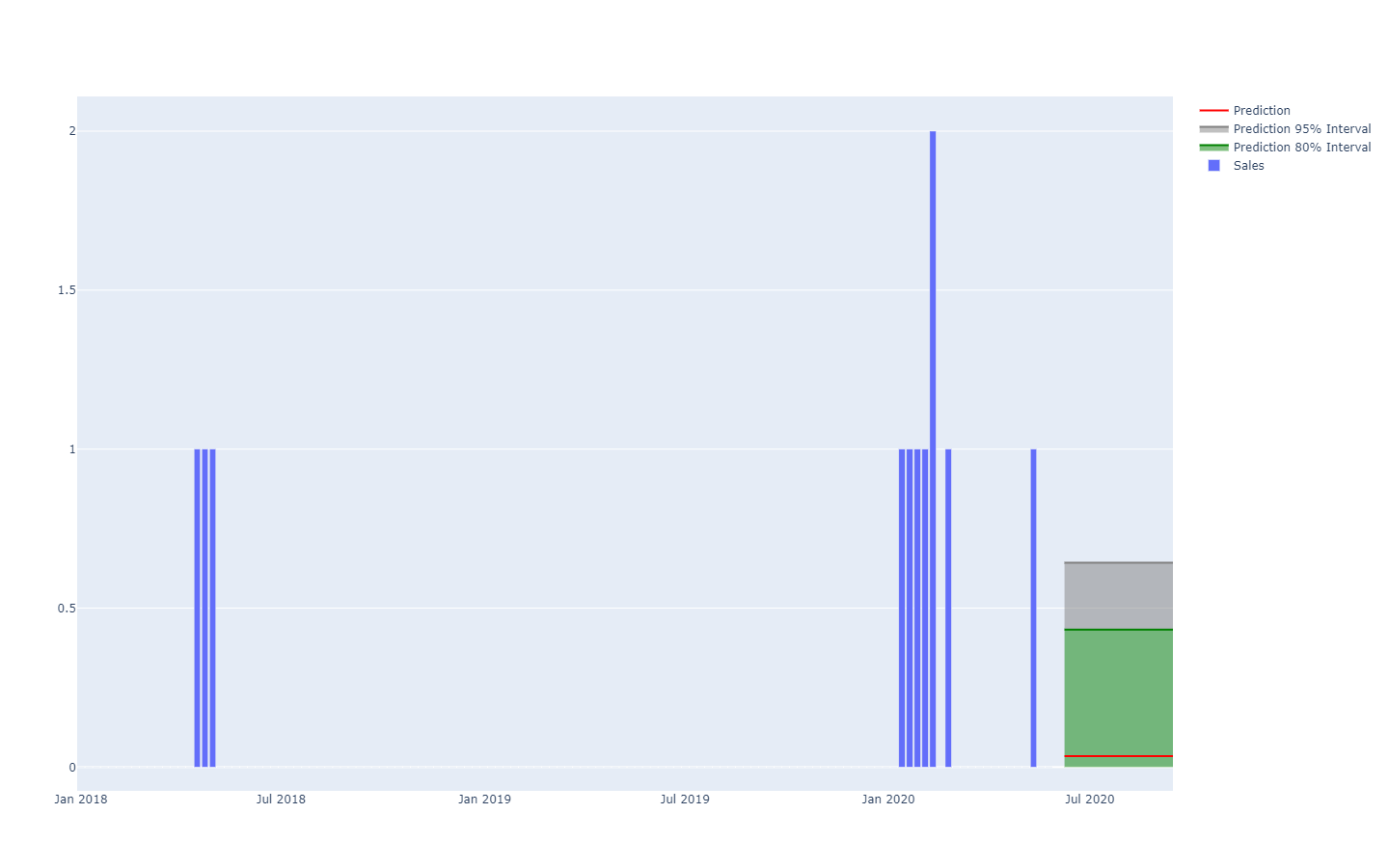
Ad esempio, non è troppo improbabile che un prodotto appena lanciato performi bene e raggiunga volumi di vendita elevati (un successo). Non è nemmeno troppo improbabile che lo stesso prodotto appena lanciato fallisca e ottenga volumi di vendita bassi (un insuccesso). Tuttavia, enormi oscillazioni quotidiane tra livelli di vendita di successo e insuccesso sono estremamente improbabili.

Gli intervalli di previsione, comunemente presenti nella letteratura della supply chain, sono in qualche modo fuorvianti. Tendono a enfatizzare situazioni a bassa incertezza che non sono rappresentative delle reali situazioni della supply chain;

Notate come questi intervalli di previsione siano esattamente le distribuzioni di probabilità, poste affiancate utilizzando uno schema di colori per delineare soglie di quantile specifiche.

Una rappresentazione migliore - cioè, che non comprometta le forti dipendenze interperiodiche - è osservare i valori cumulativi nel tempo, calcolarne i quantili, e poi differenziare per recuperare gli incrementi per periodo (vedi la prima illustrazione di una previsione probabilistica riportata all’inizio del presente articolo). La visualizzazione è la stessa, ma il significato sottostante è diverso. Ora stiamo esaminando i quantili sugli scenari, delineando gli scenari estremamente favorevoli (rispettivamente sfavorevoli).

Antipatterns delle previsioni probabilistiche

Le previsioni probabilistiche sfidano il modo in cui molte persone pensano “intuitivamente” al futuro. In questa sezione, trattiamo alcuni degli aspetti delle previsioni probabilistiche che vengono più frequentemente fraintesi.

Non esistono eventi ‘imprevedibili’

Dal punto di vista deterministic, prevedere l’esito della lotteria è impossibile, poiché le probabilità di indovinare sono “uno su un milione”. Tuttavia, da una prospettiva probabilistica, il problema è banale: ogni biglietto ha una probabilità “uno su un milione” di vincere. L’elevata varianza dell’esito non deve essere confusa con una qualche “inconoscibilità” del fenomeno stesso, che può essere perfettamente compreso, come nel caso di una lotteria. Le previsioni probabilistiche riguardano la quantificazione e la strutturazione della varianza, non l’eliminazione della stessa.

Non esistono distribuzioni ‘normali’

Le distribuzioni normali, note anche come gaussiane, sono onnipresenti sia nei libri di testo della supply chain che in quelli di fisica. Eppure, per quanto riguarda gli affari umani, quasi nulla è distribuito “normalmente”. Le distribuzioni normali, per loro natura, rendono le grandi deviazioni (rispetto alle deviazioni medie) estremamente rare, al punto da essere scartate come praticamente impossibili dal modello - ovvero probabilità inferiori a una su un miliardo. Domanda, lead time, resi sono molti pattern che categoricamente non seguono una distribuzione normale. L’unico lato positivo delle distribuzioni normali è che sono ben adatte a creare esercizi da manuale per gli studenti, poiché si prestano a soluzioni analitiche esplicite.

Scelta selettiva delle probabilità

Quando si è di fronte a una distribuzione di probabilità, è tentante selezionare un singolo punto della distribuzione, possibilmente la media o la mediana, e procedere basandosi su questo numero. Questo processo contrasta con l’essenza stessa dell’aspetto probabilistico della previsione. Le probabilità non dovrebbero essere ridotte a una singola stima puntuale, perché indipendentemente dal punto scelto, questo processo comporta una massiccia perdita di informazioni. Pertanto, per quanto possa risultare alquanto inquietante, le probabilità devono essere preservate tali per il maggior tempo possibile. Il momento del collasso è tipicamente la decisione finale nella supply chain, che massimizza i ritorni affrontando futuri incerti.

Rimozione degli outlier statistici

La maggior parte dei metodi numerici classici - saldamente radicati nella prospettiva deterministica delle previsioni (ad es. medie mobili) - si comporta in maniera inadeguata quando si incontrano outlier statistici. Pertanto, molte aziende stabiliscono processi per “pulire” manualmente i dati storici da quegli outlier. Tuttavia, questa necessità di un processo di pulizia evidenzia soltanto le carenze di quei metodi numerici. Al contrario, gli outlier statistici sono un ingrediente essenziale della previsione probabilistica in quanto contribuiscono a fornire un quadro più accurato di ciò che accade alla coda della distribuzione. In altre parole, quegli outlier sono la chiave per quantificare la probabilità di incontrarne altri.

Portare una spada a un combattimento a pistole

È necessario disporre di strumenti specializzati per manipolare le distribuzioni di probabilità. Produrre la previsione probabilistica è solo uno dei tanti passaggi per fornire un valore reale all’azienda. Molti operatori della supply chain finiscono per scartare le previsioni probabilistiche per mancanza di strumenti adatti a farne qualcosa. Numerosi software vendors aziendali hanno seguito questa tendenza e ora sostengono di supportare la “previsione probabilistica” (insieme a “AI” e “blockchain”), ma non sono mai andati oltre una mera implementazione cosmetica di alcuni modelli probabilistici (cfr. la sezione sopra). Presentare un modello di previsione probabilistica ha un valore trascurabile senza i numerosi strumenti necessari a sfruttarne i risultati numerici.

Note