00:19 Introduction
04:33 Two definitions for ‘algorithm’
08:09 Big-O
13:10 The story so far
15:11 Auxiliary sciences (recap)
17:26 Modern algorithms
19:36 Outperforming “optimality”
22:23 Data structures - 1/4 - List
25:50 Data structures - 2/4 - Tree
27:39 Data structures - 3/4 - Graph
29:55 Data structures - 4/4 - Hash table
31:30 Magic recipes - 1/2
37:06 Magic recipes - 2/2
39:17 Tensor comprehensions - 1/3 - The ‘Einstein’ notation
42:53 Tensor comprehensions - 2/3 - Facebook’s team’s breakthrough
46:52 Tensor comprehensions - 3/3 - Supply chain perspective
52:20 Meta techniques - 1/3 - Compression
56:11 Meta techniques - 2/3 - Memoization
58:44 Meta techniques - 3/3 - immutability
01:03:46 Conclusion
01:06:41 Upcoming lecture and audience questions
説明
サプライチェーンの最適化は、数多くの数値問題を解決することに依存しています。アルゴリズムは、正確な計算問題を解決するための、非常に体系化された 数値レシピ です。優れたアルゴリズムは、より少ない計算資源で優れた結果を得ることができることを意味します。サプライチェーンの具体的な要素に注目することで、アルゴリズムの性能は飛躍的に向上し、時には桁違いの改善が見込まれます。「サプライチェーン」アルゴリズムは、過去数十年で大きく進化した現代コンピュータの設計も取り入れる必要があります。
全文書き起こし

このサプライチェーン講義シリーズへようこそ。私はジョアネス・ヴェルモレルです。本日は「サプライチェーンのための現代アルゴリズム」をお届けします。優れた計算能力は、優れた サプライチェーンパフォーマンス を実現するために不可欠です。より正確な 予測 や、より微細な最適化、さらに頻繁な最適化は、すべて優れたサプライチェーンパフォーマンスを達成するために望まれるものです。常に、あなたが手にできる計算資源をほんのわずかに超えたところに、優れた数値的手法が存在します。
簡単に言えば、アルゴリズムはコンピュータの動作を速くします。アルゴリズムは数学の一分野であり、非常に活発な研究領域でもあります。この研究分野の進歩は、しばしば コンピューティングハードウェア 自体の進化を上回ります。本講義の目的は、現代アルゴリズムが何であるか、そして特に サプライチェーンの視点 から、どのように問題にアプローチしてこれらの現代アルゴリズムをサプライチェーンに最大限活用できるかを理解することです。

アルゴリズムに関しては、絶対的なリファレンスとなる一冊の本があります。それが『Introduction to Algorithms』で、1990年に初版が出版されました。これは必読の書です。プレゼンテーションと文章の質は非常に高く、この本は初版から20年間で50万部以上を売り上げ、学術作家の世代全体に影響を与えました。実際、過去10年間に出版されたサプライチェーン理論に関する多くの書籍は、この本のスタイルとプレゼンテーションから大きなインスピレーションを受けています。
個人的には、1997年にこの本を読みましたが、実際には初版のフランス語訳でした。この本は私のキャリア全体に深い影響を与え、これを読んだ後はソフトウェアの見方が一変しました。ただし一言注意すると、この本は80年代末から90年代初頭に普及していたコンピュータハードウェアの視点を採用しているため、近年の急速なハードウェア進化を考慮すると、一部の前提は時代遅れに感じられるかもしれません。例えば、本書ではメモリアクセスが、アドレスするメモリの量に関わらず常に一定時間と仮定されていますが、これは現代のコンピュータでは通用しません。
それにもかかわらず、説明の明確さとシンプルさを大幅に向上させるために単純化するという手法は、十分に合理的である場合もあると考えています。この点で本書は素晴らしい成果を上げています。本書全体で用いられている主要な前提が時代遅れであることを念頭に置くべきですが、それでも全聴衆に推奨できる絶対的なリファレンスであると私は考えています。

アルゴリズムという用語を、必ずしも馴染みのない聴衆のために明確にしましょう。アルゴリズムの古典的定義は、有限で明確に定義されたコンピュータ命令の連続であるというものです。これは教科書やWikipediaでよく見られる定義です。古典的定義にも一定の価値はありますが、アルゴリズムに込められた意図が明示されていないため、私はやや物足りなさを感じます。重要なのは、単なる命令の連続ではなく、非常に特定のコンピュータ命令の連続であるという点です。そこで、私の個人的な定義として、アルゴリズムとは本質的に、性能重視で微細な問題解決を行うソフトウェア手法である、と提案します。
この定義を詳しく見ていきましょう。まず、問題解決という側面についてです。アルゴリズムは、解決しようとする問題によって完全に特徴付けられます。この画面に表示されているのは、広く知られた人気のアルゴリズムであるクイックソートの疑似コードです。クイックソートは、データエントリが含まれた配列という状況で、すべてのエントリを昇順に整列した同一の配列を返すというソート問題を解決しようとします。アルゴリズムは、特定かつ明確に定義された問題に完全に焦点を合わせています。
第二の側面は、どのようにしてより優れたアルゴリズムと判断するかという点です。より優れたアルゴリズムとは、実質的により少ない計算資源で同じ問題を解決できる、すなわちより高速に動作するものを指します。最後に、微細な側面ですが、「アルゴリズム」という用語には、非常に基本的な問題に注目し、モジュール化された要素を無限に組み合わせて、はるかに複雑な問題を解決するという考えが含まれています。これこそがアルゴリズムの本質なのです。
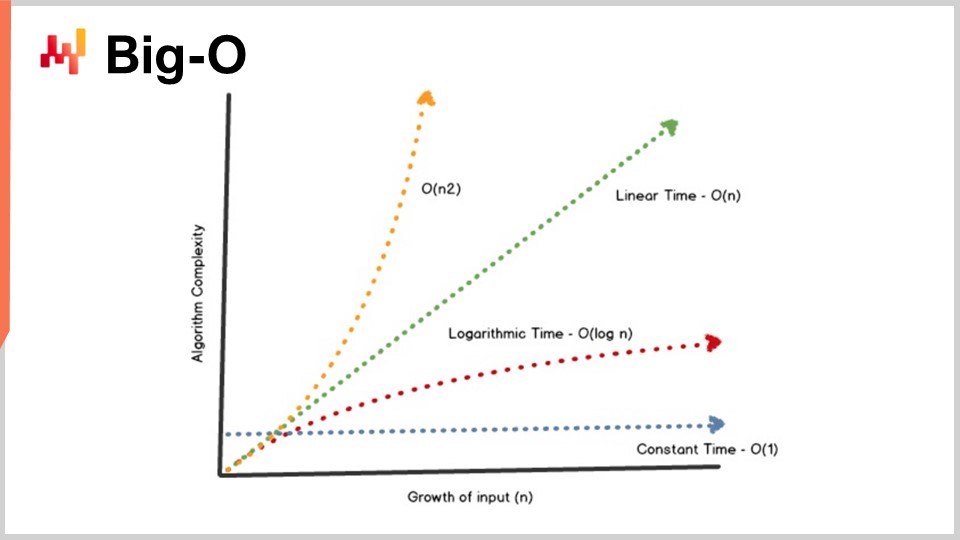
アルゴリズム理論の大きな成果の一つは、アルゴリズムの性能を非常に抽象的な方法で特徴付けることができる点にあります。本日はこの特徴付けの詳細や数学的枠組みに踏み込む時間はありませんが、アルゴリズムを特徴付けるために、漸近的な振る舞いに注目するという考え方があります。問題は、いくつかの主要なボトルネックとなる次元に依存しており、例えば先ほど説明したソート問題では、その特徴的な次元は通常、ソートすべき要素の数です。では、ソート対象の配列が非常に大きくなった場合、どのようなことが起こるのでしょうか?ここでは便宜上、この特徴的な次元を「n」と呼ぶことにします.
ここで、アルゴリズムを扱う際によく目にするビッグオー記法があります。今回は、その直感を理解していただくためにいくつかの要素を概説します。まず、例えばデータセットがあり、平均値のような単純な統計的 インジケーター を抽出したいとしましょう。もし私がビッグオー1のアルゴリズムを持っていると言えば、データセットの大きさに関わらず一定時間でこの問題(平均の計算)に対する解を返すことができるという意味です。一定時間、すなわちビッグオー1は、機械間通信のリアルタイム性を求める場合に絶対的な要件となります。もし一定時間での実行が保証されなければ、リアルタイム性能の達成は非常に困難、時には不可能です.
通常、もう一つの主要な性能指標としてビッグオーNがあります。ビッグオーNとは、対象となるデータセットのサイズに対してアルゴリズムの複雑性が厳密に線形であることを意味します。これは、データを一度または決まった回数だけ読み込む効率的な実装で問題を解決できる場合に得られるものです。ビッグオーNの複雑性は、通常バッチ処理としか相性がよくありません。オンラインでリアルタイムな処理を行う場合、データセット全体を走査するような動作は、データセットのサイズが固定されている場合を除き難しいのです.
線形性を超えて、ビッグオーN二乗があります。ビッグオーN二乗は、プロダクション環境における性能低下の甘い落とし穴とも言える興味深いケースです。これは、複雑性がデータセットのサイズに対して二次的に増大することを意味し、例えばデータ量が10倍になると性能が100倍悪化するということになります。これは、プロトタイプやテスト段階では小規模なデータを扱っているため問題に気づかない場合が多いですが、本番環境に移るとソフトウェアが非常に遅くなります。エンタープライズソフトウェア、特にサプライチェーン向けのエンタープライズソフトウェアの現場では、多くの深刻な性能問題が、特定されなかった二次アルゴリズムによって引き起こされているのが実情です。その結果、非常に遅い二次的な動作が確認されるのです。現代のコンピュータが非常に高速であるため、Nが小さい限りは大きな問題にはならなかったのですが、いざ大規模な生産データセットを扱うとなると、その影響は甚大です.
この講義は、実は私のサプライチェーン講義シリーズにおける第四章の第二講義です。第一章である序章では、サプライチェーンを学問としても実践としても捉える私の見解を紹介しました。ご覧の通り、サプライチェーンは穏やかな問題ではなく、手強い問題の集合体です。複雑な問題は、あらゆる場所に敵対的な要素が存在するため、単純な手法では対処できず、手法自体に多大な注意を払う必要があります。多くの単純な方法は、非常に目立った形で失敗します。まさにそのために、サプライチェーンの研究と管理実践の改善に適した手法に全面的に焦点を当てた第二章を構成しました。第三章はまだ完成していませんが、いわゆる「サプライチェーン・パーソネル」と呼ばれる、解決策ではなく問題そのものに焦点を当てる非常に特定の手法に絞っており、今後、第三章と本章(サプライチェーンの補助科学について)の間を交互に進める予定です.
前回の講義では、より優れた現代的なコンピューティングハードウェアによってサプライチェーン向けの計算能力が向上することを示しました。本日は、より良いソフトウェアによって計算能力が向上するという、異なる角度からのアプローチについて検討します。これがアルゴリズムの真髄です.

簡単な振り返りです。補助科学とは、本質的にサプライチェーンそのものに対する一つの視点です。今日の講義は厳密にはサプライチェーンそのものについてではなく、アルゴリズムに関するものですが、サプライチェーンの基盤として極めて重要な内容だと信じています。サプライチェーンは孤立した存在ではなく、その進展は他の隣接分野で既に達成された成果に大きく依存しています。これらの分野を、私はサプライチェーンの補助科学と呼んでいます.
この状況は、19世紀における医学と化学の関係に非常によく似ていると考えています。19世紀初頭、医学は化学に全く関心を示さず、化学は新参者であり、実際の患者に対する有効な提案とは見なされていませんでした。しかし、21世紀に突入すると、化学の知識が一切なくとも優秀な医師になれるという考えは、全くもってとんでもないものと捉えられるでしょう。優秀な化学者であっても必ずしも優秀な医師になれるわけではありませんが、体内化学について全く知識がなければ、現代医療の観点からは有能とは到底言えないというのが一般的な見解です。私の見解では、21世紀においてサプライチェーン分野も、19世紀に医学が化学を捉え始めたのとほぼ同様に、アルゴリズム分野を重要視するようになるでしょう.

アルゴリズムは広大な研究分野であり、数学の一分野でもあります。本日はその表層のみを掘り下げるに過ぎません。特に、この分野は何十年にもわたり驚くべき成果を積み重ねてきました。理論的な側面が強いとはいえ、単なる理論だけではなく、多数の発見が実際の生産現場に応用されてきたのです.
実は、現在あなたが使用しているスマートフォンやコンピューターは、元々どこかで公開された何万ものアルゴリズムを文字通り利用しています。この実績は、サプライチェーン理論に基づいていない大多数のサプライチェーンと比べると非常に印象的です。現代のコンピューターとアルゴリズムに関しては、ソフトウェアに関連するほぼすべてのものが、何十年にもわたるアルゴリズム研究の成果に完全に依存して動作しています。これは、今日私たちが使用しているほぼすべてのコンピューターの基本中の基本です。
本日の講義では、モダンなアルゴリズムに取り組むにあたって知っておくべき内容を示す、非常に示唆に富んだトピックのリストを厳選しました。まず、特にサプライチェーンにおいて、いわゆる最適なアルゴリズムをどのように上回るかについて議論します。次に、データ構造を簡単に見た後、マジックレシピ、テンソル圧縮、そして最後にメタテクニックについて説明します。
まず最初に、「サプライチェーンのためのアルゴリズム」と言ったとき、サプライチェーン固有の問題を解決するために設計されたアルゴリズムを意味しているのではないことを明確にしておきたいと思います。正しい見方は、古典的な問題に対する古典的なアルゴリズムを見直し、それらの古典的な問題をサプライチェーンの視点から再検討して、実際により良い方法が取れるかどうかを確かめることです。答えは、はい、可能です。
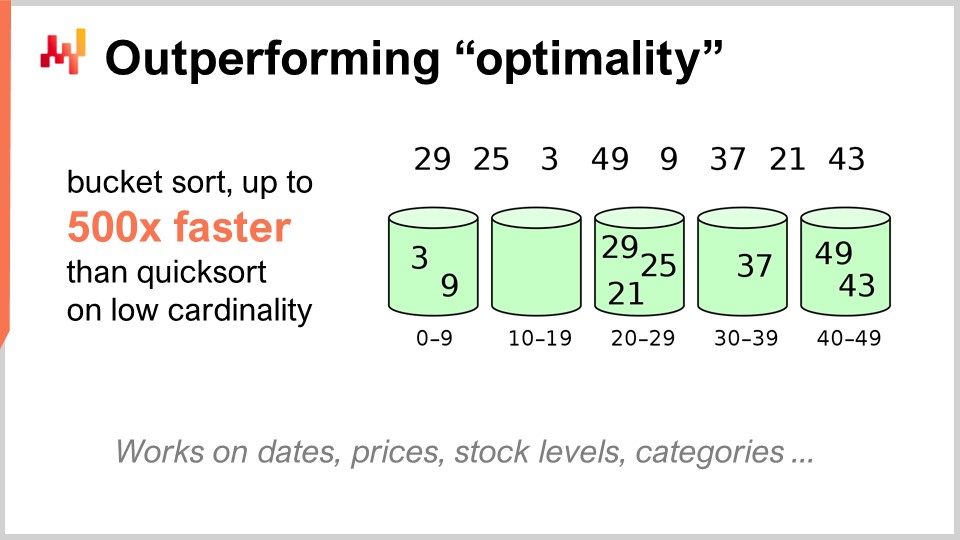
例えば、クイックソートアルゴリズムは、一般的なアルゴリズム理論によれば、クイックソート以上に任意に優れたアルゴリズムは導入できないという意味で最適とされています。つまり、この点においてクイックソートはこれ以上望めるものではありません。しかし、サプライチェーンに特化して考えると、驚異的なスピードアップを実現できるのです。特に、日付、価格、在庫レベル、カテゴリーのように、関心のあるデータセットの基数が低い場合、これらはすべて低基数のデータセットです。したがって、もし低基数という追加の仮定があれば、バケットソートを利用することができます。実運用では、クイックソートの500倍ものスピードアップを実現できる状況が数多く存在し、いわゆる最適とされるものよりも桁違いに速くなるのです。これこそが非常に重要な点であり、サプライチェーン向けアルゴリズムの活用によって得られる驚異的な成果の核心だと信じています。
私は、この見解が少なくとも二つの理由で誤っていると考えています。第一に、私たちが見てきたように、常に標準のアルゴリズムが関心の対象であるとは限らないということです。クイックソートのようないわゆる最適なアルゴリズムが存在する一方で、同じ問題をサプライチェーンの角度から見ることで、実際に莫大なスピードアップを実現できることがわかりました。つまり、クラシックなアルゴリズムを再検討し、一般のケースではなくサプライチェーンの場合において大幅な速度向上を実現するために、アルゴリズムに精通することが極めて重要なのです。
この見解が誤っていると考える第二の理由は、アルゴリズムがデータ構造と密接に関連しているという点にあります。データ構造は、データをより効率的に操作できるように整理する方法です。興味深いことに、これらのデータ構造は一種の語彙を形成しており、この語彙にアクセスすることが、サプライチェーンの状況をソフトウェアに容易に翻訳可能な形で記述するために不可欠です。素人の言葉で記述を始めると、多くの場合ソフトウェアへの翻訳が極めて困難なものになってしまいます。サプライチェーンについて何も知らないソフトウェアエンジニアにその翻訳を期待すると、トラブルの種になりかねません。むしろ、この語彙を知っていれば、アイデアをソフトウェアに容易に翻訳できる用語で直接伝えることが可能になるのです。
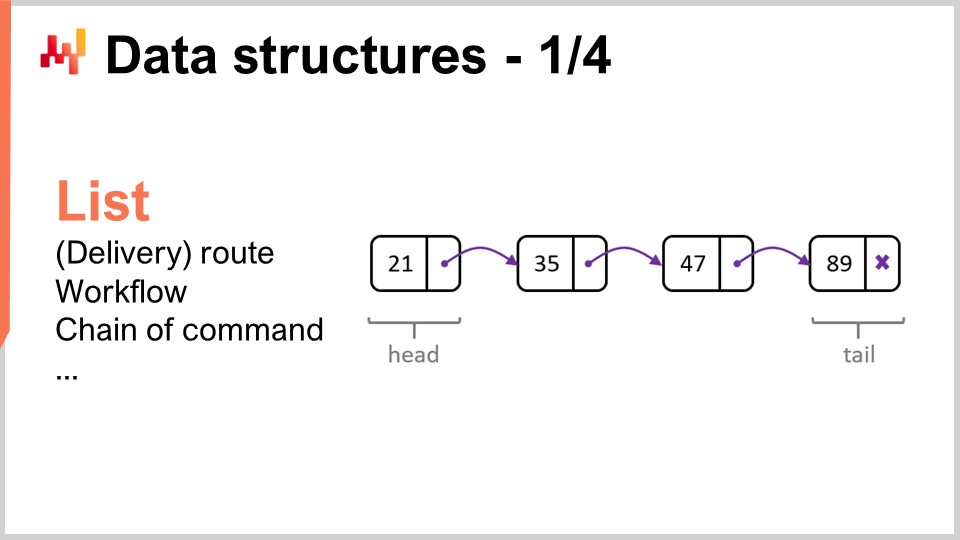
ここで、最も一般的かつシンプルなデータ構造について見直してみましょう。まずはリストです。リストは、例えば、配達ごとに1エントリずつ記述された配達ルート(すなわち、実施すべき配達の順序)を表現するために使用できます。進行に合わせて配達ルートを列挙することが可能です。また、リストは、特定の機器の製造に必要な一連の操作であるワークフローや、特定の意思決定を行うべき人物を決定する命令系統を表現するためにも利用できます。
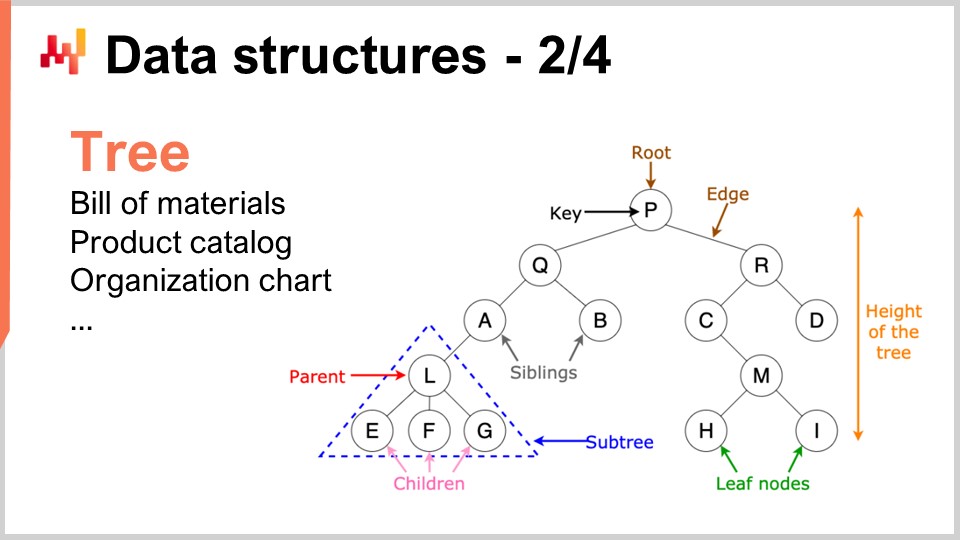
同様に、ツリーもまた遍在するデータ構造の一つです。ちなみに、アルゴリズムで用いられるツリーは逆さまで、ルートが上部に、枝が下部に配置されます。ツリーを用いれば、さまざまな階層構造を記述でき、サプライチェーンにもあらゆる階層構造が存在します。例えば、部品表はツリーであり、ある機器を製造する際、その機器はアセンブリで構成され、各アセンブリはサブアセンブリで構成され、各サブアセンブリは部品で構成されています。部品表を完全に展開すると、ツリーが得られます。同様に、製品ファミリー、製品カテゴリー、製品、サブカテゴリーなどを持つ製品カタログには、しばしばツリー状の構造が付随しています。CEOが頂点に、次いでCレベルの幹部が続く組織図もまたツリーで表現されます。アルゴリズム理論は、ツリーを効率的に処理し操作するための多数の手法とツールを提供してくれます。データをツリーとして表現できれば、これらのツリーを効率的に活用するための数学的手法の全 arsenal を手に入れたも同然です。だからこそ、これは非常に重要な分野なのです。
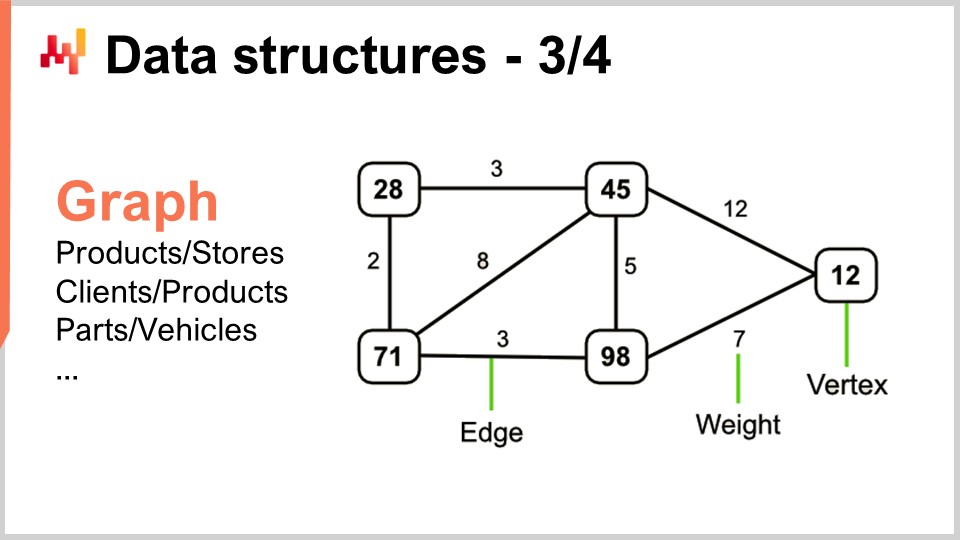
さて、グラフはあらゆる種類のネットワークを記述する手段です。ちなみに、数学的な意味でのグラフは、頂点の集合と辺の集合で構成され、辺は2つの頂点を相互に接続します。「グラフ」という用語は、グラフィックとは全く関係がないため、少々誤解を招くかもしれません。グラフは単なる数学的対象であり、図や視覚的な要素ではありません。グラフの見方を理解すれば、サプライチェーンのあらゆる場所にグラフが存在することに気づくでしょう。
いくつか例を挙げると、小売ネットワークにおける品揃えは本質的には二部グラフであり、製品と店舗を接続します。また、あるクライアントが時間の経過とともにどの商品を購入したかを記録するロイヤリティプログラムがあれば、これもまたクライアントと製品を接続する二部グラフとなります。さらに、自動車のアフターマーケットでは、修理を実施する際に対象車両と機械的に互換性のある部品のリストを示す互換性マトリックスを使用する必要があり、これ自体が一種のグラフとなります。グラフを扱うためのあらゆる種類のアルゴリズムに関する文献は膨大であり、問題をグラフ構造で特徴付けることができれば、文献で知られているすべての手法がすぐに利用可能になるため、非常に興味深いのです。
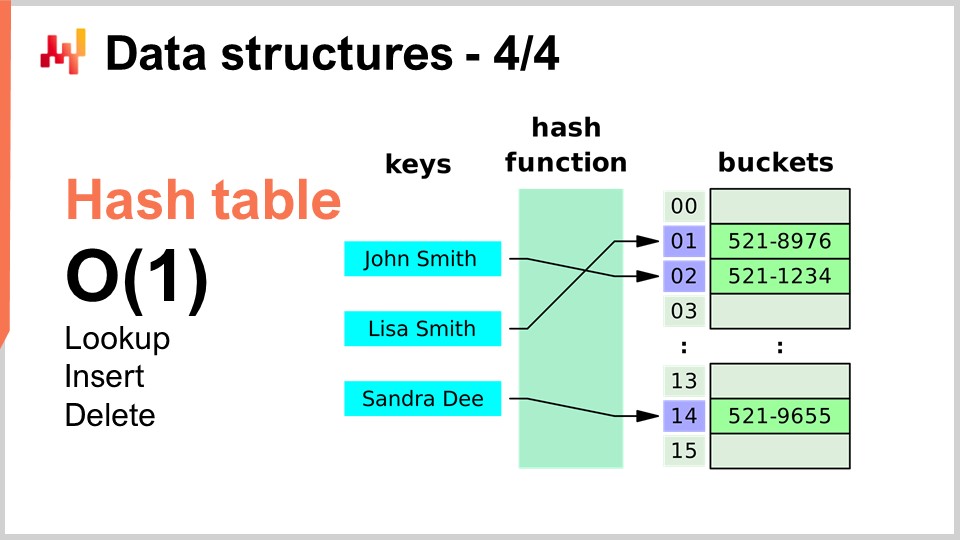
最後に、本日取り上げるデータ構造の中で最後に紹介するのはハッシュテーブルです。ハッシュテーブルは、いわばアルゴリズムの万能ナイフとも言える存在です。これまで紹介したデータ構造のいずれも現代の基準では新しいものではありませんが、ハッシュテーブルはその中でもおそらく最も新しいもので、1950年代に起源を持つため、新しいとは言えません。それにもかかわらず、ハッシュテーブルは非常に有用なデータ構造です。これはキーと値のペアを保持するコンテナであり、このコンテナを使用することで大量のデータを格納でき、探索、挿入、削除が定数時間 (Big O(1)) で行えます。すなわち、一定時間でデータを追加し、キーを使ってデータの有無を確認し、場合によってはデータを削除できるのです。これは非常に興味深く有用な仕組みです。ハッシュテーブルは文字通りあらゆる場所で見られ、他のアルゴリズム内でも広範に利用されています。
ここで一つ指摘しておきたいのは、後ほど再び触れるとおり、ハッシュテーブルの性能は利用するハッシュ関数の性能に大きく依存するということです。

さて、次はマジックレシピについて見ていきましょう。視点を完全に切り替えます。マジックナンバーは基本的にアンチパターンです。前回の講義、サプライチェーンにおけるネガティブナレッジについての講義では、アンチパターンは善意に基づいて開始されるものの、結果的にその解決策がもたらすはずの利益を打ち消すような予期せぬ結果を引き起こすと論じました。マジックナンバーはよく知られたプログラミングのアンチパターンであり、全く根拠のない定数が散在するコードを書くため、ソフトウェアの保守が非常に困難になります。多数の定数が存在すると、なぜその制約があるのか、またそれらがどのように選ばれたのかが不明瞭になってしまいます。
通常、プログラム内でマジックナンバーを見かけた場合、それらの定数を管理しやすい場所にまとめるのが望ましいです。しかしながら、定数を慎重に選ぶことで、全く予期しなかった効果が得られ、まるで魔法のように、意図しない利点がもたらされる場合もあります。これこそが、ここで紹介する非常に短いアルゴリズムの核心なのです。
サプライチェーンにおいては、しばしば一種のシミュレーションを実現したいと考えます。シミュレーションやモンテカルロ法は、サプライチェーンの無数の状況で使用できる基本的な手法の一つです。しかしながら、シミュレーションの性能は乱数生成能力に大きく依存します。シミュレーションを生成するためには、ある程度のランダム性が必要となるため、そのランダム性を生成するアルゴリズムが求められるのです。コンピューターの場合、通常は疑似乱数が用いられます―真の乱数ではなく、乱数らしく見え、統計的な特性を持つものの、実際には乱数ではありません。
そこで問題となるのは、どれほど効率的に乱数を生成できるかということです。実は、2003年にジョージ・マーサリアが発表した「Shift」と呼ばれるアルゴリズムがあり、非常に印象的です。このアルゴリズムは、2^64 - 1 ビットの完全な順列を生成する高品質な乱数を生み出します。0を固定点とし、残る64ビットの組み合わせすべて(ただし1つを除く)を循環させるのです。これは本質的に、3回の二進シフトと3回のXOR(排他的論理和)操作、合計6つの操作で実行されます。シフトもまたビット操作の一種です。
ここで注目すべきは、その中に3つのマジックナンバー、すなわち13、7、17が存在する点です。ちなみに、これらの数字はすべて素数であり、これは偶然ではありません。これら非常に特定の定数を選ぶことで、非常に高速で優れた乱数生成器が得られるのです。私が「非常に高速」と言うのは、文字通り毎秒10メガバイトの乱数を生成できるという意味です。これは実に莫大な性能です。前回の講義に戻ってみると、このアルゴリズムがなぜこれほど効率的であるかが理解できるでしょう。下位のコンピューティングハードウェア(プロセッサなど)がネイティブにサポートする命令に直接対応する6つの命令しか使われておらず、かつ分岐が一切ないのです。テストが存在しないため、実行時にプロセッサのパイプライン能力を最大限に引き出すことが可能となります。現代のプロセッサが持つ深いパイプライン能力を文字通り最大限に活用できるのです。これは非常に興味深いです。
では、このアルゴリズムを機能させるために、他の数字を選ぶことは可能でしょうか?答えはノーです。実際に機能する数字の組み合わせはせいぜい数ダース、あるいは百通り程度しかなく、その他の組み合わせでは非常に低品質な乱数生成器となってしまいます。ここに魔法のような要素が潜んでいるのです。見ての通り、これはアルゴリズム開発における最近の流れであり、予期しない二進操作の組み合わせによって、全く意図しない利点をもたらす半ば魔法の定数を見つけ出す試みなのです。乱数生成は、サプライチェーンにとって極めて重要な要素です。

しかし先ほども述べたように、ハッシュテーブルはあらゆる場所に存在しており、さらに非常に高性能な汎用ハッシュ関数を持つことにも大いに関心が寄せられています。それは存在するのか? 存在します。何十年にもわたって数多くのハッシュ関数が利用されてきましたが、2019年に記録的な性能を叩き出す別のアルゴリズムが発表されました。画面に表示されているのが、Wang Yiによる「WyHash」です。本質的には、その構造はXORShiftアルゴリズムに非常に似ています。これはXORShiftのように分岐がなく、XOR演算を用いるアルゴリズムであり、合計6つの命令(4回のXOR操作と2回のMultiply-No-Flags操作)を使用しています。
Multiply-No-Flagsとは、2つの64ビット整数間の通常の乗算を意味し、その結果、上位64ビットと下位64ビットが得られるというものです。これは現代のプロセッサにおいてハードウェアレベルで実装されている実際の命令であり、1つのコンピュータ命令として数えられます。それを2回使用しているのです。さらに、3つのマジックナンバーが16進数形式で記述されています。ちなみに、これらはすべて素数であり、再び半ば魔法のような性質を帯びています。このアルゴリズムを用いれば、暗号化目的ではないながらも、ほぼmemcpyの速度で動作する非常に優れたハッシュ関数が得られます。これは非常に高速で、極めて重要です。

さて、ここでまた全く異なる話題に切り替えましょう。ディープラーニングやその他多くの現代の機械学習手法の成功は、専用の計算ハードウェアによって大幅に高速化できる問題に対する、いくつかの重要なアルゴリズム的洞察にあります。これは、以前の講義で、スーパースカラ命令を持つプロセッサや、さらに言えばGPUやTPUについて話したときに論じた内容でもあります。この洞察がいかにしてかなり混沌とした状況から生まれたのか、もう一度振り返ってみましょう。しかしながら、ここ数年で関連する洞察は結晶化していると私は信じています。現在の状況を理解するためには、アルバート・アインシュタインが100年以上前に論文で導入したアインシュタイン記法に立ち返る必要があります。直感はシンプルです。式yが、c_yとx_yの積のi=1からi=3までの和であるとします。このように式が書かれている場合、アインシュタイン記法の直感は、和の記号を完全に省略して書くべきだと示唆しています。ソフトウェア用語で言えば、この和はforループにあたります。つまり、和を完全に省略し、慣例として変数iの意味があるすべての添字に対して和をとるのです.
この単純な直感は、非常に驚くべき、しかし好ましい二つの成果をもたらします。一つ目は設計の正確性です。和を明示的に記述すると、適切な添字が使用されず、ソフトウェアにおいては添字範囲外エラーにつながる危険があります。明示的な和を取り除き、定義上有効なすべての添字位置を採用することを宣言することで、設計段階から正しいアプローチが実現されます。これだけでも非常に重要であり、以前の講義で簡単に触れた差分可能プログラミングという配列プログラミングにも関連しています.
2つ目の洞察は、より新しいものであり今日非常に注目されている点ですが、もしあなたの問題をアインシュタイン記法が適用できる形で記述できれば、実際に大規模なハードウェア加速の恩恵を受けることができるというものです。これは革命的とも言える要素です.

その理由を理解するために、Facebook研究チームによって2018年に発表された「Tensor Comprehensions」という非常に興味深い論文があります。彼らはテンソル・コンプリヘンションという概念を導入しました。まず、この二つの単語を定義しましょう。コンピュータサイエンスの分野では、テンソルとは本質的に多次元行列のことを指します(物理学におけるテンソルは全く異なる意味を持ちます)。スカラー値は0次元のテンソル、ベクトルは1次元のテンソル、行列は2次元のテンソルであり、さらに高次元のテンソルも存在します。テンソルは、配列のような性質を備えたオブジェクトです.
コンプリヘンションとは、加算、減算、乗算、除算という基本演算およびその他の演算を備えた、いわば代数のようなものです。通常の算術代数よりも広範であるため、テンソル代数ではなくテンソル・コンプリヘンションが採用されるのです。これはより包括的ですが、完全なプログラミング言語ほどの表現力は持ち合わせていません。コンプリヘンションを用いると、何でもできる完全なプログラミング言語に比べ、制限が多くなります.
つまり、MV関数(def MV)を見れば、本質的には関数であり、MVは行列とベクトルを意味します。この場合、行列とベクトルの乗算を行っており、基本的には行列AとベクトルXの乗算を実行しています。この定義には、アインシュタイン記法が活用されており、C_i = A_ik * X_k と記述されます。iとkにはどの値を選べばよいでしょうか?答えは、これらが添字となるすべての有効な組み合わせです。有効な添字すべてに対して和をとることで、実際には行列とベクトルの乗算が実現されます.
画面下部には、同じMVメソッドがforループを用いて書き直され、値の範囲が明示的に指定されている様子が示されています。Facebook研究チームの主要な成果は、このテンソル・コンプリヘンションの構文でプログラムを書くことができれば、GPUを用いた大規模なハードウェア加速の恩恵を大いに享受できるコンパイラを開発した点にあります。基本的に、テンソル・コンプリヘンションの構文で記述できるプログラムはすべて加速されるのです。この形式でプログラムが書ければ、通常のプロセッサよりも2桁高速な大規模ハードウェア加速の恩恵を受けることになり、これはそれ自体で驚異的な成果です.

では、このアプローチをサプライチェーンの視点からどのように活用できるかを見てみましょう。現代のサプライチェーン実務で注目すべき重要な点は、確率的予測です。以前の講義で取り上げた確率的予測とは、単一の予測値を出すのではなく、関心のある変数に対してさまざまな確率を予測するという考え方です。例えば、リードタイム予測を検討してみましょう。リードタイムを予測し、確率的なリードタイム予測を行いたいのです.
さて、リードタイムを製造リードタイムと輸送リードタイムに分解できると仮定しましょう。実際には、製造リードタイムに対しては、1日、2日、3日、4日などの期間が観測される確率を示す離散的なランダム変数としての予測が大部分の場合存在します。これは、製造リードタイムの期間が観測される確率を示す大きなヒストグラムのようなものと考えることができます。そして、輸送リードタイムについても同様に、別の離散ランダム変数による確率的予測があります.
次に、合計リードタイムを計算したいとします。もし予測されたリードタイムが単なる数値であれば、単純な加算で済むところですが、ここでの予測リードタイムは数値ではなく確率分布です。したがって、これら2つの確率分布を組み合わせて、合計リードタイムの確率分布という第三の分布を得る必要があります。実際、製造リードタイムと輸送リードタイムが独立であると仮定すれば、これらのランダム変数の和を計算する操作は、1次元の畳み込みに他なりません。複雑に聞こえるかもしれませんが、実際はそれほど複雑ではありません。私が実装したもの、画面に表示されているのは、製造リードタイムの確率を示すヒストグラムを表すベクトル(A)と、輸送リードタイムの確率を示すヒストグラム(B)との間で1次元の畳み込みを実施する実装です。その結果が、これらの確率的リードタイムの和、すなわち合計時間となります。テンソル・コンプリヘンション記法を用いれば、これは非常にコンパクトな1行のアルゴリズムで記述できます.
さて、この講義の初めに紹介したBig O記法に立ち返ると、基本的にこれは二次アルゴリズムであることが分かります。NをAとBの配列の特徴的なサイズとすると、アルゴリズムはBig O(N^2)となります。前述したように、二次的な性能は予測上の悩みの中で好都合な点です。では、この問題にどう対処すればよいでしょうか?まず、これはサプライチェーンの問題であり、そこでは小さい数の法則を活用できるという点を考慮する必要があります。先の講義で議論したように、サプライチェーンは主に小さな数に関するものです。リードタイムを考える場合、たとえば400日未満であると仮定するのが合理的です。これは、確率のヒストグラムとしては既にかなり長い期間です.
つまり、結果としてBig O(N^2)ですが、Nは400未満ということになります。400という数字自体は大きく、400×400は160,000になります。これは非常に大きな数値であり、確率分布への加算は非常に基本的な操作であることを思い出してください。確率的予測を始めると、さまざまな方法で予測値を組み合わせる必要があり、基本的にはこれらの畳み込みは、ランダム変数の領域での単なる加算にすぎないため、何百万もの畳み込みを行うことになるでしょう。したがって、Nを400未満に制限していても、ハードウェア加速を導入することは大いに意義があり、これこそがテンソル・コンプリヘンションで実現できるのです.
重要なのは、そのアルゴリズムを記述できた時点で、サプライチェーンの概念に基づいた適用可能な前提を明確にし、その上で利用可能なツールキットを使ってハードウェア加速を実現することです.

次に、メタテクニックについて議論しましょう。メタテクニックは既存のアルゴリズムの上に重ね合わせることができるため非常に注目されます。つまり、もしアルゴリズムが存在するならば、その性能を向上させるためにこれらのメタテクニックのいずれかが利用できる可能性があるのです。最初の重要な洞察は圧縮です。これは、データが小さいほど処理が速くなるという単純な理由によります。前の講義で見たように、私たちは均一なメモリアクセス環境にありません。より多くのデータにアクセスするには、異なる種類の物理メモリにアクセスする必要があり、メモリ容量が増えると、はるかに効率の悪いメモリにアクセスすることになるのです。プロセッサ内部のL1キャッシュは非常に小さく、約64キロバイトですが非常に高速です。一方、RAM、すなわちメインメモリはこの小さなキャッシュより数百倍遅いですが、文字通り1テラバイトにも上ります。したがって、データをできるだけ小さく保つことは、ほぼ必ずアルゴリズムの実行速度を向上させるため、非常に重要です。この点に関して利用できる一連のトリックがあります.
まず、データを整理し、整頓することができます。これはエンタープライズソフトウェアの領域です。データに対して動作するアルゴリズムを持つ場合、しばしば解決に寄与しない未使用のデータが大量に存在します。重要なデータと無視されるデータが混在しないようにすることが不可欠です.
次に、ビットパッキングという考え方があります。ポインタなどの他の要素にフラグを埋め込むことができる状況は多数存在します。64ビットのポインタを持っていたとしても、実際に64ビットのアドレス範囲全体を必要とすることは非常に稀です。数ビットを犠牲にしてフラグを注入することで、性能低下ほとんどなくデータを最小限に抑えることができます.
また、精度の調整も可能です。サプライチェーンにおいて64ビットの浮動小数点精度が本当に必要でしょうか?実際、その精度を必要とすることは極めて稀です。通常は32ビットで十分であり、場合によっては16ビットで十分なことすらあります。精度を落とすことは些細なことと考えられるかもしれませんが、データサイズを半分に減らすことができれば、アルゴリズムの速度が単なる2倍ではなく、実際には10倍速くなることもあるのです。データのパッキングは実行速度に対して全く非線形な利点をもたらします.
最後にエントロピー符号化があります。これは本質的には圧縮ですが、ZIPアーカイブで用いられるような、圧縮効率が非常に高いアルゴリズムを必ずしも使いたいわけではありません。圧縮効率はやや劣るが、実行速度がはるかに速いものが望ましいのです.
圧縮は基本的に、メモリへの負荷を軽減するために、若干の追加CPU使用量を犠牲にするという考えに基づいており、ほぼすべての場合においてこの手法が有効です.
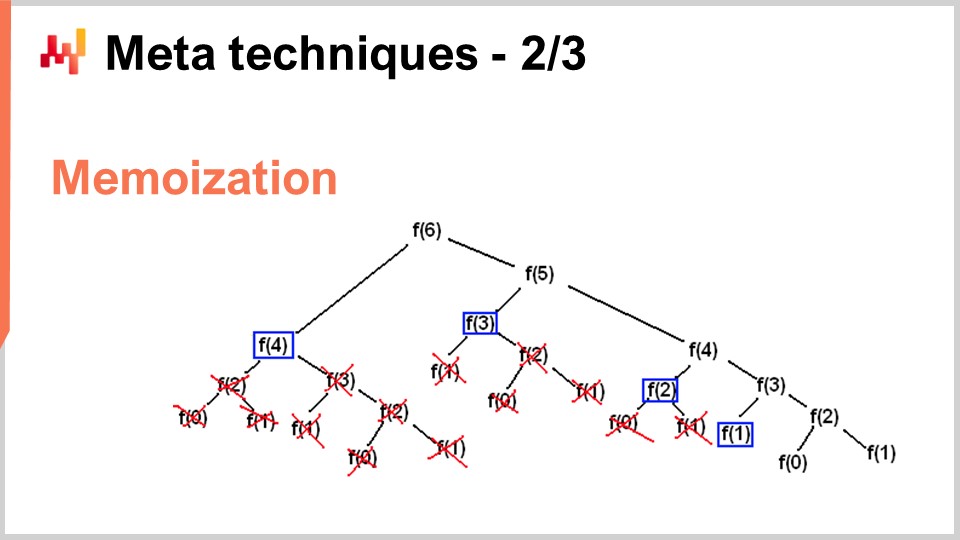
しかし、全く逆の状況―すなわち、CPU使用量を大幅に削減するためにメモリを犠牲にする―場合もあります。これこそがメモ化トリックで行っていることです。メモ化とは、ある関数が解の実行中に何度も同一の入力で呼ばれる場合、その関数を再計算する必要がないという考え方です。結果を記録して別に保管(例えばハッシュテーブルに)し、同じ関数に再度遭遇した際に、ハッシュテーブルにその入力に対応するキーや、すでに計算済みの結果が存在するかどうかを確認できるようにするのです。もしメモ化する関数が非常に計算コストの高いものであれば、劇的な高速化を実現できます。特に興味深いのは、前の講義で見たようにDRAMが非常に高価であるため、メモ化を主記憶ではなく、安価で豊富なディスクやSSDに対して行う場合です。つまり、SSDをCPU負荷軽減のために利用するという考え方であり、これは先に述べた圧縮の正反対のアプローチと言えます.
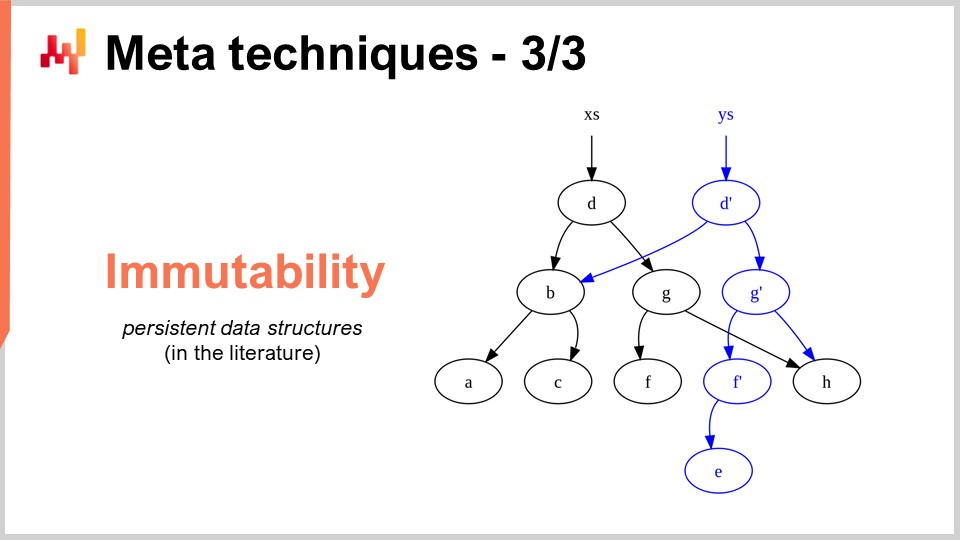
最後のメタテクニックは不変性です。不変なデータ構造とは、本質的に決して変更されないデータ構造のことを指します。つまり、変更が上書きされるのではなく、変更がその上に層状に重ねられるという考え方です。例えば、不変なハッシュテーブルでは、要素を追加すると、元のハッシュテーブルのすべての内容に新要素を加えた新たなハッシュテーブルが返されます。非常に素朴な方法としては、データ構造全体のコピーを行いそれを返す方法がありますが、これは非常に非効率です。不変なデータ構造の重要な洞察は、データ構造を変更する際、変更が必要な部分のみを実装した新しいデータ構造が返され、変更されなかった部分は元のデータ構造から再利用されるという点にあります.
リスト、ツリー、グラフ、ハッシュテーブルなど、ほぼすべての古典的なデータ構造にはそれぞれの不変版が存在します。多くの場合、これらを用いることは非常に有意義です。ちなみに、Clojureのように完全な不変性を追求している現代的なプログラミング言語も存在しますので、馴染みがある方もいらっしゃるかもしれません.
なぜこれが非常に注目されるのか?第一に、アルゴリズムの並列化を大幅に簡素化するためです。前回の講義で見たように、一般的なデスクトップコンピュータ用プロセッサで100 GHzで動作するものは見つかりません。しかし、50コアを持ち、各コアが2 GHzで動作するマシンは存在します。その多くのコアを活用するためには実行を並列化する必要があり、その並列化は競合状態(race conditions)と呼ばれる非常に厄介なバグを引き起こすリスクがあります。複数のプロセッサが同時にコンピュータの同じメモリ領域に書き込もうとするため、記述したアルゴリズムが正しいかどうかを判断するのは非常に困難になります。
しかし、もし不変データ構造を用いれば、設計上、そのような事態は決して起こりません。なぜなら、一度データ構造が提示されると決して変更されず、新たなデータ構造が常に生成されるからです。したがって、不変のアプローチを取ることでアルゴリズムの並列版をより容易に実装でき、結果として大幅なパフォーマンス向上が実現できます。なお、通常、アルゴリズムの高速化を実装する際のボトルネックは、実際にアルゴリズムを作成するのにかかる時間です。設計上、恐れを知らない並行性の原則を適用できる仕組みがあれば、関与するプログラマの数を抑えつつ、アルゴリズムの高速化をより迅速に展開できるのです。不変データ構造のもう一つの重要な利点は、デバッグが非常に容易になる点です。もしデータ構造を破壊的に変更してバグに直面すると、どのようにしてその状態に至ったのかを特定するのは非常に困難です。デバッガを使用しても、問題の原因を突き止めるのは厄介な作業です。不変データ構造の興味深い点は、変更が非破壊的であるため、以前のデータ構造の状態を確認でき、どのようにして誤った挙動に至ったのかをより容易に把握できることです。

結論として、優れたアルゴリズムはまるでスーパーパワーのように感じられます。優れたアルゴリズムによって、同じコンピューティングハードウェアからより多くの性能を引き出すことができ、その恩恵は無限に続きます。これは一度の努力で済み、その後は投入する計算資源の量を変えずに、優れた計算能力にアクセスできるという無限の利点を享受できるのです。私は、この視点がサプライチェーン管理における大幅な改善の機会を提供すると信じています。
全く異なる分野、例えばビデオゲームに目を向けると、彼らはゲーム体験に特化した独自のアルゴリズムの伝統や知見を確立しています。現代のビデオゲームで体験する驚異的なグラフィックスは、ゲーム体験の質を最大化するためにアルゴリズムスタック全体を再考することに何十年も費やしてきたコミュニティの成果です。ゲームにおいては、物理的あるいは科学的に正確な3Dモデルを持つことよりも、プレイヤーにとっての視覚体験の質を最大化することが重視され、そのために精密に調整されたアルゴリズムが使われ、見事な成果を上げています。
私は、この種の取り組みがサプライチェーン分野ではまだ始まったばかりだと考えています。企業向けサプライチェーンソフトウェアは行き詰まっており、私の見解では、現代の計算ハードウェアが持つ能力の1%すら利用できていません。これから多くの可能性があり、それらは車両ルーティングなどのサプライチェーン専用のアルゴリズムに限らず、サプライチェーンの視点から古典的なアルゴリズムを再検討することで、大幅な高速化を実現するアルゴリズムによって捉えられるのです。

さて、質問を見ていきましょう。
質問: これまでサプライチェーン特有の要素、例えば小さい数値について話してきました。もし、意思決定全体で取り扱う数値が事前に少量であると分かっている場合、どのような簡素化がもたらされるでしょうか?たとえば、最大でも1~2コンテナしか注文できないと分かっている場合、在庫報酬関数を計算する際に使用されるホリスティックな予測の粒度レベルにどのような具体的な影響があるか、何か例を挙げられますか?
まず、今日私が提示したすべてはLokadで実際に運用されています。これらの知見は、何らかの形でサプライチェーンに適用されており、Lokadで実際に利用されています。現代のソフトウェアは、計算ハードウェアの力を最大限に引き出すようには調整されていないことを理解しなければなりません。前回の講義で述べたように、現在のコンピュータは数十年前のものと比べて1000倍の能力を持っていますが、実際に1000倍速く動作するわけではなく、また、数十年前よりも格段に複雑な問題に対処できるわけでもありません。したがって、改善の大きな潜在力を過小評価してはならないのです。
この講義で紹介したバケットソートはその一例に過ぎません。サプライチェーンでは、ソート操作がいたるところで必要ですが、私の知る限り、サプライチェーンの状況にぴったり合った特殊なアルゴリズムを活用している企業向けソフトウェアは非常に稀です。さて、私たちは1~2コンテナという状況を知っている場合、その要素をLokadで活用しているでしょうか?はい、常に活用しており、そのレベルで実装可能なトリックが山ほど存在します。
これらのトリックは通常、低いレベルで行われ、利益は全体のソリューションに徐々に反映されます。コンテナ充填の問題をその構成要素にまで分解して考える必要があります。そして、今日提示したアイデアやトリックを低レベルで適用することで、利益を得ることが可能です。
例えば、コンテナについて話す場合、どの程度の数値精度が必要でしょうか?16ビットの数値、つまり16ビットの精度で十分かもしれません。それによりデータサイズが小さくなります。また、注文する異なる製品の数はどれほどでしょうか?おそらく、数千種類の製品しか注文していないので、バケットソートを利用できるのです。確率分布も低く、小さい数値で表せるため、理論上は0ユニット、1ユニット、3ユニットから無限大までのヒストグラムを持つことが可能ですが、実際に無限大まで行くことはありません。おそらく、1,000ユニットを超えるヒストグラムに遭遇するのは非常に稀であると賢く仮定できるでしょう。その場合、近似が可能です。1,000ユニットを含むコンテナに対して、必ずしも2ユニットの精度が必要というわけではないのです。近似を用い、より大きなバケットを持ったヒストグラムなどを利用することができます。これは、テンソル理解のようなアルゴリズムの原則を導入するというよりも、確かに全体を非常にクールな方法で簡素化するものですが、結果としてほとんどのアルゴリズムの高速化は、より速くなる一方でやや複雑なアルゴリズムを招くという点を示しています。通常、最も単純なアルゴリズムは効率が悪いものです。ケースに適したより適切なアルゴリズムは、記述が長く複雑になるかもしれませんが、最終的にはより速く動作するのです。これは常に当てはまるわけではありませんが、私が示したかったのは、企業向けソフトウェアを実際に構築するためには、基本的な構成要素を再検討する必要があるということです。
質問: これらの知見は、ERPベンダー、APS、そしてGTAのような最高峰のシステムにどの程度実装されているのでしょうか?
興味深いのは、これらの知見は基本的に、ほとんどの場合、トランザクションソフトウェアと完全に両立しないということです。多くの企業向けソフトウェアは、トランザクションデータベースを中核として構築され、すべてがそのデータベースを通して処理されます。このデータベースはサプライチェーン専用ではなく、金融、科学計算、医療記録など、あらゆる状況に対応できる汎用データベースなのです。
問題は、対象のソフトウェアがトランザクションデータベースを中核としている場合、私が提案した知見は設計上、実装不可能になるという点です。言い換えれば、そこから先は解決が困難になります。ビデオゲームを例に挙げると、トランザクションデータベース上に構築されたゲームはどれほどあるでしょうか?答えはゼロです。なぜなら、トランザクションデータベース上で優れたグラフィックスパフォーマンスを実現することはできないからです。トランザクションデータベースではコンピュータグラフィックスは不可能です。
トランザクションデータベースは確かに優れており、取引の完全性を保証しますが、その代償として、考え得るほぼすべてのアルゴリズムの高速化が適用できない世界に閉じ込められてしまうのです。APSについて考えると、これらのシステムには先進的な面はなく、何十年も前の設計に縛られています。そして、その根底にはトランザクションデータベースがあり、ここが過去40年ほどにわたりアルゴリズム分野から生まれた知見を適用できない原因となっているのです。
これが企業向けソフトウェア界における問題の核心です。製品設計の最初の1ヶ月で下した設計上の決定は、事実上時の終わりまで何十年もあなたを悩ませ続けるでしょう。一度特定の設計に固執すると、後からアップグレードすることはできず、その状態に縛られるのです。ちょうど、車を単に改造して電気自動車にするのではなく、優れた電気自動車を作るためには、推進エンジンが電気であるという前提のもと、車全体を再設計する必要があるのと同じです。エンジンを交換するだけでは「これで電気自動車だ」とはなりません。そう単純なものではないのです。一度電気自動車の生産を決意すると、エンジン周りの全てを見直し、最適な設計にする必要があります。残念ながら、非常にデータベース中心のERPやAPSは、これらの知見を活用することができません。こうしたトリックの恩恵を受けるための孤立したバブルを形成することは可能かもしれませんが、それは後付けのアドオンに過ぎず、コア部分に組み込まれることは決してありません。
Blue Yonderの印象的な能力についてですが、LokadはBlue Yonderの直接の競合であるため、完全に偏りのない見解を示すのは難しいです。企業向けソフトウェア市場では、競争力を維持するためにとんでもなく大胆な主張をしなければならず、私はそれらの主張に実質的な裏付けがあるとは思っていません。この市場の誰もが、実際に「印象的」と呼べるものを持っているという前提に異議を唱えます。
もし、目を見張るような極めて印象的なものを見たいなら、Unreal Engineの最新デモや、専門のビデオゲームアルゴリズムを見てください。次世代のPlayStation 5ハードウェアのコンピュータグラフィックスを考えてみてください;それは本当に驚嘆すべきものです。企業向けソフトウェアの分野で同程度の技術的成果を持つものはあるでしょうか?Lokadとしては非常に偏った意見かもしれませんが、市場全体を見ると、何十年も関係データベースの限界を追求している者の海が広がっています。時にはグラフデータベースのような他の種類のデータベースを導入することもありますが、それは私が示した知見の核心を全く捉えていません。サプライチェーンの世界に価値を提供する実質的なものは何ももたらしていないのです。
ここで聴衆に伝えたい重要なメッセージは、すべては設計の問題であるということです。企業向けソフトウェアの設計において、最初に下された決定が、初めからこれらの手法を使用できなくするものであってはならないのです。
次の講義は3週間後の水曜日、パリ時間午後3時に行われます。日付は6月13日で、今回はサプライチェーンの人材、驚くべき性格特性、そして架空の企業に関する第3章を再び取り上げます。次回はチーズについて話しましょう。それでは、その時にお会いしましょう!


